Obiectivele lecției:

Să formeze cunoștințe, deprinderi și abilități de aplicare eficientă a metodei generalizate a intervalelor, pe baza proprietății funcțiilor continue;

Formularea unui algoritm de acțiuni care conduc la transformări echivalente;

Învață-te să o aplici atunci când rezolvi inegalitățile;

Pentru a efectua transferul de cunoștințe, abilități și abilități în condiții noi.

Educațional: sistematizare, consolidare, generalizare a cunoștințelor, deprinderilor și abilităților.

Educativ: educarea necesității unei argumentări consistente cu drepturi depline, acuratețe, independență.

Dezvoltarea: dezvoltarea logicii matematice, formarea unui stil matematic de gândire (o disecție clară a cursului raționamentului), interes cognitiv.

1) Introducere, stabilirea scopului și obiectivelor lecției - 2 min.

2) Verificarea temelor - 2 min. (muncă frontală, autocontrol).

3) Fundamentarea matematică a etapelor de rezolvare a inegalităților prin metoda intervalului - 4 min (răspunsuri pregătite de elev).

4) Repetarea proprietăților inegalităților - 2 min.

5) Pregătirea pentru asimilarea (studiul) de material educațional nou prin repetarea și actualizarea cunoștințelor de bază - 5 min. (muncă frontală, răspunsuri la întrebări, situații problematice).

6) Metoda intervalului generalizat pentru rezolvarea inegalităților, înțelegere inițială - 13 min. (rezolvarea colectivă a inegalităților prin metoda intervalelor: pe tablă și în caiete).

7) Informații despre teme, instrucțiuni pentru a le face - 1 min.

8) Consolidarea noilor cunoștințe - 15 min. (muncă independentă - opțiunea 1).

9) Rezumarea lecției, reflecție - 1 min.

1) Introducere, stabilirea scopului și obiectivelor lecției. (Povestea profesorului)

1) Necesitatea unei aplicări mai ample a metodei intervalelor în școală este dictată de ideologia întregului proces de predare a matematicii. Ideea este că linia funcțională (una dintre principalele în studiul fundamentelor matematicii) primește un sprijin tehnologic puternic. Metoda intervalelor se bazează pe caracteristici atât de importante ale dependenței funcționale, cum ar fi zerourile unei funcții, intervalele de semn constant și monotonitatea. Atunci originea funcțională a ecuațiilor și inegalităților, precum și metodele de rezolvare a acestora, devine mai clară. Categoriile de continuitate ale unei funcții, comportamentul graficului acesteia în vecinătatea punctelor de discontinuitate infinită, teoremele asupra rădăcinii, constanța semnului, punctele extreme și tipurile acestora devin mai vizuale. Și toate acestea sunt legate organic într-un întreg funcțional.

Pe de altă parte, geometrizarea obiectelor de studiu utilizate este și ea de neprețuit, i.e. prezentați vizual, figurat, toate instrumentele matematice folosite de dependență funcțională.

Principiile de bază care stau la baza metodei intervalului:

• abordare funcțională (generalizată);
• încrederea pe geometrizarea proprietăților funcționale;
• vizualizarea cercetării.

Aceasta conduce la următoarele avantaje ale metodei în comparație cu altele utilizate în același gen de sarcini: simplitate și rapiditate în atingerea scopului; vizibilitate (și capacitatea de a controla sau verifica de două ori); economie în resurse de calcul și timp; amplitudinea de acoperire a întregii situații, formarea și dezvoltarea abilităților de gândire și analiză generalizate, precum și abilitățile asociate cu aceasta pentru a trage concluzii logice.

2) Verificarea temelor.(Diapozitivul numărul 4)

3) O poveste despre metoda intervalelor de rezolvare a inegalităților. (Răspunde elevul).

Fundamentarea matematică a soluției inegalităților prin metoda intervalelor.

1) Se consideră inegalitățile: (x-2)(x-3)>0. (diapozitivul numărul 5)

O puteți rezolva astfel: produsul (coeficientul) a doi factori este pozitiv dacă și numai dacă ambii factori au același semn, adică. inegalitatea este echivalentă cu combinarea a două sisteme: (diapozitivul numărul 6)

Din primul sistem obținem x >3, din al doilea x< 2.

Soluția este unirea soluțiilor celor două sisteme.

Răspuns:

Metoda grafică (diapozitivul numărul 7)

O altă metodă este metoda intervalului(diapozitivul numărul 8).

Ideea lui este următoarea.

Pe linia reală, marcați zerourile (rădăcinile) polinomului (x-2)(x-3) în picioare

în partea stângă a inegalității, adică numerele 2 și 3.

Când x >3 (în dreapta rădăcinii mai mari), atunci (x-2)(x-3)>0, deoarece fiecare factor este pozitiv.

Dacă vă deplasați de-a lungul axei într-o direcție negativă, atunci când treceți prin punctul x=3, factorul (x-3) își va schimba semnul. În produsul (x-2) (x-3) va apărea un factor negativ, ca rezultat (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Acum este ușor să notăm soluția inegalității:

Concluzie: produsul poate schimba semnul doar la trecerea prin punctele x=2 si x=3

și, prin urmare, păstrează semnul pe fiecare dintre intervalele obținute.

În acest exemplu simplu, este ușor de înțeles ideea metodei intervalului, dar nu prezintă avantaje notabile.

Raționalitatea metodei intervalului, puterea sa, vom lua în considerare următorul exemplu (diapozitivul nr. 9, 10,11, 12))

2) Rezolvați inegalitatea (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10)>0.

Pentru a rezolva această inegalitate folosind un set de sisteme, ar trebui să luăm în considerare un set de 512 sisteme cu 10 inegalități în fiecare sistem.

Să folosim metoda intervalului. Marcam zerourile polinomului pe dreapta reală. Pe intervalul x>10, polinomul va fi pozitiv, deoarece fiecare factor este pozitiv. Când trece prin fiecare rădăcină următoare, polinomul își va schimba semnul, deoarece în produs va apărea un factor negativ suplimentar. Acum este ușor să scrieți soluția inegalității folosind alternarea semnelor.

Avantajele metodei intervalului.

• simplitatea și viteza de realizare a scopului;
• vizibilitate (și capacitatea de a controla sau verifica de două ori);
• o reducere semnificativă a cantității de lucru și a timpului de calcul;
• amplitudinea de acoperire a întregii situații;
• formarea și dezvoltarea abilităților de gândire și analiză generalizate, precum și abilitățile aferente de a trage concluzii logice.

Cometariu. Este foarte convenabil să rezolvați inegalitățile, a căror parte stângă este factorizată, deoarece nu este dificil să găsiți zerouri (rădăcini).

Sarcină: Rezolvați inegalitatea folosind metoda intervalului (x+3) 3 (x-4) 2 (x-5)>0(Diapozitivul 13)

4) Repetarea proprietăților inegalităților.

a) Întrebare: Ce inegalități se numesc echivalente?

(Două inegalități sunt numite echivalente dacă orice soluție a primei inegalități este o soluție a celei de-a doua și, invers, orice soluție a celei de-a doua este o soluție a primei).

Sau: se spune că două inegalități sunt echivalente dacă mulțimile soluțiilor lor sunt aceleași.

Slide 14. Repetarea proprietăților inegalităților.

Slide 15. Răspunde la întrebare și explică.

Sunt inegalitățile egale?

1) 4x-5<0 и 4х<5

2) -2x+5>0 și 2x-5<0

3) -3x 2 +5x-7>0 și 3x 2 -5x+7<0

4) (x+1)>0 și (x 2 +5x+10)(x+1)>0

5) Lucrări frontale orale de pregătire pentru asimilarea (studiul) de material educațional nou prin repetarea și actualizarea cunoștințelor de bază.

Slide 16. Definiția unei funcții continue într-un punct.

Slide 17. Proprietatea funcțiilor continue.

Slide 18. Găsiți goluri de continuitate.

Slide 19. Găsiți greșeala.

Slide 20. Rezolvați inegalitatea verbal,
folosind o diagramă.

Slide 21, 22. Înlocuirea inegalității cu o condiție echivalentă.

Rezolvați inegalitatea

Această inegalitate este echivalentă cu condiția f(x) < 0 numărând

Prin urmare, trebuie să găsim toate valorile lui x pentru care condiția f(x) < 0.

6) Metoda intervalului generalizat pentru rezolvarea inegalităților, înțelegere inițială - 10 min. (rezolvarea colectivă a inegalităților prin metoda intervalelor: pe tablă și în caiete).

slide 23. Algoritm. Metoda generalizată de rezolvare a inegalităților.

Rezolvarea inegalităților f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 prin metoda intervalului. (Sistem)

Slide 24 și 25. Rezolvarea inegalității prin algoritm. (Comentarii la toate punctele algoritmului).

slide 26. Ilustrare grafică a soluției acestei inegalități.

Slide 27. Rezolvați inegalitatea pe tablă și în caiete .

Slide 28. Ilustrare grafică a soluției acestei inegalități.

Slide 29. Rezolvați inegalitatea pe tablă și în caiete

Slide 30. Ilustrare grafică a soluției acestei inegalități.

Slide 31, 32. Rezolvați verbal inegalitatea, conform imaginii

7) Informații despre teme.(Rezolvați prin metoda intervalului optiunea numarul 2)

8) Consolidarea noilor cunoștințe (muncă independentă, opțiunea nr. 1).

9) Rezumarea lecției, autocontrol asupra soluțiilor gata făcute (diapozitivele 33, 34, 35), repetarea algoritmului metodei generalizate a intervalelor și aplicarea acestuia.

10) Analiza asimilării materialului și a interesului studenților pentru temă. Această metodă este universală pentru rezolvarea oricăror inegalități, inclusiv raționale, cu un modul, irațional, exponențial, logaritmic, deoarece metoda intervalului reduce soluția inegalităților la rezolvarea ecuațiilor, găsirea domeniului de definiție și a valorii funcției într-un punct nu nu provoacă dificultăți. Dar a trebuit să dau exemple de inegalități unde utilizarea acestei metode nu este justificată, unde este mai rațional să se aplice alte metode de rezolvare a inegalităților.

Prezentare „Aplicarea continuității în rezolvarea inegalităților”. (35 diapozitive)

Definiție 4. O funcție se numește continuă pe un segment dacă este continuă în fiecare punct al acestui segment (în punctul a este continuă în dreapta, adică în punctul b este continuă în stânga, adică).

Toate funcțiile elementare de bază sunt continue în domeniul lor de definire.

Proprietățile funcțiilor continue pe un segment:

• 1) Dacă o funcție este continuă pe un segment, atunci ea este mărginită pe acest segment (prima teoremă Weierstrass).
• 2) Dacă o funcție este continuă pe un segment, atunci pe acest segment atinge valoarea sa minimă și valoarea sa maximă (a doua teoremă Weierstrass) (vezi Fig. 2).
• 3) Dacă o funcție este continuă pe un segment și ia valori de diferite semne la capetele sale, atunci există cel puțin un punct în interiorul segmentului astfel încât (teorema Bolzano-Cauchy).

Punctele de întrerupere a funcției și clasificarea lor

Segmentul punctului de continuitate a funcției

Punctele în care condiția de continuitate nu este îndeplinită se numesc puncte de discontinuitate ale acestei funcții. Dacă este un punct de discontinuitate al unei funcții, atunci cel puțin una dintre cele trei condiții pentru continuitatea funcției specificate în definițiile 1, 2 nu este îndeplinită în aceasta, și anume:

1) Funcția este definită în vecinătatea punctului, dar nu este definită în punctul însuși. Deci funcția considerată în exemplul 2 a) are o întrerupere într-un punct, deoarece nu este definită în acest punct.

2) Funcția este definită la un punct și vecinătatea acestuia, există limite unilaterale și, dar nu sunt egale între ele: . De exemplu, funcția din exemplul 2 b) este definită într-un punct și vecinătatea acestuia, dar, din moment ce, a.

3) Funcția este definită în punct și în împrejurimile acestuia, există limite unilaterale și, sunt egale între ele, dar nu egale cu valoarea funcției în punctul: . De exemplu, funcția. Iată punctul de întrerupere: în acest moment funcția este definită, există limite unilaterale și egale între ele, dar, adică .

Punctele de întrerupere a funcției sunt clasificate după cum urmează.

Definiție 5. Un punct se numește punct de discontinuitate al primului fel de funcție dacă există limite finite și în acest punct, dar nu sunt egale între ele: . Mărimea se numește apoi saltul funcției în punct.

Definiția 6 . Un punct se numește punct al unei discontinuități amovibile a unei funcții dacă în acest punct există limite finite și, ele sunt egale între ele: , dar funcția în sine nu este definită în punct, sau este definită, dar.

Definiție 7. Un punct se numește punct de discontinuitate al celui de-al doilea fel de funcție dacă în acest punct cel puțin una dintre limitele unilaterale (sau) nu există sau este egală cu infinitul.

Exemplul 3. Găsiți punctele de întrerupere ale următoarelor funcții și determinați tipul acestora: a) b)

Soluţie. a) Funcția este definită și continuă pe intervalele u, întrucât pe fiecare dintre aceste intervale este dată de funcții elementare continue. Prin urmare, punctele de întrerupere ale unei anumite funcții pot fi doar acele puncte în care funcția își schimbă alocarea analitică, i.e. punctele i. Să găsim limitele unilaterale ale funcției în punctul:

Deoarece limitele unilaterale există și sunt finite, dar nu sunt egale între ele, punctul este un punct de discontinuitate de primul fel. Salt de funcție:

Pentru un punct găsim.

Continuitatea unei funcții pe un interval

Nume parametru	Sens
Subiect articol:	Continuitatea unei funcții pe un interval
Rubrica (categoria tematica)	Matematica

Definiție. O funcție se numește continuă pe un interval dacă este continuă în fiecare punct al acestui interval.

Dacă funcția este definită pentru X=A si in care f(X) = f(A),

atunci ei spun că f(X) la punct și continuă pe dreapta. În mod similar, dacă f(X) = f(b), atunci spunem că la punct b această funcție lăsat continuu.

Definiție. Funcția este de obicei numită continuă pe intervalul [ A, b], dacă este continuă în fiecare dintre punctele sale (la punctul A continuu pe dreapta, la un punct b este continuă în stânga).

cea mai mare valoare funcții la = f(X) pe segmentul [ A, b f(X 1) că f(X) £ f(X 1) pentru toată lumea X Î [ A, b].

Cea mai mică valoare funcții la = f(X) pe segmentul [ A, b] se obișnuiește să se numească astfel valoarea sa f(X 2) că f(X) ³ f(X 2) pentru toată lumea X Î [ A, b].

Funcțiile care sunt continue pe un interval au o serie de proprietăți importante, care sunt exprimate prin următoarele teoreme.

Teorema 3.3.1. O funcție continuă pe segmentul [ A, b], atinge valoarea minimă pe el mși cea mai mare valoare M, adică există astfel de puncte X 1 și X 2 din acest segment, care f(X 1) = m, f(X 2) = M.

Teorema are un sens geometric simplu (vezi Fig. 2).

Teorema 3.3.2.În cazul în care funcția la = f(X) este continuă pe intervalul [ A, b] și ia valori inegale la capete f(A) = A, f(b) = B, A ¹ B, atunci indiferent de numărul C dintre A și B, există un punct Cu Î [ A, b] astfel încât f(Cu) = C.

Sensul geometric al teoremei este ilustrat în Fig.3. Orice linie dreaptă la= C, unde A< C < B (или A >C > B), intersectează graficul funcției la = f(X).

Consecinţă. Dacă funcția este continuă pe un segment și ia valori de diferite semne la capete, atunci există cel puțin un punct pe acest segment în care funcția dispare.

Sensul geometric al consecinței este ilustrat în Fig.4.

Întrebări pentru autocontrol

1. Ce funcție se numește continuă într-un punct?

2. Dați încă o definiție echivalentă prin creșterea unei funcții și a argumentelor.

3. Ce se poate spune despre suma, diferența, produsul și câtul a două funcții continue?

4. Pentru ce valori ale argumentului sunt continue toate funcțiile raționale și fracționale-raționale?

5. Când este continuă într-un punct o funcție complexă?

6. Ce se numește în mod obișnuit punctul de rupere al funcțiilor?

7. Ce puncte se numesc puncte de discontinuitate de primul fel?

8. Ce valoare se numește de obicei funcția salt?

9. Explicați conceptele de „punct de întrerupere amovibil”. Dă exemple.

10. Ce puncte se numesc puncte de discontinuitate de al doilea fel? Dă exemple.

11. Explicați conceptele: „„continuitate pe interval””, „„continuitate pe dreapta””, „„continuitate pe stânga””, „„continuitate pe segment””.

12. Definiți cele mai mari și cele mai mici valori ale funcțiilor.

13. Formulați o teoremă privind relația de continuitate pe un segment cu cele mai mari și mai mici valori ale funcției. Explica-l cu o poza.

14. Formulați o teoremă privind legătura dintre continuitatea funcțiilor pe un segment și segmentul valorilor funcției. Ilustrați semnificația sa geometrică în figură.

15. Dați o consecință a teoremei de mai sus și a interpretării sale geometrice.

PRELEGERE №4

Tema cursului: Derivată de funcție

Planul cursului: Conceptul de derivat, sensul său geometric și fizic. Reguli de bază de diferențiere. Derivată a unei funcții complexe. Unele aplicații ale derivatului.

4.1. Conceptul de derivat, sensul său geometric și fizic

Luați în considerare funcția la = f(X) specificat în intervalul ] A, b[. Lăsa XÎ ] A, b[ și X Î ] A, b[, apoi funcția crește la punctul X 0 este exprimat prin formula D la = f(X 0+D X) – f(X 0).

Definiție. Derivata functiei y = f(X) la punct X 0 este de obicei numit limita raportului dintre incrementul acestei funcții și incrementul argumentului atunci când acesta din urmă tinde spre zero:

f'(X 0) = sau y"(X 0) =.

Sensul geometric al derivatului: derivata acestei funcții într-un punct este egală cu tangentei unghiului dintre axa Ox și tangentei la graficul acestei funcții în punctul corespunzător (vezi Fig. 1):

f"(X 0) = tan a.

Definiție. Dacă funcţia f(X) este definită pe intervalul [ a, b], este continuă în fiecare punct al intervalului ( a, b), la punctul A continuu pe dreapta, la un punct b este continuu in stanga, atunci spunem ca functia f(X) continuu pe segment [a, b].

Cu alte cuvinte, funcția f(X) este continuă pe intervalul [ a, b] dacă sunt îndeplinite trei condiții:

1) "X 0 Î( a, b): f(X) = f(X 0);

2) f(X) = f(A);

3) f(X) = f(b).

Pentru funcțiile care sunt continue pe un interval avem în vedere unele proprietăți, pe care le formulăm sub forma următoarelor teoreme fără demonstrații.

Teorema 1. Dacă funcţia f(X) este continuă pe intervalul [ a, b], apoi atinge cea mai mică și cea mai mare valoare pe acest segment.

Această teoremă afirmă (Fig. 1.15) că pe segmentul [ a, b] există un astfel de punct X 1 că f(X 1) £ f(X) pentru orice X de la [ a, b] și că există un punct X 2 (X 2 О[ a, b]) astfel încât " XÎ[ a, b] (f(X 2) ³ f(X)).

Sens f(X 1) este cea mai mare pentru funcția dată pe [ a, b], A f(X 2) - cel mai mic. Denota: f(X 1) = M, f(X 2) =m. Întrucât pentru f(X) este valabilă următoarea inegalitate: " XÎ[ a, b] m£ f(X) £ M, apoi obținem următorul corolar din teorema 1.

Consecinţă. Dacă funcţia f(X) este continuă pe un segment, apoi este mărginită pe acest segment.

Teorema 2. Dacă funcţia f(X) este continuă pe intervalul [ a,b] și ia valori ale diferitelor semne la capetele segmentului, atunci există un astfel de punct interior X 0 segment [ a, b], în care funcția se transformă în 0, i.e. $ X 0 Î ( a, b) (f(X 0) = 0).

Această teoremă afirmă că graficul unei funcții y=f(X), continuu pe segmentul [ a, b], traversează axa Bou cel puţin o dată dacă valorile f(A) și f(b) au semne opuse. Deci, (Fig. 1.16) f(A) > 0, f(b) < 0 и функция f(X) dispare în puncte X 1 , X 2 , X 3 .

Teorema 3. Lasă funcția f(X) este continuă pe intervalul [ a, b], f(A) = A, f(b) = Bși A¹ B. (Fig. 1.17). Apoi pentru orice număr C, încheiat între numere Ași B, există un astfel de punct interior X 0 segment [ a, b], ce f(X 0) = C.

Consecinţă. Dacă funcţia f(X) este continuă pe intervalul [ a, b], m- cea mai mică valoare f(X), M- cea mai mare valoare a functiei f(X) pe segmentul [ a, b], atunci funcția ia (cel puțin o dată) orice valoare mîntre mși M, și, prin urmare, segmentul [ m, M] este mulțimea tuturor valorilor funcției f(X) pe segmentul [ a, b].

Rețineți că dacă funcția este continuă pe intervalul ( a, b) sau are pe segmentul [ a, b] a punctului de discontinuitate, atunci Teoremele 1, 2, 3 nu mai sunt adevărate pentru o astfel de funcție.

În concluzie, considerăm teorema privind existența unei funcții inverse.

Amintiți-vă că un interval este un segment, un interval sau un semi-interval finit sau infinit.

Teorema 4. Lăsa f(X) este continuă pe interval X, crește (sau scade) cu Xși are o gamă de valori Y. Apoi pentru funcție y=f(X) există o funcție inversă X= j(y) definit pe interval Y, continuă și în creștere (sau în scădere) pe Y cu multe sensuri X.

cometariu. Lasă funcția X= j(y) este inversă pentru funcție f(X). Deoarece argumentul este de obicei notat cu X, iar funcția prin y, atunci scriem funcția inversă ca y=j(X).

Exemplul 1. Funcţie y=x 2 (Fig. 1.8, a) pe platou X= dacă este continuă în toate punctele interne ale acestui segment și la capetele acestuia, i.e. la puncte Ași b, este continuă pe dreapta și, respectiv, pe stânga.

Teorema 1. O funcție continuă pe segmentul [ A, b], cel puțin într-un punct al acestui segment ia cea mai mare valoare și cel puțin într-un punct - cea mai mică.

Teorema afirmă că dacă funcția y = f(x) continuu pe segmentul [ A, b], atunci există cel puțin un punct x 1 Î [ A, b] astfel încât valoarea funcției f(x)în acest moment va fi cea mai mare dintre toate valorile sale de pe acest segment: f(x1) ≥ f(x). În mod similar, există un astfel de punct x2, în care valoarea funcției va fi cea mai mică dintre toate valorile de pe segment: f(x 1) ≤ f(x).

Este clar că pot exista mai multe astfel de puncte, de exemplu, figura arată că funcția f(x) ia cea mai mică valoare în două puncte x2și X 2 ".

cometariu. Afirmația teoremei poate deveni falsă dacă luăm în considerare valoarea funcției pe intervalul ( A, b). Într-adevăr, dacă luăm în considerare funcția y=x pe (0, 2), atunci este continuă pe acest interval, dar nu își atinge valorile maxime sau minime în el: atinge aceste valori la sfârșitul intervalului, dar capetele nu aparțin regiune.

De asemenea, teorema încetează să fie adevărată pentru funcțiile discontinue. Dă un exemplu.

Consecinţă. Dacă funcţia f(x) continuu pe [ A, b], atunci este mărginit pe acest segment.

Teorema 2. Lasă funcția y = f(x) continuu pe intervalul [ A, b] și ia valori ale diferitelor semne la capetele acestui segment, atunci există cel puțin un punct în interiorul segmentului x=C, unde funcția dispare: f(C)= 0, unde a< C< b

Această teoremă are o semnificație geometrică simplă: dacă punctele graficului unei funcții continue y = f(x), corespunzătoare capetelor segmentului [ A, b] se află pe părțile opuse ale axei Bou, atunci acest grafic cel puțin într-un punct al segmentului intersectează axa Bou. Este posibil ca funcțiile discontinue să nu aibă această proprietate.

Această teoremă admite următoarea generalizare.

Teorema 3 (teorema valorilor intermediare). Lasă funcția y = f(x) continuu pe intervalul [ A, b] și f(a) = A, f(b) = B. Apoi pentru orice număr Cîntre Ași B, există un astfel de punct în interiorul acestui segment CÎ [ A, b], ce f(c) = C.

Această teoremă este evidentă din punct de vedere geometric. Luați în considerare graficul funcției y = f(x). Lăsa f(a) = A, f(b) = B. Apoi orice linie y=C, Unde C- orice număr între Ași B, intersectează graficul funcției cel puțin într-un punct. Abscisa punctului de intersecție va fi acea valoare x=C, la care f(c) = C.

Astfel, o funcție continuă, care trece de la una dintre valorile sale la alta, trece în mod necesar prin toate valorile intermediare. În special:

Consecinţă. Dacă funcţia y = f(x) este continuă pe un anumit interval și ia valorile cele mai mari și cele mai mici, apoi pe acest interval ia, cel puțin o dată, orice valoare între cele mai mici și cele mai mari valori ale sale.

DERIVAT ȘI APLICAȚIILE EI. DEFINIȚIA DERIVATIVE

Să avem o funcție y=f(x), definite pe un anumit interval. Pentru fiecare valoare de argument X din acest interval funcţia y=f(x) are un anumit sens.

Luați în considerare două valori ale argumentului: initial X 0 și nou X.

Diferență x–x 0 este numit increment al argumentului x la punct X 0 și notat Δx. În acest fel, ∆x = x – x 0 (incrementul argumentului poate fi pozitiv sau negativ). Din această egalitate rezultă că x=x 0 +Δx, adică valoarea inițială a variabilei a primit o anumită creștere. Apoi, dacă la punct X 0 valoarea funcției a fost f(x 0 ), apoi la noul punct X funcția va lua valoarea f(x) = f(x 0 +∆x).

Diferență a-a 0 = f(x) – f(x 0 ) numit creșterea funcției y = f(x) la punct X 0 și este notat cu simbolul Δy. În acest fel,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

De obicei, valoarea inițială a argumentului X 0 este considerat fix iar noua valoare X- variabil. Apoi y 0 = f(x 0 ) se dovedeşte a fi constantă şi y = f(x)- variabil. incremente Δyși Δx vor fi și variabile și formula (1) arată că Dy este o funcție a variabilei Δx.

Compuneți raportul dintre incrementul funcției și incrementul argumentului

Să găsim limita acestei relații la Δx→0. Dacă această limită există, atunci se numește derivată a acestei funcții. f(x) la punct X 0 și notează f "(X 0). Asa de,

derivat această funcție y = f(x) la punct X 0 se numește limita raportului de creștere a funcției Δ y la incrementul argumentului Δ X când acesta din urmă tinde în mod arbitrar spre zero.

Rețineți că pentru aceeași funcție derivata în puncte diferite X poate lua valori diferite, de ex. derivata poate fi gândită ca o funcție a argumentului X. Aceasta functie este notata f "(X)

Derivata este notata prin simboluri f "(X y", . Valoarea specifică a derivatului la x = a notat f "(A) sau y "| x=a.

Operația de găsire a derivatei unei funcții f(x) se numeste diferentierea acestei functii.

Pentru a găsi direct derivata prin definiție, puteți aplica următoarele regula generală:

Exemple.

SENSUL MECANIC AL DERIVATULUI

Din fizică se știe că legea mișcării uniforme are forma s = v t, Unde s- calea parcursă până la momentul respectiv t, v este viteza mișcării uniforme.

Cu toate acestea, din moment ce majoritatea mișcărilor care apar în natură sunt inegale, apoi, în general, viteza și, în consecință, distanța. s va depinde de timp t, adică va fi o funcție a timpului.

Deci, lăsați punctul material să se miște în linie dreaptă într-o direcție conform legii s=s(t).

Observați un moment în timp t 0 . Până în acest moment, punctul a depășit poteca s=s(t 0 ). Să stabilim viteza v punct material la timp t 0 .

Pentru a face acest lucru, luați în considerare un alt moment în timp t 0 + Δ t. Ea corespunde distanței parcurse s =s(t 0 + Δ t). Apoi pentru intervalul de timp Δ t punctul a parcurs calea Δs =s(t 0 + Δ t)–Sf).

Să luăm în considerare relația. Se numește viteza medie în intervalul de timp Δ t. Viteza medie nu poate caracteriza cu exactitate viteza de mișcare a unui punct în acest moment t 0 (deoarece mișcarea este inegală). Pentru a exprima mai precis această viteză adevărată folosind viteza medie, trebuie să luați un interval de timp mai mic Δ t.

Deci, viteza de mișcare la un moment dat t 0 (viteza instantanee) este limita vitezei medii în intervalul de la t 0 la t 0 +Δ t când Δ t→0:

,

acestea. viteza mișcării inegale este derivata distantei parcurse in raport cu timpul.

SENSUL GEOMETRIC AL DERIVATULUI

Să introducem mai întâi definiția unei tangente la o curbă într-un punct dat.

Să avem o curbă și un punct fix pe ea M 0(vezi figura) Luați în considerare un alt punct M aceasta curba si traseaza o secanta M 0 M. Dacă punct Mîncepe să se miște de-a lungul curbei și punctul M 0 rămâne staționar, secanta își schimbă poziția. Dacă, cu o aproximare nelimitată a punctului M curbă la punct M 0 pe orice parte, secanta tinde să ia poziția unei anumite linii drepte M 0 T, apoi linia dreaptă M 0 T se numeste tangenta la curba in punctul dat M 0.

Acea., tangentă la curba la un punct dat M 0 numită poziție limită a secantei M 0 M când punctul M tinde de-a lungul curbei către un punct M 0.

Luați în considerare acum funcția continuă y=f(x) iar curba corespunzătoare acestei funcţii. Pentru o oarecare valoare X Funcția 0 ia o valoare y0=f(x0). Aceste valori X 0 și y 0 pe curbă corespunde unui punct M0 (x 0; y 0). Să dăm un argument x0 increment Δ X. Noua valoare a argumentului corespunde valorii incrementate a funcției y 0 +Δ y=f(x 0 –Δ X). Primim un punct M(x 0+Δ X; y 0+Δ y). Să desenăm o secanta M 0 M si notam cu φ unghiul format de secanta cu directia pozitiva a axei Bou. Să facem o relație și să observăm că .

Dacă acum Δ X→0, deci, datorită continuității funcției Δ la→0 și, prin urmare, punctul M, deplasându-se de-a lungul curbei, se apropie la infinit de punct M 0. Apoi secanta M 0 M va tinde să ia poziția unei tangente la curbă în punct M 0, iar unghiul φ→α la Δ X→0, unde α reprezintă unghiul dintre tangentă și direcția pozitivă a axei Bou. Deoarece funcția tg φ depinde continuu de φ la φ≠π/2, atunci la φ→α tg φ → tg α și, prin urmare, panta tangentei va fi:

acestea. f"(x)= tgα .

Astfel, geometric y "(x 0) reprezintă panta tangentei la graficul acestei funcţii în punct x0, adică pentru o valoare dată a argumentului X, derivata este egala cu tangentei unghiului format de tangenta la graficul functiei f(x)în punctul corespunzător M 0 (x; y) cu direcția pozitivă a axei Bou.

Exemplu. Aflați panta tangentei la curbă y = x 2 la punct M(-1; 1).

Am văzut deja că ( X 2)" = 2X. Dar panta tangentei la curbă este tg α = y„| x=-1 = - 2.

DIFERENȚIABILITATEA FUNCȚIILOR. CONTINUITATEA UNEI FUNCȚII DIFERENȚIABILE

Funcţie y=f(x) numit diferentiabil la un moment dat X 0 dacă are o anumită derivată în acest moment, adică dacă limita relaţiei există şi este finită.

Dacă o funcție este diferențiabilă în fiecare punct al unui segment [ A; b] sau interval ( A; b), apoi spun că asta diferentiabil pe segmentul [ A; b] sau, respectiv, în intervalul ( A; b).

Este valabilă următoarea teoremă, care stabilește o legătură între funcțiile diferențiabile și continue.

Teorema. Dacă funcţia y=f(x) diferentiabil la un moment dat x0, atunci este continuă în acest moment.

Astfel, diferențiabilitatea unei funcții implică continuitatea acesteia.

Dovada. În cazul în care un , apoi

,

unde α este o valoare infinitezimală, i.e. cantitate care tinde spre zero la Δ X→0. Dar apoi

Δ y=f "(x0) Δ X+αΔ X=> Δ y→0 la Δ X→0, adică f(x) – f(x0)→0 la X→X 0 , ceea ce înseamnă că funcția f(x) continuu la punct X 0 . Q.E.D.

Astfel, în punctele de discontinuitate, funcția nu poate avea o derivată. Afirmația inversă nu este adevărată: există funcții continue care nu sunt diferențiabile în anumite puncte (adică nu au o derivată în aceste puncte).

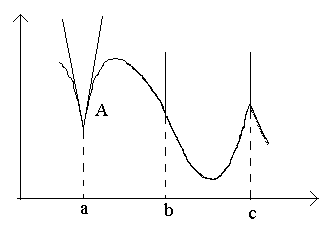
Luați în considerare punctele din figură a, b, c.

La punctul A la Δ X→0 relația nu are limită (deoarece limitele unilaterale sunt diferite pentru Δ X→0–0 și Δ X→0+0). La punctul A graficul nu are o tangentă definită, dar există două tangente unilaterale diferite cu pante la 1 și la 2. Acest tip de punct se numește punct de colț.

La punctul b la Δ X→0 raportul este de semn constant valoare infinit mare . Funcția are o derivată infinită. În acest moment, graficul are o tangentă verticală. Tip de punct - „punct de inflexiune” cu o tangentă verticală.

La punctul c derivatele unilaterale sunt cantități infinit de mari de semne diferite. În acest moment, graficul are două tangente verticale îmbinate. Tip - "cuspid" cu o tangentă verticală - un caz special al unui punct de colț.