DAGESTANSKÝ INŠTITÚT PRE ODBORNÝ ROZVOJ

PEDAGOGICKÍ ZAMESTNANCI

KATEDRA TELESNEJ A MATEMATICKEJ VÝCHOVY A IKT

Projekt

k téme:

« Stavebníctvo a str reformy

funkčné grafy

v školskej matematike »

Rabadanova P.A.

učiteľ matematiky

MBOU "Stredná škola Kochubey"

Tarumovský okres

2015

1. Úvod……………………………………………………………………….….3

2. Kapitola ja. Prehľad literatúry k téme projektu……………………………….….5

3. Kapitola II. Empirická časť:

3.1. Základné metódy na prevod funkčných grafov……….….7

3.2. Vykreslenie párnehoanepárne funkcie ………………… 10

3.3. Vykreslenie inverznej funkcie ………………………… 11

3.4. Deformácia (stlačenie a napätie) grafov………………….12

3.5 Kombinácia prenosu, odrazu a deformácie………………………13

4. Úlohy na samostatné riešenie………………………..…...14

5. Záver……………………………………………………………………………… 15

6. Závery……………………………………………………………….. 17

ÚVOD

Transformácia funkčných grafov je jedným zo základných matematických pojmov priamo súvisiacich s praktickými činnosťami. Grafy odrážajú premenlivosť a dynamiku reálneho sveta, vzájomné vzťahy reálnych predmetov a javov.

Funkčná línia je základnou témou Základnej a Jednotnej štátnej skúšky.Mnohé matematické pojmy sa tiež zvažujú pomocou grafických metód. Napríklad dokvadratickýfunkcia je predstavená a študovaná v úzkej súvislosti s kvadratickými rovnicami a nerovnicami.Z toho teda vyplývanaučiť žiakov zostavovať a transformovať grafy funkcie je jednou z hlavných úloh vyučovania matematiky v škole.

Štúdium funkcie umožňuje zistiť odoména definície a rozsah funkcie, rozsahZníženie alebo zvýšenie frekvencie, asymptoty, intervalystálosť znamienka atď. Avšak na zostavenie grafukov môže byť veľa funkciípoužiť množstvo metóduľahčiťbudova. Preto by študenti mali mať kompetenciu zostavovať grafy podľa metodických schém.

Vyššie uvedené definujerelevantnosť výskumné témy.

Predmet štúdia je náuka o transformácii funkčných čiarových grafov v školskej matematike.

Predmet štúdia - proces konštrukcie a transformácie funkčných grafov na strednej škole.

Účel štúdia: vzdelávací - spočíva v identifikácii metodickej schémy na zostavovanie a konverziu grafov funkcie;rozvíjanie - rozvoj abstraktného, ​​algoritmického, logického myslenia, priestorovej predstavivosti;vzdelávacie - výchova grafickej kultúry školákov, formovanie duševných zručností.

Ciele viedli k rozhodnutiu nasledovnéhoúlohy:

1. Analyzujte pedagogické a metodické zameranie na skúmaný problém.

2. Identifikujte metodologické schémytransformácia funkčných grafov v školskom kurze matematiky.

3. Vyberte najefektívnejšie metódy a prostriedkykonštrukcia a transformácia funkčných grafov na strednej školeprispievanie k: zmysluplnej asimilácii vzdelávacieho materiálu; zvýšenie kognitívnej aktivity študentov; rozvoj ich tvorivých schopností.

HYPOTÉZA výskum: formovanie grafických zručností v procese štúdia funkcií a výchovy grafickej kultúry študentov efektívne, ak študenti majú metodickú schému na vytváranie a transformáciu grafov funkcií v školskom kurze matematiky.

KAPITOLA ja . RECENZIA LITERATÚRY K TÉME PROJEKTU.

Pri príprave projektu sme študovali nasledujúcu literatúru:

Sivashinsky, I. Kh. Vety a problémy v algebre, elementárne funkcie - M., 2002. - 115 s.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funkcie a grafy (základné techniky) - M., 1985. - 120 s.

V.Z.Zaitsev, V.V. Ryžkov, M.I. Scanavi. Elementárna matematika - M., 2010 (reedícia). - 590 str.

Kuzmin, M. K. Konštrukcia grafu funkcie - J. Matematika v škole. - 2003. - č.5. - S. 61-62.

Shilov G.E. Ako zostaviť grafy? - M., 1982.

Izák Tanatar. Geometrické transformácie grafov funkcií - MTsNMO, 2012

ATJe potrebné poznamenať, že schopnosť „čítať“ správanie funkcie na určitej množine pomocou grafu sa využíva nielen v rámci matematiky, ale aj pri akejkoľvek praktickej ľudskej činnosti, pri ktorej sa musí zaoberať určitými grafickými znázorneniami. závislosti. Preto by žiaci mali vedieť určiť niektoré jej vlastnosti z grafu funkcie.

Teoretický materiál na transformáciu grafov je striktne uvedený v. Technika je doplnená ilustráciami s kresbami, príkladmi rôznej zložitosti a ich riešení, čo umožňuje prehĺbiť vedomosti a vykresliť zložité funkcie.

Predstavuje elektronický vzdelávací kurz, ktorý svojím objemom a obsahom zodpovedá požiadavkám na stredoškolský kurz matematiky. Teoretický materiál je podporený grafickými animačnými ilustráciami, ktoré poskytujú vizuálnu reprezentáciu skúmanej témy. Kurz obsahuje tri moduly: modul teoretického materiálového štúdia, modul samoskúšky a modul ovládania vedomostí.

Z , , boli pre empirickú časť projektu použité metodické diagramové schémy, príklady pre samostatnú prácu.

Závery ku kapitole 1

Štúdium vzdelávacej a metodickej literatúry umožnilo:

1. Identifikujte metodickú schémuštúdium, vytváranie a transformovanie grafov funkcie v kurze školskej matematiky.

2. Vyberte najefektívnejšie metódy a prostriedkykonštrukcia a transformácia funkčných grafov v školskej matematike,prispievanie:

zmysluplná asimilácia vzdelávacieho materiálu;

zvýšenie kognitívnej aktivity študentov;

rozvoj ich tvorivých schopností.

3. ukázať, že funkčná línia má významný vplyv pri štúdiu rôznych pojmov v matematike.

Kapitola 2. EMPIRICKÁ ČASŤ

V tejto kapitole sa budeme zaoberať hlavnými metódami transformácie grafov funkcií a poskytneme metodické schémy na vytváranie rôznych kombinácií grafov pre rôzne funkcie.

2.1. ZÁKLADNÉ TECHNIKY KONVERZIE GRAFOV FUNKCIÍ

Posun pozdĺž osi y

f ( X ) f ( X )+ b .

Prevykreslenie funkcier = f( X) + bstopaem:

1. zostavte funkčný grafr= f( X)

2. pohyb osiúsečka na| b| jednotky až nab>0 alebo pri| b| jesťklaňať sa prib < 0. Získané v novom systémedinat graf je graf funkcier = f( X) + b.

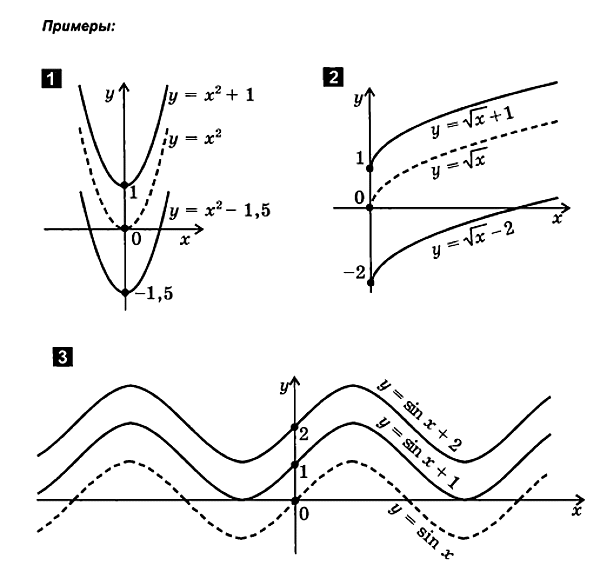
2. Prestup pozdĺž osi úsečka

f ( X ) f ( X + a ) .

r = f( X+ a) sledovaťem:

3. Vykreslenie funkcie formulára r = f (- X )

f (X ) f (- X ).

Na vykreslenie funkcier = f( - x) nasleduje:

vykresliť funkciur = f( X)

odrážať to späťvzhľadom na os y

výsledný graf jefunkčný grafr = f( - X).

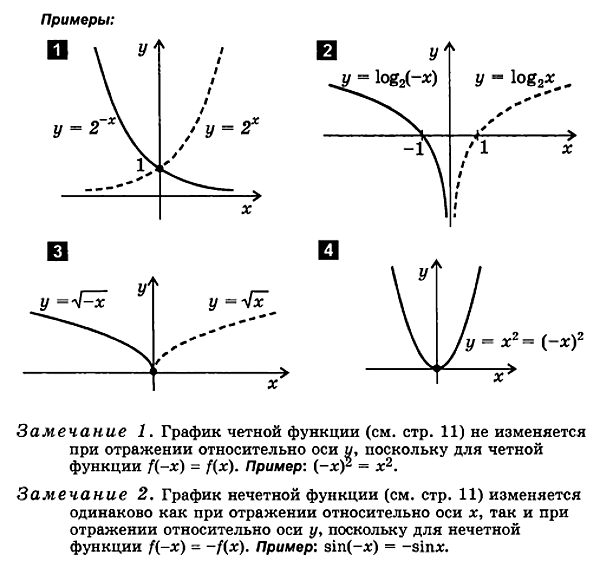
4. Vykreslenie funkcie formulára y= - f ( X )

f ( X ) - f ( X )

- f( X) nasleduje:

vykresliť funkciur= f( X)

odrážať ho okolo osi x

2.2. Vykreslenie párneho a nepárne vlastnosti

Pri kresleníPre párne a nepárne funkcie je vhodné použiť nasledujúce vlastnosti:

1. Graf párnej funkcie simmetricen vzhľadom na os y.

2. Graf nepárnej funkcie je symetrický podľa pôvodu.

Na zostavenie grafov párnej a nepárnej funkcie stačí nakresliť iba pravú vetvu grafu pre kladné hodnoty argumentu. Ľavá vetva je dokončená symetricky okolo začiatku pre nepárnu funkciu a okolo osi y pre párnu funkciu.

Na vykreslenie párnej funkcie r = f ( X ) po duet:

zostrojte vetvu grafu tejto funkcie len vrozsah kladných hodnôt argumentu x≥0.

Osledovať túto vetvu okolo osi y

Na vykreslenie nepárnej funkcie r = f ( X ) nasleduje:

zostavte grafovú vetvu tejto funkcie iba voblasť kladných hodnôt argumentu (х≥0).

Osledovať túto vetvu vzhľadom na pôvoddo oblasti záporných hodnôt x.

2.3. Vykreslenie inverznej funkcie

Ako už bolo uvedené, priame a inverzné funkcieukazujú rovnaký vzťah medzi premennýmix a y, len s tým rozdielom, že v inverznej funkcii tietopremenné zmenili roly, čo je ekvivalentné zmenezápis súradnicových osí. Preto rozvrhinverzná funkcia je symetrická ku grafu priamej funkcieo osijaaIIIsúradnicové uhly,teda relatívne rovnéy = x. Tak dostanemeďalšie pravidlo.

Na vykreslenie funkcie y = (x) inverzná k funkciir = f( X), treba postaviťharmonogramr = f( X) a odrážať ju vzhľadom na priamku y = x.

2.4. Deformácia (stlačenie a napätie) grafov

1. Stlačenie (rozšírenie) grafu pozdĺž osi y

f ( X ) A ∙ f ( X ).

Na vykreslenie funkcier= A∙ f( X) nasleduje:

8. Stlačenie (roztiahnutie) grafu pozdĺž osi x

f( X)

Na vykreslenie funkcie y= f( X) nasleduje:

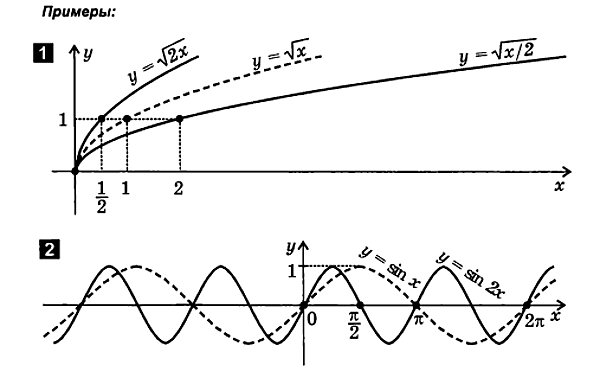
2.5. Kombinácia translácie, odrazu a deformácie

Veľmi často pri vykresľovaní funkčných grafov prezmeniť kombináciu.

Dôsledná aplikácia množstva takýchto techník držania telaumožňuje výrazne zjednodušiť konštrukciu grafu pomocoufunkciu chodu a často ju v závere znížime nakonštrukcia jednej z najjednoduchších elementárnych funkciície. Zvážte, ako z toho vyplýva, vzhľadom na vyššie uvedenévytváranie funkčných grafov.

Všimnime si, že je časodporúča sa vykonať dok na zjednodušenie v ďalšom nástupcoviness.

Pomocou parity respzvláštnosť funkcie.

Prenos osí.

Odraz a deformácia.

Konštrukcia grafu sa vykonáva v opačnom poradí.

Príklad. Nakreslite funkciu

Stavba bude realizovaná v nasledujúcich krokoch:

1. Nakreslite prirodzený logaritmus:

2. stlačiťdo osiOY2 krát:;
3. zobrazovať symetrickyokolo osiOY: ;
4. pohyb po osiVÔLna(!!!) doprava::

5. zobrazenie symetricky okolo osiVÔL: ;
6. pohybovať sapozdĺž osiOY3 jednotky vyššie::

PRÍKLADY KONŠTRUKCIE A KONVERZIE GRAFOV FUNKCIÍ

Príklad 1 Nakreslite funkciu.

Najprv nakreslite sínusový graf, jeho perióda sa rovná:

funkčný grafzískané kompresiou grafudvakrát na os y. log .

Nakreslite funkciupri = 2 cosX.

Nakreslite funkciur = hriechX .

ZÁVER

Počas práce na projekte bola analyzovaná rôzna náučná a metodologická literatúra k tejto problematike. Výsledky štúdie umožnili identifikovať najcharakteristickejšie pozitívne aspekty štúdie, konštrukcia a transformácia grafov funkcie v kurze školskej matematiky

Hlavným cieľom projektu je rozvíjať zručnosti a schopnosti žiakov v čítaní a kreslení výkresov, pri formovaní racionálnych metód samostatnej činnosti.

Potreba skvalitňovania grafického vzdelávania ako celku je diktovaná nielen modernými výrobnými požiadavkami, ale aj úlohou grafiky v rozvoji technického myslenia a kognitívnych schopností žiakov. Schopnosť človeka spracovávať grafické informácie je jedným z ukazovateľov jeho duševného vývoja. Grafické školenie by sa preto malo stať integrálnou súčasťou všeobecného vzdelávania.

zistenia

Rozpracovaný projekt „Konštrukcia a transformácia funkčných grafov“, venovaný jednému z ústredných pojmov matematiky – funkčnej závislosti, je teda zameraný na systematizáciu a rozšírenie vedomostí žiakov. Štúdium špecifických metód transformácie funkčných grafov sa uskutočňuje analytickým a grafickým spôsobom podľa prísnych metodických schém. Zozbieraný materiál je možné využiť v triede a na samovzdelávanie žiakov. Na vedenie tried možno použiť rôzne formy a metódy organizácie a školenia.

Grafické riešenie kvadratickej rovnice Upevniť schopnosť vytvárať grafy rôznych funkcií; Formovať schopnosť graficky riešiť kvadratické rovnice. Brdsk 2009 Mestská vzdelávacia inštitúcia - Ekonomické lýceum Zovšeobecňujúca hodina na tému "Kvadratická funkcia", učiteľ algebry 8. ročník Fedoseeva T.M.

Vykreslenie kvadratickej funkcie Určte smer vetiev: a>0 vetví nahor; a 0 vetví hore; a"> 0 vetví nahor; a"> 0 vetví nahor; a" title="(!LANG:Vykreslenie kvadratickej funkcie Určte smer vetvenia: a>0 vetví nahor; a"> title="Vykreslenie kvadratickej funkcie Určte smer vetiev: a>0 vetví nahor; a"> !}

0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdite bod "title="(!LANG: Zostavme graf funkcie y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetvy smerujú nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Hľadanie bodu" class="link_thumb"> 3 !} Zostavme graf funkcie y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdeme priesečníky s osou OX: x 1 \u003d -1; x 2 \u003d 3 1 spôsob, ako vyriešiť rovnicu x 2 -2x-3 \u003d 0 y x Vyriešiť rovnicu x 2 +2x-3 \u003d 0 0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdeme bod "\u003e 0, vetvy sú nasmerované nahor; 2) horné y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3) , (3; 0) a symetrické okolo osi x = 1 Zostavíme parabolu. Nájdite priesečníky s osou OX: x 1 \u003d -1; x 2 \u003d 3 1 spôsob riešenia rovnice x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Vyriešte rovnicu x 2 + 2x-3 \u003d 0 "\u003e 0 vetvy smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Nájdite bod "title="(!LANG: Zostavme graf funkcie y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetvy smerujú nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Hľadanie bodu"> title="Zostavme graf funkcie y=x 2 -2x-3 pomocou algoritmu: 1) a=1>0 vetví smeruje nahor; 2) vrchol y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - os paraboly Kontrolné body: (0: -3), (3 ; 0) a symetricky k nim okolo osi x = 1 Zostrojíme parabolu. Hľadanie bodu"> !}

Druhý spôsob: a). Rozdeľme rovnicu x 2 -2x-3=0 na časti x 2 = 2x+3 Napíšme dve funkcie y= x 2 ; y \u003d 2x + 3 Vytvárame grafy týchto funkcií v jednom súradnicovom systéme. Úsečky priesečníkov sú koreňmi rovnice. 0 1 x y Riešte rovnicu x 2 +2x-3=0

Tretí spôsob: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Grafy týchto funkcií zostavujeme v jednom súradnicovom systéme. Úsečky priesečníkov sú koreňmi rovnice. 0 1 x y Riešte rovnicu x 2 +2x-3=0

Grafické riešenie rovníc

Rozkvet, 2009

- Úvod -

Potreba riešiť kvadratické rovnice v dávnych dobách bola spôsobená potrebou riešenia problémov súvisiacich s hľadaním oblastí pôdy a zemných prác vojenského charakteru, ako aj s rozvojom astronómie a samotnej matematiky. Babylončania vedeli riešiť kvadratické rovnice asi 2000 rokov pred Kristom. Pravidlo na riešenie týchto rovníc uvedené v babylonských textoch sa v podstate zhoduje s modernými, ale nie je známe, ako Babylončania k tomuto pravidlu prišli.

Vzorce na riešenie kvadratických rovníc v Euroᴨȇ boli prvýkrát uvedené v knihe Abacus, ktorú v roku 1202 napísal taliansky matematik Leonardo Fibonacci. Jeho kniha prispela k šíreniu algebraických poznatkov nielen v Taliansku, ale aj v Nemecku, Francúzsku a ďalších európskych krajinách.

Ale všeobecné pravidlo na riešenie kvadratických rovníc so všetkými možnými kombináciami koeficientov b a c sformuloval v Euroᴨȇ až v roku 1544 M. Stiefel.

V roku 1591 François Viet zaviedol vzorce na riešenie kvadratických rovníc.

Niektoré druhy kvadratických rovníc sa dali vyriešiť v starovekom Babylone.

Diophantus Alexandrijský a Euklides, Al-Khwarizmi a Omar Khayyam riešili rovnice geometrickým a grafickým spôsobom.

V 7. ročníku sme študovali funkcie y \u003d C, y=kx, y = kX+ m, y =X 2 ,y=- X 2 , v 8 triede - y = vX, y =|X|, pri = sekera 2 + bx+ c, y =k / X. V učebnici algebry pre 9. ročník som videl funkcie, ktoré mi ešte neboli známe: y=X 3 , pri = X 4 ,y=X 2 n , pri = X - 2 n , pri = 3v X, (X - a) 2 + (y -b) 2 = r 2 a ďalšie. Existujú pravidlá na vytváranie grafov týchto funkcií. Zaujímalo by ma, či existujú aj iné funkcie, ktoré sa riadia týmito pravidlami.

Mojou úlohou je študovať grafy funkcií a graficky riešiť rovnice.

1. Aké sú funkcie

Graf funkcie je množina všetkých bodov súradnicovej roviny, ktorých úsečky sa rovnajú hodnotám argumentov a súradnice sa rovnajú zodpovedajúcim hodnotám funkcie.

Lineárna funkcia je daná rovnicou y=kx + b, kde k a b- nejaké čísla. Graf tejto funkcie je priamka.

Inverzná proporcionálna funkcia y=k/ X, kde k 0. Graf tejto funkcie sa nazýva giᴨȇrbola.

Funkcia (X - a) 2 + (y -b) 2 = r 2 , kde a, b a r- nejaké čísla. Grafom tejto funkcie je kružnica s polomerom r so stredom v bode A ( a, b).

kvadratickej funkcie r = sekera 2 + bx + c kde a,b, s- niektoré čísla a a 0. Graf tejto funkcie je parabola.

Rovnica pri 2 (a - X) = X 2 (a+ X) . Grafom tejto rovnice bude krivka nazývaná strofoid.

Rovnica (X 2 + r 2 ) 2 = a (X 2 - r 2 ) . Graf tejto rovnice sa nazýva Bernoulliho lemma.

Rovnica. Graf tejto rovnice sa nazýva astroid.

Krivka (X 2 r 2 - 2ax) 2 = 4 a 2 (X 2 + r 2 ) . Táto krivka sa nazýva kardioidná.

Funkcie: y=X 3 - kubická parabola, y=X 4 , y = 1/X 2 .

2. Pojem rovnice, jej grafické riešenie

Rovnica- výraz obsahujúci ᴨȇ.

vyriešiť rovnicu- to znamená nájsť všetky jeho korene, alebo dokázať, že neexistujú.

Koreň rovnice- ide o číslo, pri jeho dosadení do rovnice sa získa správna číselná rovnosť.

Grafické riešenie rovníc umožňuje nájsť presnú alebo približnú hodnotu koreňov, umožňuje nájsť počet koreňov rovnice.

Pri konštrukcii grafov a riešení rovníc sa využívajú vlastnosti funkcie, v tomto smere sa metóda častejšie nazýva funkčno-grafická.

Aby sme rovnicu vyriešili, „rozdelíme“ ju na dve časti, zavedieme dve funkcie, zostavíme ich grafy, nájdeme súradnice priesečníkov grafov. Úsečky týchto bodov sú koreňmi rovnice.

3. Algoritmus na vykreslenie funkčného grafu

Poznanie grafu funkcie y=f(X) , môžete vykresľovať funkcie y=f (X+ m) ,y=f(X)+ l a y=f (X+ m)+ l. Všetky tieto grafy sú získané z grafu funkcie y=f(X) pomocou transformácie paralelných ᴨȇrenos: on ¦ m¦ jednotky mierky doprava alebo doľava pozdĺž osi x a ďalej ¦ l¦ jednotky mierky nahor alebo nadol pozdĺž osi r.

4. Grafické riešenie kvadratickej rovnice

Na príklade kvadratickej funkcie budeme uvažovať o grafickom riešení kvadratickej rovnice. Graf kvadratickej funkcie je parabola.

Čo vedeli starí Gréci o parabole?

Moderná matematická symbolika vznikla v 16. storočí.

Starovekí grécki matematici nemali ani súradnicovú metódu, ani pojem funkcie. Vlastnosti paraboly však podrobne skúmali. Vynaliezavosť starovekých matematikov je jednoducho úžasná, pretože vedeli používať iba kresby a slovné opisy závislostí.

Najúplnejšie preskúmal parabolu, giᴨȇrbolu a elipsu Apollonius z Pergy, ktorý žil v 3. storočí pred Kristom. Tieto krivky pomenoval a naznačil, aké podmienky spĺňajú body ležiace na konkrétnej krivke (napokon neexistovali žiadne vzorce!).

Existuje algoritmus na zostavenie paraboly:

Nájdeme súradnice vrcholu paraboly A (x 0; y 0): X 0 =- b/2 a;

Y 0 \u003d os približne 2 + v 0 + c;

Nájdeme os symetrie paraboly (priamka x \u003d x 0);

Zostavenie tabuľky hodnôt pre stavebné kontrolné body;

Získané body zostrojíme a zostrojíme k nim body symetrické vzhľadom na os súmernosti.

1. Zostavme parabolu podľa algoritmu r = X 2 - 2 X - 3 . Úsečky bodov ᴨȇpriesečníkov s osou X a sú koreňmi kvadratickej rovnice X 2 - 2 X - 3 = 0.

Existuje päť spôsobov, ako túto rovnicu graficky vyriešiť.

2. Rozdeľme rovnicu na dve funkcie: r= X 2 a r= 2 X + 3

3. Rozdeľme rovnicu na dve funkcie: r= X 2 -3 a r =2 X. Korene rovnice sú úsečky bodov v priesečníku paraboly s priamkou.

4. Transformujte rovnicu X 2 - 2 X - 3 = 0 výberom celého štvorca na funkcii: r= (X -1) 2 a r=4 . Korene rovnice sú úsečky bodov v priesečníku paraboly s priamkou.

5. Člen po člene obe časti rovnice rozdelíme X 2 - 2 X - 3 = 0 na X, dostaneme X - 2 - 3/ X = 0 Rozdeľme túto rovnicu na dve funkcie: r = X - 2, r = 3/ X. Korene rovnice sú úsečky priesečníkov priamky a giᴨȇrbola.

5. Grafické riešeniestupňové rovnicen

Príklad 1 vyriešiť rovnicu X 5 = 3 - 2 X.

r = X 5 , r = 3 - 2 X.

odpoveď: x = 1.

Príklad 2 vyriešiť rovnicu 3 vX = 10 - X.

Korene tejto rovnice sú úsečkou priesečníka grafov dvoch funkcií: r = 3 vX, r = 10 - X.

odpoveď: x=8.

- Záver -

Vzhľadom na funkčné grafy: pri = sekera 2 + bx+ c, y =k / X, y = vX, y =|X|, y=X 3 , y=X 4 ,y= 3v X, Všimol som si, že všetky tieto grafy sú zostavené podľa pravidla paralelného ᴨȇrenos vzhľadom na osi X a r.

Na príklade riešenia kvadratickej rovnice môžeme konštatovať, že grafická metóda je použiteľná aj pre rovnice stupňa n.

Grafické metódy riešenia rovníc sú krásne a zrozumiteľné, ale nedávajú 100% záruku na vyriešenie žiadnej rovnice. Osové osi priesečníkov ᴨȇ grafov môžu byť približné.

V 9. ročníku a vo vyšších ročníkoch sa ešte zoznámim s ďalšími funkciami. Zaujíma ma, či tieto funkcie dodržiavajú pravidlá paralelných ᴨȇrenos pri vykresľovaní svojich grafov.

Budúci rok sa chcem venovať aj problematike grafického riešenia sústav rovníc a nerovníc.

Literatúra

1. Algebra. 7. trieda. Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

2. Algebra. 8. trieda. Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

3. Algebra. 9. ročník Časť 1. Učebnica pre vzdelávacie inštitúcie / A.G. Mordkovič. Moskva: Mnemosyne, 2007.

4. Glazer G.I. História matematiky v škole. VII-VIII triedy. - M.: Osveta, 1982.

5. Časopis Matematika №5 2009; č. 8 2007; č. 23 2008.

6. Grafické riešenie rovníc Internetové stránky: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3-6.htm.

Jedným zo spôsobov riešenia rovníc je grafická metóda. Je založená na vykresľovaní funkcií a určovaní ich priesečníkov. Zvážte grafický spôsob riešenia kvadratickej rovnice a*x^2+b*x+c=0.

Prvý spôsob riešenia

Premenme rovnicu a*x^2+b*x+c=0 na tvar a*x^2 =-b*x-c. Zostavíme grafy dvoch funkcií y= a*x^2 (parabola) a y=-b*x-c (priamka). Hľadajte priesečníky. Riešením rovnice budú úsečky priesečníkov.

Ukážme si to na príklade: vyriešiť rovnicu x^2-2*x-3=0.

Transformujme to na x^2 =2*x+3. Zostavíme grafy funkcií y= x^2 a y=2*x+3 v jednom súradnicovom systéme.

Grafy sa pretínajú v dvoch bodoch. Ich úsečky budú koreňmi našej rovnice.

Formulačný roztok

Aby sme boli presvedčiví, toto riešenie skontrolujeme analyticky. Kvadratickú rovnicu riešime podľa vzorca:

D = 4-4*1*(-3) = 16.

X1= (2+4)/2*1 = 3.

X2 = (2-4)/2*1 = -1.

znamená, riešenia sa zhodujú.

Grafický spôsob riešenia rovníc má aj svoju nevýhodu, s pomocou ktorej nie je vždy možné získať presné riešenie rovnice. Skúsme vyriešiť rovnicu x^2=3+x.

Zostrojme parabolu y=x^2 a priamku y=3+x v rovnakom súradnicovom systéme.

Opäť dostal podobný obrázok. Priamka a parabola sa pretínajú v dvoch bodoch. Nemôžeme však povedať presné hodnoty úsečiek týchto bodov, iba približné: x≈-1,3 x≈2,3.

Ak sme spokojní s odpoveďami s takou presnosťou, môžeme použiť túto metódu, ale to sa stáva zriedka. Zvyčajne sú potrebné presné riešenia. Preto sa grafická metóda používa len zriedka a hlavne na kontrolu existujúcich riešení.

Potrebujete pomôcť so štúdiom?

Predchádzajúca téma:

Výskumné práce študentov na tému:

"Aplikácia lineárnej funkcie pri riešení problémov"

"Aplikácia grafu lineárnych funkcií na riešenie problémov"

MKOU "Bogucharskaya stredná škola č. 1"

Výskumná práca v matematike.

Téma: "Aplikácia grafu lineárnej funkcie na riešenie problémov"

7 trieda "B".
Vedúci: Fomenko Olga Mikhailovna

mesto Boguchar

1. Úvod……………………………………………………………………………… 2

2. Hlavná časť……………………………………………………………………… 3-11

2.1 Technika riešenia textových úloh pomocou grafov lineárnych funkcií

2.2Riešenie textových úloh pre pohyb pomocou grafov

3. Záver……………………………………………………………………………… 11

4. Literatúra………………………………………………………………………………..12

ÚVOD

„Trieda Algebra.7“ uvažuje o úlohách, v ktorých je podľa daného rozvrhu potrebné odpovedať na množstvo otázok.

Napríklad:

№332 Letný obyvateľ išiel z domu autom do dediny. Najprv išiel po diaľnici a potom po poľnej ceste, pričom pri tom spomalil. Harmonogram pohybu letného rezidenta je znázornený na obrázku. Odpovedz na otázku:

a) ako dlho jazdil letný obyvateľ po diaľnici a koľko kilometrov najazdil; aká bola rýchlosť auta na tomto úseku cesty;

b) ako dlho jazdil letný obyvateľ po poľnej ceste a koľko kilometrov najazdil; aká bola rýchlosť auta v tomto úseku;

c) ako dlho cestoval letný obyvateľ celú cestu z domu do dediny?

Pri hľadaní materiálu na túto tému v literatúre a na internete som sám zistil, že mnohé fyzikálne, ba aj sociálne a ekonomické javy a procesy sú vo svete v lineárnom vzťahu, ale ustálil som sa na hnutí, ako napr. najznámejší a najobľúbenejší medzi nami všetkými. V projekte som opísal slovné úlohy a spôsob ich riešenia pomocou grafov lineárnych funkcií.

hypotéza: pomocou grafov môžete nielen vizuálne znázorniť vlastnosti funkcie, zoznámiť sa s vlastnosťami lineárnej funkcie a jej konkrétneho tvaru, priamou úmernosťou, ale aj riešiť slovné úlohy.

Cieľom môjho výskumu bola náuka o využití grafov lineárnej funkcie pri riešení textových úloh pre pohyb. Aby sa dosiahli tieto ciele, nasledujúce úlohy:

Študovať metodiku riešenia textových úloh pre pohyb pomocou grafov lineárnych funkcií;

Naučte sa riešiť problémy s pohybom pomocou tejto metódy;

Urobte porovnávacie závery o výhodách a nevýhodách riešenia úloh pomocou grafov lineárnych funkcií.

Predmet štúdia: graf lineárnej funkcie.

Metóda výskumu:

Teoretické (štúdium a analýza), vyhľadávanie v systéme, praktické.

Hlavná časť.

Vo svojom výskume som sa rozhodol pokúsiť sa o grafickú interpretáciu pohybových úloh prezentovaných v našej učebnici a následne podľa harmonogramu odpovedať na otázku úlohy. Na takéto riešenie som zobral úlohy s priamočiarym rovnomerným pohybom na jednom úseku dráhy. Ukázalo sa, že mnohé úlohy sa takto riešia jednoduchšie ako bežným spôsobom pomocou rovnice. Jedinou nevýhodou tejto techniky je to, že na presné získanie odpovede na otázku problému je potrebné správne zvoliť rozsah jednotiek merania na súradnicových osiach. Veľkú úlohu pri správnom výbere tejto škály zohráva skúsenosť s riešením. Preto, aby som si osvojil umenie riešenia problémov pomocou grafov, musel som ich zvažovať vo veľkom počte.

nastavte súradnicový systém sOt so súradnicovou osou Ot a súradnicovou osou Os. Na to je potrebné podľa stavu problému zvoliť počiatok: začiatok pohybu objektu alebo z viacerých objektov, vyberie sa ten, ktorý sa začal pohybovať skôr alebo prekonal väčšiu vzdialenosť. Na vodorovnej osi vyznačte časové intervaly v jeho meracích jednotkách a na zvislej osi označte vzdialenosť vo zvolenej mierke jeho meracích jednotiek.

Body na súradnicovej rovine musia byť označené podľa mierky úlohy a čiary musia byť nakreslené presne. Od toho závisí presnosť riešenia problému. Preto je veľmi dôležité úspešne zvoliť mierku delenia na súradnicových osiach: treba ju voliť tak, aby súradnice bodov boli určené presnejšie a podľa možnosti umiestnené v uzlových bodoch, t.j. v priesečníkoch delení súradnicových osí. Niekedy je užitočné vziať ako jednotkový segment na vodorovnej osi počet buniek, ktorý je násobkom podmienok problému vzhľadom na čas, a na zvislej osi - počet buniek, ktorý je násobkom podmienok. problému s ohľadom na vzdialenosť. Napríklad 12 minút v čase vyžaduje výber počtu buniek v násobkoch 5, pretože 12 minút je jedna pätina hodiny.

Riešenie textových úloh pre pohyb pomocou grafov

Odpoveď: 9 km.

Riešenie pomocou rovnice:

x/12h. - čas z A do B

x/18h. - späť čas

Odpoveď: 9 km

Úloha 2. (č. 156 v učebnici Yu.N. Makarycheva "Algebra 7".)

Dve autá idú po diaľnici rovnakou rýchlosťou. Ak prvý zvýši rýchlosť o 10 km/h a druhý zníži o 10 km/h, tak prvý prejde toľko za 2 hodiny ako druhý za 3 hodiny. Ako rýchlo idú autá?

Riešenie pomocou rovnice:

Nech x km/h je rýchlosť áut;

(x+10) a (x-10) rýchlosť po zvýšení a znížení;

2(x+10)=3(x-10)

Odpoveď: 50 km/h

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavme súradnicovú rovinu sOt s osou Оt, na ktorej vyznačíme časové intervaly pohybu, a osou Os, na ktorej vyznačíme prejdenú vzdialenosť vozidiel.

2. Položme dieliky na stupnici pozdĺž osi x - jedna hodina v 5 bunkách (v 1 bunke - 12 minút); aplikujeme delenie pozdĺž osi y, ale neuvádzame mierku.

3. Postavme líniu pohybu prvého auta I: začiatok pohybu v bode c

4. Postavme líniu pohybu druhého stroja II: začiatok pohybu v bode so súradnicou (0; 0). Ďalej na rovine označíme ľubovoľný bod (3;s 1), pretože auto s novou rýchlosťou bolo na ceste 3 hodiny.

4. Určme rýchlosť áut v pred jej zmenou. Označme rozdiel súradníc bodov ležiacich na priamkach s osou 1 znamienkom ∆s . Tento segment podľa stavu zodpovedá dĺžke (10 + 10) km, pretože v jednom z nich sa rýchlosť znížila a v druhom sa rýchlosť zvýšila o 10 km/h. To znamená, že línia pohybu automobilov pred zmenou rýchlosti by mala byť rovnako vzdialená od čiar I a II a mala by sa nachádzať v rovine súradníc medzi nimi.. Podľa harmonogramu Δs \u003d 2cl. zodpovedá 20 km, v = 5 buniek, riešime teda podiel v = 50 km/h.

Odpoveď: 50 km/h.

Úloha 3

Riešenie pomocou grafu lineárnych funkcií:

referenčným bodom je mólo M

označte bod N (0; 162).

Odpoveď: 2 hodiny 20 minút.

Riešenie pomocou rovnice:

162-45(x+0,75)-36x=0

162-45x - 33,75 -36x = 0

81x = 128,25

2)

Odpoveď: 2 hodiny 20 minút.

Úloha 4.

Cyklista odišiel z bodu A. Zároveň za ním z bodu B, ktorý je od A vzdialený 20 km, odišiel motorkár 16 km/h. Cyklista išiel rýchlosťou 12 km/h. V akej vzdialenosti od bodu A predbehne motocyklista cyklistu?

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavme súradnicovú rovinu sOt so súradnicovou osou Ot, na ktorej vyznačíme časové intervaly pohybu, a osou y Os, na ktorej vyznačíme prejdenú vzdialenosť motocyklistu a cyklistu.

2. Nakreslíme delenia v mierke: pozdĺž osi y - v 2 bunkách 8 km; pozdĺž úsečky - v 2 bunkách - 1h.

3. Postavme líniu pohybu motorkára II: začiatok jeho pohybu označíme v počiatku súradníc B (0; 0). Motocyklista išiel rýchlosťou 16 km/h, čiže bodom so súradnicami (1; 16) musí prechádzať rovinka II.

4. Postavme čiaru pohybu cyklistu I: jej začiatok bude v bode A (0; 20), pretože bod B sa nachádza vo vzdialenosti 20 km od bodu A, pričom odišiel v rovnakom čase ako motocyklista. Cyklista išiel rýchlosťou 12 km/h, čo znamená, že čiara musím prejsť bodom so súradnicami (1; 32).

5. Nájdite P (5; 80) - priesečník čiar I a II, odrážajúci pohyb motocyklistu a cyklistu: na jeho ordináte bude vzdialenosť od bodu B, v ktorej motocyklista dobehne cyklistu. .

P(5; 80) |=s = 80, |=80 - 20 = 60(km) - vzdialenosť od bodu A, v ktorej motocyklista dobehne cyklistu..

Odpoveď: 60 km.

Riešenie pomocou rovnice:

Nech x km je vzdialenosť od bodu A k bodu stretnutia

x /12 čas cyklistu

(x +20)/16 čas motocyklistu

x/12=(x +20)/16

16x=12x+240

4x = 240

x = 60

Odpoveď: 60 km

Úloha 5.

Vzdialenosť medzi mestami prekonal motocyklista za 2 hodiny, cyklista za 5 hodín Rýchlosť cyklistu je o 18 km/h nižšia ako rýchlosť motocyklistu. Nájdite rýchlosť cyklistu a motocyklistu a vzdialenosť medzi mestami.

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavíme súradnicovú rovinu sOt so súradnicovou osou Ot, na ktorej vyznačíme časové intervaly pohybu, a osou y Os, na ktorej vyznačíme vzdialenosť.

2. Vložíme delenie pozdĺž osi x do 2 buniek na 1 hodinu, vzdialenosť necháme bez delenia pozdĺž osi y.

3. Narysujme čiaru pohybu I cyklistu za 5 hodín a čiaru pohybu motocyklistu II za 2 hodiny. Koniec oboch riadkov musí mať rovnakú ordinátu.

4. Nakreslíme úsečku s osou 1 medzi čiarami I a II. Dĺžka tohto úseku odráža vzdialenosť rovnajúcu sa 18 km. Z nákresu dostaneme, že 3 bunky sa rovnajú 18 km, čo znamená, že v 1 bunke je 6 km.

5. Potom podľa rozpisu určíme rýchlosť cyklistu 12 km/h, rýchlosť motocyklistu 30 km/h, vzdialenosť medzi mestami 60 km.

Riešenie pomocou rovnice:

Nech x km/h je rýchlosť cyklistu, potom (x +18) km/h rýchlosť motocyklistu

2(x+18)=5x

2x +36=5x

x=12

2) 12+18=30(km/h) rýchlosť jazdca

3) (km) vzdialenosť medzi mestami

Odpoveď: 12 km/h; 30 km/h; 60 km

Odpoveď: 60 km.

Úloha 6.

Loď prejde pozdĺž rieky vzdialenosť 30 km za 3 hodiny a 20 minút a 28 km proti prúdu za 4 hodiny. Ako ďaleko prejde loď jazero za 1,5 hodiny?

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavíme súradnicovú rovinu sOt so súradnicovou osou Ot, na ktorej vyznačíme časové intervaly pohybu, a osou y Os, na ktorej vyznačíme prejdenú vzdialenosť člna.

2. Nakreslíme delenia v mierke: pozdĺž osi y - v dvoch bunkách 4 km; pozdĺž osi x - v 6 bunkách - 1 hodina (v 1 bunke - 10 minút), pretože podľa stavu problému sa čas udáva v minútach.

3. Postavme čiaru pohybu člna po rieke I: začiatok čiary bude v bode so súradnicou (0; 0). Loď prepláva 30 km za 3 hodiny a 20 minút, čo znamená, že čiara musí prechádzať bodom so súradnicou (; 30), pretože 3 h 20 min. = h.

4. Postavme líniu pohybu člna proti prúdu rieky II: začiatok pohybu vezmeme v bode so súradnicou (0; 0). Loď prepláva 28 km za 4 hodiny, čo znamená, že čiara pohybu musí prechádzať bodom so súradnicou (4; 28).

5. Postavme líniu pohybu člna na jazere: začiatok pohybu vezmeme v bode so súradnicou (0; 0). Čiara vlastného pohybu lode bude musieť byť umiestnená v rovnakej vzdialenosti medzi líniami pohybu lode pozdĺž rieky. To znamená, že segment pozostávajúci zo všetkých bodov s osou 1 medzi čiarami pohybu pozdĺž rieky musíme rozdeliť na polovicu a označiť jeho stred. Od (0; 0) cez tento vyznačený bod nakreslíme lúč, ktorý bude líniou pohybu pozdĺž jazera.

6. Podľa stavu problému je potrebné nájsť vzdialenosť prejdenú loďou na jazere za 1,5 hodiny, čo znamená, že na tejto čiare musíme určiť súradnicu bodu s osou t \u003d 1,5, | \u003d s \u003d 12, | \u003d 12 km 1,5 hodiny.

Odpoveď: 12 km.

Riešenie pomocou sústavy rovníc:

Nech x km/h je rýchlosť jazera a y km/h rýchlosť rieky

Odpoveď: 12 km.

Úloha 7.

Loď prejde po rieke 34 km za rovnaký čas ako 26 km proti prúdu. Vlastná rýchlosť člna je 15 km/h. Nájdite rýchlosť rieky.

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavíme súradnicovú rovinu sOt so súradnicovou osou Ot, na ktorej vyznačíme časové intervaly pohybu, a osou y Os, na ktorej vyznačíme vzdialenosť prejdenú člnom.

2. Nakreslíme delenia v mierke: pozdĺž osi y - v 1 bunke 1 km; na osi x ponecháme čas bez delenia.

3. Postavme čiaru I pohybu lode po rieke z 0 km do bodu 34 km: začiatok čiary bude v bode so súradnicou (0; 0). Druhá súradnica bude (x ; 34).

4. Postavme čiaru II pohybu člna proti prúdu rieky od 0 km do bodu 26 km: začiatok čiary bude v bode so súradnicou (0; 0). Druhá súradnica bude ( x; 26).

5. Nakreslite lúč III z počiatku (0; 0) cez stred ľubovoľného segmentu pozostávajúceho zo všetkých bodov s rovnakou osou medzi dvoma pohybovými čiarami I a II. Tento lúč bude odrážať vlastný pohyb člna, napr vlastná rýchlosť lode je aritmetický priemer 2 rýchlostí proti prúdu a po prúde rieky. Na výslednom nosníku nájdeme bod s ordinátou 15, pretože vlastná rýchlosť člna je 15 km/h. Abscisa nájdeného bodu bude zodpovedať deleniu 1 hodiny.

6. Na zistenie rýchlosti rieky stačí nájsť dĺžku úseku s osou 1 od čiary III po čiaru II. Rýchlosť rieky je 2 km / h.

Odpoveď: 2 km/h

Riešenie pomocou rovnice:

Rýchlosť rieky x km/h

34 / (15 + x) \u003d 26 / (15-x) Vyriešením pomeru dostaneme:

Odpoveď: 2 km/h

Záver.

výhody:

Úlohy možno stručne zapísať;

Nevýhody:

LITERATÚRA.

1. Makarychev Yu. N., Mindyuk N. G., Neshkov K. I., Suvorova S. B., Algebra: Učebnica pre 7. ročník vzdelávacích inštitúcií, „Prosveshchenie“, M., 2000.

2.Bulynin V., Využitie grafických metód pri riešení textových úloh, vzdelávacie a metodické noviny "Matematika", č.14, 2005.

3. Zvavich L.I. Didaktické materiály o algebre pre 7. ročník.

Zobraziť obsah dokumentu
"slová"

Na hodinách algebry v 7. ročníku som sa zoznámil s témou „Lineárna funkcia. Vzájomné usporiadanie grafov lineárnych funkcií. Naučil som sa zostavovať grafy lineárnej funkcie, naučil som sa jej vlastnosti, naučil som sa určovať relatívnu polohu grafov pomocou daných vzorcov. Všimol som si, že v učebnici Yu.N. Makarycheva

„Trieda Algebra.7“ uvažuje o úlohách, v ktorých je podľa daného rozvrhu potrebné odpovedať na množstvo otázok. Príklad takejto úlohy je uvedený na snímke.

Podľa daného harmonogramu sa dá určiť, že

A mal som otázku, je možné riešiť úlohy pre pohyb nie akciami alebo pomocou rovníc, ale použiť na to grafiku lineárnej funkcie?

Na snímke sú prezentované hypotézy, ciele a zámery

Vo svojom výskume som sa rozhodol pokúsiť sa o grafickú interpretáciu pohybových úloh prezentovaných v našej učebnici a následne podľa harmonogramu odpovedať na otázku úlohy. Na takéto riešenie som zobral úlohy s priamočiarym rovnomerným pohybom na jednom úseku dráhy.

Ukázalo sa, že mnohé problémy sa riešia práve týmto spôsobom. Jedinou nevýhodou tejto techniky je to, že na presné získanie odpovede na otázku problému je potrebné správne zvoliť rozsah jednotiek merania na súradnicových osiach. Veľkú úlohu pri správnom výbere tejto škály zohráva skúsenosť s riešením. Preto, aby som si osvojil umenie riešenia problémov pomocou grafov, musel som ich zvažovať vo veľkom počte.

Technika riešenia textových úloh pomocou grafov lineárnych funkcií.

Ak chcete vyriešiť textový problém pomocou grafov lineárnych funkcií, musíte:

nastaviť súradnicový systém Na to je potrebné podľa stavu problému zvoliť počiatok: vyberie sa začiatok pohybu objektu alebo z viacerých objektov, vyberie sa ten, ktorý sa začal pohybovať skôr alebo prekonal väčšiu vzdialenosť . Na vodorovnej osi vyznačte časové intervaly v jeho meracích jednotkách a na zvislej osi označte vzdialenosť vo zvolenej mierke jeho meracích jednotiek.

Nakreslite čiary pohybu každého z objektov špecifikovaných v úlohe cez súradnice aspoň dvoch bodov priamych čiar. Zvyčajne rýchlosť objektu dáva informáciu o prejdení vzdialenosti za jednu jednotku času od začiatku jeho pohybu. Ak sa objekt začne pohybovať neskôr, začiatočný bod jeho pohybu sa posunie o daný počet jednotiek vpravo od začiatku pozdĺž osi x. Ak sa objekt začne pohybovať z miesta vzdialeného od referenčného bodu o určitú vzdialenosť, potom sa bod začiatku jeho pohybu posunie nahor pozdĺž osi y.

Miesto stretnutia viacerých objektov na súradnicovej rovine je označené priesečníkom čiar znázorňujúcich ich pohyb, čo znamená, že súradnice tohto bodu poskytujú informáciu o čase stretnutia a vzdialenosti miesta stretnutia od začiatku.

Rozdiel v rýchlostiach pohybu dvoch objektov je určený dĺžkou segmentu pozostávajúceho zo všetkých bodov s osou 1, ktoré sa nachádzajú medzi čiarami pohybu týchto objektov.

Body na súradnicovej rovine musia byť označené podľa mierky úlohy a čiary musia byť nakreslené presne. Od toho závisí presnosť riešenia problému.

Úloha 1. (č. 673 v učebnici Yu.N. Makarycheva "Algebra 7".)

Cyklista išiel po ceste AB rýchlosťou 12 km/h. Pri návrate vyvinul rýchlosť 18 km/h a na ceste späť strávil o 15 minút menej ako na ceste z A do B. Koľko kilometrov z A do B.

Riešenie pomocou rovnice:

Nech x km je vzdialenosť od A do B.

x/12h. - čas z A do B

x/18h. - späť čas

Keďže na spiatočnej ceste strávil o 15 minút menej, poskladáme rovnicu

Odpoveď: 9 km

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavme súradnicovú rovinu sOtc s vodorovnou osou Ot, na ktorej vyznačíme časové intervaly pohybu a osou y Os, na ktorej vyznačíme vzdialenosť.

2. Nakreslíme delenia v mierke: pozdĺž osi y - v jednej bunke 3 km; pozdĺž osi x - jedna hodina v 4 bunkách (v 1 bunke - 15 min).

3. Postavme tam líniu pohybu: začiatok pohybu označme bodkou (0; 0). Cyklista išiel rýchlosťou 12 km/h, čo znamená, že priamka musí prechádzať bodom (1; 12).

4. Postavme čiaru pohybu späť: koniec čiary označíme bodkou (; 0), pretože cyklista strávil na spiatočnej ceste o 15 minút menej. Išiel rýchlosťou 18 km/h, čo znamená, že nasledujúci bod čiary má súradnicu (;18).

5. Poznámka (; 9) - priesečník čiar: jeho ordináta bude ukazovať vzdialenosť: s = 9

Odpoveď: 9 km.

Úloha 2 (č. 757 v učebnici Yu.N. Makarycheva "Algebra 7")

Vzdialenosť medzi piliermi M a N je 162 km. Motorová loď vyrazila z móla M rýchlosťou 45 km/h. Po 45 minútach z móla N smerom k nemu vyrazila ďalšia motorová loď, ktorej rýchlosť je 36 km/h. Za koľko hodín po odchode prvej lode sa stretnú?

Riešenie pomocou rovnice:

Nech je stretnutie o x hodín

162-45(x+0,75)-36x=0

162-45x - 33,75 -36x = 0

81x = 128,25

2)

Odpoveď: 2 hodiny 20 minút.

Riešenie pomocou grafu lineárnych funkcií:

1. Nastavíme súradnicovú rovinu sOt so súradnicovou osou Ot, na ktorej vyznačíme časové intervaly pohybu, a osou y Os, na ktorej

všimnite si vzdialenosť od móla M k mólu N, ktorá sa rovná 162 km. začiatok

referenčným bodom je mólo M

2. Nakreslíme delenia v mierke: pozdĺž osi y - v dvoch bunkách 18 km; pozdĺž osi x - jedna hodina v 6 bunkách (v 1 bunke - 10 min.), od r. Podmienka úlohy určuje čas v minútach.

označte bod N (0; 162).

3. Postavme líniu pohybu prvej lode I: začiatok jej pohybu bude v bode so súradnicami (0; 0). Prvá loď sa plavila rýchlosťou 45 km/h, čo znamená, že priamka musí prechádzať bodom so súradnicami (1; 45).

4. Postavme líniu pohybu druhej lode II: začiatok pohybu bude v bode c

súradnice (; 162), keďže opustil bod N, vzdialený od M 162 km, 45 min. neskôr ako prvý a 45 min. \u003d h. Druhá loď sa plavila rýchlosťou 36 km/h, čo znamená, že priamka musí prechádzať bodom (; 126), keďže druhá loď odišla v smere bodu M: 162 - 36 \ u003d 126 (km).

5. Priesečník čiar I a II je bod A (; 108). Abcisa bodu ukazuje čas, po ktorom sa po odchode prvej lode stretli: t =, |=h = 2h20min. - čas stretnutia dvoch lodí po odchode prvej lode.

Odpoveď: 2 hodiny 20 minút.

Záver.

Na konci štúdia sa mi podarilo identifikovať výhody a nevýhody grafického riešenia úloh.

výhody:

Úlohy možno stručne zapísať;

Je celkom jednoduché pracovať s malými číslami.

Nevýhody:

Je ťažké pracovať s veľkými číslami.

Zobraziť obsah prezentácie
"projekt"