Ano ang logarithm?

Pansin!
May mga karagdagang
materyal sa Espesyal na Seksyon 555.
Para sa mga malakas na "hindi masyadong..."
At para sa mga "sobra...")

Ano ang logarithm? Paano malutas ang mga logarithms? Ang mga tanong na ito ay nakalilito sa maraming nagtapos. Ayon sa kaugalian, ang paksa ng logarithms ay itinuturing na kumplikado, hindi maintindihan at nakakatakot. Lalo na - mga equation na may logarithms.

Ito ay ganap na hindi totoo. Ganap! ayaw maniwala? Mabuti. Ngayon, sa loob ng mga 10 - 20 minuto:

1. Intindihin ano ang logarithm.

2. Matutong lutasin ang isang buong klase ng mga exponential equation. Kahit na hindi mo pa naririnig ang tungkol sa kanila.

3. Matutong magkalkula ng mga simpleng logarithms.

Bukod dito, para dito kakailanganin mo lamang malaman ang talahanayan ng pagpaparami, at kung paano itataas ang isang numero sa isang kapangyarihan ...

Pakiramdam ko ay nagdududa ka ... Well, panatilihin ang oras! Go!

Una, lutasin ang sumusunod na equation sa iyong isip:

Kung gusto mo ang site na ito...

Siyanga pala, mayroon akong ilang mas kawili-wiling mga site para sa iyo.)

Maaari kang magsanay sa paglutas ng mga halimbawa at alamin ang iyong antas. Pagsubok na may agarang pag-verify. Pag-aaral - nang may interes!)

maaari kang maging pamilyar sa mga function at derivatives.

Kaugnay sa

ang gawain ng paghahanap ng alinman sa tatlong numero mula sa iba pang dalawa, na ibinigay, ay maaaring itakda. Ang ibinigay na a at pagkatapos ay ang N ay matatagpuan sa pamamagitan ng exponentiation. Kung ang N ay ibinigay at pagkatapos ay ang a ay matatagpuan sa pamamagitan ng pagkuha ng ugat ng kapangyarihan x (o exponentiation). Ngayon isaalang-alang ang kaso kapag, ibinigay ang a at N, ito ay kinakailangan upang mahanap ang x.

Hayaang maging positibo ang bilang N: ang bilang a ay positibo at hindi katumbas ng isa: .

Kahulugan. Ang logarithm ng numero N sa base a ay ang exponent kung saan kailangan mong itaas ang a upang makuha ang numerong N; ang logarithm ay tinutukoy ng

Kaya, sa pagkakapantay-pantay (26.1), ang exponent ay matatagpuan bilang logarithm ng N sa base a. Mga entry

may parehong kahulugan. Ang pagkakapantay-pantay (26.1) ay kung minsan ay tinatawag na pangunahing pagkakakilanlan ng teorya ng logarithms; sa katunayan, ito ay nagpapahayag ng kahulugan ng konsepto ng logarithm. Sa pamamagitan ng kahulugang ito, ang base ng logarithm a ay palaging positibo at naiiba sa pagkakaisa; ang logarithmable number N ay positibo. Ang mga negatibong numero at zero ay walang logarithms. Mapapatunayan na ang anumang numero na may ibinigay na base ay may mahusay na tinukoy na logarithm. Samakatuwid ang pagkakapantay-pantay ay nagsasangkot ng . Tandaan na ang kondisyon ay mahalaga dito, kung hindi, ang konklusyon ay hindi makatwiran, dahil ang pagkakapantay-pantay ay totoo para sa anumang mga halaga ng x at y.

Halimbawa 1. Hanapin

Solusyon. Upang makuha ang numero, kailangan mong itaas ang base 2 sa kapangyarihan Samakatuwid.

Maaari kang mag-record kapag nilulutas ang mga naturang halimbawa sa sumusunod na form:

Halimbawa 2. Hanapin .

Solusyon. Meron kami

Sa mga halimbawa 1 at 2, madali naming natagpuan ang nais na logarithm sa pamamagitan ng pagre-represent sa logarithmable na numero bilang isang antas ng base na may rational exponent. Sa pangkalahatang kaso, halimbawa, para sa atbp., hindi ito magagawa, dahil ang logarithm ay may hindi makatwirang halaga. Bigyang-pansin natin ang isang tanong na may kaugnayan sa pahayag na ito. Sa § 12 ibinigay namin ang konsepto ng posibilidad ng pagtukoy ng anumang tunay na kapangyarihan ng isang naibigay na positibong numero. Ito ay kinakailangan para sa pagpapakilala ng mga logarithms, na, sa pangkalahatan, ay maaaring hindi makatwiran na mga numero.

Isaalang-alang ang ilang mga katangian ng logarithms.

Property 1. Kung ang numero at base ay pantay, kung gayon ang logarithm ay katumbas ng isa, at, sa kabaligtaran, kung ang logarithm ay katumbas ng isa, kung gayon ang numero at base ay pantay.

Patunay. Hayaan Sa pamamagitan ng kahulugan ng logarithm, mayroon tayo at saan

Sa kabaligtaran, hayaan ang Pagkatapos sa pamamagitan ng kahulugan

Property 2. Ang logarithm ng pagkakaisa sa anumang base ay katumbas ng zero.

Patunay. Sa pamamagitan ng kahulugan ng logarithm (ang zero na kapangyarihan ng anumang positibong base ay katumbas ng isa, tingnan ang (10.1)). Mula rito

Q.E.D.

Ang kabaligtaran na pahayag ay totoo rin: kung , kung gayon N = 1. Sa katunayan, mayroon tayong .

Bago sabihin ang sumusunod na katangian ng logarithms, sumang-ayon tayo na ang dalawang numero a at b ay nasa magkabilang panig ng ikatlong numero c kung pareho silang mas malaki sa c o mas mababa sa c. Kung ang isa sa mga numerong ito ay mas malaki kaysa sa c at ang isa ay mas mababa sa c, pagkatapos ay sinasabi namin na sila ay nakahiga sa magkabilang panig ng c.

Ari-arian 3. Kung ang numero at base ay nasa parehong panig ng pagkakaisa, ang logarithm ay positibo; kung ang numero at base ay nasa magkabilang panig ng pagkakaisa, kung gayon ang logarithm ay negatibo.

Ang patunay ng property 3 ay batay sa katotohanan na ang antas ng a ay mas malaki kaysa sa isa kung ang base ay mas malaki kaysa sa isa at ang exponent ay positibo, o ang base ay mas mababa sa isa at ang exponent ay negatibo. Ang antas ay mas mababa sa isa kung ang base ay mas malaki sa isa at ang exponent ay negatibo, o ang base ay mas mababa sa isa at ang exponent ay positibo.

Mayroong apat na kaso na dapat isaalang-alang:

Ikinukulong namin ang aming sarili sa pagsusuri ng una sa kanila, isasaalang-alang ng mambabasa ang natitira sa kanyang sarili.

Hayaang ang exponent sa pagkakapantay-pantay ay hindi negatibo o katumbas ng zero, samakatuwid, ito ay positibo, ibig sabihin, na kinakailangang patunayan.

Halimbawa 3. Alamin kung alin sa mga sumusunod na logarithms ang positibo at alin ang negatibo:

Solusyon, a) dahil ang numero 15 at ang base 12 ay matatagpuan sa parehong bahagi ng yunit;

b) , dahil ang 1000 at 2 ay matatagpuan sa parehong bahagi ng yunit; sa parehong oras, hindi mahalaga na ang base ay mas malaki kaysa sa logarithmic number;

c), dahil ang 3.1 at 0.8 ay nasa magkabilang panig ng pagkakaisa;

G); bakit?

e); bakit?

Ang mga sumusunod na katangian 4-6 ay madalas na tinatawag na mga panuntunan ng logarithm: pinapayagan nila, alam ang logarithms ng ilang mga numero, upang mahanap ang logarithms ng kanilang produkto, quotient, degree ng bawat isa sa kanila.

Property 4 (ang panuntunan para sa logarithm ng produkto). Ang logarithm ng produkto ng ilang positibong numero sa isang ibinigay na base ay katumbas ng kabuuan ng logarithms ng mga numerong ito sa parehong base.

Patunay. Hayaang maibigay ang mga positibong numero.

Para sa logarithm ng kanilang produkto, isinusulat namin ang pagkakapantay-pantay (26.1) na tumutukoy sa logarithm:

Mula dito makikita natin

Ang paghahambing ng mga exponents ng una at huling mga expression, makuha namin ang kinakailangang pagkakapantay-pantay:

Tandaan na ang kondisyon ay mahalaga; ang logarithm ng produkto ng dalawang negatibong numero ay may katuturan, ngunit sa kasong ito nakukuha natin

Sa pangkalahatan, kung ang produkto ng ilang mga kadahilanan ay positibo, kung gayon ang logarithm nito ay katumbas ng kabuuan ng mga logarithms ng mga module ng mga salik na ito.

Property 5 (quotient logarithm rule). Ang logarithm ng isang quotient ng mga positibong numero ay katumbas ng pagkakaiba sa pagitan ng logarithms ng dibidendo at ng divisor, na kinuha sa parehong base. Patunay. Patuloy na paghahanap

Q.E.D.

Property 6 (panuntunan ng logarithm ng degree). Ang logarithm ng kapangyarihan ng anumang positibong numero ay katumbas ng logarithm ng numerong iyon na beses ang exponent.

Patunay. Isinulat namin muli ang pangunahing pagkakakilanlan (26.1) para sa numero :

Q.E.D.

Bunga. Ang logarithm ng root ng isang positibong numero ay katumbas ng logarithm ng root number na hinati sa exponent ng root:

Mapapatunayan natin ang bisa ng corollary na ito sa pamamagitan ng paglalahad kung paano at paggamit ng property 6.

Halimbawa 4. Logarithm sa base a:

a) (pinapalagay na ang lahat ng mga halaga b, c, d, e ay positibo);

b) (pinapalagay na ).

Solusyon, a) Maginhawang ipasa ang expression na ito sa mga fractional na kapangyarihan:

Batay sa mga pagkakapantay-pantay (26.5)-(26.7) maaari na nating isulat ang:

Napansin namin na ang mga mas simpleng operasyon ay ginagawa sa mga logarithms ng mga numero kaysa sa mga numero mismo: kapag nagpaparami ng mga numero, ang kanilang mga logarithm ay idinagdag, kapag hinati, sila ay ibabawas, atbp.

Kaya naman ginamit ang logarithms sa computational practice (tingnan ang Sec. 29).

Ang aksyon na kabaligtaran sa logarithm ay tinatawag na potentiation, ibig sabihin: ang potentiation ay ang aksyon kung saan ang numerong ito mismo ay matatagpuan sa pamamagitan ng ibinigay na logarithm ng isang numero. Sa esensya, ang potentiation ay hindi anumang espesyal na aksyon: ito ay bumababa sa pagtaas ng base sa isang kapangyarihan (katumbas ng logarithm ng numero). Ang terminong "potentiation" ay maaaring ituring na kasingkahulugan ng terminong "exponentiation".

Kapag potentiating, kinakailangang gamitin ang mga panuntunan na kabaligtaran sa mga panuntunan ng logarithm: palitan ang kabuuan ng logarithm ng logarithm ng produkto, ang pagkakaiba ng logarithm sa logarithm ng quotient, atbp. Sa partikular, kung mayroong anumang kadahilanan sa harap ng sign ng logarithm, pagkatapos ay sa panahon ng potentiation dapat itong ilipat sa indicator degrees sa ilalim ng sign ng logarithm.

Halimbawa 5. Hanapin ang N kung alam na

Solusyon. Kaugnay ng potentiation rule na kasasabi pa lang, ang mga salik na 2/3 at 1/3, na nasa harap ng mga palatandaan ng logarithms sa kanang bahagi ng pagkakapantay-pantay na ito, ay ililipat sa mga exponent sa ilalim ng mga palatandaan ng logarithms na ito; nakukuha namin

Ngayon ay pinapalitan namin ang pagkakaiba ng logarithms sa logarithm ng quotient:

para makuha ang huling fraction sa chain of equalities na ito, pinalaya namin ang nakaraang fraction mula sa irrationality sa denominator (seksyon 25).

Pag-aari 7. Kung ang base ay mas malaki kaysa sa isa, kung gayon ang mas malaking bilang ay may mas malaking logarithm (at ang mas maliit ay may mas maliit), kung ang base ay mas mababa sa isa, kung gayon ang mas malaking numero ay may mas maliit na logarithm (at ang mas maliit ang isa ay may mas malaki).

Ang ari-arian na ito ay binabalangkas din bilang panuntunan para sa logarithm ng mga hindi pagkakapantay-pantay, na parehong positibo ang mga bahagi:

Kapag kinukuha ang logarithm ng mga hindi pagkakapantay-pantay na may base na mas malaki kaysa sa isa, ang tanda ng hindi pagkakapantay-pantay ay pinapanatili, at kapag kumukuha ng logarithm na may base na mas mababa sa isa, ang tanda ng hindi pagkakapantay-pantay ay nababaligtad (tingnan din ang aytem 80).

Ang patunay ay batay sa mga katangian 5 at 3. Isaalang-alang ang kaso kapag Kung , pagkatapos at, sa pagkuha ng logarithm, nakuha namin

(a at N/M ay nasa parehong panig ng pagkakaisa). Mula rito

Kaso a ang mga sumusunod, ang mambabasa ang mag-iisip nito para sa kanyang sarili.

Ang mga logarithm, tulad ng anumang numero, ay maaaring idagdag, ibawas at i-convert sa lahat ng posibleng paraan. Ngunit dahil ang logarithms ay hindi masyadong ordinaryong mga numero, may mga panuntunan dito, na tinatawag pangunahing katangian.

Dapat mong malaman ang mga patakarang ito - walang seryosong problema sa logarithmic ang malulutas kung wala ang mga ito. Bilang karagdagan, napakakaunti sa kanila - lahat ay maaaring matutunan sa isang araw. Kaya simulan na natin.

Pagdaragdag at pagbabawas ng logarithms

Isaalang-alang ang dalawang logarithms na may parehong base: log a x at mag-log a y. Pagkatapos ay maaari silang idagdag at ibawas, at:

1. log a x+log a y= log a (x · y);
2. log a x−log a y= log a (x : y).

Kaya, ang kabuuan ng logarithms ay katumbas ng logarithm ng produkto, at ang pagkakaiba ay ang logarithm ng quotient. Mangyaring tandaan: ang pangunahing punto dito ay - parehong batayan. Kung ang mga base ay iba, ang mga patakarang ito ay hindi gagana!

Tutulungan ka ng mga formula na ito na kalkulahin ang logarithmic expression kahit na hindi isinasaalang-alang ang mga indibidwal na bahagi nito (tingnan ang aralin na "Ano ang logarithm"). Tingnan ang mga halimbawa at tingnan:

log 6 4 + log 6 9.

Dahil ang mga base ng logarithms ay pareho, ginagamit namin ang sum formula:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Isang gawain. Hanapin ang halaga ng expression: log 2 48 − log 2 3.

Ang mga base ay pareho, ginagamit namin ang formula ng pagkakaiba:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Isang gawain. Hanapin ang halaga ng expression: log 3 135 − log 3 5.

Muli, ang mga base ay pareho, kaya mayroon kaming:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Tulad ng nakikita mo, ang mga orihinal na expression ay binubuo ng "masamang" logarithms, na hindi isinasaalang-alang nang hiwalay. Ngunit pagkatapos ng mga pagbabago, medyo normal na mga numero ang lumabas. Maraming pagsubok ang nakabatay sa katotohanang ito. Oo, ang kontrol - ang mga katulad na expression sa lahat ng kabigatan (minsan - na halos walang pagbabago) ay inaalok sa pagsusulit.

Pag-alis ng exponent mula sa logarithm

Ngayon pasimplehin natin ng kaunti ang gawain. Paano kung may degree sa base o argumento ng logarithm? Kung gayon ang exponent ng degree na ito ay maaaring alisin sa sign ng logarithm ayon sa mga sumusunod na patakaran:

Madaling makita na ang huling panuntunan ay sumusunod sa kanilang unang dalawa. Ngunit ito ay mas mahusay na tandaan ito pa rin - sa ilang mga kaso ito ay makabuluhang bawasan ang halaga ng mga kalkulasyon.

Siyempre, ang lahat ng mga patakarang ito ay may katuturan kung ang ODZ logarithm ay sinusunod: a > 0, a ≠ 1, x> 0. At isa pang bagay: matutong ilapat ang lahat ng mga formula hindi lamang mula kaliwa hanggang kanan, kundi pati na rin sa kabaligtaran, i.e. maaari mong ipasok ang mga numero bago ang sign ng logarithm sa logarithm mismo. Ito ang madalas na kinakailangan.

Isang gawain. Hanapin ang halaga ng expression: log 7 49 6 .

Tanggalin natin ang antas sa argumento ayon sa unang formula:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Isang gawain. Hanapin ang halaga ng expression:

[Figure caption]

Tandaan na ang denominator ay isang logarithm na ang base at argumento ay eksaktong kapangyarihan: 16 = 2 4 ; 49 = 72. Meron kami:

[Figure caption]

Sa tingin ko ang huling halimbawa ay nangangailangan ng paglilinaw. Saan napunta ang logarithms? Hanggang sa pinakahuling sandali, nagtatrabaho lamang kami sa denominator. Iniharap nila ang base at argumento ng logarithm na nakatayo doon sa anyo ng mga degree at kinuha ang mga tagapagpahiwatig - nakakuha sila ng isang "tatlong palapag" na bahagi.

Ngayon tingnan natin ang pangunahing bahagi. Ang numerator at denominator ay may parehong numero: log 2 7. Dahil log 2 7 ≠ 0, maaari nating bawasan ang fraction - 2/4 ay mananatili sa denominator. Ayon sa mga patakaran ng aritmetika, ang apat ay maaaring ilipat sa numerator, na ginawa. Ang resulta ay ang sagot: 2.

Paglipat sa isang bagong pundasyon

Sa pagsasalita tungkol sa mga patakaran para sa pagdaragdag at pagbabawas ng mga logarithms, partikular kong binigyang-diin na gumagana lamang ang mga ito sa parehong mga base. Paano kung magkaiba ang mga base? Paano kung hindi sila eksaktong mga kapangyarihan ng parehong bilang?

Ang mga formula para sa paglipat sa isang bagong base ay dumating upang iligtas. Binubalangkas namin ang mga ito sa anyo ng isang teorama:

Hayaang mag-log ang logarithm a x. Pagkatapos ay para sa anumang numero c ganyan c> 0 at c≠ 1, ang pagkakapantay-pantay ay totoo:

[Figure caption]

Sa partikular, kung ilalagay natin c = x, nakukuha natin:

[Figure caption]

Ito ay sumusunod mula sa pangalawang pormula na ang base at ang argumento ng logarithm ay maaaring palitan, ngunit ang buong expression ay "ibinalik", i.e. ang logarithm ay nasa denominator.

Ang mga formula na ito ay bihirang makita sa mga ordinaryong numerical expression. Posibleng suriin kung gaano kaginhawa ang mga ito kapag nilulutas ang mga logarithmic equation at hindi pagkakapantay-pantay.

Gayunpaman, may mga gawain na hindi malulutas sa lahat maliban sa paglipat sa isang bagong pundasyon. Isaalang-alang natin ang ilan sa mga ito:

Isang gawain. Hanapin ang halaga ng expression: log 5 16 log 2 25.

Tandaan na ang mga argumento ng parehong logarithms ay eksaktong exponent. Kunin natin ang mga indicator: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Ngayon, i-flip natin ang pangalawang logarithm:

[Figure caption]

Dahil ang produkto ay hindi nagbabago mula sa permutation ng mga kadahilanan, mahinahon naming pinarami ang apat at dalawa, at pagkatapos ay naisip ang mga logarithms.

Isang gawain. Hanapin ang halaga ng expression: log 9 100 lg 3.

Ang batayan at argumento ng unang logarithm ay eksaktong kapangyarihan. Isulat natin ito at alisin ang mga tagapagpahiwatig:

[Figure caption]

Ngayon, alisin natin ang decimal logarithm sa pamamagitan ng paglipat sa isang bagong base:

[Figure caption]

Pangunahing logarithmic na pagkakakilanlan

Kadalasan sa proseso ng paglutas ay kinakailangan na kumatawan sa isang numero bilang isang logarithm sa isang naibigay na base. Sa kasong ito, ang mga formula ay makakatulong sa amin:

Sa unang kaso, ang numero n nagiging exponent ng argumento. Numero n maaaring maging anumang bagay, dahil ito ay ang halaga lamang ng logarithm.

Ang pangalawang formula ay talagang isang paraphrased na kahulugan. Ito ay tinatawag na pangunahing logarithmic identity.

Sa katunayan, ano ang mangyayari kung ang numero b itaas sa kapangyarihan upang b sa lawak na ito ay nagbibigay ng isang numero a? Tama: ito ang parehong numero a. Basahin muli ang talatang ito nang mabuti - maraming tao ang "nakabitin" dito.

Tulad ng mga bagong base conversion formula, ang pangunahing logarithmic identity ay minsan ang tanging posibleng solusyon.

Isang gawain. Hanapin ang halaga ng expression:

[Figure caption]

Tandaan na ang log 25 64 = log 5 8 - kinuha lamang ang parisukat mula sa base at ang argumento ng logarithm. Dahil sa mga patakaran para sa pagpaparami ng mga kapangyarihan na may parehong base, nakukuha natin ang:

[Figure caption]

Kung ang isang tao ay hindi alam, ito ay isang tunay na gawain mula sa pagsusulit :)

Logarithmic unit at logarithmic zero

Sa konklusyon, magbibigay ako ng dalawang pagkakakilanlan na mahirap tawagan ang mga katangian - sa halip, ito ay mga kahihinatnan mula sa kahulugan ng logarithm. Ang mga ito ay patuloy na matatagpuan sa mga problema at, nakakagulat, lumikha ng mga problema kahit para sa mga "advanced" na mga mag-aaral.

1. log a a Ang = 1 ay ang logarithmic unit. Tandaan minsan at para sa lahat: ang logarithm sa anumang base a mula sa mismong base na ito ay katumbas ng isa.
2. log a 1 = 0 ay logarithmic zero. Base a maaaring maging anuman, ngunit kung ang argumento ay isa, ang logarithm ay zero! kasi a Ang 0 = 1 ay isang direktang kinahinatnan ng kahulugan.

Iyon ang lahat ng mga pag-aari. Siguraduhing magsanay sa pagsasabuhay ng mga ito! I-download ang cheat sheet sa simula ng aralin, i-print ito at lutasin ang mga problema.

Kahulugan ng logarithm

Ang logarithm ng numero b sa base a ay ang exponent kung saan kailangan mong itaas ang a upang makakuha ng b.

Ang dami e sa matematika, kaugalian na tukuyin ang limitasyon kung saan ang expression ay may gawi

Numero e ay hindi makatwirang numero- isang numero na hindi katumbas ng isa, hindi ito maaaring eksaktong ipahayag alinman sa kabuuan o bilang isang fraction makatwiran numero.

Sulat e- ang unang titik ng salitang Latin exonere- upang ipagmalaki, kaya ang pangalan sa matematika exponential- exponential function.

Numero e malawakang ginagamit sa matematika, at sa lahat ng agham, sa isang paraan o iba pa gamit ang mga kalkulasyon ng matematika para sa kanilang mga pangangailangan.

Logarithms. Mga katangian ng logarithms

Kahulugan: Ang batayang logarithm ng isang positibong numero b ay ang exponent c kung saan ang numero a ay dapat na itaas upang makuha ang bilang b.

Pangunahing logarithmic na pagkakakilanlan:

7) Formula para sa paglipat sa isang bagong base:

lna = log e a, e ≈ 2.718…

Mga gawain at pagsusulit sa paksang “Logarithms. Mga katangian ng logarithms»

• Logarithms - Mga mahahalagang paksa para sa pag-uulit ng pagsusulit sa matematika

Upang matagumpay na makumpleto ang mga gawain sa paksang ito, dapat mong malaman ang kahulugan ng logarithm, ang mga katangian ng logarithms, ang pangunahing logarithmic na pagkakakilanlan, ang mga kahulugan ng decimal at natural na logarithm. Ang mga pangunahing uri ng mga gawain sa paksang ito ay mga gawain para sa pagkalkula at pag-convert ng mga logarithmic na expression. Isaalang-alang natin ang kanilang solusyon sa mga sumusunod na halimbawa.

Solusyon: Gamit ang mga katangian ng logarithms, nakukuha namin

Solusyon: gamit ang mga katangian ng degree, nakukuha namin

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Mga katangian ng logarithms, formulations at proofs.

Ang logarithms ay may ilang mga katangian na katangian. Sa artikulong ito, susuriin natin ang pangunahing mga katangian ng logarithms. Dito ibinibigay namin ang kanilang mga formulation, isulat ang mga katangian ng logarithms sa anyo ng mga formula, nagpapakita ng mga halimbawa ng kanilang aplikasyon, at nagbibigay din ng mga patunay ng mga katangian ng logarithms.

Pag-navigate sa pahina.

Mga pangunahing katangian ng logarithms, formula

Para sa kadalian ng pag-alala at paggamit, ipinakita namin pangunahing katangian ng logarithms bilang isang listahan ng mga formula. Sa susunod na seksyon, ibibigay namin ang kanilang mga pormulasyon, mga patunay, mga halimbawa ng paggamit, at mga kinakailangang paliwanag.

Unit log property: log a 1=0 para sa alinmang a>0 , a≠1 .

Ang logarithm ng isang numero na katumbas ng base: log a a=1 para sa a>0 , a≠1 .

Base power logarithm property: log a a p =p , kung saan ang a>0 , a≠1 at p ay anumang tunay na numero.

Ang logarithm ng produkto ng dalawang positibong numero: log a (x y)=log a x+log a y , a>0 , a≠1 , x>0 , y>0 ,
at ang ari-arian ng logarithm ng produkto ng n positibong numero: log a (x 1 x 2 ... x n) \u003d log a x 1 + log a x 2 + ... + log a x n, a>0, a≠1 , x 1 >0, x 2 >0, …, xn >0 .

Pribadong logarithm property: , kung saan ang a>0 , a≠1 , x>0 , y>0 .

Logarithm ng kapangyarihan ng isang numero: log a b p =p log a |b| , kung saan ang a>0 , a≠1 , b at p ay mga numero na ang antas ng b p ay may katuturan at b p >0 .

Bunga: , kung saan ang a>0 , a≠1 , n ay isang natural na bilang na mas malaki sa isa, b>0 .

Corollary 1: , a>0 , a≠1 , b>0 , b≠1 .

Corollary 2: , a>0 , a≠1 , b>0 , p at q ay mga tunay na numero, q≠0 , sa partikular, para sa b=a mayroon tayo .

Mga pahayag at patunay ng mga ari-arian

Dumaan kami sa pagbabalangkas at patunay ng mga naitala na katangian ng logarithms. Ang lahat ng mga katangian ng logarithms ay napatunayan sa batayan ng kahulugan ng logarithm at ang pangunahing logarithmic na pagkakakilanlan na sumusunod mula dito, pati na rin ang mga katangian ng degree.

Magsimula tayo sa katangian ng logarithm ng pagkakaisa. Ang pagbabalangkas nito ay ang mga sumusunod: ang logarithm ng pagkakaisa ay katumbas ng zero, iyon ay, log a 1=0 para sa alinmang a>0 , a≠1 . Ang patunay ay diretso: dahil ang isang 0 =1 para sa anumang a na nakakatugon sa mga kundisyon sa itaas a>0 at a≠1 , pagkatapos ay ang napatunayang equality log a 1=0 ay agad na sumusunod mula sa kahulugan ng logarithm.

Magbigay tayo ng mga halimbawa ng aplikasyon ng itinuturing na ari-arian: log 3 1=0 , lg1=0 at .

Lumipat tayo sa susunod na pag-aari: ang logarithm ng isang numero na katumbas ng base ay katumbas ng isa, yan ay, log a a=1 para sa a>0 , a≠1 . Sa katunayan, dahil a 1 =a para sa anumang a , pagkatapos ay sa pamamagitan ng kahulugan ng logarithm log a a=1 .

Ang mga halimbawa ng paggamit ng property na ito ng logarithms ay log 5 5=1 , log 5.6 5.6 at lne=1 .

Ang logarithm ng kapangyarihan ng isang numero na katumbas ng base ng logarithm ay katumbas ng exponent. Ang pag-aari na ito ng logarithm ay tumutugma sa isang formula ng form log a a p =p, kung saan ang a>0 , a≠1 at p ay anumang tunay na numero. Direktang sumusunod ang property na ito mula sa kahulugan ng logarithm. Tandaan na pinapayagan ka nitong agad na tukuyin ang halaga ng logarithm, kung posible na kumatawan sa numero sa ilalim ng sign ng logarithm bilang isang antas ng base, pag-uusapan natin ang higit pa tungkol dito sa artikulong pagkalkula ng logarithm.

Halimbawa, log 2 2 7 =7 , log10 -4 =-4 at .

Logarithm ng produkto ng dalawang positibong numero Ang x at y ay katumbas ng produkto ng logarithms ng mga numerong ito: log a (x y)=log a x+log a y, a>0 , a≠1 . Patunayan natin ang pag-aari ng logarithm ng produkto. Dahil sa mga katangian ng degree a log a x + log a y =a log a x a log a y , at dahil sa pamamagitan ng pangunahing logarithmic identity isang log a x =x at isang log a y =y , pagkatapos ay isang log a x a log a y =x y . Kaya, ang isang log a x+log a y =x y , kung saan ang kinakailangang pagkakapantay-pantay ay sinusundan ng kahulugan ng logarithm.

Magpakita tayo ng mga halimbawa ng paggamit ng property ng logarithm ng produkto: log 5 (2 3)=log 5 2+log 5 3 at .

Ang product logarithm property ay maaaring gawing pangkalahatan sa produkto ng isang finite number n ng positive numbers x 1 , x 2 , …, x n as log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. Ang pagkakapantay-pantay na ito ay madaling mapatunayan sa pamamagitan ng pamamaraan ng matematikal na induction.

Halimbawa, ang natural na logarithm ng isang produkto ay maaaring palitan ng kabuuan ng tatlong natural na logarithm ng mga numero 4 , e , at .

Logarithm ng quotient ng dalawang positibong numero Ang x at y ay katumbas ng pagkakaiba sa pagitan ng logarithms ng mga numerong ito. Ang property ng quotient logarithm ay tumutugma sa isang formula ng form , kung saan ang a>0 , a≠1 , x at y ay ilang positibong numero. Ang bisa ng formula na ito ay pinatunayan tulad ng formula para sa logarithm ng produkto: since , pagkatapos ay sa pamamagitan ng kahulugan ng logarithm .

Narito ang isang halimbawa ng paggamit ng property na ito ng logarithm: .

Lumipat tayo sa ari-arian ng logarithm ng degree. Ang logarithm ng isang degree ay katumbas ng produkto ng exponent at ang logarithm ng modulus ng base ng degree na ito. Isinulat namin ang pag-aari na ito ng logarithm ng degree sa anyo ng isang formula: log a b p =p log a |b|, kung saan ang a>0 , a≠1 , b at p ay mga numero na ang antas ng b p ay may katuturan at b p >0 .

Pinatunayan muna namin ang property na ito para sa positive b . Ang pangunahing logarithmic na pagkakakilanlan ay nagbibigay-daan sa amin na katawanin ang numero b bilang isang log a b , pagkatapos ay b p =(a log a b) p , at ang nagresultang expression, dahil sa power property, ay katumbas ng isang p log a b . Kaya't dumating tayo sa pagkakapantay-pantay b p =a p log a b , kung saan, sa pamamagitan ng kahulugan ng logarithm, napagpasyahan natin na log a b p =p log a b .

Ito ay nananatiling patunayan ang ari-arian na ito para sa negatibong b . Dito napapansin natin na ang expression na log a b p para sa negatibong b ay may katuturan lamang para sa kahit na mga exponent p (dahil ang halaga ng degree b p ay dapat na mas malaki kaysa sa zero, kung hindi, ang logarithm ay hindi magkakaroon ng kahulugan), at sa kasong ito b p =|b| p . Pagkatapos b p ==b| p =(a log a |b|) p =a p log a |b| , saan mag-log a b p =p mag-log a |b| .

Halimbawa, at ln(-3) 4 =4 ln|-3|=4 ln3 .

Ito ay sumusunod mula sa nakaraang pag-aari ari-arian ng logarithm mula sa ugat: ang logarithm ng ugat ng nth degree ay katumbas ng produkto ng fraction 1/n at ang logarithm ng root expression, iyon ay, kung saan ang a>0, a≠1, n ay isang natural na bilang na mas malaki sa isa, b>0.

Ang patunay ay batay sa isang pagkakapantay-pantay (tingnan ang kahulugan ng exponent na may fractional exponent), na wasto para sa anumang positive b , at ang property ng logarithm ng degree: .

Narito ang isang halimbawa ng paggamit ng property na ito: .

Ngayon patunayan natin conversion formula sa bagong base ng logarithm mabait . Upang gawin ito, sapat na upang patunayan ang bisa ng equality log c b=log a b log c a . Ang pangunahing logarithmic identity ay nagbibigay-daan sa amin na katawanin ang numero b bilang isang log a b , pagkatapos ay log c b=log c a log a b . Nananatili itong gamitin ang pag-aari ng logarithm ng degree: log c a log a b = log a b log c a . Kaya, ang equality log c b=log a b log c a ay napatunayan, na nangangahulugan na ang formula para sa paglipat sa isang bagong base ng logarithm ay napatunayan din. .

Magpakita tayo ng ilang halimbawa ng paglalapat ng katangiang ito ng logarithms: at .

Ang pormula para sa paglipat sa isang bagong base ay nagbibigay-daan sa iyo na magpatuloy sa pagtatrabaho sa mga logarithms na may "maginhawa" na base. Halimbawa, maaari itong magamit upang lumipat sa natural o decimal logarithms upang makalkula mo ang halaga ng logarithm mula sa isang talahanayan ng logarithm. Ang pormula para sa paglipat sa isang bagong base ng logarithm ay nagpapahintulot din sa ilang mga kaso na mahanap ang halaga ng isang naibigay na logarithm, kapag ang mga halaga ng ilang logarithm sa iba pang mga base ay kilala.

Ang isang espesyal na kaso ng transition formula sa isang bagong base ng logarithm para sa c=b ng form ay kadalasang ginagamit. Ipinapakita nito na ang log a b at log b a ay magkabaligtaran na mga numero. Halimbawa, .

Madalas ding ginagamit ang formula, na maginhawa kapag naghahanap ng mga halaga ng logarithm. Upang kumpirmahin ang aming mga salita, ipapakita namin kung paano kinakalkula ang halaga ng logarithm ng form gamit ito. Meron kami . Upang patunayan ang formula, sapat na ang paggamit ng formula ng paglipat sa bagong base ng logarithm a: .

Ito ay nananatiling patunayan ang mga katangian ng paghahambing ng logarithms.

Gamitin natin ang kabaligtaran na pamamaraan. Ipagpalagay na para sa isang 1 >1 , a 2 >1 at a 1 2 at para sa 0 1 log a 1 b≤log a 2 b ay totoo. Sa pamamagitan ng mga katangian ng logarithms, ang mga hindi pagkakapantay-pantay na ito ay maaaring muling isulat bilang at ayon sa pagkakabanggit, at mula sa kanila ay sumusunod na log b a 1 ≤log b a 2 at log b a 1 ≥log b a 2, ayon sa pagkakabanggit. Pagkatapos, sa pamamagitan ng mga katangian ng mga kapangyarihan na may parehong mga base, ang mga pagkakapantay-pantay b log b a 1 ≥b log b a 2 at b log b a 1 ≥b log b a 2 ay dapat masiyahan, iyon ay, a 1 ≥a 2 . Kaya, nakarating kami sa isang kontradiksyon sa kondisyon a 1 2 . Kinukumpleto nito ang patunay.

Mga pangunahing katangian ng logarithms

• Mga materyales para sa aralin
• I-download ang lahat ng mga formula

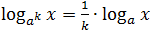
Ang mga logarithm, tulad ng anumang numero, ay maaaring idagdag, ibawas at i-convert sa lahat ng posibleng paraan. Ngunit dahil ang logarithms ay hindi masyadong ordinaryong mga numero, may mga panuntunan dito, na tinatawag pangunahing katangian.

Dapat malaman ang mga panuntunang ito - walang seryosong problema sa logarithmic ang malulutas kung wala ang mga ito. Bilang karagdagan, napakakaunti sa kanila - lahat ay maaaring matutunan sa isang araw. Kaya simulan na natin.

Pagdaragdag at pagbabawas ng logarithms

Isaalang-alang ang dalawang logarithms na may parehong base: log a x at log a y . Pagkatapos ay maaari silang idagdag at ibawas, at:

Kaya, ang kabuuan ng logarithms ay katumbas ng logarithm ng produkto, at ang pagkakaiba ay ang logarithm ng quotient. Mangyaring tandaan: ang pangunahing punto dito ay - parehong batayan. Kung ang mga base ay iba, ang mga patakarang ito ay hindi gagana!

Ang mga formula na ito ay makakatulong sa pagkalkula ng logarithmic expression kahit na ang mga indibidwal na bahagi nito ay hindi isinasaalang-alang (tingnan ang aralin na "Ano ang logarithm"). Tingnan ang mga halimbawa - at tingnan:

Isang gawain. Hanapin ang halaga ng expression: log 6 4 + log 6 9.

Dahil ang mga base ng logarithms ay pareho, ginagamit namin ang sum formula:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Isang gawain. Hanapin ang halaga ng expression: log 2 48 − log 2 3.

Ang mga base ay pareho, ginagamit namin ang formula ng pagkakaiba:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Isang gawain. Hanapin ang halaga ng expression: log 3 135 − log 3 5.

Muli, ang mga base ay pareho, kaya mayroon kaming:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Tulad ng nakikita mo, ang mga orihinal na expression ay binubuo ng "masamang" logarithms, na hindi isinasaalang-alang nang hiwalay. Ngunit pagkatapos ng mga pagbabago, medyo normal na mga numero ang lumabas. Maraming pagsubok ang nakabatay sa katotohanang ito. Oo, ang kontrol na iyon - ang mga katulad na expression sa lahat ng kaseryosohan (minsan - halos walang pagbabago) ay inaalok sa pagsusulit.

Pag-alis ng exponent mula sa logarithm

Ngayon pasimplehin natin ng kaunti ang gawain. Paano kung may degree sa base o argumento ng logarithm? Kung gayon ang exponent ng degree na ito ay maaaring alisin sa sign ng logarithm ayon sa mga sumusunod na patakaran:

• log a x n = n log a x ;
• 
• 

Madaling makita na ang huling panuntunan ay sumusunod sa kanilang unang dalawa. Ngunit ito ay mas mahusay na tandaan ito pa rin - sa ilang mga kaso ito ay makabuluhang bawasan ang halaga ng mga kalkulasyon.

Siyempre, ang lahat ng mga patakarang ito ay may katuturan kung ang ODZ logarithm ay sinusunod: a > 0, a ≠ 1, x > 0. At isa pang bagay: matutong ilapat ang lahat ng mga formula hindi lamang mula kaliwa hanggang kanan, kundi pati na rin sa kabaligtaran, i.e. maaari mong ipasok ang mga numero bago ang sign ng logarithm sa logarithm mismo. Ito ang madalas na kinakailangan.

Isang gawain. Hanapin ang halaga ng expression: log 7 49 6 .

Tanggalin natin ang antas sa argumento ayon sa unang formula:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Isang gawain. Hanapin ang halaga ng expression:

[Figure caption]

Tandaan na ang denominator ay isang logarithm na ang base at argumento ay eksaktong kapangyarihan: 16 = 2 4 ; 49 = 72. Meron kami:

[Figure caption]

Sa tingin ko ang huling halimbawa ay nangangailangan ng paglilinaw. Saan napunta ang logarithms? Hanggang sa pinakahuling sandali, nagtatrabaho lamang kami sa denominator. Iniharap nila ang base at argumento ng logarithm na nakatayo doon sa anyo ng mga degree at kinuha ang mga tagapagpahiwatig - nakakuha sila ng isang "tatlong palapag" na bahagi.

Ngayon tingnan natin ang pangunahing bahagi. Ang numerator at denominator ay may parehong numero: log 2 7. Dahil log 2 7 ≠ 0, maaari nating bawasan ang fraction - 2/4 ay mananatili sa denominator. Ayon sa mga patakaran ng aritmetika, ang apat ay maaaring ilipat sa numerator, na ginawa. Ang resulta ay ang sagot: 2.

Paglipat sa isang bagong pundasyon

Sa pagsasalita tungkol sa mga patakaran para sa pagdaragdag at pagbabawas ng mga logarithms, partikular kong binigyang-diin na gumagana lamang ang mga ito sa parehong mga base. Paano kung magkaiba ang mga base? Paano kung hindi sila eksaktong mga kapangyarihan ng parehong bilang?

Ang mga formula para sa paglipat sa isang bagong base ay dumating upang iligtas. Binubalangkas namin ang mga ito sa anyo ng isang teorama:

Hayaang ibigay ang logarithm log a x. Pagkatapos ay para sa anumang bilang c tulad na c > 0 at c ≠ 1, ang pagkakapantay-pantay ay totoo:

[Figure caption]

Sa partikular, kung ilalagay natin c = x , makukuha natin:

[Figure caption]

Ito ay sumusunod mula sa pangalawang pormula na ang base at ang argumento ng logarithm ay maaaring palitan, ngunit ang buong expression ay "ibinalik", i.e. ang logarithm ay nasa denominator.

Ang mga formula na ito ay bihirang makita sa mga ordinaryong numerical expression. Posibleng suriin kung gaano kaginhawa ang mga ito kapag nilulutas ang mga logarithmic equation at hindi pagkakapantay-pantay.

Gayunpaman, may mga gawain na hindi malulutas sa lahat maliban sa paglipat sa isang bagong pundasyon. Isaalang-alang natin ang ilan sa mga ito:

Isang gawain. Hanapin ang halaga ng expression: log 5 16 log 2 25.

Tandaan na ang mga argumento ng parehong logarithms ay eksaktong exponent. Kunin natin ang mga indicator: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Ngayon, i-flip natin ang pangalawang logarithm:

[Figure caption]

Dahil ang produkto ay hindi nagbabago mula sa permutation ng mga kadahilanan, mahinahon naming pinarami ang apat at dalawa, at pagkatapos ay naisip ang mga logarithms.

Isang gawain. Hanapin ang halaga ng expression: log 9 100 lg 3.

Ang batayan at argumento ng unang logarithm ay eksaktong kapangyarihan. Isulat natin ito at alisin ang mga tagapagpahiwatig:

[Figure caption]

Ngayon, alisin natin ang decimal logarithm sa pamamagitan ng paglipat sa isang bagong base:

[Figure caption]

Pangunahing logarithmic na pagkakakilanlan

Kadalasan sa proseso ng paglutas ay kinakailangan na kumatawan sa isang numero bilang isang logarithm sa isang naibigay na base. Sa kasong ito, ang mga formula ay makakatulong sa amin:

1. n = log a a n

2. Sa unang kaso, ang numero n ay nagiging exponent sa argumento. Ang numero n ay maaaring maging anumang bagay, dahil ito ay ang halaga lamang ng logarithm.

   Ang pangalawang formula ay talagang isang paraphrased na kahulugan. Ito ay tinatawag na pangunahing logarithmic identity.

   Sa katunayan, ano ang mangyayari kung ang bilang b ay itataas sa gayong kapangyarihan na ang bilang b sa kapangyarihang ito ay nagbibigay ng bilang a? Tama iyan: ito ay ang parehong numero a . Basahin muli ang talatang ito nang mabuti - maraming tao ang "nakabitin" dito.

   Tulad ng mga bagong base conversion formula, ang pangunahing logarithmic identity ay minsan ang tanging posibleng solusyon.

   [Figure caption]

   Tandaan na ang log 25 64 = log 5 8 - kunin lamang ang parisukat ng base at ang argumento ng logarithm. Dahil sa mga patakaran para sa pagpaparami ng mga kapangyarihan na may parehong base, nakukuha natin ang:

   [Figure caption]

   Kung ang isang tao ay hindi alam, ito ay isang tunay na gawain mula sa Unified State Examination 🙂

   Logarithmic unit at logarithmic zero

   Sa konklusyon, magbibigay ako ng dalawang pagkakakilanlan na mahirap tawagan ang mga katangian - sa halip, ito ay mga kahihinatnan mula sa kahulugan ng logarithm. Ang mga ito ay patuloy na matatagpuan sa mga problema at, nakakagulat, lumikha ng mga problema kahit para sa mga "advanced" na mga mag-aaral.

   1. Ang log a a = 1 ay ang logarithmic unit. Tandaan minsan at para sa lahat: ang logarithm sa anumang base a mula sa base na iyon mismo ay katumbas ng isa.
   2. log a 1 = 0 ay logarithmic zero. Ang base a ay maaaring maging anuman, ngunit kung ang argumento ay isa - ang logarithm ay zero! Dahil ang 0 = 1 ay direktang kinahinatnan ng kahulugan.

   Iyon ang lahat ng mga pag-aari. Siguraduhing magsanay sa pagsasabuhay ng mga ito! I-download ang cheat sheet sa simula ng aralin, i-print ito - at lutasin ang mga problema.

   Logarithm. Mga katangian ng logarithm (pagdaragdag at pagbabawas).

   Mga katangian ng logarithm sundin mula sa kahulugan nito. At kaya ang logarithm ng numero b sa pamamagitan ng dahilan a tinukoy bilang exponent kung saan dapat itaas ang isang numero a para makuha ang numero b(umiiral lamang ang logarithm para sa mga positibong numero).

   Mula sa pagbabalangkas na ito ay sumusunod na ang pagkalkula x=log a b, ay katumbas ng paglutas ng equation ax=b. Halimbawa, log 2 8 = 3 kasi 8 = 2 3 . Ang pagbabalangkas ng logarithm ay ginagawang posible upang bigyang-katwiran na kung b=a c, pagkatapos ay ang logarithm ng numero b sa pamamagitan ng dahilan a katumbas Sa. Malinaw din na ang paksa ng logarithm ay malapit na nauugnay sa paksa ng kapangyarihan ng isang numero.

   Sa logarithms, tulad ng anumang mga numero, maaari kang gumanap karagdagan, mga pagpapatakbo ng pagbabawas at magbago sa lahat ng posibleng paraan. Ngunit sa view ng katotohanan na ang logarithms ay hindi masyadong ordinaryong mga numero, ang kanilang sariling mga espesyal na patakaran ay nalalapat dito, na tinatawag pangunahing katangian.

   Pagdaragdag at pagbabawas ng logarithms.

   Kumuha ng dalawang logarithms na may parehong base: log x at mag-log a y. Pagkatapos ay alisin posible na magsagawa ng mga pagpapatakbo ng karagdagan at pagbabawas:

   Sa nakikita natin, kabuuan ng logarithms katumbas ng logarithm ng produkto, at pagkakaiba logarithms- ang logarithm ng quotient. At ito ay totoo kung ang mga numero a, X at sa positibo at isang ≠ 1.

   Mahalagang tandaan na ang pangunahing aspeto sa mga formula na ito ay ang parehong mga batayan. Kung ang mga base ay naiiba sa bawat isa, ang mga patakarang ito ay hindi nalalapat!

   Ang mga patakaran para sa pagdaragdag at pagbabawas ng mga logarithms na may parehong mga base ay binabasa hindi lamang mula kaliwa hanggang kanan, kundi pati na rin ang kabaligtaran. Bilang resulta, mayroon kaming mga theorems para sa logarithm ng produkto at ang logarithm ng quotient.

   Logarithm ng produkto dalawang positibong numero ay katumbas ng kabuuan ng kanilang mga logarithms ; paraphrasing ito teorama, makuha namin ang mga sumusunod, kung ang mga numero a, x at sa positibo at isang ≠ 1, pagkatapos:

   Logarithm ng quotient ng dalawang positibong numero ay katumbas ng pagkakaiba sa pagitan ng logarithms ng dibidendo at ng divisor. Sa madaling salita, kung ang mga numero a, X at sa positibo at isang ≠ 1, pagkatapos:

   Inilapat namin ang mga theorems sa itaas upang malutas mga halimbawa:

   Kung mga numero x at sa ay negatibo, kung gayon formula ng logarithm ng produkto nagiging walang kabuluhan. Kaya, ipinagbabawal na magsulat:

   dahil ang mga expression na log 2 (-8) at log 2 (-4) ay hindi tinukoy sa lahat (ang logarithmic function sa= log 2 X tinukoy lamang para sa mga positibong halaga ng argumento X).

   Teorama ng produkto ay naaangkop hindi lamang para sa dalawa, ngunit para din sa isang walang limitasyong bilang ng mga kadahilanan. Nangangahulugan ito na para sa bawat natural k at anumang positibong numero x 1 , x 2 , . . . ,x n may pagkakakilanlan:

   Mula sa quotient logarithm theorems isa pang pag-aari ng logarithm ang maaaring makuha. Kilalang-kilala ang log na iyon a 1= 0, samakatuwid,

   Kaya mayroong isang pagkakapantay-pantay:

   Logarithms ng dalawang magkatumbas na numero sa parehong batayan ay magkakaiba sa isa't isa lamang sa sign. Kaya:

   Logarithm. Mga katangian ng logarithms

   Logarithm. Mga katangian ng logarithms

   Isaalang-alang ang pagkakapantay-pantay. Ipaalam sa amin ang mga halaga at at gusto naming mahanap ang halaga ng .

   Ibig sabihin, naghahanap kami ng exponent kung saan kailangan mong i-cock para makuha ang .

   Hayaan ang variable ay maaaring tumagal ng anumang tunay na halaga, pagkatapos ay ang mga sumusunod na paghihigpit ay ipapataw sa mga variable: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/ >

   Kung alam natin ang mga halaga ng at , at nahaharap tayo sa gawain ng paghahanap ng hindi alam, kung gayon para sa layuning ito ay ipinakilala ang isang operasyon sa matematika, na tinatawag na logarithm.

   Upang mahanap ang halaga na ating kinukuha logarithm ng isang numero sa pundasyon :

   Ang logarithm ng isang numero sa base ay ang exponent kung saan kailangan mong itaas upang makakuha ng .

   Yan ay pangunahing logarithmic na pagkakakilanlan:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   ay mahalagang mathematical notation mga kahulugan ng logarithm.

   Ang mathematical operation logarithm ay ang kabaligtaran ng exponentiation, kaya mga katangian ng logarithms ay malapit na nauugnay sa mga katangian ng degree.

   Inilista namin ang pangunahing mga katangian ng logarithms:

   (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

   d>0″/>, 1″ pamagat=”d1″/>

   4.

   5.

   Ang sumusunod na pangkat ng mga katangian ay nagpapahintulot sa iyo na kumatawan sa exponent ng expression sa ilalim ng sign ng logarithm, o nakatayo sa base ng logarithm bilang isang coefficient bago ang sign ng logarithm:

   6.

   7.

   8.

   9.

   Ang susunod na pangkat ng mga formula ay nagpapahintulot sa iyo na pumunta mula sa isang logarithm na may isang ibinigay na base patungo sa isang logarithm na may isang arbitrary na base, at tinatawag na mga formula ng paglipat sa isang bagong base:

   10.

   12. (corollary mula sa property 11)

   

   Ang sumusunod na tatlong katangian ay hindi kilala, ngunit madalas itong ginagamit kapag nilulutas ang mga logarithmic equation, o kapag pinapasimple ang mga expression na naglalaman ng logarithms:

   13.

   14.

   15.

   Mga espesyal na kaso:

   — decimal logarithm

   — natural na logarithm

   Kapag pinasimple ang mga expression na naglalaman ng logarithms, inilalapat ang isang pangkalahatang diskarte:

   1. Kinakatawan namin ang mga decimal fraction sa anyo ng mga ordinaryong.

   2. Kinakatawan namin ang mga magkahalong numero bilang mga hindi wastong fraction.

   3. Ang mga numero sa base ng logarithm at sa ilalim ng sign ng logarithm ay nabubulok sa prime factor.

   4. Sinusubukan naming dalhin ang lahat ng logarithms sa parehong base.

   5. Ilapat ang mga katangian ng logarithms.

   Tingnan natin ang mga halimbawa ng pagpapasimple ng mga expression na naglalaman ng logarithms.

   Halimbawa 1

   Kalkulahin:

   Pasimplehin natin ang lahat ng mga exponent: ang ating gawain ay dalhin ang mga ito sa logarithms, na ang base ay kapareho ng bilang ng base ng exponent.

   ==(sa pamamagitan ng property 7)=(sa pamamagitan ng property 6) =

   Palitan ang mga indicator na nakuha natin sa orihinal na expression. Nakukuha namin:

   Sagot: 5.25

   Halimbawa 2 Kalkulahin:

   

   Dinadala namin ang lahat ng logarithms sa base 6 (sa kasong ito, ang logarithms mula sa denominator ng fraction ay "lilipat" sa numerator):

   I-decompose natin ang mga numero sa ilalim ng sign ng logarithm sa prime factor:

   Ilapat ang mga katangian 4 at 6:

   Ipinakilala namin ang kapalit

   Nakukuha namin:

   Sagot: 1

   Logarithm . Pangunahing logarithmic na pagkakakilanlan.

   Mga katangian ng logarithms. Decimal logarithm. natural na logarithm.

   logarithm positibong numero N sa base (b > 0, b 1) ay tinatawag na exponent x kung saan kailangan mong itaas ang b upang makakuha ng N .

   Ang entry na ito ay katumbas ng sumusunod: b x = N .

   MGA HALIMBAWA: log 3 81 = 4 since 3 4 = 81 ;

   log 1/3 27 = – 3 dahil (1/3) - 3 = 3 3 = 27 .

   Ang kahulugan sa itaas ng logarithm ay maaaring isulat bilang isang pagkakakilanlan:

   

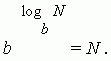
   Mga pangunahing katangian ng logarithms.

   2) log 1 = 0 dahil b 0 = 1 .

   3) Ang logarithm ng produkto ay katumbas ng kabuuan ng logarithms ng mga salik:

   4) Ang logarithm ng quotient ay katumbas ng pagkakaiba sa pagitan ng logarithms ng dibidendo at ng divisor:

   5) Ang logarithm ng degree ay katumbas ng produkto ng exponent at ang logarithm ng base nito:

   Ang kahihinatnan ng ari-arian na ito ay ang mga sumusunod: ugat ng log katumbas ng logarithm ng root number na hinati sa kapangyarihan ng root:

   

   6) Kung ang base ng logarithm ay isang degree, kung gayon ang halaga ang reciprocal ng exponent ay maaaring alisin sa rhyme log sign:

   

   Ang huling dalawang katangian ay maaaring pagsamahin sa isa:

   

   7) Ang formula para sa transition modulus (i.e. ang paglipat mula sa isang base ng logarithm patungo sa isa pang base):

   

   Sa isang partikular na kaso, kapag N = a meron kami:

   

   Decimal logarithm tinawag batayang logarithm 10. Ito ay tinutukoy lg, i.e. log 10 N= log N. Logarithms ng mga numero 10, 100, 1000, . p ay 1, 2, 3, …, ayon sa pagkakabanggit, i.e. may napakaraming positibo

   units, kung gaano karaming mga zero ang nasa logarithm number pagkatapos ng isa. Logarithms ng mga numero 0.1, 0.01, 0.001, . p ay –1, –2, –3, …, ayon sa pagkakabanggit, i.e. magkaroon ng kasing daming negatibo gaya ng may mga zero sa logarithm number bago ang isa (kabilang ang mga zero integer). Ang logarithms ng natitirang mga numero ay may fractional na bahagi na tinatawag mantissa. Ang integer na bahagi ng logarithm ay tinatawag katangian. Para sa mga praktikal na aplikasyon, ang mga decimal logarithm ay pinaka-maginhawa.

   natural na logarithm tinawag batayang logarithm e. Ito ay tinutukoy ng ln, i.e. log e N=ln N. Numero e ay hindi makatwiran, ang tinatayang halaga nito ay 2.718281828. Ito ang limitasyon kung saan ang bilang (1 + 1 / n) n na may walang limitasyong pagtaas n(cm. unang kahanga-hangang limitasyon sa pahina ng Mga Limitasyon sa Pagkakasunud-sunod ng Numero).
   Kakaibang tila, ang mga natural na logarithms ay naging napaka-maginhawa kapag nagsasagawa ng iba't ibang mga operasyon na may kaugnayan sa pagsusuri ng mga pag-andar. Pagkalkula ng base logarithms e mas mabilis kaysa sa anumang iba pang batayan.

• Ano ang kailangan mo ngayon upang magpatibay ng isang bata sa Russia? Ang pag-ampon sa Russia, bilang karagdagan sa isang responsableng personal na desisyon, ay nagsasangkot ng isang bilang ng mga pamamaraan para sa pagpapatunay ng estado ng mga kandidato. Ang mahigpit na pagpili sa yugto ng paghahanda ay nag-aambag sa higit […]
• Walang bayad ang impormasyon ng TIN o OGRN mula sa rehistro ng buwis sa buong Russia - online Sa Unified Portal of Tax Services, impormasyon sa pagpaparehistro ng estado ng mga legal na entity, indibidwal na negosyante, [...]
• Parusa para sa pagmamaneho nang walang mga dokumento (lisensya sa pagmamaneho, insurance, STS) Minsan, dahil sa pagkalimot, ang mga driver ay nasa likod ng manibela nang walang lisensya at tumatanggap ng multa para sa pagmamaneho nang walang mga dokumento. Alalahanin na ang isang motoristang nagmamanehong kasama niya ay […]
• Bulaklak para sa mga lalaki. Anong uri ng mga bulaklak ang maaari mong ibigay sa isang lalaki? Anong mga bulaklak ang maaaring ibigay sa isang lalaki? Walang gaanong "lalaki" na bulaklak, ngunit may mga ibinibigay sa mga lalaki. Isang maliit na listahan ng mga bulaklak sa harap mo: Chrysanthemums. Rosas. Mga carnation. […]
• Ang isang memo ay isang espesyal na anyo ng isang dokumento na ginagamit sa panloob na kapaligiran ng isang negosyo at nagsisilbi upang mabilis na malutas ang mga kasalukuyang problema sa produksyon. Karaniwan ang dokumentong ito ay iginuhit para sa layunin ng paggawa ng ilang […]
• Kailan at paano makukuha ang pinondohan na bahagi ng pensiyon sa Sberbank? Ang Sberbank ay isang kasosyong bangko ng pondo ng pensiyon ng estado. Sa batayan nito, ang mga mamamayan na nagbigay ng pinondohan na pensiyon ay maaaring ilipat ang pinondohan […]
• Mga allowance ng bata sa Ulyanovsk at rehiyon ng Ulyanovsk sa 2018 Bilang karagdagan, ang mga programang inaprubahan ng pederal na batas ay tumatakbo sa lahat ng mga rehiyon. Tingnan natin kung sino at anong mga benepisyo ang maaasahan. Bilang mga awtoridad sa rehiyon […]
• Detalyadong gabay sa kung paano gumawa ng kapangyarihan ng abugado upang kumatawan sa mga interes ng isang indibidwal sa hukuman Sa isang sibil o arbitrasyon na kaso, sa isang administratibo o kriminal na kaso, ang mga interes ng parehong nagsasakdal at nasasakdal ay maaaring katawanin ng isang abogado: […]

\(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)

Ipaliwanag natin nang mas madali. Halimbawa, ang \(\log_(2)(8)\) ay katumbas ng kapangyarihang \(2\) ay dapat na itaas upang makuha ang \(8\). Mula dito ay malinaw na ang \(\log_(2)(8)=3\).

Mga halimbawa:		\(\log_(5)(25)=2\)		kasi \(5^(2)=25\)
		\(\log_(3)(81)=4\)		kasi \(3^(4)=81\)
		\(\log_(2)\)\(\frac(1)(32)\) \(=-5\)		kasi \(2^(-5)=\)\(\frac(1)(32)\)

Argumento at base ng logarithm

Anumang logarithm ay may sumusunod na "anatomy":

Ang argumento ng logarithm ay karaniwang nakasulat sa antas nito, at ang base ay nakasulat sa subscript na mas malapit sa sign ng logarithm. At ang entry na ito ay binasa ng ganito: "ang logarithm ng dalawampu't lima hanggang sa base ng lima."

Paano makalkula ang logarithm?

Upang makalkula ang logarithm, kailangan mong sagutin ang tanong: sa anong antas dapat itaas ang base upang makuha ang argumento?

Halimbawa, kalkulahin ang logarithm: a) \(\log_(4)(16)\) b) \(\log_(3)\)\(\frac(1)(3)\) c) \(\log_(\ sqrt (5))(1)\) d) \(\log_(\sqrt(7))(\sqrt(7))\) e) \(\log_(3)(\sqrt(3))\)

a) Sa anong kapangyarihan dapat itaas ang \(4\) upang makuha ang \(16\)? Halatang pangalawa. kaya naman:

\(\log_(4)(16)=2\)

\(\log_(3)\)\(\frac(1)(3)\) \(=-1\)

c) Sa anong kapangyarihan dapat itaas ang \(\sqrt(5)\) upang makuha ang \(1\)? At anong antas ang gumagawa ng anumang numero bilang isang yunit? Syempre zero!

\(\log_(\sqrt(5))(1)=0\)

d) Sa anong kapangyarihan dapat itaas ang \(\sqrt(7)\) upang makuha ang \(\sqrt(7)\)? Sa una - anumang numero sa unang antas ay katumbas ng sarili nito.

\(\log_(\sqrt(7))(\sqrt(7))=1\)

e) Sa anong kapangyarihan dapat itaas ang \(3\) upang makuha ang \(\sqrt(3)\)? Mula sa alam namin na iyon ay isang fractional na kapangyarihan, at samakatuwid ang square root ay ang kapangyarihan ng \(\frac(1)(2)\) .

\(\log_(3)(\sqrt(3))=\)\(\frac(1)(2)\)

Halimbawa : Kalkulahin ang logarithm \(\log_(4\sqrt(2))(8)\)

Solusyon :

\(\log_(4\sqrt(2))(8)=x\)		Kailangan nating hanapin ang halaga ng logarithm, tukuyin natin ito bilang x. Ngayon ay gamitin natin ang kahulugan ng logarithm: \(\log_(a)(c)=b\) \(\Leftrightarrow\) \(a^(b)=c\)
\((4\sqrt(2))^(x)=8\)		Anong mga link ang \(4\sqrt(2)\) at \(8\)? Dalawa, dahil ang parehong mga numero ay maaaring kinakatawan ng dalawa: \(4=2^(2)\) \(\sqrt(2)=2^(\frac(1)(2))\) \(8=2^(3)\)
\(((2^(2)\cdot2^(\frac(1)(2))))^(x)=2^(3)\)		Sa kaliwa, ginagamit namin ang mga katangian ng degree: \(a^(m)\cdot a^(n)=a^(m+n)\) at \((a^(m))^(n)=a ^(m\cdot n)\)
\(2^(\frac(5)(2)x)=2^(3)\)		Ang mga base ay pantay, nagpapatuloy kami sa pagkakapantay-pantay ng mga tagapagpahiwatig
\(\frac(5x)(2)\) \(=3\)		I-multiply ang magkabilang panig ng equation sa \(\frac(2)(5)\)
		Ang resultang ugat ay ang halaga ng logarithm

Sagot : \(\log_(4\sqrt(2))(8)=1,2\)

Bakit naimbento ang logarithm?

Upang maunawaan ito, lutasin natin ang equation: \(3^(x)=9\). Itugma lang ang \(x\) para gumana ang pagkakapantay-pantay. Siyempre, \(x=2\).

Ngayon lutasin ang equation: \(3^(x)=8\).Ano ang katumbas ng x? Iyon ang punto.

Ang pinaka mapanlikha ay magsasabi: "Ang X ay mas mababa ng kaunti sa dalawa." Paano eksaktong isusulat ang numerong ito? Upang masagot ang tanong na ito, nakabuo sila ng logarithm. Salamat sa kanya, ang sagot dito ay maaaring isulat bilang \(x=\log_(3)(8)\).

Gusto kong bigyang-diin na \(\log_(3)(8)\), pati na rin anumang logarithm ay isang numero lamang. Oo, mukhang hindi karaniwan, ngunit ito ay maikli. Dahil kung gusto naming isulat ito bilang isang decimal, magiging ganito ang hitsura: \(1.892789260714.....\)

Halimbawa : Lutasin ang equation \(4^(5x-4)=10\)

Solusyon :

\(4^(5x-4)=10\)		Ang \(4^(5x-4)\) at \(10\) ay hindi maaaring bawasan sa parehong base. Kaya dito hindi mo magagawa nang wala ang logarithm. Gamitin natin ang kahulugan ng logarithm: \(a^(b)=c\) \(\Leftrightarrow\) \(\log_(a)(c)=b\)
\(\log_(4)(10)=5x-4\)		I-flip ang equation upang ang x ay nasa kaliwa
\(5x-4=\log_(4)(10)\)		Bago tayo. Ilipat ang \(4\) sa kanan. At huwag matakot sa logarithm, ituring ito bilang isang normal na numero.
\(5x=\log_(4)(10)+4\)		Hatiin ang equation sa 5
\(x=\)\(\frac(\log_(4)(10)+4)(5)\)		Narito ang ating ugat. Oo, mukhang hindi karaniwan, ngunit ang sagot ay hindi pinili.

Sagot : \(\frac(\log_(4)(10)+4)(5)\)

Decimal at natural na logarithms

Gaya ng nakasaad sa kahulugan ng logarithm, ang base nito ay maaaring maging anumang positibong numero maliban sa isang \((a>0, a\neq1)\). At sa lahat ng posibleng mga base, mayroong dalawa na madalas na nangyayari na ang isang espesyal na maikling notasyon ay naimbento para sa mga logarithms sa kanila:

Natural logarithm: isang logarithm na ang base ay ang Euler number \(e\) (katumbas ng humigit-kumulang \(2.7182818…\)), at ang logarithm ay isinusulat bilang \(\ln(a)\).

Yan ay, Ang \(\ln(a)\) ay kapareho ng \(\log_(e)(a)\)

Decimal logarithm: Ang logarithm na ang base ay 10 ay nakasulat na \(\lg(a)\).

Yan ay, Ang \(\lg(a)\) ay kapareho ng \(\log_(10)(a)\), kung saan ang \(a\) ay ilang numero.

Pangunahing logarithmic na pagkakakilanlan

Ang logarithms ay may maraming katangian. Ang isa sa kanila ay tinatawag na "Basic logarithmic identity" at ganito ang hitsura:

\(a^(\log_(a)(c))=c\)

Direktang sumusunod ang property na ito mula sa kahulugan. Tingnan natin kung paano eksaktong lumitaw ang formula na ito.

Alalahanin ang maikling kahulugan ng logarithm:

kung \(a^(b)=c\), kung gayon \(\log_(a)(c)=b\)

Ibig sabihin, ang \(b\) ay kapareho ng \(\log_(a)(c)\). Pagkatapos ay maaari nating isulat ang \(\log_(a)(c)\) sa halip na \(b\) sa formula \(a^(b)=c\) . Ito ay naging \(a^(\log_(a)(c))=c\) - ang pangunahing logarithmic identity.

Maaari mong mahanap ang natitirang mga katangian ng logarithms. Sa kanilang tulong, maaari mong pasimplehin at kalkulahin ang mga halaga ng mga expression na may logarithms, na mahirap direktang kalkulahin.

Halimbawa : Hanapin ang halaga ng expression na \(36^(\log_(6)(5))\)

Solusyon :

Sagot : \(25\)

Paano magsulat ng isang numero bilang isang logarithm?

Tulad ng nabanggit sa itaas, ang anumang logarithm ay isang numero lamang. Totoo rin ang kabaligtaran: anumang numero ay maaaring isulat bilang logarithm. Halimbawa, alam namin na ang \(\log_(2)(4)\) ay katumbas ng dalawa. Pagkatapos ay maaari mong isulat ang \(\log_(2)(4)\) sa halip na dalawa.

Ngunit ang \(\log_(3)(9)\) ay katumbas din ng \(2\), kaya maaari mo ring isulat ang \(2=\log_(3)(9)\) . Katulad din sa \(\log_(5)(25)\), at sa \(\log_(9)(81)\), atbp. Ibig sabihin, lumalabas

\(2=\log_(2)(4)=\log_(3)(9)=\log_(4)(16)=\log_(5)(25)=\log_(6)(36)=\ log_(7)(49)...\)

Kaya, kung kailangan natin, maaari nating isulat ang dalawa bilang isang logarithm na may anumang base kahit saan (kahit sa isang equation, kahit sa isang expression, kahit na sa isang hindi pagkakapantay-pantay) - isinusulat lang natin ang squared base bilang isang argumento.

Ito ay pareho sa isang triple - maaari itong isulat bilang \(\log_(2)(8)\), o bilang \(\log_(3)(27)\), o bilang \(\log_(4)( 64) \) ... Dito isinulat namin ang base sa kubo bilang isang argumento:

\(3=\log_(2)(8)=\log_(3)(27)=\log_(4)(64)=\log_(5)(125)=\log_(6)(216)=\ log_(7)(343)...\)

At kasama ang apat:

\(4=\log_(2)(16)=\log_(3)(81)=\log_(4)(256)=\log_(5)(625)=\log_(6)(1296)=\ log_(7)(2401)...\)

At may minus one:

\(-1=\) \(\log_(2)\)\(\frac(1)(2)\) \(=\) \(\log_(3)\)\(\frac(1)( 3)\) \(=\) \(\log_(4)\)\(\frac(1)(4)\) \(=\) \(\log_(5)\)\(\frac(1 )(5)\) \(=\) \(\log_(6)\)\(\frac(1)(6)\) \(=\) \(\log_(7)\)\(\frac (1)(7)\)\(...\)

At kasama ang isang ikatlo:

\(\frac(1)(3)\) \(=\log_(2)(\sqrt(2))=\log_(3)(\sqrt(3))=\log_(4)(\sqrt( 4))=\log_(5)(\sqrt(5))=\log_(6)(\sqrt(6))=\log_(7)(\sqrt(7))...\)

Anumang numero \(a\) ay maaaring katawanin bilang isang logarithm na may base \(b\): \(a=\log_(b)(b^(a))\)

Halimbawa : Hanapin ang halaga ng isang expression \(\frac(\log_(2)(14))(1+\log_(2)(7))\)

Solusyon :

Sagot : \(1\)