Instruction
Use pi to find the radius from the known area of a circle. This constant specifies the proportion between the diameter of a circle and the length of its border (circle). The circumference of a circle is the maximum area of the plane that it is possible to cover with its help, and the diameter is equal to two radii, therefore, the area with the radius also correlate with each other with a proportion that can be expressed in terms of Pi. This constant (π) is defined as the area (S) and the squared radius (r) of the circle. It follows from this that the radius can be expressed as the square root of the quotient of dividing the area by the number Pi: r=√(S/π).
For a long time, Erastofen headed the Library of Alexandria, the most famous library of the ancient world. In addition to the fact that he calculated the size of our planet, he made a number of important inventions and discoveries. Invented a simple method to determine prime numbers, now called "Erastothenes' sieve".
He drew a "map of the world", in which he showed all parts of the world known at that time to the ancient Greeks. The map was considered one of the best for its time. He developed a system of longitude and latitude and a calendar that included leap years. Invented the armillary sphere, a mechanical device used by early astronomers to demonstrate and predict the apparent movement of stars in the sky. He also compiled a star catalog, which included 675 stars.
Sources:
- The Greek scientist Eratosthenes of Cyrene for the first time in the world calculated the radius of the Earth
- Eratosthenes "Calculation of Earth" s Circumference
- Eratosthenes
How to find the area of a circle? First find the radius. Learn to solve simple and complex problems.
A circle is a closed curve. Any point on the circle line will be the same distance from the center point. A circle is a flat figure, so solving problems with finding the area is easy. In this article, we will look at how to find the area of a circle inscribed in a triangle, trapezoid, square, and described around these figures.
To find the area of a given figure, you need to know what the radius, diameter and number π are.
Radius R is the distance bounded by the center of the circle. The lengths of all R-radii of one circle will be equal.
Diameter D is a line between any two points on a circle that passes through the center point. The length of this segment is equal to the length of the R-radius times 2.
Number π is a constant value, which is equal to 3.1415926. In mathematics, this number is usually rounded up to 3.14.
The formula for finding the area of a circle using the radius:


Examples of solving tasks for finding the S-area of a circle through the R-radius:
A task: Find the area of a circle if its radius is 7 cm.
Solution: S=πR², S=3.14*7², S=3.14*49=153.86 cm².
Answer: The area of the circle is 153.86 cm².
The formula for finding the S-area of a circle in terms of the D-diameter is:
Examples of solving tasks for finding S, if D is known:
————————————————————————————————————————-
A task: Find the S of the circle if its D is 10 cm.
Solution: P=π*d²/4, P=3.14*10²/4=3.14*100/4=314/4=78.5 cm².
Answer: The area of a flat round figure is 78.5 cm².
Finding the S circle if the circumference is known:
First, find what the radius is. The circumference is calculated by the formula: L=2πR, respectively, the radius R will be equal to L/2π. Now we find the area of the circle using the formula through R.
Consider the solution on the example of the problem:
———————————————————————————————————————-
A task: Find the area of a circle if the circumference L is known - 12 cm.
Solution: First we find the radius: R=L/2π=12/2*3.14=12/6.28=1.91.
Now we find the area through the radius: S=πR²=3.14*1.91²=3.14*3.65=11.46 cm².
Answer: The area of a circle is 11.46 cm².


Finding the area of a circle inscribed in a square is easy. The side of the square is the diameter of the circle. To find the radius, you need to divide the side by 2.
The formula for finding the area of a circle inscribed in a square is:
Examples of solving problems on finding the area of a circle inscribed in a square:
———————————————————————————————————————
Task #1: The side of a square figure is known, which is equal to 6 centimeters. Find the S-area of the inscribed circle.
Solution: S=π(a/2)²=3.14(6/2)²=3.14*9=28.26 cm².
Answer: The area of a flat round figure is 28.26 cm².
————————————————————————————————————————
Task #2: Find S of a circle inscribed in a square figure and its radius if one side is a=4 cm.
Decide like this: First find R=a/2=4/2=2 cm.
Now let's find the area of the circle S=3.14*2²=3.14*4=12.56 cm².
Answer: The area of a flat round figure is 12.56 cm².


It is a little more difficult to find the area of a round figure circumscribed by a square. But, knowing the formula, you can quickly calculate this value.
The formula for finding S of a circle circumscribed about a square figure:
Examples of solving tasks for finding the area of a circle described near a square figure:
A task




A circle that is inscribed in a triangular figure is a circle that touches all three sides of the triangle. A circle can be inscribed in any triangular figure, but only one. The center of the circle will be the point of intersection of the bisectors of the angles of the triangle.
The formula for finding the area of a circle inscribed in an isosceles triangle is:


When the radius is known, the area can be calculated using the formula: S=πR².
The formula for finding the area of a circle inscribed in a right triangle is:


Examples of solving tasks:
Task #1


If in this problem you also need to find the area of a circle with a radius of 4 cm, then this can be done using the formula: S=πR²
Task #2


Solution:


Now that you know the radius, you can find the area of the circle in terms of the radius. See the formula above.
Task #3


Area of a circle circumscribed about a right-angled and isosceles triangle: formula, examples of problem solving
All formulas for finding the area of a circle come down to the fact that you first need to find its radius. When the radius is known, then finding the area is simple, as described above.
The area of a circle circumscribed about a right-angled and isosceles triangle is found by the following formula:


Examples of problem solving:


Here is another example of solving a problem using Heron's formula.


Solving such problems is difficult, but they can be mastered if you know all the formulas. Students solve such problems in the 9th grade.
Area of a circle inscribed in a rectangular and isosceles trapezoid: formula, examples of problem solving
An isosceles trapezoid has two equal sides. A rectangular trapezoid has one angle equal to 90º. Consider how to find the area of a circle inscribed in a rectangular and isosceles trapezoid using the example of solving problems.
For example, a circle is inscribed in an isosceles trapezoid, which at the point of contact divides one side into segments m and n.
To solve this problem, you need to use the following formulas:


The area of a circle inscribed in a rectangular trapezoid is found using the following formula:


If the lateral side is known, then you can find the radius through this value. The height of the side of the trapezoid is equal to the diameter of the circle, and the radius is half the diameter. Accordingly, the radius is R=d/2.
Examples of problem solving:


A trapezoid can be inscribed in a circle when the sum of its opposite angles is 180º. Therefore, only an isosceles trapezoid can be inscribed. The radius for calculating the area of a circle circumscribed about a rectangular or isosceles trapezoid is calculated using the following formulas:




Examples of problem solving:


Solution: The large base in this case passes through the center, since an isosceles trapezoid is inscribed in a circle. The center divides this base exactly in half. If the base AB is 12, then the radius R can be found as follows: R=12/2=6.
Answer: The radius is 6.
In geometry, it is important to know the formulas. But it is impossible to remember all of them, so even in many exams it is allowed to use a special form. However, it is important to be able to find the right formula for solving a particular problem. Practice solving different problems for finding the radius and area of a circle to be able to correctly substitute formulas and get accurate answers.
Video: Mathematics | Calculating the area of a circle and its parts
- This is a flat figure, which is a set of points equidistant from the center. All of them are at the same distance and form a circle.
A line segment that connects the center of a circle with points on its circumference is called radius. In each circle, all radii are equal to each other. A line joining two points on a circle and passing through the center is called diameter. The formula for the area of a circle is calculated using a mathematical constant - the number π ..
It is interesting : Number pi. is the ratio of the circumference of a circle to the length of its diameter and is a constant value. The value π = 3.1415926 was used after the work of L. Euler in 1737.
The area of a circle can be calculated using the constant π. and the radius of the circle. The formula for the area of a circle in terms of radius looks like this:
![]()
Consider an example of calculating the area of a circle using the radius. Let a circle with radius R = 4 cm be given. Let's find the area of the figure.
The area of our circle will be equal to 50.24 square meters. cm.
There is a formula the area of a circle through the diameter. It is also widely used to calculate the required parameters. These formulas can be used to find .

Consider an example of calculating the area of a circle through the diameter, knowing its radius. Let a circle be given with a radius R = 4 cm. First, let's find the diameter, which, as you know, is twice the radius.
Now we use the data for the example of calculating the area of a circle using the above formula:
As you can see, as a result we get the same answer as in the first calculations.
Knowledge of the standard formulas for calculating the area of a circle will help in the future to easily determine sector area and it is easy to find the missing quantities.
We already know that the formula for the area of a circle is calculated through the product of the constant value π and the square of the radius of the circle. The radius can be expressed in terms of the circumference of a circle and substitute the expression in the formula for the area of a circle in terms of the circumference:
Now we substitute this equality into the formula for calculating the area of a circle and get the formula for finding the area of \u200b\u200bthe circle, through the circumference

Consider an example of calculating the area of a circle through the circumference. Let a circle be given with length l = 8 cm. Let's substitute the value in the derived formula: 
The total area of the circle will be 5 square meters. cm.
Area of a circle circumscribed around a square

It is very easy to find the area of a circle circumscribed around a square.
This will require only the side of the square and knowledge of simple formulas. The diagonal of the square will be equal to the diagonal of the circumscribed circle. Knowing the side a, it can be found using the Pythagorean theorem: from here.
After we find the diagonal, we can calculate the radius: .
And then we substitute everything into the basic formula for the area of a circle circumscribed around a square:
Circles require a more careful approach and are much less common in B5 tasks. At the same time, the general solution scheme is even simpler than in the case of polygons (see lesson " Areas of polygons on a coordinate grid »).
All that is required in such tasks is to find the radius of the circle R . Then you can calculate the area of the circle using the formula S = πR 2 . It also follows from this formula that it suffices to find R 2 for the solution.
To find these values, it is enough to indicate on the circle a point lying at the intersection of the grid lines. And then use the Pythagorean theorem. Consider specific examples of calculating the radius:
A task. Find the radii of the three circles shown in the figure:
Let's perform additional constructions in each circle:
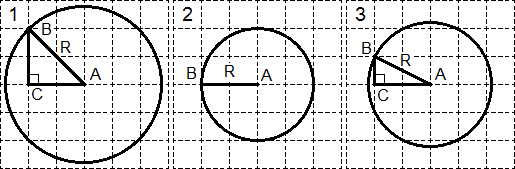
In each case point B is chosen on the circle so as to lie at the intersection of the grid lines. Point C in circles 1 and 3 completes the figure to a right triangle. It remains to find the radii:
Consider triangle ABC in the first circle. According to the Pythagorean theorem: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.
For the second circle, everything is obvious: R = AB = 2.
The third case is similar to the first. From the triangle ABC according to the Pythagorean theorem: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 1 2 + 2 2 \u003d 5.
Now we know how to find the radius of a circle (or at least its square). Therefore, we can find the area. There are tasks where it is required to find the area of a sector, and not the entire circle. In such cases, it is easy to find out what part of the circle is this sector, and thus find the area.
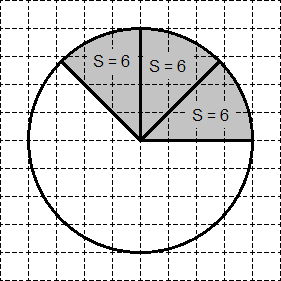
A task. Find the area S of the shaded sector. Indicate S / π in your answer.
Obviously, the sector is one quarter of the circle. Therefore, S = 0.25 S of the circle.
It remains to find the S of the circle - the area of the circle. To do this, we will perform an additional construction:
Triangle ABC is a right triangle. By the Pythagorean theorem, we have: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.
Now we find the area of the circle and the sector: S of the circle = πR 2 = 8π; S = 0.25 S circle = 2π.
Finally, the desired value is equal to S /π = 2.
Sector area with unknown radius
This is a completely new type of task, there was nothing like it in 2010-2011. By condition, we are given a circle of a certain area (namely, the area, not the radius!). Then, inside this circle, a sector is allocated, the area of which is required to be found.
The good news is that these problems are the easiest of all the problems in the square, which are in the exam in mathematics. In addition, the circle and sector are always placed on the coordinate grid. Therefore, to learn how to solve such problems, just take a look at the picture:

Let the original circle have area S of the circle = 80. Then it can be divided into two sectors of area S = 40 each (see step 2). Similarly, each of these "half" sectors can be divided in half again - we get four sectors of area S = 20 each (see step 3). Finally, you can divide each of these sectors into two more - we get 8 sectors - "little pieces". The area of each of these "chunks" will be S = 10.
Please note: there is no smaller division in any USE task in mathematics! Thus, the algorithm for solving problem B-3 is as follows:
- Cut the original circle into 8 sectors - "pieces". The area of each of them is exactly 1/8 of the area of the entire circle. For example, if according to the condition the circle has the area S of the circle = 240, then the “lumps” have the area S = 240: 8 = 30;
- Find out how many "lumps" fit in the original sector, the area of which you want to find. For example, if our sector contains 3 “lumps” with an area of 30, then the area of the desired sector is S = 3 30 = 90. This will be the answer.
That's all! The problem is solved practically orally. If you still don't understand something, buy a pizza and cut it into 8 pieces. Each such piece will be the same sector - "chunk" that can be combined into larger pieces.
And now let's look at examples from the trial exam:
A task. A circle with an area of 40 is drawn on checkered paper. Find the area of the shaded figure.
So, the area of the circle is 40. Divide it into 8 sectors - each with an area of S = 40: 5 = 8. We get:
Obviously, the shaded sector consists of exactly two "small" sectors. Therefore, its area is 2 5 = 10. That's the whole solution!
A task. A circle with an area of 64 is drawn on checkered paper. Find the area of the shaded figure.
Again, divide the entire circle into 8 equal sectors. It is obvious that the area of one of them just needs to be found. Therefore, its area is S = 64: 8 = 8.
A task. A circle with an area of 48 is drawn on checkered paper. Find the area of the shaded figure.
Again, divide the circle into 8 equal sectors. The area of each of them is equal to S = 48: 8 = 6. Exactly three sectors - "smear" are placed in the desired sector (see figure). Therefore, the area of the desired sector is 3 6 = 18.