Shekhovtsov Viktor Anatolievich Private teacher at the IMS "INTERAKTIV".
One of the solutions real options GIA-2010
mathematics.
Information taken from the website http://www.ctege.org/
The table shows the standards for running 30 meters for students in grade 9. Estimate the result of the girl who ran this distance in 5.92 s.
Mark "5"
Mark "4"
Mark "3"
Standard not met
Therefore, the mark "3". Explanation: if the results are greater than or equal to 5.95 s, the standard is not met. ^ ANSWER: 3).
The area of land in the farm is distributed as follows: pastures occupy 14 hectares, arable land - 10 hectares. What is the approximate percentage of the area covered by pastures?
171%
0,58%
1,4%
The total land area on the farm is 14 + 10 = 24 ha. Compose and solve the proportion:
^ ANSWER: 1).
Solution.
If the number is under the sign square root is not a square rational number, then the square root of this number is an irrational number. AT this case the problem is solved in the following way:
^ ANSWER: 2).
Answer:______________
Solution.
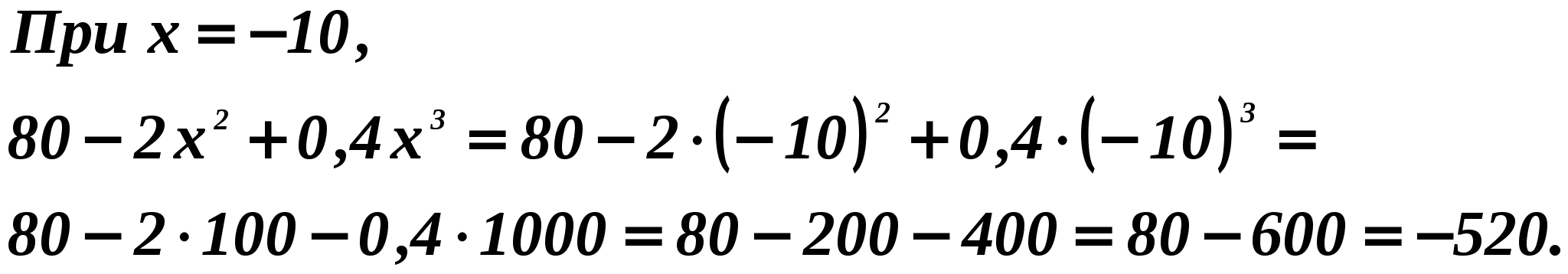
^ ANSWER: -520.
Write an expression to calculate the shaded portion of the rectangle.
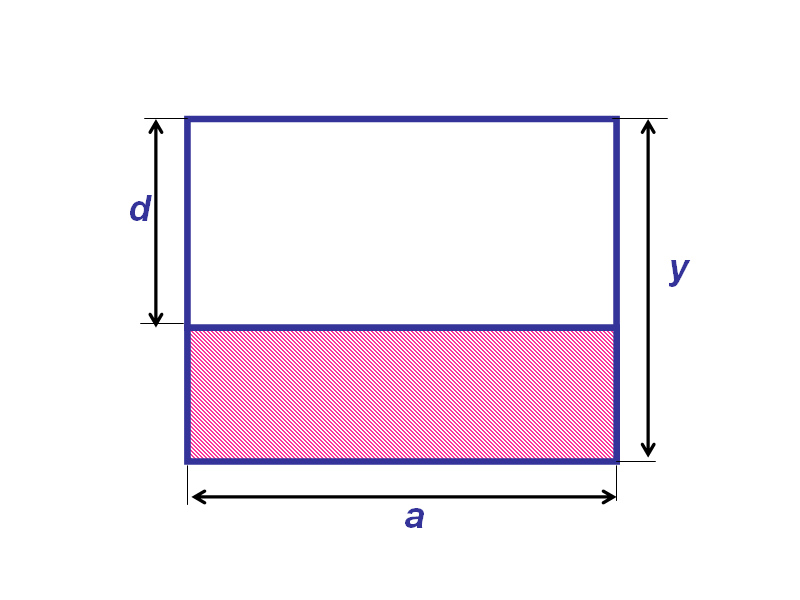
Answer:____________________
Solution.
The length of the shaded rectangle is a , width y-d. Therefore, its area is a(y-d).
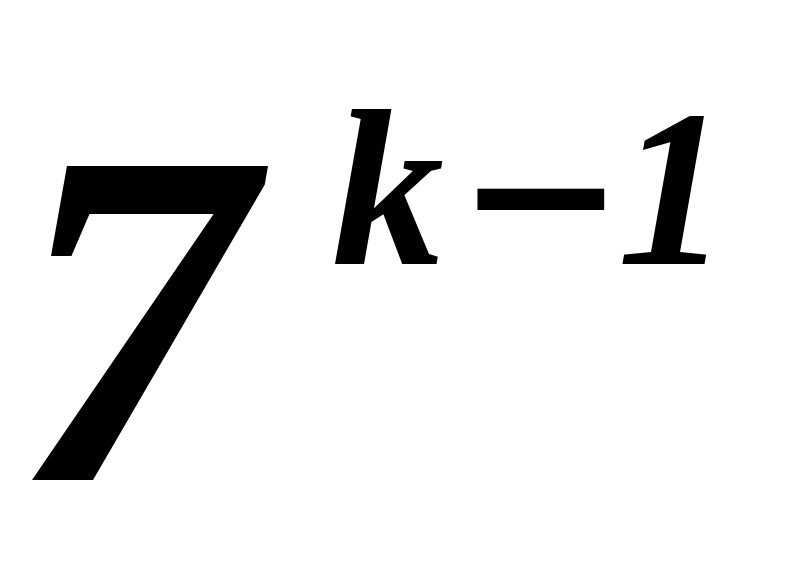
Solution.
^ ANSWER: 2).
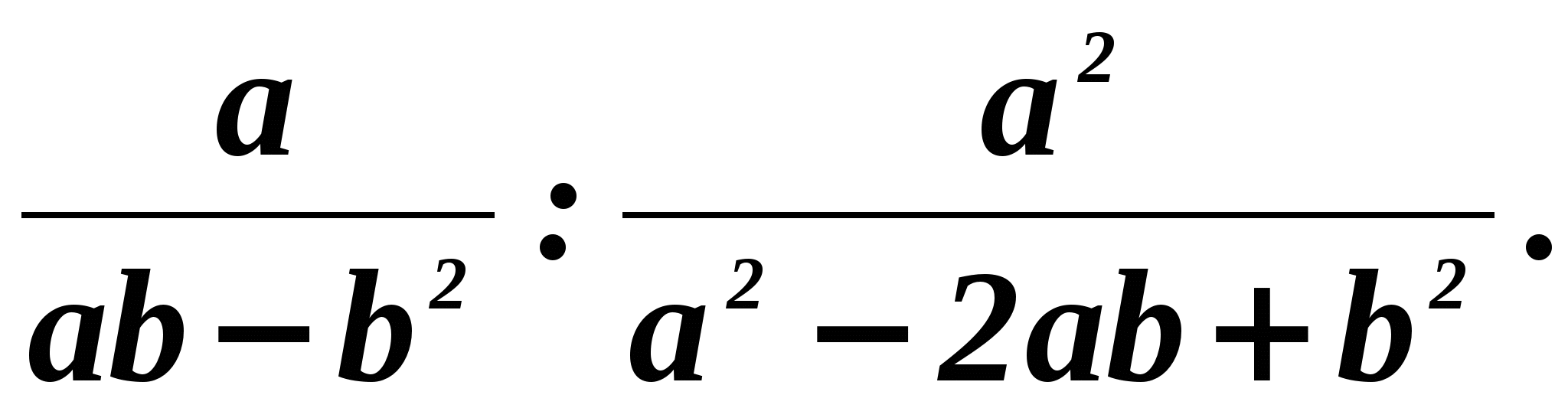
Answer:___________
Solution.
ANSWER: 
.
In which case the transformation is performed wrong?
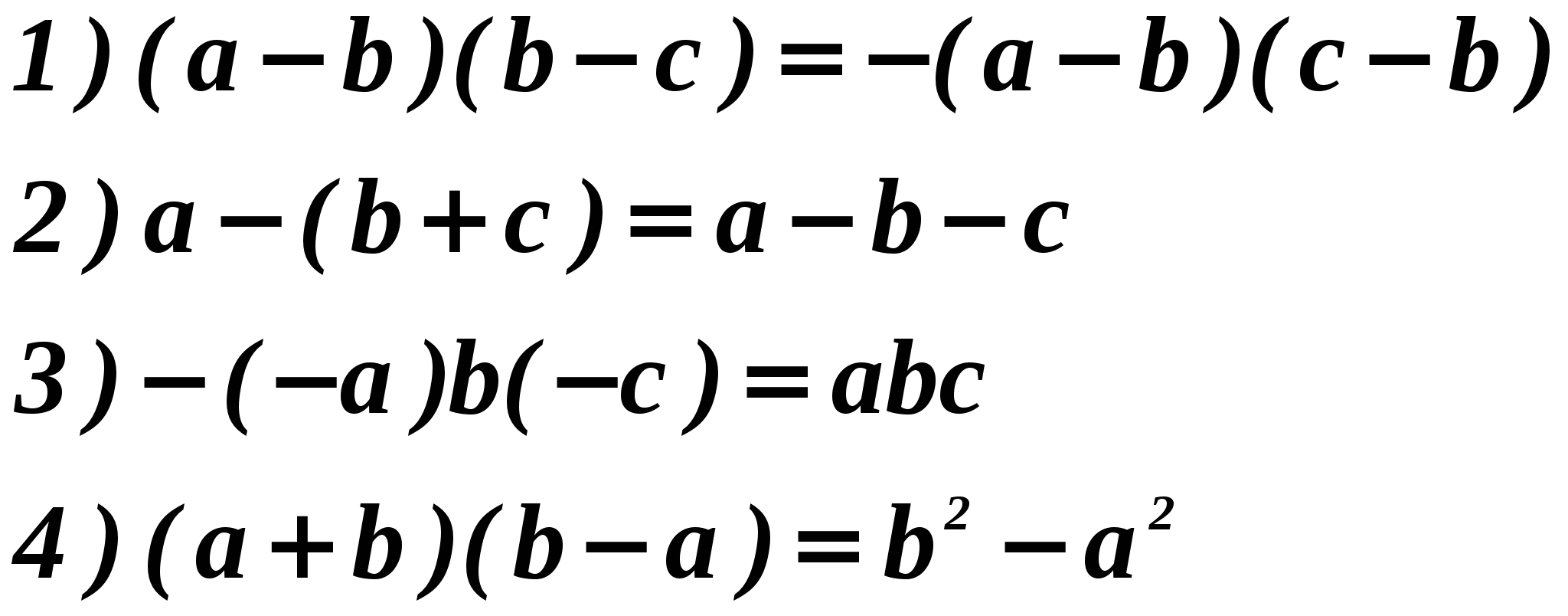
Solution.
You can simply transform one of the parts of the equality and if the other part is obtained, then the transformation is done correctly.
^ ANSWER: 3).
Answer:__________.
Solution.
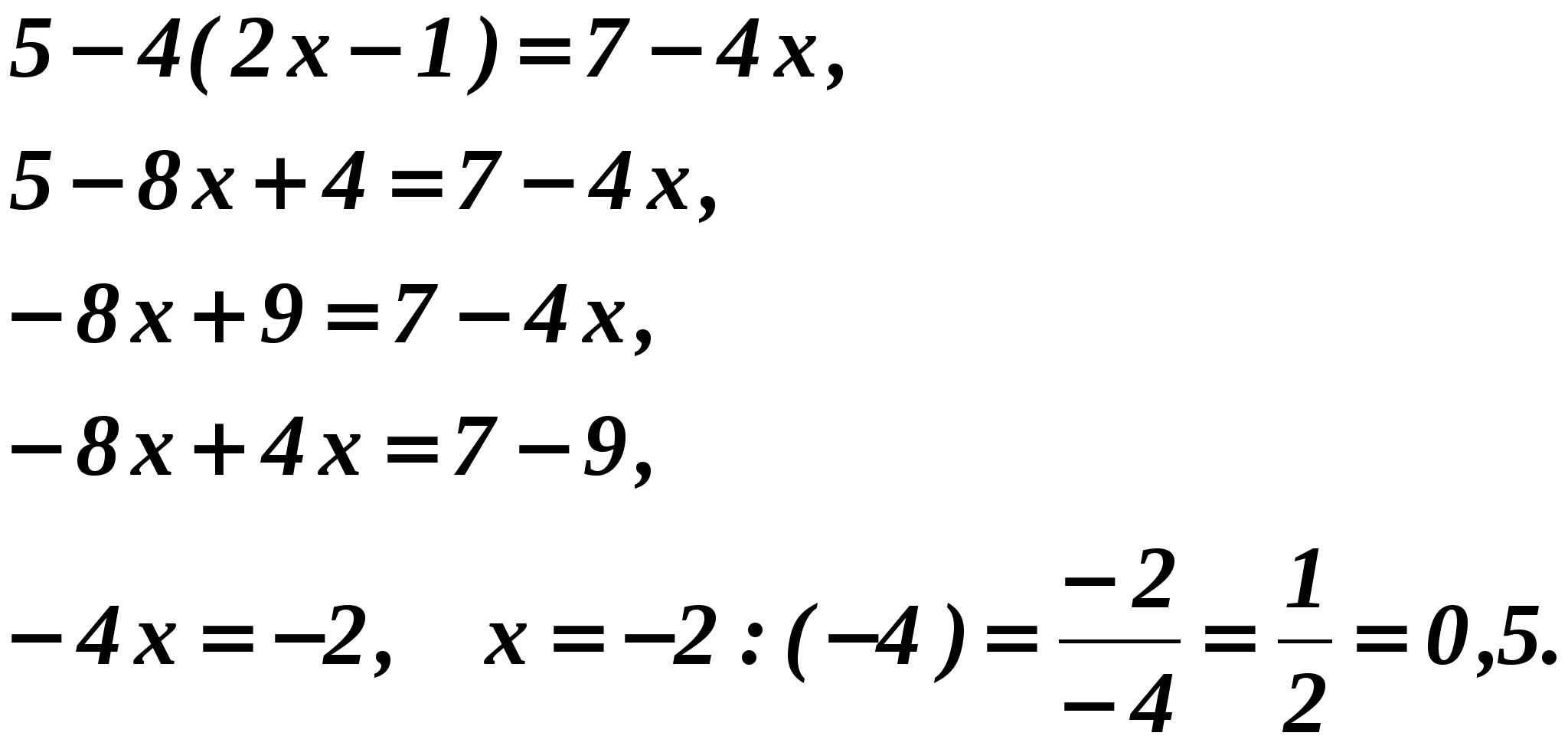
^ ANSWER: 0.5.
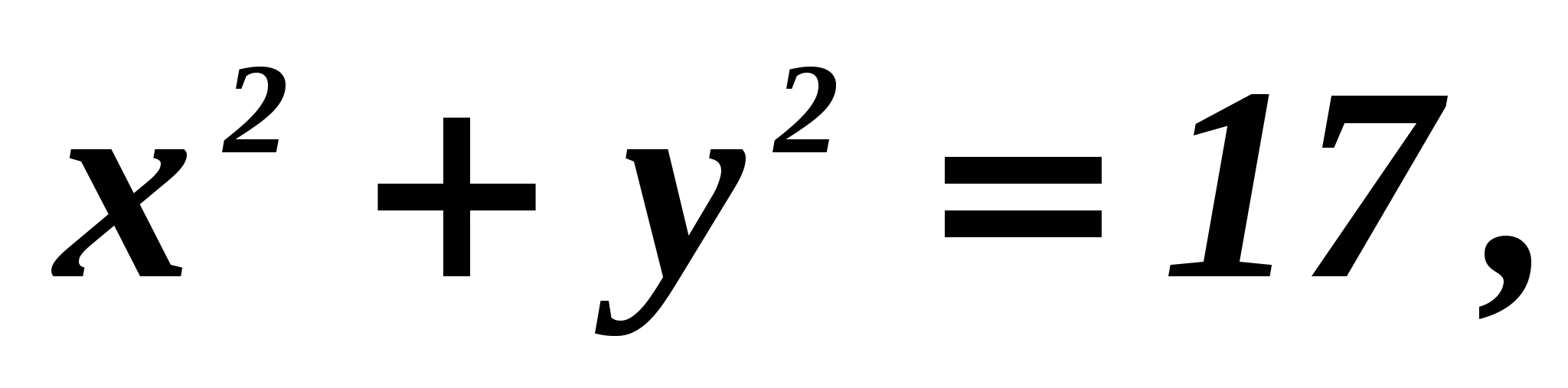
Answer:_____________
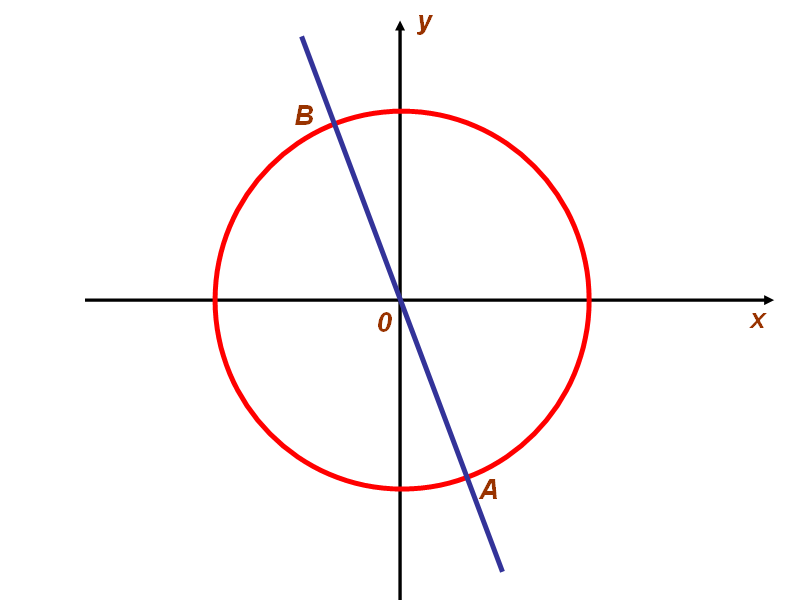
Solution.
We compose and solve the system of equations:
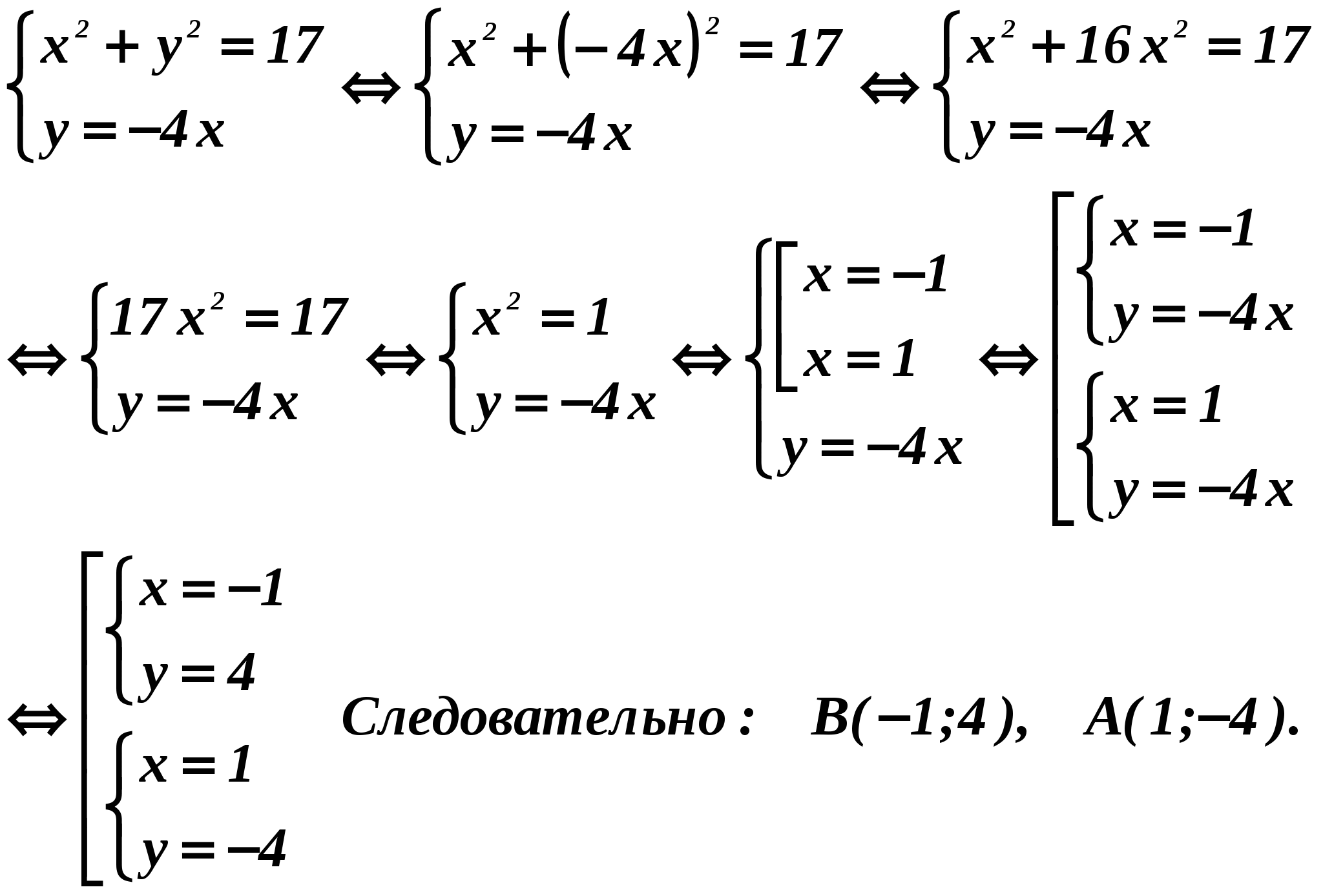
^ ANSWER: (-1;4).
Read the task:
^ Let the motorcyclist's speed be x km/h. Which equation corresponds to the condition of the problem?
Solution.
Let's make a table according to the condition of the problem.
According to the condition of the problem, a motorcyclist and a cyclist traveled the same distance from the city to the village, so we have the equation: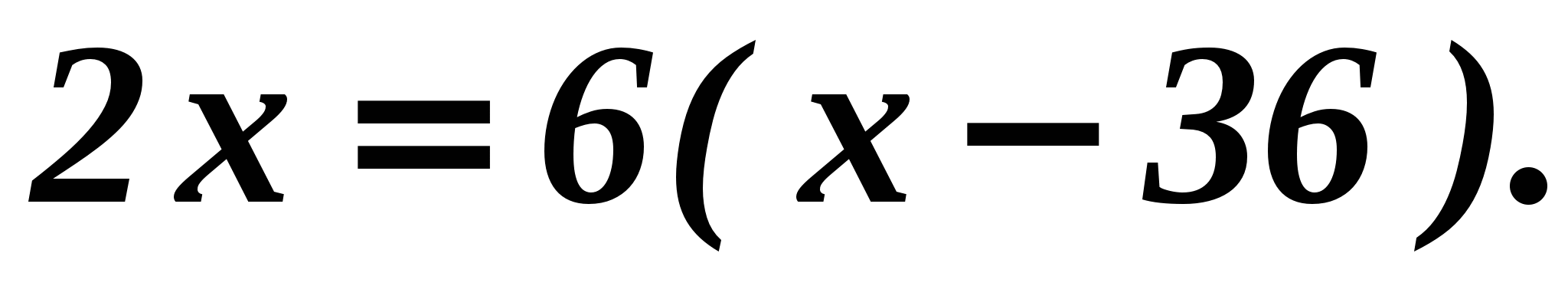 
^ ANSWER: 3).
Three sequences, among which there is an arithmetic progression and a geometric progression, are given by the first few terms. Specify for each sequence the statement corresponding to it.
^ STATEMENT SEQUENCES
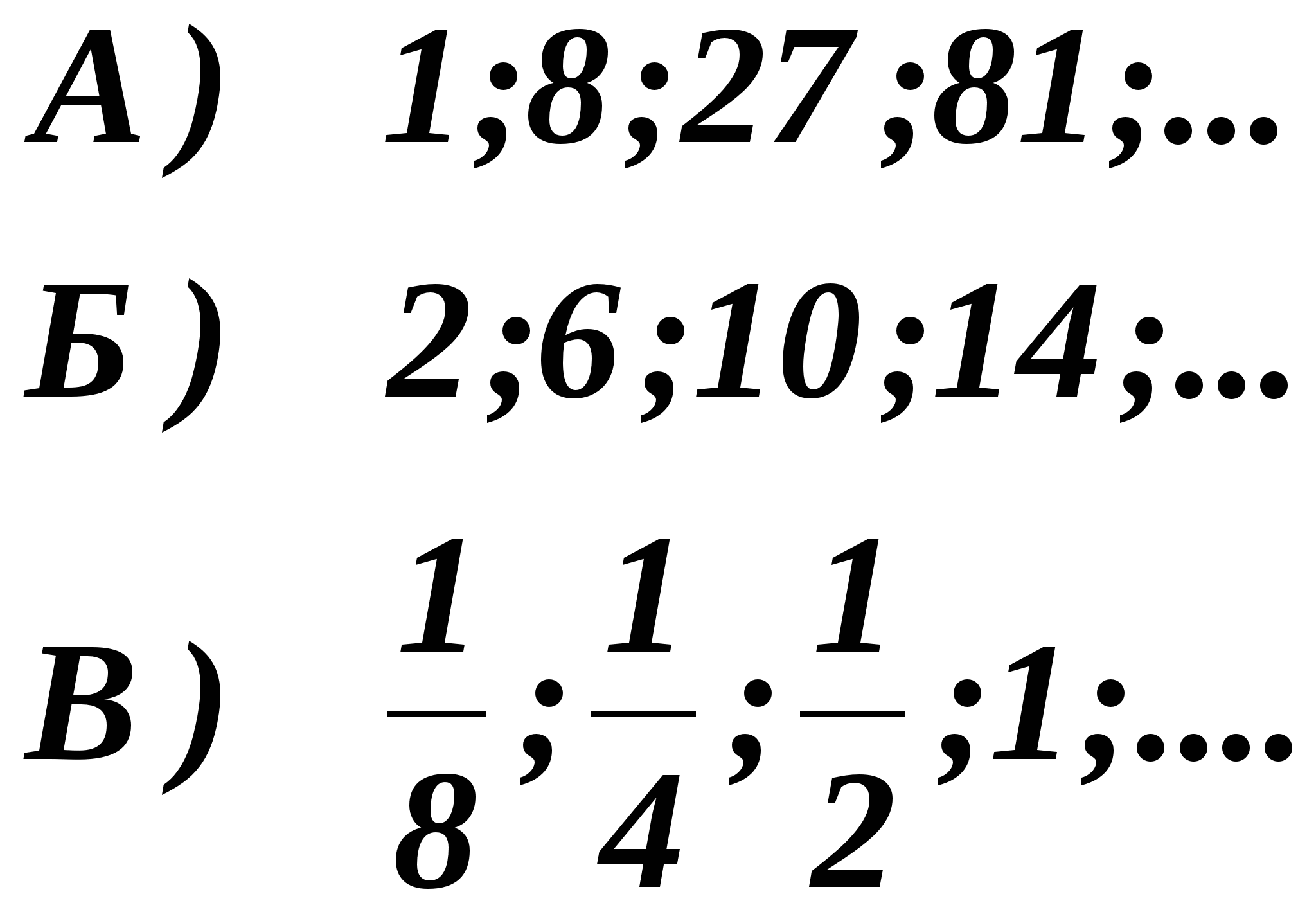
3. Consistency
is neither arithmetic
chesic or geometric
progression.
Answer:
| BUT | B | AT |
AT arithmetic progression the difference between neighboring terms is constant. This condition is met by sequence B):
AT geometric progression the quotient of neighboring members is constant. This condition is met by the sequence B): 
The members of the sequence A) do not fit either the definition of a geometric or the definition of an arithmetic progression.
ANSWER:
| BUT | B | AT |
| 3 | 1 | 2 |
Answer:___________
Solution.
Numbers are marked on the coordinate line a, b, c.
^ Which of the differences a - b, a - c, c - b positive?
a - b, 2) a - c, 3) c - b, 4) none of them.
Solution.
On the coordinate line, the larger of the two numbers is located to the right. That's why:
^ ANSWER: 3).
15. Specify a straight line that has no common points with the graph of the function 
Solution.
The easiest way is to solve it graphically.
Obviously, only a straight y=0 has no common points with the graph of the function y=-x 2 – 4. ^ ANSWER: 4).
The second way (for those who are too lazy to draw).
A purely analytical solution is also possible. Compiling quadratic equations and find out if they have roots.
^ ANSWER: 4).
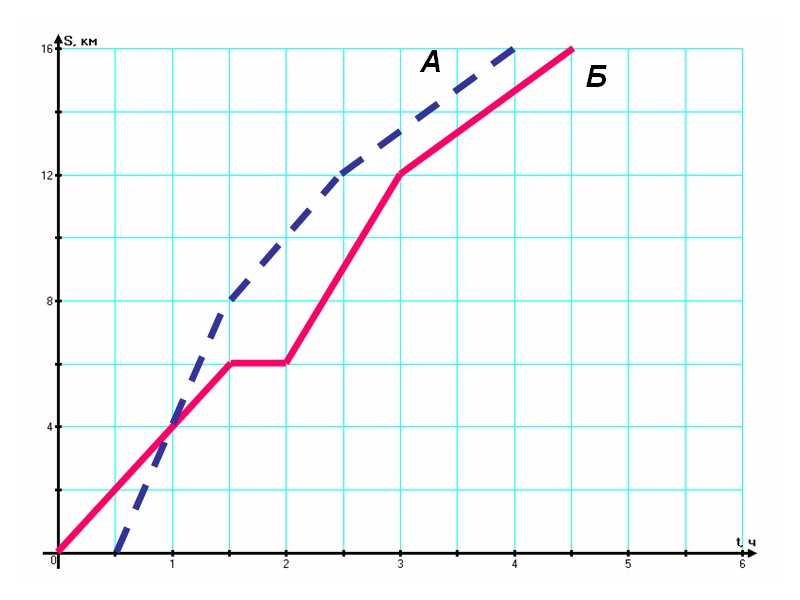
Two groups of tourists - A and B - left the camp site "Yuzhnaya" and went along the same route to the camp site "Severnaya". The figure shows the graphs of their movement. Which of the two groups spent less time on the first 12 km and by how many hours?
Solution.
Group A started moving at a time equal to 0 h 30 min and was 12 km from the Yuzhnaya base at 2 h 30 min. That is, the travel time is 2 hours. Group B traveled the same path from 0:00 to 3:00. That is, its travel time is 3 hours. That is, for the first 12 km of the journey, group A spent 1 hour less than group B.
^ Of the 500 monitors on sale, an average of 15 do not work.
Ovvet___________
Solution.
Let's denote the event A - a randomly purchased monitor works. According to classical definition event probabilities:
^ ANSWER: 0.97.
The cost (in rubles) of a pack of Nezhenka butter in the shops of the microdistrict is recorded: 26, 32, 31, 33, 24, 27, 37. How much does the arithmetic mean of this set of numbers differ from its median?
Solution.
Let's sort this set of numbers in ascending order: 24, 26, 27, 31, 32, 33, 37. Since the number of elements in the series is odd, the median is the value that occupies the middle number series. That is M = 31.
Let's calculate the arithmetic mean of this set of numbers. 
Write the equation of a straight line parallel to a straight line y = 4x - 5 , and passing through the point C(4;9).
The slopes of the parallel lines are equal. Type equation 
describes all lines in the plane xOy,
parallel to a straight line 
To calculate the parameter b
Substitute the coordinates of point C into the equation.
-2, -1, 0, 1, 2.
^ ANSWER: -2, -1, 0, 1, 2.
Three tourists leave the camp site in one direction with an interval of 30 minutes. The first travels at a speed of 3 km/h, the second at a speed of 4 km/h. The third tourist catches up with the first, and after another 30 minutes. catches up with the second. Find the speed of the third tourist.
At the time of the start of the third tourist, the first one will already be 3 km from the camp site. Let the speed of the third tourist bex km/h
, then the speed of approach of the first and third tourists is equal to(x - 3) km / h.
Therefore, the third tourist will catch up with the first at a time equal to 
after leaving the camp site. At the start of the third tourist, the second one is at a distance equal to 
. The speed of approach of the third and second tourist is equal to(x - 4) km / h.
Therefore, the third tourist will catch up with the second at a time equal to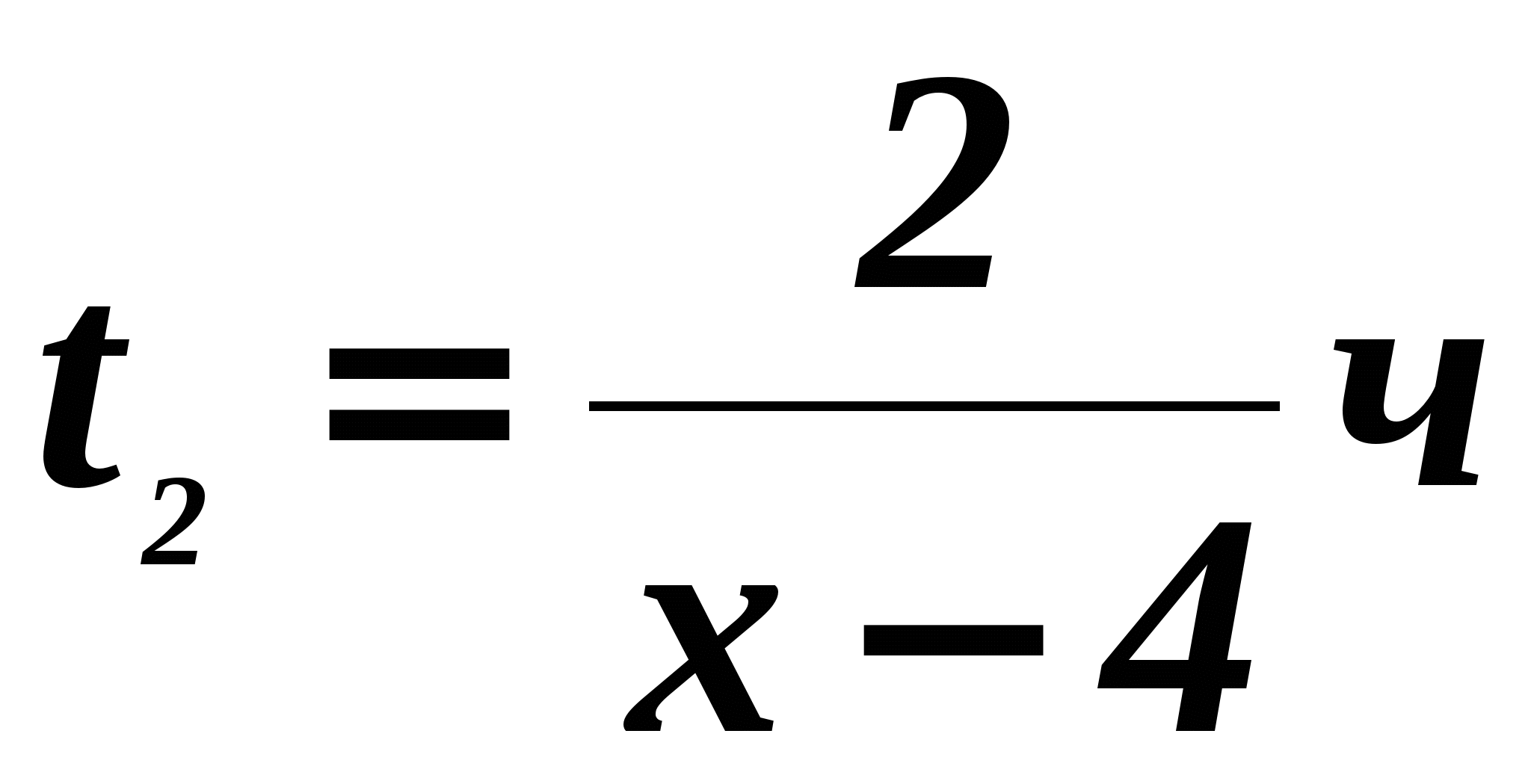 
after leaving the camp. By condition 
.
Let's make and solve the equation:
The first root does not fit the meaning of the problem, therefore, the speed of the third tourist is 5 km/h.
ANSWER: 5 km/h.
The schedules of the movement of tourists are fully consistent with the result.
Follow the tasks of this part with a record of the solution.
Find the value of the expression 41a-11b+15 if \frac(4a-9b+3)(9a-4b+3)=5
Show answer
\begin(array)(l)\frac(4a-9b+3)(9a-4b+3)=5\\4a-9b+3=5(9a-4b+3)\\4a-9b+3= 45a-20b+15\\41a-19b=-12\end(array)
41a-19b+15=-12+15=3
Employees of three enterprises of the holding received bonuses. The bonus to employees of the first enterprise was 30% of the bonuses to employees of the third enterprise, and the bonus to employees of the third enterprise was 70% of the bonus of the second. The bonus to employees of the second enterprise exceeds the bonus to employees of the third by 120 thousand rubles. What is the amount of the total premium accrued by the holding to all three enterprises? Give your answer in thousand rubles.
Show answer
Let the sum of the premium of the second enterprise be equal to x thousand rubles. Then the sum of the premium of the third enterprise is 0.7x thousand rubles, and the sum of the premium of the first enterprise is 0.3 * 0.7x thousand rubles. The bonus to employees of the second enterprise exceeds the bonus to employees of the third by (x - 0.7x) thousand rubles, and by the condition - by 120 thousand rubles.
Let's make the equation: x - 0.7x \u003d 120
Having solved the equation, we get: x \u003d 400. Then the amount of the total premium is (x + 0.7x + 0.3 * 0.7x) thousand rubles. Substituting x=400, we get 764 thousand rubles
Plot the function y=x^2-\vert4x+5\vert and determine for what values of m the line y = m has exactly three common points.
Show answer
Let's open the module: at 4x + 5< 0 функция задаётся формулой у = х 2 + 4х + 5,
and for 4x + 5 \geq 0 - by the formula y \u003d x 2 - 4x - 5, i.e.:
y=\left\(\begin(array)(l)x^2+4x+5,\;when\;x<-\frac54\\х^2-4х-5,\;при\;х\geq-\frac54\end{array}\right.
For all x< -5/4 строим график функции у = х 2 + 4х + 5 = (х + 2) 2 + 1 - это парабола без растяжений, ветви вверх, вершина в точке (-2;1).
Now for all x \geq -5/4 we build y \u003d x 2 - 4x - 5 \u003d (x - 2) 2 - 9 - a parabola without stretching, branches up, top (2; -9). The result should be the following:
The straight line y \u003d m is parallel to the OX axis. It can be seen from the graph that at y = 1 and y = 25/16, this line intersects the graph at three points. y \u003d 25/16 is determined from the conditions x \u003d -5/4 and y \u003d (x + 2) 2 +1.
Answer: (1; 25/16)
The point H is the base of the height BH drawn from the vertex of the right angle B of the right triangle ABC. A circle with diameter BH intersects sides AB and CB at points P and K, respectively. Find RK if VN = 13.
Show answer
Right triangle BPK is inscribed in a circle, then PK is the diameter, so BH=PK=13
Quadrilateral ABCD with diagonal AC is inscribed in a circle, AB 2 + BC 2 = AC 2. Prove that S ABCD = 1/2 (AB BC + AD DC).
A circle can be inscribed in an isosceles trapezoid. Find the distance from the point of intersection of the diagonals of a trapezoid to its larger base if the perimeter of the trapezoid is 68 and the area is 255.
