Ongelman muotoilu

Tehtävänä on perehdyttää käyttäjä numeeristen menetelmien peruskäsitteisiin, kuten determinantti- ja käänteimatriisiin, sekä erilaisiin tapoihin laskea niitä. Tässä teoreettisessa raportissa yksinkertaisella ja ymmärrettävällä kielellä esitellään ensin peruskäsitteet ja määritelmät, joiden pohjalta tehdään jatkotutkimusta. Käyttäjällä ei välttämättä ole erityisosaamista numeeristen menetelmien ja lineaarialgebran alalla, mutta hän pystyy helposti hyödyntämään tämän työn tuloksia. Selvyyden vuoksi on annettu C ++ -ohjelmointikielellä kirjoitettu ohjelma matriisideterminantin laskemiseksi useilla menetelmillä. Ohjelmaa käytetään laboratoriotelineenä raportin kuvien luomiseen. Ja myös tutkimusmenetelmiä lineaaristen algebrallisten yhtälöiden järjestelmien ratkaisemiseksi suoritetaan. Käänteimatriisin laskemisen hyödyttömyys on todistettu, joten paperi tarjoaa optimaalisempia tapoja ratkaista yhtälöitä ilman sitä. Selitetään, miksi determinanttien ja käänteisten matriisien laskentamenetelmiä on niin monia erilaisia ​​ja niiden puutteita analysoidaan. Myös determinantin laskennan virheet huomioidaan ja saavutettu tarkkuus arvioidaan. Työssä käytetään venäjän termien lisäksi myös niiden englanninkielisiä vastineita ymmärtämään, millä nimillä numeerisia toimenpiteitä kirjastoista etsitään ja mitä niiden parametrit tarkoittavat.

Perusmääritelmät ja yksinkertaiset ominaisuudet

Determinantti

Esitetään minkä tahansa kertaluvun neliömatriisin determinantin määritelmä. Tämä määritelmä tulee toistuva, eli määrittääksesi mikä on järjestysmatriisin determinantti, sinun on jo tiedettävä, mikä on järjestysmatriisin determinantti. Huomaa myös, että determinantti on olemassa vain neliömatriiseille.

Neliömatriisin determinanttia merkitään tai det .

Määritelmä 1. määräävä tekijä neliömatriisi toinen tilausnumero kutsutaan .

määräävä tekijä neliömatriisi järjestyksessä , kutsutaan numeroksi

missä on järjestysmatriisin determinantti, joka saadaan matriisista poistamalla ensimmäinen rivi ja sarake numerolla .

Selvyyden vuoksi kirjoitamme ylös, kuinka voit laskea neljännen kertaluvun matriisin determinantin:

Kommentti. Poikkeustapauksissa käytetään määritelmään perustuvaa varsinaista determinanttien laskentaa kolmannen asteen matriiseille. Laskenta suoritetaan pääsääntöisesti muiden algoritmien mukaan, joita käsitellään myöhemmin ja jotka vaativat vähemmän laskentatyötä.

Kommentti. Määritelmässä 1 olisi tarkempaa sanoa, että determinantti on funktio, joka on määritelty neliöjärjestyksen matriisien joukossa ja ottaa arvot numerojoukosta.

Kommentti. Kirjallisuudessa termin "determinantti" sijasta käytetään myös termiä "determinantti", jolla on sama merkitys. Sanasta "determinantti" ilmestyi nimitys det.

Tarkastellaan joitain determinanttien ominaisuuksia, jotka muotoilemme väitteiden muodossa.

Lausunto 1. Matriisia transponoitaessa determinantti ei muutu, eli .

Lausuma 2. Neliömatriisien tulon determinantti on yhtä suuri kuin tekijöiden determinanttien tulo, eli .

Lausunto 3. Jos matriisin kaksi riviä vaihdetaan, sen determinantti vaihtaa etumerkkiä.

Lausunto 4. Jos matriisissa on kaksi identtistä riviä, sen determinantti on nolla.

Jatkossa meidän on lisättävä merkkijonoja ja kerrottava merkkijono numerolla. Suoritamme nämä toiminnot riveille (sarakkeille) samalla tavalla kuin rivimatriiseille (sarakematriiseille), eli elementti elementiltä. Tuloksena on rivi (sarake), joka ei yleensä vastaa alkuperäisen matriisin rivejä. Rivien (sarakkeiden) lisäämisen ja niiden numerolla kertomisen yhteydessä voidaan puhua myös rivien (sarakkeiden) lineaarisista yhdistelmistä eli summista numeerisilla kertoimilla.

Lausunto 5. Jos matriisin rivi kerrotaan luvulla, sen determinantti kerrotaan tällä luvulla.

Lausunto 6. Jos matriisi sisältää nollarivin, niin sen determinantti on nolla.

Lausunto 7. Jos yksi matriisin riveistä on yhtä suuri kuin toinen kerrottuna luvulla (rivit ovat verrannollisia), matriisin determinantti on nolla.

Lausunto 8. Olkoon matriisin i:s rivi tältä . Sitten, jossa matriisi saadaan matriisista korvaamalla i. rivi rivillä , ja matriisi saadaan korvaamalla i:s rivi rivillä .

Lausunto 9. Jos yksi matriisin rivistä lisätään toiseen, kerrottuna numerolla, matriisin determinantti ei muutu.

Lausunto 10. Jos yksi matriisin riveistä on lineaarinen yhdistelmä sen muista riveistä, matriisin determinantti on nolla.

Määritelmä 2. Algebrallinen lisäys Matriisielementille kutsutaan lukua, joka on yhtä suuri kuin , jossa on matriisista poistamalla i. rivi ja j:s sarake saadun matriisin determinantti. Matriisielementin algebrallinen komplementti on merkitty .

Esimerkki. Päästää . Sitten

Kommentti. Algebrallisten lisäysten avulla 1 determinantin määritelmä voidaan kirjoittaa seuraavasti:

Lausunto 11. Determinantin hajottaminen mielivaltaisessa merkkijonossa.

Matriisideterminantti täyttää kaavan

Esimerkki. Laskea .

Ratkaisu. Käytetään kolmannen rivin laajennusta, se on kannattavampaa, koska kolmannella rivillä kaksi numeroa kolmesta on nollia. Saada

Lausunto 12. Neliömatriisille, jonka järjestys on , meillä on suhde .

Lausunto 13. Kaikki riveille formuloidun determinantin ominaisuudet (lauseet 1 - 11) pätevät myös sarakkeille, erityisesti j:nnen sarakkeen determinantin hajotelma pätee. ja tasa-arvo osoitteessa .

Lausunto 14. Kolmiomatriisin determinantti on yhtä suuri kuin sen päädiagonaalin elementtien tulo.

Seuraus. Identiteettimatriisin determinantti on yhtä suuri kuin yksi, .

Johtopäätös. Yllä luetellut ominaisuudet mahdollistavat riittävän korkean asteen matriisien determinanttien löytämisen suhteellisen pienellä määrällä laskelmia. Laskenta-algoritmi on seuraava.

Algoritmi nollien luomiseksi sarakkeeseen. Olkoon se vaadittava laskemaan järjestysdeterminantti . Jos , vaihda ensimmäinen rivi ja mikä tahansa muu rivi, jonka ensimmäinen elementti ei ole nolla. Seurauksena on, että determinantti , on sama kuin uuden matriisin determinantti päinvastaisella merkillä. Jos jokaisen rivin ensimmäinen alkio on nolla, niin matriisissa on nollasarake ja lauseiden 1, 13 mukaan sen determinantti on nolla.

Joten katsomme sen jo alkuperäisessä matriisissa . Jätä ensimmäinen rivi ennalleen. Lisätään toiselle riville ensimmäinen rivi kerrottuna numerolla . Sitten toisen rivin ensimmäinen elementti on yhtä suuri .

Uuden toisen rivin jäljellä olevat elementit merkitään , . Uuden matriisin determinantti lauseen 9 mukaan on yhtä suuri kuin . Kerro ensimmäinen rivi numerolla ja lisää se kolmanteen. Uuden kolmannen rivin ensimmäinen elementti on yhtä suuri kuin

Uuden kolmannen rivin jäljellä olevat elementit merkitään , . Uuden matriisin determinantti lauseen 9 mukaan on yhtä suuri kuin .

Jatkamme nollien saamista merkkijonojen ensimmäisten elementtien sijaan. Lopuksi kerromme ensimmäisen rivin numerolla ja lisäämme sen viimeiselle riville. Tuloksena on matriisi, jota merkitään ja jolla on muoto

ja . Matriisin determinantin laskemiseksi käytämme ensimmäisen sarakkeen laajennusta

Siitä lähtien

Järjestysmatriisin determinantti on oikealla puolella. Käytämme siihen samaa algoritmia, ja matriisin determinantin laskenta supistetaan järjestysmatriisin determinantin laskentaan. Prosessi toistetaan, kunnes saavutetaan toisen kertaluvun determinantti, joka lasketaan määritelmän mukaan.

Jos matriisilla ei ole erityisiä ominaisuuksia, ei ole mahdollista merkittävästi vähentää laskelmien määrää verrattuna ehdotettuun algoritmiin. Toinen tämän algoritmin hyvä puoli on, että tietokoneelle on helppo kirjoittaa ohjelma suurten kertalukujen matriisien determinanttien laskemiseksi. Determinanttien laskentaan tarkoitetuissa vakioohjelmissa tätä algoritmia käytetään pienin muutoksin, jotka liittyvät pyöristysvirheiden ja syötetietojen virheiden vaikutuksen minimoimiseen tietokonelaskelmissa.

Esimerkki. Laske matriisideterminantti .

Ratkaisu. Ensimmäinen rivi jätetään ennalleen. Toiselle riville lisäämme ensimmäisen, kerrottuna numerolla:

Determinantti ei muutu. Kolmannelle riville lisäämme ensimmäisen, kerrottuna numerolla:

Determinantti ei muutu. Neljännelle riville lisäämme ensimmäisen, kerrottuna numerolla:

Determinantti ei muutu. Tuloksena saamme

Saman algoritmin avulla laskemme oikeanpuoleisen kertaluvun 3 matriisin determinantin. Jätämme ensimmäisen rivin ennalleen, toiselle riville lisäämme ensimmäisen, kerrottuna numerolla :

Kolmannelle riville lisäämme ensimmäisen, kerrottuna numerolla :

Tuloksena saamme

Vastaus. .

Kommentti. Vaikka laskelmissa käytettiin murtolukuja, tulos oli kokonaisluku. Todellakin, käyttämällä determinanttien ominaisuuksia ja sitä tosiasiaa, että alkuperäiset luvut ovat kokonaislukuja, toiminnot murtolukujen kanssa voitaisiin välttää. Mutta insinöörikäytännössä luvut ovat erittäin harvoin kokonaislukuja. Siksi determinantin elementit ovat pääsääntöisesti desimaalimurtolukuja, eikä laskelmien yksinkertaistamiseksi ole suositeltavaa käyttää temppuja.

käänteinen matriisi

Määritelmä 3. Matriisia kutsutaan käänteinen matriisi neliömatriisille jos .

Määritelmästä seuraa, että käänteimatriisi on neliömatriisi, joka on samaa luokkaa kuin matriisi (muuten yksi tuloista tai ei olisi määritelty).

Matriisin käänteismatriisi on merkitty . Eli jos on olemassa, niin .

Käänteismatriisin määritelmästä seuraa, että matriisi on matriisin käänteinen, eli . Matriisit ja voidaan sanoa olevan käänteisiä toisilleen tai keskenään käänteisiä.

Jos matriisin determinantti on nolla, sen käänteistä ei ole olemassa.

Koska käänteimatriisin löytämiseksi on tärkeää, onko matriisin determinantti yhtä suuri kuin nolla vai ei, otamme käyttöön seuraavat määritelmät.

Määritelmä 4. Kutsutaan neliömatriisia rappeutunut tai erityinen matriisi, jos ja ei-degeneroitunut tai ei-singulaarinen matriisi, jos.

lausunto. Jos käänteimatriisi on olemassa, se on ainutlaatuinen.

lausunto. Jos neliömatriisi on ei-degeneroitunut, niin sen käänteinen on olemassa ja (1) missä ovat algebralliset lisäykset elementteihin .

Lause. Käänteinen matriisi neliömatriisille on olemassa, jos ja vain jos matriisi on ei-singulaarinen, käänteimatriisi on ainutlaatuinen ja kaava (1) on voimassa.

Kommentti. Erityistä huomiota tulee kiinnittää algebrallisten lisäysten ottamisiin paikkoihin käänteismatriisikaavassa: ensimmäinen indeksi näyttää numeron sarakkeessa, ja toinen on numero rivit, johon laskettu algebrallinen komplementti tulee kirjoittaa.

Esimerkki. .

Ratkaisu. Determinantin löytäminen

Koska , niin matriisi on ei-degeneroitunut, ja sen käänteisarvo on olemassa. Algebrallisten lisäysten etsiminen:

Muodostetaan käänteismatriisi sijoittamalla löydetyt algebralliset lisäykset siten, että ensimmäinen indeksi vastaa saraketta ja toinen riviä: (2)

Tuloksena oleva matriisi (2) on vastaus ongelmaan.

Kommentti. Edellisessä esimerkissä olisi tarkempaa kirjoittaa vastaus näin:
(3)

Merkintä (2) on kuitenkin kompaktimpi ja sen avulla on helpompi suorittaa lisälaskelmia, jos sellaisia ​​on. Siksi vastauksen kirjoittaminen muotoon (2) on parempi, jos matriisien alkiot ovat kokonaislukuja. Ja päinvastoin, jos matriisin elementit ovat desimaalilukuja, on parempi kirjoittaa käänteismatriisi ilman tekijää edessä.

Kommentti. Käänteimatriisia etsittäessä joudut suorittamaan melko paljon laskutoimituksia ja epätavallisen säännön algebrallisten summausten järjestämiseksi lopullisessa matriisissa. Siksi virheen mahdollisuus on suuri. Virheiden välttämiseksi sinun tulee tehdä tarkistus: laske alkuperäisen matriisin tulo lopullisella tavalla tai toisessa. Jos tuloksena on identiteettimatriisi, käänteismatriisi löytyy oikein. Muussa tapauksessa sinun on etsittävä virhettä.

Esimerkki. Etsi matriisin käänteisarvo .

Ratkaisu. - olemassa.

Vastaus: .

Johtopäätös. Käänteimatriisin löytäminen kaavan (1) avulla vaatii liian monta laskutoimitusta. Neljännen ja korkeamman asteen matriiseille tämä ei ole hyväksyttävää. Todellinen algoritmi käänteismatriisin löytämiseksi annetaan myöhemmin.

Determinantti- ja käänteimatriisin laskeminen Gaussin menetelmällä

Gaussin menetelmää voidaan käyttää determinantti- ja käänteimatriisin löytämiseen.

Nimittäin matriisideterminantti on yhtä suuri kuin det .

Käänteismatriisi löydetään ratkaisemalla lineaarisia yhtälöjärjestelmiä Gaussin eliminointimenetelmällä:

Missä on identiteettimatriisin j:s sarake, on vaadittu vektori.

Tuloksena olevat ratkaisuvektorit - muodostavat luonnollisesti matriisin sarakkeet, koska .

Determinantin kaavat

1. Jos matriisi on epäsingulaarinen, niin ja (johtavien elementtien tulo).

Koska käänteimatriisin löytämiseksi on tärkeää, onko matriisin determinantti yhtä suuri kuin nolla vai ei, otamme käyttöön seuraavat määritelmät.

Määritelmä 14.9 Kutsutaan neliömatriisia rappeutunut tai erityinen matriisi, jos ja ei-degeneroitunut tai ei-singulaarinen matriisi, jos.

Tarjous 14.21 Jos käänteimatriisi on olemassa, se on ainutlaatuinen.

Todiste. Olkoon kaksi matriisia ja matriisin käänteisarvo. Sitten

Tämän seurauksena,.

Cramerin sääntö.

Olkoon matriisiyhtälö AX=B

Missä ; on determinantista saatu determinantti D korvaus i-th sarake matriisin vapaiden jäsenten sarakkeella B:

Todiste Lause on jaettu kolmeen osaan:

1. Järjestelmän (1) ratkaisu on olemassa ja on ainutlaatuinen.

2. Yhtälöt (2) ovat seurausta matriisiyhtälöstä (1).

3. Yhtälöt (2) sisältävät matriisiyhtälön (1).

Koska , on olemassa myös ainutlaatuinen käänteimatriisi .
Kerrotaan vasemmalla olevan matriisiyhtälön (1) molemmat osat luvulla , saadaan tämän yhtälön ratkaisu:

ainutlaatuisuus käänteismatriisi todistaa lauseen ensimmäisen osan.

Siirrytään todistukseen henkilökohtainen kirjeenvaihto kaavojen (1) ja (2) välissä.

Käyttämällä kaavaa (4) saamme lausekkeen for i-th elementti. Tätä varten sinun on kerrottava i-matriisin rivi

saraketta kohden B.

Olettaen että i- liittyvän matriisin rivi koostuu algebrallisista lisäyksistä, saamme seuraavan tuloksen:

Cramerin kaavojen johtaminen on valmis. Osoittakaamme nyt, että ilmaisuja

Muutetaan summausjärjestys tuloksena olevan lausekkeen oikealla puolella:

missä on delta Kronecker -symboli.

Ottaen huomioon, että delta-symboli poistaa yhden indeksin summauksen, saamme vaaditun tuloksen:

Monimutkaiset luvut: Ideana on määritellä uusia objekteja tuttujen avulla. Reaaliluvut sijaitsevat suoralla viivalla. Kun siirrymme tasolle, saamme kompleksiluvut. Määritelmä: Kompleksiluku on reaalilukupari z = (a,b). Lukua a = Re z kutsutaan reaaliosaksi ja b = Im z kompleksiluvun z imaginaariosaksi.

Operaatiot kompleksiluvuille: Kompleksiluvut z1 z2 ovat Z1 = z2 ⇔ Re z1 = Re z2 & Im z1 = Im z2. Lisäys: Z=z1+z2. ⇔Rez=Rez1+Rez2 & Imz1+ Imz2. Numero (0,0) on merkitty 0:lla. Tämä on neutraali elementti. Varmistetaan, että kompleksilukujen summauksella on samanlaisia ​​ominaisuuksia kuin reaalilukujen yhteenlaskemisella. (1. Z1+ z2 = z2 + z1 – kommutatiivisuus; 2. Z1 + (z2 + z3) = (z1 + z2) + z3 – assosiatiivisuus; 3. Z1 + 0 = z1 - nollan olemassaolo (neutraali elementti); 4. z + (−z) = 0 - vastakkaisen alkion olemassaolo). Kertominen: z= z1 z2⇔Re z=Re z1 Re z2-Im z1 Im z2 & Im z1=Im z1 Re z2+Im z2 Re z1. Kompleksiluku z on reaaliakselilla, jos Imz = 0 . Tällaisten lukujen operaatioiden tulokset ovat samat kuin tavallisten reaalilukujen operaatioiden tulokset. Kompleksilukujen kertolaskulla on sulkemisen, kommutatiivisuuden ja assosiatiivisuuden ominaisuudet. Lukua (1,0) merkitään 1. Se on kertomalla neutraali alkio Jos a∈ R, z ∈C , niin Re(az) = aRe z, Im(az) = a Imz . Määritelmä Numero (0,1) on merkitty i ja sitä kutsutaan imaginaariyksiköksi. Tässä merkinnässä saadaan kompleksiluvun esitys algebrallisessa muodossa: z = a + ib, a,b∈ R. i = -1.(a,b)=(a,0)+(0,b);(a,0)+b(0,1)=a+ib=z; (a1+ib)(a2+ib2)=a1a2+i(a1b2+1-a2b1)-blb2; (a+ib)(1+0i)=a+ib; z(a,b), z(0+i0)=0; z! = 0; a 2 + b 2 > 0 (a + ib) (a-ib / a 2 + b 2) = 1. Numeroa kutsutaan konjugaatti z:hen, jos Re =Rez; Olen =- olen z.

= + ; = ; z =(a+ib)(a-ib)=a 2 +b 2 Luvun z moduuli on reaaliluku| z |= . Reilu kaava| z| 2 = z Määritelmästä seuraa, että z ≠ 0⇔| z|≠ 0. z -1 = /|z| 2 (1)

Kompleksiluvun trigonometrinen muoto: a=rcos(t); b=r sin(t). Z=a+ib=r(cos(t)+isin(t))(2) kompleksiluvun t-argumentti. Z1=z2 =>|z1|=|z2|

arg(z1)-arg(z2)=2pk.

Z1=r1(cos(t1)+isin(t1), Z2=r2(cos(t2)+isin(t2)), Z3=z1 z2=T1T2(cos(t1+t2)+isin(t1+t2)( yksi)

Arg(z1z2)=arg(z1)+arg(z2) (2)

Z!=0 z-1 = /|z| 2 =1/r(cos(-t)+i(sin(-t)) Z=r(cos(t)+istn(t))

R(cos(t)-isin(t))

Määritelmä: Asteen n juuri yksiköstä on yhtälön ratkaisu z n =1 Ehdotus. Yhtenäisyydellä on n erillistä n:nnettä juurta. Ne kirjoitetaan muodossa z = cos(2 π k / n) + isin(2 π k / n), k = 0,..., n −1 . Lause. Kompleksilukujen joukossa yhtälöllä on aina n ratkaisua Z=r(cos(t)+isin(t)); z n =r n (cos(nt)+isin(nt))=1(cos(0)+isin(0))=>z n =1 .Z-kokonaisluvut. K kuuluu Z:hen. k=2=E2=E n-1 En; En = 1; En+p =Ep. Siten on todistettu, että yhtälön ratkaisut ovat säännöllisen n-kulmion kärkipisteitä ja yksi pisteistä osuu yhteen 1:n kanssa.

z 0:n n:s juuri. Z k \u003d Z 0; Z0 = 0 => Z = 0; Z° = 0; Z = r(cos(t)-isin(t)); Z 0 \u003d r 0 (cos (t0) + isin (t0)); r0!=0; Z n \u003d r n (cos (nt) + isin (nt))

r n \u003d r 0, nt-t 0 \u003d 2pk; r=; t=(2pk+t0)/n; z= (cos((2pk+t0)/n)+isin((2pk+t0)/n)= (cos t0/n+isin t0/n)(cos(2pk/n)+isin(2pk/n) )=Z1Ek;z=z1Ek;Z1n=z0, k=0, n=1

Matriisit. Määritelmä: M × n -matriisi on suorakaiteen muotoinen taulukko, joka sisältää m riviä ja n saraketta, joiden alkiot ovat reaali- tai kompleksilukuja. Matriisielementeillä on kaksoisindeksit.

Jos m = n, niin se on neliömatriisi, jonka kertaluku on m, ja saman indeksin omaavat elementit muodostavat matriisin päädiagonaalin.

Matriisioperaatiot: Määritelmä: Kutsutaan kahta matriisia A,B

yhtä suuri, jos niiden koot ovat samat ja A = B,1≤ i ≤ m,1≤ j ≤ n

Lisäys. Samankokoiset matriisit otetaan huomioon. Määritelmä:C = A + B ⇔ C = A + B, ∀i, j Tuomita. Matriisilisäys on kommutatiivista, assosiatiivista, siinä on neutraali elementti ja jokaiselle matriisille on vastakkainen elementti.

Neutraali alkio on nollamatriisi, jonka kaikki alkiot ovat yhtä suuria kuin 0. Sitä merkitään Θ:llä.

Kertominen. m × n matriisia A merkitään Amn . Määritelmä: C mk =A mn B nk ó

C= Huomaa, että kertominen ei yleensä ole kommutatiivista. Suljetus on voimassa kiinteän kokoiselle neliömatriisille. Olkoon kolme matriisia Amn , Bnk , Ckr. Sitten (AB)C = A(BC). Jos on olemassa kolmen matriisin tulo, se on assosiatiivinen.

Kronecker-symboli δij . Se on 1, jos indeksit täsmäävät, ja 0 muussa tapauksessa. Määritelmä. Identiteettimatriisi I n on kertalukua n oleva neliömatriisi, jonka yhtälöt n I n [ i | j] = δij Tuomita. Yhtälöt I m ​​A mn =A mn I n =A mn

Matriisien yhteen- ja kertolasku on yhdistetty distributiivisuuden lailla. A(B+C)=AB+AC; (A+B)C=AC+BC;(A(B+C)= = = +

Matriisitransponointi. Transponoitu matriisi on matriisi, joka saadaan alkuperäisestä korvaamalla rivit sarakkeilla.

(A+B) T = A T + B T

(AB) T \u003d B T A T; (AB) T \u003d (AB) \u003d \u003d (B T A T)

Matriisin kertominen luvulla. Luvun a ja matriisin A mn tuloa kutsutaan uudeksi matriiksi B=aA

1*A=A;a(A+B)=aA+aB;(a+b)A=aA+bA;

A(BC)=(aB)C=B(aC); (ab)A=a(bA)=b(aA)

lineaarinen avaruus(L) kentän F yli kutsutaan vektoreiden joukoksi L=(α,β..)

1.α+β=β+α(kommutatiivisuus) 2.α+(β+γ)= (α+β)+γ, (ab)α=a(bα)(assosiatiivisuus) 3.α+θ=α, α∙1=α(neutraalin olemassaolo) 4.α+(-α)=θ (vastakohdan olemassaolo)

a(a+p)=aa+aβ, (a+b)a=aa+ba. Dokumentaatio (|(a+b)α|=|a+b||α|, |aα|=|a||α|,|bα|=|b||α|, a ja b>0, |a +b|=a+b,|a|=a,|b|=b.) aα+(-a)α=θ, (a+0)α=aα

Esimerkki lineaarisesta avaruudesta on joukko kiinteän kokoisia matriiseja, joissa on yhteen- ja luvulla kertomisoperaatioita.

Lineaaristen vektorien järjestelmää kutsutaan lineaarisesti riippuvainen, jos 1.a 1 ,a 2 ..a n ≠0 2. a 1 α 1 ,a 2 α 2 ..a n α n =θ Jos järjestelmä ei ole lineaarisesti riippuvainen, niin se on lineaarisesti riippumaton. Tarkastellaan 1. n=1 α 1 riippuvat. a 1 ≠0, a 1 α 1 = θ, a 1 -1 (a 1 α 1) = a 1 -1 ∙ θ= θ, (a 1 -1 a 1) α 1 =1 ∙α 1 = α 1 ; 2. n=2 α1,α2 riippuvat. a 1 < 0, a 1 a 1 + a 2 a 2 = θ, a 1 = - a 1 - 1 a 2 a 2 = b 2 a 2; 3.n≥2 α 1 ..α n riippuvat. a 1 ≠0, α 1 =Σ k =2 n b k α k, 1α 1 - Σ k =2 n b k α k = θ, (1,b 2 ..b n)≠0

Tuomita: Useamman kuin yhden vektorin sisältävä vektorijärjestelmä on lineaarisesti riippuvainen, jolloin jokin järjestelmän vektori on muiden lineaarinen yhdistelmä.

Jos vektorijärjestelmä sisältää lineaarisesti riippuvan alijärjestelmän, niin koko järjestelmä on lineaarisesti riippuvainen. Asiakirja m =θ, a 1 ..a n ,0..0≠0.) Jos järjestelmä sisältää nollavektorin, niin se on lineaarisesti riippuvainen. Lineaarisen avaruuden lause: (Ollaan 2 vektorijärjestelmää α 1 ..α m, β 1 ..β n. Vektorijärjestelmä α ilmaistaan ​​β:na, jos jokainen vektori α on lineaarinen yhdistelmä β α i = Σ k =1 n a ik β k , (α ) ( (β), (β) ( (γ) → (α) ( (γ)) Lause: Kun annetaan 2 vektorijärjestelmää, α on riippumaton ja (α) ( (β)→m≤n Osoitetaan, että α 1 ..α m +1 β 1 ..β m (α) ( (β)→(α ) riippuu (Todistetaan induktiolla. m=1: α 1 =a 11 β 1, α 2 =a 21 β 1. a 11 =0→ α 1 =θ. a 11 α 2 – a 21 α 1 = a 11 a 21 β 1 - a 21 a 11 β 1 = θ. α 1 = a 11 β 1 + .. a 1 n -1 β n -1 .. α n = a n 1 β 1 + .. a nn -1 β n - 1 Jos kaikki kertoimet =0 a 11 =a 12 =..=a 1 n -1 =0→ α 1 =θ→ koko järjestelmä on lineaarisesti riippuvainen a 1 n -1 ≠0 α 2 ′= α 2 – с 2 α 1 =b 21 β 1 +.. + b 2 n - 2 β n -2, c 2 =a 2 n -1 / a 1 n -1, α 3 ′ = α 3 - с 3 α 1 . α n ′= α n –с n α 1. Esiinduktion avulla on olemassa nollasta poikkeava lukujoukko d 2 ..d n: d 2 α 2 ′+d 3 α 3 ′+.. d n α n ′=θ , d 2 ( α 2 –с 2 α 1)+d 3 (α 3 – с 3 α 1)+.. d n (α n –с n α 1)=θ, (α) ( (β) , m>n →(α )riippuu jos (α) riippumaton →m≤n)

MLNP-max.line.independent.subsystem. Olkoon jonkin osajärjestelmän vektorijärjestelmä α 1 ..α n. α i 1 ..α in kutsutaan MLIS:ksi, jos 1. α 1 ..α n on riippumaton2. α i 1 ..α ir , α ij riippuu. Jokainen järjestelmän vektori on lineaarinen yhdistelmä MLLM-vektoreita. ( α i 1 ..α ir , α ij riippuvainen a i 1 α i 1 +.. a ir α ir +a ij α ij =θ

a i 1 ..a ir , a ij ≠0 jos a ij =0 → a i 1 α i 1 +.. a ir α ir =θ a i 1 ..a ir =0 ristiriita a ij ≠0 α ij = a ij - 1 (-a i 1 α i 1 -.. a ir α ir) (α 1 .. α n) ( (α i 1 .. α ir)

Seuraus: Mikä tahansa 2 MLIS:ää yhdestä vektorijärjestelmästä sisältää saman määrän vektoreita (α i 1 ..α ir) ( (α j 1 ..α jk) , (α j 1 .. α jk) ( (α i 1 . .α ir ) k≤r, r≤k →r=k MLLM-vektorien lukumäärä on ns. sijoitus alkuperäinen järjestelmä. Lineaarisen avaruuden tapauksessa (vektorijärjestelmä koostuu kaikista avaruuden vektoreista) MLLM mb on joko äärellinen tai ääretön. Käsittelemme viimeistä tapausta. Vektorien lukumäärä (rank) on lineaariavaruuden ulottuvuus. MLNP-pohja. Suunnattujen segmenttien tila. Muodostuu kaksi ei-kollineaarista vektoria pohja tason vektoreiden avaruudessa. α 3 = α 1 ′ + α 2 ′ = a 1 α 1 + a 2 α 2 . 3 vektoria lineaarisesti riippuvainen α 3 =a 1 α 1 + a 2 α 2 . Komplanaarisuus - 3 vektorit ovat saman tason suuntaisia ​​α 4 = α 4 ′+ α 5 ′ , α 4 ′=a 1 α 1 + a 2 α 2 , α 5 ′= a 3 α 3 , α 4 1 + a 2 a 2 + a 3 a 3 . n pituisten merkkijonojen avaruus. α= Tuomita: N-pituisten merkkijonojen avaruuden mitat ovat n. (ξ 1 =<1…0>ξ2 =<0,1…0>.. n =<0…1>,a 1 ξ 1 + a 2 ξ 2 +.. a n ξ n =θ=<0,..0> → a 1 =a 2 =..a n =0 (lineaarinen riippumattomuus) β= β= b 1 ξ 1 + b 2 ξ 2 +.. b n ξ n →pituisten n merkkijonojen avaruudessa on dimensio ja n.

Matrix sijoitus.

Kahta vektorijärjestelmää α ja β kutsutaan ekvivalenteiksi, jos kutakin vektoria

α(β(ilmaistu) ja β(α.

Tuomita. Vastaavien järjestelmien rivit ovat samat.

α i 1 , α i 2 ,…, α ir – MLLM α , β i 1 , β i 2 ,…, β ik – MLLM β , α i 1 , α i 2 ,…, α ir< β < β i 1 , β i 2 ,…, β ik → r<=k

α:n ja β:n vaihto → r>=k >>> Tästä syystä r=k.

Määritelmä. Olkoon matriisi A=

α i =

Matrix sijoitus A:ta kutsutaan tästä matriisista koostuvan vektorien järjestelmän α1, α2,…, αm arvoksi >>rank(A)-rank

Määritelmän perusteella on selvää, että kun sarakkeet järjestetään uudelleen, järjestys ei muutu. Osoitetaan, että kun sarakkeet järjestetään uudelleen, sijoitus ei myöskään muutu.

A'=

α'i=

Lineaarinen riippuvainen:

b 1 α 1 + b 2 α 2 +…+ b m α m = θ, b 1 a 11 + b 2 a 21 +…+b m a m 1 = 0, b 1 α' 1 + b 2 α' 2 +…+ b m α' m , b 1 a 11 +b 2 a 21 +…+b m a m 1 = 0

Se on yhtä suuri kuin jonkin rivin tai sarakkeen alkioiden ja niiden algebrallisten komplementtien tulojen summa, ts. , jossa i 0 on kiinteä.
Lauseketta (*) kutsutaan determinantin D hajotukseksi rivin i 0 alkioiden suhteen.

Palvelutehtävä. Tämä palvelu on suunniteltu etsimään matriisin determinantti verkosta suorittamalla koko ratkaisu Word-muodossa. Lisäksi ratkaisumalli luodaan Excelissä.

Ohje. Valitse matriisin mitta ja napsauta Seuraava.

Matriisiulottuvuus 2 3 4 5 6 7 8 9 10

Determinantin laskemiseen on kaksi tapaa: määritelmän mukaan ja jaottelu rivin tai sarakkeen mukaan. Jos haluat löytää determinantin luomalla nollia johonkin riveistä tai sarakkeista, voit käyttää tätä laskinta.

Algoritmi determinantin löytämiseksi

1. Matriiseille, joiden kertaluku on n=2, determinantti lasketaan kaavalla: Δ=a 11 *a 22 -a 12 *a 21
2. Matriiseille, joiden kertaluku on n=3, determinantti lasketaan algebrallisten yhteenlaskujen tai Sarrus menetelmä.
3. Matriisi, jonka dimensio on suurempi kuin kolme, hajotetaan algebrallisiksi summauksiksi, joille lasketaan niiden determinantit (alaikäiset). Esimerkiksi, 4. asteen matriisideterminantti löytyy laajentamalla rivejä tai sarakkeita (katso esimerkki).

Matriisin funktioita sisältävän determinantin laskemiseen käytetään standardimenetelmiä. Laske esimerkiksi 3. asteen matriisin determinantti:

Käytetään ensimmäisen rivin laajennusta.
Δ = sin(x)× + 1× = 2sin(x)cos(x)-2cos(x) = sin(2x)-2cos(x)

Determinanttien laskentamenetelmät

Determinantin löytäminen algebrallisten lisäysten avulla on yleinen menetelmä. Sen yksinkertaistettu versio on determinantin laskenta Sarrus-säännöllä. Kuitenkin, kun matriisiulottuvuus on suuri, käytetään seuraavia menetelmiä:

1. determinantin laskeminen tilauksen vähentämisellä
2. determinantin laskeminen Gaussin menetelmällä (pelkistämällä matriisi kolmion muotoon).

Excelissä determinantin laskemiseen käytetään funktiota = MOPRED (solualue).

Determinanttien sovellettu käyttö

Determinantit lasketaan pääsääntöisesti tietylle järjestelmälle neliömatriisin muodossa. Harkitse tietyntyyppisiä tehtäviä matriisideterminantin löytäminen. Joskus on löydettävä tuntematon parametri a, jonka determinantti olisi yhtä suuri kuin nolla. Tätä varten on tarpeen laatia yhtälö determinantille (esimerkiksi kolmion sääntö) ja laskemalla sen arvoon 0 parametri a .
jaottelu sarakkeiden mukaan (ensimmäisen sarakkeen mukaan):
Minor for (1,1): Poista ensimmäinen rivi ja ensimmäinen sarake matriisista.
Etsitään tälle alaikäiselle ratkaiseva tekijä. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6.

Määritetään (2,1) molli: tätä varten poistamme matriisista toisen rivin ja ensimmäisen sarakkeen.

Etsitään tälle alaikäiselle ratkaiseva tekijä. ∆ 2,1 = (0 (-2)-2 (-2)) = 4 . Minor for (3,1): Poista 3. rivi ja 1. sarake matriisista.
Etsitään tälle alaikäiselle ratkaiseva tekijä. ∆ 3,1 = (0 1-2 (-2)) = 4
Päädeterminantti on: ∆ = (1 (-6)-3 4+1 4) = -14

Etsitään determinantti rivilaajennuksella (ensimmäisellä rivillä):
Minor for (1,1): Poista ensimmäinen rivi ja ensimmäinen sarake matriisista.

Etsitään tälle alaikäiselle ratkaiseva tekijä. ∆ 1,1 \u003d (2 (-2) -2 1) \u003d -6. Minor for (1,2): Poista 1. rivi ja 2. sarake matriisista. Lasketaan tämän alaikäisen determinantti. ∆ 1,2 \u003d (3 (-2) -1 1) \u003d -7. Ja löytääksemme molliarvon (1,3):lle, poistamme ensimmäisen rivin ja kolmannen sarakkeen matriisista. Etsitään tälle alaikäiselle ratkaiseva tekijä. ∆ 1,3 = (3 2-1 2) = 4
Löydämme päädeterminantin: ∆ \u003d (1 (-6) -0 (-7) + (-2 4)) \u003d -14

M lineaarisen yhtälön järjestelmä, jossa on n tuntematonta kutsutaan muotojärjestelmäksi

missä aij ja b i (i=1,…,m; b=1,…,n) ovat joitain tunnettuja numeroita ja x 1,…,x n- tuntematon. Kertoimien merkinnöissä aij ensimmäinen indeksi i tarkoittaa yhtälön numeroa ja toista j on tuntemattoman numero, jossa tämä kerroin on.

Tuntemattomien kertoimet kirjoitetaan matriisin muotoon , jota kutsumme järjestelmämatriisi.

Numerot yhtälöiden oikealla puolella b 1,…,b m nimeltään ilmaisia ​​jäseniä.

Aggregaatti n numeroita c 1,…,c n nimeltään päätös tämän järjestelmän, jos jokaisesta järjestelmän yhtälöstä tulee yhtälö sen jälkeen, kun siihen on korvattu lukuja c 1,…,c n vastaavien tuntemattomien sijaan x 1,…,x n.

Tehtävämme on löytää ratkaisuja järjestelmään. Tässä tapauksessa voi syntyä kolme tilannetta:

Lineaariyhtälöjärjestelmää, jolla on vähintään yksi ratkaisu, kutsutaan liitos. Muuten, ts. jos järjestelmällä ei ole ratkaisuja, niin sitä kutsutaan yhteensopimaton.

Harkitse tapoja löytää ratkaisuja järjestelmään.

MATRIISIMENETELMÄ LINEAARIEN YHTÄLÖJÄRJESTELMIEN RATKAISEMINEN

Matriisit mahdollistavat lineaarisen yhtälöjärjestelmän lyhyen kirjoittamisen. Olkoon 3 yhtälöjärjestelmä, jossa on kolme tuntematonta:

Harkitse järjestelmän matriisia 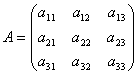ja matriisisarakkeet tuntemattomista ja vapaista jäsenistä

Etsitään tuote

nuo. tuotteen tuloksena saamme tämän järjestelmän yhtälöiden vasemmat puolet. Sitten, käyttämällä matriisiyhtälön määritelmää, tämä järjestelmä voidaan kirjoittaa muodossa

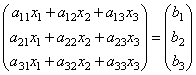tai lyhyempi A∙X = B.

Tässä matriiseja A ja B tunnetaan, ja matriisi X tuntematon. Hänet on löydettävä, koska. sen elementit ovat tämän järjestelmän ratkaisu. Tätä yhtälöä kutsutaan matriisiyhtälö.

Olkoon matriisideterminantti eri kuin nolla | A| ≠ 0. Sitten matriisiyhtälö ratkaistaan ​​seuraavasti. Kerro vasemmalla olevan yhtälön molemmat puolet matriisilla A-1, matriisin käänteis A: . Koska A -1 A = E ja E∙X = X, niin saadaan matriisiyhtälön ratkaisu muodossa X = A -1 B .

Huomaa, että koska käänteimatriisi löytyy vain neliömatriiseille, matriisimenetelmä voi ratkaista vain ne järjestelmät, joissa yhtälöiden määrä on sama kuin tuntemattomien lukumäärä. Järjestelmän matriisimerkintä on kuitenkin mahdollista myös siinä tapauksessa, että yhtälöiden lukumäärä ei ole yhtä suuri kuin tuntemattomien lukumäärä, niin matriisi A ei ole neliö ja siksi on mahdotonta löytää ratkaisua järjestelmään muodossa X = A -1 B.

Esimerkkejä. Ratkaise yhtälöjärjestelmiä.

CRAMERIN SÄÄNTÖ

Tarkastellaan 3 lineaarisen yhtälön järjestelmää, joissa on kolme tuntematonta:

Kolmannen kertaluvun determinantti, joka vastaa järjestelmän matriisia, ts. koostuu kertoimista tuntemattomissa,

nimeltään järjestelmän määräävä tekijä.

Muodostamme kolme muuta determinanttia seuraavasti: korvaamme peräkkäin 1, 2 ja 3 saraketta determinantissa D vapaiden termien sarakkeella

Sitten voimme todistaa seuraavan tuloksen.

Lause (Cramerin sääntö). Jos järjestelmän determinantti on Δ ≠ 0, niin tarkasteltavalla järjestelmällä on yksi ja vain yksi ratkaisu, ja

Todiste. Tarkastellaan siis kolmen yhtälön järjestelmää, jossa on kolme tuntematonta. Kerro järjestelmän 1. yhtälö algebrallisella komplementilla A 11 elementti a 11, 2. yhtälö - päällä A21 ja 3. - päällä A 31:

Lisätään nämä yhtälöt:

Harkitse tämän yhtälön jokaista sulkua ja oikeaa puolta. Lauseen mukaan determinantin laajenemisesta 1. sarakkeen elementtien suhteen

Samalla tavalla voidaan osoittaa, että ja .

Lopulta se on helppo nähdä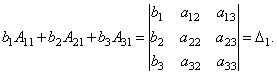

Siten saamme tasa-arvon: .

Tämän seurauksena,.

Yhtälöt ja johdetaan samalla tavalla, mistä seuraa lauseen väite.

Näin ollen todetaan, että jos järjestelmän determinantti on Δ ≠ 0, niin järjestelmällä on ainutlaatuinen ratkaisu ja päinvastoin. Jos järjestelmän determinantti on nolla, niin systeemillä on joko ääretön joukko ratkaisuja tai ei ole ratkaisuja, ts. yhteensopimaton.

Esimerkkejä. Ratkaise yhtälöjärjestelmä

GAUSS-MENETELMÄ

Aiemmin käsitellyillä menetelmillä voidaan ratkaista vain sellaisia ​​järjestelmiä, joissa yhtälöiden lukumäärä on sama kuin tuntemattomien lukumäärä ja järjestelmän determinantin on oltava eri kuin nolla. Gaussin menetelmä on yleismaailmallisempi ja sopii järjestelmiin, joissa on mikä tahansa määrä yhtälöitä. Se koostuu tuntemattomien peräkkäisestä poistamisesta järjestelmän yhtälöistä.

Tarkastellaan jälleen kolmen yhtälön järjestelmää, jossa on kolme tuntematonta:

.

Jätämme ensimmäisen yhtälön ennalleen, ja 2. ja 3:sta jätämme pois sisältävät termit x 1. Tätä varten jaamme toisen yhtälön arvolla a 21 ja kerro - a 11 ja lisää sitten 1. yhtälöllä. Samalla tavalla jaamme kolmannen yhtälön a 31 ja kerro - a 11 ja lisää se sitten ensimmäiseen. Tämän seurauksena alkuperäinen järjestelmä on seuraavanlainen:

Nyt, viimeisestä yhtälöstä, poistamme termin sisältävän x2. Voit tehdä tämän jakamalla kolmannen yhtälön luvulla, kertomalla ja lisäämällä sen toiseen. Sitten meillä on yhtälöjärjestelmä:

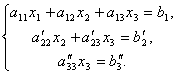
Siksi se on helppo löytää viimeisestä yhtälöstä x 3, sitten 2. yhtälöstä x2 ja lopuksi 1. päivästä - x 1.

Gaussin menetelmää käytettäessä yhtälöt voidaan tarvittaessa vaihtaa keskenään.

Usein uuden yhtälöjärjestelmän kirjoittamisen sijaan he rajoittuvat kirjoittamaan järjestelmän laajennetun matriisin:

ja tuo se sitten kolmion tai diagonaalin muotoon käyttämällä alkeismuunnoksia.

Vastaanottaja alkeellisia muunnoksia matriisit sisältävät seuraavat muunnokset:

1. rivien tai sarakkeiden permutaatio;
2. merkkijonon kertominen nollasta poikkeavalla luvulla;
3. lisäämällä yhdelle riville muita rivejä.

Esimerkkejä: Ratkaise yhtälöjärjestelmä Gaussin menetelmällä.

Järjestelmällä on siis ääretön määrä ratkaisuja.

2.Jos │A│=0, niin matriisi A on degeneroitunut ja käänteismatriisia A -1 ei ole olemassa.

Jos matriisin A determinantti ei ole nolla, niin käänteismatriisi on olemassa.

3. Etsi A T transponoituna A:ksi.

4. Etsi transponoidun matriisin alkioiden algebralliset komplementit ja muodosta niistä adjunktinen matriisi. 5. Laskemme käänteismatriisin kaavan mukaan: 6. Tarkista käänteimatriisin laskennan oikeellisuus sen määritelmän perusteella A -1 ∙A = A ∙A -1 = E.

· №28

· M x n -matriisissa, poistamalla mahdolliset rivit ja sarakkeet, voidaan valita k:nnen kertaluvun neliömatriisit, joissa k≤min(m; n). Tällaisten alimatriisien determinantteja kutsutaan matriisin A k:nnen kertaluvun minoreiksi.

· Matriisin A ranking on tämän matriisin nollasta poikkeavien molempien korkein kertaluku.

· Matriisin A järjestys on merkitty A:lla tai r(A:lla).

· Määritelmästä seuraa:

· 1) m x n kokoisen matriisin järjestys ei ylitä sen pienintä kokoa, ts. r(A) < min (m; n).

· 2) r(A)=0 jos ja vain jos kaikki matriisin alkiot ovat nolla, ts. A = 0.

· 3) N:nnen kertaluvun neliömatriisille r(A) = n jos ja vain jos matriisi A on epäsingulaarinen.

· Yleisesti ottaen matriisin arvon määrittäminen laskemalla kaikki alaikäiset on melko työlästä. Tämän tehtävän helpottamiseksi käytetään perusmuunnoksia, jotka säilyttävät matriisin arvon:

· 1) Nollarivin (sarakkeen) hylkääminen.

· 2) Matriisin rivin (sarakkeen) kaikkien elementtien kertominen nollasta poikkeavalla luvulla.

· 3) Matriisin rivien (sarakkeiden) järjestyksen muuttaminen.

· 4) Lisäämällä yhden rivin (sarakkeen) jokaiseen elementtiin toisen rivin (sarakkeen) vastaavat elementit kerrottuna millä tahansa numerolla.

· 5) Matriisitransponointi.

· Lause. Matriisin arvo ei muutu matriisin alkeismuunnosten yhteydessä.

№31

— Olkoon yhtälöiden lukumäärä järjestelmässä (1) yhtä suuri kuin muuttujien lukumäärä, ts. m = n. Tällöin järjestelmän matriisi on neliö, ja sen determinanttia Δ=│А│ kutsutaan järjestelmän determinantiksi.

— Oletetaan, että │А│ ei ole nolla, niin on olemassa käänteimatriisi A -1 .

— Kerrotaan vasemmanpuoleisen matriisin yhtälön molemmat osat käänteismatriisilla A -1, saadaan:

— A -1 (AX) \u003d A -1 B.

Yhtälöjärjestelmän ratkaisu käänteismatriisimenetelmällä on sarakematriisi:

X \u003d A -1 B.

(A -1 A)X \u003d EX \u003d X

— Cramerin lause. Olkoon Δ järjestelmän A matriisin determinantti ja Δ j sen matriisin determinantti, joka saadaan matriisista korvaamalla j. sarake vapaiden termien sarakkeella. Sitten jos Δ ei ole nolla, järjestelmällä on ainutlaatuinen ratkaisu, joka on määritelty Cramerin kaavoilla:

missä j=1..n.

№33

—
Gaussin menetelmä - muuttujien peräkkäisen eliminoinnin menetelmä - koostuu siitä, että alkeismuunnosten avulla yhtälöjärjestelmä pelkistetään vastaavaksi porras- tai kolmiotyyppiseksi järjestelmäksi.

— Harkitse matriisia:

— tätä matriisia kutsutaan järjestelmän (1) laajennetuksi matriisiksi, koska se sisältää järjestelmän A matriisin lisäksi vapaita jäseniä.

№26

— N-ulotteinen vektori on n:n reaaliluvun järjestynyt joukko, joka on kirjoitettu muodossa X=(x 1,x 2,...x n) , missä x i on vektorin X i:s komponentti.

— Kaksi n-ulotteista vektoria ovat samanarvoisia silloin ja vain, jos niiden vastaavat komponentit ovat yhtä suuret, ts. X=Y jos x i =y i, i=1…n.

Vektoriavaruudeksi kutsutaan joukkoa reaalikomponentteja vektoreita, joissa on määritelty operaatiot vektorien yhteenlaskemiseksi ja vektorin kertomiseksi luvulla, jotka täyttävät yllä olevat ominaisuudet.

— Vektoriavaruutta R kutsutaan n-ulotteiseksi, jos siinä on n lineaarisesti riippumatonta vektoria ja mikä tahansa n + 1 vektoria on jo riippuvainen. Lukua n kutsutaan vektoriavaruuden R dimensioksi ja sitä merkitään dim(R).

№29

Lineaariset operaattorit

— Määritelmä. Jos annetaan laki (sääntö), jonka mukaan jokainen avaruuden vektori x liittyy yhteen avaruuden vektoriin y

sitten he sanovat: että operaattori (muunnos, kartoitus) A(x) on annettu, joka toimii välillä - ja

kirjoita y=A(x).

— Operaattoria kutsutaan lineaariseksi, jos jollekin avaruuden vektorille x ja y

ja mikä tahansa luku λ, seuraavat suhteet pätevät:

№37

— Olkoon А joukko, joka koostuu äärellisestä määrästä alkioita a 1 , a 2 , a 3 …a n . Ryhmiä voidaan muodostaa joukon A eri elementeistä. Jos jokaisessa ryhmässä on sama määrä elementtejä m (m n:stä), niiden sanotaan muodostavan n alkuaineen yhdisteitä, joissa kussakin on m. On olemassa kolmenlaisia ​​yhteyksiä: sijoittelut, yhdistelmät ja permutaatiot.

— liitännät, joista kukin sisältää joukon A kaikki n alkiota ja jotka siksi eroavat toisistaan ​​vain alkioiden järjestyksessä, kutsutaan n elementin permutaatioiksi. Tällaisten permutaatioiden lukumäärä on merkitty symbolilla Р n .

№35

Klassinen todennäköisyyden määritelmä perustuu tapahtumien tasatodennäköisyyden käsitteeseen.

Tapahtumien vastaavuus tarkoittaa, ettei ole mitään syytä suosia yhtä niistä toisiin nähden.

Tarkastellaan testiä, jonka seurauksena tapahtuma A voi tapahtua. Jokaista tulosta, jossa tapahtuma A tapahtuu, kutsutaan suotuisaksi tapahtumaksi A.

Tapahtuman A todennäköisyys (merkitty P(A)) on tapahtumalle A suotuisten tulosten lukumäärän (merkitty k:llä) suhde kaikkien testitulosten lukumäärään - N eli. P(A) = k/N.

— Klassisesta todennäköisyyden määritelmästä seuraa seuraavat ominaisuudet:

— Minkä tahansa tapahtuman todennäköisyys on nollan ja yhden välillä.

— Tietyn tapahtuman todennäköisyys on yhtä suuri kuin yksi.

— Mahdottoman tapahtuman todennäköisyys on nolla

№39, 40

— Lisäyslause. Jos A ja B ovat ristiriidassa, niin P(A + B) = P(A) + P(B)