Diskreetin satunnaismuuttujan dispersio (sironta). D(X) on matemaattinen odotus satunnaismuuttujan neliöidylle poikkeamalle sen matemaattisesta odotuksesta
1 omaisuus. Vakion C dispersio on nolla; D(C) = 0.
Todiste. Varianssin määritelmän mukaan D(C) = M( 2 ).
Odotuksen ensimmäisestä ominaisuudesta D(C) = M[(C – C) 2 ] = M(0) = 0.
2 omaisuutta. Vakiokerroin voidaan ottaa pois dispersiomerkistä neliöimällä se:
D(CX) = C 2 D(X)
Todiste. Varianssin määritelmän mukaan D(CX) = M( 2 )
Toisesta odotusominaisuudesta D(CX)=M( 2 )= C 2 M( 2 )=C 2 D(X)
3 omaisuutta. Kahden riippumattoman satunnaismuuttujan summan varianssi on yhtä suuri kuin näiden muuttujien varianssien summa:
D = D[X] + D.
Todiste. Varianssin laskentakaavan mukaan meillä on
D(X + Y) = M[(X + Y) 2 ] − 2
Avaamalla sulut ja käyttämällä useiden määrien summan ja kahden riippumattoman satunnaismuuttujan tulon matemaattisen odotuksen ominaisuuksia saadaan
D(X + Y) = M − 2 = M(X2) + 2M(X)M(Y) + M(Y2) − M2(X) − 2M(X)M(Y) − M2(Y) = ( M(X2) − 2)+(M(Y2) − 2) = D(X) + D(Y). Joten D(X + Y) = D(X) + D(Y)
4 omaisuutta. Kahden riippumattoman satunnaismuuttujan eron varianssi on yhtä suuri kuin niiden varianssien summa:
D(X − Y) = D(X) + D(Y)
Todiste. Kolmannen ominaisuuden perusteella D(X − Y) = D(X) + D(–Y). Toisella kiinteistöllä
D(X − Y) = D(X) + (–1) 2 D(Y) tai D(X − Y) = D(X) + D(Y)
Satunnaismuuttujien järjestelmien numeeriset ominaisuudet. Korrelaatiokerroin, korrelaatiokertoimen ominaisuudet.
korrelaatiohetki. Satunnaismuuttujien välisen riippuvuuden ominaisuus on matemaattinen odotus poikkeamien tulosta ja niiden jakaumien keskuksista (kuten satunnaismuuttujan matemaattista odotusta joskus kutsutaan), jota kutsutaan korrelaatiomomentiksi tai kovarianssiksi:
Diskreettien arvojen korrelaatiomomentin laskemiseen käytetään seuraavaa kaavaa:
ja jatkuville määrille - kaava:
Korrelaatiokerroin satunnaismuuttujien X ja Y rxy on korrelaatiomomentin suhde arvojen keskihajonnan tuloon:
- korrelaatiokerroin;
Korrelaatiokertoimen ominaisuudet:
1. Jos X ja Y ovat riippumattomia satunnaismuuttujia, niin r = 0;
2. -1≤ r ≤1 Lisäksi, jos |r| =1, silloin X:n ja Y:n välillä on funktionaalinen, nimittäin lineaarinen suhde;
3. r kuvaa M(XY):n suhteellista arvoa M(X)M(Y):n poikkeamalle, ja koska poikkeama tapahtuu vain riippuvaisille suureille, jolloin r luonnehtii riippuvuuden tiukkuutta.
Lineaarinen regressiofunktio.
Tarkastellaan kaksiulotteista satunnaismuuttujaa (X, Y), jossa X ja Y ovat riippuvaisia satunnaismuuttujia. Esitämme yhtä suureista toisen funktiona. Rajoitumme Y:n likimääräiseen esitykseen (tarkka approksimaatio on yleisesti ottaen mahdotonta) X:n lineaarifunktiona:
missä α ja β ovat määritettäviä parametreja.
Lause. Lineaarinen keskineliön regressio Y:llä X on muoto
missä m x = M(X), m y = M(Y), σ x = √D(X), σ y = √D(Y), r=µ xy /(σ x σ y)- X- ja Y-arvojen korrelaatiokerroin.
Kutsutaan kerrointa β=rσ y /σ x regressiokerroin Y - X ja suora viiva
kutsutaan suoraan keskimääräinen neliöregressio
Y:stä X:ään.
Markovin epätasa-arvo.
Toteamus Markovin epätasa-arvosta
Jos satunnaismuuttujalla X ei ole negatiivisia arvoja, niin todennäköisyys, että se saa jonkin arvon, joka ylittää positiivisen luvun A, on enintään murto-osa, ts.
ja todennäköisyys, että se saa jonkin arvon, joka ei ylitä positiivista lukua A, ei ole pienempi kuin ts.
Chebyshevin epätasa-arvo.
Chebyshevin epätasa-arvo. Todennäköisyys, että satunnaismuuttujan X poikkeama sen matemaattisesta odotuksesta absoluuttisena arvona on pienempi kuin positiivinen luku ε, vähintään 1 −D[X]ε 2
P(|X – M(X)|< ε) ≥ 1 –D(X)ε 2
Todiste. Koska tapahtumat koostuvat eriarvoisuuksien ymmärtämisestä
P(|X−M(X)|< ε) и P(|X – M(X)| ≥ε) противоположны, то сумма их вероятностей равна единице, т. е.
P(|X – M(X)|< ε) + P(|X – M(X)| ≥ ε) = 1.
Tästä johtuu todennäköisyys, josta olemme kiinnostuneita
P(|X – M(X)|< ε) = 1 − P(|X – M(X)| > ε).
Siten ongelma rajoittuu todennäköisyyden P(|X –M(X)| ≥ ε) laskemiseen.
Kirjoitetaan lauseke satunnaismuuttujan X varianssille
D(X) = 2p1 + 2p2 +. . . + 2 pn
Kaikki tämän summan ehdot eivät ole negatiivisia. Hylätään termit, joille |x i – M(X)|< ε (для оставшихся слагаемых |x j – M(X)| ≥ ε), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,
D(X) ≥ 2 p k+1 + 2 p k+2+. . . + 2 pn
Epäyhtälön |x j –M(X)| molemmat osat ≥ ε (j = k+1, k+2, . . ., n) ovat positiivisia, joten ne neliöimällä saadaan ekvivalentti epäyhtälö |x j – M(X)| 2 ≥ε 2. Korvataan jokainen tekijä jäljellä olevalla summalla
|xj – M(X)| 2 luvulla ε 2 (tässä tapauksessa epäyhtälö voi vain kasvaa), saamme
D(X) ≥ ε 2 (p k+1 + p k+2 + . . . + p n)
Summauslauseen mukaan todennäköisyyksien summa on p k+1 +p k+2 +. . .+p n on todennäköisyys, että X ottaa yhden arvoista x k+1 +x k+2 + riippumatta siitä, mikä. . .+x n , ja minkä tahansa niistä poikkeama tyydyttää epäyhtälön |x j – M(X)| ≥ ε. Tästä seuraa, että summa p k+1 + p k+2 + . . . + p n ilmaisee todennäköisyyden
P(|X – M(X)| ≥ ε).
Tämä mahdollistaa D(X):n epäyhtälön kirjoittamisen uudelleen muotoon
D(X) ≥ ε 2 P(|X – M(X)| ≥ ε)
P(|X – M(X)|≥ ε) ≤D(X)/ε 2
Lopulta saamme
P(|X – M(X)|< ε) ≥D(X)/ε 2
Tšebyshevin lause.
Tšebyshevin lause. Jos - pareittain riippumattomia satunnaismuuttujia ja niiden varianssit ovat tasaisesti rajoitettuja (älä ylitä vakiolukua Kanssa ), ei väliä kuinka pieni positiivinen luku onε , epätasa-arvon todennäköisyys
on mielivaltaisen lähellä yksikköä, jos satunnaismuuttujien määrä on riittävän suuri.
Toisin sanoen lauseen ehdoilla
Todiste. Otetaan huomioon uusi satunnaismuuttuja - satunnaismuuttujien aritmeettinen keskiarvo
Etsitään matemaattinen odotus X. Käyttämällä matemaattisen odotuksen ominaisuuksia (matemaattisen odotuksen merkistä voidaan ottaa vakiotekijä, summan matemaattinen odotus on yhtä suuri kuin ehtojen matemaattisten odotusten summa) , saamme
| (1) |
Kun sovelletaan Tšebyševin epäyhtälöä X:ään, meillä on
tai ottaen huomioon suhde (1)
Varianssin ominaisuuksia käyttämällä (vakiokerroin voidaan ottaa pois varianssimerkistä neliöimällä; riippumattomien satunnaismuuttujien summan varianssi on yhtä suuri kuin termien varianssien summa) saadaan
Ehdolla kaikkien satunnaismuuttujien dispersioita rajoittaa vakioluku C, ts. on epätasa-arvoa:
 (2)
|
Korvaamalla (2):n oikean puolen epätasa-arvoon (1) (miksi jälkimmäistä voidaan vain vahvistaa), meillä on
Siten, siirtymällä rajaan muodossa n→∞, saamme
Lopuksi, koska todennäköisyys ei voi olla suurempi kuin yksi, voimme vihdoin kirjoittaa
Lause on todistettu.
Bernoullin lause.
Bernoullin lause. Jos kussakin n:stä riippumattomasta kokeesta tapahtuman A todennäköisyys p on vakio, niin todennäköisyys on mielivaltaisen lähellä yksikköä, että suhteellisen frekvenssin poikkeama todennäköisyydestä p absoluuttisessa arvossa on mielivaltaisen pieni, jos kokeiden määrä on riittävän suuri.
Toisin sanoen, jos ε on mielivaltaisen pieni positiivinen luku, niin lauseen ehdoilla meillä on yhtäläisyys
Todiste. Merkitse x1 diskreetti satunnaismuuttuja - tapahtuman esiintymisten lukumäärä ensimmäisessä testissä, läpi x2- toisessa, ..., X n- sisään n th testi. On selvää, että kukin suureista voi saada vain kaksi arvoa: 1 (tapahtuma A on tapahtunut) todennäköisyydellä p ja 0 (tapahtumaa ei tapahtunut) todennäköisyydellä .
Aihe 8.12. Satunnaismuuttujan dispersio.
O. Satunnaismuuttujan varianssi on matemaattinen odotus satunnaismuuttujan neliöidylle poikkeamalle sen matemaattisesta odotuksesta.
Dispersio kuvaa satunnaismuuttujan arvojen dispersioastetta suhteessa sen matemaattiseen odotukseen. Jos kaikki satunnaismuuttujan arvot keskittyvät tiiviisti sen matemaattisen odotuksen ympärille ja suuret poikkeamat matemaattisesta odotuksesta ovat epätodennäköisiä, tällaisella satunnaismuuttujalla on pieni hajonta. Jos satunnaismuuttujan arvot ovat hajallaan ja on suuri todennäköisyys suurille poikkeamille matemaattisesta odotuksesta, niin tällaisella satunnaismuuttujalla on suuri hajonta.
Diskreetin satunnaismuuttujan varianssin määritelmää käyttämällä varianssin laskentakaava voidaan esittää seuraavasti:
Voit johtaa toisen kaavan varianssin laskemiseksi:
Näin ollen satunnaismuuttujan varianssi on yhtä suuri kuin satunnaismuuttujan neliön matemaattisen odotuksen ja sen matemaattisen odotuksen neliön välinen ero.
Dispersioominaisuudet.
Jätämme tämän kiinteistön ilman todisteita.
Binomijakauman laki.
Olkoon numerot annettu n kuuluu N ja p(0 <p< yksi). Sitten jokaiselle välin kokonaisluvulle voidaan määrittää todennäköisyys, joka lasketaan Bernoullin kaavalla. Otetaan satunnaismuuttujan jakautumislaki (kutsutaanko sitä B(betta))
Sanotaan, että satunnaismuuttuja jakautuu Bernoullin lain mukaan. Tällainen satunnaismuuttuja on tapahtuman A esiintymistiheys n toistuvat riippumattomat kokeet, jos jokaisessa kokeessa tapahtuma A tapahtuu todennäköisyydellä p.
Harkitse erillistä i- e testi. Sen perustulosten tilalla on muoto
Satunnaismuuttujan jakautumislakia käsiteltiin edellisessä aiheessa
varten i= 1,2, ... , n saamme järjestelmän n riippumattomia satunnaismuuttujia, joilla on samat jakautumissäännöt. 
Esimerkki.
Kontrolliin valituista 20 tuotenäytteestä 4 osoittautui epästandardiksi. Arvioidaan todennäköisyys, että tuotteen satunnaisesti valittu kopio ei täytä standardia suhteessa R*= 4/20 = 0,2.
Kuten X satunnainen arvo, R* on myös satunnaismuuttuja. Arvot R* voi vaihdella kokeesta toiseen (tarkasteltavana olevassa tapauksessa koe on 20 tuotteen satunnainen valinta ja kontrolli). Mikä on matemaattinen odotus R*? Sikäli kuin X on satunnaismuuttuja, joka edustaa onnistumisten määrää n Bernoullin testi, M( x) = np. Satunnaismuuttujan matemaattiselle odotukselle R* määritelmän mukaan saamme: M(p*) = M(x/n), mutta n tässä on vakio, joten odotusominaisuuden mukaan
M(p*) = 1/n*M(x)=1/n np=p
Siten "keskiarvo" on todellinen arvo R, mikä on odotettavissa. Tämä on arviointiominaisuus R* määriä R on nimi: R* on puolueeton arviointi varten R. Ei systemaattista poikkeamaa arvioidun parametrin arvosta R vahvistaa arvon käyttökelpoisuuden R* arviona. Jätämme kysymyksen arvion oikeellisuudesta toistaiseksi avoimeksi.
Matemaattinen odotus ja varianssi ovat yleisimmin käytetyt satunnaismuuttujan numeeriset ominaisuudet. Ne kuvaavat jakauman tärkeimpiä piirteitä: sen sijaintia ja hajontaastetta. Monissa käytännön ongelmissa täydellistä, tyhjentävää kuvausta satunnaismuuttujasta - jakauman laista - ei joko voida saada ollenkaan tai sitä ei tarvita ollenkaan. Näissä tapauksissa ne rajoittuvat satunnaismuuttujan likimääräiseen kuvaukseen numeeristen ominaisuuksien avulla.
Matemaattista odotusta kutsutaan usein yksinkertaisesti satunnaismuuttujan keskiarvoksi. Satunnaismuuttujan dispersio on dispersion ominaisuus, satunnaismuuttujan hajonta sen matemaattisen odotuksen ympärille.
Diskreetin satunnaismuuttujan matemaattinen odotus
Lähestytään matemaattisen odotuksen käsitettä lähtemällä ensin diskreetin satunnaismuuttujan jakauman mekaanisesta tulkinnasta. Olkoon yksikkömassa jakautunut x-akselin pisteiden kesken x1 , x 2 , ..., x n, ja jokaisella materiaalipisteellä on sitä vastaava massa p1 , p 2 , ..., p n. On valittava yksi piste x-akselilta, joka luonnehtii koko materiaalipistejärjestelmän sijaintia ottaen huomioon niiden massat. On luonnollista ottaa materiaalipistejärjestelmän massakeskipiste sellaiseksi pisteeksi. Tämä on satunnaismuuttujan painotettu keskiarvo X, jossa kunkin pisteen abskissa xi tulee "painolla", joka on yhtä suuri kuin vastaava todennäköisyys. Näin saadun satunnaismuuttujan keskiarvo X kutsutaan sen matemaattiseksi odotukseksi.
Diskreetin satunnaismuuttujan matemaattinen odotus on kaikkien sen mahdollisten arvojen ja näiden arvojen todennäköisyyksien tulojen summa:
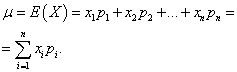
Esimerkki 1 Järjestettiin win-win arpajaiset. Voittoja on 1000, joista 400 kukin on 10 ruplaa. 300-20 ruplaa 200-100 ruplaa kukin. ja 100-200 ruplaa kukin. Mikä on yhden lipun ostavan henkilön keskimääräinen voitto?
Päätös. Keskimääräinen voitto saadaan, jos voittojen kokonaismäärä, joka on 10*400 + 20*300 + 100*200 + 200*100 = 50 000 ruplaa, jaetaan 1000:lla (voittojen kokonaismäärä). Sitten saamme 50 000/1000 = 50 ruplaa. Mutta lauseke keskimääräisen vahvistuksen laskemiseksi voidaan esittää myös seuraavassa muodossa:
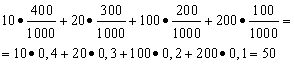
Toisaalta näissä olosuhteissa voittojen määrä on satunnaismuuttuja, joka voi ottaa arvot 10, 20, 100 ja 200 ruplaa. todennäköisyyksillä 0,4; 0,3; 0,2; 0.1. Tästä syystä odotettu keskimääräinen voitto on yhtä suuri kuin voittojen koon ja niiden saamisen todennäköisyyden tulojen summa.
Esimerkki 2 Kustantaja päätti julkaista uuden kirjan. Hän aikoo myydä kirjan 280 ruplalla, josta 200 annetaan hänelle, 50 kirjakaupalle ja 30 kirjailijalle. Taulukossa on tietoa kirjan julkaisukustannuksista ja todennäköisyydestä myydä tietty määrä kirjan kappaleita.
Selvitä julkaisijan odotettu tuotto.
Päätös. Satunnaismuuttuja "voitto" on yhtä suuri kuin myyntitulojen ja kustannusten välinen erotus. Esimerkiksi, jos kirjaa myydään 500 kappaletta, myyntitulot ovat 200 * 500 = 100 000 ja julkaisukustannukset ovat 225 000 ruplaa. Näin kustantaja kohtaa 125 000 ruplan tappiota. Seuraavassa taulukossa on yhteenveto satunnaismuuttujan - voitto - odotetuista arvoista:
| Määrä | Voitto xi | Todennäköisyys pi | xi p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Kaikki yhteensä: | 1,00 | 25000 |
Siten saamme julkaisijan tuoton matemaattisen odotuksen:
.
Esimerkki 3 Mahdollisuus lyödä yhdellä laukauksella p= 0,2. Määritä niiden kuorien kulutus, jotka antavat matemaattisen odotuksen osumien lukumäärästä, joka on yhtä suuri kuin 5.
Päätös. Ilmaisemme saman odotuskaavan, jota olemme käyttäneet tähän asti x- kuorien kulutus:
.
Esimerkki 4 Määritä satunnaismuuttujan matemaattinen odotus x osumien määrä kolmella laukauksella, jos todennäköisyys osua jokaisella laukauksella p = 0,4 .
Vihje: etsi satunnaismuuttujan arvojen todennäköisyys arvolla Bernoullin kaava .
Odotusominaisuudet
Harkitse matemaattisen odotuksen ominaisuuksia.
Kiinteistö 1. Vakion arvon matemaattinen odotus on yhtä suuri kuin tämä vakio:
Kiinteistö 2. Vakiotekijä voidaan ottaa pois odotusmerkistä:
Kiinteistö 3. Satunnaismuuttujien summan (eron) matemaattinen odotus on yhtä suuri kuin niiden matemaattisten odotusten summa (ero):
Kiinteistö 4. Satunnaismuuttujien tulon matemaattinen odotus on yhtä suuri kuin niiden matemaattisten odotusten tulo:
Kiinteistö 5. Jos kaikki satunnaismuuttujan arvot X vähennä (lisää) samalla numerolla Kanssa, niin sen matemaattinen odotus pienenee (nousee) samalla luvulla:
Kun ei voi rajoittua vain matemaattisiin odotuksiin
Useimmissa tapauksissa vain matemaattinen odotus ei pysty kuvaamaan satunnaismuuttujaa riittävästi.
Olkoon satunnaismuuttujat X ja Y annetaan seuraavilla jakelulailla:
| Merkitys X | Todennäköisyys |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Merkitys Y | Todennäköisyys |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Näiden suureiden matemaattiset odotukset ovat samat - yhtä kuin nolla:
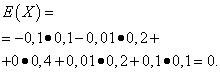
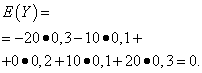
Niiden jakautuminen on kuitenkin erilainen. Satunnainen arvo X voi ottaa vain arvoja, jotka poikkeavat vähän matemaattisesta odotuksesta ja satunnaismuuttujasta Y voi ottaa arvoja, jotka poikkeavat merkittävästi matemaattisista odotuksista. Samankaltainen esimerkki: keskipalkan perusteella ei voida arvioida korkea- ja matalapalkkaisten osuutta. Toisin sanoen matemaattisella odotuksella ei voi arvioida, mitkä poikkeamat siitä ovat, ainakin keskimäärin, mahdollisia. Tätä varten sinun on löydettävä satunnaismuuttujan varianssi.
Diskreetin satunnaismuuttujan dispersio
dispersio diskreetti satunnaismuuttuja X kutsutaan matemaattiseksi odotukseksi neliön poikkeamasta matemaattisesta odotuksesta:
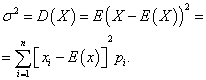
Satunnaismuuttujan keskihajonta X on sen varianssin neliöjuuren aritmeettinen arvo:
.
Esimerkki 5 Laske satunnaismuuttujien varianssit ja keskihajonnat X ja Y, jonka jakautumislait on annettu yllä olevissa taulukoissa.
Päätös. Satunnaismuuttujien matemaattiset odotukset X ja Y, kuten yllä todettiin, ovat nolla. Dispersiokaavan mukaan E(X)=E(y)=0 saamme:
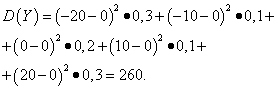
Sitten satunnaismuuttujien keskihajonnat X ja Y muodostavat
.
Näin ollen samoilla matemaattisilla odotuksilla satunnaismuuttujan varianssi X hyvin pieni ja satunnainen Y- merkittävä. Tämä johtuu niiden jakautumisen eroista.
Esimerkki 6 Sijoittajalla on 4 vaihtoehtoista sijoitushanketta. Taulukkoon on koottu tiedot näiden projektien odotetusta tuotosta vastaavalla todennäköisyydellä.
| Projekti 1 | Projekti 2 | Projekti 3 | Projekti 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Etsi kullekin vaihtoehdolle matemaattinen odotusarvo, varianssi ja keskihajonta.
Päätös. Osoitetaan, kuinka nämä suuret lasketaan kolmannelle vaihtoehdolle:
Taulukossa on yhteenveto löydetyistä arvoista kaikille vaihtoehdoille.
Kaikilla vaihtoehdoilla on samat matemaattiset odotukset. Tämä tarkoittaa, että pitkällä aikavälillä kaikilla on samat tulot. Keskihajonta voidaan tulkita riskin mittana - mitä suurempi se on, sitä suurempi on sijoituksen riski. Sijoittaja, joka ei halua suurta riskiä, valitsee projektin 1, koska sillä on pienin keskihajonta (0). Jos sijoittaja pitää parempana riskiä ja korkeaa tuottoa lyhyessä ajassa, hän valitsee projektin, jolla on suurin keskihajonta - projekti 4.
Dispersion ominaisuudet
Esitetään dispersion ominaisuudet.
Kiinteistö 1. Vakioarvon hajonta on nolla:
Kiinteistö 2. Vakiokerroin voidaan ottaa pois dispersiomerkistä neliöimällä se:
.
Kiinteistö 3. Satunnaismuuttujan varianssi on yhtä suuri kuin tämän arvon neliön matemaattinen odotus, josta vähennetään itse arvon matemaattisen odotuksen neliö:
,
missä 
.
Kiinteistö 4. Satunnaismuuttujien summan (eron) varianssi on yhtä suuri kuin niiden varianssien summa (ero):
Esimerkki 7 Tiedetään, että diskreetti satunnaismuuttuja X ottaa vain kaksi arvoa: −3 ja 7. Lisäksi tunnetaan matemaattinen odotus: E(X) = 4. Etsi diskreetin satunnaismuuttujan varianssi.
Päätös. Merkitse p todennäköisyys, jolla satunnaismuuttuja saa arvon x1 = −3 . Sitten arvon todennäköisyys x2 = 7 tulee olemaan 1 − p. Johdetaan yhtälö matemaattiselle odotukselle:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
mistä saamme todennäköisyydet: p= 0,3 ja 1 − p = 0,7 .
Satunnaismuuttujan jakautumislaki:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
Laskemme tämän satunnaismuuttujan varianssin käyttämällä varianssin ominaisuuden 3 kaavaa:
D(X) = 2,7 + 34,3 − 16 = 21 .
Etsi itse satunnaismuuttujan matemaattinen odotus ja katso sitten ratkaisu
Esimerkki 8 Diskreetti satunnaismuuttuja X ottaa vain kaksi arvoa. Se ottaa suuremman arvon 3 todennäköisyydellä 0,4. Lisäksi satunnaismuuttujan varianssi tunnetaan D(X) = 6. Etsi satunnaismuuttujan matemaattinen odotus.
Esimerkki 9 Urna sisältää 6 valkoista ja 4 mustaa palloa. Urnasta otetaan 3 palloa. Valkoisten pallojen lukumäärä vedettyjen pallojen joukossa on diskreetti satunnaismuuttuja X. Etsi tämän satunnaismuuttujan matemaattinen odotus ja varianssi.
Päätös. Satunnainen arvo X voi ottaa arvot 0, 1, 2, 3. Vastaavat todennäköisyydet voidaan laskea todennäköisyyksien kertolasku sääntö. Satunnaismuuttujan jakautumislaki:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Tästä johtuu tämän satunnaismuuttujan matemaattinen odotus:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Tietyn satunnaismuuttujan varianssi on:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Jatkuvan satunnaismuuttujan matemaattinen odotus ja dispersio
Jatkuvalle satunnaismuuttujalle matemaattisen odotuksen mekaaninen tulkinta säilyttää saman merkityksen: massakeskipiste yksikkömassalle, joka jakautuu jatkuvasti x-akselille tiheydellä f(x). Toisin kuin diskreetti satunnaismuuttuja, jonka funktion argumentti xi muuttuu äkillisesti, jatkuvan satunnaismuuttujan argumentti muuttuu jatkuvasti. Mutta jatkuvan satunnaismuuttujan matemaattinen odotus liittyy myös sen keskiarvoon.
Jotta voit löytää jatkuvan satunnaismuuttujan matemaattisen odotuksen ja varianssin, sinun on löydettävä määrätyt integraalit . Jos jatkuvan satunnaismuuttujan tiheysfunktio annetaan, se tulee suoraan integrandiin. Jos on annettu todennäköisyysjakaumafunktio, niin sen eriyttämisellä täytyy löytää tiheysfunktio.
Jatkuvan satunnaismuuttujan kaikkien mahdollisten arvojen aritmeettista keskiarvoa kutsutaan sen matemaattinen odotus, merkitty tai .
Edellisessä annoimme joukon kaavoja, joiden avulla voimme löytää funktioiden numeeriset ominaisuudet, kun argumenttien jakautumislait tunnetaan. Usein funktioiden numeeristen ominaisuuksien löytämiseksi ei kuitenkaan tarvitse tietää edes argumenttien jakautumislakeja, vaan riittää, että tietää vain osa niiden numeerisista ominaisuuksista; tässä tapauksessa pärjätään ilman jakelulakeja ollenkaan. Funktioiden numeeristen ominaisuuksien määrittäminen argumenttien annetuilla numeerisilla ominaisuuksilla on laajalti käytössä todennäköisyysteoriassa ja mahdollistaa useiden ongelmien ratkaisemisen yksinkertaistamisen merkittävästi. Suurimmaksi osaksi tällaiset yksinkertaistetut menetelmät liittyvät lineaarisiin funktioihin; kuitenkin jotkin alkeelliset epälineaariset funktiot sallivat myös tämän lähestymistavan.
Tässä esittelemme lukuisia funktioiden numeerisia ominaisuuksia koskevia lauseita, jotka kokonaisuutena edustavat hyvin yksinkertaista laitteistoa näiden ominaisuuksien laskemiseen, ja niitä voidaan soveltaa monenlaisiin olosuhteisiin.
1. Ei-satunnaisen muuttujan matemaattinen odotus
Ilmoitettu ominaisuus on melko ilmeinen; se voidaan todistaa pitämällä ei-satunnaista muuttujaa tietyntyyppisenä satunnaismuuttujana, jolla on yksi mahdollinen arvo todennäköisyydellä yksi; sitten matemaattisen odotuksen yleisen kaavan mukaan:
.
2. Ei-satunnaisen muuttujan dispersio
Jos on ei-satunnainen arvo, niin
3. Matemaattisen odotuksen merkin ylittävän ei-satunnaisen muuttujan poistaminen
, (10.2.1)
eli ei-satunnainen arvo voidaan ottaa pois odotusmerkistä.
Todiste.
a) Epäjatkuville määrille
b) Jatkuville määrille
.
4. Ei-satunnaisen arvon poistaminen varianssin ja keskihajonnan etumerkistä
If on ei-satunnainen muuttuja ja on satunnainen, niin
, (10.2.2)
eli ei-satunnainen arvo voidaan ottaa pois dispersiomerkistä neliöimällä se.
Todiste. Varianssin määritelmän mukaan
Seuraus
,
eli ei-satunnainen arvo voidaan ottaa pois keskihajonnan etumerkistä sen absoluuttisella arvolla. Todiste saadaan poimimalla neliöjuuri kaavasta (10.2.2) ja ottamalla huomioon, että r.s.c. on pohjimmiltaan positiivinen arvo.
5. Satunnaismuuttujien summan matemaattinen odotus
Osoittakaamme, että mille tahansa kahdelle satunnaismuuttujalle ja
eli kahden satunnaismuuttujan summan matemaattinen odotus on yhtä suuri kuin niiden matemaattisten odotusten summa.
Tämä ominaisuus tunnetaan odotuslisäyslauseena.
Todiste.
a) Olkoon epäjatkuvien satunnaismuuttujien järjestelmä. Sovelletaan satunnaismuuttujien summaan yleiskaavaa (10.1.6) kahden argumentin funktion matemaattiselle odotukselle:
.
Ho ei ole muuta kuin kokonaistodennäköisyys, että arvo saa arvon:
;
siten,
.
Samalla tavalla todistamme sen
,
ja lause on todistettu.
b) Olkoon jatkuva satunnaismuuttujien järjestelmä. Kaavan (10.1.7) mukaan
. (10.2.4)
Muunnetaan ensimmäinen integraali (10.2.4):
;
samoin
,
ja lause on todistettu.
On erityisesti huomattava, että matemaattisten odotusten yhteenlaskulause pätee kaikille satunnaismuuttujille - sekä riippuville että riippumattomille.
Odotuslisäyslause voidaan yleistää mielivaltaiseen määrään termejä:
, (10.2.5)
eli useiden satunnaismuuttujien summan matemaattinen odotus on yhtä suuri kuin niiden matemaattisten odotusten summa.
Sen todistamiseksi riittää täydellisen induktion menetelmän soveltaminen.
6. Lineaarifunktion matemaattinen odotus
Harkitse useiden satunnaisten argumenttien lineaarista funktiota:
missä ovat ei-satunnaiset kertoimet. Todistetaan se
, (10.2.6)
eli lineaarifunktion keskiarvo on yhtä suuri kuin argumenttien keskiarvon sama lineaarifunktio.
Todiste. Käyttämällä summauslausetta m.o. ja sääntö ottaa ei-satunnainen muuttuja pois m. o:n merkistä, saamme:
.
7. Dispeptämä satunnaismuuttujien summa
Kahden satunnaismuuttujan summan varianssi on yhtä suuri kuin niiden varianssien summa plus kaksinkertainen korrelaatiomomentti:
Todiste. Merkitse
Matemaattisten odotusten summauslauseen mukaan
Siirrytään satunnaismuuttujista vastaaviin keskitettyihin muuttujiin . Kun vähennetään termi kerrallaan yhtäläisyydestä (10.2.8) yhtäläisyydestä (10.2.9), saadaan:
Varianssin määritelmän mukaan
Q.E.D.
Summan varianssin kaava (10.2.7) voidaan yleistää mihin tahansa määrään termejä:
,
(10.2.10)
missä on arvojen korrelaatiomomentti, summan alla oleva merkki tarkoittaa, että summaus koskee kaikkia mahdollisia satunnaismuuttujien parittaisia yhdistelmiä 
.
Todistus on samanlainen kuin edellinen ja seuraa polynomin neliön kaavasta.
Kaava (10.2.10) voidaan kirjoittaa toisessa muodossa:
, (10.2.11)
jossa kaksoissumma ulottuu kaikkiin suureiden järjestelmän korrelaatiomatriisin alkioihin , joka sisältää sekä korrelaatiomomentit että varianssit.
Jos kaikki satunnaismuuttujat , jotka sisältyvät järjestelmään, ovat korreloimattomia (eli osoitteessa ), kaava (10.2.10) on muodossa:
, (10.2.12)
eli korreloimattomien satunnaismuuttujien summan varianssi on yhtä suuri kuin termien varianssien summa.
Tämä väite tunnetaan varianssin yhteenlaskulauseena.
8. Lineaarifunktion dispersio
Tarkastellaan useiden satunnaismuuttujien lineaarista funktiota.
missä ovat ei-satunnaiset muuttujat.
Osoitetaan, että tämän lineaarisen funktion dispersio ilmaistaan kaavalla
, (10.2.13)
missä on määrien korrelaatiomomentti , .
Todiste. Esitellään merkintä:
. (10.2.14)
Soveltamalla kaavaa (10.2.10) summan varianssille lausekkeen (10.2.14) oikealle puolelle ja ottaen huomioon, että saadaan:
missä on määrien korrelaatiomomentti:
.
Lasketaan tämä hetki. Meillä on:
;
samoin
Kun tämä lauseke korvataan lausekkeella (10.2.15), saadaan kaava (10.2.13).
Erityistapauksessa, kun kaikki määrät korreloimaton, kaava (10.2.13) saa muodon:
, (10.2.16)
eli korreloimattomien satunnaismuuttujien lineaarisen funktion varianssi on yhtä suuri kuin kertoimien neliöiden ja vastaavien argumenttien varianssien tulojen summa.
9. Satunnaismuuttujien tulon matemaattinen odotus
Kahden satunnaismuuttujan tulon matemaattinen odotus on yhtä suuri kuin niiden matemaattisten odotusten tulo plus korrelaatiomomentti:
Todiste. Jatkamme korrelaatiomomentin määritelmästä:
Muunnamme tämän lausekkeen käyttämällä matemaattisen odotuksen ominaisuuksia:
joka ilmeisesti vastaa kaavaa (10.2.17).
Jos satunnaismuuttujat eivät korreloi, kaava (10.2.17) saa muotoa:
eli kahden korreloimattoman satunnaismuuttujan tulon keskiarvo on yhtä suuri kuin niiden keskiarvon tulo.
Tämä lause tunnetaan odotuskerto-lauseena.
Kaava (10.2.17) ei ole muuta kuin ilmaus järjestelmän toisesta sekakeskihetkestä toisen sekoitettuna alkumomentin ja matemaattisten odotusten suhteen:
. (10.2.19)
Tätä lauseketta käytetään usein käytännössä korrelaatiomomenttia laskettaessa samalla tavalla kuin yhden satunnaismuuttujan varianssi lasketaan usein toisen alkuhetken ja matemaattisen odotuksen kautta.
Odotuskertoloreema voidaan myös yleistää mielivaltaiseen määrään tekijöitä, vain tässä tapauksessa sen soveltamiseen ei riitä, että suureet ovat korreloimattomia, vaan tarvitaan myös joidenkin korkeampien sekoitusmomenttien katoamista, joiden lukumäärä riippuu mm. termien määrä tuotteessa. Nämä ehdot täyttyvät varmasti, jos tuotteeseen sisältyvät satunnaismuuttujat ovat riippumattomia. Tässä tapauksessa
, (10.2.20)
eli riippumattomien satunnaismuuttujien tulon matemaattinen odotus on yhtä suuri kuin heidän matemaattisten odotustensa tulo.
Tämä väite voidaan helposti todistaa täydellisellä induktiolla.
10. Riippumattomien satunnaismuuttujien tulon hajonta
Todistetaan tämä riippumattomille muuttujille
Todiste. Merkitään. Varianssin määritelmän mukaan
Koska määrät ovat riippumattomia, ja
Riippumattomille määrät ovat myös riippumattomia; siten,
,
Mutta ei ole mitään muuta kuin määrän toinen alkumomentti, ja siksi se ilmaistaan varianssina:
;
samoin
.
Korvaamalla nämä lausekkeet kaavaan (10.2.22) ja tuomalla vastaavat termit, päädymme kaavaan (10.2.21).
Siinä tapauksessa, että keskitetyt satunnaismuuttujat kerrotaan (arvot, joiden matemaattiset odotukset ovat yhtä suuria kuin nolla), kaava (10.2.21) saa muotoa:
, (10.2.23)
eli riippumattomien keskitettyjen satunnaismuuttujien tulon varianssi on yhtä suuri kuin niiden varianssien tulo.
11. Satunnaismuuttujien summan korkeammat momentit
Joissakin tapauksissa on tarpeen laskea riippumattomien satunnaismuuttujien summan korkeammat momentit. Todistakaamme joitain toisiinsa liittyviä suhteita.
1) Jos suuret ovat riippumattomia, niin
Todiste.
mistä odotuskertalauseella
Mutta minkä tahansa suuren ensimmäinen keskeinen momentti on nolla; kaksi keskimmäistä termiä katoavat ja kaava (10.2.24) todistetaan.
Relaatio (10.2.24) voidaan helposti yleistää induktiolla mielivaltaiseen määrään riippumattomia termejä:
. (10.2.25)
2) Kahden riippumattoman satunnaismuuttujan summan neljäs keskusmomentti ilmaistaan kaavalla
missä ovat ja dispersiot.
Todistus on täsmälleen sama kuin edellinen.
Täydellisen induktion menetelmällä on helppo todistaa kaavan (10.2.26) yleistyminen mielivaltaiseen määrään riippumattomia termejä.
Satunnaismuuttujan dispersio ja sen ominaisuudet.
Monilla satunnaismuuttujilla on sama matemaattinen odotus, mutta erilaiset mahdolliset arvot. Siksi yksi matemaattinen odotus ei riitä karakterisoimaan satunnaismuuttujaa.
Anna tulot X ja Y(dollareissa) kahdesta yrityksestä saadaan jakaumilla:
Joskus on kätevää käyttää toista kaavaa, joka voidaan saada käyttämällä matemaattisen odotuksen ominaisuuksia,
Dispersio on olemassa, jos sarja (vastaavasti integraali) konvergoi.
Ei-negatiivinen luku 
nimeltään keskihajonta Satunnaismuuttuja X. Sillä on satunnaismuuttujan ulottuvuus X ja määrittelee jonkin standardin rms-dispersiovälin, joka on symmetrinen suhteessa matemaattiseen odotukseen. Arvoa kutsutaan joskus standardipoikkeamaksi.
Satunnaismuuttujaa kutsutaan keskitetty, jos. Satunnaismuuttujaa kutsutaan normalisoitunut(vakio) jos .
Jatketaan esimerkkiä. Laske kahden yrityksen tulojen varianssi:
Vertaamalla varianssia näemme, että toisen yrityksen tulot vaihtelevat enemmän kuin ensimmäisen.
Dispersion ominaisuudet.
1. Vakioarvon hajonta on nolla, ts. , jos vakio. Tämä on ilmeistä, koska vakioarvon matemaattinen odotusarvo on sama kuin vakioarvo, ts. .
2. Vakiokerroin C voidaan ottaa pois dispersiomerkistä neliöimällä se ensin.
Todella,
3. Kahden riippumattoman satunnaismuuttujan algebrallisen summan varianssi on yhtä suuri kuin niiden varianssien summa, ts.
Ilmaisua kutsutaan X:n ja Y:n kovarianssi(katso Aihe 4, §2). Riippumattomien satunnaismuuttujien kovarianssi on nolla, ts.
Käyttämällä tätä yhtälöä voit lisätä matemaattisen odotuksen ominaisuuksien luetteloon. Jos satunnaismuuttujat X ja Y ovat riippumattomia, silloin tuotteen matemaattinen odotus on yhtä suuri kuin matemaattisten odotusten tulo, nimittäin:
Jos satunnaismuuttuja muunnetaan lineaarisesti, ts. , sitten
.
Esimerkki 1. Anna sen tuottaa n riippumattomat testit, tapahtuman todennäköisyys MUTTA joista jokaisessa on vakio ja yhtä suuri p. Mikä on tapahtuman esiintymisten lukumäärän varianssi MUTTA näissä kokeissa?
Päätös. Antaa olla tapahtuman esiintymisten lukumäärä MUTTA ensimmäisessä kokeilussa on tapahtuman esiintymisten lukumäärä MUTTA toisessa testissä ja niin edelleen. Sitten tapahtuman esiintymisten kokonaismäärä MUTTA sisään n koettelemukset ovat yhtä suuria
Käyttämällä dispersion ominaisuutta 3 saamme
Tässä olemme käyttäneet sitä tosiasiaa 
, i= (katso esimerkit 1 ja 2, kohta 3.3.1.).
Esimerkki 2. Anna X - talletuksen määrä (dollareina) pankissa - todennäköisyysjakauman avulla
| X | ||||||
| i = | 0,01 | 0,03 | 0,10 | 0,30 | 0,5 | 0,06 |
Etsi keskimääräinen panoksen määrä ja varianssi.
Päätös. Keskimääräinen talletussumma on yhtä suuri kuin matemaattinen odotus
Varianssin laskemiseen käytämme kaavaa
D (X) \u003d 8196 - 7849,96 \u003d 348,04.
Vakiopoikkeama
Hetkiä.
Jotta voidaan ottaa huomioon satunnaismuuttujan mahdollisten arvojen vaikutus matemaattiseen odotukseen X, jotka ovat suuria, mutta joilla on pieni todennäköisyys, on suositeltavaa ottaa huomioon satunnaismuuttujan positiivisen kokonaisluvun potenssin matemaattiset odotukset.
