Neliöyhtälön graafinen ratkaisu Vahvistaa kykyä rakentaa eri funktioiden kuvaajia; Muodostaa kyky ratkaista toisen asteen yhtälöitä graafisesti. Projekti aiheesta "Funktion graafien muuntaminen"

Neliöyhtälön graafinen ratkaisu Vahvistaa kykyä rakentaa eri funktioiden kuvaajia; Muodostaa kyky ratkaista toisen asteen yhtälöitä graafisesti. Brdsk 2009 Kunnallinen oppilaitos - Talouslyseo Yleistävä oppitunti aiheesta "Kvadraattinen funktio", algebra luokka 8 opettaja Fedoseeva T.M.

Neliöfunktion piirtäminen Määritä haarojen suunta: a>0 haarautuu ylöspäin; a 0 haaraa ylöspäin; a"> 0 haaraa ylös; a"> 0 haaraa ylös; a" title="(!LANG:Neliöfunktion piirtäminen Haaroittamisen suunta: a>0 haarautuu ylöspäin; a"> title="Neliöfunktion piirtäminen Määritä haarojen suunta: a>0 haarautuu ylöspäin; a"> !}

0 haaraa on suunnattu ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Etsi piste "title="(!LANG: Tehdään funktio y=x 2 -2x-3 kuvaajasta algoritmilla: 1) a=1>0 haarat suunnataan ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Pisteen löytäminen" class="link_thumb"> 3 !} Rakennetaan funktion y=x 2 -2x-3 graafi algoritmilla: 1) a=1>0 haarat suunnataan ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Löydämme leikkauspisteet OX-akselin kanssa: x 1 \u003d -1; x 2 \u003d 3 1 tapa ratkaista yhtälö x 2 -2x-3 \u003d 0 y x Ratkaise yhtälö x 2 +2x-3 \u003d 0 0 haaraa on suunnattu ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Löydämme pisteen "\u003e 0 oksat on suunnattu ylöspäin; 2) ylä y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - akseli paraabelin ohjauspisteet: (0: -3) , (3; 0) ja symmetrisesti x = 1-akselin suhteen Rakennamme paraabelin.Etsi OX-akselin leikkauspisteet: x 1 \u003d -1; x 2 \u003d 3 1 tapa ratkaista yhtälö x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Ratkaise yhtälö x 2 + 2x-3 \u003d 0 "\u003e 0 haaraa on suunnattu ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Etsi piste "title="(!LANG: Tehdään funktio y=x 2 -2x-3 kuvaajasta algoritmilla: 1) a=1>0 haarat suunnataan ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Pisteen löytäminen"> title="Rakennetaan funktion y=x 2 -2x-3 graafi algoritmilla: 1) a=1>0 haarat suunnataan ylöspäin; 2) huippupiste y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - paraabelin akseli Ohjauspisteet: (0: -3), (3) ; 0) ja symmetrinen niille x-akselin ympäri = 1 Rakennamme paraabelin. Pisteen löytäminen"> !}

Toinen tapa: a). Jaetaan yhtälö x 2 -2x-3=0 osiin x 2 = 2x+3 Kirjoitetaan kaksi funktiota y= x 2 ; y \u003d 2x + 3 Rakennamme näiden funktioiden kuvaajia yhteen koordinaattijärjestelmään. Leikkauspisteiden abskissat ovat yhtälön juuret. 0 1 x y Ratkaise yhtälö x 2 +2x-3=0

Kolmas tapa: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Rakennamme näiden funktioiden kuvaajia yhteen koordinaattijärjestelmään. Leikkauspisteiden abskissat ovat yhtälön juuret. 0 1 x y Ratkaise yhtälö x 2 +2x-3=0

Yhtälöiden graafinen ratkaisu

Kunnon päivä, 2009

Johdanto

Muinaisina aikoina tarve ratkaista toisen asteen yhtälöitä johtui tarpeesta ratkaista sotilasluonteisten maa-alueiden ja maanrakennustöiden löytämiseen liittyviä ongelmia sekä itse tähtitieteen ja matematiikan kehitystä. Babylonialaiset osasivat ratkaista toisen asteen yhtälöitä noin 2000 eaa. Babylonilaisissa teksteissä esitetty sääntö näiden yhtälöiden ratkaisemiseksi on olennaisesti sama kuin nykyajan sääntö, mutta ei tiedetä, kuinka babylonialaiset päätyivät tähän sääntöön.

Kaavat toisen asteen yhtälöiden ratkaisemiseksi Euroopassa esitettiin ensimmäisen kerran Abacus-kirjassa, jonka italialainen matemaatikko Leonardo Fibonacci kirjoitti vuonna 1202. Hänen kirjansa edisti algebrallisen tiedon leviämistä ei vain Italiassa, vaan myös Saksassa, Ranskassa ja muissa Euroopan maissa.

Mutta yleisen säännön toisen asteen yhtälöiden ratkaisemiseksi kaikilla mahdollisilla kertoimien b ja c yhdistelmillä muotoiltiin Euroopassa vasta vuonna 1544 M. Stiefelin toimesta.

Vuonna 1591 François Viet esitteli kaavoja toisen asteen yhtälöiden ratkaisemiseksi.

Joitakin toisenlaisia yhtälöitä voitiin ratkaista muinaisessa Babylonissa.

Diophantus Aleksandrialainen ja Euclid , Al-Khwarizmi ja Omar Khayyam ratkaisi yhtälöitä geometrisesti ja graafisesti.

7. luokalla opiskelimme toimintoja y \u003d C, y= kx , y = kx + m , y = x 2 ,y = - x 2 , 8 luokalla - y = √ x , y = |x |, y= kirves 2 + bx + c , y = k / x. 9. luokan algebraoppikirjassa näin funktioita, joita en vielä tuntenut: y= x 3 , y= x 4 ,y= x 2 n , y= x - 2 n , y= 3 √x , ( x – a ) 2 + (y - b ) 2 = r 2 ja muut. Näiden funktioiden kuvaajien muodostamiseen on olemassa säännöt. Mietin, onko muita toimintoja, jotka noudattavat näitä sääntöjä.

Työni on tutkia funktiokaavioita ja ratkaista yhtälöitä graafisesti.

1. Mitkä ovat toiminnot

Funktion kuvaaja on joukko koordinaattitason kaikkia pisteitä, joiden abskissat ovat yhtä suuria kuin argumenttien arvot ja ordinaatit ovat yhtä suuria kuin funktion vastaavat arvot.

Lineaarinen funktio saadaan yhtälöstä y= kx + b, missä k ja b- joitain numeroita. Tämän funktion kaavio on suora.

Käänteinen suhteellinen funktio y= k / x, missä k¹ 0. Tämän funktion kuvaajaa kutsutaan hyperboliksi.

Toiminto ( x – a ) 2 + (y – b ) 2 = r 2 , missä a , b ja r- joitain numeroita. Tämän funktion kuvaaja on ympyrä, jonka säde on r ja jonka keskipiste on piste A ( a , b).

neliöfunktio y = kirves 2 + bx + c missä a, b , Kanssa- joitain numeroita ja a¹ 0. Tämän funktion kuvaaja on paraabeli.

Yhtälö v 2 ( a – x ) = x 2 ( a + x ) . Tämän yhtälön kuvaaja on käyrä, jota kutsutaan strophoidiksi.

Yhtälö ( x 2 + y 2 ) 2 = a ( x 2 – y 2 ) . Tämän yhtälön kuvaajaa kutsutaan Bernoullin lemniskaatiksi.

Yhtälö. Tämän yhtälön kuvaajaa kutsutaan astroidiksi.

Käyrä (x 2 y 2 - 2 a x) 2 \u003d 4 a 2 (x 2 + y 2). Tätä käyrää kutsutaan kardioidiksi.

Toiminnot: y= x 3 - kuutioinen paraabeli, y= x 4 , y = 1/ x 2 .

2. Yhtälön käsite, sen graafinen ratkaisu

Yhtälö on lauseke, joka sisältää muuttujan.

ratkaise yhtälö- tämä tarkoittaa kaikkien sen juurten löytämistä tai sen todistamista, että niitä ei ole olemassa.

Yhtälön juuri on luku, joka yhtälöön korvattuna tuottaa oikean numeerisen yhtälön.

Yhtälöiden ratkaiseminen graafisesti avulla voit löytää juurien tarkan tai likimääräisen arvon, voit löytää yhtälön juurien lukumäärän.

Kaavioiden piirtämisessä ja yhtälöiden ratkaisemisessa käytetään funktion ominaisuuksia, joten menetelmää kutsutaan usein funktionaaliseksi graafiseksi.

Yhtälön ratkaisemiseksi "jaamme" sen kahteen osaan, esittelemme kaksi funktiota, rakennamme niiden kaaviot, etsimme kaavioiden leikkauspisteiden koordinaatit. Näiden pisteiden abskissat ovat yhtälön juuret.

3. Algoritmi funktion kuvaajan muodostamiseksi

Funktion kaavion tunteminen y= f ( x ) , voit piirtää funktioita y= f ( x + m ) ,y= f ( x )+ l ja y= f ( x + m )+ l. Kaikki nämä kaaviot saadaan funktion kaaviosta y= f ( x ) käyttämällä rinnakkaiskäännösmuunnosta: on │ m │ skaalausyksiköt oikealle tai vasemmalle x-akselia pitkin ja edelleen │ l │ skaalausyksiköt ylös tai alas akselia pitkin y .

4. Toisen yhtälön graafinen ratkaisu

Tarkastellaan toisen asteen yhtälön graafista ratkaisua neliöfunktion esimerkin avulla. Neliöfunktion kuvaaja on paraabeli.

Mitä muinaiset kreikkalaiset tiesivät parabolista?

Nykyaikainen matemaattinen symboliikka syntyi 1500-luvulla.

Muinaisilla kreikkalaisilla matemaatikoilla ei ollut koordinaattimenetelmää eikä funktion käsitettä. He kuitenkin tutkivat paraabelin ominaisuuksia yksityiskohtaisesti. Muinaisten matemaatikoiden kekseliäisyys on yksinkertaisesti hämmästyttävää, koska he pystyivät käyttämään vain piirustuksia ja sanallisia kuvauksia riippuvuuksista.

Täysin tutkittu paraabeli, hyperbola ja ellipsi Apollonius Pergalainen, joka asui 3. vuosisadalla eKr. Hän antoi myös nimet näille käyrälle ja osoitti, mitkä ehdot tietyllä käyrällä olevat pisteet täyttävät (eihän siellä ollut kaavoja!).

Paraabelin rakentamiseen on algoritmi:

Löydämme paraabelin A (x 0; y 0) kärjen koordinaatit: x 0 =- b /2 a ;

Y 0 \u003d ax noin 2 + in 0 + c;

Löydämme paraabelin symmetria-akselin (suora x \u003d x 0);

Arvotaulukon laatiminen rakennuksen ohjauspisteille;

Rakennamme saadut pisteet ja rakennamme niille symmetrisiä pisteitä symmetria-akselin suhteen.

1. Muodostetaan paraabeli algoritmin mukaan y = x 2 – 2 x – 3 . Akselin ja leikkauspisteiden abskissit x ja ovat toisen asteen yhtälön juuret x 2 – 2 x – 3 = 0.

On viisi tapaa ratkaista tämä yhtälö graafisesti.

2. Jaetaan yhtälö kahteen funktioon: y = x 2 ja y = 2 x + 3

3. Jaetaan yhtälö kahteen funktioon: y = x 2 –3 ja y =2 x. Yhtälön juuret ovat paraabelin ja suoran leikkauspisteiden abskissat.

4. Muunna yhtälö x 2 – 2 x – 3 = 0 valitsemalla funktion koko neliö: y = ( x –1) 2 ja y =4. Yhtälön juuret ovat paraabelin ja suoran leikkauspisteiden abskissat.

5. Jaamme termit termeiltä yhtälön molemmat osat x 2 – 2 x – 3 = 0 päällä x, saamme x – 2 – 3/ x = 0 Jaetaan tämä yhtälö kahteen funktioon: y = x – 2, y = 3/ x . Yhtälön juuret ovat suoran ja hyperbelin leikkauspisteiden abskissat.

5. Graafinen asteyhtälöiden ratkaisu n

Esimerkki 1 ratkaise yhtälö x 5 = 3 – 2 x .

y = x 5 , y = 3 – 2 x .

Vastaus: x = 1.

Esimerkki 2 ratkaise yhtälö 3 √ x = 10 – x .

Tämän yhtälön juuret ovat kahden funktion kaavioiden leikkauspisteen abskissa: y = 3 √ x , y = 10 – x .

Vastaus: x=8.

Johtopäätös

Kun otetaan huomioon funktiokaaviot: y= kirves 2 + bx + c , y = k / x , y = √ x , y = |x |, y= x 3 , y= x 4 ,y= 3 √x , Huomasin, että kaikki nämä graafit on rakennettu akseleihin nähden rinnakkaiskäännöksen säännön mukaan x ja y .

Käyttämällä esimerkkiä toisen asteen yhtälön ratkaisusta voidaan päätellä, että graafinen menetelmä soveltuu myös n-asteisiin yhtälöihin.

Graafiset menetelmät yhtälöiden ratkaisemiseksi ovat kauniita ja ymmärrettäviä, mutta ne eivät anna 100% takuuta yhdenkään yhtälön ratkaisemisesta. Kuvaajien leikkauspisteiden abskissat voivat olla likimääräisiä.

9. luokalla ja vanhemmilla luokilla tulen vielä tutustumaan muihin toimintoihin. Olen kiinnostunut tietämään, noudattavatko nämä funktiot rinnakkaiskäännöksen sääntöjä piirtäessään graafiaan.

Ensi vuonna haluan pohtia myös yhtälö- ja epäyhtälöjärjestelmien graafisen ratkaisun kysymyksiä.

Kirjallisuus

1. Algebra. 7. luokka. Osa 1. Oppikirja oppilaitoksille / A.G. Mordkovich. Moskova: Mnemosyne, 2007.

2. Algebra. 8. luokka. Osa 1. Oppikirja oppilaitoksille / A.G. Mordkovich. Moskova: Mnemosyne, 2007.

3. Algebra. Luokka 9 Osa 1. Oppikirja oppilaitoksille / A.G. Mordkovich. Moskova: Mnemosyne, 2007.

4. Glazer G.I. Matematiikan historia koulussa. VII-VIII luokat. – M.: Enlightenment, 1982.

5. Journal Mathematics №5 2009; nro 8 2007; Nro 23 2008.

6. Yhtälöiden graafinen ratkaisu Internet-sivustot: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Yhtälöiden graafinen ratkaisu

Kunnon päivä, 2009

Johdanto

Mutta yleisen säännön toisen asteen yhtälöiden ratkaisemiseksi kaikilla mahdollisilla kertoimien b ja c yhdistelmillä muotoiltiin Euroopassa vasta vuonna 1544 M. Stiefelin toimesta.

Vuonna 1591 François Viet esitteli kaavoja toisen asteen yhtälöiden ratkaisemiseksi.

Joitakin toisenlaisia yhtälöitä voitiin ratkaista muinaisessa Babylonissa.

Diophantus Aleksandrialainen ja Euclid, Al-Khwarizmi ja Omar Khayyam ratkaisi yhtälöitä geometrisesti ja graafisesti.

7. luokalla opiskelimme toimintoja y \u003d C, y=kx, y =kx+ m, y =x 2,y = -x 2, 8 luokalla - y = √x, y =|x|, y=kirves2 + bx+ c, y =k/ x. 9. luokan algebraoppikirjassa näin funktioita, joita en vielä tuntenut: y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– a) 2 + (y -b) 2 = r 2 ja muut. Näiden funktioiden kuvaajien muodostamiseen on olemassa säännöt. Mietin, onko muita toimintoja, jotka noudattavat näitä sääntöjä.

Työni on tutkia funktiokaavioita ja ratkaista yhtälöitä graafisesti.

1. Mitkä ovat toiminnot

Funktion kuvaaja on joukko koordinaattitason kaikkia pisteitä, joiden abskissat ovat yhtä suuria kuin argumenttien arvot ja ordinaatit ovat yhtä suuria kuin funktion vastaavat arvot.

Lineaarinen funktio saadaan yhtälöstä y=kx+ b, missä k ja b- joitain numeroita. Tämän funktion kaavio on suora.

Käänteinen suhteellinen funktio y=k/ x, jossa k ¹ 0. Tämän funktion kuvaajaa kutsutaan hyperboliksi.

Toiminto (x– a) 2 + (y -b) 2 = r2 , missä a, b ja r- joitain numeroita. Tämän funktion kuvaaja on ympyrä, jonka säde on r ja jonka keskipiste on piste A ( a, b).

neliöfunktio y= kirves2 + bx+ c missä a,b, Kanssa- joitain numeroita ja a¹ 0. Tämän funktion kuvaaja on paraabeli.

Yhtälö klo2 (a– x) = x2 (a+ x) . Tämän yhtälön kuvaaja on käyrä, jota kutsutaan strophoidiksi.

/>Yhtälö (x2 + y2 ) 2 = a(x2 – y2 ) . Tämän yhtälön kuvaajaa kutsutaan Bernoullin lemniskaatiksi.

Yhtälö. Tämän yhtälön kuvaajaa kutsutaan astroidiksi.

Käyrä (x2 y2 – 2 x)2 =4 a2 (x2 +y2 ) . Tätä käyrää kutsutaan kardioidiksi.

Toiminnot: y=x 3 - kuutioinen paraabeli, y=x 4, y = 1/x 2.

2. Yhtälön käsite, sen graafinen ratkaisu

Yhtälö on lauseke, joka sisältää muuttujan.

ratkaise yhtälö- tämä tarkoittaa kaikkien sen juurten löytämistä tai sen todistamista, että niitä ei ole olemassa.

Yhtälön juuri on luku, joka yhtälöön korvattuna tuottaa oikean numeerisen yhtälön.

Yhtälöiden ratkaiseminen graafisesti avulla voit löytää juurien tarkan tai likimääräisen arvon, voit löytää yhtälön juurien lukumäärän.

Kaavioiden piirtämisessä ja yhtälöiden ratkaisemisessa käytetään funktion ominaisuuksia, joten menetelmää kutsutaan usein funktionaaliseksi graafiseksi.

3. Algoritmi funktion kuvaajan muodostamiseksi

Funktion kaavion tunteminen y=f(x) , voit piirtää funktioita y=f(x+ m) ,y=f(x)+ l ja y=f(x+ m)+ l. Kaikki nämä kaaviot saadaan funktion kaaviosta y=f(x) käyttämällä rinnakkaiskäännösmuunnosta: on │ m│ skaalausyksiköt oikealle tai vasemmalle x-akselia pitkin ja edelleen │ l│ skaalausyksiköt ylös tai alas akselia pitkin y.

4. Toisen yhtälön graafinen ratkaisu

Tarkastellaan toisen asteen yhtälön graafista ratkaisua neliöfunktion esimerkin avulla. Neliöfunktion kuvaaja on paraabeli.

Mitä muinaiset kreikkalaiset tiesivät parabolista?

Nykyaikainen matemaattinen symboliikka syntyi 1500-luvulla.

Paraabelin rakentamiseen on algoritmi:

Etsi paraabelin A (x0; y0) kärjen koordinaatit: X=- b/2 a;

y0=aho2+in0+s;

Etsi paraabelin symmetria-akseli (suora x=x0);

SIVUNVAIHTO--

Arvotaulukon laatiminen rakennuksen ohjauspisteille;

Rakennamme saadut pisteet ja rakennamme niille symmetrisiä pisteitä symmetria-akselin suhteen.

1. Muodostetaan paraabeli algoritmin mukaan y= x2 – 2 x– 3 . Akselin ja leikkauspisteiden abskissit x ja ovat toisen asteen yhtälön juuret x2 – 2 x– 3 = 0.

On viisi tapaa ratkaista tämä yhtälö graafisesti.

2. Jaetaan yhtälö kahteen funktioon: y= x2 ja y= 2 x+ 3

3. Jaetaan yhtälö kahteen funktioon: y= x2 –3 ja y=2 x. Yhtälön juuret ovat paraabelin ja suoran leikkauspisteiden abskissat.

4. Muunna yhtälö x2 – 2 x– 3 = 0 valitsemalla funktion koko neliö: y= (x–1) 2 ja y=4. Yhtälön juuret ovat paraabelin ja suoran leikkauspisteiden abskissat.

5. Jaamme termit termeiltä yhtälön molemmat osat x2 – 2 x– 3 = 0 päällä x, saamme x– 2 – 3/ x= 0 Jaetaan tämä yhtälö kahteen funktioon: y= x– 2, y= 3/ x. Yhtälön juuret ovat suoran ja hyperbelin leikkauspisteiden abskissat.

5. Graafinen asteyhtälöiden ratkaisun

Esimerkki 1 ratkaise yhtälö x5 = 3 – 2 x.

y= x5 , y= 3 – 2 x.

Vastaus: x = 1.

Esimerkki 2 ratkaise yhtälö 3 √ x= 10 – x.

Tämän yhtälön juuret ovat kahden funktion kaavioiden leikkauspisteen abskissa: y= 3 √ x, y= 10 – x.

Vastaus: x=8.

Johtopäätös

Kun otetaan huomioon funktiokaaviot: y=kirves2 + bx+ c, y =k/ x, y = √x, y =|x|, y=x 3, y=x 4,y= 3√x, Huomasin, että kaikki nämä graafit on rakennettu akseleihin nähden rinnakkaiskäännöksen säännön mukaan x ja y.

Käyttämällä esimerkkiä toisen asteen yhtälön ratkaisusta voidaan päätellä, että graafinen menetelmä soveltuu myös n-asteisiin yhtälöihin.

Ensi vuonna haluan pohtia myös yhtälö- ja epäyhtälöjärjestelmien graafisen ratkaisun kysymyksiä.

Kirjallisuus

1. Algebra. 7. luokka. Osa 1. Oppikirja oppilaitoksille / A.G. Mordkovich. Moskova: Mnemosyne, 2007.

2. Algebra. 8. luokka. Osa 1. Oppikirja oppilaitoksille / A.G. Mordkovich. Moskova: Mnemosyne, 2007.

3. Algebra. Luokka 9 Osa 1. Oppikirja oppilaitoksille / A.G. Mordkovich. Moskova: Mnemosyne, 2007.

4. Glazer G.I. Matematiikan historia koulussa. VII-VIII luokat. – M.: Enlightenment, 1982.

5. Journal Mathematics №5 2009; nro 8 2007; Nro 23 2008.

6. Yhtälöiden graafinen ratkaisu Internet-sivustot: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Tässä videotunnissa aiheena "Funktion y \u003d x 2. Yhtälöiden graafinen ratkaisu. Tämän oppitunnin aikana opiskelijat pääsevät tutustumaan uuteen yhtälöiden ratkaisutapaan - graafiseen, joka perustuu funktiokaavioiden ominaisuuksien tuntemiseen. Opettaja näyttää, kuinka funktio y=x 2 ratkaistaan graafisesti.

Aihe:Toiminto

Oppitunti:Toiminto. Yhtälöiden graafinen ratkaisu

Yhtälöiden graafinen ratkaisu perustuu funktiokaavioiden ja niiden ominaisuuksien tuntemiseen. Listaamme funktiot, joiden kuvaajat tunnemme:

1), kaavio on x-akselin suuntainen suora viiva, joka kulkee y-akselin pisteen kautta. Harkitse esimerkkiä: y=1:

Eri arvoille saamme perheen x-akselin suuntaisia suoria viivoja.

2) Suora verrannollisuusfunktio tämän funktion kuvaaja on origon kautta kulkeva suora. Harkitse esimerkkiä:

Olemme jo rakentaneet nämä kaaviot aiemmilla oppitunneilla, muista, että jokaisen rivin rakentamiseksi sinun on valittava piste, joka täyttää sen, ja otettava origo toiseksi pisteeksi.

Muista kertoimen k rooli: funktion kasvaessa suoran ja x-akselin positiivisen suunnan välinen kulma on terävä; kun funktio pienenee, suoran ja x-akselin positiivisen suunnan välinen kulma on tylppä. Lisäksi kahden samanmerkkisen parametrin k välillä on seuraava suhde: positiiviselle k:lle, mitä suurempi se on, sitä nopeammin funktio kasvaa, ja negatiivisella funktio pienenee nopeammin suurilla k moduloarvoilla.

3) Lineaarinen funktio. Kun - saamme leikkauspisteen y-akselin kanssa ja kaikki tällaiset suorat kulkevat pisteen (0; m) kautta. Lisäksi funktion kasvaessa suoran ja x-akselin positiivisen suunnan välinen kulma on terävä; kun funktio pienenee, suoran ja x-akselin positiivisen suunnan välinen kulma on tylppä. Ja tietysti k:n arvo vaikuttaa funktion arvon muutosnopeuteen.

neljä). Tämän funktion kuvaaja on paraabeli.

Harkitse esimerkkejä.

Esimerkki 1 - ratkaise yhtälö graafisesti:

Emme tunne tämän tyyppisiä funktioita, joten meidän on muutettava annettu yhtälö, jotta voimme työskennellä tunnettujen funktioiden kanssa:

Saimme tuttuja funktioita yhtälön molemmissa osissa:

Rakennetaan funktioiden kuvaajia:

Kaavioissa on kaksi leikkauspistettä: (-1; 1); (2; 4)

Tarkastetaan löytyykö ratkaisu oikein, korvaa koordinaatit yhtälöön:

Ensimmäinen kohta löytyy oikein.

, , , , , ,

Toinen kohta löytyy myös oikein.

Joten yhtälön ratkaisut ovat ja

Toimimme samalla tavalla kuin edellisessä esimerkissä: muunnamme annetun yhtälön meille tunnetuiksi funktioiksi, piirrämme niiden graafit, etsimme leikkausvirrat ja osoitamme tästä ratkaisut.

Saamme kaksi toimintoa:

Rakennetaan kaavioita:

Näissä kaavioissa ei ole leikkauspisteitä, mikä tarkoittaa, että annetulla yhtälöllä ei ole ratkaisuja

Johtopäätös: tällä oppitunnilla kävimme läpi tuntemiamme funktioita ja niiden kuvaajia, muistimme niiden ominaisuudet ja pohdimme graafista tapaa ratkaista yhtälöitä.

1. Dorofejev G.V., Suvorova S.B., Bunimovich E.A. et al. Algebra 7. 6. painos. M.: Valaistuminen. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. ja muut Algebra 7 .M .: Koulutus. 2006

Tehtävä 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et ai., Algebra 7, nro 494, s. 110;

Tehtävä 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. ja muut Algebra 7, nro 495, kohta 110;

Tehtävä 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et ai., Algebra 7, nro 496, s. 110;

DAGESTAN Ammattimaisen kehityksen instituutti

PEDAGOGINEN HENKILÖSTÖ

FYSIKAALISEN JA MATEMAATISEN KOULUTUKSEN SEKÄ ICT:N LAITOS

Projekti

aiheesta:

« Rakentaminen ja s uudistuksia

funktiokaavioita

koulumatematiikassa »

Rabadanova P.A.

matematiikan opettaja

MBOU "Kochubeyn lukio"

Tarumovskyn alueella

2015

1. Johdanto………………………………………………………………….….3

2. Luku minä. Katsaus hankkeen aiheeseen liittyvään kirjallisuuteen……………………………….….5

3. Luku II. Empiirinen osa:

3.1. Perusmenetelmät funktiokaavioiden muuntamiseen……….….7

3.2. Piirrä parillinenjaparittomat funktiot…………….. 10

3.3. Käänteisfunktion piirtäminen………………………… 11

3.4. Kuvaajien muodonmuutos (puristus ja jännitys).………………….12

3.5 Siirron, heijastuksen ja muodonmuutoksen yhdistelmä………………………………………………………

4. Itsenäisen ratkaisun tehtävät……………………………………..14

5. Johtopäätös………………………………………………………………… 15

6. Johtopäätökset…………………………………………………………..………17

JOHDANTO

Funktiokaavioiden muuntaminen on yksi matemaattisista peruskäsitteistä, jotka liittyvät suoraan käytännön toimintaan. Kaaviot heijastavat todellisen maailman vaihtelua ja dynaamisuutta, todellisten esineiden ja ilmiöiden keskinäisiä suhteita.

Toiminnallinen linja on perusaihe, jota käsitellään perus- ja yhtenäistetyissä valtiokokeissa.Myös monia matemaattisia käsitteitä tarkastellaan graafisilla menetelmillä. Esimerkiksi siihenneliöllinenfunktiota esitellään ja tutkitaan läheisessä yhteydessä toisen asteen yhtälöiden ja epäyhtälöiden kanssa.Tästä seuraa siisfunktion kuvaajien rakentamisen ja muuntamisen opettaminen on yksi matematiikan kouluopetuksen päätehtävistä.

Toiminnon tutkiminen mahdollistaa sen selvittämisenmäärittelyalue ja toiminnon laajuus, laajuusLaskevat tai kasvavat nopeudet, asymptootit, intervallitmerkkivakio jne. Kuitenkin graafin rakentamiseksikov monia toimintoja voi ollakäyttää useita menetelmiähelpottaarakennus. Siksi opiskelijoilla tulisi olla kyky rakentaa kaavioita metodologisten kaavioiden mukaan.

Yllä oleva määritteleemerkityksellisyys tutkimusaiheita.

Tutkimuksen kohde on tutkimus funktionaalisten viivakaavioiden muunnoksista koulumatematiikassa.

Opintojen aihe - funktiokaavioiden rakentamis- ja muunnosprosessi lukiossa.

Tutkimuksen tarkoitus: koulutus - koostuu metodologisen järjestelmän tunnistamisesta funktion graafien muodostamiseksi ja muuntamiseksi;kehittymässä - abstraktin, algoritmisen, loogisen ajattelun, spatiaalisen mielikuvituksen kehittäminen;koulutuksellinen - koululaisten graafisen kulttuurin koulutus, henkisten taitojen kehittäminen.

Tavoitteet johtivat seuraavaan päätökseentehtävät:

1. Analysoi tutkittavan ongelman koulutus- ja metodologiset tiedot.

2. Tunnista metodologiset suunnitelmatfunktiokaavioiden muunnos matematiikan koulukurssilla.

3. Valitse tehokkaimmat menetelmät ja keinotfunktiokaavioiden rakentaminen ja muuntaminen lukiossaedistää: oppimateriaalin mielekästä omaksumista; opiskelijoiden kognitiivisen toiminnan lisääminen; luovien kykyjensä kehittämiseen.

HYPOTEESI tutkimus: graafisten taitojen muodostuminen toimintojen opiskeluprosessissa ja opiskelijoiden graafisen kulttuurin koulutus tehokas, jos opiskelijoilla on menetelmällinen kaavio funktiokaavioiden rakentamiseen ja muuntamiseen koulun matematiikan kurssilla.

LUKU minä . KATSAUS PROJEKTIN AIHEESSA KIRJOITTAMISEEN.

Projektia valmistautuessamme tutkimme seuraavaa kirjallisuutta:

Sivashinsky, I. Kh. Algebran lauseita ja ongelmia, alkeisfunktioita - M., 2002. - 115 s.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funktiot ja graafit (perustekniikat) - M., 1985. - 120 s

V.Z. Zaitsev, V.V. Ryžkov, M.I. Scanavi. Elementary Mathematics - M., 2010 (uudelleenjulkaisu). - 590 s.

Kuzmin, M. K. Funktion graafin rakentaminen - J. Matematiikka koulussa. - 2003. - Nro 5. - S. 61-62.

Shilov G.E. Kuinka rakentaa kaavioita? - M., 1982.

Isaac Tanatar. Funktioiden kuvaajien geometriset muunnokset - MTsNMO, 2012

ATOn huomattava, että kykyä "lukea" funktion käyttäytyminen tietyssä joukossa graafin avulla ei käytetä vain matematiikan aikana, vaan myös kaikessa ihmisen käytännön toiminnassa, jossa hänen on käsiteltävä tiettyä grafiikkaa. riippuvuuksien esitykset. Siksi opiskelijoiden tulisi pystyä määrittämään joitakin sen ominaisuuksia funktion kaaviosta.

Graafisten muunnoksen teoreettinen materiaali on tiukasti määritelty kohdassa. Tekniikkaan liittyy piirustuskuvituksia, vaihtelevan monimutkaisuuden esimerkkejä ja niiden ratkaisuja, mikä mahdollistaa tiedon syventämisen ja monimutkaisten funktioiden piirtämisen.

Edustaa sähköistä koulutusta, jonka tilavuus ja sisältö täyttävät lukion matematiikan kurssin vaatimukset. Teoreettista materiaalia tukevat graafiset animaatiokuvitukset, jotka antavat visuaalisen esityksen tutkittavasta aiheesta. Kurssi sisältää kolme moduulia: teoreettisen materiaalin opiskelumoduulin, itsetutkiskelumoduulin ja tiedonhallintamoduulin.

Projektin empiirisessä osassa käytettiin menetelmällisistä kartoituskaavioista , , esimerkkejä itsenäiseen työskentelyyn.

Johtopäätökset luvusta 1

Opetus- ja metodisen kirjallisuuden tutkiminen mahdollisti:

1. Tunnista metodologinen suunnitelmafunktion kuvaajien tutkiminen, rakentaminen ja muuntaminen koulun matematiikan kurssilla.

2. Valitse tehokkaimmat menetelmät ja keinotfunktiokaavioiden rakentaminen ja muuntaminen koulumatematiikassa,osallistuminen:

opetusmateriaalin mielekäs omaksuminen;

opiskelijoiden kognitiivisen toiminnan lisääminen;

luovien kykyjensä kehittämiseen.

3. näytä se funktionaalisella linjalla on merkittävä vaikutus matematiikan eri käsitteiden tutkimiseen.

Luku 2. EMPIIRINEN OSA

Tässä luvussa tarkastellaan päämenetelmiä funktiograafien muuntamiseen ja annetaan metodologisia kaavioita erilaisten kaavioiden yhdistelmien rakentamiseen eri funktioille.

2.1. PERUSTEKNIIKAT FUNKTIOKUVIOJEN MUUNTAMINEN

Käännös y-akselia pitkin

f ( x ) f ( x )+ b .

vartenfunktion piirtämineny = f( x) + bjäljittääem:

1. rakentaa funktiokaavioy= f( x)

2. siirrä akseliaabskissa päällä| b| yksiköt ylös klob>0 tai klo| b| syödäkumartuab < 0. Hankittu uudessa järjestelmässädinat-graafi on funktion kuvaajay = f( x) + b.

2. Siirto pitkin kirveet abskissa

f ( x ) f ( x + a ) .

y = f( x+ a) jälkiäem:

3. Muodon funktion piirtäminen y = f (- x )

f (x ) f (- x ).

Piirrä funktioy = f( - x) seuraavasti:

piirrä funktioy = f( x)

heijastaa sitä takaisinsuhteessa y-akseliin

tuloksena oleva kaavio onfunktiokaavioy = f( - X).

4. Muodon funktion piirtäminen y= - f ( x )

f ( x ) - f ( x )

- f( x) seuraavasti:

piirrä funktioy= f( x)

heijastaa sitä x-akselin ympäri

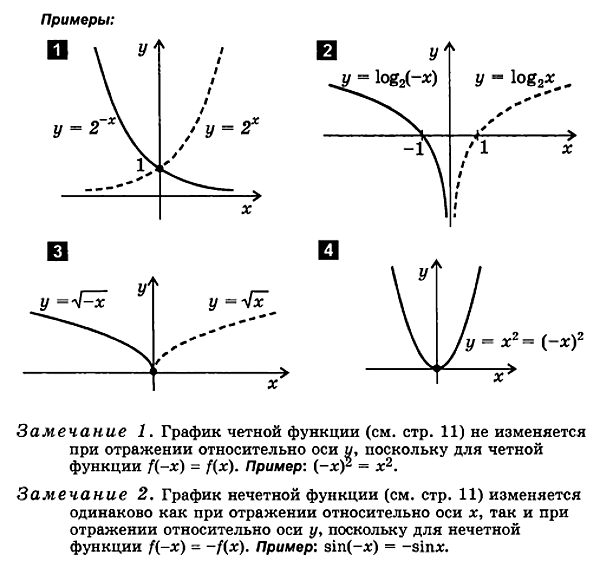
2.2. Piirrä parillinen ja outoja ominaisuuksia

SuunniteltaessaParillisille ja parittomille funktioille on kätevää käyttää seuraavia ominaisuuksia:

1. Parillisen funktion simmetin kuvaajaricen suhteessa y-akseliin.

2. Parittoman funktion kuvaaja on symmetrinen origon suhteen.

Parillisen ja parittoman funktion kaavioiden rakentamiseksi riittää, että piirretään vain kaavion oikea haara argumentin positiivisille arvoille. Parittoman funktion vasen haara täydentyy symmetrisesti origon ympäri ja parillisen funktion y-akselin ympäri.

Piirrä parillinen funktio y = f ( x ) jälkeen duetto:

rakentaa tämän funktion kaavion haara vain sisäänargumentin positiivisten arvojen alue x≥0.

Opiirrä tämä haara y-akselin ympäri

Parittoman funktion piirtäminen y = f ( x ) seuraa:

rakentaa tämän funktion graafihaara vain sisäänargumentin positiivisten arvojen alue (х≥0).

Ojäljittää tämän haaran alkuperän suhteennegatiivisten x-arvojen alueelle.

2.3. Käänteisfunktion piirtäminen

Kuten jo todettiin, suorat ja käänteiset funktiotosoittavat saman muuttujien välisen suhteenx ja y, sillä ainoalla erolla, että käänteisfunktiossa nämämuuttujat ovat vaihtaneet rooleja, mikä vastaa muuttumistakoordinaattiakselien merkintä. Siksi aikataulukäänteisfunktio on symmetrinen suoran funktion kuvaajallepuolittajastaminäjaIIIkoordinaattikulmat,eli suhteellisen suoray = x. Siten saammeseuraava sääntö.

Piirrä funktio y = (x) käänteinen funktiolley = f( x), pitäisi rakentaaajoittaay = f( x) ja heijastaa sitä suoran y = x suhteen.

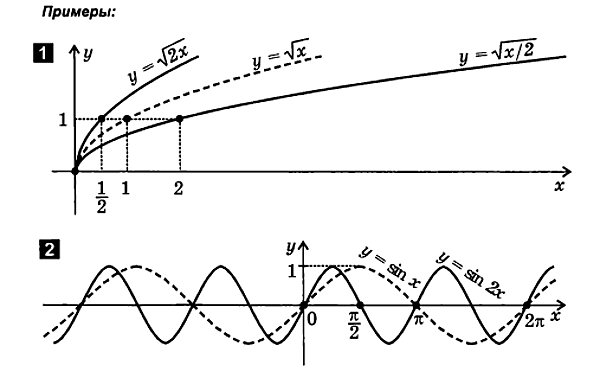
2.4. Kuvaajien muodonmuutos (puristus ja jännitys).

1. Kuvaajan pakkaus (laajennus) y-akselia pitkin

f ( x ) A ∙ f ( x ).

Piirrä funktioy= A∙ f( x) seuraavasti:

8. Kuvaajan pakkaus (laajennus) x-akselia pitkin

f( x)

Piirrä funktio y= f( x) seuraa:

2.5. Translaation, heijastuksen ja muodonmuutoksen yhdistelmä

Hyvin usein piirrettäessä funktiokaavioitamuuta yhdistelmää.

Useiden tällaisten asentotekniikoiden johdonmukainen soveltaminenmahdollistaa huomattavasti graafin rakentamisen yksinkertaistamisenjuoksutoimintoa ja usein vähentää sitä lopultayhden yksinkertaisin perusfunktion rakentaminentoimenpiteitä. Mieti, miten se seuraa edellä olevan perusteellarakentaa funktiokaavioita.

Huomaa, että on aikaon suositeltavaa suorittaa yksinkertaistustelakka seuraavassa seuraajassaness.

Käyttämällä pariteettia taifunktion omituisuus.

Akselien siirto.

Heijastus ja muodonmuutos.

Kaavion rakentaminen suoritetaan päinvastaisessa järjestyksessä.

Esimerkki. Piirrä funktio

Rakentaminen toteutetaan seuraavissa vaiheissa:

1. piirrä luonnollinen logaritmi:

2. puristaaakselilleOY2 kertaa:;
3. näyttää symmetrisestiakselin suhteenOY: ;
4. liikkua akselia pitkinHÄRKÄpäällä(!!!) oikealle::

5. näytä symmetrisesti akselin ympäriHÄRKÄ: ;
6. liikkuaakselia pitkinOY3 yksikköä ylöspäin::

ESIMERKKEJÄ FUNKTIKOAFIJIEN RAKENTAMISESTA JA MUUNNISTAMISTA

Esimerkki 1 Piirrä funktio.

Piirrä ensin sinigraafi, sen jakso on yhtä suuri kuin:

funktiokaaviosaadaan pakkaamalla kuvaajakahdesti y-akselille. Hirsi .

Piirrä funktioklo = 2 cosX.

Piirrä funktioy = syntix .

PÄÄTELMÄ

Projektityön aikana analysoitiin erilaista opetus- ja metodologista kirjallisuutta aiheesta. Tutkimuksen tulokset mahdollistivat tutkimuksen tunnusomaisimmat positiiviset puolet, funktion kuvaajien rakentaminen ja muunnos koulun matematiikan kurssilla

Hankkeen päätavoitteena on kehittää opiskelijoiden taitoja ja kykyjä piirustusten lukemisessa ja piirtämisessä, rationaalisten itsenäisen toiminnan menetelmien muodostamisessa.

Graafisen koulutuksen parantamisen tarvetta kokonaisuutena sanelevat paitsi nykyaikaiset tuotantovaatimukset, myös grafiikan rooli opiskelijoiden teknisen ajattelun ja kognitiivisten kykyjen kehittämisessä. Ihmisen kyky käsitellä graafista tietoa on yksi hänen henkisen kehityksensä mittareista. Siksi graafisen koulutuksen tulisi olla olennainen osa yleissivistävää koulutusta.

johtopäätöksiä

Niinpä kehitetty projekti "Funktiograafien rakentaminen ja muuntaminen", joka on omistettu yhdelle matematiikan keskeisistä käsitteistä - funktionaalisesta riippuvuudesta, keskittyy opiskelijoiden tiedon systematisointiin ja laajentamiseen. Spesifisten funktiokaavioiden muuntamismenetelmien tutkimus suoritetaan analyyttisesti ja graafisesti tiukkojen metodologisten kaavioiden mukaisesti. Kerättyä materiaalia voidaan käyttää luokkahuoneessa ja opiskelijoiden itsekoulutuksessa. Luokkien johtamiseen voidaan käyttää erilaisia organisointi- ja koulutusmuotoja ja -menetelmiä.

Portaali opiskelijalle. Itseharjoittelu

AIHEESEEN LIITTYVÄT ARTIKKELIT