განმარტება 9.3.ვექტორი X დაურეკა საკუთარი ვექტორიმატრიცები მაგრამთუ არის ასეთი რიცხვი λ, რომ თანასწორობა მოქმედებს: მაგრამ X= λ X, ანუ მიმართვის შედეგი X მატრიცით მოცემული წრფივი ტრანსფორმაცია მაგრამ, არის ამ ვექტორის გამრავლება რიცხვზე λ . თავად ნომერი λ დაურეკა საკუთარი ნომერიმატრიცები მაგრამ.

ჩანაცვლება ფორმულებში (9.3) x` j = λx j,ვიღებთ განტოლებათა სისტემას საკუთარი ვექტორის კოორდინატების დასადგენად:

. (9.5)

ამ წრფივ ერთგვაროვან სისტემას ექნება არატრივიალური ამოხსნა მხოლოდ იმ შემთხვევაში, თუ მისი მთავარი განმსაზღვრელი არის 0 (კრამერის წესი). ამ პირობის ჩაწერით ფორმაში:

ვიღებთ განტოლებას საკუთრივ მნიშვნელობების დასადგენად λ დაურეკა დამახასიათებელი განტოლება. მოკლედ, ის შეიძლება წარმოდგენილი იყოს შემდეგნაირად:

| A-λE | = 0, (9.6)

რადგან მისი მარცხენა მხარე არის მატრიცის განმსაზღვრელი A-λE. პოლინომიის მიმართ λ | A-λE| დაურეკა დამახასიათებელი მრავალწევრიმატრიცები A.

დამახასიათებელი მრავალწევრის თვისებები:

1) წრფივი გარდაქმნის დამახასიათებელი პოლინომი არ არის დამოკიდებული საფუძვლის არჩევანზე. მტკიცებულება. (იხ. (9.4)), მაგრამ აქედან გამომდინარე, . ამრიგად, ეს არ არის დამოკიდებული საფუძვლის არჩევანზე. აქედან გამომდინარე, და | A-λE| არ იცვლება ახალ ბაზაზე გადასვლისას.

2) თუ მატრიცა მაგრამწრფივი ტრანსფორმაცია არის სიმეტრიული(ისინი. ა ი = ა ჯი), მაშინ დამახასიათებელი განტოლების (9.6) ყველა ფესვი რეალური რიცხვია.

საკუთარი მნიშვნელობების და საკუთრივ ვექტორების თვისებები:

1) თუ ჩვენ ვირჩევთ საფუძველს საკუთრივ ვექტორებიდან x 1, x 2, x 3 საკუთარი მნიშვნელობების შესაბამისი λ 1, λ 2, λ 3მატრიცები მაგრამ, მაშინ ამ საფუძველზე A წრფივ ტრანსფორმაციას აქვს დიაგონალური მატრიცა:

(9.7) ამ თვისების დადასტურება გამომდინარეობს საკუთრივ ვექტორების განმარტებიდან.

2) თუ ტრანსფორმაციის საკუთრივ მნიშვნელობები მაგრამგანსხვავებულია, მაშინ მათ შესაბამისი საკუთრივვექტორები წრფივად დამოუკიდებელია.

3) თუ მატრიცის დამახასიათებელი მრავალწევრი მაგრამაქვს სამი განსხვავებული ფესვი, შემდეგ გარკვეულწილად მატრიცა მაგრამაქვს დიაგონალური ფორმა.

ვიპოვოთ მატრიცის საკუთრივ მნიშვნელობები და საკუთრივვექტორები, გავაკეთოთ დამახასიათებელი განტოლება: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

იპოვეთ თითოეული ნაპოვნი მნიშვნელობის შესაბამისი საკუთარი ვექტორების კოორდინატები λ. (9.5)-დან გამომდინარეობს, რომ თუ X (1) ={x 1, x 2, x 3) არის შესაბამისი საკუთრივვექტორი λ 1 = -2, მაშინ

არის თანამშრომლობითი, მაგრამ განუსაზღვრელი სისტემა. მისი ამოხსნა შეიძლება დაიწეროს როგორც X (1) ={ა,0,-ა), სადაც a არის ნებისმიერი რიცხვი. კერძოდ, თუ თქვენ მოითხოვთ, რომ | x (1) |=1, X (1) =

ჩანაცვლება სისტემაში (9.5) λ 2 =3, ვიღებთ სისტემას მეორე საკუთარი ვექტორის კოორდინატების დასადგენად - x (2) ={y1, y2, y3}:

, სად X (2) ={ბ,-ბ,ბ) ან, გათვალისწინებული | x (2) |=1, x (2) =

ამისთვის λ 3 = 6 იპოვნეთ საკუთარი ვექტორი x (3) ={z1, z2, z3}:

, x (3) ={გ,2c,c) ან ნორმალიზებულ ვერსიაში

x (3) = ჩანს რომ X (1) X (2) = აბ-აბ= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = ძვ.წ- 2ძვ.წ+ძვ.წ= 0. ამრიგად, ამ მატრიცის საკუთრივ ვექტორები წყვილი ორთოგონალურია.

ლექცია 10

კვადრატული ფორმები და მათი კავშირი სიმეტრიულ მატრიცებთან. სიმეტრიული მატრიცის საკუთრივ ვექტორების და საკუთრივ მნიშვნელობების თვისებები. კვადრატული ფორმის შემცირება კანონიკურ ფორმამდე.

განმარტება 10.1.კვადრატული ფორმარეალური ცვლადები x 1, x 2,…, x nამ ცვლადებთან მიმართებაში მეორე ხარისხის პოლინომი ეწოდება, რომელიც არ შეიცავს პირველი ხარისხის თავისუფალ წევრს და ტერმინებს.

კვადრატული ფორმების მაგალითები:

(ნ = 2),

(ნ = 3). (10.1)

გაიხსენეთ სიმეტრიული მატრიცის განმარტება, რომელიც მოცემულია ბოლო ლექციაში:

განმარტება 10.2.კვადრატული მატრიცა ეწოდება სიმეტრიული, თუ , ანუ თუ მატრიცის ელემენტები სიმეტრიული მთავარი დიაგონალის მიმართ ტოლია.

სიმეტრიული მატრიცის საკუთრივ მნიშვნელობებისა და საკუთრივვექტორების თვისებები:

1) სიმეტრიული მატრიცის ყველა საკუთრივ მნიშვნელობა რეალურია.

მტკიცებულება (ამისთვის ნ = 2).

მოდით მატრიცა მაგრამროგორც ჩანს: . მოდით გავაკეთოთ დამახასიათებელი განტოლება:

(10.2) იპოვეთ დისკრიმინანტი:

მაშასადამე, განტოლებას მხოლოდ რეალური ფესვები აქვს.

2) სიმეტრიული მატრიცის საკუთრივვექტორები ორთოგონალურია.

მტკიცებულება (ამისთვის ნ= 2).

საკუთრივ ვექტორების კოორდინატები და უნდა აკმაყოფილებდეს განტოლებებს.

დიაგონალური ტიპის მატრიცები ყველაზე მარტივად არის მოწყობილი. ჩნდება კითხვა, შესაძლებელია თუ არა ისეთი საფუძვლის პოვნა, რომლითაც ხაზოვანი ოპერატორის მატრიცას დიაგონალური ფორმა ექნება. ასეთი საფუძველი არსებობს.
მოცემულია წრფივი სივრცე R n და მასში მოქმედი წრფივი ოპერატორი A; ამ შემთხვევაში ოპერატორი A იღებს R n-ს, ანუ A:R n → R n.

განმარტება. არანულოვან ვექტორს უწოდებენ A ოპერატორის საკუთრივ ვექტორს, თუ ოპერატორი A ითარგმნება მის კოლინარულ ვექტორად, ანუ . რიცხვს λ ეწოდება საკუთრივ ვექტორის შესაბამისი ოპერატორის საკუთრივ მნიშვნელობა ან საკუთრივ მნიშვნელობა.
ჩვენ აღვნიშნავთ საკუთრივ მნიშვნელობების და საკუთრივვექტორების ზოგიერთ თვისებას.
1. საკუთრივ ვექტორების ნებისმიერი წრფივი კომბინაცია ოპერატორის A, რომელიც შეესაბამება იმავე საკუთრივ მნიშვნელობას λ არის საკუთრივ ვექტორი იგივე საკუთრივ მნიშვნელობით.
2. საკუთრივ ვექტორები ოპერატორი A წყვილი განსხვავებული საკუთარი მნიშვნელობებით λ 1 , λ 2 , ..., λ m წრფივად დამოუკიდებელია.
3. თუ საკუთარი მნიშვნელობები λ 1 =λ 2 = λ m = λ, მაშინ საკუთარი მნიშვნელობა λ შეესაბამება არაუმეტეს m წრფივად დამოუკიდებელ საკუთრივექტორებს.

ასე რომ, თუ არსებობს n წრფივად დამოუკიდებელი საკუთარი ვექტორები შეესაბამება სხვადასხვა საკუთრივ მნიშვნელობებს λ 1 , λ 2 , ..., λ n , მაშინ ისინი წრფივად დამოუკიდებელნი არიან, შესაბამისად, ისინი შეიძლება იქნას მიღებული როგორც R n სივრცის საფუძველი. მოდით ვიპოვოთ წრფივი ოპერატორის A მატრიცის ფორმა მისი საკუთრივვექტორების საფუძველზე, რისთვისაც ვმოქმედებთ A ოპერატორთან საბაზისო ვექტორებზე: მაშინ .
ამრიგად, A ხაზოვანი ოპერატორის მატრიცას მისი საკუთრივვექტორების საფუძველზე აქვს დიაგონალური ფორმა, ხოლო ოპერატორი A-ს საკუთარი მნიშვნელობები დიაგონალზეა.
არის თუ არა სხვა საფუძველი, რომლითაც მატრიცას აქვს დიაგონალური ფორმა? ამ კითხვაზე პასუხი მოცემულია შემდეგი თეორემით.

თეორემა. წრფივი A ოპერატორის მატრიცას საფუძველში (i = 1..n) აქვს დიაგონალური ფორმა, თუ და მხოლოდ იმ შემთხვევაში, თუ საფუძვლის ყველა ვექტორი არის A ოპერატორის საკუთარი ვექტორები.

საკუთარი მნიშვნელობებისა და საკუთრივვექტორების პოვნის წესი

მოდით ვექტორი , სადაც x 1 , x 2 , …, x n - ვექტორის კოორდინატები საფუძველთან შედარებით და არის წრფივი ოპერატორის A საკუთრივ ვექტორი, რომელიც შეესაბამება λ საკუთრივ მნიშვნელობას, ე.ი. ეს კავშირი შეიძლება დაიწეროს მატრიცის სახით

. (*)

განტოლება (*) შეიძლება ჩაითვალოს განტოლებად საპოვნელად და, ანუ ჩვენ გვაინტერესებს არატრივიალური ამონახსნები, ვინაიდან საკუთრივვექტორი არ შეიძლება იყოს ნული. ცნობილია, რომ წრფივი განტოლებათა ერთგვაროვანი სისტემის არატრივიალური ამონახსნები არსებობს, თუ და მხოლოდ მაშინ, თუ det(A - λE) = 0. ამრიგად, იმისათვის, რომ λ იყოს A ოპერატორის საკუთრივ მნიშვნელობა, აუცილებელია და საკმარისია, რომ det(A - λE). ) = 0.
თუ განტოლება (*) დეტალურად არის დაწერილი კოორდინატების სახით, მაშინ მივიღებთ წრფივი ერთგვაროვანი განტოლებების სისტემას:

(1)
სადაც არის ხაზოვანი ოპერატორის მატრიცა.

სისტემას (1) აქვს არანულოვანი ამონახსნი, თუ მისი განმსაზღვრელი D ნულის ტოლია

ჩვენ მივიღეთ განტოლება საკუთარი მნიშვნელობების საპოვნელად.
ამ განტოლებას ეწოდება დამახასიათებელი განტოლება, ხოლო მის მარცხენა მხარეს - მატრიცის (ოპერატორი) A დამახასიათებელი პოლინომი. თუ დამახასიათებელ მრავალწევრს არ აქვს ნამდვილი ფესვები, მაშინ A მატრიცას არ აქვს საკუთარი ვექტორები და ვერ დაიყვანება დიაგონალურ ფორმამდე.
მოდით λ 1 , λ 2 , …, λ n იყოს დამახასიათებელი განტოლების რეალური ფესვები და მათ შორის შეიძლება იყოს ჯერადი. ამ მნიშვნელობების თავის მხრივ (1) სისტემაში ჩანაცვლებით, ჩვენ ვპოულობთ საკუთრივ ვექტორებს.

მაგალითი 12. წრფივი ოპერატორი A მოქმედებს R 3-ში კანონის მიხედვით, სადაც x 1 , x 2 , .., x n არის ვექტორის კოორდინატები საფუძველში. , , . იპოვეთ ამ ოპერატორის საკუთრივ მნიშვნელობები და საკუთრივვექტორები.
გადაწყვეტილება. ჩვენ ვაშენებთ ამ ოპერატორის მატრიცას:
.
ჩვენ ვქმნით სისტემას საკუთარი ვექტორების კოორდინატების დასადგენად:

ჩვენ ვადგენთ დამახასიათებელ განტოლებას და ვხსნით მას:

.
λ 1,2 = -1, λ 3 = 3.
თუ შევცვლით λ = -1 სისტემაში, გვაქვს:
ან
როგორც , მაშინ არის ორი დამოკიდებული ცვლადი და ერთი თავისუფალი ცვლადი.
მოდით x 1 იყოს თავისუფალი უცნობი, მაშინ ჩვენ ვხსნით ამ სისტემას ნებისმიერი გზით და ვპოულობთ ამ სისტემის ზოგად ამონახსნებს: ამონახსნების ფუნდამენტური სისტემა შედგება ერთი ამოხსნისგან, ვინაიდან n - r = 3 - 2 = 1.
საკუთრივვექტორთა სიმრავლეს, რომელიც შეესაბამება λ = -1 საკუთრივ მნიშვნელობას, აქვს ფორმა: , სადაც x 1 არის ნებისმიერი რიცხვი, გარდა ნულისა. მოდით ავირჩიოთ ერთი ვექტორი ამ ნაკრებიდან, მაგალითად, x 1 = 1 დაყენებით: .
ანალოგიურად კამათით, ჩვენ ვპოულობთ საკუთრივ ვექტორს, რომელიც შეესაბამება λ = 3 საკუთრივ მნიშვნელობას: .
R 3 სივრცეში საფუძველი შედგება სამი წრფივად დამოუკიდებელი ვექტორისგან, მაგრამ ჩვენ მივიღეთ მხოლოდ ორი წრფივად დამოუკიდებელი საკუთრივვექტორი, საიდანაც R3-ში საფუძველი არ შეიძლება ჩამოყალიბდეს. შესაბამისად, წრფივი ოპერატორის A მატრიცა ვერ დაიყვანება დიაგონალურ ფორმამდე.

მაგალითი 13 მოცემულია მატრიცა .
1. დაამტკიცეთ, რომ ვექტორი არის A მატრიცის საკუთრივვექტორი. იპოვეთ ამ საკუთრივვექტორის შესაბამისი საკუთრივ მნიშვნელობა.
2. იპოვეთ საფუძველი, რომელშიც A მატრიცას აქვს დიაგონალური ფორმა.
გადაწყვეტილება.
1. თუ , მაშინ არის საკუთრივვექტორი

.
ვექტორი (1, 8, -1) არის საკუთარი ვექტორი. საკუთარი მნიშვნელობა λ = -1.
მატრიცას აქვს დიაგონალური ფორმა, რომელიც შედგება საკუთარი ვექტორებისგან. ერთ-ერთი მათგანი ცნობილია. მოდი ვიპოვოთ დანარჩენი.
ჩვენ ვეძებთ საკუთრივ ვექტორებს სისტემიდან:

დამახასიათებელი განტოლება: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
იპოვეთ საკუთრივვექტორი, რომელიც შეესაბამება λ = -3 საკუთრივ მნიშვნელობას:

ამ სისტემის მატრიცის რანგი უდრის ორს და უდრის უცნობთა რაოდენობას, ამიტომ ამ სისტემას აქვს მხოლოდ ნულოვანი ამონახსნი x 1 = x 3 = 0. x 2 აქ შეიძლება იყოს არაფერი, გარდა ნულისა, მაგალითად, x 2 = 1. ამრიგად, ვექტორი (0 ,1,0) არის λ = -3 შესაბამისი საკუთრივვექტორი. მოდით შევამოწმოთ:
.
თუ λ = 1, მაშინ მივიღებთ სისტემას
მატრიცის წოდება არის ორი. გადახაზეთ ბოლო განტოლება.
მოდით x 3 იყოს თავისუფალი უცნობი. შემდეგ x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
თუ დავუშვებთ x 3 = 1, გვაქვს (-3,-9,1) - საკუთრივ ვექტორი, რომელიც შეესაბამება λ = 1 საკუთრივ მნიშვნელობას. შეამოწმეთ:

.
ვინაიდან საკუთრივ მნიშვნელობები რეალური და განსხვავებულია, მათ შესაბამისი ვექტორები წრფივად დამოუკიდებელია, ამიტომ ისინი შეიძლება იქნას მიღებული როგორც საფუძველი R3-ში. ამრიგად, საფუძველში , , A მატრიცას აქვს ფორმა:
.
წრფივი ოპერატორის A:R n → R n ყველა მატრიცა არ შეიძლება დაიყვანოს დიაგონალურ ფორმამდე, ვინაიდან ზოგიერთი წრფივი ოპერატორისთვის შეიძლება იყოს n-ზე ნაკლები წრფივი დამოუკიდებელი საკუთრივექტორები. თუმცა, თუ მატრიცა არის სიმეტრიული, მაშინ ზუსტად m წრფივი დამოუკიდებელი ვექტორები შეესაბამება m სიმრავლის დამახასიათებელი განტოლების ფესვს.

განმარტება. სიმეტრიული მატრიცა არის კვადრატული მატრიცა, რომელშიც ელემენტები, რომლებიც სიმეტრიულია მთავარ დიაგონალთან მიმართებაში, ტოლია, ანუ რომელშიც .
შენიშვნები. 1. სიმეტრიული მატრიცის ყველა საკუთრივ მნიშვნელობა რეალურია.
2. სიმეტრიული მატრიცის საკუთრივ ვექტორები, რომლებიც შეესაბამება წყვილ-წყვილად სხვადასხვა საკუთრივ მნიშვნელობებს, ორთოგონალურია.
როგორც შესწავლილი აპარატის ერთ-ერთი მრავალრიცხოვანი გამოყენება, განვიხილავთ მეორე რიგის მრუდის ფორმის განსაზღვრის პრობლემას.

A მატრიცით, თუ არის რიცხვი l ისეთი, რომ AX = lX.

ამ შემთხვევაში იწოდება რიცხვი l საკუთარი ღირებულება X ვექტორის შესაბამისი ოპერატორი (მატრიცა A).

სხვა სიტყვებით რომ ვთქვათ, საკუთრივ ვექტორი არის ვექტორი, რომელიც წრფივი ოპერატორის მოქმედებით გარდაიქმნება კოლინურ ვექტორად, ე.ი. უბრალოდ გაამრავლე რაღაც რიცხვზე. ამის საპირისპიროდ, არასწორი ვექტორების გარდაქმნა უფრო რთულია.

ჩვენ ვწერთ საკუთრივ ვექტორის განმარტებას, როგორც განტოლებათა სისტემას:

მოდით გადავიტანოთ ყველა ტერმინი მარცხენა მხარეს:

ბოლო სისტემა შეიძლება დაიწეროს მატრიცის სახით შემდეგნაირად:

(A - lE)X \u003d O

მიღებულ სისტემას ყოველთვის აქვს ნულოვანი ამონახსნი X = O. ისეთ სისტემებს, რომლებშიც ყველა თავისუფალი წევრი ნულის ტოლია, ე.წ. ერთგვაროვანი. თუ ასეთი სისტემის მატრიცა არის კვადრატი, ხოლო მისი განმსაზღვრელი არ არის ნულის ტოლი, მაშინ კრამერის ფორმულების მიხედვით, ყოველთვის მივიღებთ უნიკალურ ამონახსნებს - ნულს. შეიძლება დადასტურდეს, რომ სისტემას აქვს არანულოვანი ამონახსნები, თუ და მხოლოდ იმ შემთხვევაში, თუ ამ მატრიცის განმსაზღვრელი ნულის ტოლია, ე.ი.

|A - lE| = = 0

ეს განტოლება უცნობი l-ით ე.წ დამახასიათებელი განტოლება (დამახასიათებელი მრავალწევრი) მატრიცა A (წრფივი ოპერატორი).

შეიძლება დადასტურდეს, რომ ხაზოვანი ოპერატორის დამახასიათებელი პოლინომი არ არის დამოკიდებული საფუძვლის არჩევანზე.

მაგალითად, ვიპოვოთ ხაზოვანი ოპერატორის საკუთრივ მნიშვნელობები და საკუთრივვექტორები, რომლებიც მოცემულია A = მატრიცით.

ამისთვის ვადგენთ დამახასიათებელ განტოლებას |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; საკუთარი მნიშვნელობები l 1 = (2 - 12) / 2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

საკუთარი ვექტორების საპოვნელად, ჩვენ ვხსნით განტოლებების ორ სისტემას

(A + 5E) X = O

(A - 7E) X = O

პირველი მათგანისთვის გაფართოებული მატრიცა მიიღებს ფორმას

,

საიდანაც x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, ე.ი. X (1) \u003d (- (2/3) s; s).

მეორე მათგანისთვის გაფართოებული მატრიცა მიიღებს ფორმას

,

საიდანაც x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, ე.ი. X (2) \u003d ((2/3) s 1; s 1).

ამრიგად, ამ წრფივი ოპერატორის საკუთრივ ვექტორები არის (-(2/3)c; c) ფორმის ვექტორები (-5) და ((2/3)c 1; c 1) ფორმის ყველა ვექტორი. საკუთარი მნიშვნელობა 7.

შეიძლება დადასტურდეს, რომ A ოპერატორის მატრიცა, რომელიც შედგება მისი საკუთრივვექტორებისგან, დიაგონალურია და აქვს ფორმა:

,

სადაც l i არის ამ მატრიცის საკუთარი მნიშვნელობები.

პირიქითაც მართალია: თუ მატრიცა A ზოგიერთ საფუძველში დიაგონალურია, მაშინ ამ საფუძვლის ყველა ვექტორი იქნება ამ მატრიცის საკუთრივ ვექტორები.

ასევე შეიძლება დადასტურდეს, რომ თუ წრფივ ოპერატორს აქვს n წყვილი განსხვავებული საკუთარი მნიშვნელობები, მაშინ შესაბამისი საკუთრივექტორები წრფივად დამოუკიდებელია და ამ ოპერატორის მატრიცას შესაბამის ბაზაზე აქვს დიაგონალური ფორმა.

ეს ავხსნათ წინა მაგალითით. ავიღოთ თვითნებური არანულოვანი მნიშვნელობები c და c 1 , მაგრამ ისეთი, რომ ვექტორები X (1) და X (2) წრფივად დამოუკიდებელი იყოს, ე.ი. საფუძველს შექმნიდა. მაგალითად, მოდით c \u003d c 1 \u003d 3, შემდეგ X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

მოდით გადავამოწმოთ ამ ვექტორების წრფივი დამოუკიდებლობა:

12 ≠ 0. ამ ახალ საფუძველზე, A მატრიცა მიიღებს A * = ფორმას.

ამის დასადასტურებლად ვიყენებთ ფორმულას A * = C -1 AC. ჯერ ვიპოვოთ C -1.

C -1 = ;

კვადრატული ფორმები

კვადრატული ფორმა f (x 1, x 2, x n) n ცვლადიდან ეწოდება ჯამი, რომლის თითოეული წევრი არის ან ერთ-ერთი ცვლადის კვადრატი, ან ორი განსხვავებული ცვლადის ნამრავლი, აღებული გარკვეული კოეფიციენტით: f (x 1 , x 2, x n) = (a ij = a ji).

მატრიცა A, რომელიც შედგება ამ კოეფიციენტებისგან, ე.წ მატრიცაკვადრატული ფორმა. ყოველთვის არის სიმეტრიულიმატრიცა (ანუ მატრიცა სიმეტრიულია მთავარი დიაგონალის მიმართ, a ij = a ji).

მატრიცული აღნიშვნისას კვადრატულ ფორმას აქვს ფორმა f(X) = X T AX, სადაც

Ნამდვილად

მაგალითად, დავწეროთ კვადრატული ფორმა მატრიცის სახით.

ამისათვის ჩვენ ვპოულობთ კვადრატული ფორმის მატრიცას. მისი დიაგონალური ელემენტები უდრის კოეფიციენტებს ცვლადების კვადრატებზე, ხოლო დარჩენილი ელემენტები უდრის კვადრატული ფორმის შესაბამისი კოეფიციენტების ნახევარს. Ისე

მოდით, X ცვლადების მატრიცა-სვეტი მივიღოთ მატრიცა-სვეტის Y არადეგენერაციული წრფივი გარდაქმნით, ე.ი. X = CY, სადაც C არის n რიგის არადეგენერირებული მატრიცა. მაშინ კვადრატული ფორმა f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

ამრიგად, C არადეგენერაციული წრფივი ტრანსფორმაციის დროს კვადრატული ფორმის მატრიცა იღებს ფორმას: A * = C T AC.

მაგალითად, ვიპოვოთ კვადრატული ფორმა f(y 1, y 2) მიღებული კვადრატული ფორმიდან f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 წრფივი გარდაქმნით.

კვადრატული ფორმა ეწოდება კანონიკური(Მას აქვს კანონიკური შეხედულება) თუ მისი ყველა კოეფიციენტი a ij = 0 i ≠ j-სთვის, ე.ი.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

მისი მატრიცა დიაგონალურია.

თეორემა(მტკიცებულება აქ არ არის მოცემული). ნებისმიერი კვადრატული ფორმა შეიძლება შემცირდეს კანონიკურ ფორმამდე არადეგენერაციული ხაზოვანი ტრანსფორმაციის გამოყენებით.

მაგალითად, კანონიკურ ფორმამდე მივიყვანოთ კვადრატული ფორმა
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

ამისათვის ჯერ აირჩიეთ x 1 ცვლადის სრული კვადრატი:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

ახლა ჩვენ ვირჩევთ სრულ კვადრატს x 2 ცვლადისთვის:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

შემდეგ არადეგენერაციული წრფივი ტრანსფორმაცია y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 და y 3 \u003d x 3 მოაქვს ამ კვადრატულ ფორმას კანონიკურ ფორმამდე f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

გაითვალისწინეთ, რომ კვადრატული ფორმის კანონიკური ფორმა ორაზროვნად არის განსაზღვრული (იგივე კვადრატული ფორმა კანონიკურ ფორმამდე შეიძლება შემცირდეს სხვადასხვა გზით). თუმცა, სხვადასხვა მეთოდით მიღებულ კანონიკურ ფორმებს არაერთი საერთო თვისება აქვთ. კერძოდ, კვადრატული ფორმის დადებითი (უარყოფითი) კოეფიციენტების მქონე ტერმინების რაოდენობა არ არის დამოკიდებული იმაზე, თუ როგორ მცირდება ფორმა ამ ფორმამდე (მაგალითად, განხილულ მაგალითში ყოველთვის იქნება ორი უარყოფითი და ერთი დადებითი კოეფიციენტი). ამ თვისებას კვადრატული ფორმების ინერციის კანონი ეწოდება.

მოდით გადავამოწმოთ ეს იგივე კვადრატული ფორმის კანონიკურ ფორმაზე სხვაგვარად შემცირებით. დავიწყოთ ტრანსფორმაცია x 2 ცვლადით:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, სადაც y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 და y 3 = x 1. აქ უარყოფითი კოეფიციენტი -3 y 1-ზე და ორი დადებითი კოეფიციენტი 3 და 2 y 2 და y 3-ზე (და სხვა მეთოდის გამოყენებით მივიღეთ უარყოფითი კოეფიციენტი (-5) y 2-ზე და ორი დადებითი კოეფიციენტი: 2 y 1-ზე. და 1/20 y 3-ისთვის).

აქვე უნდა აღინიშნოს, რომ კვადრატული ფორმის მატრიცის რანგი, ე.წ კვადრატული ფორმის წოდება, უდრის კანონიკური ფორმის არანულოვანი კოეფიციენტების რაოდენობას და არ იცვლება წრფივი გარდაქმნებისას.

კვადრატული ფორმა f(X) ეწოდება დადებითად (უარყოფითი) გარკვეულითუ ცვლადის ყველა მნიშვნელობისთვის, რომლებიც ერთდროულად არ არის ნულის ტოლი, ეს დადებითია, ე.ი. f(X) > 0 (უარყოფითი, ე.ი.
f(X)< 0).

მაგალითად, კვადრატული ფორმა f 1 (X) \u003d x 1 2 + x 2 2 არის დადებითი განსაზღვრული, რადგან არის კვადრატების ჯამი და კვადრატული ფორმა f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 არის უარყოფითი განსაზღვრული, რადგან წარმოადგენს ის შეიძლება წარმოდგენილი იყოს როგორც f 2 (X) \u003d - (x 1 - x 2) 2.

უმეტეს პრაქტიკულ სიტუაციებში, გარკვეულწილად უფრო რთულია კვადრატული ფორმის ნიშან-განსაზღვრულის დადგენა, ამიტომ ამისთვის გამოიყენება შემდეგი თეორემებიდან ერთ-ერთი (ჩვენ ვაყალიბებთ მათ მტკიცებულებების გარეშე).

თეორემა. კვადრატული ფორმა არის დადებითი (უარყოფითი) განსაზღვრული, თუ და მხოლოდ იმ შემთხვევაში, თუ მისი მატრიცის ყველა საკუთარი მნიშვნელობა დადებითია (უარყოფითი).

თეორემა(სილვესტერის კრიტერიუმი). კვადრატული ფორმა დადებითია განსაზღვრული, თუ და მხოლოდ იმ შემთხვევაში, თუ ამ ფორმის მატრიცის ყველა ძირითადი მინორი დადებითია.

მაიორი (კუთხა) მინორი n-ე რიგის A მატრიცის k-ე წესრიგს ეწოდება მატრიცის განმსაზღვრელი, რომელიც შედგება A (A) მატრიცის პირველი k რიგებისა და სვეტებისგან.

გაითვალისწინეთ, რომ უარყოფით-განსაზღვრული კვადრატული ფორმებისთვის, ძირითადი მცირეწლოვანთა ნიშნები ერთმანეთს ენაცვლება, ხოლო პირველი რიგის მინორი უარყოფითი უნდა იყოს.

მაგალითად, ჩვენ განვიხილავთ კვადრატულ ფორმას f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 ნიშნის განსაზღვრულობისთვის.

= (2 - ლ)*
*(3 - ლ) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. ამიტომ, კვადრატული ფორმა დადებითი განსაზღვრულია.

მეთოდი 2. მატრიცის პირველი რიგის მთავარი მინორი A D 1 = a 11 = 2 > 0. მეორე რიგის მთავარი მინორი D 2 = = 6 - 4 = 2 > 0. ამიტომ, სილვესტერის კრიტერიუმის მიხედვით, კვადრატული ფორმა დადებითი განსაზღვრულია.

ჩვენ განვიხილავთ ნიშნის განსაზღვრულობის სხვა კვადრატულ ფორმას, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

მეთოდი 1. ავაშენოთ А = კვადრატული ფორმის მატრიცა. დამახასიათებელ განტოლებას ექნება ფორმა = (-2 - ლ)*
*(-3 - ლ) - 4 = (6 + 2ლ + 3ლ + ლ 2) - 4 = ლ 2 + 5ლ + 2 = 0; D = 25 - 8 = 17;
. ამიტომ, კვადრატული ფორმა უარყოფითი განსაზღვრულია.

მეთოდი 2. მატრიცის პირველი რიგის მთავარი მინორი A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. მაშასადამე, სილვესტერის კრიტერიუმის მიხედვით, კვადრატული ფორმა უარყოფითი განსაზღვრულია (ძირითადი არასრულწლოვანთა ნიშნები ერთმანეთს ენაცვლება, დაწყებული მინუსიდან).

და როგორც სხვა მაგალითი, ჩვენ განვიხილავთ კვადრატულ ფორმას f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 ნიშნის განსაზღვრულობისთვის.

მეთოდი 1. ავაშენოთ А = კვადრატული ფორმის მატრიცა. დამახასიათებელ განტოლებას ექნება ფორმა = (2 - ლ)*
*(-3 - ლ) - 4 = (-6 - 2ლ + 3ლ + ლ 2) - 4 = ლ 2 + ლ - 10 = 0; D = 1 + 40 = 41;
.

ამ რიცხვებიდან ერთი უარყოფითია, მეორე კი დადებითი. საკუთრივ მნიშვნელობების ნიშნები განსხვავებულია. მაშასადამე, კვადრატული ფორმა არ შეიძლება იყოს არც უარყოფითი და არც დადებითი განსაზღვრული, ე.ი. ეს კვადრატული ფორმა არ არის ნიშან-განსაზღვრული (მას შეუძლია მიიღოს ნებისმიერი ნიშნის მნიშვნელობები).

მეთოდი 2. მატრიცის პირველი რიგის მთავარი მინორი A D 1 = a 11 = 2 > 0. მეორე რიგის მთავარი მინორი D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

ერთგვაროვანი წრფივი განტოლებების სისტემა

ერთგვაროვანი წრფივი განტოლებათა სისტემა არის ფორმის სისტემა

გასაგებია, რომ ამ შემთხვევაში , იმიტომ ამ განმსაზღვრელში ერთ-ერთი სვეტის ყველა ელემენტი ნულის ტოლია.

ვინაიდან უცნობები ფორმულებით არის ნაპოვნი , მაშინ იმ შემთხვევაში, როდესაც Δ ≠ 0, სისტემას აქვს უნიკალური ნულოვანი ამონახსნი x = წ = ზ= 0. თუმცა, ბევრ პრობლემაში საინტერესოა კითხვა, აქვს თუ არა ერთგვაროვან სისტემას ამონახსნები ნულის გარდა.

თეორემა.იმისათვის, რომ წრფივი ერთგვაროვანი განტოლებათა სისტემას ჰქონდეს არანულოვანი ამონახსნი, აუცილებელია და საკმარისი, რომ Δ ≠ 0.

ასე რომ, თუ განმსაზღვრელი Δ ≠ 0, მაშინ სისტემას აქვს უნიკალური ამონახსნი. თუ Δ ≠ 0, მაშინ წრფივი ერთგვაროვანი განტოლებათა სისტემას აქვს ამონახსნების უსასრულო რაოდენობა.

მაგალითები.

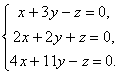
საკუთრივ ვექტორები და მატრიცის საკუთრივ მნიშვნელობები

მიეცით კვადრატული მატრიცა , Xარის რაღაც მატრიცა-სვეტი, რომლის სიმაღლე ემთხვევა მატრიცის წესრიგს ა. .

ბევრ პრობლემაში უნდა განიხილოს განტოლება X

სადაც λ არის რაღაც რიცხვი. ნათელია, რომ ნებისმიერი λ-სთვის ამ განტოლებას აქვს ნულოვანი ამონახსნი.

რიცხვი λ, რომლისთვისაც ამ განტოლებას აქვს არანულოვანი ამონახსნები, ეწოდება საკუთარი ღირებულებამატრიცები ა, ა Xასეთი λ ეწოდება საკუთარი ვექტორიმატრიცები ა.

ვიპოვოთ მატრიცის საკუთრივვექტორი ა. Იმდენად, რამდენადაც ე∙X=X, მაშინ მატრიცული განტოლება შეიძლება გადაიწეროს როგორც ან . გაფართოებული ფორმით, ეს განტოლება შეიძლება გადაიწეროს როგორც წრფივი განტოლებათა სისტემა. მართლა .

Და, შესაბამისად

ასე რომ, ჩვენ მივიღეთ ერთგვაროვანი წრფივი განტოლებების სისტემა კოორდინატების დასადგენად x 1, x2, x 3ვექტორი X. იმისათვის, რომ სისტემას ჰქონდეს არანულოვანი ამონახსნები, აუცილებელია და საკმარისია, რომ სისტემის განმსაზღვრელი იყოს ნულის ტოლი, ე.ი.

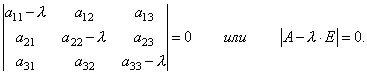
ეს არის მე-3 ხარისხის განტოლება λ-სთან მიმართებაში. ჰქვია დამახასიათებელი განტოლებამატრიცები ადა ემსახურება λ საკუთრივ მნიშვნელობების განსაზღვრას.

თითოეული საკუთარი მნიშვნელობა λ შეესაბამება საკუთრივ ვექტორს X, რომლის კოორდინატები განისაზღვრება სისტემიდან λ-ის შესაბამისი მნიშვნელობით.

მაგალითები.

ვექტორული ალგებრა. ვექტორის კონცეფცია

ფიზიკის სხვადასხვა დარგის შესწავლისას არის სიდიდეები, რომლებიც მთლიანად განისაზღვრება მათი რიცხვითი მნიშვნელობების დაყენებით, მაგალითად, სიგრძე, ფართობი, მასა, ტემპერატურა და ა.შ. ასეთ მნიშვნელობებს სკალარული ეწოდება. თუმცა მათ გარდა არის სიდიდეებიც, რომელთა დადგენისთვის, გარდა რიცხვითი მნიშვნელობისა, ასევე აუცილებელია ვიცოდეთ მათი მიმართულება სივრცეში, მაგალითად, სხეულზე მოქმედი ძალა, სიჩქარე და აჩქარება. სხეულის როდესაც ის მოძრაობს სივრცეში, მაგნიტური ველის სიძლიერე სივრცეში მოცემულ წერტილში და ა.შ. ასეთ სიდიდეებს ვექტორულ სიდიდეებს უწოდებენ.

მოდით შემოვიტანოთ მკაცრი განმარტება.

მიმართულების სეგმენტიდავარქვათ სეგმენტი, რომლის ბოლოებთან შედარებით ცნობილია რომელია პირველი და რომელი მეორე.

ვექტორიმიმართული სეგმენტი ეწოდება, რომელსაც აქვს გარკვეული სიგრძე, ე.ი. ეს არის გარკვეული სიგრძის სეგმენტი, რომელშიც მისი შემზღუდველი ერთ-ერთი წერტილი აღებულია როგორც დასაწყისი, ხოლო მეორე - როგორც დასასრული. Თუ აარის ვექტორის დასაწყისი, ბარის მისი დასასრული, მაშინ ვექტორი აღინიშნება სიმბოლოთი, გარდა ამისა, ვექტორი ხშირად აღინიშნება ერთი ასოთი. ნახატზე ვექტორი მითითებულია სეგმენტით, ხოლო მისი მიმართულება ისრით.

მოდულიან გრძელივექტორს ეწოდება მიმართული სეგმენტის სიგრძე, რომელიც განსაზღვრავს მას. აღინიშნება || ან ||.

ეგრეთ წოდებული ნულოვანი ვექტორი, რომლის დასაწყისი და დასასრული ემთხვევა, ასევე მოიხსენიება როგორც ვექტორები. აღნიშნულია. ნულოვანი ვექტორს არ აქვს განსაზღვრული მიმართულება და მისი მოდული უდრის ნულს ||=0.

ვექტორები და ე.წ კოლინარულითუ ისინი განლაგებულია იმავე ხაზზე ან პარალელურ ხაზებზე. ამ შემთხვევაში, თუ ვექტორები და თანაბრად არის მიმართული, ჩვენ დავწერთ საპირისპიროდ.

იმავე სიბრტყის პარალელურად სწორ ხაზებზე განლაგებულ ვექტორებს უწოდებენ თანაპლენარული.

ორი ვექტორი და ე.წ თანაბარითუ ისინი ხაზოვანია, აქვთ იგივე მიმართულება და ტოლია სიგრძით. ამ შემთხვევაში დაწერეთ.

ვექტორთა თანასწორობის განმარტებიდან გამომდინარეობს, რომ ვექტორი შეიძლება გადავიდეს თავის პარალელურად, მისი საწყისი სივრცის ნებისმიერ წერტილში განთავსებით.

მაგალითად.

ხაზოვანი ოპერაციები ვექტორებზე

1. ვექტორის გამრავლება რიცხვზე.

   ვექტორის ნამრავლი λ რიცხვით არის ახალი ვექტორი ისეთი, რომ:

   ვექტორისა და რიცხვის λ ნამრავლი აღინიშნება .

   

   Მაგალითად,არის ვექტორი, რომელიც მიმართულია ვექტორის იმავე მიმართულებით და აქვს ვექტორის სიგრძის ნახევარი.

   შეყვანილ ოპერაციას აქვს შემდეგი თვისებები:

2. ვექტორების დამატება.

   მოდით და იყოს ორი თვითნებური ვექტორი. მიიღეთ თვითნებური წერტილი ოდა ააგეთ ვექტორი. ამის შემდეგ, წერტილიდან აგადადო ვექტორი . ვექტორი, რომელიც აკავშირებს პირველი ვექტორის დასაწყისს მეორის დასასრულთან, ეწოდება ჯამიამ ვექტორების და აღინიშნება .

   

   ვექტორის დამატების ფორმულირებულ განმარტებას ე.წ პარალელოგრამის წესი, ვინაიდან ვექტორების იგივე ჯამის მიღება შესაძლებელია შემდეგნაირად. დააყენეთ წერტილი ოვექტორები და. ააგეთ პარალელოგრამი ამ ვექტორებზე OABC. რადგან ვექტორები , მაშინ ვექტორი , რომელიც არის წვეროდან გამოყვანილი პარალელოგრამის დიაგონალი ო, აშკარად იქნება ვექტორების ჯამი .

   

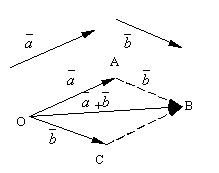
   მარტივია შემდეგის შემოწმება ვექტორის დამატების თვისებები.

3. ვექტორების განსხვავება.

   მოცემულ ვექტორთან კოლინარული ვექტორი, სიგრძით ტოლი და საპირისპიროდ მიმართული, ეწოდება საწინააღმდეგოვექტორი ვექტორისთვის და აღინიშნება . საპირისპირო ვექტორი შეიძლება ჩაითვალოს ვექტორის გამრავლების შედეგად λ = –1: .