ამ უტოლობების გადატანა ზღვარზე, როგორც Δ x→ 0 და იმის გათვალისწინებით, რომ წარმოებული ვ "(x 0) არსებობს და, შესაბამისად, ლიმიტი მარცხნივ არ არის დამოკიდებული იმაზე, თუ როგორ Δ x→ 0, ვიღებთ: Δ-სთვის x → 0 – 0 ვ"(x 0) ≥ 0 და Δ-ზე x → 0 + 0 ვ"(x 0) ≤ 0. ვინაიდან ვ"(x 0) განსაზღვრავს რიცხვს, მაშინ ეს ორი უტოლობა თავსებადია მხოლოდ იმ შემთხვევაში, თუ ვ"(x 0) = 0.

დადასტურებული თეორემა ამბობს, რომ მაქსიმალური და მინიმალური ქულები შეიძლება იყოს მხოლოდ იმ არგუმენტის მნიშვნელობებს შორის, რომლებისთვისაც წარმოებული ქრება.

ჩვენ განვიხილეთ შემთხვევა, როდესაც ფუნქციას აქვს წარმოებული გარკვეული სეგმენტის ყველა წერტილში. რა ხდება მაშინ, როდესაც წარმოებული არ არსებობს? განვიხილოთ მაგალითები.

მაგალითები.

1. წ=|x|.

   ფუნქციას არ აქვს წარმოებული წერტილში x=0 (ამ ეტაპზე ფუნქციის გრაფიკს არ აქვს განსაზღვრული ტანგენსი), მაგრამ ამ დროს ფუნქციას აქვს მინიმუმი, რადგან წ(0)=0 და ყველასთვის x≠ 0წ > 0.



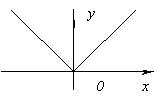
ფუნქციას არ აქვს წარმოებული at x=0, რადგან ის მიდის უსასრულობამდე როცა x=0. მაგრამ ამ ეტაპზე ფუნქციას აქვს მაქსიმუმი.



ფუნქციას არ აქვს წარმოებული at x=0 იმიტომ ზე x→0. ამ ეტაპზე ფუნქციას არც მაქსიმუმი აქვს და არც მინიმუმი. მართლაც, f(x)=0 და ზე x<0f(x)<0, а при x>0f(x)>0.



ამრიგად, მოცემული მაგალითებიდან და ჩამოყალიბებული თეორემიდან ირკვევა, რომ ფუნქციას შეიძლება ჰქონდეს ექსტრემუმი მხოლოდ ორ შემთხვევაში: 1) იმ წერტილებში, სადაც წარმოებული არსებობს და უდრის ნულს; 2) იმ წერტილში, სადაც წარმოებული არ არსებობს.

თუმცა, თუ რაღაც მომენტში x 0 ჩვენ ეს ვიცით f" (x 0 ) =0, მაშინ აქედან არ შეიძლება დავასკვნათ, რომ წერტილში x 0 ფუნქციას აქვს ექსტრემუმი.

მაგალითად. .



მაგრამ მიუთითეთ x=0 არ არის უკიდურესი წერტილი, რადგან ამ წერტილის მარცხნივ ფუნქციის მნიშვნელობები მდებარეობს ღერძის ქვემოთ. ოქსი, და ზემოთ მარჯვნივ.

არგუმენტის მნიშვნელობები ფუნქციის დომენიდან, რომლისთვისაც ფუნქციის წარმოებული ქრება ან არ არსებობს, ეწოდება კრიტიკული წერტილები.




ზემოაღნიშნულიდან გამომდინარეობს, რომ ფუნქციის უკიდურესი წერტილები კრიტიკულ წერტილებს შორისაა და, თუმცა, ყველა კრიტიკული წერტილი არ არის ექსტრემალური წერტილი. მაშასადამე, ფუნქციის უკიდურესობის მოსაძებნად, თქვენ უნდა იპოვოთ ფუნქციის ყველა კრიტიკული წერტილი და შემდეგ შეამოწმოთ თითოეული ეს წერტილი ცალ-ცალკე მაქსიმალური და მინიმალური. ამისათვის ემსახურება შემდეგი თეორემა.

თეორემა 2. (საკმარისი პირობაა ექსტრემის არსებობისთვის.)დაე, ფუნქცია იყოს უწყვეტი კრიტიკული წერტილის შემცველ რაღაც ინტერვალზე x 0 და დიფერენცირებადია ამ ინტერვალის ყველა წერტილში (გარდა, შესაძლოა, თავად წერტილისა x 0). თუ ამ წერტილში მარცხნიდან მარჯვნივ გადასვლისას წარმოებული ცვლის ნიშანს პლუსიდან მინუსზე, მაშინ წერტილში x = x 0 ფუნქციას აქვს მაქსიმუმი. თუ გავლისას x 0 მარცხნიდან მარჯვნივ, წარმოებული ცვლის ნიშანს მინუსდან პლუსზე, შემდეგ ფუნქციას აქვს მინიმალური ამ ეტაპზე.

ამრიგად, თუ

მტკიცებულება. ჯერ ვივარაუდოთ, რომ გავლისას x 0, წარმოებული ცვლის ნიშანს პლუსიდან მინუსზე, ე.ი. ყველასთვის xპუნქტთან ახლოს x 0 f "(x)> 0 ამისთვის x< x 0 , f"(x)< 0 ამისთვის x > x 0 . მოდით გამოვიყენოთ ლაგრანგის თეორემა განსხვავებაზე f(x) - f(x 0 ) = f "(c) (x- x 0), სადაც გშორის დევს xდა x 0 .

1. დაე იყოს x< x 0 . მერე გ< x 0 და f "(c)> 0. Ისე f "(c) (x-x 0)< 0 და, შესაბამისად,

   f(x) - f(x 0 )< 0, ე.ი. f(x)< f(x 0 ).

2. დაე იყოს x > x 0 . მერე c> x 0 და ვ"(გ)< 0. ნიშნავს f "(c) (x-x 0)< 0. Ისე f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .

ამრიგად, ყველა ღირებულებისთვის xსაკმარისად ახლოს x 0 f(x)< f(x 0 ) . და ეს იმას ნიშნავს, რომ იმ წერტილში x 0 ფუნქციას აქვს მაქსიმუმი.

ანალოგიურად დადასტურებულია მინიმალური თეორემის მეორე ნაწილიც.



მოდით ილუსტრაციით ამ თეორემის მნიშვნელობა სურათზე. დაე იყოს f" (x 1 ) =0 და ნებისმიერისთვის x,საკმარისად ახლოს x 1, უტოლობები

f"(x)< 0 საათზე x< x 1 , f "(x)> 0 საათზე x > x 1 .

შემდეგ წერტილის მარცხნივ x 1 ფუნქცია იზრდება და მცირდება მარჯვნივ, შესაბამისად, როდის x = x 1 ფუნქცია გაზრდიდან კლებამდე მიდის, ანუ აქვს მაქსიმუმი.

ანალოგიურად, შეიძლება განიხილოს პუნქტები x 2 და x 3 .


სქემატურად, ყოველივე ზემოთქმული შეიძლება გამოსახული იყოს სურათზე:

y=f(x) ფუნქციის შესწავლის წესი ექსტრემისთვის

1. იპოვნეთ ფუნქციის ფარგლები f(x).
2. იპოვეთ ფუნქციის პირველი წარმოებული f"(x).
3. ამისათვის განსაზღვრეთ კრიტიკული წერტილები:
   1. იპოვნეთ განტოლების ნამდვილი ფესვები f"(x)=0;
   2. იპოვნეთ ყველა ღირებულება xრომლის მიხედვითაც წარმოებული f"(x)არ არსებობს.
4. განსაზღვრეთ წარმოებულის ნიშანი კრიტიკული წერტილის მარცხნივ და მარჯვნივ. ვინაიდან წარმოებულის ნიშანი მუდმივი რჩება ორ კრიტიკულ წერტილს შორის, საკმარისია წარმოებულის ნიშნის დადგენა ნებისმიერ წერტილში მარცხნივ და ერთ წერტილში კრიტიკული წერტილიდან მარჯვნივ.
5. გამოთვალეთ ფუნქციის მნიშვნელობა უკიდურეს წერტილებში.

მაგალითები. შეისწავლეთ ფუნქციები მინიმალური და მაქსიმალური.




ფუნქციის ყველაზე დიდი და მინიმალური მნიშვნელობები ინტერსეპტზე

ყველაზე დიდისეგმენტზე ფუნქციის მნიშვნელობა ყველაზე დიდია ამ სეგმენტზე მის ყველა მნიშვნელობას შორის და სულ მცირეარის ყველაზე პატარა მისი ყველა ღირებულებიდან.

განიხილეთ ფუნქცია y=f(x)უწყვეტი სეგმენტზე [ ა, ბ]. როგორც ცნობილია, ასეთი ფუნქცია აღწევს თავის მაქსიმალურ და მინიმალურ მნიშვნელობებს, ან სეგმენტის საზღვარზე, ან მის შიგნით. თუ ფუნქციის მაქსიმალური ან მინიმალური მნიშვნელობა მიღწეულია სეგმენტის შიდა წერტილში, მაშინ ეს მნიშვნელობა არის ფუნქციის მაქსიმუმი ან მინიმალური, ანუ მიიღწევა კრიტიკულ წერტილებში.

ამრიგად, ჩვენ ვიღებთ შემდეგს სეგმენტზე ფუნქციის უდიდესი და უმცირესი მნიშვნელობების პოვნის წესი [ ა, ბ] :

1. იპოვეთ ფუნქციის ყველა კრიტიკული წერტილი ინტერვალში ( ა, ბ) და გამოთვალეთ ფუნქციის მნიშვნელობები ამ წერტილებში.
2. გამოთვალეთ ფუნქციის მნიშვნელობები სეგმენტის ბოლოებში x=a, x=b.
3. ყველა მიღებული მნიშვნელობიდან აირჩიეთ ყველაზე დიდი და პატარა.

>> ექსტრემები

ექსტრემალური ფუნქცია

ექსტრემის განმარტება

ფუნქცია y = f(x) ეწოდება იზრდება (მცირდება) რაღაც ინტერვალში, თუ x 1-ისთვის< x 2 выполняется неравенство (f (x 1) < f (x 2) (f (x 1) >f(x2)).

თუ დიფერენცირებადი ფუნქცია y \u003d f (x) სეგმენტზე იზრდება (მცირდება), მაშინ მისი წარმოებული ამ სეგმენტზე f " (x)> 0

(ვ"(x)< 0).

Წერტილი x შესახებ დაურეკა ადგილობრივი მაქსიმალური წერტილი (მინიმალური f (x) ფუნქციის ) თუ არის წერტილის მეზობლობა x o, ყველა წერტილისთვის, რომლის უტოლობა f (x)≤ f (x o) (f (x)≥ f (x o )).

მაქსიმალური და მინიმალური ქულები ეწოდება ექსტრემალური წერტილებიდა ფუნქციის მნიშვნელობები ამ წერტილებში არის მისი უკიდურესი.

ექსტრემალური წერტილები

აუცილებელი პირობები ექსტრემისთვის . თუ წერტილი x შესახებ არის f (x) ფუნქციის უკიდურესი წერტილი, შემდეგ ან f " (x o ) = 0, ან ვ(x o ) არ არსებობს. ასეთ წერტილებს ე.წ კრიტიკული,სადაც თავად ფუნქცია განისაზღვრება კრიტიკულ წერტილში. ფუნქციის უკიდურესობა უნდა ვეძებოთ მის კრიტიკულ წერტილებს შორის.

პირველი საკმარისი პირობა. დაე იყოს x შესახებ - კრიტიკული წერტილი. თუ ვ" (x ) წერტილის გავლისას x შესახებ ცვლის პლუს ნიშანს მინუსზე, შემდეგ წერტილში x oფუნქციას აქვს მაქსიმუმი, წინააღმდეგ შემთხვევაში აქვს მინიმუმი. თუ წარმოებული არ ცვლის ნიშანს კრიტიკულ წერტილში გავლისას, მაშინ წერტილში x შესახებ არ არის ექსტრემუმი.

მეორე საკმარისი პირობა. აქვს f(x) ფუნქციას
ვ" (x ) წერტილის სიახლოვეს x შესახებ და მეორე წარმოებული სწორედ იმ წერტილში x o. თუ ვ"(x o) = 0, >0 ( <0), то точка x oარის f(x) ფუნქციის ლოკალური მინიმალური (მაქსიმალური) წერტილი. თუ =0, მაშინ ან უნდა გამოიყენოთ პირველი საკმარისი პირობა, ან ჩართოთ უფრო მაღალი პირობა.

სეგმენტზე ფუნქცია y \u003d f (x) შეიძლება მიაღწიოს უმცირეს ან უდიდეს მნიშვნელობას კრიტიკულ წერტილებში ან სეგმენტის ბოლოებში.

მაგალითი 3.22.

გადაწყვეტილება.როგორც ვ " (

ამოცანები ფუნქციის ექსტრემის პოვნისთვის

მაგალითი 3.23. ა

გადაწყვეტილება. xდა წ წ
0 ≤ x≤
> 0, ხოლო x >a /4 ს " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение ფუნქციები კვ.. ერთეულები).

მაგალითი 3.24. p ≈

გადაწყვეტილება.გვ
S"
R = 2, H = 16/4 = 4.

მაგალითი 3.22.იპოვეთ f (x) = 2x 3 - 15x 2 + 36x - 14 ფუნქციის უკიდურესი.

გადაწყვეტილება.როგორც ვ " (x) \u003d 6x 2 - 30x +36 \u003d 6 (x -2) (x - 3), შემდეგ ფუნქციის კრიტიკული წერტილები x 1 \u003d 2 და x 2 \u003d 3. უკიდურესი წერტილები შეიძლება იყოს მხოლოდ ამ ქულები. ვინაიდან x 1 \u003d 2 წერტილის გავლისას წარმოებული ცვლის ნიშანს პლუსიდან მინუსზე, მაშინ ამ ეტაპზე ფუნქციას აქვს მაქსიმუმი. x 2 \u003d 3 წერტილის გავლისას, წარმოებული ცვლის ნიშანს მინუსიდან პლუსზე, შესაბამისად, x 2 \u003d 3 წერტილში ფუნქციას აქვს მინიმუმი. ფუნქციის მნიშვნელობების გამოთვლა წერტილებში
x 1 = 2 და x 2 = 3, ჩვენ ვპოულობთ ფუნქციის უკიდურესობას: მაქსიმალური f (2) = 14 და მინიმალური f (3) = 13.

მაგალითი 3.23.ქვის კედელთან სწორკუთხა უბნის აგებაა საჭირო, რომ სამი მხრიდან მავთულის ბადით შემოღობოს, მეოთხე მხრიდან კი კედელს შეუერთდეს. ამისათვის არსებობს აქსელის ხაზოვანი მეტრი. რა თანაფარდობით ექნება საიტს ყველაზე დიდი ფართობი?

გადაწყვეტილება.მიუთითეთ საიტის მხარეები მეშვეობით xდა წ. საიტის ფართობი უდრის S = xy. დაე იყოს წარის კედლის მიმდებარე მხარის სიგრძე. შემდეგ, პირობით, ტოლობა 2x + y = a უნდა იყოს. ამიტომ y = a - 2x და S = x (a - 2x), სადაც
0 ≤ x≤ a /2 (ბალიშის სიგრძე და სიგანე არ შეიძლება იყოს უარყოფითი). S "= a - 4x, a - 4x = 0 x = a/4-ისთვის, საიდანაც
y \u003d a - 2 × a / 4 \u003d a / 2. Იმდენად, რამდენადაც x = a /4 ერთადერთი კრიტიკული წერტილია, მოდით შევამოწმოთ, იცვლება თუ არა წარმოებულის ნიშანი ამ წერტილში გავლისას. x a /4 S"-სთვის> 0, ხოლო x >a /4 ს " < 0, значит, в точке x=a /4 функция S имеет максимум. Значение ფუნქციები S(a/4) = a/4(a - a/2) = a 2/8 (კვ.. ერთეულები). ვინაიდან S არის უწყვეტი და მისი მნიშვნელობები S(0) და S(a /2) ბოლოებში ნულის ტოლია, მაშინ ნაპოვნი მნიშვნელობა იქნება ფუნქციის უდიდესი მნიშვნელობა. ამრიგად, საიტის ყველაზე ხელსაყრელი ასპექტის თანაფარდობა პრობლემის მოცემულ პირობებში არის y = 2x.

მაგალითი 3.24.საჭიროა V=16 ტევადობის დახურული ცილინდრული ავზის დამზადება p ≈ 50 მ 3. როგორი უნდა იყოს ავზის ზომები (რადიუსი R და სიმაღლე H), რომ მის დასამზადებლად გამოიყენოს ყველაზე ნაკლები მასალა?

გადაწყვეტილება.ცილინდრის მთლიანი ზედაპირის ფართობი არის S = 2გვ R(R+H). ჩვენ ვიცით ცილინდრის მოცულობა V = p R 2 N Þ N \u003d V / p R 2 \u003d 16 p / p R 2 \u003d 16 / R 2. ასე რომ, S(R) = 2გვ (R2+16/R). ჩვენ ვპოულობთ ამ ფუნქციის წარმოებულს:
S"(R) \u003d 2 p (2R- 16 / R 2) \u003d 4 p (R- 8 / R 2). S" (R) = 0 R 3 = 8-ისთვის, შესაბამისად,
R = 2, H = 16/4 = 4.

ფუნქციები, საერთოდ არ არის აუცილებელი იცოდეთ პირველი და მეორე წარმოებულების არსებობის შესახებ და გაიგოთ მათი ფიზიკური მნიშვნელობა. ჯერ უნდა გესმოდეთ შემდეგი:

• ფუნქციის უკიდურესი მაქსიმიზაცია ან, პირიქით, ფუნქციის მნიშვნელობის მინიმიზაცია თვითნებურად მცირე სამეზობლოში;
• უკიდურეს წერტილში არ უნდა იყოს ფუნქციის შეწყვეტა.

ახლა კი იგივე, მხოლოდ მარტივი სიტყვებით. შეხედეთ ბურთულიანი კალმის წვერს. თუ კალამი მოთავსებულია ვერტიკალურად, ნაწერის ბოლოს, მაშინ ბურთის შუა ნაწილი იქნება უკიდურესი წერტილი - უმაღლესი წერტილი. ამ შემთხვევაში მაქსიმუმზე ვსაუბრობთ. ახლა, თუ კალამი ჩააბრუნეთ ჩაწერის ბოლოებით, მაშინ ბურთის შუაში უკვე იქნება ფუნქციის მინიმუმი. აქ მოცემული ფიგურის დახმარებით შეგიძლიათ წარმოიდგინოთ ჩამოთვლილი მანიპულაციები საკანცელარიო ფანქრისთვის. ამრიგად, ფუნქციის უკიდურესობა ყოველთვის კრიტიკული წერტილებია: მისი მაქსიმუმი ან მინიმალური. დიაგრამის მიმდებარე მონაკვეთი შეიძლება იყოს თვითნებურად მკვეთრი ან გლუვი, მაგრამ ის უნდა არსებობდეს ორივე მხრიდან, მხოლოდ ამ შემთხვევაში წერტილი არის ექსტრემი. თუ სქემა მხოლოდ ერთ მხარეს არის, ეს წერტილი არ იქნება ექსტრემუმი, მაშინაც კი, თუ ექსტრემალური პირობები დაკმაყოფილებულია მის ერთ მხარეს. ახლა მოდით შევისწავლოთ ფუნქციის ექსტრემა მეცნიერული თვალსაზრისით. იმისათვის, რომ წერტილი ჩაითვალოს ექსტრემულად, აუცილებელია და საკმარისია:

• პირველი წარმოებული იყო ნულის ტოლი ან არ არსებობდა წერტილში;
• პირველი წარმოებული ცვლის ნიშანს ამ ეტაპზე.

მდგომარეობა გარკვეულწილად განსხვავებულად არის განმარტებული უმაღლესი რიგის წარმოებულების თვალსაზრისით: წერტილში დიფერენცირებადი ფუნქციისთვის საკმარისია კენტი რიგის წარმოებული, რომელიც არ არის ნულის ტოლი, მაშინ როცა ყველა ქვედა რიგის წარმოებული უნდა იყოს არსებობს და იყოს ნულის ტოლი. ეს არის თეორემების უმარტივესი ინტერპრეტაცია სახელმძღვანელოებიდან, მაგრამ უბრალო ადამიანებისთვის ღირს ამ საკითხის მაგალითით ახსნა. საფუძველი არის ჩვეულებრივი პარაბოლა. დაუყოვნებლივ გააკეთეთ დაჯავშნა, ნულოვან წერტილში მას აქვს მინიმალური. ცოტა მათემატიკა:

• პირველი წარმოებული (X 2) | = 2X, ნულოვანი წერტილისთვის 2X = 0;
• მეორე წარმოებული (2X) | = 2, ნულოვანი წერტილისთვის 2 = 2.

ასე მარტივი გზით, ილუსტრირებულია პირობები, რომლებიც განსაზღვრავენ ფუნქციის უკიდურესობებს როგორც პირველი რიგის წარმოებულებისთვის, ასევე უმაღლესი რიგის წარმოებულებისთვის. ამას შეიძლება დაემატოს, რომ მეორე წარმოებული არის კენტი რიგის იგივე წარმოებული, ნულის არატოლი, რომელიც ნახსენები იყო ოდნავ მაღლა. როდესაც საქმე ეხება ორი ცვლადის ფუნქციის უკიდურესობას, ორივე არგუმენტისთვის პირობები უნდა იყოს დაკმაყოფილებული. როდესაც ხდება განზოგადება, მაშინ თამაშში შედის ნაწილობრივი წარმოებულები. ანუ ისეთ წერტილში უკიდურესობის არსებობისთვის აუცილებელია, რომ ორივე პირველი რიგის წარმოებული იყოს ნულის ტოლი, ან ერთი მათგანი მაინც არ არსებობს. ექსტრემის არსებობის საკმარისობისთვის გამოკვლეულია გამოხატულება, რომელიც არის განსხვავება მეორე რიგის წარმოებულების ნამრავლსა და ფუნქციის შერეული მეორე რიგის წარმოებულის კვადრატს შორის. თუ ეს გამოხატულება მეტია ნულზე, მაშინ არის ექსტრემუმი, ხოლო თუ არის ნულის ტოლობა, მაშინ კითხვა რჩება ღია და საჭიროა დამატებითი კვლევა.