ასევე იქნება ამოცანები დამოუკიდებელი გადაწყვეტისთვის, რომლებზეც შეგიძლიათ ნახოთ პასუხები.

ვექტორის კონცეფცია

სანამ ყველაფერს გაიგებთ ვექტორებისა და მათზე მოქმედებების შესახებ, შეხედეთ მარტივი პრობლემის გადაჭრას. არსებობს თქვენი საწარმოს ვექტორი და თქვენი ინოვაციური შესაძლებლობების ვექტორი. მეწარმეობის ვექტორი მიგიყვანთ 1-ლ მიზნამდე, ხოლო ინოვაციური შესაძლებლობების ვექტორი - მიზნის 2-მდე. თამაშის წესები ისეთია, რომ ამ ორი ვექტორის მიმართულებით ერთდროულად ვერ მოძრაობ და ერთდროულად ორ მიზანს მიაღწევ. ვექტორები ურთიერთქმედებენ, ან, მათემატიკურად რომ ვთქვათ, ვექტორებზე რაიმე ოპერაცია ხორციელდება. ამ ოპერაციის შედეგია „შედეგი“ ვექტორი, რომელიც მიგიყვანთ მიზნ 3-მდე.

ახლა მითხარით: რომელი მოქმედების შედეგია ვექტორებზე „Enterprise“ და „Innovative Abilities“ ვექტორი „შედეგი“? თუ დაუყოვნებლივ ვერ იტყვით, ნუ იმედგაცრუებთ. ამ გაკვეთილის შესწავლისას თქვენ შეძლებთ ამ კითხვაზე პასუხის გაცემას.

როგორც ზემოთ ვნახეთ, ვექტორი აუცილებლად რაღაც წერტილიდან მოდის ასწორ ხაზზე რაღაც მომენტამდე ბ. შესაბამისად, თითოეულ ვექტორს აქვს არა მხოლოდ რიცხვითი მნიშვნელობა - სიგრძე, არამედ ფიზიკური და გეომეტრიული მიმართულებაც. აქედან გამომდინარეობს ვექტორის პირველი, უმარტივესი განმარტება. ამრიგად, ვექტორი არის მიმართული სეგმენტი, რომელიც მიდის წერტილიდან ააზრამდე ბ. აღნიშნულია ასე:

და სხვანაირად დავიწყოთ ვექტორული ოპერაციები , უნდა გავეცნოთ ვექტორის კიდევ ერთ განმარტებას.

ვექტორი არის წერტილის ერთგვარი წარმოდგენა, რომლის მიღწევაც შესაძლებელია რაიმე საწყისი წერტილიდან. მაგალითად, სამგანზომილებიანი ვექტორი ჩვეულებრივ იწერება როგორც (x, y, z) . მარტივად რომ ვთქვათ, ეს რიცხვები გვიჩვენებს, თუ რამდენად შორს უნდა გაიაროთ სამი სხვადასხვა მიმართულებით, რათა მიხვიდეთ პუნქტამდე.

მიეცით ვექტორი. სადაც x = 3 (მარჯვენა ხელი მარჯვნივ მიუთითებს) წ = 1 (მარცხენა ხელი წინ არის მიმართული) ზ = 5 (წერტილის ქვეშ არის კიბე, რომელიც მიდის ზემოთ). ამ მონაცემებიდან თქვენ იპოვით პუნქტს მარჯვენა ხელით მითითებული მიმართულებით 3 მეტრის სიარულით, შემდეგ მარცხენა ხელით მითითებული მიმართულებით 1 მეტრით, შემდეგ კი კიბე გელოდებათ და 5 მეტრის ასვლისას საბოლოოდ იპოვით. საკუთარ თავს ბოლო ეტაპზე.

ყველა სხვა ტერმინი არის ზემოთ წარმოდგენილი ახსნის დახვეწა, რომელიც აუცილებელია ვექტორებზე სხვადასხვა ოპერაციებისთვის, ანუ პრაქტიკული პრობლემების გადასაჭრელად. მოდით გავიაროთ ეს უფრო მკაცრი განმარტებები, ვისაუბროთ ტიპურ ვექტორულ პრობლემებზე.

ფიზიკური მაგალითებივექტორული სიდიდეები შეიძლება იყოს სივრცეში მოძრავი მატერიალური წერტილის გადაადგილება, ამ წერტილის სიჩქარე და აჩქარება, ასევე მასზე მოქმედი ძალა.

გეომეტრიული ვექტორიწარმოდგენილია ორგანზომილებიან და სამგანზომილებიან სივრცეში სახით მიმართული სეგმენტი. ეს არის სეგმენტი, რომელსაც აქვს დასაწყისი და დასასრული.

Თუ აარის ვექტორის დასაწყისი და ბარის მისი დასასრული, მაშინ ვექტორი აღინიშნება სიმბოლოთი ან ერთი პატარა ასოთი. ნახატზე ვექტორის ბოლო მითითებულია ისრით (ნახ. 1).

სიგრძე(ან მოდული) გეომეტრიული ვექტორის არის სეგმენტის სიგრძე, რომელიც ქმნის მას

ორ ვექტორს ე.წ თანაბარი , თუ შესაძლებელია მათი გაერთიანება (როდესაც მიმართულებები ემთხვევა) პარალელური თარგმნით, ე.ი. თუ ისინი პარალელურია, მიუთითეთ ერთი და იგივე მიმართულებით და აქვთ ტოლი სიგრძე.

ფიზიკაში ხშირად განიხილება დამაგრებული ვექტორები, მოცემულია განაცხადის წერტილის, სიგრძისა და მიმართულების მიხედვით. თუ ვექტორის გამოყენების წერტილს მნიშვნელობა არ აქვს, მაშინ მისი გადატანა შესაძლებელია, სიგრძისა და მიმართულების შენარჩუნება სივრცის ნებისმიერ წერტილში. ამ შემთხვევაში ვექტორი ეწოდება უფასო. ჩვენ ვეთანხმებით მხოლოდ განხილვას თავისუფალი ვექტორები.

ხაზოვანი მოქმედებები გეომეტრიულ ვექტორებზე

გავამრავლოთ ვექტორი რიცხვზე

ვექტორული პროდუქტი თითო რიცხვზევექტორს უწოდებენ ვექტორიდან მიღებულ ვექტორს (at) ან შეკუმშვით (at) ჯერ, და ვექტორის მიმართულება შენარჩუნებულია თუ და შებრუნებული თუ. (ნახ. 2)

განმარტებიდან გამომდინარეობს, რომ ვექტორები და = ყოველთვის განლაგებულია ერთ ან პარალელურ ხაზებზე. ასეთ ვექტორებს ე.წ კოლინარული. (ასევე შეიძლება ითქვას, რომ ეს ვექტორები პარალელურია, მაგრამ ვექტორულ ალგებრაში ჩვეულებრივად ვამბობთ "კოლნეარულს".) პირიქითაც მართალია: თუ ვექტორები და ხაზოვანია, მაშინ ისინი დაკავშირებულია მიმართებით.

მაშასადამე, ტოლობა (1) გამოხატავს ორი ვექტორის თანამიმართულობის პირობას.

ვექტორული შეკრება და გამოკლება

ვექტორების დამატებისას ეს უნდა იცოდეთ ჯამივექტორები და ეწოდება ვექტორი , რომლის დასაწყისი ემთხვევა ვექტორის დასაწყისს , ხოლო დასასრული - ვექტორის დასასრულს , იმ პირობით , რომ ვექტორის დასაწყისი მიმაგრებულია ვექტორის ბოლოს . (ნახ. 3)

ეს განსაზღვრება შეიძლება გადანაწილდეს ვექტორების ნებისმიერ სასრულ რაოდენობაზე. შეუშვით მოცემული სივრცე ნუფასო ვექტორები. რამდენიმე ვექტორის დამატებისას მათი ჯამი მიიღება დახურვის ვექტორად, რომლის დასაწყისი ემთხვევა პირველი ვექტორის დასაწყისს, ხოლო დასასრული ბოლო ვექტორის დასასრულს. ანუ თუ ვექტორის დასაწყისს ვამაგრებთ ვექტორის ბოლოს, ხოლო ვექტორის დასაწყისს ვექტორის ბოლოს და ა.შ. და ბოლოს, ვექტორის ბოლომდე - ვექტორის დასაწყისი, მაშინ ამ ვექტორების ჯამი არის დახურვის ვექტორი. , რომლის დასაწყისი ემთხვევა პირველი ვექტორის დასაწყისს და რომლის დასასრული ემთხვევა ბოლო ვექტორის დასასრულს . (ნახ. 4)

ტერმინებს ვექტორის კომპონენტებს უწოდებენ და ჩამოყალიბებული წესია მრავალკუთხედის წესი. ეს მრავალკუთხედი შეიძლება არ იყოს ბრტყელი.

როდესაც ვექტორი მრავლდება რიცხვზე -1, საპირისპირო ვექტორი მიიღება. ვექტორები და აქვთ იგივე სიგრძე და საპირისპირო მიმართულებები. მათი ჯამი იძლევა ნულოვანი ვექტორი, რომლის სიგრძე ნულია. ნულოვანი ვექტორის მიმართულება არ არის განსაზღვრული.

ვექტორულ ალგებრაში არ არის საჭირო გამოკლების მოქმედების ცალკე განხილვა: ვექტორის გამოკლება ვექტორს ნიშნავს საპირისპირო ვექტორის დამატებას ვექტორს, ე.ი.

მაგალითი 1გამოთქმის გამარტივება:

.

,

ანუ ვექტორების დამატება და რიცხვებით გამრავლება შეიძლება ისე, როგორც მრავალწევრები (კერძოდ, ასევე გამოსახულებების გამარტივების ამოცანები). ჩვეულებრივ, ვექტორებით წრფივი მსგავსი გამონათქვამების გამარტივების აუცილებლობა ჩნდება ვექტორების ნამრავლების გამოთვლამდე.

მაგალითი 2ვექტორები და ემსახურება ABCD პარალელოგრამის დიაგონალებს (ნახ. 4a). გამოხატეთ ვექტორებით , , და , რომლებიც ამ პარალელოგრამის გვერდებია.

გადაწყვეტილება. პარალელოგრამის დიაგონალების გადაკვეთის წერტილი ორად ყოფს თითოეულ დიაგონალს. ამოცანის პირობებში საჭირო ვექტორების სიგრძე გვხვდება ან ვექტორების ჯამების ნახევარში, რომლებიც ქმნიან სამკუთხედს სასურველთან, ან ნახევარი განსხვავება (დამოკიდებულია ვექტორის მიმართულებაზე, რომელიც ემსახურება დიაგონალს). ან, როგორც ამ უკანასკნელ შემთხვევაში, მინუს ნიშნით აღებული თანხის ნახევარი. შედეგი არის პრობლემის პირობებში საჭირო ვექტორები:

არსებობს ყველა საფუძველი დასაჯერებლად, რომ თქვენ ახლა სწორად უპასუხეთ კითხვას "საწარმო" და "ინოვაციური შესაძლებლობების" ვექტორების შესახებ ამ გაკვეთილის დასაწყისში. სწორი პასუხი: ეს ვექტორები ექვემდებარება შეკრების ოპერაციას.

გადაჭრით ამოცანები ვექტორებზე დამოუკიდებლად და შემდეგ გადახედეთ ამონახსნებს

როგორ მოვძებნოთ ვექტორთა ჯამის სიგრძე?

ამ პრობლემას განსაკუთრებული ადგილი უჭირავს ვექტორებთან ოპერაციებში, რადგან ის გულისხმობს ტრიგონომეტრიული თვისებების გამოყენებას. ვთქვათ, თქვენ გაქვთ შემდეგი დავალება:

ვექტორების სიგრძის გათვალისწინებით და ამ ვექტორების ჯამის სიგრძე . იპოვეთ ამ ვექტორების სხვაობის სიგრძე.

ამ და სხვა მსგავსი პრობლემების გადაწყვეტილებები და მათი გადაჭრის ახსნა-განმარტებები - გაკვეთილზე " ვექტორული შეკრება: ვექტორთა ჯამის სიგრძე და კოსინუსების თეორემა ".

და თქვენ შეგიძლიათ შეამოწმოთ ასეთი პრობლემების გადაწყვეტა ონლაინ კალკულატორი "სამკუთხედის უცნობი გვერდი (ვექტორის შეკრება და კოსინუსების თეორემა)" .

სად არის ვექტორების პროდუქტები?

ვექტორის მიერ ვექტორის ნამრავლები არ არის წრფივი მოქმედებები და განიხილება ცალკე. და გვაქვს გაკვეთილები "ვექტორთა წერტილოვანი პროდუქტი" და "ვექტორების ვექტორული და შერეული პროდუქტი".

ვექტორის პროექცია ღერძზე

ვექტორის პროექცია ღერძზე ტოლია დაპროექტებული ვექტორის სიგრძისა და ვექტორსა და ღერძს შორის კუთხის კოსინუსის ნამრავლის:

როგორც ცნობილია, წერტილის პროექცია ახაზზე (სიბრტყეზე) არის ამ წერტილიდან ხაზამდე (სიბრტყეზე) ჩამოშვებული პერპენდიკულარულის საფუძველი.

მოდით - თვითნებური ვექტორი (ნახ. 5) და და - მისი დასაწყისის პროგნოზები (პუნქტები ა) და ბოლო (წერტილები ბ) თითო ღერძზე ლ. (პუნქტის პროექციის ასაგებად ა) პირდაპირ დახაზეთ წერტილი აწრფის პერპენდიკულარული სიბრტყე. ხაზისა და სიბრტყის გადაკვეთა განსაზღვრავს საჭირო პროექციას.

ვექტორის კომპონენტი l ღერძზეამ ღერძზე მდებარე ისეთ ვექტორს უწოდებენ, რომლის დასაწყისი ემთხვევა დასაწყისის პროექციას, ხოლო დასასრული - ვექტორის დასასრულის პროექციას.

ვექტორის პროექცია ღერძზე ლდარეკა ნომერზე

,

ამ ღერძზე კომპონენტის ვექტორის სიგრძის ტოლია, მიღებული პლუსის ნიშნით, თუ კომპონენტის მიმართულება ემთხვევა ღერძის მიმართულებას ლდა მინუს ნიშნით, თუ ეს მიმართულებები საპირისპიროა.

ვექტორული პროგნოზების ძირითადი თვისებები ღერძზე:

1. ერთ ღერძზე თანაბარი ვექტორების პროგნოზები ერთმანეთის ტოლია.

2. როდესაც ვექტორი მრავლდება რიცხვზე, მისი პროექცია მრავლდება იმავე რიცხვზე.

3. ვექტორთა ჯამის პროექცია რომელიმე ღერძზე ტოლია ვექტორების ტერმინების იმავე ღერძზე პროექციების ჯამს.

4. ვექტორის პროექცია ღერძზე უდრის დაპროექტებული ვექტორის სიგრძისა და ვექტორსა და ღერძს შორის კუთხის კოსინუსის ნამრავლს:

.

გადაწყვეტილება. მოდით გავაპროექტოთ ვექტორები ღერძზე ლროგორც განსაზღვრულია ზემოთ მოცემულ თეორიულ მითითებაში. ნახ.5ა-დან აშკარაა, რომ ვექტორთა ჯამის პროექცია უდრის ვექტორთა პროგნოზების ჯამს. ჩვენ ვიანგარიშებთ ამ პროგნოზებს:

ჩვენ ვპოულობთ ვექტორთა ჯამის საბოლოო პროექციას:

ვექტორის კავშირი მართკუთხა დეკარტის კოორდინატულ სისტემასთან სივრცეში

გაცნობა მართკუთხა დეკარტის კოორდინატთა სისტემა სივრცეში შესაბამის გაკვეთილზე მოხდა, სასურველია გახსენით იგი ახალ ფანჯარაში.

კოორდინატთა ღერძების მოწესრიგებულ სისტემაში 0xyzღერძი ოქსიდაურეკა x-ღერძი, ღერძი 0 წ – y-ღერძიდა ღერძი 0z – აპლიკაციის ღერძი.

თვითნებური წერტილით მკოსმოსური კავშირის ვექტორი

დაურეკა რადიუსის ვექტორიქულები მდა დააპროექტეთ იგი თითოეულ კოორდინატულ ღერძზე. მოდით აღვნიშნოთ შესაბამისი პროგნოზების მნიშვნელობები:

ნომრები x, y, zდაურეკა M წერტილის კოორდინატები, შესაბამისად აბსცისა, ორდინატიდა აპლიკაციადა იწერება რიცხვების მოწესრიგებული წერტილით: M(x; y; z)(ნახ. 6).

ერთეული სიგრძის ვექტორს, რომლის მიმართულება ემთხვევა ღერძის მიმართულებას, ეწოდება ერთეული ვექტორი(ან ორტომი) ცულები. აღნიშნეთ მიერ

შესაბამისად კოორდინატთა ღერძების ერთეული ვექტორები ოქსი, ოი, ოზი

თეორემა.ნებისმიერი ვექტორი შეიძლება დაიშალოს კოორდინატთა ღერძების ერთეულ ვექტორებად:

(2)

ტოლობას (2) ეწოდება ვექტორის გაფართოება კოორდინატთა ღერძების გასწვრივ. ამ გაფართოების კოეფიციენტები არის ვექტორის პროგნოზები კოორდინატთა ღერძებზე. ამრიგად, ვექტორის გაფართოების კოეფიციენტები (2) კოორდინატთა ღერძების გასწვრივ არის ვექტორის კოორდინატები.

სივრცეში გარკვეული კოორდინატთა სისტემის არჩევის შემდეგ, ვექტორი და მისი სამმაგი კოორდინატები ცალსახად განსაზღვრავენ ერთმანეთს, ამიტომ ვექტორი შეიძლება დაიწეროს სახით

(2) და (3) სახით ვექტორული გამოსახულებები იდენტურია.

კოლინარული ვექტორების მდგომარეობა კოორდინატებში

როგორც უკვე აღვნიშნეთ, ვექტორებს უწოდებენ კოლინარული, თუ ისინი დაკავშირებულია მიმართებით

მოდით ვექტორები . ეს ვექტორები კოლინარულია, თუ ვექტორების კოორდინატები დაკავშირებულია მიმართებით

,

ანუ ვექტორების კოორდინატები პროპორციულია.

მაგალითი 6მოცემული ვექტორები . ეს ვექტორები თანამიმდევრულია?

გადაწყვეტილება. მოდით გავარკვიოთ ამ ვექტორების კოორდინატების თანაფარდობა:

.

ვექტორების კოორდინატები პროპორციულია, მაშასადამე, ვექტორები არის კოლინარული ან, რაც იგივეა, პარალელური.

ვექტორის სიგრძე და მიმართულება კოსინუსები

კოორდინატთა ღერძების ურთიერთპერპენდიკულარულობის გამო ვექტორის სიგრძე

უდრის ვექტორებზე აგებული მართკუთხა პარალელეპიპედის დიაგონალის სიგრძეს

და გამოიხატება თანასწორობით

(4)

ვექტორი მთლიანად განისაზღვრება ორი წერტილის მითითებით (დასაწყისი და დასასრული), ამიტომ ვექტორის კოორდინატები შეიძლება გამოისახოს ამ წერტილების კოორდინატებში.

მოცემულ კოორდინატულ სისტემაში ვექტორის დასაწყისი იყოს წერტილში

და დასასრული არის წერტილი

თანასწორობიდან

ამას მოჰყვება

ან კოორდინატის სახით

აქედან გამომდინარე, ვექტორის კოორდინატები ტოლია ვექტორის დასასრულისა და დასაწყისის ამავე სახელწოდების კოორდინატების სხვაობებზე. . ფორმულა (4) ამ შემთხვევაში იღებს ფორმას

ვექტორის მიმართულება განისაზღვრება მიმართულების კოსინუსები . ეს არის კუთხეების კოსინუსები, რომლებსაც ვექტორი ქმნის ღერძებთან ოქსი, ოიდა ოზი. დავნიშნოთ ეს კუთხეები შესაბამისად α , β და γ . შემდეგ ამ კუთხეების კოსინუსები შეიძლება ვიპოვოთ ფორმულებით

ვექტორის მიმართულების კოსინუსები ასევე არის ვექტორის ვექტორის კოორდინატები და, შესაბამისად, ვექტორის ვექტორის

.

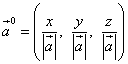
იმის გათვალისწინებით, რომ ვექტორული ვექტორის სიგრძე უდრის ერთ ერთეულს, ანუ

,

მივიღებთ შემდეგ ტოლობას მიმართულების კოსინუსებისთვის:

მაგალითი 7იპოვეთ ვექტორის სიგრძე x = (3; 0; 4).

გადაწყვეტილება. ვექტორის სიგრძეა

მაგალითი 8მოცემული ქულები:

გაარკვიეთ არის თუ არა ამ წერტილებზე აგებული სამკუთხედი ტოლფერდა.

გადაწყვეტილება. ვექტორული სიგრძის ფორმულის (6) გამოყენებით ვიპოვით გვერდების სიგრძეებს და გავარკვიეთ, არის თუ არა ტოლი ორი მათგანი:

ნაპოვნია ორი თანაბარი გვერდი, ამიტომ არ არის საჭირო მესამე გვერდის სიგრძის ძებნა და მოცემული სამკუთხედი არის ტოლფერდა.

მაგალითი 9იპოვეთ ვექტორის სიგრძე და მისი მიმართულების კოსინუსები თუ .

გადაწყვეტილება. ვექტორული კოორდინატები მოცემულია:

.

ვექტორის სიგრძე უდრის ვექტორის კოორდინატების კვადრატების ჯამის კვადრატულ ფესვს:

.

მიმართულების კოსინუსების პოვნა:

თავად გადაწყვიტეთ პრობლემა ვექტორებზე და შემდეგ გადახედეთ გამოსავალს

მოქმედებები ვექტორებზე მოცემული კოორდინატების სახით

ორი ვექტორი და მოცემული იყოს მათი პროგნოზებით:

მოდით მივუთითოთ მოქმედებები ამ ვექტორებზე.

გვერდი 1 2-დან

Კითხვა 1.რა არის ვექტორი? როგორ განისაზღვრება ვექტორები?
უპასუხე.მიმართულ სეგმენტს ვექტორს დავარქმევთ (სურ. 211). ვექტორის მიმართულება განისაზღვრება მისი დასაწყისისა და დასასრულის მითითებით. ნახატზე ვექტორის მიმართულება აღინიშნება ისრით. ვექტორების აღსანიშნავად, ჩვენ გამოვიყენებთ პატარა ლათინურ ასოებს a, b, c, ... . თქვენ ასევე შეგიძლიათ დანიშნოთ ვექტორი მისი დასაწყისისა და დასასრულის მითითებით. ამ შემთხვევაში პირველ რიგში ვექტორის დასაწყისი მოთავსებულია. სიტყვის "ვექტორის" ნაცვლად, ისარი ან ტირე ზოგჯერ მოთავსებულია ვექტორის ასოების აღნიშვნის ზემოთ. ვექტორი 211-ზე შეიძლება აღვნიშნოთ შემდეგნაირად:

\(\overline(a)\), \(\overrightarrow(a)\) ან \(\overline(AB)\), \(\overrightarrow(AB)\).

კითხვა 2.რომელ ვექტორებს ეწოდება თანაბრად მიმართული (საპირისპიროდ მიმართული)?
უპასუხე.ვექტორები \(\overline(AB)\) და \(\overline(CD)\) ამბობენ, რომ თანაბრად მიმართულია, თუ ნახევარხაზები AB და CD თანაბრად არის მიმართული.
ვექტორებს \(\overline(AB)\) და \(\overline(CD)\) უწოდებენ საპირისპიროდ მიმართულებს, თუ ნახევარხაზები AB და CD საპირისპიროა მიმართული.
ნახაზზე 212, ვექტორებს \(\overline(a)\) და \(\overline(b)\) აქვთ იგივე მიმართულება, ხოლო ვექტორებს \(\overline(a)\) და \(\overline(c) \) აქვს საპირისპირო მიმართულებები.

კითხვა 3.რა არის ვექტორის აბსოლუტური მნიშვნელობა?
უპასუხე.ვექტორის აბსოლუტური მნიშვნელობა (ან მოდული) არის ვექტორის გამომსახველი სეგმენტის სიგრძე. \(\overline(a)\) ვექტორის აბსოლუტური მნიშვნელობა აღინიშნება |\(\overline(a)\)|-ით.

კითხვა 4.რა არის ნულოვანი ვექტორი?
უპასუხე.ვექტორის დასაწყისი შეიძლება ემთხვეოდეს მის დასასრულს. ასეთ ვექტორს დაერქმევა ნულოვანი ვექტორი. ნულოვანი ვექტორი აღინიშნა ნულით ტირეთი (\(\overline(0)\)). ნულოვანი ვექტორის მიმართულებაზე არავინ საუბრობს. ნულოვანი ვექტორის აბსოლუტური მნიშვნელობა ითვლება ნულის ტოლად.

კითხვა 5.რომელ ვექტორებს უწოდებენ ტოლს?
უპასუხე.ნათქვამია, რომ ორი ვექტორი ტოლია, თუ ისინი გაერთიანებულია პარალელური გადაცემით. ეს ნიშნავს, რომ არსებობს პარალელური ტრანსლაცია, რომელიც თარგმნის ერთი ვექტორის დასაწყისს და დასასრულს, შესაბამისად, მეორე ვექტორის დასაწყისსა და დასასრულს.

კითხვა 6.დაამტკიცეთ, რომ ტოლ ვექტორებს აქვთ ერთი და იგივე მიმართულება და ტოლია აბსოლუტური მნიშვნელობით. და პირიქით: თანაბრად მიმართული ვექტორები, რომლებიც ტოლია აბსოლუტური მნიშვნელობით, ტოლია.
უპასუხე.პარალელური ტრანსლაციისას ვექტორი ინარჩუნებს მიმართულებას, ისევე როგორც აბსოლუტურ მნიშვნელობას. ეს ნიშნავს, რომ თანაბარ ვექტორებს აქვთ იგივე მიმართულება და ტოლია აბსოლუტური სიდიდით.
დაე, \(\overline(AB)\) და \(\overline(CD)\) იყოს თანაბრად მიმართული ვექტორები ტოლი აბსოლუტური სიდიდით (ნახ. 213). პარალელური ტრანსლაცია, რომელიც C წერტილიდან A წერტილამდე მიიყვანს, აერთიანებს ნახევრად წრფე CD-ს ნახევრად AB-ს, რადგან ისინი თანაბრად არიან მიმართული. და რადგან AB და CD სეგმენტები ტოლია, მაშინ D წერტილი ემთხვევა B წერტილს, ე.ი. პარალელური ტრანსლაცია თარგმნის ვექტორს \(\overline(CD)\) ვექტორად \(\overline(AB)\). აქედან გამომდინარე, ვექტორები \(\overline(AB)\) და \(\overline(CD)\) ტოლია, როგორც საჭიროა.

კითხვა 7.დაამტკიცეთ, რომ ნებისმიერი წერტილიდან შეიძლება მოცემული ვექტორის ტოლი ვექტორის დახატვა და მხოლოდ ერთი.
უპასუხე.მოდით CD იყოს ხაზი და ვექტორი \(\overline(CD)\) იყოს CD წრფის ნაწილი. მოდით AB იყოს წრფე, რომელშიც მიდის წრფე CD პარალელური გადათარგმნისას, \(\overline(AB)\) იყოს ვექტორი, რომელშიც გადადის ვექტორი \(\overline(CD)\) პარალელური გადათარგმნისას, და აქედან გამომდინარე ვექტორები. \(\ overline(AB)\) და \(\overline(CD)\) ტოლია, ხოლო AB და CD ხაზები პარალელურია (იხ. სურ. 213). როგორც ვიცით, მოცემულ წრფეზე არ მდებარე წერტილის მეშვეობით შესაძლებელია სიბრტყეზე მოცემულის პარალელურად მაქსიმუმ ერთი წრფის დახატვა (პარალელური წრფეების აქსიომა). მაშასადამე, A წერტილის მეშვეობით შეიძლება ერთი წრფის დახატვა CD წრფის პარალელურად. ვინაიდან ვექტორი \(\overline(AB)\) არის AB წრფის ნაწილი, შესაძლებელია A წერტილის გავლით გავავლოთ ერთი ვექტორი \(\overline(AB)\), რომელიც უდრის ვექტორს \(\overline. (CD)\).

კითხვა 8.რა არის ვექტორული კოორდინატები? რა არის ვექტორის აბსოლუტური მნიშვნელობა a 1, a 2 კოორდინატებით?
უპასუხე.მოდით ვექტორი \(\overline(a)\) დაიწყოს A 1 წერტილიდან (x 1 ; y 1) და დასრულდეს A 2 წერტილით (x 2 ; y 2). \(\overline(a)\) ვექტორის კოორდინატები იქნება რიცხვები a 1 = x 2 - x 1 , a 2 = y 2 - y 1 . ვექტორის კოორდინატებს დავდებთ ვექტორის ასოს აღნიშვნის გვერდით, ამ შემთხვევაში \(\overline(a)\) (a 1 ; a 2) ან უბრალოდ \((\overline(a 1 ; a 2 ))\ ). ნულოვანი ვექტორის კოორდინატები ნულის ტოლია.
ორ წერტილს შორის მანძილის გამოხატვის ფორმულიდან გამომდინარეობს, რომ ვექტორის აბსოლუტური მნიშვნელობა a 1, a 2 კოორდინატებით არის \(\sqrt(a^2 1 + a^2 2)\).

კითხვა 9.დაამტკიცეთ, რომ თანაბარ ვექტორებს აქვთ შესაბამისად თანაბარი კოორდინატები, ხოლო ვექტორებს შესაბამისი ტოლი კოორდინატები ტოლია.
უპასუხე.მოდით A 1 (x 1 ; y 1) და A 2 (x 2 ; y 2) იყოს ვექტორის \(\overline(a)\) დასაწყისი და დასასრული. ვინაიდან მის ტოლი \(\overline(a)\) ვექტორი \(\overline(a)\) ვექტორიდან მიიღება პარალელური გადათარგმნით, მაშინ მისი დასაწყისი და დასასრული იქნება შესაბამისად A" 1 (x 1 + c). ; y 1 + d ), A" 2 (x 2 + c; y 2 ​​+ d). ეს აჩვენებს, რომ ორივე ვექტორს \(\overline(a)\) და \(\overline(a")\) აქვთ იგივე კოორდინატები: x 2 - x 1 , y 2 - y 1 .
ახლა დავამტკიცოთ საპირისპირო მტკიცება. \(\overline(A 1 A 2)\) და \(\overline(A" 1 A" 2)\) ვექტორების შესაბამისი კოორდინატები ტოლი იყოს. ვამტკიცებთ, რომ ვექტორები ტოლია.
მოდით x" 1 და y" 1 იყოს A" 1 წერტილის კოორდინატები და x" 2, y" 2 იყოს A" 2 წერტილის კოორდინატები. თეორემის პირობით x 2 - x 1 \u003d x "2 - x" 1, y 2 - y 1 \u003d y "2 - y" 1. აქედან გამომდინარე, x "2 = x 2 + x" 1 - x 1, y" 2 = y 2 + y" 1 - y 1. ფორმულებით მოცემული პარალელური თარგმანი

x" = x + x" 1 - x 1, y" = y + y" 1 - y 1,

გადასცემს A 1 წერტილს A" 1 წერტილს, ხოლო A 2 წერტილს A" 2 წერტილს, ე.ი. ვექტორები \(\overline(A 1 A 2)\) და \(\overline(A" 1 A" 2)\) ტოლია, როგორც საჭიროა.

კითხვა 10.განსაზღვრეთ ვექტორების ჯამი.
უპასუხე.\(\overline(a)\) და \(\overline(b)\) ვექტორების ჯამი a 1 , a 2 და b 1 , b 2 არის ვექტორი \(\overline(c)\) კოორდინატები a 1 + b 1 , a 2 + b a 2 , ე.ი.

\(\overline(a) (a 1 ; a 2) + \overline(b)(b 1 ; b 2) = \overline(c) (a 1 + b 1 ; a 2 + b 2)\).

შექმნის თარიღი: 2009-04-11 15:25:51
ბოლო რედაქტირება: 2012-02-08 09:19:45

დიდი ხნის განმავლობაში არ მინდოდა ამ სტატიის დაწერა - ვფიქრობდი, როგორ წარმომედგინა მასალა. თქვენ ასევე გჭირდებათ სურათების დახატვა. მაგრამ, როგორც ჩანს, დღეს ვარსკვლავები წარმატებით ჩამოყალიბდნენ და იქნება სტატია ვექტორების შესახებ. თუმცა, ეს მხოლოდ პროექტია. სამომავლოდ ამ სტატიას დავყოფ რამდენიმე ცალკეულ ნაწილად - საკმარისი მასალაა. ასევე, სტატია თანდათან გაუმჯობესდება: მასში ცვლილებებს შევიტან – იმიტომ. ერთ სხდომაზე ყველა ასპექტის გამოვლენა შეუძლებელი იქნება.

ვექტორები შეიტანეს მათემატიკაში მეცხრამეტე საუკუნეში იმ რაოდენობების აღსაწერად, რომელთა აღწერა რთული იყო სკალარული მნიშვნელობების გამოყენებით.

ვექტორები ფართოდ გამოიყენება კომპიუტერული თამაშების განვითარებაში. ისინი გამოიყენება არა მხოლოდ ტრადიციულად - ისეთი რაოდენობების აღსაწერად, როგორიცაა ძალა ან სიჩქარე, არამედ ისეთ სფეროებშიც, რომლებსაც თითქოს არაფერი აქვთ საერთო ვექტორებთან: ფერების შენახვა, ჩრდილების შექმნა.

სკალარები და ვექტორები

პირველ რიგში, შეგახსენებთ, რა არის სკალარი და რით განსხვავდება იგი ვექტორისგან.

სკალარული მნიშვნელობები ინახავს გარკვეულ მნიშვნელობას: მასა, მოცულობა. ანუ ეს არის ერთეული, რომელსაც ახასიათებს მხოლოდ ერთი რიცხვი (მაგალითად, რაღაცის ოდენობა).

ვექტორი, განსხვავებით სკალარისაგან, აღწერილია ორი მნიშვნელობის გამოყენებით: სიდიდე და მიმართულება.

მნიშვნელოვანი განსხვავება ვექტორებსა და კოორდინატებს შორის: ვექტორები არ არის მიბმული კონკრეტულ მდებარეობაზე! კიდევ ერთხელ, ვექტორში მთავარია სიგრძე და მიმართულება.

ვექტორი აღინიშნება ლათინური ანბანის თამამი ასოებით. Მაგალითად: ა, ბ, ვ.

პირველ სურათზე ხედავთ, როგორ აღინიშნება ვექტორი სიბრტყეზე.

ვექტორები სივრცეში

სივრცეში ვექტორების გამოხატვა შესაძლებელია კოორდინატების გამოყენებით. მაგრამ ჯერ ერთი კონცეფცია უნდა შემოვიტანოთ:

წერტილის რადიუსის ვექტორი

ავიღოთ რაღაც წერტილი M(2,1) სივრცეში. წერტილის რადიუსის ვექტორი არის ვექტორი, რომელიც იწყება საწყისიდან და მთავრდება წერტილში.

რაც აქ გვაქვს, სხვა არაფერია, თუ არა ვექტორი OM. ვექტორული საწყისი კოორდინატები (0,0), ბოლო კოორდინატები (2,1). ავღნიშნოთ ეს ვექტორი როგორც ა.

ამ შემთხვევაში ვექტორი შეიძლება დაიწეროს შემდეგნაირად ა = <2, 1>. ეს არის ვექტორის კოორდინატთა ფორმა ა.

ვექტორის კოორდინატებს უწოდებენ მის კომპონენტებს ღერძებთან მიმართებაში. მაგალითად, 2 არის ვექტორული კომპონენტი ა x-ღერძის შესახებ.

მოდით კიდევ ერთხელ ვისაუბროთ იმაზე, თუ რა არის წერტილის კოორდინატები. წერტილის კოორდინატი (მაგალითად, x) არის წერტილის პროექცია ღერძზე, ე.ი. წერტილიდან ღერძზე ჩამოშვებული პერპენდიკულარულის ფუძე. ჩვენს მაგალითში 2.

მაგრამ დავუბრუნდეთ პირველ სურათს. აქ გვაქვს ორი წერტილი A და B. წერტილების კოორდინატები იყოს (1,1) და (3,3). ვექტორი ვამ შემთხვევაში ის შეიძლება განისაზღვროს როგორც ვ = <3-1, 3-1>. ვექტორი, რომელიც მდებარეობს სამგანზომილებიან სივრცეში ორ წერტილში, ასე გამოიყურება:

ვ =

არა მგონია აქ რაიმე პრობლემა იყოს.

გავამრავლოთ ვექტორი სკალარზე

ვექტორი შეიძლება გამრავლდეს სკალარული მნიშვნელობებით:

კ ვ = =

ამ შემთხვევაში, სკალარული მნიშვნელობა მრავლდება ვექტორის თითოეულ კომპონენტთან.

თუ k > 1, მაშინ ვექტორი გაიზრდება, თუ k არის ერთზე ნაკლები, მაგრამ ნულზე მეტი, ვექტორი შემცირდება სიგრძეში. თუ k ნულზე ნაკლებია, მაშინ ვექტორი შეიცვლის მიმართულებას.

ერთეული ვექტორები

ერთეული ვექტორები არის ვექტორები, რომელთა სიგრძე ერთის ტოლია. გაითვალისწინეთ, რომ ვექტორი კოორდინატებით<1,1,1>ერთის ტოლი არ იქნება! ვექტორის სიგრძის პოვნა აღწერილია ქვემოთ.

არსებობს ეგრეთ წოდებული ორტები - ეს არის ერთეული ვექტორები, რომლებიც მიმართულებით ემთხვევა კოორდინატთა ღერძებს. მე- x ღერძის ერთეული ვექტორი, ჯ- y ღერძის ერთეული ვექტორი, კ- z ღერძის ერთეული ვექტორი.

სადაც მე = <1,0,0>, ჯ = <0,1,0>, კ = <0,0,1>.

ახლა ჩვენ ვიცით, რა არის ვექტორის გამრავლება სკალარზე და რა არის ერთეული ვექტორები. ახლა შეგვიძლია დავწეროთ ვვექტორული სახით.

ვ= v x მე+vy ჯ+vz კ, სადაც v x, v y, v z არის ვექტორის შესაბამისი კომპონენტები

ვექტორის დამატება

წინა ფორმულის სრულად გასაგებად, თქვენ უნდა გესმოდეთ, თუ როგორ მუშაობს ვექტორის დამატება.

აქ ყველაფერი მარტივია. აიღეთ ორი ვექტორი v1 = და v2 =

v1 + v2 =

ჩვენ უბრალოდ ვამატებთ ორი ვექტორის შესაბამის კომპონენტებს.

სხვაობა გამოითვლება იმავე გზით.

საუბარია მათემატიკურ ფორმაზე. სისრულისთვის, ღირს იმის გათვალისწინება, თუ როგორი იქნება ვექტორების დამატება და გამოკლება გრაფიკულად.

ორი ვექტორის დასამატებლად ა+ბ. ჩვენ უნდა დავამთხვიოთ ვექტორის დასაწყისი ბდა ვექტორის დასასრული ა. შემდეგ, ვექტორის დასაწყისს შორის ადა ვექტორის დასასრული ბდახაზეთ ახალი ვექტორი. სიცხადისთვის იხილეთ მეორე ფიგურა (ასო "ა").

ვექტორების გამოკლებისთვის, თქვენ უნდა დააკავშიროთ ორი ვექტორის დასაწყისი და დახაზოთ ახალი ვექტორი მეორე ვექტორის ბოლოდან პირველის ბოლომდე. მეორე სურათი (ასო "ბ") გვიჩვენებს, როგორ გამოიყურება.

ვექტორის სიგრძე და მიმართულება

ჯერ სიგრძეს გადავხედოთ.

სიგრძე არის ვექტორის რიცხვითი მნიშვნელობა, მიმართულების მიუხედავად.

სიგრძე განისაზღვრება ფორმულით (სამგანზომილებიანი ვექტორისთვის):

ვექტორული კომპონენტების კვადრატების ჯამის კვადრატული ფესვი.

ნაცნობი ფორმულა, არა? ზოგადად, ეს არის სეგმენტის სიგრძის ფორმულა

ვექტორის მიმართულება განისაზღვრება ვექტორსა და კოორდინატთა ღერძებს შორის წარმოქმნილი კუთხეების მიმართულების კოსინუსებით. მიმართულების კოსინუსების საპოვნელად გამოიყენება შესაბამისი კომპონენტები და სიგრძე (სურათი მოგვიანებით იქნება).

ვექტორების წარმოდგენა პროგრამებში

ვექტორები შეიძლება წარმოდგენილი იყოს პროგრამებში სხვადასხვა გზით. როგორც ჩვეულებრივი ცვლადების, რომელიც არაეფექტურია, ასევე მასივების, კლასების და სტრუქტურების დახმარებით.

float vector3 = (1,2,3); // მასივი ვექტორული სტრუქტურის ვექტორის3 შესანახად // სტრუქტურა ვექტორების შესანახად ( float x,y,z; );

ვექტორების შენახვის უდიდეს შესაძლებლობებს იძლევა კლასები. კლასებში ჩვენ შეგვიძლია აღვწეროთ არა მხოლოდ თავად ვექტორი (ცვლადები), არამედ ვექტორული ოპერაციები (ფუნქციები).

ვექტორების წერტილოვანი ნამრავლი

ვექტორული გამრავლების ორი ტიპი არსებობს: ვექტორული და სკალარული.

სკალარული პროდუქტის გამორჩეული თვისება ის არის, რომ შედეგი ყოველთვის იქნება სკალარული მნიშვნელობა, ე.ი. ნომერი.

აქ ღირს ამ მომენტისთვის ყურადღების მიქცევა. თუ ამ ოპერაციის შედეგი არის ნული, მაშინ ორი ვექტორი პერპენდიკულარულია - მათ შორის კუთხე 90 გრადუსია. თუ შედეგი ნულზე მეტია, კუთხე 90 გრადუსზე ნაკლებია. თუ შედეგი ნულზე ნაკლებია, კუთხე 90 გრადუსზე მეტია.

ეს ოპერაცია წარმოდგენილია შემდეგი ფორმულით:

ა · ბ= a x * b x + a y * b y + a z * b z

სკალარული ნამრავლი არის ორი ვექტორის შესაბამისი კომპონენტების ნამრავლების ჯამი. იმათ. ვიღებთ x "s ორი ვექტორიდან, ვამრავლებთ, შემდეგ ვამატებთ y" s-ის ნამრავლს და ა.შ.

ვექტორების ჯვარედინი ნამრავლი

ორი ვექტორის ჯვარედინი ნამრავლის შედეგი იქნება ამ ვექტორების პერპენდიკულარული ვექტორი.

ა x ბ =

ამ ფორმულას ჯერ არ განვიხილავთ დეტალურად. გარდა ამისა, ამის დამახსოვრება საკმაოდ რთულია. ამ საკითხს განმსაზღვრელ ფაქტორების გაცნობის შემდეგ დავუბრუნდებით.

ისე, ზოგადი განვითარებისთვის სასარგებლოა ვიცოდეთ, რომ მიღებული ვექტორის სიგრძე უდრის ვექტორებზე აგებული პარალელოგრამის ფართობს. ადა ბ.

ვექტორის ნორმალიზაცია

ნორმალიზებული ვექტორი არის ვექტორი, რომლის სიგრძე ერთია.

ნორმალიზებული ვექტორის პოვნის ფორმულა შემდეგია - ვექტორის ყველა კომპონენტი უნდა დაიყოს სიგრძით:

ვ n= ვ/|ვ| =

შემდგომი სიტყვა

როგორც მოგეხსენებათ, ვექტორები არ არის რთული გასაგები. ჩვენ განვიხილეთ რამდენიმე ოპერაცია ვექტორებზე.

„მათემატიკა“ განყოფილების შემდეგ სტატიებში განვიხილავთ მატრიცებს, დეტერმინანტებს, წრფივი განტოლებათა სისტემებს. ეს ყველაფერი თეორიაა.

ამის შემდეგ ჩვენ გადავხედავთ მატრიცის გარდაქმნებს. სწორედ მაშინ მიხვდებით, თუ რამდენად მნიშვნელოვანია მათემატიკა კომპიუტერული თამაშების შექმნაში. ეს თემა უბრალოდ პრაქტიკა გახდება ყველა წინა თემისთვის.

ვექტორები. მოქმედებებიზემოთვექტორები. ᲡᲙᲐᲚᲐᲠᲣᲚᲘ,

ვექტორი, ვექტორების შერეული პროდუქტი.

1. ვექტორები, მოქმედებები ვექტორებზე.

ძირითადი განმარტებები.

განმარტება 1.სიდიდეს, რომელიც სრულად ხასიათდება მისი რიცხვითი მნიშვნელობით არჩეულ ერთეულთა სისტემაში, ეწოდება სკალარულიან სკალარული .

(სხეულის წონა, მოცულობა, დრო და ა.შ.)

განმარტება 2.რაოდენობას, რომელსაც ახასიათებს რიცხვითი მნიშვნელობა და მიმართულება, ეწოდება ვექტორი ან ვექტორი .

(გადაადგილება, ძალა, სიჩქარე და ა.შ.)

აღნიშვნები: , ან , .

გეომეტრიული ვექტორი არის მიმართული სეგმენტი.

ვექტორისთვის - წერტილი მაგრამ- საწყისი წერტილი ATარის ვექტორის დასასრული.

განმარტება 3.მოდული ვექტორი არის AB სეგმენტის სიგრძე.

განმარტება 4.ვექტორს, რომლის მოდულიც არის ნული, ეწოდება ნული , მითითებულია.

განმარტება 5.პარალელურ ხაზებზე ან იმავე წრფეზე მდებარე ვექტორებს უწოდებენ კოლინარული . თუ ორ კოლინარულ ვექტორს აქვს ერთი და იგივე მიმართულება, მაშინ მათ უწოდებენ თანამიმართული .

განმარტება 6.განიხილება ორი ვექტორი თანაბარი , თუ ისინი თანარეჟისორი და ტოლია მოდულით.

მოქმედებები ვექტორებზე.

1) ვექტორების დამატება.

დეფ. 6.ჯამი ორი ვექტორი და არის ამ ვექტორებზე აგებული პარალელოგრამის დიაგონალი, რომელიც მოდის მათი გამოყენების საერთო წერტილიდან (პარალელოგრამის წესი).

ნახ.1.

დეფ. 7.სამი ვექტორის ჯამი არის ამ ვექტორებზე აგებული პარალელეპიპედის დიაგონალი (პარალელეპიპედის წესი).

დეფ. რვა.Თუ მაგრამ, AT, თან არის თვითნებური წერტილები, შემდეგ + = (სამკუთხედის წესი).

ნახ.2

დანამატის თვისებები.

1 შესახებ . + = + (გადაადგილების კანონი).

2 შესახებ . + ( + ) = ( + ) + = ( + ) + (ასოციაციური კანონი).

3 შესახებ . + (– ) + .

2) ვექტორების გამოკლება.

დეფ. ცხრა.ქვეშ განსხვავება ვექტორები და ვექტორის გაგება = -ისეთი რომ + = .

პარალელოგრამში ეს სხვაა დიაგონალი SD (იხ. ნახ. 1).

3) ვექტორის გამრავლება რიცხვზე.

დეფ. ათი. მუშაობა ვექტორი სკალარამდე კ ვექტორი ეწოდება

= კ = კ ,

გრძელი კა , და მიმართულება, რომელიც:

1. ემთხვევა ვექტორის მიმართულებას თუ კ > 0;

2. ვექტორის მიმართულების საპირისპირო თუ კ < 0;

3. თვითნებურად თუ კ = 0.

ვექტორის რიცხვზე გამრავლების თვისებები.

1 შესახებ . (კ + ლ ) = კ + ლ .

კ ( + ) = კ + კ .

2 ო . კ (ლ ) = (კლ ) .

3 ო . 1  = , (–1)  = – , 0  = .

ვექტორული თვისებები.

დეფ. თერთმეტი.ორი ვექტორი და ე.წ კოლინარული თუ ისინი მდებარეობს პარალელური ხაზებიან ზე ერთი სწორი ხაზი.

ნულოვანი ვექტორი კოლინარულია ნებისმიერი ვექტორის მიმართ.

თეორემა 1.ორი არანულოვანი ვექტორი და კოლინარული,  როცა ისინი პროპორციულია ე.ი.

= კ , კ - სკალარული.

დეფ. 12.სამი ვექტორი , , ეწოდება თანაპლენარული თუ ისინი პარალელურად არიან რომელიმე სიბრტყის ან დევს მასში.

თეორემა 2.სამი არანულოვანი ვექტორი, თანაპლენარული,  როცა ერთი მათგანი არის დანარჩენი ორის წრფივი კომბინაცია, ე.ი.

= კ + ლ , კ , ლ - სკალარები.

ვექტორის პროექცია ღერძზე.

თეორემა 3.ვექტორის პროექცია ღერძზე (მიმართული ხაზი) ლუდრის ვექტორის მიმართულებასა და ღერძის მიმართულებას შორის კუთხის სიგრძისა და კოსინუსის ნამრავლს, ე.ი. = ა  გ os  ,  = ( , ლ).

2. ვექტორული კოორდინატები

დეფ. ცამეტი.ვექტორული პროგნოზები კოორდინატთა ღერძებზე ოჰ, OU, ოზიდაურეკა ვექტორული კოორდინატები. აღნიშვნა:  ა x , ა წ , ა ზ .

ვექტორის სიგრძე:

მაგალითი:გამოთვალეთ ვექტორის სიგრძე.

გადაწყვეტილება:

მანძილი წერტილებს შორის და გამოითვლება ფორმულით: .

მაგალითი:იპოვეთ მანძილი M (2,3,-1) და K (4,5,2) წერტილებს შორის.

მოქმედებები ვექტორებზე კოორდინატულ ფორმაში.

მოცემული ვექტორები = ა x , ა წ , ა ზ და = ბ x , ბ წ , ბ ზ .

1. (  )= ა x  ბ x , ა წ  ბ წ , ა ზ  ბ ზ .

2.  =   ა x ,  ა წ ,  ა ზ, სად  - სკალარული.

ვექტორების სკალარული ნამრავლი.

განმარტება:ორი ვექტორის სკალარული ნამრავლის ქვეშ და

გაგებულია, როგორც რიცხვი, რომელიც ტოლია ამ ვექტორების სიგრძისა და მათ შორის კუთხის კოსინუსების ნამრავლის, ე.ი. = , - კუთხე ვექტორებს შორის და .

წერტილოვანი პროდუქტის თვისებები:

1.  =

2. ( + ) =

3.

4.

5. , სად არის სკალარები.

6. ორი ვექტორი პერპენდიკულარულია (ორთოგონალური), თუ .

7. თუ და მხოლოდ თუ .

სკალარული პროდუქტი კოორდინატულ ფორმაში აქვს ფორმა: , სად და .

მაგალითი:იპოვეთ ვექტორების სკალარული ნამრავლი და

გადაწყვეტილება:

ვექტორების დამჭერი ვექტორები.

განმარტება: ორი ვექტორის ვექტორული ნამრავლი და გაგებულია, როგორც ვექტორი, რომლისთვისაც:

მოდული ტოლია ამ ვექტორებზე აგებული პარალელოგრამის ფართობის, ე.ი. , სად არის კუთხე ვექტორებს შორის და

ეს ვექტორი პერპენდიკულარულია გამრავლებულ ვექტორებზე, ე.ი.

თუ ვექტორები არასწორხაზოვანია, მაშინ ისინი ქმნიან ვექტორთა მარჯვენა სამეულს.

ჯვარედინი პროდუქტის თვისებები:

1. როდესაც იცვლება ფაქტორების თანმიმდევრობა, ვექტორული ნამრავლი ცვლის თავის ნიშანს საპირისპიროდ, ინარჩუნებს მოდულს, ე.ი.

2 .ვექტორული კვადრატი უდრის ნულოვან ვექტორს, ე.ი.

3 .სკალარული ფაქტორი შეიძლება ამოღებულ იქნას ვექტორული ნამრავლის ნიშნიდან, ე.ი.

4 .ნებისმიერი სამი ვექტორისთვის ტოლობა

5 .აუცილებელი და საკმარისი პირობა ორი ვექტორის კოლინარობისთვის და :

ვექტორული პროდუქტი კოორდინატთა ფორმით.

თუ ვექტორების კოორდინატები და , მაშინ მათი ვექტორული ნამრავლი გვხვდება ფორმულით:

.

შემდეგ ჯვარედინი პროდუქტის განმარტებიდან გამომდინარეობს, რომ პარალელოგრამის ფართობი აგებულია ვექტორებზე და გამოითვლება ფორმულით:

მაგალითი:გამოთვალეთ სამკუთხედის ფართობი წვეროებით (1;-1;2), (5;-6;2), (1;3;-1).

გადაწყვეტილება: .

შემდეგ სამკუთხედის ABC ფართობი გამოითვლება შემდეგნაირად:

,

ვექტორების შერეული პროდუქტი.

განმარტება:ვექტორების შერეული (ვექტორულ-სკალარული) ნამრავლი არის რიცხვი, რომელიც განისაზღვრება ფორმულით: .

შერეული პროდუქტის თვისებები:

1. შერეული პროდუქტი არ იცვლება მისი ფაქტორების ციკლური პერმუტაციით, ე.ი. .

2. როდესაც ორი მეზობელი ფაქტორი ერთმანეთს ენაცვლება, შერეული პროდუქტი ცვლის თავის ნიშანს საპირისპიროდ, ე.ი. .

3 .აუცილებელი და საკმარისი პირობა სამი ვექტორის თანაპლანსური იყოს : =0.

4 .სამი ვექტორის შერეული ნამრავლი უდრის ამ ვექტორებზე აგებული პარალელეპიპედის მოცულობას, აღებული პლუსის ნიშნით, თუ ეს ვექტორები ქმნიან მარჯვენა სამეულს და მინუს ნიშნით, თუ ქმნიან მარცხენა სამეულს, ე.ი. .

თუ ცნობილია კოორდინატებივექტორები , შემდეგ შერეული პროდუქტი გვხვდება ფორმულით:

მაგალითი:გამოთვალეთ ვექტორების შერეული ნამრავლი.

გადაწყვეტილება:

3. ვექტორთა სისტემის საფუძველი.

განმარტება.ვექტორთა სისტემა გაგებულია, როგორც რამდენიმე ვექტორი, რომელიც მიეკუთვნება იმავე სივრცეს რ.

კომენტარი.თუ სისტემა შედგება ვექტორების სასრული რაოდენობისგან, მაშინ ისინი აღინიშნება ერთი და იგივე ასოებით სხვადასხვა ინდექსებით.

მაგალითი.

განმარტება. ფორმის ნებისმიერი ვექტორი = ეწოდება ვექტორთა წრფივი კომბინაცია. რიცხვები არის წრფივი კომბინაციის კოეფიციენტები.

მაგალითი. .

განმარტება. თუ ვექტორი არის ვექტორების წრფივი კომბინაცია , მაშინ ვამბობთ, რომ ვექტორი წრფივად არის გამოხატული ვექტორების მიხედვით .

განმარტება.ვექტორთა სისტემა ე.წ წრფივი დამოუკიდებელი, თუ სისტემის არცერთი ვექტორი არ შეიძლება იყოს დანარჩენი ვექტორების წრფივი კომბინაცია. წინააღმდეგ შემთხვევაში, სისტემას ეწოდება წრფივი დამოკიდებული.

მაგალითი. ვექტორული სისტემა წრფივად დამოკიდებული, რადგან ვექტორი .

საბაზისო განმარტება.ვექტორთა სისტემა ქმნის საფუძველს, თუ:

1) ის არის ხაზოვანი დამოუკიდებელი,

2) მასში არსებული სივრცის ნებისმიერი ვექტორი წრფივად არის გამოხატული.

მაგალითი 1სივრცის საფუძველი: .

2. ვექტორთა სისტემაში ვექტორები არის საფუძველი: , იმიტომ წრფივად გამოხატული ვექტორებით.

კომენტარი.ვექტორების მოცემული სისტემის საფუძვლის მოსაძებნად საჭიროა:

1) ჩაწერეთ ვექტორების კოორდინატები მატრიცაში,

2) ელემენტარული გარდაქმნების გამოყენებით, მიიტანეთ მატრიცა სამკუთხა ფორმამდე,

3) მატრიცის არანულოვანი რიგები იქნება სისტემის საფუძველი,

4) ვექტორების რაოდენობა საფუძველში უდრის მატრიცის რანგს.

განმარტება

ვექტორი(ლათინურიდან. ვექტორი"-" ტარება") - სწორი ხაზის მიმართული სეგმენტი სივრცეში ან სიბრტყეზე.

გრაფიკულად, ვექტორი გამოსახულია, როგორც გარკვეული სიგრძის მიმართული სწორი ხაზის სეგმენტი. ვექტორი, რომლის დასაწყისი არის წერტილში და დასასრული წერტილში, აღინიშნება როგორც (ნახ. 1). ასევე, ვექტორი შეიძლება აღინიშნოს ერთი პატარა ასოთი, მაგალითად, .

თუ სივრცეში მოცემულია კოორდინატთა სისტემა, მაშინ ვექტორი შეიძლება ცალსახად იყოს მითითებული მისი კოორდინატების სიმრავლით. ანუ ვექტორი გაგებულია, როგორც ობიექტი, რომელსაც აქვს მნიშვნელობა (სიგრძე), მიმართულება და გამოყენების წერტილი (ვექტორის დასაწყისი).

ვექტორული გამოთვლების დასაწყისი გამოჩნდა 1831 წელს გერმანელი მათემატიკოსის, მექანიკოსის, ფიზიკოსის, ასტრონომისა და ამზომველის იოჰან კარლ ფრიდრიხ გაუსის (1777-1855) ნაშრომებში. ვექტორებთან ოპერაციებზე ნაშრომები გამოაქვეყნა ირლანდიელმა მათემატიკოსმა, მექანიკოსმა და თეორიულმა ფიზიკოსმა, სერ უილიამ როუან ჰამილტონმა (1805-1865), როგორც მისი კვატერნიონის გაანგარიშების ნაწილი. მეცნიერმა შემოგვთავაზა ტერმინი „ვექტორი“ და აღწერს რამდენიმე ოპერაცია ვექტორებზე. ვექტორული გაანგარიშება შემდგომში განვითარდა ბრიტანელი ფიზიკოსის, მათემატიკოსისა და მექანიკოსის ჯეიმს კლერკ მაქსველის (1831-1879) ელექტრომაგნიტიზმზე მუშაობის წყალობით. 1880-იან წლებში გამოიცა ამერიკელი ფიზიკოსის, ფიზიკოქიმიკოსის, მათემატიკოსისა და მექანიკოსის ჯოსია უილარდ გიბსის (1839-1903) წიგნი "ვექტორული ანალიზის ელემენტები". თანამედროვე ვექტორული ანალიზი 1903 წელს აღწერა ინგლისელმა თვითნასწავლმა მეცნიერმა, ინჟინერმა, მათემატიკოსმა და ფიზიკოსმა ოლივერ ჰევისაიდმა (1850-1925).

განმარტება

სიგრძეან ვექტორული მოდულიარის მიმართული სეგმენტის სიგრძე, რომელიც განსაზღვრავს ვექტორს. დანიშნულია როგორც.

ვექტორების ძირითადი ტიპები

ნულოვანი ვექტორიეწოდება ვექტორს, რომლის საწყისი და დასასრული წერტილი ერთნაირია. ნულოვანი ვექტორის სიგრძე არის ნული.

ვექტორებს, რომლებიც პარალელურად არიან იმავე წრფეზე ან დევს იმავე წრფეზე, ეწოდება კოლინარული(ნახ. 2).

თანამიმართულითუ მათი მიმართულებები იგივეა.

სურათზე 2, ეს არის ვექტორები და . ვექტორების თანამიმართულება აღინიშნება შემდეგნაირად: .

ორ ხაზოვანი ვექტორი ეწოდება საპირისპირო მიმართულებებითუ მათი მიმართულებები საპირისპიროა.

ფიგურაში 3, ეს არის ვექტორები და . Დანიშნულება: .