អនុញ្ញាតឱ្យ zq - ចំណុចឯកវចនៈនៃអនុគមន៍ f(z), t.s. f(z)ប៉ុន្តែគឺជាការវិភាគនៅចំណុចនេះ (ជាពិសេស, អាចនឹងមិនត្រូវបានកំណត់នៅវា). ប្រសិនបើមានសង្កាត់ដែលត្រូវបានគេវាយដំបែបនេះ zq (ឧ. សំណុំ O z - zq f(z) គឺជាពាក្យចម្លែក ហ្សូហៅ ចំណុចឯកវចនៈដាច់ដោយឡែកមុខងារ f(z)និយមន័យនេះក៏ត្រូវបានរក្សាទុកនៅក្នុងករណីនេះ។ zn = oo ប្រសិនបើអ៊ីយ៉ូតគឺជាសង្កាត់ដែលវាយលុកនៃចំនុចមួយ។ zq = oo យល់ពីសំណុំ z >ខ្ញុំ - រូបរាងនៃរង្វង់មួយចំនួនដែលផ្តោតលើប្រភពដើម។ និយាយម្យ៉ាងទៀតចំណុចឯកវចនៈ zq ត្រូវបានគេនិយាយថាដាច់ដោយឡែកប្រសិនបើមានសង្កាត់នៃចំណុចនេះដែលមាន ist ចំណុចឯកវចនៈផ្សេងទៀតខុសពី zq គ្រប់ទីកន្លែងខាងក្រោម យើងពិចារណាតែចំណុចឯកវចនៈនៃតួអក្សរតម្លៃតែមួយ (មុខងារ f(z)សន្មតថាមានតែមួយគត់) ។
អាស្រ័យលើឥរិយាបថនៃមុខងារ f(z)នៅ z -> zqមានបីប្រភេទនៃចំណុចឯកវចនៈ។ ចំណុចឯកវចនៈដាច់ដោយឡែក មុខងារ zq f(z)ហៅថា៖
1) ចំណុចឯកវចនៈដែលអាចដកចេញបាន។ប្រសិនបើមានដែនកំណត់កំណត់
2) បង្គោលប្រសិនបើមានដែនកំណត់ 
3) ចំណុចសំខាន់,ប្រសិនបើ f(z) មិនមានដែនកំណត់ ឬដែនកំណត់គ្មានកំណត់សម្រាប់ z-> zq ។
ឧទាហរណ៍ 26.1 ។ ចូរយើងបង្ហាញថាចំនុចឯកវចនៈទាំងបីប្រភេទត្រូវបានដឹង។ ពិចារណា f(z)= ចំណុច zq = 0 គឺដាច់ឆ្ងាយ
ចំណុចឯកវចនៈនៃមុខងារនេះ។ ដោយប្រើរូបមន្ត (22.12) យើងទទួលបានការពង្រីក
ពីវាបន្ទាប់មកថាមាន lim fi(z)= 1. ដូច្នេះ zq = 0 គឺ
គឺជាចំណុចឯកវចនៈដែលអាចដកចេញបាននៃមុខងារ fi(z)
មុខងារ f'j(z) =--- មានបង្គោលនៅចំណុចមួយ។ ហ្សូ= 1 ព្រោះ
2 r“X
ឥឡូវពិចារណាមុខងារ )z(z)= e 1 ^ r ហើយបង្ហាញថា ហ្សូ = O គឺជាចំណុចឯកវចនៈដ៏សំខាន់នៃមុខងារនេះ។ ពេលខំប្រឹង zដល់សូន្យតាមអ័ក្សពិត ដែនកំណត់ខាងឆ្វេង និងស្តាំនៃអនុគមន៍ f (z)ខុសគ្នា៖ lim ជាមួយ 1 / 1 = 0, លីម ជាមួយ 1 /* = os. នេះបញ្ជាក់ថា
x->0-0 x->0+O
អ្វី f:i(z)មិនមានដែនកំណត់ ឬដែនកំណត់គ្មានកំណត់សម្រាប់ 2 ->
អូ, i.e. zq = 0 គឺជាចំណុចឯកវចនៈដ៏សំខាន់នៃអនុគមន៍នេះ។ (ចំណាំថាចំណុចនេះមាននិន្នាការ z-iyទៅសូន្យនៅលើអនុគមន៍អ័ក្សស្រមៃ 
គ្មានដែនកំណត់អ្វីទាំងអស់។ )
ជាការពិតណាស់ ក៏មានចំណុចឯកវចនៈដែលមិនដាច់ពីគ្នាផងដែរ។ ឧទាហរណ៍។ មុខងារមានបង្គោលនៅចំណុច z n = -, ទំ= ±1, ±2,...
អាស្រ័យហេតុនេះ Zq = 0 គឺជាចំណុចឯកវចនៈដែលមិនដាច់ពីគ្នានៃអនុគមន៍នេះ៖ នៅក្នុងសង្កាត់ណាមួយ (តូចតាមអំពើចិត្ត) នៃចំណុចនេះមានចំណុចឯកវចនៈផ្សេងទៀត g ទំ។
អនុញ្ញាតឱ្យ ហ្សូ-ចំណុចឯកវចនៈដាច់ដោយឡែកចុងក្រោយនៃអនុគមន៍ f(z)បន្ទាប់មក f(z)គឺស្រដៀងគ្នានៅក្នុងសង្កាត់មួយចំនួន 0 Zo នៃចំណុច ហ្សូសង្កាត់នេះអាចចាត់ទុកថាជារង្វង់ដែលមានកាំខាងក្នុង r = 0។ តាមទ្រឹស្តីបទ 25.1 នៅក្នុងសង្កាត់ដែលកំពុងពិចារណា មុខងារ f(z)អាចត្រូវបានពង្រីកនៅក្នុងស៊េរី Laurent (25.2) ។ យើងនឹងបង្ហាញថាឥរិយាបថនៃអនុគមន៍សម្រាប់ 2 -> zq (ឧ. ប្រភេទនៃចំណុចឯកវចនៈ ហ្សូ)អាស្រ័យលើទម្រង់នៃផ្នែកសំខាន់នៃការរលួយ (25.2); កាលៈទេសៈនេះពន្យល់ពីប្រភពដើមនៃពាក្យ "ផ្នែកសំខាន់" ។
ទ្រឹស្តីបទ ២G.២. ចំនុចឯកវចនៈឯកវចនៈ zo នៃអនុគមន៍ f(z) គឺអាចដកចេញបាន ប្រសិនបើការពង្រីក Lorap នៅក្នុងសង្កាត់ដែលបែកខ្ញែកនៃចំណុចនេះមាន oid
ទាំងនោះ។ មានតែផ្នែកត្រឹមត្រូវ។, ហើយមេគុណទាំងអស់នៃផ្នែកសំខាន់គឺស្មើនឹងគ្រាប់។
ភស្តុតាង។ 1. អនុញ្ញាតឱ្យ ហ្សូគឺជាចំណុចឯកវចនៈដែលអាចដកចេញបាន។ អនុញ្ញាតឱ្យយើងបង្ហាញថាការពង្រីក Laurent នៃមុខងារ f(z)មានទម្រង់ (26.1) ។ ចាប់តាំងពីចំណុចឯកវចនៈ ហ្សូអាចដកចេញបាន បន្ទាប់មកមានដែនកំណត់កំណត់ f(z) = ក.អាស្រ័យហេតុនេះ f(z)មានព្រំប្រទល់នៅក្នុងសង្កាត់ដែលវាយដំមួយចំនួន 0 z - zq នៃចំណុច ហ្សូទាំងនោះ។ )(z) សម្រាប់ទាំងអស់គ្នា zពីសង្កាត់នេះ។ យកណាមួយ។ រ. U р /?| ហើយប្រើរូបមន្ត (25.3) សម្រាប់មេគុណនៃស៊េរី Laurent៖
សម្រាប់មេគុណនៃផ្នែកសំខាន់នៃការពង្រីក n =- 1,-2, ... សម្រាប់តម្លៃបែបនេះ ទំយើងមាន ទំ ~ n-e 0 នៅ រ-> 0. ចាប់តាំងពីតម្លៃ រអាចត្រូវបានជ្រើសរើសតូចតាមអំពើចិត្ត លោក~"អាចមានទំហំតូចតាមអំពើចិត្ត។ តាំងពី |c t,| ^ លោក ~ នហើយ cn មិនអាស្រ័យលើ p បន្ទាប់មក cn = 0 សម្រាប់ និង= - 1, -2, ... ដែលត្រូវបង្ហាញ។
2. ឥឡូវនេះ ចូរយើងសន្មត់ថា ការពង្រីក Laurent មានទម្រង់ (26.1)។ ស៊េរី (26.1) គឺជាស៊េរីថាមពល និង។ ដូច្នេះហើយវាមិនត្រឹមតែនៅក្នុងការវាយប្រហារប៉ុណ្ណោះទេ ប៉ុន្តែក៏នៅក្នុងសង្កាត់ទាំងមូលដែរ។ z-zq រួមទាំងចំណុច ហ្សូ;ចំនួនទឹកប្រាក់របស់វា។ S(z)គឺជាការវិភាគសម្រាប់ z និង S(z) = )(z)នៅ 0 z - ហ្សូរ.ដូច្នេះមានកម្រិតកំណត់កំណត់ )(z)\u003d Pm 5 (r) \u003d 5 (r) - ដូច្នេះ ចំណុចឯកវចនៈ zq
Z->Zo Z-*Zo
ដែលអាចចោលបាន។ ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។
មតិយោបល់។ វាធ្វើតាមពីភស្តុតាងនៃទ្រឹស្តីបទដែលថានៅក្នុងសង្កាត់ដែលដាល់ 0 z - zo នៃចំណុចឯកវចនៈដែលអាចដកចេញបាន មុខងារ f(z)ស្របគ្នានឹងមុខងារ S(r) ដែលជាការវិភាគនៅក្នុងសង្កាត់ទាំងមូល z - ហ្សូ ដូច្នេះប្រសិនបើយើងដាក់ /(th) = S(zq), បន្ទាប់មកដោយមិនផ្លាស់ប្តូរតម្លៃនៃមុខងារ f(z)នៅចំណុចណាមួយនៃសង្កាត់ដែលត្រូវបានវាយលុក យើងធ្វើការវិភាគមុខងារនេះក្នុង r, i.e. "លុប" មុខងារ។ នេះពន្យល់ពីពាក្យ "ឯកវចនៈដែលអាចដកចេញបាន" ។ វាជារឿងធម្មតាក្នុងការពិចារណាចំណុចបែបនេះជាទៀងទាត់ ហើយមិនមែនជាចំណុចឯកវចនៈនៃមុខងារនោះទេ។ f(z)
ពិចារណាឧទាហរណ៍មុខងារ
ក្នុងឧទាហរណ៍ 26.1 វាត្រូវបានបង្ហាញថា Pm (n) = 1. i.e. ចំណុចឯកវចនៈ
zq = 0 គឺអាចដកចេញបាន។ ការកំណត់ /i(0) = 1 ដោយហេតុនេះ យើងលុបបំបាត់ឯកវចនៈ និងទទួលបានមុខងារដែលវិភាគនៅចំណុច zq = 0 (ហើយនៅក្នុងយន្តហោះទាំងមូល C) ។
ឥឡូវនេះ ចូរយើងកំណត់លក្ខណៈបង្គោលនៅក្នុងលក្ខខណ្ឌនៃការពង្រីក Laurent ។
ទ្រឹស្តីបទ 26.3 ។ ចំណុចឯកវចនៈដាច់ស្រយាល Zo នៃអនុគមន៍ f(z) គឺជាបង្គោលប្រសិនបើ និងបានតែប្រសិនបើ, នៅពេលដែលផ្នែកសំខាន់នៃការពង្រីក Laurent ជាមួយមជ្ឈមណ្ឌល Zq មានតែចំនួនកំណត់ជាក់លាក់ប៉ុណ្ណោះ។
ពីមេគុណសូន្យជាមួយ n៖
ភស្តុតាង។ 1. អនុញ្ញាតឱ្យ zq - បង្គោល, i.e. lim /( z) = អូ។
អនុញ្ញាតឱ្យយើងបង្ហាញថាការពង្រីក Laurent នៃមុខងារ f(z)មានទម្រង់ (2G.2) ។ ចាប់តាំងពីលីម f(z)= អូ។ បន្ទាប់មកមានសង្កាត់មួយដែលត្រូវបានគេវាយចេញពីចំណុចនោះ។
គី zq ត្រង់ណា f(z)គឺវិភាគហើយគ្មានសូន្យ។ បន្ទាប់មកមុខងារ g(z) = 1 /f(z)នឹងត្រូវបានវិភាគផងដែរនៅក្នុងសង្កាត់ punctured នេះ, និង lim g(z)= 0. ដូច្នេះ ហ្សូតើអាចចោលបាន *-? *0
ចំណុចឯកវចនៈនៃមុខងារ g(z)ចូរកំណត់ឡើងវិញ g(z)នៅចំណុច ហ្សូ, ដាក់ g(zo)= 0. បន្ទាប់មក g(z)ក្លាយជាការវិភាគនៅក្នុងសង្កាត់ទាំងមូលនៃចំណុច (មិនវាយដំ) z 0 ,និង z0នឹងជាសូន្យឯកោរបស់វា។ បញ្ជាក់ដោយ នពហុគុណ (លំដាប់) នៃសូន្យនេះ។ ដូចដែលត្រូវបានបង្ហាញនៅក្នុង§23 នៅក្នុងសង្កាត់មួយនៃចំណុច មុខងារ zq g(z)តំណាងក្នុងទម្រង់ (សូមមើល (២៣.២))
និង (z$) ច 0 និង y>(z)ត្រូវបានវិភាគនៅក្នុងសង្កាត់មួយចំនួននៃចំណុច ហ្សូ-ដោយសារតែ ip(z)បន្តនៅចំណុច ហ្សូនិង g>(zo) F 0" បន្ទាប់មក ip(z)មិនមានលេខសូន្យនៅក្នុងសង្កាត់មួយចំនួននៃចំណុចនេះទេ។ ដូច្នេះមុខងារ 1 /-p(z)ក៏នឹងមានការវិភាគនៅក្នុងសង្កាត់នេះផងដែរ ហើយដូច្នេះ ពង្រីកនៅក្នុងវានៅក្នុងស៊េរី Taylor៖
ការបើកតង្កៀប និងការផ្លាស់ប្តូរការរចនានៃមេគុណ យើងសរសេរការពង្រីកចុងក្រោយក្នុងទម្រង់
កន្លែងណា c_jv = 1> o f 0. ដូច្នេះ ផ្នែកសំខាន់នៃការពង្រីក Laurent នៃ f(r) មានតែចំនួនកំណត់នៃលក្ខខណ្ឌប៉ុណ្ណោះ។ យើងបានមកដល់សមភាពដែលត្រូវការ (26.2) ។
2. អនុញ្ញាតឱ្យនៅក្នុងសង្កាត់ punctured នៃចំណុចមួយ។ ទីមុខងារ )(z)ត្រូវបានតំណាងដោយការពង្រីក Laurent (26.2) (ក្នុងទម្រង់ពង្រីកបន្ថែមទៀត សូមមើល (26.3)) ដែលជាផ្នែកសំខាន់ដែលមានតែចំនួនកំណត់នៃលក្ខខណ្ឌ និង ជាមួយ-ឃ" f 0. យើងត្រូវតែបញ្ជាក់ Zq - បង្គោលមុខងារ f(z)គុណសមភាព (26.3) ដោយ (ច - ជី o) iV យើងទទួលបានមុខងារ
ស៊េរីនៅក្នុង (26.4) គឺជាស៊េរីថាមពលដែលបំប្លែងទៅជាមុខងារវិភាគមិនត្រឹមតែនៅក្នុងការវាយលុកប៉ុណ្ណោះទេ ប៉ុន្តែក៏មាននៅក្នុងសង្កាត់ទាំងមូលនៃចំណុចផងដែរ។ Zq ដូច្នេះមុខងារ h(z)ក្លាយជាការវិភាគនៅក្នុងសង្កាត់នេះ ប្រសិនបើយើងពង្រីកវានៅក្នុងទី ដោយការកំណត់ h(zo)= s_dg f 0. បន្ទាប់មក
ដូច្នេះចំនុច o គឺជាបង្គោល ហើយទ្រឹស្តីបទ 26.3 ត្រូវបានបញ្ជាក់។
ពហុគុណ (លំដាប់) នៃអនុគមន៍សូន្យ g(z)= 1//(r) ត្រូវបានហៅ លំដាប់បង្គោលមុខងារ / (r) ។ ប្រសិនបើ ក ន-លំដាប់នៃបង្គោលគឺ th, បន្ទាប់មក g(z)= (r - Zo)N ip(z),និងទៅ) ច 0 ហើយដូចដែលបានបង្ហាញនៅក្នុងផ្នែកដំបូងនៃភស្តុតាងនៃទ្រឹស្តីបទ 26.3 ការពង្រីក f(r) មានទម្រង់ (26.3) ដែល c_/v f 0. ផ្ទុយទៅវិញ ប្រសិនបើ f(r) ពង្រីកទៅក្នុងស៊េរី (26.3) និង e-z F 0 បន្ទាប់មក
t.s. ន-លំដាប់នៃបង្គោលនៃអនុគមន៍ f(r) ។ ដោយវិធីនេះ លំដាប់នៃបង្គោល zq នៃអនុគមន៍/(G) គឺស្មើនឹងចំនួនមេគុណមិនសូន្យឈានមុខគេនៃផ្នែកសំខាន់នៃការពង្រីក Laurent នៅក្នុងសង្កាត់ដែលដាច់នៃចំនុច zq(ឧ. ស្មើនឹងលេខបែបនេះ អិនអ្វីដែល s_dg f 0 និង sp= 0 នៅ ទំ > ន).
អនុញ្ញាតឱ្យយើងបង្ហាញការអះអាងខាងក្រោមដែលងាយស្រួល) សម្រាប់កម្មវិធី។
កូរ៉ូឡារី 26.4 ។ ចំនុច zq គឺជាបង្គោលនៃលំដាប់ N នៃការប្រឌិត/(G) ប្រសិនបើ ហើយប្រសិនបើ/(G) តំណាងក្នុងទម្រង់
ដែល h(z) គឺជាមុខងារវិភាគនៅក្នុងសង្កាត់នៃចំនុចមួយ។ទី និង h(zo) f 0.
ភស្តុតាង។ មុខងារ cp(z) = l/h(z)គឺជាការវិភាគនៅក្នុងសង្កាត់មួយចំនួននៃចំណុច r. លក្ខខណ្ឌនៃកូរ៉ូឡារី 26.4 គឺស្មើនឹងចំណុចដូចខាងក្រោម៖
នោះហើយជាមូលហេតុដែល zq - ពហុគុណសូន្យ នមុខងារ g(z)ដូច្នេះហើយ បង្គោលពហុគុណ នមុខងារ / (2) ។
II ឧទាហរណ៍ 26.5 ។ ស្វែងរកចំណុចឯកវចនៈដាច់ដោយឡែកនៃអនុគមន៍ 
និងកំណត់ប្រភេទរបស់ពួកគេ។
D e u c tio n. ចំនុចដែល (z 2 + 1 )(z+ H) 2 = 0. ប្រសិនបើ z 2 អិល- 1 = 0 បន្ទាប់មក 2 = ±rប្រសិនបើ (z 4- H) 2 = 0 បន្ទាប់មក z= -៣. ដូច្នេះមុខងារមានចំណុចឯកវចនៈបី z= r, 22 = -r, Z3 = - 3. ពិចារណា z:
G -បង្គោលលំដាប់ទីមួយ (យើងប្រើ Corollary 26.4) ។ វាអាចត្រូវបានបញ្ជាក់ស្រដៀងគ្នាថា 22 = -iក៏ជាបង្គោលនៃលំដាប់ទីមួយផងដែរ។ សម្រាប់រយៈពេល 2 ម៉ោងយើងមាន:
ចូរយើងឆ្លងកាត់ការពិចារណាលើចំណុចឯកវចនៈសំខាន់ៗ។
ទ្រឹស្តីបទ 26.6 ។ ចំនុចឯកវចនៈឯកវចនៈ zq នៃអនុគមន៍ f(z) គឺជាឯកវចនៈសំខាន់ ប្រសិនបើផ្នែកសំខាន់នៃការពង្រីក Laurent ដែលស្ថិតនៅចំកណ្តាល zq មានភាពខុសគ្នាជាច្រើនពី។ សូន្យ, មេគុណជាមួយទំ។
ភស្តុតាង។ ទ្រឹស្តីបទ 26.6 ធ្វើតាមដោយផ្ទាល់ពីទ្រឹស្តីបទ 26.2 និង 26.3 ។ ជាការពិតប្រសិនបើចំណុច zq គឺជាឯកវចនៈដ៏សំខាន់ បន្ទាប់មកផ្នែកសំខាន់នៃការពង្រីក Laurent មិនអាចអវត្តមាន ឬមានចំនួនកំណត់នៃពាក្យ (បើមិនដូច្នេះទេ ចំណុច Zq នឹងអាចដកចេញបានឬបង្គោល) ។ ដូច្នេះចំនួនពាក្យនៅក្នុងផ្នែកសំខាន់ត្រូវតែគ្មានកំណត់។
ផ្ទុយទៅវិញ ប្រសិនបើផ្នែកសំខាន់មានសមាជិកច្រើនមិនចេះចប់ Zq មិនអាចជាចំណុចចល័ត ឬបង្គោលទេ។ អាស្រ័យហេតុនេះ ចំណុចនេះមានសារៈសំខាន់ជាឯកវចនៈ។
យោងតាមនិយមន័យ ចំណុចឯកវចនៈសំខាន់ត្រូវបានកំណត់លក្ខណៈដោយការពិតដែលថាមុខងារ f(2) មិនមានកំណត់ ឬដែនកំណត់គ្មានកំណត់សម្រាប់ z ->zq គំនិតពេញលេញបន្ថែមទៀតអំពីរបៀបដែលឥរិយាបថមិនទៀងទាត់នៃមុខងារមួយស្ថិតនៅក្នុងសង្កាត់នៃចំណុចឯកវចនៈសំខាន់មួយត្រូវបានផ្តល់ដោយទ្រឹស្តីបទខាងក្រោម។
ទ្រឹស្តីបទ 26.7 (ទ្រឹស្តីបទ Sochocki) ។ ប្រសិនបើ zq ជាឯកវចនៈសំខាន់ នោះចំនុចនៃអនុគមន៍ f(z), បន្ទាប់មកសម្រាប់លេខស្មុគស្មាញណាមួយ។អិល រួមទាំង A =អូ មានលំដាប់នៃចំណុច z n ដូចថា z n -> zo និងលីម f(zn) = ប៉ុន្តែ
n->os
ភស្តុតាង។ ពិចារណាករណីដំបូង ក =អូ នៅក្នុងផ្នែកដំបូងនៃភស្តុតាងនៃទ្រឹស្តីបទ 2G.2 យើងបានបង្កើតឡើងថាប្រសិនបើ f(z)ត្រូវបានចងនៅក្នុងសង្កាត់មួយចំនួននៃចំណុច r0 បន្ទាប់មកមេគុណទាំងអស់ c, n = - 1, - 2, ... នៃផ្នែកសំខាន់គឺស្មើនឹងសូន្យ (ហើយជាលទ្ធផលឯកវចនៈនៅក្នុង th គឺអាចដកចេញបាន) ។ ដោយសារតាមការសន្មត់ r0 គឺជាចំណុចឯកវចនៈដ៏សំខាន់ មុខងារ f(r) គឺមិនជាប់ព្រំដែននៅក្នុងសង្កាត់ណាមួយនៃចំនុច r0 ។ ចូរយើងយកសង្កាត់តូចចង្អៀតមួយចំនួន 0 Z បែបនោះ។ f(zi) > 1 (ប្រសិនបើ |/(r)| z - zo R/2 មានចំនុចមួយ។ z-2 ដែលជាកន្លែងដែល |/(dd)| > 2, etc.: នៅក្នុងសង្កាត់ចាក់អង្រែលើ O 71. វាច្បាស់ណាស់ថា rn -e ទៅ ហើយ lim /(r«) = oo ។ ដូច្នេះក្នុងករណី A = oo ទ្រឹស្តីបទ 26.7
បញ្ជាក់។
អនុញ្ញាតឱ្យឥឡូវនេះ A fអូ សន្មត់ជាដំបូងថាមានសង្កាត់ 0
= -yy---- នឹងធ្វើការវិភាគនៅក្នុងសង្កាត់ដែលរងការវាយប្រហារនេះ ហើយជាលទ្ធផល
/(G) - ប៉ុន្តែ
ដូច្នេះ r គឺជាចំណុចឯកវចនៈដាច់ស្រយាលនៃអនុគមន៍Φ(r)។ សូមបង្ហាញ។ r0 គឺជាចំណុចឯកវចនៈសំខាន់នៃΦ(r)។ សូមឱ្យវាខុស។ បន្ទាប់មកមានដែនកំណត់ lim Φ(r) មិនថាកំណត់ ឬគ្មានកំណត់។ ដោយសារតែ
/(r) = A + បន្ទាប់មក Hsh /(r) ក៏មានដែរ ដែលផ្ទុយនឹងលក្ខខណ្ឌ
F(g) ~ :-*z 0
ទិដ្ឋភាពនៃទ្រឹស្តីបទ។ ដូច្នេះ r0 គឺជាចំណុចឯកវចនៈសំខាន់នៃអនុគមន៍Φ(r)។ យោងតាមអ្វីដែលបានបង្ហាញខាងលើមានលំដាប់នៃចំណុច r n ដូចជា r n o និង lim Φ(r n) = oo ។ ពីទីនេះ
យើងបានបង្ហាញការអះអាងចាំបាច់ក្រោមការសន្មតថា f(r) F Aនៅក្នុងសង្កាត់មួយចំនួននៃចំណុច r. ចូរយើងសន្មត់ថានេះមិនមែនជាការពិត, i.e. នៅក្នុងសង្កាត់តូចតាចណាមួយដែលវាយលុកតាមអំពើចិត្តនៃចំណុច th មានចំណុចបែបនេះ G",នោះ f(r") = A. បន្ទាប់មកសម្រាប់ណាមួយ។ ទំនៅក្នុងសង្កាត់ដែលវាយដំ 0 f(z u) = L. ដូច្នេះការអះអាងដែលត្រូវការគឺពិត ទំ- យូ
ក្នុងគ្រប់ករណីទាំងអស់ ហើយទ្រឹស្តីបទ 26.7 ត្រូវបានបញ្ជាក់។
យោងតាមទ្រឹស្តីបទ 26.7 របស់ Sokhotsky នៅក្នុងសង្កាត់ណាមួយ (តូចតាមអំពើចិត្ត) វាយលុកសង្កាត់នៃចំណុចឯកវចនៈសំខាន់ មុខងារ f(r) យកតម្លៃតាមអំពើចិត្តទៅនឹងចំនួនណាមួយនៅក្នុងយន្តហោះស្មុគស្មាញ C ។
ដើម្បីសិក្សាចំណុចឯកវចនៈដាច់ស្រយាល ការពង្រីក Taylor ដ៏ល្បីនៃមុខងារបឋមជាមូលដ្ឋាន ជាញឹកញាប់មានប្រយោជន៍។
ឧទាហរណ៍ 2G.8. កំណត់ប្រភេទនៃចំណុចឯកវចនៈ zq = 0 សម្រាប់អនុគមន៍
ដោះស្រាយ និង e. យើងពង្រីកភាគយក និងភាគបែងនៅក្នុងស៊េរី Taylor ក្នុងអំណាចនៃ r. ជំនួសទៅក្នុង (22.11) 3 zជំនួសឱ្យ r និងដក 1 យើងទទួលបាន
ដោយប្រើ (22.12) យើងទទួលបានការពង្រីកនៃភាគបែង៖
ស៊េរីនៅក្នុងការពង្រីកទាំងនេះបញ្ចូលគ្នានៅក្នុងយន្តហោះស្មុគស្មាញទាំងមូល€។ យើងមាន
និង /2(2) គឺស្រដៀងគ្នានៅក្នុងសង្កាត់នៃចំណុច ហ្សូ = 0 (និងសូម្បីតែនៅក្នុងយន្តហោះទាំងមូល) និង /2(20) ច 0 បន្ទាប់មក h(z)ក៏មានការវិភាគផងដែរនៅក្នុងសង្កាត់មួយចំនួននៃចំណុច gF 0។ យោងតាម កូរ៉ូឡារី 26.4 ចំណុច ហ្សូ = 0 គឺជាបង្គោលនៃលំដាប់ N = ៤.
II ឧទាហរណ៍ 26.9 ។ ស្វែងរកចំណុចឯកវចនៈនៃអនុគមន៍ f(z)= sin j - និងកំណត់ប្រភេទរបស់ពួកគេ។
P e ក្នុង e និង e. អនុគមន៍មានចំនុចឯកវចនៈចុងក្រោយតែមួយ zq = 1. នៅចំណុចផ្សេងទៀតពី C, អនុគមន៍ w =--- ការវិភាគ; ដូច្នេះមុខងារនៃអំពើបាប វនឹងមានការវិភាគ។
ការជំនួសនៅក្នុងការពង្រីកស៊ីនុស (22.12) - ជំនួសឱ្យ r យើងទទួលបាន
យើងបានទទួលការពង្រីកមុខងារអំពើបាបនៅក្នុងស៊េរី Laurent នៅក្នុងសង្កាត់ដែលត្រូវបានវាយដំនៃចំនុច 20 = 1។ ចាប់តាំងពីការពង្រីកលទ្ធផលមានពាក្យជាច្រើនគ្មានកំណត់ជាមួយនឹងអំណាចអវិជ្ជមាន (r - 1) បន្ទាប់មក zq = 1 គឺជាចំណុចឯកវចនៈដ៏សំខាន់ (ក្នុងករណីនេះការពង្រីក Laurent មានផ្នែកសំខាន់ប៉ុណ្ណោះ ហើយផ្នែកត្រឹមត្រូវគឺអវត្តមាន)។
ចំណាំថាក្នុងករណីនេះ វាក៏អាចបង្កើតលក្ខណៈនៃឯកវចនៈដោយផ្ទាល់ពីនិយមន័យ ដោយមិនចាំបាច់ងាកទៅរកការពង្រីកស៊េរី។ ជាការពិតមានលំដាប់ (r") និង (2") មកបញ្ចូលគ្នា ហ្សូ= 1 ហើយដូច្នេះ f(z"n)= 1, / (2") = 0 (បញ្ជាក់លំដាប់បែបនេះដោយខ្លួនឯង) ដូច្នេះ, f(z)គ្មានដែនកំណត់នៅពេលណា z -> 1 ហើយដូច្នេះចំណុច zq - 1 ជាឯកវចនៈសំខាន់។
ចូរយើងណែនាំអំពីគំនិតនៃការពង្រីក Laurent នៃមុខងារនៅក្នុងសង្កាត់នៃចំណុចមួយ។ Zq = 00 ហើយពិចារណាពីការតភ្ជាប់រវាងការពង្រីកនិងលក្ខណៈនៃឯកវចនៈនៅចំណុចនេះ។ ចំណាំថានិយមន័យនៃចំណុចឯកវចនៈដាច់ស្រយាល និងប្រភេទរបស់វា (អាចដកចេញបាន បង្គោល ឬជាឯកវចនៈសំខាន់) អនុវត្តទៅលើករណី zq = oc មិនផ្លាស់ប្តូរ។ ប៉ុន្តែទ្រឹស្តីបទ 26.2 ។ 26.3 និង 26.6 ដែលទាក់ទងនឹងធម្មជាតិនៃការពង្រីក Laurent ចាំបាច់ត្រូវផ្លាស់ប្តូរ។ ចំណុចសំខាន់គឺសមាជិក c n (z - 2o) ទំ។ ទំ= -1,-2,..., ផ្នែកសំខាន់, កំណត់ "ភាពមិនទៀងទាត់" នៃមុខងារនៅជិតចំណុចបញ្ចប់ Zq ដូចដែល 2 ទំនោរទៅ oo ពួកគេនឹងប្រព្រឹត្ត "ត្រឹមត្រូវ" (ទំនោរទៅ 0) ។ ផ្ទុយទៅវិញសមាជិកនៃផ្នែកធម្មតាជាមួយ ទំ= 1,2, ... នឹងមានទំនោរទៅ oo; ពួកគេកំណត់លក្ខណៈនៃឯកវចនៈនៅក្នុង Zq = អូ។ ដូច្នេះផ្នែកសំខាន់នៃការពង្រីកនៅក្នុងសង្កាត់ oo នឹងជាលក្ខខណ្ឌដែលមានអំណាចវិជ្ជមាន Pនិងត្រឹមត្រូវ - ជាមួយអវិជ្ជមាន។
សូមណែនាំអថេរថ្មីមួយ w =១២. មុខងារ tv= 1/2, ពង្រីកដូច្នេះ u(oo) = 0, មួយទៅមួយ និងអនុលោមតាមផែនទីសង្កាត់ z > Rពិន្ទុ zq = 00 ក្នុងសង្កាត់ |w| wq = 0. ប្រសិនបើអនុគមន៍ f(z)ការវិភាគនៅក្នុងសង្កាត់ដែលមានការវាយដំ រ z Zq = oc បន្ទាប់មកអនុគមន៍ G(w) = f(l/w)នឹងត្រូវបានវិភាគនៅក្នុងសង្កាត់ពណ៌លឿង 0 wo = 0 ។ ចាប់តាំងពីសម្រាប់ 2 -> oo នឹងមាន វ-> 0 បន្ទាប់មក
នោះហើយជាមូលហេតុដែល G(w)មាននៅចំណុច wq = 0 គឺជាឯកវចនៈនៃប្រភេទដូចគ្នាទៅនឹង f(z)នៅចំណុច Zq = 00 ។ អនុញ្ញាតឱ្យយើងពង្រីកមុខងារ G(w) នៅក្នុងស៊េរី Laurent នៅក្នុងសង្កាត់ដែលវាយដំនៃចំនុច wo = 0:
ផលបូកនៅជ្រុងខាងស្តាំនៃ (26.5) តំណាងឱ្យផ្នែកត្រឹមត្រូវ និងសំខាន់នៃការពង្រីក រៀងគ្នា។ ចូរបន្តទៅអថេរ z,ការជំនួស w = 1/z៖ 
តំណាង ទំ\u003d -A *, 6 * \u003d 6_ " \u003d ជាមួយទំហើយកត់សំគាល់វា។ G(l/z) = f(z), យើងទទួលបាន
ការរលាយ (2G.G) ត្រូវបានគេហៅថា ការពង្រីក Laurent នៃអនុគមន៍ f(z) នៅក្នុងសង្កាត់ដែលបែកខ្ញែកនៃចំនុច zq= អូ។ ផលបូកដំបូងនៅក្នុង (2G.6) ត្រូវបានគេហៅថា ផ្នែកខាងស្តាំហើយផលបូកទីពីរគឺ ផ្នែកដ៏សំខាន់ការរលួយនេះ។ ដោយសារផលបូកទាំងនេះត្រូវគ្នាទៅនឹងផ្នែកត្រឹមត្រូវ និងសំខាន់នៃការពង្រីក (26.5) ការពង្រីក (26.6) បំពេញអាណាឡូកនៃទ្រឹស្តីបទ 26.2, 26.3 និង 26.6។ ដូច្នេះទ្រឹស្តីបទខាងក្រោមគឺជា analogue នៃទ្រឹស្តីបទ 26.2 ។
ទ្រឹស្តីបទ 26.10 ។ ចំណុចឯកវចនៈដាច់ដោយឡែកZq - os (មុខងារ/(G) គឺអាចដកចេញបានប្រសិនបើការពង្រីក Laurent ក្នុងសង្កាត់ដែលត្រូវបានគេវាយចេញពីចំណុចនេះមានទម្រង់
t.s. មានតែផ្នែកត្រឹមត្រូវ។
យើងដាក់ /(oo) = សហ។អនុគមន៍ដែលកំណត់ដោយស៊េរី (26.7) រួមគ្នាក្នុងសង្កាត់ z > Rពិន្ទុ 2o \u003d oc, ហៅ ការវិភាគនៅចំណុច z o = អូ។ (ចំណាំថានិយមន័យនេះគឺស្មើនឹងការវិភាគនៃមុខងារ G(w) នៅចំណុច វ៉ូ = 0.)
ឧទាហរណ៍ 26.11 ។ ស៊ើបអង្កេតចំណុចឯកវចនៈ zq = oo នៃអនុគមន៍
ដោយសារដែនកំណត់គឺកំណត់ ហ្សូ = oo គឺជាចំណុចឯកវចនៈដែលអាចដកចេញបាននៃអនុគមន៍ f(r)។ ប្រសិនបើយើងដាក់ /(oo) = lim J(z)= 0 បន្ទាប់មក f(z)នឹងក្លាយជា
tic នៅចំណុច ហ្សូ= os ។ ចូរយើងបង្ហាញពីរបៀបស្វែងរកការពង្រីកដែលត្រូវគ្នា (26.7)។ ចូរបន្តទៅអថេរ វ = 1 fzការជំនួស z= 1 /?e យើងទទួលបាន
(សមភាពចុងក្រោយមានសុពលភាពនៅក្នុងសង្កាត់ដែលវាយដំនៃចំនុច ww = 0 ប៉ុន្តែយើងនឹងពង្រីកនិយមន័យ (7(0) = 0)) ។ អនុគមន៍លទ្ធផលមានចំណុចឯកវចនៈ w =±i, w =-1/3 និងនៅចំណុច Wq = 0 គឺជាការវិភាគ។ មុខងារពង្រីក G(w)ដោយដឺក្រេ វ(ដូចដែលបានធ្វើនៅក្នុងឧទាហរណ៍ 25.7) ហើយជំនួសទៅក្នុងស៊េរីថាមពលលទ្ធផល w = 1/zមនុស្សម្នាក់អាចទទួលបានការពង្រីក (26.7) នៃមុខងារ f(z)
ទ្រឹស្តីបទ 26.3 សម្រាប់ករណី ហ្សូ=oo នឹងត្រូវបានសរសេរឡើងវិញក្នុងទម្រង់ខាងក្រោម។
ទ្រឹស្តីបទ 26.12 ។ ចំណុចឯកវចនៈដាច់ដោយឡែកទៅ = អូក មុខងារ f(z) គឺជាបង្គោលប្រសិនបើ ហើយប្រសិនបើផ្នែកសំខាន់នៃការពង្រីក Laurent (26.6) មានតែចំនួនកំណត់នៃមេគុណដែលមិនមែនជាសូន្យជាមួយ ":
នៅទីនេះ ស៊េរីគឺជាផ្នែកធម្មតា ហើយពហុនាមវង់ក្រចកគឺជាផ្នែកសំខាន់នៃការពង្រីក។ ពហុគុណនៃបង្គោលក្នុង oc ត្រូវបានកំណត់ថាជាពហុគុណនៃបង្គោល wq = 0 មុខងារ G(z)វាងាយមើលឃើញថាពហុគុណនៃបង្គោលស្របគ្នានឹងលេខ ននៅក្នុង (26.8) ។
Q p | (i 2 + 1) (z + 3) ២
កិច្ចការមួយ។ បង្ហាញថាមុខងារ f(z) =-- -- មាននៅក្នុង
ចំណុច ហ្សូ = oo pole order 3.
ទ្រឹស្តីបទ 26.6 លើចំណុចឯកវចនៈសំខាន់មួយត្រូវបានសរសេរឡើងវិញសម្រាប់ករណី ហ្សូ= os ស្ទើរតែ verbatim ហើយយើងមិនរស់នៅលើវានៅក្នុងលម្អិតទេ។
ចំណុចឯកវចនៈ នៅក្នុងគណិតវិទ្យា។ 1) ចំណុចឯកវចនៈនៃខ្សែកោងដែលផ្តល់ដោយសមីការ F ( x, y) = 0, - ចំណុច M 0 ( x 0 , y 0) ដែលដេរីវេភាគទាំងពីរនៃអនុគមន៍ F ( x, y) បាត់៖ លើសពីនេះទៀត មិនមែនគ្រប់ដេរីវេភាគទីពីរទាំងអស់នៃអនុគមន៍ F ( x, y) នៅចំណុច M 0 ស្មើនឹងសូន្យ បន្ទាប់មក O. t. ត្រូវបានគេហៅថាទ្វេដង។ ប្រសិនបើរួមជាមួយការបាត់ខ្លួននៃនិស្សន្ទវត្ថុទីមួយនៅចំណុច M 0 និស្សន្ទវត្ថុទីពីរទាំងអស់នឹងរលាយបាត់ ប៉ុន្តែមិនមែននិស្សន្ទវត្ថុទីបីទាំងអស់ស្មើនឹងសូន្យទេ នោះ O. t. ត្រូវបានគេហៅថាបីដង ហើយដូច្នេះនៅលើ។ នៅពេលសិក្សារចនាសម្ព័ន្ធនៃខ្សែកោងនៅជិត O. t ពីរដងតួនាទីសំខាន់មួយត្រូវបានលេងដោយសញ្ញានៃកន្សោម ប្រសិនបើ Δ > 0 នោះ O. t. ត្រូវបានគេហៅថាដាច់ឆ្ងាយ។ ឧទាហរណ៍ខ្សែកោង y 2 − x 4 + 4x 2= 0 ប្រភពដើមគឺជា O. t. ដាច់ឆ្ងាយ (សូមមើល អង្ករ។ មួយ។
) ប្រសិនបើ Δ x 2 + y 2 + a 2) 2 - 4a 2 x 2 − a 4= 0 ប្រភពដើមនៃកូអរដោនេគឺ nodal O. t. (សូមមើល អង្ករ។ ២
) ប្រសិនបើ Δ = 0 នោះខ្សែកោង O. t. គឺដាច់ពីគ្នា ឬកំណត់ដោយការពិតដែលថាសាខាផ្សេងគ្នានៃខ្សែកោងមានតង់សង់ទូទៅនៅចំណុចនេះ ឧទាហរណ៍៖ តង់សង់ និងបង្កើតជាចំណុច ដូចជាខ្សែកោង y 2 − x 3= 0 (សូមមើល អង្ករ។ ៣
, ក); b) cusp នៃប្រភេទទី 2 - សាខាផ្សេងគ្នានៃខ្សែកោងមានទីតាំងនៅផ្នែកម្ខាងនៃតង់សង់ទូទៅដូចជាខ្សែកោង
(y − x 2)2 - x 5= 0 (សូមមើល អង្ករ។ ៣
, ខ); គ) ចំណុចនៃការទំនាក់ទំនងដោយខ្លួនឯង (សម្រាប់ខ្សែកោង y 2 − x 4= 0 ប្រភពដើមគឺជាចំណុចនៃទំនាក់ទំនងដោយខ្លួនឯង; (សង់ទីម៉ែត។ អង្ករ។ ៣
, ក្នុង) រួមជាមួយ O. t. ដែលបានបញ្ជាក់មាន O. t. ជាច្រើនទៀតដែលមានឈ្មោះពិសេស; ឧទាហរណ៍ ចំណុច asymptotic គឺជាចំណុចកំពូលនៃវង់ដែលមានចំនួនវេនគ្មានកំណត់ (សូមមើលរូបភព។ អង្ករ។ បួន
) ចំណុចបំបែក ចំណុចជ្រុង។ល។ 2) ចំណុចឯកវចនៈនៃសមីការឌីផេរ៉ង់ស្យែល គឺជាចំណុចមួយដែលទាំងភាគយក និងភាគបែងនៃផ្នែកខាងស្តាំនៃសមីការឌីផេរ៉ង់ស្យែលបាត់ក្នុងពេលដំណាលគ្នា (សូមមើល សមីការឌីផេរ៉ង់ស្យែល) ដែល P និង Q គឺជាមុខងារដែលអាចផ្លាស់ប្តូរបានជាបន្តបន្ទាប់។ សន្មត់ថា O. t. មានទីតាំងនៅប្រភពដើម និងប្រើរូបមន្ត Taylor (សូមមើល។ រូបមន្ត Taylor) យើងអាចតំណាង Eq.(1) as កន្លែងដែល P 1 ( x, y) និង Q 1 ( x, y) គឺគ្មានដែនកំណត់ទាក់ទងនឹង មានន័យថា ប្រសិនបើ λ 1 ≠ λ 2 និង λ 1 λ 2 > 0 ឬ λ 1 = λ 2 នោះ O. t. គឺជាថ្នាំង។ ខ្សែកោងអាំងតេក្រាលទាំងអស់ឆ្លងកាត់ចំណុចនៃសង្កាត់តូចមួយគ្រប់គ្រាន់នៃថ្នាំងចូលទៅក្នុងវា។ ប្រសិនបើ λ 1 ≠ λ 2 និង λ 1 λ 2 i β, α ≠ 0 និង β ≠ 0 នោះ O. t. គឺជាការផ្តោតអារម្មណ៍; ខ្សែកោងអាំងតេក្រាលទាំងអស់ដែលឆ្លងកាត់ចំណុចនៅក្នុងសង្កាត់តូចមួយគ្រប់គ្រាន់នៃការផ្តោតអារម្មណ៍គឺជាវង់ដែលមានចំនួនវេនគ្មានកំណត់នៅក្នុងសង្កាត់តូចណាមួយនៃការផ្តោតអារម្មណ៍។ ប្រសិនបើចុងក្រោយ λ 1,2 = ± ខ្ញុំβ, β ≠ 0 បន្ទាប់មកតួអក្សររបស់ O. t. មិនត្រូវបានកំណត់ដោយពាក្យលីនេអ៊ែរក្នុងការពង្រីក P ( x, y) និង Q ( x, y) ដូចករណីទាំងអស់ខាងលើ។ នៅទីនេះ O. t. អាចជាការផ្តោតអារម្មណ៍ ឬកណ្តាល ឬវាអាចមានតួអក្សរស្មុគស្មាញជាង។ នៅក្នុងសង្កាត់នៃមជ្ឈមណ្ឌលនេះ ខ្សែកោងអាំងតេក្រាលទាំងអស់ត្រូវបានបិទ និងមានចំណុចកណ្តាលនៅខាងក្នុងពួកគេ។ ដូច្នេះឧទាហរណ៍ ចំណុច (0, 0) គឺជាថ្នាំងសម្រាប់សមីការ នៅ" = 2u/x(λ 1 = 1, λ 2 = 2; សូមមើល អង្ករ។ ៥
, ក) និង y" = u/x(λ 1 = λ 2 = 1; សូមមើល អង្ករ។ ៥
, b) សមីការ y" = -y/x(λ 1 = −1, λ 2 = 1 ; សង់ទីម៉ែត។ អង្ករ។ ៦
), ការផ្តោតអារម្មណ៍សម្រាប់សមីការ y" =(x + y) /
(x - y) (λ 1 = 1 - ខ្ញុំ, λ 2 = 1 + ខ្ញុំ; សង់ទីម៉ែត។ អង្ករ។ ៧
) និងមជ្ឈមណ្ឌលសម្រាប់សមីការ y" = -x / y(λ 1 = -i, λ 2 = ខ្ញុំ; សង់ទីម៉ែត។ អង្ករ។ ប្រាំបី
). ប្រសិនបើ x, y) និង Q ( x, y) ត្រូវបានវិភាគ , សង្កាត់នៃ O. t. នៃលំដាប់ខ្ពស់ជាងនេះអាចត្រូវបានបែងចែកទៅជាតំបន់: D 1 - ពោរពេញទៅដោយខ្សែកោងអាំងតេក្រាល, ចុងទាំងពីរចូលទៅក្នុង O. t. (តំបន់រាងពងក្រពើ), D 2 - ពោរពេញទៅដោយខ្សែកោងអាំងតេក្រាល, ចុងម្ខាងចូលទៅក្នុង O. t. (តំបន់ប៉ារ៉ាបូល) និង D 3 - តំបន់ដែលចងដោយខ្សែកោងអាំងតេក្រាលពីរដែលរួមបញ្ចូលនៅក្នុង O. t. រវាងនោះមានខ្សែកោងអាំងតេក្រាលនៃប្រភេទនៃអ៊ីពែបូឡាស (តំបន់លើសឈាម) (សូមមើល។ អង្ករ។ ៩
) ប្រសិនបើមិនមានខ្សែកោងអាំងតេក្រាលចូលទៅក្នុងចំណុច O. នោះចំណុច O. ត្រូវបានគេហៅថាជាចំណុចនៃប្រភេទស្ថេរភាព។ សង្កាត់នៃស្ថេរភាព O. t. មានខ្សែកោងអាំងតេក្រាលបិទជិតដែលមាន O. t. នៅខាងក្នុងខ្លួនវារវាងវង់ដែលស្ថិតនៅ (សូមមើលរូបភព។ អង្ករ។ ដប់
). ការសិក្សានៃសមីការឌីផេរ៉ង់ស្យែល O.t. មានន័យថា ការសិក្សាអំពីអាកប្បកិរិយារបស់ក្រុមគ្រួសារនៃខ្សែកោងអាំងតេក្រាលនៅក្នុងសង្កាត់ O.t. M. Lyapunovក, ក. Poincaréនិងល)។ 3) ចំណុចឯកវចនៈនៃអនុគមន៍វិភាគតម្លៃតែមួយ - ចំណុចដែលការវិភាគនៃអនុគមន៍ត្រូវបានបំពាន (សូមមើល។ មុខងារវិភាគ) ប្រសិនបើមានសង្កាត់ O.t. កដោយឥតគិតថ្លៃពី O. t. ផ្សេងទៀតបន្ទាប់មកចំណុច កត្រូវបានគេហៅថាដាច់ឆ្ងាយ O. t. ប្រសិនបើ កគឺជា O. t. ដាច់ស្រយាល ហើយមានកំណត់ A ត្រូវបានគេហៅថា O. t ដែលអាចដកចេញបាន។ f(ក)= ខវាគឺអាចធ្វើទៅបានដើម្បីសម្រេចបាន។ កនឹងក្លាយជាចំណុចធម្មតានៃមុខងារដែលបានកែតម្រូវ។ ឧទាហរណ៍ ចំណុច z= 0 គឺជា O.T ដែលអាចដកចេញបានសម្រាប់អនុគមន៍ f 1 ( z) = f(z), ប្រសិនបើ z≠ 0 និង f 1(0),=1, ចំណុច z= 0 គឺជាចំណុចធម្មតា [ f 1 (z) គឺជាការវិភាគនៅចំណុច z= 0]។ ប្រសិនបើ ក ក- ឯកវចនៈ O. t. និង a ត្រូវបានគេហៅថា បង្គោល ឬចំណុចឯកវចនៈនៃមុខងារ f(z) ប្រសិនបើស៊េរី Laurent) ដំណើរការ f(z) នៅក្នុងសង្កាត់នៃ O. t. ដាច់ស្រយាលមិនមានថាមពលអវិជ្ជមានទេ។ z - ក, ប្រសិនបើ ក- O. t. ដែលអាចដកចេញបាន មានចំនួនកំណត់នៃថាមពលអវិជ្ជមាន z - ក, ប្រសិនបើ ក- បង្គោល (ក្នុងករណីនេះលំដាប់នៃបង្គោល រត្រូវបានកំណត់ថាជាថាមពលខ្ពស់បំផុតនៃ a - ចំណុចឯកវចនៈសំខាន់។ ឧទាហរណ៍សម្រាប់មុខងារ ចំណុច z= 0 គឺជាបង្គោលនៃលំដាប់ រ, សម្រាប់មុខងារ ចំណុច z= 0 គឺជាចំណុចឯកវចនៈដ៏សំខាន់។ នៅលើព្រំដែននៃរង្វង់នៃការបញ្ចូលគ្នានៃស៊េរីថាមពលត្រូវតែមានយ៉ាងហោចណាស់មួយ O. t. នៃអនុគមន៍ដែលតំណាងនៅក្នុងរង្វង់នេះដោយស៊េរីថាមពលដែលបានផ្តល់ឱ្យ។ ចំណុចព្រំដែនទាំងអស់នៃដែនអត្ថិភាពនៃមុខងារវិភាគតម្លៃតែមួយ (ព្រំដែនធម្មជាតិ) គឺជាចំណុចព្រំដែននៃមុខងារនេះ។ ដូច្នេះចំនុចទាំងអស់នៃរង្វង់ឯកតា | z| = 1 គឺពិសេសចំពោះមុខងារ សម្រាប់មុខងារវិភាគពហុតម្លៃ គោលគំនិតនៃ "O. t" ពិបាកជាង។ បន្ថែមពីលើ O. t. នៅក្នុងសន្លឹកដាច់ដោយឡែកនៃផ្ទៃ Riemann នៃអនុគមន៍ (នោះគឺ O. t. នៃធាតុវិភាគតម្លៃតែមួយ) ចំនុចសាខាណាមួយក៏ជា O. t. នៃអនុគមន៍ផងដែរ។ ចំណុចសាខាដាច់ស្រយាលនៃផ្ទៃ Riemann (ឧទាហរណ៍ ចំណុចសាខាដែលនៅក្នុងសង្កាត់មួយចំនួនរបស់ពួកគេមិនមានមុខងារ O.t. ផ្សេងទៀតនៅក្នុងស្លឹកណាមួយទេ) ត្រូវបានចាត់ថ្នាក់ដូចខាងក្រោម។ ប្រសិនបើ a គឺជាចំណុចសាខាដាច់ស្រយាលនៃលំដាប់កំណត់ ហើយមាន finite a វាត្រូវបានគេហៅថា បង្គោលសំខាន់។ ប្រសិនបើ ក កគឺជាចំនុចសាខាដាច់ស្រយាលនៃលំដាប់គ្មានកំណត់ ហើយ a ត្រូវបានគេហៅថា transcendental O. t. ចំនុចសាខាដាច់ស្រយាលផ្សេងទៀតទាំងអស់ត្រូវបានគេហៅថា ចំនុចសំខាន់ឯកវចនៈសំខាន់។ ឧទាហរណ៍៖ ចំណុច z= 0 គឺជាចំណុចសំខាន់ធម្មតានៃអនុគមន៍ f ( z) = កំណត់ហេតុ zនិងចំណុចសំខាន់ឯកវចនៈសំខាន់នៃមុខងារ f (z) = កំណត់ហេតុអំពើបាប z. O. t. ណាមួយ លើកលែងតែមួយដែលអាចដកចេញបាន គឺជាឧបសគ្គដល់ការបន្តវិភាគ ពោលគឺការបន្តវិភាគតាមខ្សែកោងដែលឆ្លងកាត់ O. t. ដែលមិនអាចដកចេញបានគឺមិនអាចទៅរួចទេ។ សព្វវចនាធិប្បាយសូវៀតដ៏អស្ចារ្យ។ - អិមៈសព្វវចនាធិប្បាយសូវៀត.
1969-1978
.
p = 2, 3, …)
សូមមើលអ្វីដែល "ចំណុចពិសេស" មាននៅក្នុងវចនានុក្រមផ្សេងទៀត៖
ពិន្ទុនៅទីនេះ។ សូមមើលផងដែរនូវចំណុចឯកវចនៈ (សមីការឌីផេរ៉ង់ស្យែល)។ លក្ខណៈ ឬឯកវចនៈក្នុងគណិតវិទ្យា គឺជាចំណុចមួយដែលវត្ថុគណិតវិទ្យា (ជាធម្មតាមុខងារ) មិនត្រូវបានកំណត់ ឬមានឥរិយាបទមិនទៀងទាត់ (ឧទាហរណ៍ ចំណុចដែល……. Wikipedia
មុខងារវិភាគគឺជាចំណុចមួយដែលលក្ខខណ្ឌនៃការវិភាគត្រូវបានបំពាន។ ប្រសិនបើមុខងារវិភាគ f(z) ត្រូវបានកំណត់នៅក្នុងសង្កាត់មួយចំនួននៃចំណុច z0 គ្រប់ទីកន្លែង… សព្វវចនាធិប្បាយរូបវិទ្យា
មុខងារវិភាគគឺជាចំណុចដែលការវិភាគនៃអនុគមន៍មួយត្រូវបានបំពាន… វចនានុក្រមសព្វវចនាធិប្បាយធំ
ចំណុចឯកវចនៈ- — [Ya.N. Luginsky, M.S. Fezi Zhilinskaya, Yu.S. Kabirov ។ វចនានុក្រមអង់គ្លេសរុស្ស៊ីនៃវិស្វកម្មអគ្គិសនី និងឧស្សាហកម្មថាមពល ទីក្រុងម៉ូស្គូ ឆ្នាំ 1999] ប្រធានបទវិស្វកម្មអគ្គិសនី គំនិតជាមូលដ្ឋាន EN ចំណុចឯកវចនៈ ... សៀវភៅណែនាំអ្នកបកប្រែបច្ចេកទេស
1) OT នៃអនុគមន៍វិភាគ f(z) គឺជាឧបសគ្គដល់ការបន្តវិភាគនៃធាតុនៃអនុគមន៍ f(z) នៃអថេរ z តាមបណ្តោយផ្លូវមួយចំនួននៅលើយន្តហោះនៃអថេរនេះ។ សូមអោយអនុគមន៍វិភាគ f(z) កំណត់ដោយមួយចំនួន...... សព្វវចនាធិប្បាយគណិតវិទ្យា
មុខងារវិភាគ ចំណុចដែលការវិភាគនៃមុខងារត្រូវបានបំពាន។ * * * SINGULAR POINT A SINGULAR POINT នៃអនុគមន៍វិភាគ ចំណុចមួយដែលការវិភាគរបស់អនុគមន៍ត្រូវបានបំពាន ... វចនានុក្រមសព្វវចនាធិប្បាយ
ចំណុចឯកវចនៈ- ypatingasis taškas statusas T sritis automatika atitikmenys: engl ។ vok ចំណុចឯកវចនៈ ឯកវចនៈ Punkt, m rus ។ ចំណុចឯកវចនៈ fpranc ។ ភាគល្អិតចំណុច, m; point singulier, m … Automatikos terminų žodynas
ស៊េរី Taylor បម្រើជាឧបករណ៍ដ៏មានប្រសិទ្ធភាពសម្រាប់សិក្សាមុខងារដែលវិភាគក្នុងរង្វង់ zol ដើម្បីសិក្សាមុខងារដែលវិភាគនៅក្នុងតំបន់ annular វាប្រែថាវាអាចបង្កើតការពង្រីកនៅក្នុងថាមពលវិជ្ជមាន និងអវិជ្ជមាន (z - zq) នៃ ទម្រង់ដែលធ្វើអោយការពង្រីក Taylor ជាទូទៅ ស៊េរី (1) ដែលយល់ថាជាផលបូកនៃស៊េរីពីរត្រូវបានគេហៅថាស៊េរី Laurent ។ វាច្បាស់ណាស់ថាតំបន់នៃការបញ្ចូលគ្នានៃស៊េរី (1) គឺជាផ្នែកទូទៅនៃតំបន់នៃការបញ្ចូលគ្នានៃស៊េរី (2) ។ ចូរយើងស្វែងរកនាង។ តំបន់នៃការបញ្ចូលគ្នានៃស៊េរីទី 1 គឺជារង្វង់ដែលកាំត្រូវបានកំណត់ដោយរូបមន្ត Cauchy-Hadamard នៅខាងក្នុងរង្វង់នៃការបញ្ចូលគ្នា ស៊េរី (3) បង្រួបបង្រួមទៅជាមុខងារវិភាគ ហើយនៅក្នុងរង្វង់នៃកាំតូចជាងណាមួយវាបញ្ចូលគ្នាយ៉ាងពិតប្រាកដ។ និងស្មើភាពគ្នា។ ស៊េរីទីពីរគឺជាស៊េរីថាមពលដែលទាក់ទងទៅនឹងអថេរ។ ស៊េរី (5) បញ្ចូលគ្នានៅក្នុងរង្វង់នៃការបញ្ចូលគ្នារបស់វាទៅនឹងមុខងារវិភាគនៃអថេរស្មុគ្រស្មាញ m-*oo ហើយនៅក្នុងរង្វង់នៃកាំតូចជាងណាមួយវាបញ្ចូលគ្នាយ៉ាងពិតប្រាកដ និងស្មើគ្នា។ ដែលមានន័យថាតំបន់នៃការបញ្ចូលគ្នានៃស៊េរី (4) គឺជារូបរាងនៃរង្វង់ - ប្រសិនបើបន្ទាប់មកមានតំបន់រួមនៃការបញ្ចូលគ្នានៃស៊េរី (3) និង (4) - រង្វង់មូលដែលស៊េរី (1) បម្លែងទៅជាមុខងារវិភាគ។ លើសពីនេះទៅទៀតនៅក្នុងចិញ្ចៀនណាមួយវាបញ្ចូលគ្នាយ៉ាងពិតប្រាកដនិងស្មើភាពគ្នា។ ឧទាហរណ៍ 1. កំណត់តំបន់នៃការបញ្ចូលគ្នានៃស៊េរី rad Laurent ឯកវចនៈឯកវចនៈដាច់ស្រយាល និងការចាត់ថ្នាក់របស់ពួកគេ (z) ដែលមានតម្លៃទោល និង apolitical នៅក្នុងរង្វង់មូល អាចត្រូវបានតំណាងនៅក្នុងរង្វង់នេះថាជាផលបូកនៃស៊េរីបញ្ចូលគ្នាដែលមានមេគុណ Cn ត្រូវបានកំណត់ និងគណនាដោយរូបមន្តដែល 7p ជារង្វង់នៃកាំ m អនុញ្ញាតឱ្យយើងជួសជុលចំណុចបំពាន z នៅខាងក្នុងរង្វង់ R យើងបង្កើតរង្វង់ដោយមានចំណុចកណ្តាលនៅចំណុច r ដែលរ៉ាឌីបំពេញវិសមភាពហើយពិចារណាចិញ្ចៀនថ្មី។ យោងតាមទ្រឹស្ដីអាំងតេក្រាល Cauchy សម្រាប់ដែនដែលតភ្ជាប់គុណយើងមាន សម្រាប់ចំណុចទាំងអស់ £តាមបណ្តោយរង្វង់ 7d* ទំនាក់ទំនងនៃផលបូកនៃស៊េរីដែលរួមបញ្ចូលគ្នាស្មើភាពគ្នា 1 1 គឺពេញចិត្ត។ ដូច្នេះប្រភាគ ^ អាចតំណាងជា vi- /" / នៅក្នុងវិធីផ្សេងគ្នាបន្តិច សម្រាប់ចំណុចទាំងអស់ ξ នៅលើ រង្វង់ ir> យើងមានទំនាក់ទំនង ដូច្នេះប្រភាគ ^ អាចត្រូវបានតំណាងថាជាផលបូកនៃស៊េរីរួមផ្សំគ្នាក្នុងរូបមន្ត (10) និង (12) គឺជាមុខងារវិភាគក្នុងរង្វង់មូលមួយ។ ដូច្នេះ តាមទ្រឹស្តីបទរបស់ Cauchy តម្លៃនៃអាំងតេក្រាលដែលត្រូវគ្នាមិនផ្លាស់ប្តូរទេ ប្រសិនបើរង្វង់ 7/r និង 7r/ ត្រូវបានជំនួសដោយរង្វង់ណាមួយ។ នេះអនុញ្ញាតឱ្យយើងបញ្ចូលគ្នានូវរូបមន្ត (10) និង (12)។ ការជំនួសអាំងតេក្រាលនៅជ្រុងខាងស្តាំនៃរូបមន្ត (8) ជាមួយនឹងកន្សោមរបស់វា (9) និង (11) រៀងគ្នា យើងទទួលបានការពង្រីកដែលចង់បាន។ ចាប់តាំងពី z គឺជាអំពើតាមអំពើចិត្ត។ ចំនុចនៃសង្វៀន វាធ្វើតាមដែលស៊េរី (14) បង្រួបបង្រួមទៅនឹងមុខងារ f(z) នៅគ្រប់ទីកន្លែងនៅក្នុងសង្វៀននេះ ហើយនៅក្នុងសង្វៀនណាមួយ ស៊េរីនឹងបង្រួបបង្រួមមុខងារនេះយ៉ាងពិតប្រាកដ និងស្មើភាពគ្នា។ ឥឡូវនេះ ចូរយើងបង្ហាញថា ការខូចទ្រង់ទ្រាយនៃទម្រង់ (៦) គឺមានតែមួយគត់។ សន្មតថាការរលួយមួយទៀតកើតឡើង។ បន្ទាប់មកនៅគ្រប់កន្លែងនៅក្នុងរង្វង់ R យើងមាននៅលើរង្វង់ដែលស៊េរី (15) ចូលគ្នាស្មើគ្នា។ គុណផ្នែកទាំងពីរនៃសមភាព (ដែល m ជាចំនួនគត់ថេរ ហើយបញ្ចូលពាក្យស៊េរីទាំងពីរដោយពាក្យ។ ជាលទ្ធផល យើងទទួលបាននៅផ្នែកខាងឆ្វេង និងនៅខាងស្តាំ - Csh ។ ដូច្នេះ (4, \u003d St. ចាប់តាំងពី m គឺជាលេខតាមអំពើចិត្ត បន្ទាប់មកស៊េរីសមភាពចុងក្រោយ (6) ដែលមេគុណត្រូវបានគណនាដោយរូបមន្ត (7) ត្រូវបានគេហៅថាស៊េរី Laurent នៃអនុគមន៍ f(z) ក្នុងរង្វង់ 7) សម្រាប់មេគុណនៃស៊េរី Laurent គឺ កម្រប្រើក្នុងការអនុវត្តណាស់ ព្រោះជាក្បួនពួកគេទាមទារការគណនាដ៏ស្មុគស្មាញ។ ជាធម្មតា ប្រសិនបើអាចធ្វើបាន ការពង្រីកមុខងារបឋមរបស់ Taylor ដែលត្រៀមរួចជាស្រេចត្រូវបានប្រើប្រាស់។ ដោយផ្អែកលើភាពពិសេសនៃការពង្រីក វិធីសាស្ត្រស្របច្បាប់ណាមួយនាំទៅរកលទ្ធផលដូចគ្នា។ ឧទាហរណ៍ 2 ពិចារណាលើការពង្រីកស៊េរី Laurent នៃមុខងារនៃដែនផ្សេងៗគ្នា ដោយសន្មត់ថា Fuiscius /(r) មានចំនុចឯកវចនៈពីរ៖ ដូច្នេះហើយមាន ring domains បី ហើយផ្តោតលើចំណុច r = 0. ក្នុងផ្នែកនីមួយៗដែលមុខងារ f(r) ត្រូវបានវិភាគ៖ ក) រង្វង់គឺជាផ្នែកខាងក្រៅរបស់រង្វង់ (រូបភាព 27) ។ អនុញ្ញាតឱ្យយើងស្វែងរកការពង្រីក Laurent នៃមុខងារ /(z) នៅក្នុងតំបន់នីមួយៗនៃតំបន់ទាំងនេះ។ យើងតំណាងឱ្យ /(z) ជាផលបូកនៃប្រភាគបឋម a) ទំនាក់ទំនងនៃការផ្លាស់ប្តូររង្វង់ (16) ដូចខាងក្រោមដោយប្រើរូបមន្តសម្រាប់ផលបូកនៃលក្ខខណ្ឌនៃដំណើរការធរណីមាត្រ យើងទទួលបាន ខ) ចិញ្ចៀនសម្រាប់អនុគមន៍ -z នៅតែបញ្ចូលគ្នានៅក្នុងរង្វង់នេះ ចាប់តាំងពីស៊េរី (19) សម្រាប់អនុគមន៍ j^j សម្រាប់ |z| > 1 ខុសគ្នា។ ដូច្នេះហើយ យើងបំប្លែងអនុគមន៍ /(z) ដូចខាងក្រោម៖ ការអនុវត្តរូបមន្ត (១៩) ម្ដងទៀត យើងទទួលបានថាស៊េរីនេះរួមគ្នាសម្រាប់។ ការជំនួសការពង្រីក (18) និង (21) ទៅក្នុងទំនាក់ទំនង (20) យើងទទួលបាន គ) ផ្នែកខាងក្រៅនៃរង្វង់សម្រាប់អនុគមន៍ -z ជាមួយ |z| > 2 diverges និងស៊េរី (21) សម្រាប់អនុគមន៍ ចូរយើងតំណាងឱ្យអនុគមន៍ /(z) ក្នុងទម្រង់ខាងក្រោម៖ /<*> ដោយប្រើរូបមន្ត (18) និង (19) យើងទទួលបាន OR 1 ឧទាហរណ៍នេះបង្ហាញថាសម្រាប់មុខងារដូចគ្នា f(z) ការពង្រីក Laurent ដែលនិយាយជាទូទៅមានទម្រង់ផ្សេងគ្នាសម្រាប់ចិញ្ចៀនផ្សេងគ្នា។ ឧទាហរណ៍ 3. ស្វែងរក decomposition នៃ 8 Laurent series នៃ function Laurent series Isolated singular point and their classification in annular region A យើងប្រើតំណាងនៃអនុគមន៍ f(z) ក្នុងទម្រង់ខាងក្រោម៖ និងបំប្លែងពាក្យទីពីរដោយប្រើ រូបមន្តសម្រាប់ផលបូកនៃលក្ខខណ្ឌនៃដំណើរការធរណីមាត្រ យើងទទួលបាន ការជំនួសកន្សោមដែលបានរកឃើញទៅក្នុងរូបមន្ត (22) យើងមានឧទាហរណ៍ទី 4 យើងមានអនុញ្ញាតឱ្យការពង្រីកនេះមានសុពលភាពសម្រាប់ចំណុចណាមួយ z Ф 0. ក្នុងករណីនេះ តំបន់ annular គឺជាយន្តហោះស្មុគស្មាញទាំងមូលជាមួយនឹងចំណុចមួយដែលបានបោះចោល z - 0 ។ តំបន់នេះអាចត្រូវបានកំណត់ដោយទំនាក់ទំនងដូចខាងក្រោមៈ មុខងារនេះគឺវិភាគ នៅក្នុងតំបន់ ពីរូបមន្ត (13) សម្រាប់មេគុណនៃស៊េរី Laurent ដោយហេតុផលដូចគ្នានឹងកថាខណ្ឌមុន មនុស្សម្នាក់អាចទទួលបានវិសមភាព Kouiw ។ ប្រសិនបើអនុគមន៍ f(z) ត្រូវបានចងនៅលើរង្វង់មួយ ដែល M ជាថេរ) នោះចំនុចឯកវចនៈដាច់ស្រយាល A ចំនុច zo ត្រូវបានគេហៅថាចំនុចឯកវចនៈឯកវចនៈឯកវចនៈនៃអនុគមន៍ f(z) ប្រសិនបើមានសង្កាត់ annular នៃចំនុច ( សំណុំនេះជួនកាលត្រូវបានគេហៅផងដែរថាជាសង្កាត់ដែលត្រូវបានវាយលុកនៃចំណុច 2o) ដែលមុខងារ f(z) មានតម្លៃតែមួយ និងការវិភាគ។ នៅចំណុច zo ខ្លួនវា មុខងារមិនត្រូវបានកំណត់ ឬមិនមានតម្លៃតែមួយ និងការវិភាគ។ បីប្រភេទនៃចំណុចឯកវចនៈត្រូវបានសម្គាល់អាស្រ័យលើឥរិយាបថនៃអនុគមន៍ /(z) នៅពេលខិតជិតចំណុច zo ។ ចំណុចឯកវចនៈដាច់ស្រយាលមួយត្រូវបានគេនិយាយថា: 1) ដកចេញបានប្រសិនបើមានកំណត់ 2) pmusach ប្រសិនបើ 3) ចំណុចឯកវចនៈសំខាន់ប្រសិនបើមុខងារ f(z) មិនមានដែនកំណត់សម្រាប់ ទ្រឹស្តីបទ 16. ចំនុចឯកវចនៈដាច់ស្រយាល z0 នៃអនុគមន៍ f(z) គឺជាចំណុចឯកវចនៈដែលអាចដកចេញបាន ប្រសិនបើ និងលុះត្រាតែការពង្រីក Laurent នៃអនុគមន៍ f(z) នៅក្នុងសង្កាត់នៃចំនុច zo មិនមានផ្នែកសំខាន់ ពោលគឺ មានទម្រង់ Let zo - ចំណុចឯកវចនៈដែលអាចដកចេញបាន។ បន្ទាប់មកមានអនុគមន៍កំណត់ ហេតុដូច្នេះហើយ អនុគមន៍ f(z) ត្រូវបានចងនៅក្នុងសង្កាត់ procological នៃចំណុច r។ យើងកំណត់ដោយគុណធម៌នៃវិសមភាព Cauchy ចាប់តាំងពីវាអាចជ្រើសរើស p ជាតូចតាមអំពើចិត្ត បន្ទាប់មកមេគុណទាំងអស់នៅ អំណាចអវិជ្ជមាន (z - 20) គឺស្មើនឹងសូន្យ៖ ផ្ទុយទៅវិញ អនុញ្ញាតឱ្យ Laurent ពង្រីកមុខងារ /(r) នៅក្នុងសង្កាត់នៃចំណុច zq មានតែផ្នែកត្រឹមត្រូវប៉ុណ្ណោះ ពោលគឺវាមានទម្រង់ (23) និង, ជាលទ្ធផល Taylor ។ វាងាយស្រួលមើលថាសម្រាប់ z -* z0 អនុគមន៍ /(r) មានតម្លៃកំណត់៖ ទ្រឹស្តីបទ 17. ចំនុចឯកវចនៈឯកវចនៈ zq នៃអនុគមន៍ f(z) គឺអាចដកចេញបានប្រសិនបើអនុគមន៍ J(z) គឺ ជាប់ព្រំប្រទល់នៅក្នុងសង្កាត់មួយចំនួននៃចំណុច zq, Zgmechai មិនមែនទេ។ អនុញ្ញាតឱ្យ r0 ជាចំណុចឯកវចនៈដែលអាចដកចេញបាននៃ f(r) ។ សន្មត់ថាយើងទទួលបានថាអនុគមន៍ f (r) គឺជាការវិភាគនៅក្នុងរង្វង់មួយចំនួនដែលស្ថិតនៅកណ្តាលចំណុច th ។ នេះកំណត់ឈ្មោះចំណុច - ចោល។ ទ្រឹស្តីបទ 18. ចំនុចឯកវចនៈដាច់ស្រយាល zq នៃអនុគមន៍ f(z) គឺជាបង្គោល ប្រសិនបើផ្នែកសំខាន់នៃការពង្រីក Laurent នៃអនុគមន៍ f(z) នៅក្នុងសង្កាត់នៃចំនុចមានលេខកំណត់ (និងវិជ្ជមាន) នៃពាក្យមិនមែនសូន្យ ពោលគឺមានទម្រង់ 4 អនុញ្ញាតឱ្យ z0 ជាបង្គោល។ ចាប់តាំងពីពេលនោះមកមានសង្កាត់មួយដែលត្រូវបានវាយលុកនៃចំណុច z0 ដែលមុខងារ f(z) គឺជាការវិភាគនិងមិនសូន្យ។ បន្ទាប់មក មុខងារវិភាគត្រូវបានកំណត់នៅក្នុងសង្កាត់នេះ ហើយហេតុដូចនេះហើយ ចំណុច zq គឺជាចំណុចឯកវចនៈ (សូន្យ) នៃអនុគមន៍ ឬដែល h(z) គឺជាមុខងារវិភាគ h(z0) ∩ 0. គឺជាការវិភាគនៅក្នុងសង្កាត់នៃ ចំនុច zq ហេតុដូច្នេះហើយ យើងទទួលបានវាពីណា ឥលូវនេះ ចូរយើងសន្មត់ថា អនុគមន៍ f(z) មានការរលួយនៃទម្រង់ (24) នៅក្នុងសង្កាត់ដែលដាច់នៃចំនុច zo ។ នេះមានន័យថានៅក្នុងសង្កាត់នេះ មុខងារ f(z) ត្រូវបានវិភាគរួមគ្នាជាមួយមុខងារ។ សម្រាប់អនុគមន៍ g(z) ការពង្រីកមានសុពលភាពដែលវាច្បាស់ណាស់ថា zq គឺជាចំណុចឯកវចនៈដែលអាចដកចេញបាននៃអនុគមន៍ g(z) ហើយមាន បន្ទាប់មកអនុគមន៍មាននិន្នាការនៅ 0 - បង្គោលនៃអនុគមន៍មានភាពសាមញ្ញមួយទៀត ការពិត។ ចំនុច Zq គឺជាបង្គោលនៃអនុគមន៍ f(z) ប្រសិនបើ និងលុះត្រាតែអនុគមន៍ g(z) = y អាចត្រូវបានពង្រីកទៅជាអនុគមន៍វិភាគនៅក្នុងសង្កាត់នៃចំនុច zq ដោយកំណត់ g(z0) = 0។ លំដាប់ នៃបង្គោលនៃអនុគមន៍ f(z) ត្រូវបានគេហៅថាលំដាប់សូន្យនៃអនុគមន៍ jfa ។ ទ្រឹស្តីបទ ១៦ និង ១៨ បញ្ជាក់ពីការអះអាងខាងក្រោម។ ទ្រឹស្តីបទ 19. ឯកវចនៈឯកវចនៈដាច់ស្រយាលគឺឯកវចនៈយ៉ាងសំខាន់ប្រសិនបើផ្នែកសំខាន់នៃការពង្រីក Laurent នៅក្នុងសង្កាត់ដែលបែកខ្ញែកនៃចំណុចនេះមានពាក្យមិនសូន្យជាច្រើន។ ឧទាហរណ៍ 5. ចំនុចឯកវចនៈនៃអនុគមន៍គឺ zo = 0។ យើងមាន Laurent Series Isolated singular point និងការចាត់ថ្នាក់របស់ពួកគេ ដូច្នេះហើយ zo = 0 គឺជាចំនុចឯកវចនៈដែលអាចដកចេញបាន។ ការពង្រីកអនុគមន៍ /(z) នៅក្នុងស៊េរី Laurent នៅក្នុងតំបន់ជុំវិញនៃចំនុចសូន្យមានតែផ្នែកត្រឹមត្រូវប៉ុណ្ណោះ៖ Example7. f(z) = ចំណុចឯកវចនៈនៃអនុគមន៍ f(z) គឺ zq = 0។ ពិចារណាពីឥរិយាបថនៃអនុគមន៍នេះនៅលើអ័ក្សពិត និងស្រមើស្រមៃ៖ នៅលើអ័ក្សពិតនៅ x 0 នៅលើអ័ក្សស្រមើស្រមៃ ដូច្នេះហើយ ក៏មិនកំណត់ ឬ ដែនកំណត់គ្មានកំណត់ f(z) នៅ z -* 0 មិនមានទេ។ ដូច្នេះចំនុច r0 = 0 គឺជាចំណុចឯកវចនៈសំខាន់នៃអនុគមន៍ f(z)។ ចូរយើងស្វែងរកការពង្រីក Laurent នៃអនុគមន៍ f(z) នៅក្នុងសង្កាត់នៃចំនុចសូន្យ។ សម្រាប់ស្មុគ្រស្មាញ C ណាមួយដែលយើងមាន យើងកំណត់។ បន្ទាប់មកការពង្រីក Laurent មានចំនួនគ្មានកំណត់នៃលក្ខខណ្ឌដែលមានថាមពលអវិជ្ជមាន z ។
គំរូដែលបានពិពណ៌នាដោយប្រព័ន្ធនៃសមីការឌីផេរ៉ង់ស្យែលស្វយ័តពីរ។
យន្តហោះដំណាក់កាល។ ដំណាក់កាលបញ្ឈរ។ វិធីសាស្រ្ត isocline ។ isoclines សំខាន់ៗ។ ស្ថិរភាពរដ្ឋ។ ប្រព័ន្ធលីនេអ៊ែរ។ ប្រភេទចំណុចសំខាន់ៗ៖ ថ្នាំង កែប ការផ្តោតអារម្មណ៍ កណ្តាល។ ឧទាហរណ៍៖ ប្រតិកម្មគីមីលំដាប់ទីមួយ។
លទ្ធផលគួរឱ្យចាប់អារម្មណ៍បំផុតលើគំរូគុណភាពនៃលក្ខណៈសម្បត្តិនៃប្រព័ន្ធជីវសាស្រ្តត្រូវបានទទួលនៅលើគំរូនៃសមីការឌីផេរ៉ង់ស្យែលពីរ ដែលអនុញ្ញាតឱ្យមានការសិក្សាគុណភាពដោយប្រើវិធីសាស្ត្រ យន្តហោះដំណាក់កាល. ពិចារណាប្រព័ន្ធនៃសមីការឌីផេរ៉ង់ស្យែលធម្មតាស្វយ័តពីរនៃទម្រង់ទូទៅ
(4.1)
P(x,y), Q(x,y)- មុខងារបន្តដែលបានកំណត់នៅក្នុងដែនមួយចំនួន ជីយន្តហោះ Euclidean ( x, y- កូអរដោណេ Cartesian) ហើយមាននៅក្នុងផ្នែកនេះ និស្សន្ទវត្ថុបន្តនៃលំដាប់មិនទាបជាងទីមួយ។
តំបន់ ជីអាចមានទាំងគ្មានដែនកំណត់ ឬមានកំណត់។ ប្រសិនបើអថេរ x, yមានអត្ថន័យជីវសាស្រ្តជាក់លាក់ (ការប្រមូលផ្តុំសារធាតុ ភាពសម្បូរបែបនៃប្រភេទសត្វ) ភាគច្រើនជាតំបន់ ជីគឺជា quadrant វិជ្ជមាននៃយន្តហោះពាក់កណ្តាលខាងស្តាំ៖
0 £ x< ¥ ,0 £ y< ¥ .
ការប្រមូលផ្តុំសារធាតុឬភាពសម្បូរបែបនៃប្រភេទសត្វក៏អាចត្រូវបានកំណត់ពីខាងលើដោយបរិមាណនៃនាវាឬដោយតំបន់នៃជម្រក។ បន្ទាប់មកជួរនៃអថេរមានទម្រង់៖
0 £ x< x 0 , 0 £ y< y 0 .
អថេរ x, yការផ្លាស់ប្តូរពេលវេលាស្របតាមប្រព័ន្ធនៃសមីការ (4.1) ដូច្នេះស្ថានភាពនៃប្រព័ន្ធនីមួយៗត្រូវគ្នាទៅនឹងតម្លៃនៃអថេរមួយគូ ( x, y).
|
|
ផ្ទុយទៅវិញ សម្រាប់គូនៃអថេរនីមួយៗ ( x, y) ត្រូវគ្នាទៅនឹងស្ថានភាពជាក់លាក់នៃប្រព័ន្ធ។
ពិចារណាលើយន្តហោះដែលមានអ័ក្សកូអរដោនេ ដែលតម្លៃនៃអថេរត្រូវបានគ្រោងទុក x, y. រាល់ចំណុច មយន្តហោះនេះត្រូវគ្នាទៅនឹងស្ថានភាពជាក់លាក់នៃប្រព័ន្ធ។ យន្តហោះបែបនេះត្រូវបានគេហៅថា យន្តហោះដំណាក់កាល ហើយពណ៌នាអំពីចំនួនសរុបនៃរដ្ឋទាំងអស់នៃប្រព័ន្ធ។ ចំណុច M(x, y) ត្រូវបានគេហៅថា ចំណុចពណ៌នា ឬតំណាង។
អនុញ្ញាតឱ្យនៅពេលដំបូង t = t 0 តំណាងឱ្យចំណុចកូអរដោណេ ម 0 (x(t 0), y(t 0)). រាល់ពេលបន្ទាប់នៅក្នុងពេលវេលា tចំណុចពណ៌នានឹងផ្លាស់ទីទៅតាមការផ្លាស់ប្តូរតម្លៃនៃអថេរ x(t), y(t). សំណុំនៃចំណុច ម(x(t), y(t)) នៅលើយន្តហោះដំណាក់កាល ទីតាំងដែលត្រូវគ្នានឹងស្ថានភាពនៃប្រព័ន្ធក្នុងដំណើរការផ្លាស់ប្តូរអថេរតាមពេលវេលា x(t), y(t)យោងតាមសមីការ (៤.១) ត្រូវបានគេហៅថា គន្លងដំណាក់កាល។
សំណុំនៃគន្លងដំណាក់កាលសម្រាប់តម្លៃដំបូងផ្សេងគ្នានៃអថេរផ្តល់នូវ "បញ្ឈរ" ដែលអាចមើលឃើញយ៉ាងងាយស្រួលនៃប្រព័ន្ធ។ អាគារ បញ្ឈរដំណាក់កាលអនុញ្ញាតឱ្យអ្នកទាញការសន្និដ្ឋានអំពីលក្ខណៈនៃការផ្លាស់ប្តូរនៅក្នុងអថេរ x, yដោយមិនដឹងពីដំណោះស្រាយវិភាគនៃប្រព័ន្ធសមីការដើម(4.1).
ដើម្បីពណ៌នាបញ្ឈរដំណាក់កាល វាចាំបាច់ត្រូវបង្កើតវាលវ៉ិចទ័រនៃទិសដៅសម្រាប់គន្លងប្រព័ន្ធនៅចំណុចនីមួយៗនៃប្លង់ដំណាក់កាល។ ដោយបញ្ជាក់ចំនួនបន្ថែមឃ t>0,យើងទទួលបានការកើនឡើងដែលត្រូវគ្នា។ ឃ xនិង ឃ yពីកន្សោម៖
ឃ x=P(x,y)ឃ t,
ឃ y=Q(x,y)ឃ t.
ទិសដៅវ៉ិចទ័រ dy/dxនៅចំណុច ( x, y) អាស្រ័យលើសញ្ញានៃមុខងារ P(x, y), Q(x, y)ហើយអាចត្រូវបានផ្តល់ឱ្យដោយតារាង:
|
P(x,y)>0,Q(x,y)>0 |
|
|
P(x,y)<0,Q(x,y)<0 |
|
|
P(x,y)>0,Q(x,y)<0 |
|
|
P(x,y)<0,Q(x,y)>0 |
|
.(4.2)
ដំណោះស្រាយចំពោះសមីការនេះ។ y=y(x, គ), ឬដោយប្រយោល។ ច(x, y)=c,កន្លែងណា ជាមួយគឺជាថេរនៃការធ្វើសមាហរណកម្ម ផ្តល់ឱ្យក្រុមគ្រួសារនៃខ្សែកោងអាំងតេក្រាលនៃសមីការ (4.2) - គន្លងដំណាក់កាលប្រព័ន្ធ (4.1) នៅលើយន្តហោះ x, y.
វិធីសាស្រ្ត Isocline
ដើម្បីបង្កើតរូបតំណាក់កាល មួយប្រើ វិធីសាស្រ្ត isocline -បន្ទាត់ត្រូវបានគូរនៅលើប្លង់ដំណាក់កាលដែលប្រសព្វខ្សែកោងអាំងតេក្រាលនៅមុំជាក់លាក់មួយ។ សមីការ isocline ងាយស្រួលក្នុងការទទួលបានពី (4.2) ។ តោះដាក់
កន្លែងណា ប៉ុន្តែ– ថេរជាក់លាក់មួយ។ អត្ថន័យ ប៉ុន្តែតំណាងឱ្យតង់សង់នៃជម្រាលនៃតង់សង់ទៅគន្លងដំណាក់កាល ហើយអាចយកតម្លៃពី -¥ ទៅ + ¥ . ការជំនួសជំនួស dy/dxក្នុង (4.2) បរិមាណ ប៉ុន្តែយើងទទួលបានសមីការ isocline៖
.(4.3)
សមីការ (4.3) កំណត់នៅចំណុចនីមួយៗនៃយន្តហោះ តង់សង់តែមួយគត់ទៅនឹងខ្សែកោងអាំងតេក្រាលដែលត្រូវគ្នា លើកលែងតែចំណុចដែល P(x,y)= 0, សំណួរ (x, y) = 0 ដែលទិសដៅនៃតង់សង់ក្លាយជាមិនកំណត់ ចាប់តាំងពីតម្លៃនៃដេរីវេក្លាយជាមិនកំណត់៖
.
ចំណុចនេះគឺជាចំណុចប្រសព្វនៃ isoclines ទាំងអស់ - ចំណុចពិសេស។វាបាត់ក្នុងពេលដំណាលគ្នានូវនិស្សន្ទវត្ថុនៃអថេរ xនិង y.
ដូច្នេះនៅចំណុចឯកវចនៈអត្រានៃការផ្លាស់ប្តូរនៃអថេរគឺស្មើនឹងសូន្យ។ ដូច្នេះចំនុចឯកវចនៈនៃសមីការឌីផេរ៉ង់ស្យែលនៃគន្លងដំណាក់កាល (4.2) ត្រូវគ្នាទៅនឹង ស្ថានភាពស្ថានីនៃប្រព័ន្ធ(4.1) ហើយកូអរដោនេរបស់វាគឺជាតម្លៃស្ថានីនៃអថេរ x, y ។
ចំណាប់អារម្មណ៍ពិសេសគឺ isoclines សំខាន់ៗ៖
dy/dx=0, ទំ(x, y)=0 – isocline នៃតង់ហ្សង់ផ្ដេក និង
dy/dx=¥ , សំណួរ(x, y)=0 – isocline នៃតង់សង់បញ្ឈរ។
ដោយសាងសង់ isoclines សំខាន់និងស្វែងរកចំណុចប្រសព្វរបស់ពួកគេ។ (x, y) កូអរដោនេដែលបំពេញលក្ខខណ្ឌ៖
ដូច្នេះយើងនឹងរកឃើញចំណុចប្រសព្វនៃ isoclines ទាំងអស់នៃយន្តហោះដំណាក់កាល ដែលទិសដៅនៃតង់ហ្សង់ទៅគន្លងដំណាក់កាលគឺមិនកំណត់។ វា - ចំណុចឯកវចនៈដែលត្រូវគ្នា។ ស្ថានភាពស្ថានីនៃប្រព័ន្ធ(រូបភាព 4.2) ។
ប្រព័ន្ធ (4.1) មានស្ថានភាពស្ថានីជាច្រើន ដោយសារមានចំនុចប្រសព្វនៃ isoclines សំខាន់នៅលើយន្តហោះដំណាក់កាល។
គន្លងដំណាក់កាលនីមួយៗត្រូវគ្នាទៅនឹងបណ្តុំនៃចលនានៃប្រព័ន្ធថាមវន្តដែលឆ្លងកាត់រដ្ឋដូចគ្នា និងខុសគ្នាពីគ្នាទៅវិញទៅមកតែនៅដើមនៃសេចក្តីយោងពេលវេលាប៉ុណ្ណោះ។
 |
|
ប្រសិនបើលក្ខខណ្ឌនៃទ្រឹស្តីបទ Cauchy ត្រូវបានពេញចិត្ត នោះតាមរយៈចំណុចនីមួយៗនៃលំហ x, y, tឆ្លងកាត់ខ្សែកោងអាំងតេក្រាលតែមួយ។ ដូចគ្នាដែរ ដោយសារស្វ័យភាព សម្រាប់គន្លងដំណាក់កាល៖ គន្លងដំណាក់កាលតែមួយគត់ឆ្លងកាត់ចំណុចនីមួយៗនៃប្លង់ដំណាក់កាល។
ស្ថិរភាពរដ្ឋ
សូមឱ្យប្រព័ន្ធមានលំនឹង។
បន្ទាប់មកចំណុចតំណាងមានទីតាំងនៅចំណុចឯកវចនៈមួយនៃប្រព័ន្ធ ដែលតាមនិយមន័យ៖
.
ថាតើចំនុចឯកវចនៈមានស្ថេរភាពឬអត់ ត្រូវបានកំណត់ដោយថាតើចំនុចតំណាងទុកឬអត់ជាមួយនឹងគម្លាតតូចមួយពីស្ថានភាពស្ថានី។ ដូចដែលបានអនុវត្តទៅប្រព័ន្ធនៃសមីការពីរ និយមន័យនៃស្ថេរភាពនៅក្នុងភាសាអ៊ី, ឃដូចខាងក្រោម។
ស្ថានភាពលំនឹងមានស្ថេរភាព ប្រសិនបើសម្រាប់តំបន់ណាមួយនៃគម្លាតពីស្ថានភាពលំនឹង (អ៊ី )តំបន់អាចត្រូវបានបញ្ជាក់ ឃ (អ៊ី )ជុំវិញស្ថានភាពលំនឹង និងមានទ្រព្យសម្បត្តិដែលគ្មានគន្លងដែលចាប់ផ្តើមនៅក្នុងតំបន់ ឃ នឹងមិនឈានដល់ព្រំដែនទេ។ អ៊ី . (រូបភាព ៤.៤)
 |
|
សម្រាប់ថ្នាក់ធំនៃប្រព័ន្ធ - ប្រព័ន្ធរដុប – ធម្មជាតិនៃឥរិយាបទដែលមិនផ្លាស់ប្តូរជាមួយនឹងការផ្លាស់ប្តូរតិចតួចនៃប្រភេទនៃសមីការ ព័ត៌មានអំពីប្រភេទនៃឥរិយាបទនៅក្នុងតំបន់ជុំវិញនៃស្ថានីអាចទទួលបានដោយការសិក្សាមិនមែនដើមឡើយ ប៉ុន្តែបានធ្វើឱ្យសាមញ្ញ លីនេអ៊ែរប្រព័ន្ធ។
ប្រព័ន្ធលីនេអ៊ែរ។
ពិចារណាប្រព័ន្ធនៃសមីការលីនេអ៊ែរពីរ៖
.(4.4)
នៅទីនេះ a, b, c, ឃ- ថេរ, x, y- កូអរដោនេ Cartesian នៅលើយន្តហោះដំណាក់កាល។
ដំណោះស្រាយទូទៅនឹងត្រូវបានស្វែងរកក្នុងទម្រង់៖
.(4.5)
ជំនួសកន្សោមទាំងនេះនៅក្នុង (4.4) ហើយកាត់បន្ថយដោយ អ៊ី លីត្រ t:
(4.6)
ប្រព័ន្ធពិជគណិតនៃសមីការ (4.6) ជាមួយនឹងមិនស្គាល់ ក, ខមានដំណោះស្រាយមិនសូន្យ លុះត្រាតែកត្តាកំណត់របស់វា ដែលផ្សំឡើងដោយមេគុណមិនស្គាល់ គឺស្មើនឹងសូន្យ៖
.
ការពង្រីកកត្តាកំណត់នេះ យើងទទួលបានសមីការលក្ខណៈនៃប្រព័ន្ធ៖
.(4.7)
ដំណោះស្រាយនៃសមីការនេះផ្តល់តម្លៃនៃសូចនាករលីត្រ 1,2 នៅក្រោមតម្លៃដែលមិនមែនជាសូន្យអាចធ្វើទៅបានសម្រាប់ កនិង ខដំណោះស្រាយនៃសមីការ (៤.៦) ។ តម្លៃទាំងនេះគឺ
.(4.8)
ប្រសិនបើកន្សោមរ៉ាឌីកាល់គឺអវិជ្ជមានលីត្រ 1,2 លេខបន្សំស្មុគស្មាញ។ សន្មតថាឫសទាំងពីរនៃសមីការ (4.7) មានផ្នែកពិតមិនមែនសូន្យ ហើយថាមិនមានឫសច្រើនទេ។ បន្ទាប់មកដំណោះស្រាយទូទៅនៃប្រព័ន្ធ (4.4) អាចត្រូវបានតំណាងថាជាការរួមបញ្ចូលគ្នាលីនេអ៊ែរនៃនិទស្សន្តជាមួយនិទស្សន្តលីត្រ 1 , លីត្រ 2 :
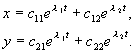(4.9)
ដើម្បីវិភាគធម្មជាតិនៃគន្លងដែលអាចកើតមាននៃប្រព័ន្ធនៅលើយន្តហោះដំណាក់កាលយើងប្រើ ការផ្លាស់ប្តូរកូអរដោណេលីនេអ៊ែរ,ដែលនឹងនាំមកនូវប្រព័ន្ធ ទម្រង់ Canonical៖
,(4.10)
ដែលអនុញ្ញាតឱ្យតំណាងងាយស្រួលជាងនៅលើយន្តហោះដំណាក់កាលបើប្រៀបធៀបទៅនឹងប្រព័ន្ធដើម (4.4) ។ សូមណែនាំកូអរដោនេថ្មី។ξ , η យោងតាមរូបមន្ត៖
(4.1)
វាត្រូវបានគេស្គាល់ពីវគ្គនៃពិជគណិតលីនេអ៊ែរថាប្រសិនបើផ្នែកពិតមិនស្មើនឹងសូន្យលីត្រ 1 , លីត្រ 2 ប្រព័ន្ធដើម (4.4) ដោយមានជំនួយពីការបំលែង (4.11) តែងតែអាចផ្លាស់ប្តូរទៅជាទម្រង់ Canonical (4.10) ហើយឥរិយាបថរបស់វានៅលើយន្តហោះដំណាក់កាលអាចត្រូវបានសិក្សាξ , η . ពិចារណាករណីផ្សេងៗដែលអាចបង្ហាញខ្លួនឯងនៅទីនេះ។
ឫស λ 1 , λ 2 - មានសុពលភាព និងសញ្ញាដូចគ្នា។
ក្នុងករណីនេះមេគុណបំប្លែងគឺពិតប្រាកដ យើងផ្លាស់ទីពីយន្តហោះពិតx, yទៅកាន់យន្តហោះពិត ξ, η ។ បែងចែកសមីការទីពីរ (4.10) ដោយទីមួយយើងទទួលបាន:
.(4.12)
ការរួមបញ្ចូលសមីការនេះយើងរកឃើញ:
កន្លែងណា .(4.13)
អនុញ្ញាតឱ្យយើងយល់ស្របដោយ λ 2 ឫសគល់នៃសមីការលក្ខណៈជាមួយនឹងម៉ូឌុលធំ ដែលមិនបំពានលើភាពទូទៅនៃហេតុផលរបស់យើង។ បន្ទាប់មកចាប់តាំងពីក្នុងករណីដែលកំពុងពិចារណាឫស λ 1 , λ2 - មានសុពលភាព និងសញ្ញាដូចគ្នាក>1 ហើយយើងកំពុងដោះស្រាយជាមួយនឹងខ្សែកោងអាំងតេក្រាលនៃប្រភេទ parabolic ។
ខ្សែកោងអាំងតេក្រាលទាំងអស់ (លើកលែងតែអ័ក្ស η ដែលត្រូវនឹង ) ប៉ះនៅប្រភពដើមនៃអ័ក្ស ξ, ដែលជាខ្សែកោងអាំងតេក្រាលនៃសមីការ (៤.១១)។ ប្រភពដើមនៃកូអរដោនេគឺជាចំណុចឯកវចនៈ។
ឥឡូវនេះ ចូរយើងស្វែងរកទិសដៅនៃចលនារបស់ចំណុចតំណាងតាមគន្លងដំណាក់កាល។ ប្រសិនបើ λ 1 , λ 2 គឺអវិជ្ជមាន បន្ទាប់មក ដូចដែលអាចមើលឃើញពីសមីការ (4.10), |ξ|, |η| ថយចុះតាមពេលវេលា។ ចំណុចតំណាងខិតទៅជិតប្រភពដើម ប៉ុន្តែមិនដែលឈានដល់វាឡើយ។ បើមិនដូច្នោះទេ នេះនឹងផ្ទុយពីទ្រឹស្តីបទរបស់ Cauchy ដែលចែងថា មានតែគន្លងដំណាក់កាលមួយប៉ុណ្ណោះ ដែលឆ្លងកាត់ចំណុចនីមួយៗនៃប្លង់ដំណាក់កាល។
ចំណុចឯកវចនៈបែបនេះ ដែលខ្សែកោងអាំងតេក្រាលឆ្លងកាត់ គ្រាន់តែជាក្រុមនៃប៉ារ៉ាបូឡា 
ឆ្លងកាត់ប្រភពដើមត្រូវបានគេហៅថាថ្នាំង (រូបភព។ 4.5)
Knot-type equilibrium state at λ 1 , λ 2 < 0 មានស្ថេរភាពយោងទៅតាម Lyapunov ចាប់តាំងពីចំណុចតំណាងផ្លាស់ទីតាមបណ្តោយខ្សែកោងអាំងតេក្រាលទាំងអស់ឆ្ពោះទៅរកប្រភពដើមនៃកូអរដោនេ។ វា។ knot ស្ថិរភាព. ប្រសិនបើ λ 1 , λ 2 > 0 បន្ទាប់មក |ξ|, |η| កើនឡើងតាមពេលវេលា ហើយចំណុចតំណាងផ្លាស់ទីឆ្ងាយពីប្រភពដើម។ ក្នុងករណីនេះចំណុចឯកវចនៈ– ថ្នាំងមិនស្ថិតស្ថេរ .
នៅលើយន្តហោះដំណាក់កាល x, y លក្ខណៈគុណភាពទូទៅនៃឥរិយាបទនៃខ្សែកោងអាំងតេក្រាលនឹងនៅតែមាន ប៉ុន្តែតង់ហ្សង់ទៅខ្សែកោងអាំងតេក្រាលនឹងមិនស្របគ្នានឹងអ័ក្សកូអរដោនេទេ។ មុំទំនោរនៃតង់សង់ទាំងនេះនឹងត្រូវបានកំណត់ដោយសមាមាត្រនៃមេគុណ α , β , γ , δ នៅក្នុងសមីការ (4.11) ។
ឫស λ 1 , λ 2 មានសុពលភាព និងមានសញ្ញាផ្សេងៗគ្នា។
បម្លែងពីកូអរដោនេ x, y ដើម្បីសំរបសំរួល ξ, η ពិតម្តងទៀត។ សមីការសម្រាប់អថេរ Canonical ម្តងទៀតមានទម្រង់ (4.10) ប៉ុន្តែឥឡូវនេះសញ្ញា λ 1 , λ 2 ខុសគ្នា។ សមីការគន្លងដំណាក់កាលមានទម្រង់:
កន្លែងណា ,(4.14)
ការរួមបញ្ចូល (4.14) យើងរកឃើញ
(4.15)
វា។ សមីការកំណត់ក្រុមគ្រួសារនៃខ្សែកោងនៃប្រភេទអ៊ីពែរបូល ដែលអ័ក្សសំរបសំរួលទាំងពីរគឺជា asymtotes (នៅ ក=1 យើងនឹងមានគ្រួសារនៃ isosceles hyperbolas). អ័ក្សកូអរដោនេក៏ជាខ្សែកោងអាំងតេក្រាលក្នុងករណីនេះផងដែរ។– ទាំងនេះនឹងជាខ្សែកោងអាំងតេក្រាលតែមួយគត់ដែលឆ្លងកាត់ប្រភពដើម។ គ្នា។ដែលក្នុងនោះមានគន្លងបីដំណាក់កាល: នៃចលនាពីរឆ្ពោះទៅរកស្ថានភាពលំនឹងមួយ (ឬឆ្ងាយពីស្ថានភាពលំនឹង) និងពីស្ថានភាពលំនឹង។ ខ្សែកោងអាំងតេក្រាលផ្សេងទៀតទាំងអស់។– គឺជាអ៊ីពែបូឡា ដែលមិនឆ្លងកាត់ប្រភពដើម (រូបភព។ 4.6) ចំណុចឯកវចនៈនេះត្រូវបានគេហៅថា "អាប ». បន្ទាត់កម្រិតនៅជិតខ្នងភ្នំមានឥរិយាបទដូចជាគន្លងតំណាក់កាលដែលនៅជិតខ្នងសេះ។
ចូរយើងពិចារណាពីធម្មជាតិនៃចលនានៃចំណុចតំណាងតាមបណ្តោយគន្លងដំណាក់កាលនៅជិតស្ថានភាពលំនឹង។ អនុញ្ញាតឱ្យឧទាហរណ៍λ 1 >0 , λ 2<0 . បន្ទាប់មកចំណុចតំណាងដាក់នៅលើអ័ក្ស ξ នឹងផ្លាស់ទីឆ្ងាយពីប្រភពដើម ហើយដាក់នៅលើអ័ក្ស η – នឹងចូលទៅជិតប្រភពដើមនៃកូអរដោនេដោយមិនកំណត់, ដោយមិនឈានដល់វាក្នុងពេលវេលាកំណត់. កន្លែងណាដែលចំណុចតំណាងគឺនៅពេលដំបូង (លើកលែងតែចំណុចឯកវចនៈ និងចំណុចនៅលើ asymptote η =0), នៅទីបំផុតវានឹងផ្លាស់ទីឆ្ងាយពីស្ថានភាពលំនឹង ទោះបីជានៅដើមដំបូង វាផ្លាស់ទីតាមខ្សែកោងអាំងតេក្រាលមួយឆ្ពោះទៅកាន់ចំណុចឯកវចនៈ.
វាច្បាស់ណាស់។ Saddle-type singular point តែងតែមិនស្ថិតស្ថេរ . មានតែនៅក្រោមលក្ខខណ្ឌដំបូងដែលបានជ្រើសរើសពិសេសនៅលើ asymptote ប៉ុណ្ណោះ។η =0 ប្រព័ន្ធនឹងឈានដល់ស្ថានភាពលំនឹង។ ទោះជាយ៉ាងណាក៏ដោយនេះមិនផ្ទុយនឹងការអះអាងដែលថាប្រព័ន្ធមិនស្ថិតស្ថេរនោះទេ។ ប្រសិនបើអ្នករាប់, ថាស្ថានភាពដំបូងទាំងអស់នៃប្រព័ន្ធនៅលើយន្តហោះដំណាក់កាលគឺប្រហែលស្មើគ្នា បន្ទាប់មកប្រូបាប៊ីលីតេនៃស្ថានភាពដំបូងបែបនេះដែលត្រូវគ្នានឹងចលនាក្នុងទិសដៅទៅ ចំណុចឯកវចនៈស្មើនឹងសូន្យ។ ដូច្នេះចលនាពិតប្រាកដណាមួយនឹងដកប្រព័ន្ធចេញពីស្ថានភាពលំនឹង។ត្រលប់ទៅកូអរដោណេx,y,យើងទទួលបានរូបភាពគុណភាពដូចគ្នានៃធម្មជាតិនៃចលនានៃគន្លងជុំវិញប្រភពដើម។
ព្រំដែនរវាងករណីដែលបានពិចារណានៃថ្នាំង និងអាបគឺជាករណីពេលណា ឧទាហរណ៍មួយនៃសូចនាករលក្ខណៈ λ 1 , បាត់ ដែលកើតឡើងនៅពេលដែលកត្តាកំណត់នៃប្រព័ន្ធ- កន្សោម adbc=0(សូមមើលរូបមន្ត 4.8 ). ក្នុងករណីនេះ មេគុណនៃសមីការផ្នែកខាងស្តាំ (4.4) គឺសមាមាត្រគ្នាទៅវិញទៅមក។:
ហើយប្រព័ន្ធមានលំនឹងរបស់វាបញ្ជាក់ចំណុចទាំងអស់នៃបន្ទាត់:
ខ្សែកោងអាំងតេក្រាលដែលនៅសល់គឺជាគ្រួសារនៃបន្ទាត់ប៉ារ៉ាឡែលដែលមានជម្រាលមួយ។ ស្របតាមចំណុចតំណាងទាំងចូលទៅជិតស្ថានភាពលំនឹង ឬផ្លាស់ទីចេញពីវា អាស្រ័យលើសញ្ញានៃឫសទីពីរនៃសមីការលក្ខណៈ λ 2 = a+d។(រូប ៤. ៧ ) ក្នុងករណីនេះកូអរដោនេនៃស្ថានភាពលំនឹងអាស្រ័យលើតម្លៃដំបូងនៃអថេរ។
ឫស λ 1 , λ 2 – ស្មុគស្មាញរួម
ក្នុងករណីនេះសម្រាប់ការពិតxនិង yយើងនឹង មានបន្សំស្មុគស្មាញ ξ , η (4.10) . ទោះជាយ៉ាងណាក៏ដោយ តាមរយៈការណែនាំការបំប្លែងកម្រិតមធ្យមមួយបន្ថែមទៀត វាក៏អាចធ្វើទៅបានផងដែរក្នុងករណីនេះដើម្បីកាត់បន្ថយការពិចារណាទៅជាការបំលែងឯកតាលីនេអ៊ែរពិតប្រាកដ។ តោះដាក់:
(4.16)
កន្លែងណា ក, ខ,និង u,v – តម្លៃពិត។ វាអាចត្រូវបានបង្ហាញថាការផ្លាស់ប្តូរពីx, yទៅ u,v នៅក្រោមការសន្មត់របស់យើង ពិតប្រាកដ លីនេអ៊ែរ ភាពដូចគ្នាជាមួយនឹងកត្តាកំណត់មិនសូន្យ។ ដោយសារសមីការ(៤.១០, ៤.១៦) យើងមាន៖
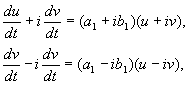
កន្លែងណា
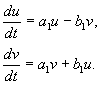(4.17)
បែងចែកសមីការទីពីរដោយទីមួយ, យើងទទួលបាន:
ដែលងាយស្រួលដាក់បញ្ចូលគ្នា, ប្រសិនបើយើងប្តូរទៅប្រព័ន្ធកូអរដោណេប៉ូល។ (r, φ ) . បន្ទាប់ពីការជំនួសយើងទទួលបានពីកន្លែងណា៖
.(4.18)
ដូច្នេះនៅលើយន្តហោះដំណាក់កាលu, vយើងកំពុងដោះស្រាយជាមួយក្រុមគ្រួសារនៃវង់លោការីត ដែលនីមួយៗមានចំណុច asymptotic នៅប្រភពដើម។ចំណុចឯកវចនៈដែលជាចំណុច asymptotic នៃខ្សែកោងអាំងតេក្រាលទាំងអស់ដែលមានទម្រង់ជាវង់, មិត្តរួមគ្នានៅក្នុងមិត្ត, បានហៅ ការផ្តោតអារម្មណ៍ ( រូប ៤.៨ ) .
ចូរយើងពិចារណាពីធម្មជាតិនៃចលនានៃចំណុចតំណាងនៅតាមបណ្តោយគន្លងដំណាក់កាល។ គុណទីមួយនៃសមីការ (4.17) ដោយយូនិងទីពីរទៅ vហើយបន្ថែមយើងទទួលបាន៖
កន្លែងណា
អនុញ្ញាតឱ្យ ក 1 < 0 (ក 1 = ឡើងវិញλ ) . ចំណុចតំណាងបន្ទាប់មកបន្តទៅជិតប្រភពដើមដោយមិនឈានដល់វាក្នុងរយៈពេលកំណត់។ នេះមានន័យថាគន្លងដំណាក់កាលគឺបង្វិលវង់ និងត្រូវគ្នាទៅនឹងលំយោលដែលសើមអថេរ។ វា - ការផ្តោតអារម្មណ៍ថេរ .
នៅក្នុងករណីនៃការផ្តោតអារម្មណ៍មានស្ថេរភាពដូចនៅក្នុងករណីនៃថ្នាំងដែលមានស្ថេរភាពមិនត្រឹមតែលក្ខខណ្ឌ Lyapunov ត្រូវបានគេពេញចិត្តនោះទេប៉ុន្តែក៏មានតម្រូវការតឹងរ៉ឹងបន្ថែមទៀត។ ពោលគឺសម្រាប់គម្លាតដំបូងណាមួយ ប្រព័ន្ធនឹងត្រឡប់មកជិតដូចការចង់បានទៅទីតាំងលំនឹង។ ស្ថេរភាពបែបនេះ ដែលគម្លាតដំបូងមិនត្រឹមតែមិនកើនឡើងប៉ុណ្ណោះទេ ប៉ុន្តែការពុកផុយ ទំនោរទៅសូន្យ ត្រូវបានគេហៅថា ស្ថេរភាពដាច់ខាត .
ប្រសិនបើនៅក្នុងរូបមន្ត (4.18) ក 1 >0 បន្ទាប់មកចំណុចតំណាងផ្លាស់ទីឆ្ងាយពីប្រភពដើម ហើយយើងកំពុងដោះស្រាយ ការផ្តោតអារម្មណ៍មិនស្ថិតស្ថេរ . នៅពេលផ្លាស់ទីពីយន្តហោះu,vទៅយន្តហោះដំណាក់កាលx, yវង់ក៏នឹងនៅតែជាវង់ដែរ ប៉ុន្តែនឹងត្រូវខូចទ្រង់ទ្រាយ។
ពិចារណាករណីនេះនៅពេលក 1
=0
. ដំណាក់កាលគន្លងនៅលើយន្តហោះu, vវានឹងមានរង្វង់ 
ដែលនៅលើយន្តហោះx, yសមរាងពងក្រពើ:
ដូច្នេះនៅក ១=0 តាមរយៈចំណុចពិសេសមួយ។x= 0y= 0 គ្មានខ្សែកោងអាំងតេក្រាលឆ្លងកាត់ទេ។ ចំណុចឯកវចនៈដាច់ស្រយាលបែបនេះ ដែលនៅជិតខ្សែកោងអាំងតេក្រាល គឺជាខ្សែកោងបិទ ជាពិសេស រាងពងក្រពើដែលបង្កប់នៅក្នុងគ្នាទៅវិញទៅមក និងបិទភ្ជាប់ចំណុចឯកវចនៈ ត្រូវបានគេហៅថា ចំណុចកណ្តាល។
ដូចនេះ លំនឹងទាំងប្រាំមួយប្រភេទគឺអាចធ្វើទៅបាន អាស្រ័យលើលក្ខណៈនៃឫសគល់នៃសមីការលក្ខណៈ (៤.៧)។ ទិដ្ឋភាពនៃគន្លងដំណាក់កាលនៅលើយន្តហោះ x, yសម្រាប់ករណីទាំងប្រាំមួយនេះ ត្រូវបានបង្ហាញនៅក្នុងរូបភព។ ៤.៩.
អង្ករ។ ៤.៩.ប្រភេទនៃរូបភាពដំណាក់កាលនៅក្នុងសង្កាត់នៃស្ថានភាពស្ថានីសម្រាប់ប្រព័ន្ធសមីការលីនេអ៊ែរ (4.4) ។
ស្ថានភាពលំនឹងទាំងប្រាំប្រភេទគឺរដុប ធម្មជាតិរបស់វាមិនផ្លាស់ប្តូរជាមួយនឹងការផ្លាស់ប្តូរតិចតួចគ្រប់គ្រាន់នៅក្នុងផ្នែកខាងស្តាំនៃសមីការ (4.4) ។ ក្នុងករណីនេះ ការផ្លាស់ប្តូរគួរតែមានទំហំតូចមិនត្រឹមតែនៅខាងស្តាំដៃប៉ុណ្ណោះទេ ប៉ុន្តែវាក៏មាននៅក្នុងនិស្សន្ទវត្ថុលំដាប់ទីមួយរបស់ពួកគេផងដែរ។ ស្ថានភាពលំនឹងទីប្រាំមួយ - ចំណុចកណ្តាល - មិនរឹង។ ជាមួយនឹងការផ្លាស់ប្តូរតិចតួចនៅក្នុងប៉ារ៉ាម៉ែត្រនៃផ្នែកខាងស្តាំនៃសមីការវាចូលទៅក្នុងការផ្តោតអារម្មណ៍ថេរឬមិនស្ថិតស្ថេរ។
ដ្យាក្រាម bifurcation
ចូរយើងណែនាំការសម្គាល់៖
.
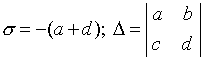(4.11)
បន្ទាប់មកសមីការលក្ខណៈអាចត្រូវបានសរសេរជាទម្រង់៖
.
(4.12)
ពិចារណាយន្តហោះដែលមានកូអរដោណេរាងចតុកោណ ស , ឃ ហើយសម្គាល់លើវានូវតំបន់ដែលត្រូវគ្នាទៅនឹងស្ថានភាពលំនឹងមួយ ឬប្រភេទផ្សេងទៀត ដែលត្រូវបានកំណត់ដោយធម្មជាតិនៃឫសគល់នៃសមីការលក្ខណៈ
.(4.13)
លក្ខខណ្ឌសម្រាប់ស្ថេរភាពនៃស្ថានភាពលំនឹងនឹងជាវត្តមាននៃផ្នែកពិតអវិជ្ជមាននៃ yលីត្រ 1 និង លីត្រ 2 . លក្ខខណ្ឌចាំបាច់ និងគ្រប់គ្រាន់សម្រាប់ការនេះគឺការបំពេញវិសមភាពស > 0, ឃ > 0 . នៅលើដ្យាក្រាម (4.15) លក្ខខណ្ឌនេះត្រូវគ្នាទៅនឹងចំណុចដែលមានទីតាំងនៅត្រីមាសទីមួយនៃយន្តហោះប៉ារ៉ាម៉ែត្រ។ ចំណុចឯកវចនៈនឹងជាការផ្តោតអារម្មណ៍ប្រសិនបើលីត្រ 1 និង លីត្រ 2 ស្មុគស្មាញ។ លក្ខខណ្ឌនេះត្រូវគ្នាទៅនឹងចំណុចទាំងនោះនៃយន្តហោះដែល , ទាំងនោះ។ ចំណុចរវាងសាខាពីរនៃប៉ារ៉ាបូឡាស 2 = 4 ឃ. ចំណុច Semiaxis ស = 0, ឃ> 0 ត្រូវគ្នាទៅនឹងស្ថានភាពលំនឹងនៃប្រភេទកណ្តាល។ ដូចគ្នានេះដែរលីត្រ 1 និង លីត្រ 2 - មានសុពលភាពប៉ុន្តែសញ្ញាផ្សេងគ្នា, i.e. ចំនុចឯកវចនៈនឹងជាក្រវ៉ាត់ប្រសិនបើ ឃ<0, ល។ ជាលទ្ធផលយើងទទួលបានដ្យាក្រាមភាគថាសនៃយន្តហោះប៉ារ៉ាម៉ែត្រ ស, ឃចូលទៅក្នុងតំបន់ដែលត្រូវគ្នាទៅនឹងប្រភេទផ្សេងៗនៃរដ្ឋលំនឹង។
អង្ករ។ ៤.១០.ដ្យាក្រាម bifurcation
សម្រាប់ប្រព័ន្ធសមីការលីនេអ៊ែរ ៤.៤
ប្រសិនបើមេគុណនៃប្រព័ន្ធលីនេអ៊ែរ a, b, c, ឃអាស្រ័យលើប៉ារ៉ាម៉ែត្រមួយចំនួន បន្ទាប់មកនៅពេលដែលប៉ារ៉ាម៉ែត្រនេះត្រូវបានផ្លាស់ប្តូរ តម្លៃក៏នឹងផ្លាស់ប្តូរផងដែរ។ស , ឃ . នៅពេលឆ្លងកាត់ព្រំដែន លក្ខណៈនៃដំណាក់កាលបញ្ឈរផ្លាស់ប្តូរគុណភាព។ ដូច្នេះព្រំដែនបែបនេះត្រូវបានគេហៅថាព្រំដែន bifurcation - នៅលើជ្រុងផ្ទុយគ្នានៃព្រំដែនប្រព័ន្ធមានពីរដំណាក់កាលផ្សេងគ្នា topologically ហើយតាមនោះមានពីរប្រភេទផ្សេងគ្នានៃឥរិយាបទ។
ដ្យាក្រាមបង្ហាញពីរបៀបដែលការផ្លាស់ប្តូរបែបនេះអាចកើតឡើង។ ប្រសិនបើយើងមិនរាប់បញ្ចូលករណីពិសេស - ប្រភពដើមនៃកូអរដោណេ - នោះវាងាយមើលឃើញថា សោអាចចូលទៅក្នុងថ្នាំង មានស្ថេរភាព ឬមិនស្ថិតស្ថេរនៅពេលឆ្លងកាត់អ័ក្ស y ។ ថ្នាំងដែលមានស្ថេរភាពអាចផ្លាស់ទីទៅកែប ឬការផ្តោតអារម្មណ៍មានស្ថេរភាព ហើយដូច្នេះនៅលើ។ ចំណាំថាថ្នាំងមានស្ថេរភាព-ការផ្តោតអារម្មណ៍មានស្ថេរភាព និងថ្នាំងមិនស្ថិតស្ថេរ-ការផ្លាស់ប្តូរការផ្តោតអារម្មណ៍មិនស្ថិតស្ថេរគឺមិនមែនជាការបំប្លែងទេ ចាប់តាំងពីធាតុកំពូលនៃលំហដំណាក់កាលមិនផ្លាស់ប្តូរក្នុងករណីនេះ។ យើងនឹងនិយាយលម្អិតបន្ថែមទៀតអំពីសណ្ឋានដីនៃលំហដំណាក់កាល និងដំណើរផ្លាស់ប្តូរនៃការបំប្លែងក្នុងមេរៀនទី ៦។
នៅក្រោមការផ្លាស់ប្តូរ bifurcation ធម្មជាតិនៃស្ថេរភាពនៃចំណុចឯកវចនៈផ្លាស់ប្តូរ។ ឧទាហរណ៍ ការផ្តោតអារម្មណ៍មានស្ថេរភាពតាមរយៈមជ្ឈមណ្ឌលអាចប្រែទៅជាការផ្តោតអារម្មណ៍មិនស្ថិតស្ថេរ។ ការបំបែកនេះត្រូវបានគេហៅថា Andronov-Hopf bifurcationតាមឈ្មោះរបស់អ្នកវិទ្យាសាស្ត្រដែលបានសិក្សាវា។ ជាមួយនឹង bifurcation នេះនៅក្នុងប្រព័ន្ធ nonlinear វដ្តដែនកំណត់មួយត្រូវបានកើត ហើយប្រព័ន្ធនេះក្លាយជាលំយោលដោយខ្លួនឯង (សូមមើលការបង្រៀនទី 8) ។
ឧទាហរណ៍។ ប្រព័ន្ធប្រតិកម្មគីមីលីនេអ៊ែរ
សារធាតុ Xហូរចូលពីខាងក្រៅក្នុងអត្រាថេរ ប្រែទៅជាសារធាតុ Y និងក្នុងអត្រាសមាមាត្រទៅនឹងកំហាប់នៃសារធាតុ យត្រូវបានយកចេញពីលំហប្រតិកម្ម។ ប្រតិកម្មទាំងអស់មានលំដាប់ទីមួយ លើកលែងតែការហូរចូលនៃរូបធាតុពីខាងក្រៅដែលមានលំដាប់សូន្យ។ គ្រោងការណ៍ប្រតិកម្មមើលទៅដូចនេះ៖
(4.14)
និងត្រូវបានពិពណ៌នាដោយប្រព័ន្ធសមីការ៖
(4.15)
យើងទទួលបានការប្រមូលផ្តុំនៅស្ថានីដោយស្មើផ្នែកខាងស្តាំទៅសូន្យ៖
.(4.16)
ពិចារណាពីរូបភាពដំណាក់កាលនៃប្រព័ន្ធ។ ចូរយើងបែងចែកសមីការទីពីរនៃប្រព័ន្ធ (4.16) ដោយទីមួយ។ យើងទទួលបាន:
.(4.17)
សមីការ (4.17) កំណត់ឥរិយាបថនៃអថេរនៅលើប្លង់ដំណាក់កាល។ អនុញ្ញាតឱ្យយើងបង្កើតរូបភាពដំណាក់កាលនៃប្រព័ន្ធនេះ។ ដំបូងយើងគូរ isoclines សំខាន់នៅលើយន្តហោះដំណាក់កាល។ សមីការនៃ isocline នៃតង់សង់បញ្ឈរ៖
សមីការសម្រាប់ isocline នៃតង់សង់ផ្ដេក៖
ចំណុចឯកវចនៈ (ស្ថានភាពស្ថានី) ស្ថិតនៅចំនុចប្រសព្វនៃ isoclines សំខាន់។
ឥឡូវនេះអនុញ្ញាតឱ្យយើងកំណត់នៅមុំណាដែលអ័ក្សកូអរដោនេកាត់ខ្សែកោងអាំងតេក្រាល។
ប្រសិនបើ ក x= 0 បន្ទាប់មក។
ដូច្នេះតង់សង់នៃជម្រាលនៃតង់សង់ទៅខ្សែកោងអាំងតេក្រាល។ y=y(x),ឆ្លងកាត់អ័ក្ស y x=0, គឺអវិជ្ជមាននៅក្នុងយន្តហោះពាក់កណ្តាលខាងលើ (រំលឹកថាអថេរ x, yមានតម្លៃប្រមូលផ្តុំ ហើយដូច្នេះយើងចាប់អារម្មណ៍តែលើ quadrant ខាងស្តាំខាងលើនៃយន្តហោះដំណាក់កាល)។ ក្នុងករណីនេះតម្លៃនៃតង់សង់នៃមុំទំនោរនៃតង់សង់កើនឡើងជាមួយនឹងចម្ងាយពីប្រភពដើម។
ពិចារណាអ័ក្ស y= 0. នៅចំនុចប្រសព្វនៃអ័ក្សនេះ ខ្សែកោងអាំងតេក្រាលត្រូវបានពិពណ៌នាដោយសមីការ
នៅ តង់សង់នៃជម្រាលនៃខ្សែកោងអាំងតេក្រាលឆ្លងកាត់អ័ក្ស abscissa គឺវិជ្ជមាន ហើយកើនឡើងពីសូន្យទៅគ្មានដែនកំណត់ជាមួយនឹងការកើនឡើង x.
នៅ។
បន្ទាប់មក ជាមួយនឹងការកើនឡើងបន្ថែមទៀត តង់សង់នៃជម្រាលមានការថយចុះនៅក្នុងតម្លៃដាច់ខាត នៅសល់អវិជ្ជមាន និងមានទំនោរទៅ -1 នៅ x ® ¥ . ដោយដឹងពីទិសដៅនៃតង់សង់ទៅខ្សែកោងអាំងតេក្រាលនៅលើ isoclines សំខាន់ និងនៅលើអ័ក្សកូអរដោនេ វាងាយស្រួលក្នុងការបង្កើតរូបភាពទាំងមូលនៃគន្លងដំណាក់កាល។
 |
|
ធម្មជាតិនៃស្ថេរភាពនៃចំណុចឯកវចនៈនឹងត្រូវបានបង្កើតឡើងដោយប្រើវិធីសាស្ត្រ Lyapunov ។ កត្តាកំណត់លក្ខណៈនៃប្រព័ន្ធមានទម្រង់៖
.
ការពង្រីកកត្តាកំណត់ យើងទទួលបានសមីការលក្ខណៈនៃប្រព័ន្ធ៖ , i.e. ឫសគល់នៃសមីការលក្ខណៈគឺអវិជ្ជមានទាំងពីរ។ ដូច្នេះស្ថានភាពស្ថានីនៃប្រព័ន្ធគឺជាថ្នាំងដែលមានស្ថេរភាព។ ទន្ទឹមនឹងនេះការប្រមូលផ្តុំសារធាតុ Xទំនោរទៅរកស្ថានភាពស្ថានីតែងតែជាឯកតា ការប្រមូលផ្តុំនៃសារធាតុ Y អាចឆ្លងកាត់អប្បបរមា ឬអតិបរមា។ របប Oscillatory នៅក្នុងប្រព័ន្ធបែបនេះគឺមិនអាចទៅរួចទេ។
