Šajā nodarbībā mēs runāsim par eksponenciālajām un logaritmiskajām funkcijām. Tos parasti pēta kopā, jo tie ir savstarpēji apgriezti. Mēs runāsim par šo funkciju izmantošanu, par to, kāpēc šīs funkcijas ir izvēlētas izpētei.

Eksponenciālo funkciju izmanto, lai aprakstītu visas parādības, kuras mēs saucam par lavīnu procesiem. Skaidrāk sakot, tie ir procesi, kuros lieluma izmaiņas ir proporcionālas jau esošajam lieluma daudzumam (jo vairāk, jo vairāk tas mainās; jo mazāk, jo mazāk mainās).

Šāda procesa piemērs ir baktēriju vairošanās. Apsvērsim šādu uzdevumu. Glāzē ir viena baktērija. Katru sekundi tas sadalās divās baktērijās, jaunas baktērijas arī sadalās divās katrā sekundē utt. Minūtes laikā viss stikls bija piepildīts ar baktērijām. Cik baktēriju glāzē bija sekundi pirms tam?

Gribētos teikt, ka bija iepildīts nedaudz mazāk par veselu glāzi, kaut kur, bet pareizā atbilde ir: pusglāze. Ja piepilda pusi glāzes, tad pēc sekundes katra baktērija sadalīsies daļās, un tās piepildīs visu glāzi. Kā redzat, pirmā glāzes puse tika piepildīta sekundēs, bet otrā puse tika piepildīta tikai sekundē.

Kūstošie ledāji

Noteikti visi ir dzirdējuši par ledus kušanas problēmu uz planētas. Kāpēc notiek šādi apledošanas un, gluži otrādi, sasilšanas procesi? Viņi bija agrāk, lai gan tagad viņi saka, ka cilvēka darbībai ir galvenā ietekme uz viņu ātrumu. Ir dažādas hipotēzes, bet tas nav tik svarīgi.

Vēl svarīgāk ir tas, ka ledus daudzuma samazināšana palielina absorbētās saules enerģijas daudzumu. Tas ir, jo mazāk ledus kļūst, jo ātrāk tas izkusīs. Process ir eksponenciāls vai, citiem vārdiem sakot, sevi izsaucošs, pašbarojošs.

Šāds process ir aprakstīts eksponenciāla funkcija (vai eksponenciāla): (1. att.). - bāze, , , un - eksponents, mainīgā vērtība.

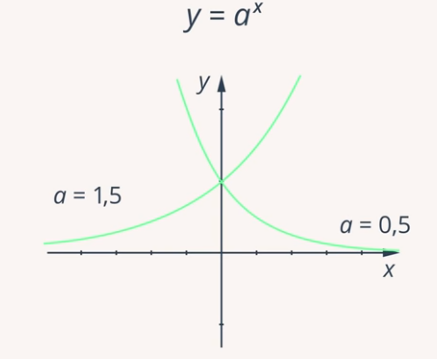
Rīsi. 1. Funkcijas grafiks

Vēl viens daudziem pazīstamas eksponenciālās funkcijas piemērs ir saliktie procenti. Ja mēs ieliekam naudu bankā par noteiktu procentu, kamēr mēs naudu neizņemam, un procenti tiek iekasēti par visu pieejamo summu, tad summa, ko mēs saņemsim periodos: , kur ir sākotnējais depozīts, ir procentu likme, ir pagājušo periodu skaits (gadi, mēneši utt.). Sākumā apjoms augs lēni, bet pēc tam pieaugums paātrināsies.

Vēl viens labs piemērs. Ja paaugstinām līdz pakāpei, tad iegūstam aptuveni, bet pakāpē tas ir praktiski. Ja šo piemēru uzrāda procentu veidā, tad pirmajā gadījumā tiek iekasēta diena, tad pēc gada summa pieaugs par koeficientu. Un otrajā gadījumā tiek izņemts viens procents dienā, tad pēc gada gandrīz nekas nepaliks.

Tajā pašā laikā viena no eksponenciālās funkcijas raksturīgajām iezīmēm ir tāda, ka saskaņā ar šādu shēmu summa nevar samazināties. Līdzīgs kodolfizikas piemērs ir pussabrukšanas periods. Radioaktīvajiem elementiem ir pussabrukšanas periods, piemēram, ar gadiem vielas masa samazināsies uz pusi (2. att.).

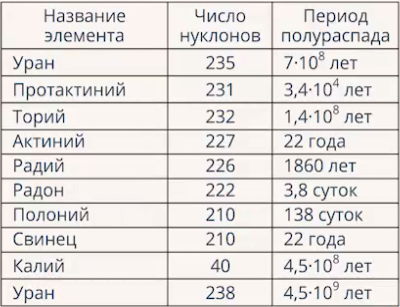
Rīsi. 2. Dažu elementu pussabrukšanas periodu tabula

Tas ir, ja mums bija kilograms vielas, tad pirmajos gados pazudīs grams vielas (diezgan daudz), bet nākamajos - jau grams utt. Un tad būs periods, kad ar gadiem aizies aptuveni grams vielas. Šis ir eksponenta samazināšanās piemērs.

Ja ņemam vērā visu funkciju kopu un no tām atlasām tās, kurām ir šāda īpašība: , tad tas tiks apmierināts eksponenciālajām funkcijām: .