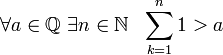Din punct de vedere istoric, primul numere întregi$N$, ca urmare a recalculării farts. Mulțimea acestor numere este infinită și formează o serie naturală $N=\(1, 2, 3, ..., n, ...\)$. În acest set, operațiile de adunare și înmulțire sunt fezabile. Pentru efectuarea operației de scădere au fost necesare numere noi, ceea ce a dus la apariția unui set de numere întregi: $Z$. $Z=N_+\cup N_- \cup \(0\)$. Astfel, în mulțimea numerelor întregi se efectuează întotdeauna operațiile de adunare, înmulțire, scădere.
Numere rationale
Nevoia de a efectua împărțirea a condus la mulțimea numerelor raționale $Q$. $Q=\(\frac(m)(n), m\în Z, n\în N\)$.
Definiție. Două numere raționale sunt egale: $\frac(m_1)(n_1)=\frac(m_2)(n_2)$ - dacă $m_1\cdot n_2=n_1\cdot m_2$. Aceasta înseamnă că fiecare Numar rational poate fi reprezentat unic ca o fracție ireductibilă $\frac(m)(n)$. $gcd(m, n)=1$.
Proprietăţile mulţimii numerelor raţionale
1. Ca urmare operatii aritmetice peste numere raționale (adunare, înmulțire, scădere, împărțire, cu excepția împărțirii la zero), se obține un număr rațional.
2. Mulțimea numerelor raționale este ordonată, adică pentru orice pereche de numere raționale $a$ și $b$ sau $a
3. Mulțimea numerelor raționale este densă, adică pentru orice pereche de numere raționale $a$ și $b$ există un număr rațional $c$ astfel încât $a Orice număr rațional pozitiv poate fi întotdeauna reprezentat ca o fracție zecimală: fie periodic finit, fie infinit. De exemplu: $\frac(3)(5)=0,6$, $\frac(1)(3)=0,333...=0,(3)$. $\frac(m)(n)=a_0,a_1a_1...a_kb_1b_2b_3...b_nb_1b_2b_3...b_n...$. $b_1b_2b_3...b_n...$ - se numește perioada fracției zecimale, unde nu toți $b_i=0$. Rețineți că o fracție finită poate fi scrisă ca o fracție periodică infinită cu zero în perioadă. $\frac(m)(n)=a_0,a_1a_1...a_k000000...$, $a_k\ne0$. Cu toate acestea, o altă reprezentare a numerelor raționale ca fracție zecimală este mai comună: $\frac(m)(n)=a_0,a_1a_1...(a_k-1)999...$. Numerele raționale negative $-\frac(m)(n)$ sunt scrise ca expansiune zecimală a unui număr rațional de forma $\frac(m)(n)$ luate cu semnul opus. Numărul $0$ este reprezentat ca $0,000...$. Astfel, orice număr rațional este întotdeauna reprezentabil ca o fracție periodică zecimală infinită care nu conține $0$ în perioadă, cu excepția numărului $0$ însuși. Această vedere este singura. Mulțimea numerelor raționale este închisă sub patru operații aritmetice. Totuși, în mulțimea numerelor raționale, soluția celei mai simple ecuații de forma $x^2-n=0$ nu are întotdeauna loc. Prin urmare, este necesar să se introducă numere noi. Să arătăm că printre numerele raționale nu există niciun număr al cărui pătrat să fie egal cu trei. Dovada se realizează prin metoda contradicţiei. Să presupunem că există un număr rațional $\frac(m)(n)$ astfel încât pătratul său să fie trei: $\left(\frac(m)(n)\right)^2=3\;\;\;( 1 )$. $\frac(m^2)(n^2)=3$, $m^2=3n^2.\;\;\;(2)$ Partea dreaptă a egalității (2) este divizibil cu 3. Prin urmare, $m^2$ este și el divizibil cu 3, deci $m$ este divizibil cu 3, ceea ce înseamnă că $m=3k$. Înlocuind în ecuația (2), obținem: $3k^2=n^2.\;\;\;(3)$ Partea stângă a lui $(3)$ este divizibilă cu $3$, deci partea dreaptă este, de asemenea, divizibilă cu $3$. Prin urmare, $n^2$ este divizibil cu $3$, deci $n$ este de asemenea divizibil cu $3$, de unde $n=3p$. Ca rezultat, obținem: $\frac(m)(n)=\frac(3k)(3p)$, adică fracția $\frac(m)(n)$ s-a dovedit a fi reductibilă, ceea ce contrazice ipoteza . Aceasta înseamnă că printre numerele raționale nu există un astfel de număr, al cărui pătrat este egal cu trei. Dar există un număr al cărui pătrat este trei. Poate fi reprezentat ca o fracție neperiodică infinită. Și avem un nou tip de numere. Să le numim iraționale. Definiție. Un număr irațional este orice fracție neperiodică infinită. Mulțimea tuturor fracțiilor neperiodice infinite se numește mulțime de numere iraționale și se notează cu $I$. Unirea mulțimii numerelor raționale $Q$ și a numerelor iraționale $I$ dă mulțimea numerelor reale $R$: $Q\cup I=R$. Astfel, orice număr real poate fi reprezentat ca o fracție zecimală infinită: periodic în cazul unui număr rațional și neperiodic în cazul unui număr irațional. Pentru numerele reale $a=a_0,a_1a_2a_3\ldots a_n\ldots$, $b=b_0,b_1b_2b_3\ldots b_n\ldots$ comparația este următoarea: 1) Fie $a$ și $b$ ambele pozitive: $a>0$, $b>0$, apoi: $a=b$ dacă pentru orice $k$ $a_k=b_k$; $a>b$ dacă $\există s$ $\forall k 2) Fie $a>0$, $b<0$, или иначе: $b<0 3) Fie $a$ și $b$ ambele negative: $a<0$, $b<0$, тогда: $a=b$ dacă pentru $-a=-b$; Există numere de altă natură - operația de extragere a rădăcinii pătrate duce adesea la ele (și nu numai asta, pur și simplu nu o știm încă). Deci, trebuie să cunoaștem noile numere mai detaliat. Dar mai întâi, să încercăm să sistematizăm cunoștințele noastre despre numerele „vechi”, adică raționale. 1. Câteva simboluri ale limbajului matematic
Acestea erau numere întregi, fracții comune, fracții zecimale. Pentru toate aceste numere, puteți folosi aceeași notație, despre care vom discuta acum. 5 = 5,00000... = 5,(0). Același lucru este valabil și pentru numărul 8,377: 8,377 = 8,377000... = 8,377(0). Pentru a face totul frumos, ei spun așa: 8,377 este o fracție zecimală finită, iar 8,377000 ... este o fracție zecimală infinită. În general, orice număr rațional poate fi scris ca o fracție periodică zecimală infinită. Cometariu.
Această concluzie este convenabilă pentru teorie, dar nu foarte convenabilă pentru practică. La urma urmei, dacă este dată fracția zecimală finală 8,377, atunci de ce este necesar să o scrieți sub forma 8,377 (0)? Prin urmare, ei spun de obicei acest lucru: orice număr rațional poate fi scris ca o fracție zecimală finită sau ca o fracție periodică zecimală infinită. Mulțimea numerelor raționale se notează și poate fi scrisă astfel: Se dovedește că intrări diferite pot reprezenta aceeași fracție, de exemplu, și , (toate fracțiile care pot fi obținute una de la alta prin înmulțirea sau împărțirea cu același număr natural reprezintă același număr rațional). Întrucât împărțind numărătorul și numitorul unei fracții la cel mai mare divizor comun al lor, se poate obține singura reprezentare ireductibilă a unui număr rațional, se poate vorbi despre mulțimea lor ca pe o mulțime ireductibil fracții cu numărător întreg între prima și numitor natural: Iată cel mai mare divizor comun al numerelor și . Mulțimea numerelor raționale este o generalizare naturală a mulțimii numerelor întregi. Este ușor de observat că, dacă un număr rațional are un numitor, atunci este un număr întreg. Mulțimea numerelor raționale este peste tot densă pe axa numerelor: între oricare două numere raționale diferite există cel puțin un număr rațional (și, prin urmare, o mulțime infinită de numere raționale). Cu toate acestea, se dovedește că mulțimea numerelor raționale are o cardinalitate numărabilă (adică toate elementele sale pot fi renumerotate). Rețineți, apropo, că până și grecii antici erau convinși de existența unor numere care nu pot fi reprezentate ca o fracție (de exemplu, au demonstrat că nu există un număr rațional al cărui pătrat este 2). Proprietăți Proprietăți de bază Mulțimea numerelor raționale satisface șaisprezece proprietăți de bază care pot fi obținute cu ușurință din proprietățile numerelor întregi. Proprietăți suplimentare Toate celelalte proprietăți inerente numerelor raționale nu sunt evidențiate ca fiind de bază, deoarece, în general, ele nu se mai bazează direct pe proprietățile numerelor întregi, ci pot fi demonstrate pe baza proprietăților de bază date sau direct prin definiția lui. vreun obiect matematic. Există o mulțime de astfel de proprietăți suplimentare. Este logic să cităm doar câteva dintre ele. 25..Mulțimea J de numere iraționale Exemple de numere iraționale: Setul de numere iraționale este notat cu litera engleză majusculă [ai] - „I”. Între mulțimea numerelor, numerele iraționale ocupă un loc aparte. Ele nu sunt incluse în numerele raționale. Numere irationale(spre deosebire de cele raționale) nu poate fi reprezentată ca o fracție a / b , unde a ∈ Z (a aparține numerelor întregi), b∈N (b aparține numerelor naturale). 26. Mulțimea R de numere reale numar real De la Wikipedia, enciclopedia liberă Salt la: navigare, căutare Real, sau numar real- o abstractizare matematică care a apărut din necesitatea de a măsura mărimile geometrice și fizice ale lumii înconjurătoare, precum și de a efectua operații precum extragerea unei rădăcini, calcularea logaritmilor, rezolvarea ecuațiilor algebrice. Linia numerică Dacă în procesul de numărare au apărut numerele naturale, numerele raționale - din necesitatea de a opera cu părți ale unui întreg, atunci numerele reale sunt destinate măsurării cantităților continue. Astfel, extinderea stocului de numere luat în considerare a condus la mulțimea numerelor reale, care, pe lângă numerele raționale, include și alte elemente numite numere irationale. Conceptul de număr real poate fi vizualizat folosind linie numerică. Dacă alegeți o direcție pe o dreaptă, un punct de plecare și o unitate de lungime pentru măsurarea segmentelor, atunci fiecare număr real poate fi asociat cu un anumit punct pe această dreaptă și invers, fiecare punct va reprezenta câteva, și mai mult. , doar unul, număr real. Din cauza acestei corespondențe, termenul linie numerică este de obicei folosit ca sinonim pentru mulțimea numerelor reale. Conceptul de număr real a parcurs un drum lung de a deveni. Chiar și în Grecia antică, în școala lui Pitagora, care punea numerele întregi și relațiile lor ca bază pentru tot, existența cantități incomensurabile(incomensurabilitate a laturii și diagonalei unui pătrat), adică, în terminologia modernă, numere care nu sunt raționale. În urma acesteia, Eudoxus din Cnidus a încercat să construiască o teorie generală a numărului care să includă cantități incomensurabile. După aceea, timp de mai bine de două mii de ani, nimeni nu a simțit nevoia unei definiții precise a conceptului de număr real, în ciuda extinderii treptate a acestui concept. Abia în a doua jumătate a secolului al XIX-lea, când dezvoltarea analizei matematice a necesitat restructurarea fundamentelor sale la un nou nivel de rigoare, mai înalt, a fost creată o teorie riguroasă a numerelor reale în lucrările lui K. Weierstrass, R. Dedekind. , G. Cantor, E. Heine, S. Mere . Din punctul de vedere al matematicii moderne, mulțimea numerelor reale este un câmp ordonat continuu. Această definiție, sau un sistem echivalent de axiome, definește exact conceptul de număr real în sensul că există un singur câmp ordonat continuu până la izomorfism. Mulțimea numerelor reale are o notație standard - R("R bold") sau (ing. tablă îndrăzneață„R”) din lat. realis- valabil. 27. Sisteme numerice Notaţie- o metodă simbolică de scriere a numerelor, reprezentarea numerelor folosind caractere scrise. Notaţie: Sistemele numerice sunt împărțite în pozițional, nepoziționalăși amestecat.Numere irationale
Numere reale
Compararea numerelor reale
Luați în considerare, de exemplu, numărul întreg 5, fracția comună și zecimala 8,377. Numărul întreg 5 poate fi scris ca o zecimală infinită: 5,0000... Decimalul 8,377 poate fi scris și ca o zecimală infinită fracție zecimală: 8,377000... Pentru număr, să folosim metoda „diviziunii unghiulare”:
După cum puteți vedea, începând de la a doua cifră după virgulă, se repetă același grup de numere: 18, 18, 18, .... Astfel = 0,3181818... . Pe scurt, se scrie astfel: 0,3 (18). Un grup de cifre care se repetă după virgulă zecimală se numește perioadă, iar fracția zecimală în sine este numită fracție periodică zecimală infinită.
fracție periodică zecimală infinită. Pentru a face acest lucru, scrieți numărul 0 în perioada:
Astfel, numărul 5, și numărul și numărul 8,377 au fost scrise ca o fracție periodică zecimală infinită.![]()