Anweisung

Verwenden Sie pi, um den Radius aus der bekannten Fläche eines Kreises zu ermitteln. Diese Konstante gibt das Verhältnis zwischen dem Durchmesser eines Kreises und der Länge seines Randes (Kreises) an. Der Umfang eines Kreises ist die maximale Fläche der Ebene, die mit seiner Hilfe abgedeckt werden kann, und der Durchmesser ist gleich zwei Radien, daher kann die Fläche mit dem Radius auch mit einem Anteil korrelieren, der miteinander korrelieren kann in Form von Pi ausgedrückt werden. Diese Konstante (π) ist definiert als die Fläche (S) und der quadrierte Radius (r) des Kreises. Daraus folgt, dass der Radius als Quadratwurzel des Quotienten aus der Teilung der Fläche durch die Zahl Pi ausgedrückt werden kann: ​​r=√(S/π).

Erastofen leitete lange Zeit die Bibliothek von Alexandria, die berühmteste Bibliothek der Antike. Abgesehen davon, dass er die Größe unseres Planeten berechnete, machte er eine Reihe wichtiger Erfindungen und Entdeckungen. Erfand eine einfache Methode zur Bestimmung von Primzahlen, die heute als "Sieb des Erastothenes" bezeichnet wird.

Er zeichnete eine „Weltkarte“, in der er alle Teile der Welt zeigte, die den alten Griechen damals bekannt waren. Die Karte galt als eine der besten ihrer Zeit. Er entwickelte ein Längen- und Breitengradsystem und einen Kalender mit Schaltjahren. Erfand die Armillarsphäre, ein mechanisches Gerät, das von frühen Astronomen verwendet wurde, um die scheinbare Bewegung von Sternen am Himmel zu demonstrieren und vorherzusagen. Er stellte auch einen Sternenkatalog zusammen, der 675 Sterne umfasste.

Quellen:

• Der griechische Wissenschaftler Eratosthenes von Cyrene hat zum ersten Mal auf der Welt den Radius der Erde berechnet
• Eratosthenes „Berechnung des Erdumfangs“.
• Eratosthenes

Wie findet man die Fläche eines Kreises? Finden Sie zuerst den Radius. Lernen Sie, einfache und komplexe Probleme zu lösen.

Ein Kreis ist eine geschlossene Kurve. Jeder Punkt auf der Kreislinie hat den gleichen Abstand vom Mittelpunkt. Ein Kreis ist eine flache Figur, daher ist es einfach, Probleme beim Auffinden des Bereichs zu lösen. In diesem Artikel werden wir uns ansehen, wie man die Fläche eines Kreises findet, der in ein Dreieck, ein Trapez, ein Quadrat eingeschrieben und um diese Figuren herum beschrieben ist.

Um die Fläche einer bestimmten Figur zu finden, müssen Sie den Radius, den Durchmesser und die Zahl π kennen.

Radius R ist die Entfernung, die durch den Mittelpunkt des Kreises begrenzt wird. Die Längen aller R-Radien eines Kreises sind gleich.

Durchmesser D ist eine Linie zwischen zwei beliebigen Punkten auf einem Kreis, die durch den Mittelpunkt verläuft. Die Länge dieses Segments ist gleich der Länge des R-Radius mal 2.

Zahl π ist ein konstanter Wert, der gleich 3,1415926 ist. In der Mathematik wird diese Zahl üblicherweise auf 3,14 aufgerundet.

Die Formel zum Ermitteln der Fläche eines Kreises anhand des Radius:

Beispiele zum Lösen von Aufgaben zum Finden der S-Fläche eines Kreises durch den R-Radius:

Aufgabe: Finden Sie die Fläche eines Kreises, wenn sein Radius 7 cm beträgt.

Entscheidung: S=πR², S=3,14*7², S=3,14*49=153,86 cm².

Antworten: Die Fläche des Kreises beträgt 153,86 cm².

Die Formel zum Ermitteln der S-Fläche eines Kreises in Bezug auf den D-Durchmesser lautet:

Beispiele für das Lösen von Aufgaben zum Finden von S, wenn D bekannt ist:

————————————————————————————————————————-

Aufgabe: Finden Sie das S des Kreises, wenn sein D 10 cm beträgt.

Entscheidung: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 cm².

Antworten: Die Fläche einer flachen runden Figur beträgt 78,5 cm².

Bestimmung des S-Kreises bei bekanntem Umfang:

Finden Sie zuerst heraus, was der Radius ist. Der Umfang wird nach folgender Formel berechnet: L=2πR bzw. der Radius R ist gleich L/2π. Jetzt finden wir die Fläche des Kreises mit der Formel durch R.

Betrachten Sie die Lösung am Beispiel des Problems:

———————————————————————————————————————-

Aufgabe: Finden Sie die Fläche eines Kreises, wenn der Umfang L bekannt ist - 12 cm.

Entscheidung: Zuerst finden wir den Radius: R=L/2π=12/2*3,14=12/6,28=1,91.

Nun finden wir die Fläche durch den Radius: S=πR²=3,14*1,91²=3,14*3,65=11,46 cm².

Antworten: Die Fläche eines Kreises beträgt 11,46 cm².

Es ist einfach, die Fläche eines Kreises zu finden, der in ein Quadrat eingeschrieben ist. Die Seite des Quadrats ist der Durchmesser des Kreises. Um den Radius zu finden, musst du die Seite durch 2 teilen.

Die Formel zum Ermitteln der Fläche eines Kreises, der in ein Quadrat eingeschrieben ist, lautet:

Beispiele für die Lösung von Problemen beim Ermitteln der Fläche eines Kreises, der in ein Quadrat eingeschrieben ist:

———————————————————————————————————————

Aufgabe 1: Die Seite einer quadratischen Figur ist bekannt, die 6 Zentimetern entspricht. Finden Sie den S-Bereich des Inkreises.

Entscheidung: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 cm².

Antworten: Die Fläche einer flachen runden Figur beträgt 28,26 cm².

————————————————————————————————————————

Aufgabe Nr. 2: Finden Sie S eines Kreises, der in eine quadratische Figur eingeschrieben ist, und seinen Radius, wenn eine Seite a = 4 cm ist.

Entscheide dich so: Finde zuerst R=a/2=4/2=2 cm.

Finden wir nun die Fläche des Kreises S=3,14*2²=3,14*4=12,56 cm².

Antworten: Die Fläche einer flachen runden Figur beträgt 12,56 cm².

Etwas schwieriger ist es, die von einem Quadrat umschriebene Fläche einer runden Figur zu finden. Aber wenn Sie die Formel kennen, können Sie diesen Wert schnell berechnen.

Die Formel zum Finden von S eines Kreises, der um eine quadratische Figur umschrieben ist:

Beispiele für das Lösen von Aufgaben zum Finden der Fläche eines Kreises, der in der Nähe einer quadratischen Figur beschrieben wird:

Aufgabe

Ein Kreis, der in eine dreieckige Figur eingeschrieben ist, ist ein Kreis, der alle drei Seiten des Dreiecks berührt. Ein Kreis kann in jede dreieckige Figur eingeschrieben werden, aber nur in eine. Der Mittelpunkt des Kreises ist der Schnittpunkt der Winkelhalbierenden des Dreiecks.

Die Formel zum Ermitteln der Fläche eines Kreises, der in ein gleichschenkliges Dreieck eingeschrieben ist, lautet:

Wenn der Radius bekannt ist, kann die Fläche mit der Formel berechnet werden: S=πR².

Die Formel zum Ermitteln der Fläche eines Kreises, der in ein rechtwinkliges Dreieck eingeschrieben ist, lautet:

Beispiele zum Lösen von Aufgaben:

Aufgabe 1

Wenn Sie in diesem Problem auch die Fläche eines Kreises mit einem Radius von 4 cm finden müssen, können Sie dies mit der Formel tun: S=πR²

Aufgabe Nr. 2

Entscheidung:

Jetzt, wo du den Radius kennst, kannst du die Fläche des Kreises in Bezug auf den Radius finden. Siehe obige Formel.

Aufgabe Nr. 3

Fläche eines um ein rechtwinkliges und gleichschenkliges Dreieck umschriebenen Kreises: Formel, Beispiele zur Problemlösung

Alle Formeln zum Ermitteln der Fläche eines Kreises laufen darauf hinaus, dass Sie zuerst seinen Radius ermitteln müssen. Wenn der Radius bekannt ist, ist das Auffinden der Fläche einfach, wie oben beschrieben.

Die Fläche eines um ein rechtwinkliges und gleichschenkliges Dreieck umschriebenen Kreises ergibt sich aus der folgenden Formel:

Beispiele für Problemlösungen:

Hier ist ein weiteres Beispiel für die Lösung eines Problems mit der Heron-Formel.

Das Lösen solcher Probleme ist schwierig, aber sie können gemeistert werden, wenn Sie alle Formeln kennen. Schüler lösen solche Probleme in der 9. Klasse.

Fläche eines Kreises, der in ein rechteckiges und gleichschenkliges Trapez eingeschrieben ist: Formel, Beispiele zur Problemlösung

Ein gleichschenkliges Trapez hat zwei gleiche Seiten. Ein rechteckiges Trapez hat einen Winkel von 90º. Überlegen Sie am Beispiel der Lösung von Problemen, wie Sie die Fläche eines Kreises finden, der in ein rechteckiges und gleichschenkliges Trapez eingeschrieben ist.

Beispielsweise wird einem gleichschenkligen Trapez ein Kreis einbeschrieben, der an der Berührungsstelle eine Seite in Segmente m und n teilt.

Um dieses Problem zu lösen, müssen Sie die folgenden Formeln verwenden:

Die Fläche eines Kreises, der in ein rechteckiges Trapez eingeschrieben ist, wird mit der folgenden Formel ermittelt:

Wenn die laterale Seite bekannt ist, dann können Sie den Radius durch diesen Wert finden. Die Höhe der Seite des Trapezes ist gleich dem Durchmesser des Kreises und der Radius ist der halbe Durchmesser. Dementsprechend ist der Radius R = d/2.

Beispiele für Problemlösungen:

Ein Trapez kann einem Kreis einbeschrieben werden, wenn die Summe seiner gegenüberliegenden Winkel 180º beträgt. Daher kann nur ein gleichschenkliges Trapez eingeschrieben werden. Der Radius zur Berechnung der Fläche eines um ein rechteckiges oder gleichschenkliges Trapez umschriebenen Kreises wird nach folgenden Formeln berechnet:

Beispiele für Problemlösungen:

Entscheidung: Die große Basis geht in diesem Fall durch die Mitte, da einem Kreis ein gleichschenkliges Trapez einbeschrieben ist. Die Mitte teilt diese Basis genau in zwei Hälften. Wenn die Basis AB 12 ist, dann kann der Radius R wie folgt ermittelt werden: R=12/2=6.

Antworten: Der Radius ist 6.

In der Geometrie ist es wichtig, die Formeln zu kennen. Aber es ist unmöglich, sich alle zu merken, daher ist es sogar in vielen Prüfungen erlaubt, ein spezielles Formular zu verwenden. Es ist jedoch wichtig, die richtige Formel zur Lösung eines bestimmten Problems finden zu können. Üben Sie das Lösen verschiedener Probleme zum Ermitteln des Radius und der Fläche eines Kreises, um Formeln richtig ersetzen zu können und genaue Antworten zu erhalten.

Video: Mathematik | Berechnung der Fläche eines Kreises und seiner Teile

- Dies ist eine flache Figur, bei der es sich um eine Reihe von Punkten handelt, die gleich weit vom Mittelpunkt entfernt sind. Alle sind gleich weit entfernt und bilden einen Kreis.

Eine Strecke, die den Mittelpunkt eines Kreises mit Punkten auf seinem Umfang verbindet, heißt Radius. In jedem Kreis sind alle Radien einander gleich. Eine Linie, die zwei Punkte auf einem Kreis verbindet und durch den Mittelpunkt verläuft, heißt Durchmesser. Die Formel für die Fläche eines Kreises wird mit einer mathematischen Konstante berechnet - der Zahl π ..

Das ist interessant : Die Zahl Pi. ist das Verhältnis des Umfangs eines Kreises zur Länge seines Durchmessers und ist ein konstanter Wert. Der Wert π = 3,1415926 wurde nach der Arbeit von L. Euler im Jahr 1737 verwendet.

Die Fläche eines Kreises kann mit der Konstanten π berechnet werden. und der Radius des Kreises. Die Formel für die Fläche eines Kreises in Bezug auf den Radius sieht so aus:

Betrachten Sie ein Beispiel für die Berechnung der Fläche eines Kreises mit dem Radius. Gegeben sei ein Kreis mit Radius R = 4 cm. Finden wir die Fläche der Figur.

Die Fläche unseres Kreises beträgt 50,24 Quadratmeter. cm.

Es gibt eine Formel die Fläche eines Kreises durch den Durchmesser. Es wird auch häufig verwendet, um die erforderlichen Parameter zu berechnen. Diese Formeln können verwendet werden, um zu finden.

Betrachten Sie ein Beispiel für die Berechnung der Fläche eines Kreises durch den Durchmesser, wobei Sie seinen Radius kennen. Gegeben sei ein Kreis mit einem Radius R = 4 cm. Zuerst suchen wir den Durchmesser, der bekanntlich doppelt so groß ist wie der Radius.


Jetzt verwenden wir die Daten für das Beispiel der Berechnung der Fläche eines Kreises mit der obigen Formel:

Wie Sie sehen, erhalten wir als Ergebnis die gleiche Antwort wie bei den ersten Berechnungen.

Die Kenntnis der Standardformeln zur Berechnung der Kreisfläche hilft in Zukunft bei der einfachen Bestimmung Sektor Bereich und es ist einfach, die fehlenden Mengen zu finden.

Wir wissen bereits, dass sich die Formel für die Kreisfläche aus dem Produkt des konstanten Wertes π und dem Quadrat des Kreisradius errechnet. Der Radius kann in Bezug auf den Umfang eines Kreises ausgedrückt werden und den Ausdruck in der Formel für die Fläche eines Kreises in Bezug auf den Umfang ersetzen:
Jetzt setzen wir diese Gleichheit in die Formel zur Berechnung der Kreisfläche ein und erhalten die Formel zur Ermittlung der Kreisfläche durch den Umfang

Betrachten Sie ein Beispiel für die Berechnung der Fläche eines Kreises durch den Umfang. Gegeben sei ein Kreis mit der Länge l = 8 cm, ersetzen wir den Wert in der abgeleiteten Formel:

Die Gesamtfläche des Kreises beträgt 5 Quadratmeter. cm.

Fläche eines um ein Quadrat umschriebenen Kreises

Es ist sehr einfach, die Fläche eines um ein Quadrat umschriebenen Kreises zu finden.

Dies erfordert nur die Seite des Quadrats und die Kenntnis einfacher Formeln. Die Diagonale des Quadrats ist gleich der Diagonale des umschriebenen Kreises. Wenn man die Seite a kennt, kann man sie mit dem Satz des Pythagoras finden: von hier.
Nachdem wir die Diagonale gefunden haben, können wir den Radius berechnen: .
Und dann setzen wir alles in die Grundformel für die Fläche eines um ein Quadrat umschriebenen Kreises ein:

Kreise erfordern eine sorgfältigere Herangehensweise und kommen bei B5-Aufgaben viel seltener vor. Gleichzeitig ist das allgemeine Lösungsschema noch einfacher als bei Polygonen (siehe Lektion " Flächen von Polygonen auf einem Koordinatengitter »).

Alles, was bei solchen Aufgaben erforderlich ist, ist, den Radius des Kreises R zu finden. Dann können Sie die Fläche des Kreises mit der Formel S = πR 2 berechnen. Aus dieser Formel folgt auch, dass es genügt, R 2 für die Lösung zu finden.

Um die angegebenen Werte zu finden, reicht es aus, auf dem Kreis einen Punkt anzugeben, der am Schnittpunkt der Gitterlinien liegt. Und dann den Satz des Pythagoras verwenden. Betrachten Sie spezifische Beispiele für die Berechnung des Radius:

Aufgabe. Ermitteln Sie die Radien der drei in der Abbildung gezeigten Kreise:

Führen wir in jedem Kreis zusätzliche Konstruktionen durch:

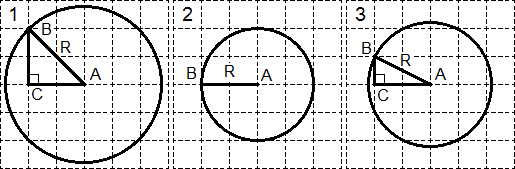
Auf dem Kreis wird jeweils der Punkt B so gewählt, dass er im Schnittpunkt der Gitterlinien liegt. Punkt C in den Kreisen 1 und 3 vervollständigt die Figur zu einem rechtwinkligen Dreieck. Es bleibt die Radien zu finden:

Betrachten Sie das Dreieck ABC im ersten Kreis. Nach dem Satz des Pythagoras: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.

Für den zweiten Kreis ist alles klar: R = AB = 2.

Der dritte Fall ähnelt dem ersten. Aus dem Dreieck ABC nach dem Satz des Pythagoras: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 1 2 + 2 2 \u003d 5.

Jetzt wissen wir, wie man den Radius eines Kreises (oder zumindest sein Quadrat) findet. Daher können wir den Bereich finden. Es gibt Aufgaben, bei denen es erforderlich ist, die Fläche eines Sektors und nicht den gesamten Kreis zu finden. In solchen Fällen ist es einfach, herauszufinden, welcher Teil des Kreises dieser Sektor ist, und somit die Fläche zu finden.

Aufgabe. Suchen Sie den Bereich S des schattierten Sektors. Geben Sie in Ihrer Antwort S / π an.

Offensichtlich ist der Sektor ein Viertel des Kreises. Daher ist S = 0,25 S des Kreises.

Es bleibt das S des Kreises zu finden - die Fläche des Kreises. Dazu führen wir eine zusätzliche Konstruktion durch:

Das Dreieck ABC ist ein rechtwinkliges Dreieck. Nach dem Satz des Pythagoras haben wir: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.

Jetzt finden wir die Fläche des Kreises und den Sektor: S des Kreises = πR 2 = 8π; S = 0,25 S Kreis = 2π.

Schließlich ist der gewünschte Wert gleich S /π = 2.

Sektorgebiet mit unbekanntem Radius

Dies ist eine völlig neue Art von Aufgabe, 2010-2011 gab es nichts Vergleichbares. Als Bedingung erhalten wir einen Kreis mit einer bestimmten Fläche (nämlich der Fläche, nicht dem Radius!). Dann wird innerhalb dieses Kreises ein Sektor zugewiesen, dessen Bereich gefunden werden muss.

Die gute Nachricht ist, dass diese Aufgaben die einfachsten von allen Aufgaben im Quadrat sind, die in der Prüfung in Mathematik stehen. Außerdem werden Kreis und Sektor immer auf dem Koordinatengitter platziert. Um zu erfahren, wie man solche Probleme löst, werfen Sie einfach einen Blick auf das Bild:

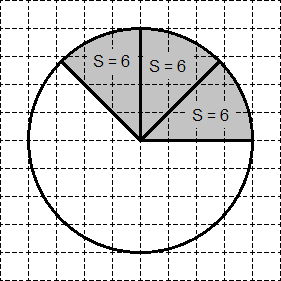
Der ursprüngliche Kreis habe die Kreisfläche S = 80. Dann kann er in zwei Sektoren mit der Fläche S = 40 geteilt werden (siehe Schritt 2). Ebenso kann jeder dieser "halben" Sektoren wieder in zwei Hälften geteilt werden - wir erhalten vier Sektoren der Fläche S = 20 (siehe Schritt 3). Schließlich können Sie jeden dieser Sektoren in zwei weitere unterteilen - wir erhalten 8 Sektoren - "kleine Stücke". Die Fläche jedes dieser „Stücke“ beträgt S = 10.

Bitte beachten Sie: Es gibt keine kleinere Unterteilung in jeder USE-Aufgabe in der Mathematik! Somit lautet der Algorithmus zum Lösen von Problem B-3 wie folgt:

1. Schneiden Sie den ursprünglichen Kreis in 8 Sektoren - "Stücke". Die Fläche von jedem von ihnen beträgt genau 1/8 der Fläche des gesamten Kreises. Hat zum Beispiel der Kreis laut Bedingung die Fläche S des Kreises = 240, dann haben die „Klumpen“ die Fläche S = 240: 8 = 30;
2. Finden Sie heraus, wie viele "Klumpen" in den ursprünglichen Sektor passen, den Bereich, den Sie finden möchten. Wenn unser Sektor beispielsweise 3 „Klumpen“ mit einer Fläche von 30 enthält, beträgt die Fläche des gewünschten Sektors S = 3 30 = 90. Dies ist die Antwort.

Das ist alles! Das Problem wird praktisch mündlich gelöst. Wenn Sie immer noch etwas nicht verstehen, kaufen Sie eine Pizza und schneiden Sie sie in 8 Stücke. Jedes dieser Stücke wird derselbe Sektor sein - "Chunk", der zu größeren Stücken kombiniert werden kann.

Und jetzt schauen wir uns Beispiele aus der Probeprüfung an:

Aufgabe. Auf kariertes Papier wird ein Kreis mit einer Fläche von 40 gezeichnet.Suchen Sie die Fläche der schattierten Figur.

Die Fläche des Kreises beträgt also 40. Teilen Sie ihn in 8 Sektoren auf - jeder mit einer Fläche von S = 40: 5 = 8. Wir erhalten:

Offensichtlich besteht der schraffierte Sektor aus genau zwei "kleinen" Sektoren. Daher ist seine Fläche 2 5 = 10. Das ist die vollständige Lösung!

Aufgabe. Auf kariertes Papier wird ein Kreis mit einer Fläche von 64 gezeichnet.Suchen Sie die Fläche der schattierten Figur.

Teilen Sie den gesamten Kreis erneut in 8 gleiche Sektoren. Offensichtlich muss nur der Bereich von einem von ihnen gefunden werden. Daher ist seine Fläche S = 64: 8 = 8.

Aufgabe. Auf kariertes Papier wird ein Kreis mit einer Fläche von 48 gezeichnet.Suchen Sie die Fläche der schattierten Figur.

Teilen Sie den Kreis erneut in 8 gleiche Sektoren. Die Fläche von jedem von ihnen ist gleich S = 48: 8 = 6. Genau drei Sektoren – „klein“ – werden im gewünschten Sektor platziert (siehe Abbildung). Daher ist die Fläche des gewünschten Sektors 3 6 = 18.