Bei der Vorbereitung auf die Prüfung in Mathematik müssen die Studierenden ihre Kenntnisse in Algebra und Geometrie systematisieren. Ich möchte alle bekannten Informationen kombinieren, zum Beispiel wie man die Fläche einer Pyramide berechnet. Außerdem ausgehend von den Grund- und Seitenflächen bis zur gesamten Oberfläche. Wenn die Situation bei den Seitenflächen klar ist, da es sich um Dreiecke handelt, dann ist die Basis immer eine andere.
Was tun, wenn man die Fläche der Basis der Pyramide findet?
Es kann absolut jede Figur sein: von einem beliebigen Dreieck bis zu einem n-Eck. Und diese Basis kann zusätzlich zu dem Unterschied in der Anzahl der Winkel eine reguläre Figur oder eine falsche sein. Bei den für Schüler interessanten USE-Aufgaben gibt es nur Aufgaben mit den richtigen Figuren an der Basis. Daher werden wir nur über sie sprechen.
rechtwinkliges Dreieck
Das ist gleichseitig. Eine, bei der alle Seiten gleich sind und mit dem Buchstaben "a" gekennzeichnet sind. In diesem Fall wird die Fläche der Basis der Pyramide nach folgender Formel berechnet:
S = (a 2 * √3) / 4.
Quadrat
Die Formel zur Berechnung seiner Fläche ist die einfachste, hier ist "a" wieder die Seite:
Beliebiges reguläres n-Eck
Die Seite eines Polygons hat die gleiche Bezeichnung. Für die Anzahl der Ecken wird der lateinische Buchstabe n verwendet.
S = (n * a 2) / (4 * tg (180º/n)).

Wie ist bei der Berechnung der Seiten- und Gesamtfläche vorzugehen?
Da die Basis eine regelmäßige Figur ist, sind alle Seiten der Pyramide gleich. Außerdem ist jedes von ihnen ein gleichschenkliges Dreieck, da die Seitenkanten gleich sind. Um dann die seitliche Fläche der Pyramide zu berechnen, benötigen Sie eine Formel, die aus der Summe identischer Monome besteht. Die Anzahl der Terme wird durch die Anzahl der Seiten der Basis bestimmt.
Die Fläche eines gleichschenkligen Dreiecks wird nach der Formel berechnet, bei der das halbe Produkt der Basis mit der Höhe multipliziert wird. Diese Höhe in der Pyramide wird Apothem genannt. Seine Bezeichnung ist "A". Die allgemeine Formel für die Seitenfläche lautet:
S \u003d ½ P * A, wobei P der Umfang der Basis der Pyramide ist.
Es gibt Situationen, in denen die Seiten der Basis nicht bekannt sind, aber die Seitenkanten (c) und der flache Winkel an ihrem Scheitel (α) gegeben sind. Dann soll eine solche Formel verwendet werden, um die seitliche Fläche der Pyramide zu berechnen:
S = n/2 * in 2 sin α .

Aufgabe 1
Bedingung. Finden Sie die Gesamtfläche der Pyramide, wenn ihre Basis mit einer Seite von 4 cm liegt und das Apothem einen Wert von √3 cm hat.
Lösung. Sie müssen mit der Berechnung des Umfangs der Basis beginnen. Da es sich um ein regelmäßiges Dreieck handelt, ist P \u003d 3 * 4 \u003d 12 cm Da das Apothem bekannt ist, können Sie sofort die Fläche der gesamten Seitenfläche berechnen: ½ * 12 * √3 = 6 √3cm2.
Für ein Dreieck an der Basis wird der folgende Flächenwert erhalten: (4 2 * √3) / 4 \u003d 4√3 cm 2.
Um die Gesamtfläche zu bestimmen, müssen Sie die beiden resultierenden Werte addieren: 6√3 + 4√3 = 10√3 cm 2.
Antworten. 10√3 cm2.
Aufgabe Nr. 2
Bedingung. Es gibt eine regelmäßige viereckige Pyramide. Die Seitenlänge der Basis beträgt 7 mm, die Seitenkante 16 mm. Sie müssen seine Oberfläche kennen.
Lösung. Da das Polyeder viereckig und regelmäßig ist, ist seine Grundfläche ein Quadrat. Nachdem Sie die Flächen der Grund- und Seitenflächen gelernt haben, können Sie die Fläche der Pyramide berechnen. Die Formel für das Quadrat ist oben angegeben. Und bei den Seitenflächen sind alle Seiten des Dreiecks bekannt. Daher können Sie die Formel von Heron verwenden, um ihre Flächen zu berechnen.
Die ersten Berechnungen sind einfach und führen zu dieser Zahl: 49 mm 2. Für den zweiten Wert müssen Sie den Halbumfang berechnen: (7 + 16 * 2): 2 = 19,5 mm. Jetzt können Sie die Fläche eines gleichschenkligen Dreiecks berechnen: √ (19,5 * (19,5-7) * (19,5-16) 2) = √2985,9375 = 54,644 mm 2. Es gibt nur vier solcher Dreiecke, also musst du sie bei der Berechnung der endgültigen Zahl mit 4 multiplizieren.
Es stellt sich heraus: 49 + 4 * 54,644 \u003d 267,576 mm 2.
Antworten. Der Sollwert beträgt 267,576 mm 2.
Aufgabe Nr. 3
Bedingung. Für eine regelmäßige viereckige Pyramide müssen Sie die Fläche berechnen. Darin beträgt die Seite des Quadrats 6 cm und die Höhe 4 cm.
Lösung. Am einfachsten ist es, die Formel mit dem Produkt aus Umfang und Apothem zu verwenden. Der erste Wert ist leicht zu finden. Der zweite ist etwas schwieriger.
Wir müssen uns an den Satz des Pythagoras erinnern und bedenken, dass er aus der Höhe der Pyramide und dem Apothem, der Hypotenuse, gebildet wird. Das zweite Bein ist gleich der halben Seite des Quadrats, da die Höhe des Polyeders in seine Mitte fällt.
Der gesuchte Apothem (die Hypotenuse eines rechtwinkligen Dreiecks) ist √(3 2 + 4 2) = 5 (cm).
Jetzt können Sie den gewünschten Wert berechnen: ½ * (4 * 6) * 5 + 6 2 \u003d 96 (cm 2).
Antworten. 96 cm2.

Aufgabe Nr. 4
Bedingung. Die richtige Seite seiner Basis beträgt 22 mm, die Seitenrippen 61 mm. Welche Fläche hat die Seitenfläche dieses Polyeders?
Lösung. Die Argumentation darin ist die gleiche wie in Problem Nr. 2 beschrieben. Nur gab es eine Pyramide mit einem Quadrat an der Basis, und jetzt ist es ein Sechseck.
Zunächst wird die Fläche der Basis nach der obigen Formel berechnet: (6 * 22 2) / (4 * tg (180º / 6)) \u003d 726 / (tg30º) \u003d 726√3 cm 2.
Jetzt müssen Sie den halben Umfang eines gleichschenkligen Dreiecks herausfinden, das eine Seitenfläche ist. (22 + 61 * 2): 2 = 72 cm Es bleibt übrig, die Fläche jedes solchen Dreiecks mit der Heron-Formel zu berechnen, sie dann mit sechs zu multiplizieren und zu der zu addieren, die sich für die herausgestellt hat Base.
Berechnungen mit der Heron-Formel: √ (72 * (72-22) * (72-61) 2) \u003d √ 435600 \u003d 660 cm 2. Berechnungen, die die Seitenfläche ergeben: 660 * 6 \u003d 3960 cm 2. Es bleibt, sie zu addieren, um die gesamte Oberfläche herauszufinden: 5217,47≈5217 cm 2.
Antworten. Basis - 726√3 cm 2, Seitenfläche - 3960 cm 2, Gesamtfläche - 5217 cm 2.
Die Oberfläche der Pyramide. In diesem Artikel werden wir mit Ihnen Probleme mit regulären Pyramiden betrachten. Ich möchte Sie daran erinnern, dass eine regelmäßige Pyramide eine Pyramide ist, deren Basis ein regelmäßiges Polygon ist, die Spitze der Pyramide wird in die Mitte dieses Polygons projiziert.
Die Seitenfläche einer solchen Pyramide ist ein gleichschenkliges Dreieck.Die Höhe dieses Dreiecks, gezeichnet von der Spitze einer regelmäßigen Pyramide, wird Apothem genannt, SF ist ein Apothem:
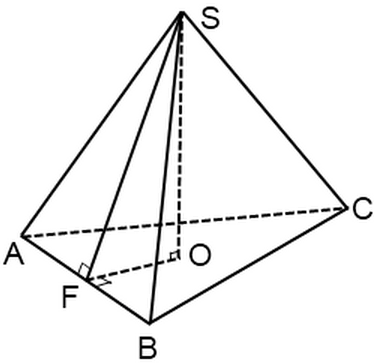
Bei der unten vorgestellten Art von Problemen ist es erforderlich, die Oberfläche der gesamten Pyramide oder die Fläche ihrer Seitenfläche zu finden. Der Blog hat bereits mehrere Probleme mit regulären Pyramiden betrachtet, bei denen die Frage nach dem Finden von Elementen (Höhe, Basiskante, Seitenkante) aufgeworfen wurde.
Bei den Prüfungsaufgaben werden in der Regel regelmäßige dreieckige, viereckige und sechseckige Pyramiden berücksichtigt. Ich habe keine Probleme mit regelmäßigen fünfeckigen und siebeneckigen Pyramiden gesehen.
Die Formel für die Fläche der gesamten Oberfläche ist einfach - Sie müssen die Summe der Fläche der Basis der Pyramide und der Fläche ihrer Seitenfläche finden:
![]()
Betrachten Sie die Aufgaben:
Die Seiten der Basis einer regelmäßigen viereckigen Pyramide sind 72, die Seitenkanten sind 164. Finden Sie die Oberfläche dieser Pyramide.

Die Oberfläche der Pyramide ist gleich der Summe der Flächen der Seitenfläche und der Basis:
*Die Seitenfläche besteht aus vier flächengleichen Dreiecken. Die Basis der Pyramide ist ein Quadrat.
Die Fläche der Seite der Pyramide kann berechnet werden mit:

Somit ist die Oberfläche der Pyramide:
Antwort: 28224
Die Seiten der Basis einer regelmäßigen sechseckigen Pyramide sind 22, die Seitenkanten sind 61. Finden Sie die Fläche der Seitenfläche dieser Pyramide.

Die Basis einer regelmäßigen sechseckigen Pyramide ist ein regelmäßiges Sechseck.
Die Seitenfläche dieser Pyramide besteht aus sechs Flächen gleicher Dreiecke mit den Seiten 61,61 und 22:
Finden Sie die Fläche eines Dreiecks mit der Heron-Formel:

Die Seitenfläche ist also:
![]()
Antwort: 3240
*In den oben vorgestellten Aufgaben könnte die Fläche der Seitenfläche mit einer anderen Dreiecksformel ermittelt werden, aber dafür müssen Sie das Apothem berechnen.
27155. Finden Sie die Oberfläche einer regelmäßigen viereckigen Pyramide, deren Basisseiten 6 und deren Höhe 4 ist.

Um die Oberfläche einer Pyramide zu finden, müssen wir die Fläche der Grundfläche und die Fläche der Seitenfläche kennen:
Die Fläche der Basis beträgt 36, da es sich um ein Quadrat mit einer Seite von 6 handelt.
Die Seitenfläche besteht aus vier Flächen, die gleiche Dreiecke sind. Um die Fläche eines solchen Dreiecks zu finden, müssen Sie seine Basis und Höhe (Apothem) kennen:
* Die Fläche eines Dreiecks ist gleich dem halben Produkt aus der Basis und der zu dieser Basis gezogenen Höhe.
Die Basis ist bekannt, sie ist gleich sechs. Finden wir die Höhe. Betrachten Sie ein rechtwinkliges Dreieck (gelb hervorgehoben):

Ein Bein ist gleich 4, da dies die Höhe der Pyramide ist, das andere ist gleich 3, da es gleich der halben Kante der Basis ist. Wir können die Hypotenuse mit dem Satz des Pythagoras finden:
![]()
Die Fläche der Seitenfläche der Pyramide ist also:

Somit ist die Oberfläche der gesamten Pyramide:
Antwort: 96
27069. Die Seiten der Basis einer regelmäßigen viereckigen Pyramide sind 10, die Seitenkanten sind 13. Finden Sie die Oberfläche dieser Pyramide.
27070. Die Seiten der Basis einer regelmäßigen sechseckigen Pyramide sind 10, die Seitenkanten sind 13. Finden Sie die Fläche der Seitenfläche dieser Pyramide.
Es gibt auch Formeln für die Seitenfläche einer regelmäßigen Pyramide. In einer regelmäßigen Pyramide ist die Basis eine orthogonale Projektion der Seitenfläche, daher:
P- Umfang der Basis, l- Apothem der Pyramide
*Diese Formel basiert auf der Formel für die Fläche eines Dreiecks.
Wenn Sie mehr darüber erfahren möchten, wie diese Formeln abgeleitet werden, verpassen Sie es nicht, folgen Sie der Veröffentlichung von Artikeln.Das ist alles. Viel Glück!
Mit freundlichen Grüßen Alexander Krutitskikh.
P.S: Ich wäre Ihnen dankbar, wenn Sie in sozialen Netzwerken über die Website berichten.
Die Fläche der Seitenfläche einer beliebigen Pyramide ist gleich der Summe der Flächen ihrer Seitenflächen. Bei einer regelmäßigen Pyramide ist es sinnvoll, eine spezielle Formel zum Ausdrücken dieser Fläche anzugeben. Gegeben sei also eine regelmäßige Pyramide, an deren Basis ein regelmäßiges n-Eck mit einer Seite gleich a liegt. Sei h die Höhe der Seitenfläche, auch genannt Apothema Pyramiden. Die Fläche einer Seitenfläche beträgt 1/2 ah, und die gesamte Seitenfläche der Pyramide hat eine Fläche von n/2 ha. Da na der Umfang der Basis der Pyramide ist, können wir die gefundene Formel wie folgt schreiben :
Seitenfläche einer regelmäßigen Pyramide ist gleich dem Produkt ihres Apothems mal dem halben Umfang der Basis.
Hinsichtlich Gesamtfläche, dann fügen Sie einfach den Bereich der Basis zur Seite hinzu.
Eingeschriebene und umschriebene Sphäre und Kugel. Es sei darauf hingewiesen, dass der Mittelpunkt der in die Pyramide eingeschriebenen Kugel am Schnittpunkt der Winkelhalbierenden der inneren Diederwinkel der Pyramide liegt. Der Mittelpunkt der in der Nähe der Pyramide beschriebenen Kugel liegt am Schnittpunkt von Ebenen, die durch die Mittelpunkte der Kanten der Pyramide und senkrecht zu ihnen verlaufen.

Pyramidenstumpf. Wenn die Pyramide von einer Ebene parallel zu ihrer Basis geschnitten wird, wird der Teil genannt, der zwischen der Schnittebene und der Basis eingeschlossen ist Pyramidenstumpf. Die Abbildung zeigt eine Pyramide, deren Teil über der Schnittebene liegt, wir erhalten einen Pyramidenstumpf. Es ist klar, dass die zu verwerfende kleine Pyramide homothetisch zur großen Pyramide ist, wobei das Zentrum der Homothetie an der Spitze liegt. Der Ähnlichkeitskoeffizient ist gleich dem Höhenverhältnis: k = h 2 /h 1 oder Seitenrippen oder anderen entsprechenden linearen Abmessungen beider Pyramiden. Wir wissen, dass die Flächen ähnlicher Figuren als Quadrate mit linearen Abmessungen in Beziehung stehen; so sind die Flächen der Basen beider Pyramiden (d.h. die Basen des Pyramidenstumpfes verschont) wie folgt verwandt
Dabei ist S 1 die Fläche der unteren Basis und S 2 die Fläche der oberen Basis des Pyramidenstumpfes. Die Seitenflächen der Pyramiden stehen im gleichen Verhältnis. Es gibt eine ähnliche Regel für Volumen.
Volumen ähnlicher Körper sind als Würfel ihrer linearen Dimensionen verwandt; Beispielsweise sind die Volumen der Pyramiden als Produkte ihrer Höhe mit der Fläche ihrer Grundflächen verbunden, woraus sich unsere Regel unmittelbar ergibt. Sie hat einen ganz allgemeinen Charakter und folgt unmittelbar daraus, dass der Band immer die Dimension der dritten Potenz der Länge hat. Unter Verwendung dieser Regel leiten wir eine Formel ab, die das Volumen eines Pyramidenstumpfes in Bezug auf die Höhe und die Flächen der Basen ausdrückt.
Gegeben sei ein Pyramidenstumpf mit der Höhe h und den Grundflächen S 1 und S 2 . Wenn wir uns vorstellen, dass es auf die volle Pyramide erweitert wird, dann kann der Ähnlichkeitskoeffizient der vollen Pyramide und der kleinen Pyramide leicht als Wurzel des Verhältnisses S 2 /S 1 gefunden werden. Die Höhe des Pyramidenstumpfes wird ausgedrückt als h = h 1 - h 2 = h 1 (1 - k). Nun haben wir für das Volumen des Pyramidenstumpfes (V 1 und V 2 bezeichnen die Volumina der vollen und kleinen Pyramiden)
Pyramidenstumpf-Volumenformel

Die Formel für den Flächeninhalt S der Mantelfläche eines regelmäßigen Pyramidenstumpfes leiten wir aus den Umfängen P 1 und P 2 der Grundflächen und der Länge des Apothems a her. Wir argumentieren genauso wie bei der Ableitung der Volumenformel. Wir ergänzen die Pyramide mit dem oberen Teil, wir haben P 2 \u003d kP 1, S 2 \u003d k 2 S 1, wobei k der Ähnlichkeitskoeffizient ist, P 1 und P 2 die Umfänge der Basen und S 1 und S 2 sind die Pferde der Seitenflächen der gesamten resultierenden Pyramide bzw. ihrer Spitze. Für die Seitenfläche finden wir (a 1 und a 2 - Apotheme der Pyramiden, a \u003d a 1 - a 2 \u003d a 1 (1-k))
Formel für die Seitenfläche eines regelmäßigen Pyramidenstumpfes

Typische geometrische Probleme in der Ebene und im dreidimensionalen Raum sind die Probleme der Flächenbestimmung verschiedener Figuren. In diesem Artikel stellen wir die Formel für die Fläche der Seitenfläche einer regelmäßigen viereckigen Pyramide vor.
Was ist eine Pyramide?
Lassen Sie uns eine streng geometrische Definition einer Pyramide geben. Angenommen, es gibt ein Polygon mit n Seiten und n Ecken. Wir wählen einen beliebigen Punkt im Raum, der nicht in der Ebene des angegebenen n-Ecks liegt, und verbinden ihn mit jedem Eckpunkt des Polygons. Wir erhalten eine Figur mit einem gewissen Volumen, die als n-gonale Pyramide bezeichnet wird. Lassen Sie uns zum Beispiel in der Abbildung unten zeigen, wie eine fünfeckige Pyramide aussieht.
Zwei wichtige Elemente jeder Pyramide sind ihre Basis (n-Eck) und ihre Spitze. Diese Elemente sind durch n Dreiecke miteinander verbunden, die im Allgemeinen nicht gleich sind. Die von oben nach unten fallende Senkrechte wird als Höhe der Figur bezeichnet. Wenn es die Basis im geometrischen Zentrum schneidet (fällt mit dem Massenmittelpunkt des Polygons zusammen), wird eine solche Pyramide als gerade Linie bezeichnet. Wenn zusätzlich zu dieser Bedingung die Grundfläche ein regelmäßiges Vieleck ist, dann heißt die gesamte Pyramide regelmäßig. Die folgende Abbildung zeigt, wie regelmäßige Pyramiden mit dreieckiger, viereckiger, fünfeckiger und sechseckiger Basis aussehen.

Die Oberfläche der Pyramide
Bevor man sich der Frage nach dem Flächeninhalt der Seitenfläche einer regelmäßigen viereckigen Pyramide zuwendet, sollte man sich näher mit dem Begriff der Fläche selbst befassen.
Wie oben erwähnt und in den Figuren gezeigt, wird jede Pyramide durch einen Satz von Flächen oder Seiten gebildet. Eine Seite ist die Basis und n Seiten sind Dreiecke. Die Oberfläche der ganzen Figur ist die Summe der Flächen jeder ihrer Seiten.
Es ist bequem, die Oberfläche am Beispiel einer sich entfaltenden Figur zu studieren. Ein Scan für eine regelmäßige viereckige Pyramide ist in den folgenden Abbildungen dargestellt.

Wir sehen, dass seine Oberfläche gleich der Summe von vier Flächen identischer gleichschenkliger Dreiecke und der Fläche eines Quadrats ist.
Die Gesamtfläche aller Dreiecke, die die Seiten der Figur bilden, wird als Fläche der Seitenfläche bezeichnet. Als nächstes zeigen wir, wie man es für eine regelmäßige viereckige Pyramide berechnet.
Seitenfläche einer rechteckigen regelmäßigen Pyramide
Um die Seitenfläche der angegebenen Figur zu berechnen, wenden wir uns wieder dem obigen Sweep zu. Angenommen, wir kennen die Seite der quadratischen Grundfläche. Lassen Sie es uns mit dem Symbol a bezeichnen. Es ist ersichtlich, dass jedes der vier identischen Dreiecke eine Basis der Länge a hat. Um ihre Gesamtfläche zu berechnen, müssen Sie diesen Wert für ein Dreieck kennen. Aus dem Verlauf der Geometrie ist bekannt, dass die Fläche des Dreiecks S t gleich dem Produkt aus der Basis und der Höhe ist, die halbiert werden sollte. Also:
Wobei h b die Höhe des gleichschenkligen Dreiecks zur Basis a ist. Für eine Pyramide ist diese Höhe das Apothem. Nun bleibt noch, den resultierenden Ausdruck mit 4 zu multiplizieren, um die Fläche S b der Seitenfläche für die betreffende Pyramide zu erhalten:
Sb = 4*St = 2*hb*a.
Diese Formel enthält zwei Parameter: das Apothem und die Seite der Basis. Wenn letzteres in den meisten Problemstellungen bekannt ist, dann muss ersteres unter Kenntnis anderer Größen berechnet werden. Hier sind die Formeln zur Berechnung von Apotema h b für zwei Fälle:
- wenn die Länge der Seitenrippe bekannt ist;
- wenn die Höhe der Pyramide bekannt ist.
Wenn wir die Länge der Seitenkante (der Seite eines gleichschenkligen Dreiecks) mit dem Symbol L bezeichnen, dann wird das Apotema h b durch die Formel bestimmt:
h b \u003d √ (L 2 - a 2 / 4).
Dieser Ausdruck ist das Ergebnis der Anwendung des Satzes des Pythagoras für das Seitenflächendreieck.
Wenn die Höhe h der Pyramide bekannt ist, kann das Apotema h b wie folgt berechnet werden:
h b = √(h 2 + a 2 /4).
Es ist auch nicht schwierig, diesen Ausdruck zu erhalten, wenn wir ein rechtwinkliges Dreieck innerhalb der Pyramide betrachten, die durch die Beine h und a / 2 und die Hypotenuse h b gebildet wird.
Wir werden zeigen, wie man diese Formeln anwendet, indem wir zwei interessante Probleme lösen.
Problem mit bekannter Oberfläche
Es ist bekannt, dass die Fläche der Seitenfläche eines Vierecks 108 cm 2 beträgt. Es ist notwendig, den Wert der Länge seines Apothems h zu berechnen, wenn die Höhe der Pyramide 7 cm beträgt.
Wir schreiben die Formel für die Fläche S b der Mantelfläche durch die Höhe. Wir haben:
Sb = 2*√(h 2 + a 2 /4) *a.
Hier haben wir einfach die entsprechende Apotema-Formel in den Ausdruck für S b eingesetzt. Lassen Sie uns beide Seiten der Gleichung quadrieren:
S b 2 \u003d 4 * a 2 * h 2 + a 4.
Um den Wert von a zu finden, nehmen wir eine Änderung der Variablen vor:
t 2 + 4*h 2 *t - S b 2 = 0.
Wir ersetzen nun die bekannten Werte und lösen die quadratische Gleichung:
t 2 + 196*t - 11664 = 0.
Wir haben nur die positive Wurzel dieser Gleichung geschrieben. Dann sind die Seiten der Basis der Pyramide gleich:
a = √t = √47,8355 ≈ 6,916 cm.
Um die Länge des Apotemas zu erhalten, verwenden Sie einfach die Formel:
h b \u003d √ (h 2 + a 2 / 4) \u003d √ (7 2 + 6,916 2 / 4) ≈ 7,808 cm.
Seitenfläche der Cheopspyramide
Lassen Sie uns den Wert der seitlichen Oberfläche für die größte ägyptische Pyramide bestimmen. Es ist bekannt, dass an seiner Basis ein Quadrat mit einer Seitenlänge von 230,363 Metern liegt. Die Höhe des Bauwerks betrug ursprünglich 146,5 Meter. Setzen Sie diese Zahlen in die entsprechende Formel für S b ein, erhalten wir:
S b \u003d 2 * √ (h 2 + a 2 / 4) * a \u003d 2 * √ (146,5 2 + 230,363 2 / 4) * 230,363 ≈ 85860 m 2.
Der gefundene Wert ist etwas größer als die Fläche von 17 Fußballfeldern.
In dieser Lektion:
- Aufgabe 1. Finden Sie die Gesamtfläche der Pyramide
- Aufgabe 2. Finden Sie die Fläche der Seitenfläche einer regelmäßigen dreieckigen Pyramide
.
Notiz . Wenn Sie ein Problem in Geometrie lösen müssen, das nicht hier ist, schreiben Sie darüber im Forum. In Aufgaben wird anstelle des Symbols "Quadratwurzel" die Funktion sqrt () verwendet, bei der sqrt das Quadratwurzelsymbol ist und der Wurzelausdruck in Klammern angegeben ist. Für einfache Wurzelausdrücke kann das Zeichen „√“ verwendet werden.
Aufgabe 1. Finden Sie die Gesamtoberfläche einer regelmäßigen Pyramide
Die Höhe der Basis einer regelmäßigen dreieckigen Pyramide beträgt 3 cm, und der Winkel zwischen der Seitenfläche und der Basis der Pyramide beträgt 45 Grad.Finden Sie die Gesamtfläche der Pyramide
Lösung.
An der Basis einer regelmäßigen dreieckigen Pyramide liegt ein gleichseitiges Dreieck.
Um das Problem zu lösen, verwenden wir daher die Eigenschaften eines regelmäßigen Dreiecks: 
Wir kennen die Höhe des Dreiecks, woraus wir seine Fläche ableiten können.
h = √3/2a
a = h / (√3/2)
a = 3 / (√3/2)
a = 6 / √3
Von wo aus wird die Fläche der Basis gleich sein:
S = √3/4 ein 2
S = √3/4 (6 / √3) 2
S = 3√3
Um die Fläche der Seitenfläche zu finden, berechnen wir die Höhe KM. Der OKM-Winkel beträgt laut Problemstellung 45 Grad.
Auf diese Weise:
OK / MK = cos 45
Verwenden wir die Wertetabelle trigonometrischer Funktionen und ersetzen die bekannten Werte.
OK / MK = √2/2
Wir berücksichtigen, dass OK gleich dem Radius des Inkreises ist. Dann
OK = √3/6 a
OK = √3/6 * 6/√3 = 1
Dann
OK / MK = √2/2
1 / MK = √2/2
MK = 2/√2
Die Fläche der Seitenfläche ist dann gleich dem halben Produkt aus Höhe und Grundfläche des Dreiecks.
Seite = 1/2 (6 / √3) (2/√2) = 6/√6
Somit ist die Gesamtfläche der Pyramide gleich
S = 3√3 + 3 * 6/√6
S = 3√3 + 18/√6
Antworten: 3√3 + 18/√6
Aufgabe 2. Finden Sie die seitliche Oberfläche einer regelmäßigen Pyramide
In einer regelmäßigen dreieckigen Pyramide beträgt die Höhe 10 cm und die Seite der Basis 16 cm . Finden Sie die Seitenfläche .Lösung.
Da die Basis einer regelmäßigen dreieckigen Pyramide ein gleichseitiges Dreieck ist, ist AO der Radius des umschriebenen Kreises um die Basis.
(Es folgt von)
Der Radius eines um ein gleichseitiges Dreieck umschriebenen Kreises ergibt sich aus seinen Eigenschaften 
Daher ist die Länge der Kanten einer regelmäßigen dreieckigen Pyramide gleich:
AM 2 = MO 2 + AO 2
die Höhe der Pyramide ist bekannt durch die Bedingung (10 cm), AO = 16√3/3
AM 2 = 100 + 256/3
AM = √(556/3)
Jede Seite der Pyramide ist ein gleichschenkliges Dreieck. Die Fläche eines gleichschenkligen Dreiecks ergibt sich aus der ersten Formel unten 
S = 1/2 * 16 Quadrat((√(556/3) + 8) (√(556/3) - 8))
S = 8 Quadrat((556/3) - 64)
S = 8 Quadrat(364/3)
S = 16 Quadratmeter (91/3)
Da alle drei Flächen einer regelmäßigen Pyramide gleich sind, ist die seitliche Oberfläche gleich
3S = 48√(91/3)
Antworten: 48 √(91/3)
Aufgabe 3. Finden Sie die Gesamtfläche einer regelmäßigen Pyramide
Die Seite einer regelmäßigen dreieckigen Pyramide beträgt 3 cm und der Winkel zwischen der Seitenfläche und der Basis der Pyramide beträgt 45 Grad. Finden Sie die Gesamtfläche der Pyramide.
Lösung.
Da die Pyramide regelmäßig ist, hat sie an ihrer Basis ein gleichseitiges Dreieck. Also die Fläche der Basis ist 
Also = 9 * √3/4
Um die Fläche der Seitenfläche zu finden, berechnen wir die Höhe KM. Der OKM-Winkel beträgt laut Problemstellung 45 Grad.
Auf diese Weise:
OK / MK = cos 45
Lassen Sie uns verwenden

