Streuung (Streuung) einer diskreten Zufallsvariablen D(X) ist die mathematische Erwartung der quadrierten Abweichung einer Zufallsvariablen von ihrer mathematischen Erwartung
1 Eigentum. Die Streuung der Konstanten C ist Null; D (C) = 0.
Nachweisen. Nach Definition der Varianz ist D(C) = M( 2 ).
Aus der ersten Eigenschaft des Erwartungswerts folgt D(C) = M[(C – C) 2 ] = M(0) = 0.
2 Eigentum. Der konstante Faktor lässt sich aus dem Streuungszeichen herausnehmen, indem man ihn quadriert:
D(CX) = C2D(X)
Nachweisen. Nach Definition der Varianz ist D(CX) = M( 2 )
Aus der zweiten Erwartungseigenschaft D(CX)=M( 2 )= C 2 M( 2 )=C 2 D(X)
3 Eigentum. Die Varianz der Summe zweier unabhängiger Zufallsvariablen ist gleich der Summe der Varianzen dieser Variablen:
D = D[X] + D.
Nachweisen. Nach der Formel zur Berechnung der Varianz haben wir
D(X + Y) = M[(X + Y) 2 ] − 2
Wenn wir die Klammern öffnen und die Eigenschaften des mathematischen Erwartungswerts der Summe mehrerer Größen und des Produkts zweier unabhängiger Zufallsvariablen verwenden, erhalten wir
D(X + Y) = M − 2 = M(X2) + 2M(X)M(Y) + M(Y2) − M2(X) − 2M(X)M(Y) − M2(Y) = ( M(X2) − 2)+(M(Y2) − 2) = D(X) + D(Y). Also D(X + Y) = D(X) + D(Y)
4 Eigentum. Die Varianz der Differenz zweier unabhängiger Zufallsvariablen ist gleich der Summe ihrer Varianzen:
D(X − Y) = D(X) + D(Y)
Nachweisen. Aufgrund der dritten Eigenschaft ist D(X − Y) = D(X) + D(–Y). Durch die zweite Eigenschaft
D(X − Y) = D(X) + (–1) 2 D(Y) oder D(X − Y) = D(X) + D(Y)
Numerische Eigenschaften von Systemen von Zufallsvariablen. Korrelationskoeffizient, Eigenschaften des Korrelationskoeffizienten.
Korrelationsmoment. Das Merkmal der Abhängigkeit zwischen Zufallsvariablen ist die mathematische Erwartung des Produkts der Abweichungen und ihrer Verteilungszentren (wie die mathematische Erwartung einer Zufallsvariablen manchmal genannt wird), die als Korrelationsmoment oder Kovarianz bezeichnet wird:
Zur Berechnung des Korrelationsmoments diskreter Werte wird die folgende Formel verwendet:
und für kontinuierliche Mengen - die Formel:
Korrelationskoeffizient rxy der Zufallsvariablen X und Y ist das Verhältnis des Korrelationsmoments zum Produkt der Standardabweichungen der Werte:
- Korrelationskoeffizient;
Eigenschaften des Korrelationskoeffizienten:
1. Wenn X und Y unabhängige Zufallsvariablen sind, dann ist r = 0;
2. –1 ≤ r ≤ 1. Außerdem, wenn |r| =1, dann besteht zwischen X und Y ein funktionaler, nämlich ein linearer Zusammenhang;
3. r charakterisiert den relativen Wert der Abweichung von M(XY) von M(X)M(Y), und seit Abweichung nur für abhängige Größen stattfindet, dann charakterisiert r die Enge der Abhängigkeit.
Lineare Regressionsfunktion.
Stellen Sie sich eine zweidimensionale Zufallsvariable (X, Y) vor, wobei X und Y abhängige Zufallsvariablen sind. Wir stellen eine der Größen als Funktion der anderen dar. Wir beschränken uns auf eine ungefähre Darstellung (exakte Näherung ist im Allgemeinen unmöglich) von Y als lineare Funktion von X:
wobei α und β zu bestimmende Parameter sind.
Satz. Lineare Mean-Square-Regression Y auf X hat die Form
wo m x =M(X), m y =M(Y), σ x =√D(X), σ y =√D(Y), r=µ xy /(σ x σ y)- Korrelationskoeffizient von X- und Y-Werten.
Der Koeffizient β=rσ y /σ x wird aufgerufen Regressionskoeffizienten Y bis X und eine gerade Linie
direkt genannt mittlere quadratische Regression
Y bis X.
Markovsche Ungleichung.
Erklärung der Markovschen Ungleichung
Wenn es keine negativen Werte der Zufallsvariablen X gibt, dann ist die Wahrscheinlichkeit, dass sie einen Wert annimmt, der die positive Zahl A übersteigt, nicht mehr als ein Bruchteil, d.h.
und die Wahrscheinlichkeit, dass es einen Wert annimmt, der eine positive Zahl A nicht überschreitet, ist nicht kleiner als , d.h.
Chebyshevs Ungleichung.
Chebyshevs Ungleichung. Die Wahrscheinlichkeit, dass die Abweichung einer Zufallsvariablen X von ihrem mathematischen Erwartungswert kleiner als eine positive Zahl ε ist, nicht kleiner als 1 − D[X]ε 2
P(|X – M(X)|< ε) ≥ 1 –D(X)ε 2
Nachweisen. Da die Ereignisse in der Verwirklichung von Ungleichheiten bestehen
P(|X−M(X)|< ε) и P(|X – M(X)| ≥ε) противоположны, то сумма их вероятностей равна единице, т. е.
P(|X – M(X)|< ε) + P(|X – M(X)| ≥ ε) = 1.
Daher interessiert uns die Wahrscheinlichkeit
P(|X – M(X)|< ε) = 1 − P(|X – M(X)| > ε).
Damit reduziert sich das Problem auf die Berechnung der Wahrscheinlichkeit P(|X –M(X)| ≥ ε).
Schreiben wir einen Ausdruck für die Varianz der Zufallsvariablen X
D(X) = 2p1 + 2p2 + . . . + 2 pn
Alle Terme dieser Summe sind nichtnegativ. Wir verwerfen diejenigen Terme, für die |x i – M(X)|< ε (для оставшихся слагаемых |x j – M(X)| ≥ ε), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,
D(X) ≥ 2pk+1 + 2pk+2 + . . . + 2 pn
Beide Teile der Ungleichung |x j –M(X)| ≥ ε (j = k+1, k+2, . . ., n) sind positiv, daher erhalten wir durch Quadrieren die äquivalente Ungleichung |x j – M(X)| 2 ≥ε 2. Ersetzen jedes der Faktoren in der verbleibenden Summe
|xj – M(X)| 2 durch die Zahl ε 2 (in diesem Fall kann die Ungleichung nur zunehmen) erhalten wir
D(X) ≥ ε 2 (p k+1 + p k+2 + . . . + p n)
Nach dem Additionstheorem ist die Summe der Wahrscheinlichkeiten p k+1 + p k+2 +. . .+p n ist die Wahrscheinlichkeit, dass X einen, egal welchen, der Werte x k+1 +x k+2 + annimmt. . .+x n , und für jeden von ihnen erfüllt die Abweichung die Ungleichung |x j – M(X)| ≥ ε. Daraus folgt, dass die Summe p k+1 + p k+2 + . . . + p n drückt die Wahrscheinlichkeit aus
P(|X – M(X)| ≥ ε).
Dies erlaubt uns, die Ungleichung für D(X) umzuschreiben als
D(X) ≥ ε 2 P(|X – M(X)| ≥ ε)
P(|X – M(X)|≥ ε) ≤ D(X)/ε 2
Endlich bekommen wir
P(|X – M(X)|< ε) ≥D(X)/ε 2
Chebyshevs Theorem.
Chebyshevs Theorem. Wenn ein - paarweise unabhängige Zufallsvariablen, deren Varianzen gleichmäßig begrenzt sind (eine konstante Zahl nicht überschreiten Mit ), dann egal wie klein die positive Zahl istε , die Wahrscheinlichkeit der Ungleichheit
willkürlich nahe an Eins liegen, wenn die Anzahl der Zufallsvariablen groß genug ist.
Mit anderen Worten, unter den Bedingungen des Theorems
Nachweisen. Lassen Sie uns eine neue Zufallsvariable in Betracht ziehen - das arithmetische Mittel der Zufallsvariablen
Finden wir den mathematischen Erwartungswert X. Unter Verwendung der Eigenschaften des mathematischen Erwartungswerts (ein konstanter Faktor kann aus dem Vorzeichen des mathematischen Erwartungswerts genommen werden, der mathematische Erwartungswert der Summe ist gleich der Summe der mathematischen Erwartungswerte der Terme) , wir erhalten
| (1) |
Wenden wir die Tschebyscheff-Ungleichung auf X an, haben wir
oder unter Berücksichtigung der Beziehung (1)
Unter Verwendung der Eigenschaften der Varianz (der konstante Faktor kann durch Quadrieren aus dem Varianzzeichen herausgenommen werden; die Varianz der Summe unabhängiger Zufallsvariablen ist gleich der Summe der Varianzen der Terme) erhalten wir
Durch die Bedingung werden die Streuungen aller Zufallsvariablen durch eine konstante Zahl C begrenzt, d.h. Es gibt Ungleichheiten:
 (2)
|
Setzen wir die rechte Seite von (2) in die Ungleichung (1) ein (warum letztere nur verstärkt werden kann), haben wir
Wenn wir also zum Grenzwert für n→∞ übergehen, erhalten wir
Da die Wahrscheinlichkeit eins nicht überschreiten kann, können wir endlich schreiben
Der Satz ist bewiesen.
Satz von Bernoulli.
Satz von Bernoulli. Wenn in jedem von n unabhängigen Versuchen die Wahrscheinlichkeit p für das Eintreten des Ereignisses A konstant ist, dann liegt die Wahrscheinlichkeit beliebig nahe bei Eins, dass die Abweichung der relativen Häufigkeit von der betragsmäßigen Wahrscheinlichkeit p bei der Anzahl der Versuche beliebig klein sein wird ist groß genug.
Mit anderen Worten, wenn ε eine beliebig kleine positive Zahl ist, dann haben wir unter den Bedingungen des Satzes die Gleichheit
Nachweisen. Bezeichne mit x1 diskrete Zufallsvariable - die Anzahl der Vorkommen des Ereignisses im ersten Test, durch x2- in dieser Sekunde, ..., Xn- in n te Prüfung. Es ist klar, dass jede der Größen nur zwei Werte annehmen kann: 1 (Ereignis A ist eingetreten) mit der Wahrscheinlichkeit p und 0 (das Ereignis ist nicht eingetreten) mit Wahrscheinlichkeit .
Thema 8.12. Streuung einer Zufallsvariablen.
Ö. Die Varianz einer Zufallsvariablen ist die mathematische Erwartung der quadrierten Abweichung einer Zufallsvariablen von ihrer mathematischen Erwartung.
Streuung charakterisiert den Grad der Streuung der Werte einer Zufallsvariablen relativ zu ihrer mathematischen Erwartung. Wenn alle Werte einer Zufallsvariablen eng um ihre mathematische Erwartung konzentriert sind und große Abweichungen von der mathematischen Erwartung unwahrscheinlich sind, dann hat eine solche Zufallsvariable eine kleine Streuung. Wenn die Werte einer Zufallsvariablen streuen und die Wahrscheinlichkeit großer Abweichungen von der mathematischen Erwartung hoch ist, dann hat eine solche Zufallsvariable eine große Streuung.
Unter Verwendung der Definition der Varianz kann für eine diskrete Zufallsvariable die Formel zur Berechnung der Varianz wie folgt dargestellt werden:
Sie können eine andere Formel zur Berechnung der Varianz ableiten:
Die Varianz einer Zufallsvariablen ist also gleich der Differenz zwischen dem mathematischen Erwartungswert des Quadrats der Zufallsvariablen und dem Quadrat ihres mathematischen Erwartungswerts.
Dispersionseigenschaften.
Wir verlassen diese Eigenschaft ohne Beweis.
Binomialverteilungsgesetz.
Lassen Sie sich Zahlen geben n gehört N und p(0 <p< ein). Dann kann jeder ganzen Zahl aus dem Intervall eine Wahrscheinlichkeit zugeordnet werden, die mit der Bernoulli-Formel berechnet wird. Lassen Sie uns das Verteilungsgesetz einer Zufallsvariablen erhalten (nennen wir es B(betta))
Wir werden sagen, dass die Zufallsvariable nach dem Bernoulli-Gesetz verteilt ist. Eine solche Zufallsvariable ist die Häufigkeit des Auftretens des Ereignisses A in n wiederholte unabhängige Versuche, wenn in jedem Versuch Ereignis A mit einer Wahrscheinlichkeit eintritt p.
Betrachten Sie eine separate ich- e-Test. Der Raum elementarer Ergebnisse hat dafür die Form
Das Verteilungsgesetz einer Zufallsvariablen wurde im vorherigen Thema betrachtet
Für ich= 1,2, ... , n Wir bekommen das System von n unabhängige Zufallsvariablen mit den gleichen Verteilungsgesetzen. 
Beispiel.
Von den 20 zur Kontrolle ausgewählten Produktproben erwiesen sich 4 als nicht standardisiert. Schätzen wir die Wahrscheinlichkeit, dass eine zufällig ausgewählte Kopie des Produkts den Standard nicht erfüllt, anhand des Verhältnisses ab R *= 4/20 = 0,2.
Als X Zufallswert, R * ist ebenfalls eine Zufallsvariable. Werte R * kann von Experiment zu Experiment variieren (im betrachteten Fall handelt es sich bei dem Experiment um eine zufällige Auswahl und Kontrolle von 20 Produkten). Was ist die mathematische Erwartung R *? Soweit X ist eine Zufallsvariable, die die Anzahl der Erfolge in darstellt n Bernoulli-Test, M( x) = np. Für die mathematische Erwartung einer Zufallsvariablen R* per Definition erhalten wir: M(p*) = M(x/n), sondern n hier ist eine Konstante, also durch die Erwartungseigenschaft
M(p*) = 1/n*M(x)=1/n np=p
Somit ist „Durchschnitt“ der wahre Wert R, was zu erwarten ist. Dies ist die Bewertungseigenschaft R* Mengen R hat den Namen: R* ist ein unvoreingenommen Auswertung für R. Keine systematische Abweichung vom Wert des geschätzten Parameters R bestätigt die Machbarkeit der Verwendung des Wertes R* als Schätzung. Die Frage nach der Genauigkeit der Schätzung lassen wir vorerst offen.
Mathematischer Erwartungswert und Varianz sind die am häufigsten verwendeten numerischen Merkmale einer Zufallsvariablen. Sie charakterisieren die wichtigsten Merkmale der Verteilung: ihre Position und ihren Streuungsgrad. Bei vielen Problemen der Praxis ist eine vollständige, erschöpfende Beschreibung einer Zufallsvariablen - des Verteilungsgesetzes - entweder gar nicht möglich oder gar nicht erforderlich. Sie beschränken sich in diesen Fällen auf die näherungsweise Beschreibung einer Zufallsvariablen durch numerische Merkmale.
Der mathematische Erwartungswert wird oft einfach als Durchschnittswert einer Zufallsvariablen bezeichnet. Die Streuung einer Zufallsvariablen ist ein Merkmal der Streuung, die Streuung einer Zufallsvariablen um ihre mathematische Erwartung.
Mathematische Erwartung einer diskreten Zufallsvariablen
Nähern wir uns dem Konzept der mathematischen Erwartung, indem wir zunächst von der mechanischen Interpretation der Verteilung einer diskreten Zufallsvariablen ausgehen. Die Einheitsmasse sei auf die Punkte der x-Achse verteilt x1 , x 2 , ..., x n, und jeder materielle Punkt hat eine ihm entsprechende Masse aus p1 , p 2 , ..., p n. Es ist erforderlich, einen Punkt auf der x-Achse auszuwählen, der die Position des gesamten Systems materieller Punkte unter Berücksichtigung ihrer Massen charakterisiert. Es liegt nahe, als solchen Punkt den Schwerpunkt des Systems materieller Punkte zu nehmen. Dies ist der gewichtete Durchschnitt der Zufallsvariablen X, in der die Abszisse jedes Punktes ist xich tritt mit einem "Gewicht" gleich der entsprechenden Wahrscheinlichkeit ein. Der so erhaltene Mittelwert der Zufallsvariablen X wird als mathematischer Erwartungswert bezeichnet.
Der mathematische Erwartungswert einer diskreten Zufallsvariablen ist die Summe der Produkte aller ihrer möglichen Werte und der Wahrscheinlichkeiten dieser Werte:
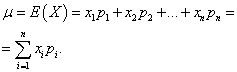
Beispiel 1 Organisierte eine Win-Win-Lotterie. Es gibt 1000 Gewinne, von denen 400 jeweils 10 Rubel sind. 300 - 20 Rubel pro Stück 200 - 100 Rubel pro Stück. und jeweils 100 - 200 Rubel. Was ist der durchschnittliche Gewinn für eine Person, die ein Ticket kauft?
Entscheidung. Wir finden den durchschnittlichen Gewinn, wenn die Gesamtgewinnsumme, die 10*400 + 20*300 + 100*200 + 200*100 = 50.000 Rubel entspricht, durch 1000 dividiert wird (die Gesamtgewinnsumme). Dann bekommen wir 50000/1000 = 50 Rubel. Der Ausdruck zur Berechnung des durchschnittlichen Gewinns kann aber auch in folgender Form dargestellt werden:
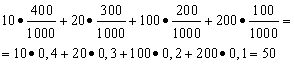
Andererseits ist die Höhe des Gewinns unter diesen Bedingungen eine Zufallsvariable, die die Werte von 10, 20, 100 und 200 Rubel annehmen kann. mit Wahrscheinlichkeiten von jeweils 0,4; 0,3; 0,2; 0,1. Daher ist die erwartete durchschnittliche Auszahlung gleich der Summe der Produkte aus der Höhe der Auszahlungen und der Wahrscheinlichkeit, sie zu erhalten.
Beispiel 2 Der Verlag beschloss, ein neues Buch zu veröffentlichen. Er wird das Buch für 280 Rubel verkaufen, von denen 200 an ihn, 50 an die Buchhandlung und 30 an den Autor gehen. Die Tabelle gibt Auskunft über die Kosten für die Veröffentlichung eines Buches und die Wahrscheinlichkeit, eine bestimmte Anzahl von Exemplaren des Buches zu verkaufen.
Ermitteln Sie den erwarteten Gewinn des Publishers.
Entscheidung. Die Zufallsvariable „Gewinn“ ist gleich der Differenz zwischen dem Erlös aus dem Verkauf und den Kosten der Kosten. Wenn beispielsweise 500 Exemplare eines Buches verkauft werden, betragen die Einnahmen aus dem Verkauf 200 * 500 = 100.000 und die Veröffentlichungskosten 225.000 Rubel. Damit droht dem Verlag ein Verlust von 125.000 Rubel. Die folgende Tabelle fasst die erwarteten Werte der Zufallsvariablen - Gewinn zusammen:
| Anzahl | Profitieren xich | Wahrscheinlichkeit pich | xich p ich |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Gesamt: | 1,00 | 25000 |
Damit erhalten wir die mathematische Erwartung des Verlagsgewinns:
.
Beispiel 3 Chance, mit einem Schuss zu treffen p= 0,2. Bestimmen Sie den Verbrauch von Granaten, die die mathematische Erwartung einer Trefferzahl von 5 liefern.
Entscheidung. Aus derselben Erwartungsformel, die wir bisher verwendet haben, drücken wir aus x- Verbrauch von Muscheln:
.
Beispiel 4 Bestimmen Sie den mathematischen Erwartungswert einer Zufallsvariablen x Anzahl der Treffer bei drei Schüssen, wenn die Wahrscheinlichkeit, mit jedem Schuss zu treffen p = 0,4 .
Tipp: Finden Sie die Wahrscheinlichkeit der Werte einer Zufallsvariablen heraus Bernoulli-Formel .
Erwartungseigenschaften
Betrachten Sie die Eigenschaften der mathematischen Erwartung.
Eigentum 1. Die mathematische Erwartung eines konstanten Werts ist gleich dieser Konstante:
Eigenschaft 2. Der konstante Faktor kann aus dem Erwartungszeichen herausgenommen werden:
Eigenschaft 3. Die mathematische Erwartung der Summe (Differenz) von Zufallsvariablen ist gleich der Summe (Differenz) ihrer mathematischen Erwartung:
Eigenschaft 4. Die mathematische Erwartung des Produkts von Zufallsvariablen ist gleich dem Produkt ihrer mathematischen Erwartungen:
Eigenschaft 5. Wenn alle Werte der Zufallsvariablen X um die gleiche Zahl verringern (erhöhen). Mit, dann verringert (erhöht) sich seine mathematische Erwartung um dieselbe Zahl:
Wenn Sie sich nicht nur auf mathematische Erwartungen beschränken können
In den meisten Fällen kann nur die mathematische Erwartung eine Zufallsvariable nicht angemessen charakterisieren.
Lassen Sie Zufallsvariablen X und Y sind durch folgende Verteilungsgesetze gegeben:
| Bedeutung X | Wahrscheinlichkeit |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Bedeutung Y | Wahrscheinlichkeit |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Die mathematischen Erwartungen dieser Größen sind die gleichen - gleich Null:
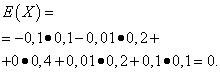
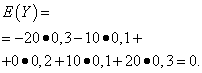
Ihre Verteilung ist jedoch unterschiedlich. Zufallswert X kann nur Werte annehmen, die sich geringfügig von der mathematischen Erwartung und der Zufallsvariablen unterscheiden Y kann Werte annehmen, die deutlich von der mathematischen Erwartung abweichen. Ein ähnliches Beispiel: Der Durchschnittslohn lässt keine Aussage über den Anteil von Hoch- und Niedrigverdienern zu. Mit anderen Worten, durch mathematische Erwartung kann man nicht beurteilen, welche Abweichungen davon zumindest im Durchschnitt möglich sind. Dazu müssen Sie die Varianz einer Zufallsvariablen ermitteln.
Streuung einer diskreten Zufallsvariablen
Streuung diskrete Zufallsvariable X heißt der mathematische Erwartungswert des Quadrats seiner Abweichung vom mathematischen Erwartungswert:
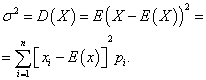
Die Standardabweichung einer Zufallsvariablen X ist der arithmetische Wert der Quadratwurzel seiner Varianz:
.
Beispiel 5 Berechnen Sie Varianzen und Standardabweichungen von Zufallsvariablen X und Y, deren Verteilungsgesetze in den obigen Tabellen angegeben sind.
Entscheidung. Mathematische Erwartungen an Zufallsvariablen X und Y, wie oben festgestellt, gleich Null sind. Nach der Dispersionsformel für E(X)=E(j)=0 erhalten wir:
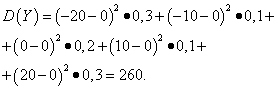
Dann die Standardabweichungen von Zufallsvariablen X und Y bilden
.
Also bei gleichen mathematischen Erwartungen die Varianz der Zufallsvariablen X sehr klein und willkürlich Y- von Bedeutung. Dies ist eine Folge der unterschiedlichen Verteilung.
Beispiel 6 Der Investor hat 4 alternative Investitionsprojekte. Die Tabelle fasst die Daten zum erwarteten Gewinn in diesen Projekten mit der entsprechenden Wahrscheinlichkeit zusammen.
| Projekt 1 | Projekt 2 | Projekt 3 | Projekt 4 |
| 500, P=1 | 1000, P=0,5 | 500, P=0,5 | 500, P=0,5 |
| 0, P=0,5 | 1000, P=0,25 | 10500, P=0,25 | |
| 0, P=0,25 | 9500, P=0,25 |
Finden Sie für jede Alternative den mathematischen Erwartungswert, die Varianz und die Standardabweichung.
Entscheidung. Lassen Sie uns zeigen, wie diese Größen für die 3. Alternative berechnet werden:
Die Tabelle fasst die gefundenen Werte für alle Alternativen zusammen.
Alle Alternativen haben die gleiche mathematische Erwartung. Das bedeutet, dass langfristig alle das gleiche Einkommen haben. Die Standardabweichung kann als Risikomaß interpretiert werden – je größer sie ist, desto größer ist das Risiko der Investition. Ein Investor, der kein großes Risiko eingehen möchte, wird Projekt 1 wählen, weil es die kleinste Standardabweichung (0) hat. Wenn der Investor Risiko und hohe Renditen in kurzer Zeit bevorzugt, wählt er das Projekt mit der größten Standardabweichung - Projekt 4.
Dispersionseigenschaften
Lassen Sie uns die Eigenschaften der Dispersion darstellen.
Eigentum 1. Die Streuung eines konstanten Wertes ist Null:
Eigenschaft 2. Der konstante Faktor lässt sich aus dem Streuungszeichen herausnehmen, indem man ihn quadriert:
.
Eigenschaft 3. Die Varianz einer Zufallsvariablen ist gleich der mathematischen Erwartung des Quadrats dieses Werts, von der das Quadrat der mathematischen Erwartung des Werts selbst abgezogen wird:
,
wo 
.
Eigenschaft 4. Die Varianz der Summe (Differenz) von Zufallsvariablen ist gleich der Summe (Differenz) ihrer Varianzen:
Beispiel 7 Es ist bekannt, dass eine diskrete Zufallsvariable X nimmt nur zwei Werte an: −3 und 7. Außerdem ist die mathematische Erwartung bekannt: E(X) = 4 . Finden Sie die Varianz einer diskreten Zufallsvariablen.
Entscheidung. Bezeichne mit p die Wahrscheinlichkeit, mit der eine Zufallsvariable einen Wert annimmt x1 = −3 . Dann die Wahrscheinlichkeit des Wertes x2 = 7 wird 1 − sein p. Lassen Sie uns die Gleichung für die mathematische Erwartung herleiten:
E(X) = x 1 p + x 2 (1 − p) = −3p + 7(1 − p) = 4 ,
woher wir die Wahrscheinlichkeiten bekommen: p= 0,3 und 1 − p = 0,7 .
Das Verteilungsgesetz einer Zufallsvariablen:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
Die Varianz dieser Zufallsvariablen berechnen wir mit der Formel aus Eigenschaft 3 der Varianz:
D(X) = 2,7 + 34,3 − 16 = 21 .
Finden Sie selbst den mathematischen Erwartungswert einer Zufallsvariablen und sehen Sie sich dann die Lösung an
Beispiel 8 Diskrete Zufallsvariable X nimmt nur zwei Werte an. Es nimmt den größeren Wert 3 mit einer Wahrscheinlichkeit von 0,4 an. Außerdem ist die Varianz der Zufallsvariablen bekannt D(X) = 6 . Finden Sie den mathematischen Erwartungswert einer Zufallsvariablen.
Beispiel 9 Eine Urne enthält 6 weiße und 4 schwarze Kugeln. 3 Kugeln werden aus der Urne genommen. Die Anzahl der weißen Kugeln unter den gezogenen Kugeln ist eine diskrete Zufallsvariable X. Finden Sie den mathematischen Erwartungswert und die Varianz dieser Zufallsvariablen.
Entscheidung. Zufallswert X kann die Werte 0, 1, 2, 3 annehmen. Daraus lassen sich die entsprechenden Wahrscheinlichkeiten berechnen Regel der Multiplikation von Wahrscheinlichkeiten. Das Verteilungsgesetz einer Zufallsvariablen:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Daher die mathematische Erwartung dieser Zufallsvariablen:
M(X) = 3/10 + 1 + 1/2 = 1,8 .
Die Varianz einer gegebenen Zufallsvariablen ist:
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Mathematische Erwartung und Streuung einer kontinuierlichen Zufallsvariablen
Für eine kontinuierliche Zufallsvariable behält die mechanische Interpretation der mathematischen Erwartung die gleiche Bedeutung: der Massenschwerpunkt für eine Einheitsmasse, die kontinuierlich auf der x-Achse mit Dichte verteilt ist f(x). Im Gegensatz zu einer diskreten Zufallsvariablen, für die das Funktionsargument xichändert sich abrupt, bei einer kontinuierlichen Zufallsvariablen ändert sich das Argument kontinuierlich. Aber auch der mathematische Erwartungswert einer stetigen Zufallsvariablen hängt mit ihrem Mittelwert zusammen.
Um den mathematischen Erwartungswert und die Varianz einer kontinuierlichen Zufallsvariablen zu finden, müssen Sie bestimmte Integrale finden . Ist eine Dichtefunktion einer kontinuierlichen Zufallsvariablen gegeben, so geht sie direkt in den Integranden ein. Wenn eine Wahrscgegeben ist, müssen Sie durch Differenzieren die Dichtefunktion finden.
Das arithmetische Mittel aller möglichen Werte einer kontinuierlichen Zufallsvariablen wird als sein bezeichnet mathematische Erwartung, gekennzeichnet durch oder .
In der vorherigen haben wir eine Reihe von Formeln angegeben, die es uns ermöglichen, die numerischen Eigenschaften von Funktionen zu finden, wenn die Verteilungsgesetze der Argumente bekannt sind. Um jedoch die numerischen Eigenschaften von Funktionen zu finden, ist es in vielen Fällen nicht einmal notwendig, die Verteilungsgesetze von Argumenten zu kennen, sondern es reicht aus, nur einige ihrer numerischen Eigenschaften zu kennen; dabei verzichten wir komplett auf Verteilungsgesetze. Die Bestimmung der numerischen Eigenschaften von Funktionen durch gegebene numerische Eigenschaften der Argumente ist in der Wahrscheinlichkeitstheorie weit verbreitet und ermöglicht es, die Lösung einer Reihe von Problemen erheblich zu vereinfachen. Meist beziehen sich solche vereinfachten Verfahren auf lineare Funktionen; einige elementare nichtlineare Funktionen erlauben jedoch auch diesen Ansatz.
In der Gegenwart stellen wir eine Reihe von Sätzen über die numerischen Eigenschaften von Funktionen vor, die in ihrer Gesamtheit einen sehr einfachen Apparat zur Berechnung dieser Eigenschaften darstellen, der unter einer Vielzahl von Bedingungen anwendbar ist.
1. Mathematische Erwartung einer nicht zufälligen Variablen
Die angegebene Eigenschaft ist ziemlich offensichtlich; es kann bewiesen werden, indem man eine Nicht-Zufallsvariable als einen bestimmten Typ einer Zufallsvariablen betrachtet, mit einem möglichen Wert mit einer Wahrscheinlichkeit von eins; dann nach der allgemeinen Formel für den mathematischen Erwartungswert:
.
2. Streuung einer nicht zufälligen Variablen
Wenn es sich um einen nicht zufälligen Wert handelt, dann
3. Entfernung einer Nicht-Zufallsvariable über das Zeichen der mathematischen Erwartung hinaus
, (10.2.1)
d.h. ein nicht zufälliger Wert kann aus dem Erwartungszeichen herausgenommen werden.
Nachweisen.
a) Für diskontinuierliche Mengen
b) Für kontinuierliche Mengen
.
4. Entfernen eines nicht zufälligen Werts für das Vorzeichen der Varianz und der Standardabweichung
If ist eine Nicht-Zufallsvariable und ist dann zufällig
, (10.2.2)
d.h. ein nicht zufälliger Wert kann durch Quadrieren aus dem Streuungszeichen herausgenommen werden.
Nachweisen. Per Definition von Varianz
Folge
,
d.h. ein nicht zufälliger Wert kann durch seinen Absolutwert aus dem Vorzeichen der Standardabweichung herausgenommen werden. Den Beweis erhalten wir, indem wir aus der Formel (10.2.2) die Quadratwurzel ziehen und berücksichtigen, dass der r.s.c. ist ein im Wesentlichen positiver Wert.
5. Mathematischer Erwartungswert der Summe von Zufallsvariablen
Beweisen wir das für zwei beliebige Zufallsvariablen und
d.h. der mathematische Erwartungswert der Summe zweier Zufallsvariablen ist gleich der Summe ihrer mathematischen Erwartungswerte.
Diese Eigenschaft ist als Erwartungsadditionssatz bekannt.
Nachweisen.
a) Sei ein System von unstetigen Zufallsvariablen. Wenden wir auf die Summe von Zufallsvariablen die allgemeine Formel (10.1.6) für den mathematischen Erwartungswert einer Funktion zweier Argumente an:
.
Ho ist nichts anderes als die Gesamtwahrscheinlichkeit, dass der Wert den Wert annehmen wird:
;
somit,
.
Auf ähnliche Weise werden wir das beweisen
,
und der Satz ist bewiesen.
b) Sei ein System stetiger Zufallsvariablen. Nach der Formel (10.1.7)
. (10.2.4)
Wir transformieren das erste der Integrale (10.2.4):
;
gleichfalls
,
und der Satz ist bewiesen.
Es sollte besonders darauf hingewiesen werden, dass das Theorem der Addition mathematischer Erwartungen für beliebige Zufallsvariablen gilt - sowohl für abhängige als auch für unabhängige.
Der Erwartungsadditionssatz kann auf eine beliebige Anzahl von Termen verallgemeinert werden:
, (10.2.5)
d.h. der mathematische Erwartungswert der Summe mehrerer Zufallsvariablen ist gleich der Summe ihrer mathematischen Erwartungswerte.
Zum Beweis genügt es, die Methode der vollständigen Induktion anzuwenden.
6. Mathematische Erwartung einer linearen Funktion
Betrachten Sie eine lineare Funktion mehrerer zufälliger Argumente:
wo sind nicht zufällige Koeffizienten. Lassen Sie uns das beweisen
, (10.2.6)
dh der Mittelwert einer linearen Funktion ist gleich der gleichen linearen Funktion des Mittelwerts der Argumente.
Nachweisen. Unter Verwendung des Additionssatzes m.o. und der Regel, eine nicht zufällige Variable aus dem Vorzeichen von m. o. herauszunehmen, erhalten wir:
.
7. Anzepdiese Summe von Zufallsvariablen
Die Varianz der Summe zweier Zufallsvariablen ist gleich der Summe ihrer Varianzen plus dem doppelten Korrelationsmoment:
Nachweisen. Bezeichnen
Nach dem Additionssatz der mathematischen Erwartungen
Gehen wir von Zufallsvariablen zu den entsprechenden zentrierten Variablen über. Wenn wir Term für Term von Gleichheit (10.2.8) Gleichheit (10.2.9) subtrahieren, haben wir:
Per Definition von Varianz
Q.E.D.
Formel (10.2.7) für die Varianz der Summe lässt sich auf beliebig viele Terme verallgemeinern:
,
(10.2.10)
wobei das Korrelationsmoment der Werte ist, das Vorzeichen unter der Summe bedeutet, dass die Summation für alle möglichen paarweisen Kombinationen von Zufallsvariablen gilt 
.
Der Beweis ist ähnlich wie der vorherige und folgt aus der Formel für das Quadrat eines Polynoms.
Formel (10.2.10) kann auch in anderer Form geschrieben werden:
, (10.2.11)
wobei sich die Doppelsumme auf alle Elemente der Korrelationsmatrix des Mengensystems erstreckt , die sowohl Korrelationsmomente als auch Varianzen enthält.
Wenn alle Zufallsvariablen , die im System enthalten sind, unkorreliert sind (d. h. bei ), Formel (10.2.10) nimmt die Form an:
, (10.2.12)
d.h. die Varianz der Summe unkorrelierter Zufallsvariablen ist gleich der Summe der Varianzen der Terme.
Dieser Satz ist als Varianzadditionssatz bekannt.
8. Dispersion einer linearen Funktion
Betrachten Sie eine lineare Funktion mehrerer Zufallsvariablen.
wo sind Nicht-Zufallsvariablen.
Lassen Sie uns beweisen, dass die Streuung dieser linearen Funktion durch die Formel ausgedrückt wird
, (10.2.13)
wo ist das Korrelationsmoment der Größen , .
Nachweisen. Führen wir die Notation ein:
. (10.2.14)
Wenden wir die Formel (10.2.10) für die Varianz der Summe auf die rechte Seite des Ausdrucks (10.2.14) an und berücksichtigen wir, dass wir erhalten:
wo ist das Korrelationsmoment der Größen:
.
Lassen Sie uns diesen Moment berechnen. Wir haben:
;
gleichfalls
Setzen wir diesen Ausdruck in (10.2.15) ein, gelangen wir zu Formel (10.2.13).
Im besonderen Fall, wenn alle Mengen unkorreliert, Formel (10.2.13) hat die Form:
, (10.2.16)
d.h. die Varianz einer linearen Funktion unkorrelierter Zufallsvariablen ist gleich der Summe der Produkte der Quadrate der Koeffizienten und der Varianzen der entsprechenden Argumente.
9. Mathematische Erwartung des Produkts von Zufallsvariablen
Die mathematische Erwartung des Produkts zweier Zufallsvariablen ist gleich dem Produkt ihrer mathematischen Erwartungen plus dem Korrelationsmoment:
Nachweisen. Wir gehen von der Definition des Korrelationsmoments aus:
Wir transformieren diesen Ausdruck mit den Eigenschaften der mathematischen Erwartung:
was offensichtlich äquivalent zu Formel (10.2.17) ist.
Wenn Zufallsvariablen unkorreliert sind, dann nimmt Formel (10.2.17) die Form an:
d.h. der Mittelwert des Produkts zweier unkorrelierter Zufallsvariablen ist gleich dem Produkt ihrer Mittelwerte.
Diese Aussage ist als Erwartungsmultiplikationssatz bekannt.
Formel (10.2.17) ist nichts anderes als ein Ausdruck des zweiten gemischten zentralen Moments des Systems in Bezug auf das zweite gemischte Anfangsmoment und mathematische Erwartungen:
. (10.2.19)
Dieser Ausdruck wird in der Praxis häufig bei der Berechnung des Korrelationsmoments verwendet, so wie für eine Zufallsvariable häufig die Varianz über das zweite Anfangsmoment und den mathematischen Erwartungswert berechnet wird.
Der Erwartungsmultiplikationssatz lässt sich auch auf beliebig viele Faktoren verallgemeinern, nur reicht es in diesem Fall für seine Anwendung nicht aus, dass die Größen unkorreliert sind, sondern es ist erforderlich, dass auch einige höhere gemischte Momente verschwinden, deren Anzahl davon abhängt die Anzahl der Begriffe im Produkt. Diese Bedingungen sind sicherlich erfüllt, wenn die im Produkt enthaltenen Zufallsvariablen unabhängig sind. In diesem Fall
, (10.2.20)
d.h. die mathematische Erwartung des Produkts unabhängiger Zufallsvariablen ist gleich dem Produkt ihrer mathematischen Erwartungen.
Dieser Satz kann leicht durch vollständige Induktion bewiesen werden.
10. Streuung des Produkts unabhängiger Zufallsvariablen
Beweisen wir das für unabhängige Größen
Nachweisen. Lassen Sie uns bezeichnen. Per Definition von Varianz
Da die Größen unabhängig sind, und
Für unabhängig sind die Größen auch unabhängig; somit,
,
Aber es gibt nichts anderes als das zweite Anfangsmoment der Größe und wird daher in Form der Varianz ausgedrückt:
;
gleichfalls
.
Wenn wir diese Ausdrücke in Formel (10.2.22) einsetzen und ähnliche Terme einbringen, gelangen wir zu Formel (10.2.21).
Für den Fall, dass zentrierte Zufallsvariablen multipliziert werden (Werte mit mathematischen Erwartungen gleich Null), nimmt die Formel (10.2.21) die Form an:
, (10.2.23)
d.h. die Varianz des Produkts unabhängiger zentrierter Zufallsvariablen ist gleich dem Produkt ihrer Varianzen.
11. Höhere Momente der Summe von Zufallsvariablen
In manchen Fällen ist es notwendig, die höheren Momente der Summe unabhängiger Zufallsvariablen zu berechnen. Lassen Sie uns einige verwandte Beziehungen beweisen.
1) Wenn die Größen unabhängig sind, dann
Nachweisen.
woher nach dem Erwartungsmultiplikationssatz
Aber das erste zentrale Moment für jede Menge ist Null; zwei mittlere Terme verschwinden, und Formel (10.2.24) ist bewiesen.
Beziehung (10.2.24) lässt sich leicht per Induktion auf eine beliebige Anzahl unabhängiger Terme verallgemeinern:
. (10.2.25)
2) Das vierte zentrale Moment der Summe zweier unabhängiger Zufallsvariablen wird durch die Formel ausgedrückt
wo sind die Dispersionen von und .
Der Beweis ist genau derselbe wie der vorherige.
Mit der Methode der vollständigen Induktion ist es einfach, die Verallgemeinerung der Formel (10.2.26) auf eine beliebige Anzahl unabhängiger Terme zu beweisen.
Streuung einer Zufallsvariablen und ihrer Eigenschaften.
Viele Zufallsvariablen haben dieselbe mathematische Erwartung, aber unterschiedliche mögliche Werte. Daher reicht eine mathematische Erwartung nicht aus, um eine Zufallsvariable zu charakterisieren.
Lassen Sie das Einkommen X und Y(in Dollar) von zwei Firmen werden durch Verteilungen gegeben:
Manchmal ist es bequem, eine andere Formel zu verwenden, die durch Verwendung der Eigenschaften der mathematischen Erwartung erhalten werden kann,
Die Dispersion liegt vor, wenn die Reihe (bzw. das Integral) konvergiert.
Nicht negative Zahl 
namens Standardabweichung zufällige Variable X. Sie hat die Dimension einer Zufallsvariablen X und definiert ein Standard-RMS-Dispersionsintervall, symmetrisch in Bezug auf die mathematische Erwartung. Der Wert wird manchmal als Standardabweichung bezeichnet.
Die Zufallsvariable wird aufgerufen zentriert, Wenn . Die Zufallsvariable wird aufgerufen normalisiert(Standard) wenn .
Fahren wir mit dem Beispiel fort. Berechnen Sie die Varianz des Einkommens zweier Unternehmen:
Beim Vergleich der Varianz sehen wir, dass das Einkommen des zweiten Unternehmens stärker variiert als das des ersten.
Dispersionseigenschaften.
1. Die Streuung eines konstanten Wertes ist gleich Null, d.h. , Wenn Konstante. Dies ist offensichtlich, da der konstante Wert eine mathematische Erwartung hat, die gleich dem konstanten Wert ist, d.h. .
2. Konstanter Multiplikator C kann aus dem Streuungszeichen herausgenommen werden, indem man es zuerst quadriert.
Wirklich,
3. Die Varianz der algebraischen Summe zweier unabhängiger Zufallsvariablen ist gleich der Summe ihrer Varianzen, d.h.
Der Ausdruck wird aufgerufen Kovarianz von X und Y(siehe Thema 4, §2). Für unabhängige Zufallsvariablen ist die Kovarianz Null, d.h.
Mit dieser Gleichheit können Sie die Liste der Eigenschaften der mathematischen Erwartung erweitern. Wenn die Zufallsvariablen X und Y unabhängig sind, dann ist die mathematische Erwartung des Produkts gleich dem Produkt der mathematischen Erwartungen, nämlich:
Wird die Zufallsvariable linear transformiert, d.h. , dann
.
Beispiel 1. Lassen Sie es produzieren n unabhängige Tests, Eintrittswahrscheinlichkeit eines Ereignisses SONDERN in denen jeweils konstant und gleich ist p. Wie groß ist die Varianz der Anzahl der Vorkommen des Ereignisses? SONDERN in diesen Studien?
Entscheidung. Sei die Anzahl des Auftretens des Ereignisses SONDERN im ersten Versuch ist die Anzahl des Auftretens des Ereignisses SONDERN im zweiten Test usw. Dann die Gesamtzahl des Auftretens des Ereignisses SONDERN in n Prüfungen gleich
Unter Verwendung von Eigenschaft 3 der Dispersion erhalten wir
Hier haben wir die Tatsache ausgenutzt, dass 
, ich= (siehe Beispiele 1 und 2, Punkt 3.3.1.).
Beispiel 2. Lass X - die Höhe der Einlage (in Dollar) bei der Bank - gegeben durch die Wahrscheinlichkeitsverteilung
| X | ||||||
| ich = | 0,01 | 0,03 | 0,10 | 0,30 | 0,5 | 0,06 |
Ermitteln Sie den durchschnittlichen Beitragsbetrag und die Varianz.
Entscheidung. Der durchschnittliche Einzahlungsbetrag entspricht der mathematischen Erwartung
Um die Varianz zu berechnen, verwenden wir die Formel
D (X) \u003d 8196 - 7849,96 \u003d 348,04.
Standardabweichung
Momente.
Um den Einfluss dieser möglichen Werte der Zufallsvariablen auf die mathematische Erwartung zu berücksichtigen X, die groß sind, aber eine geringe Wahrscheinlichkeit haben, ist es ratsam, die mathematischen Erwartungen einer positiven ganzzahligen Potenz einer Zufallsvariablen zu berücksichtigen.
