Bestimmte Integrale online auf der Website, um das von Studenten und Schülern behandelte Material zu konsolidieren. Und üben Sie Ihre praktischen Fähigkeiten. Eine vollständige Online-Lösung bestimmter Integrale für Sie in wenigen Augenblicken hilft Ihnen, alle Phasen des Prozesses zu bestimmen. Online-Integrale - Online-bestimmtes Integral. Bestimmte Online-Integrale auf der Website zur vollständigen Konsolidierung des von Studenten und Schülern behandelten Materials und zur Schulung ihrer praktischen Fähigkeiten. Eine vollständige Online-Lösung bestimmter Integrale für Sie in wenigen Augenblicken hilft Ihnen, alle Phasen des Prozesses zu bestimmen. Online-Integrale - Online-bestimmtes Integral. Für uns scheint die Online-Bildung eines bestimmten Integrals nichts Übernatürliches zu sein, da wir dieses Thema anhand eines Buches von prominenten Autoren studiert haben. Ein großes Dankeschön an sie und wir drücken diesen Personen unseren Respekt aus. Es hilft, im Handumdrehen den definitiven integralen Online-Service zur Berechnung solcher Probleme zu ermitteln. Geben Sie einfach die richtigen Daten ein und alles wird gut! Jedes bestimmte Integral als Lösung des Problems wird die Alphabetisierung der Schüler erhöhen. Das ist der Traum eines jeden Faultiers, und wir sind keine Ausnahme, wir geben es ehrlich zu. Wenn Sie es trotzdem schaffen, das bestimmte Integral mit der kostenlosen Lösung online zu berechnen, dann schreiben Sie bitte die Website-Adresse an alle, die sie verwenden möchten. Teilen Sie, wie es so schön heißt, einen nützlichen Link – und freundliche Menschen werden Ihnen für das Geschenk danken. Es wird sehr interessant sein, ein Problem zu analysieren, bei dem ein bestimmtes Integral vom Taschenrechner selbst gelöst wird und nicht auf Kosten Ihrer kostbaren Zeit. Deshalb sind sie Maschinen, um Menschen zu pflügen. Die Online-Lösung bestimmter Integrale ist jedoch nicht für jeden Standort geeignet, und dies ist leicht zu überprüfen, nämlich, es reicht aus, ein komplexes Beispiel zu nehmen und zu versuchen, es mit jedem dieser Dienste zu lösen. Sie werden den Unterschied auf Ihrer eigenen Haut spüren. Oft wird es ziemlich schwierig, online ohne Mühe ein eindeutiges Integral zu finden, und Ihre Antwort wird vor dem Hintergrund des Gesamtbildes des Ergebnisses lächerlich aussehen. Es wäre besser, zuerst den Kurs eines jungen Kämpfers zu nehmen. Jede Online-Lösung uneigentlicher Integrale reduziert sich zunächst auf die Berechnung des Unbestimmten und dann durch die Grenzwerttheorie in der Regel auf die Berechnung einseitiger Grenzwerte aus den mit den substituierten Grenzwerten A und B erhaltenen Ausdrücken definitives Integral online mit einer detaillierten Lösung, die Sie angegeben haben, sind wir zu dem Schluss gekommen, dass Sie im fünften Schritt einen Fehler gemacht haben, nämlich bei der Verwendung der Chebyshev-Variablenänderungsformel. Seien Sie bei Ihrer nächsten Entscheidung sehr vorsichtig. Wenn Ihr Online-Rechner Ihr definitives Integral beim ersten Mal nicht berechnen konnte, lohnt es sich zunächst, die schriftlichen Daten in den entsprechenden Formularen auf der Website zu überprüfen. Stellen Sie sicher, dass alles in Ordnung ist und gehen Sie, Go-Go! Die Hürde für jeden Schüler ist die Berechnung uneigentlicher Integrale online mit dem Lehrer selbst, da dies entweder eine Klausur oder ein Kolloquium oder nur ein Test an einem Paar ist, sobald Ihnen der gegebene Online-Rechner für uneigentliche Integrale zur Verfügung steht , fahren Sie dann sofort die angegebene Funktion ein, ersetzen Sie die angegebenen Integrationsgrenzen und klicken Sie auf die Schaltfläche Lösen, woraufhin Ihnen eine vollständige detaillierte Antwort zur Verfügung steht. Und doch ist es gut, wenn es eine so wunderbare Website als Website gibt, denn sie ist sowohl kostenlos als auch einfach zu bedienen und enthält auch viele Abschnitte. die Studenten jeden Tag verwenden, einer von ihnen ist nur ein bestimmtes Integral online mit der Lösung in vollem Umfang. Im selben Abschnitt können Sie das uneigentliche Integral online mit einer ausführlichen Lösung für weitere Anwendungen der Antwort sowohl am Institut als auch in der Ingenieurarbeit berechnen. Es scheint, dass es nicht jedem schwer fällt, online ein bestimmtes Integral zu bestimmen, wenn man ein solches Beispiel vorher ohne obere und untere Schranke löst, also nicht das Leibniz-Integral, sondern das unbestimmte Integral. Aber hier stimmen wir Ihnen kategorisch nicht zu, da es auf den ersten Blick so erscheinen mag, aber es gibt einen signifikanten Unterschied, nehmen wir alles auseinander. Die Lösung liefert ein solches bestimmtes Integral nicht in expliziter Form, sondern durch Umwandlung des Ausdrucks in einen Grenzwert. Mit anderen Worten, man muss zuerst das Integral durch Ersetzen der symbolischen Werte der Grenzen lösen und dann die Grenze entweder im Unendlichen oder an einem bestimmten Punkt berechnen. Von hier aus bedeutet die Berechnung eines bestimmten Integrals online mit einer kostenlosen Lösung nichts anderes, als die exakte Lösung mit der Newton-Leibniz-Formel darzustellen. Wenn wir unser bestimmtes Integral betrachten, hilft Ihnen der Rechner, es in wenigen Sekunden direkt vor Ihren Augen zu berechnen. Einen solchen Ansturm braucht jeder, der die Aufgabe schnellstmöglich bewältigen und für persönliche Angelegenheiten frei sein will. Sie sollten nicht nach Websites im Internet suchen, die Sie auffordern, sich zu registrieren, dann Geld auf das Guthaben aufzufüllen, und das alles für einen klugen Kerl, der die Lösung bestimmter Integrale angeblich online vorbereitet. Denken Sie daran, dass die Adresse Math24 ein kostenloser Dienst zur Lösung vieler mathematischer Probleme ist. Wir helfen Ihnen unter anderem dabei, online ein bestimmtes Integral zu finden. Um dies sicherzustellen, überprüfen Sie bitte unsere Erklärung mit konkreten Beispielen. Geben Sie den Integranden in das entsprechende Feld ein, geben Sie dann entweder unendliche Grenzwerte an (in diesem Fall wird die Lösung uneigentlicher Integrale berechnet und online erhalten), oder setzen Sie Ihre numerischen oder symbolischen Grenzen und das eindeutige Online-Integral mit einer detaillierten Lösung wird auf der Seite angezeigt, nachdem Sie auf die Schaltfläche "Lösung" geklickt haben. Ist es nicht wahr - es ist sehr einfach, erfordert keine zusätzlichen Aktionen von Ihnen, kostenlos, was das Wichtigste ist, und gleichzeitig effektiv. Sie können den Service selbst nutzen, damit Ihnen der definitiv integrale Online-Rechner den maximalen Nutzen bringt und Sie einen komfortablen Zustand erhalten, ohne sich auf die Komplexität aller Rechenprozesse zu belasten, lassen Sie uns alles für Sie tun und demonstrieren Sie die volle Leistungsfähigkeit der Computertechnologie in der modernen Welt. Wenn Sie in den Dschungel der komplexesten Formeln eintauchen und die Berechnung uneigentlicher Integrale online studieren, ist dies lobenswert und Sie können die Möglichkeit einer Doktorarbeit in Anspruch nehmen, aber zurück zur Realität des Studentenlebens . Und wer ist Student? Zunächst einmal ist dies ein junger Mann, energisch und fröhlich, der Zeit haben möchte, sich zu entspannen und seine Hausaufgaben zu machen! Deshalb haben wir uns um die Studenten gekümmert, die versuchen, einen ungeeigneten integralen Online-Rechner in der Weite des globalen Netzwerks zu finden, und hier ist es für Ihre Aufmerksamkeit - die Website ist der nützlichste Online-Löser für junge Leute. Übrigens, obwohl sich unser Service als Assistent für Studenten und Schüler präsentiert, ist er für jeden Ingenieur voll und ganz geeignet, da wir alle Arten von Aufgaben erledigen können und deren Lösung in einem professionellen Format präsentiert wird. Beispielsweise bieten wir online ein bestimmtes Integral mit einer schrittweisen Lösung in vollständiger Form an, d. h. jedem logischen Block (Teilaufgabe) wird ein eigener Datensatz mit allen Berechnungen im Zuge des allgemeinen Lösungsprozesses zugeordnet. Dies vereinfacht natürlich die Wahrnehmung mehrstufiger sequentieller Layouts und ist daher der Vorteil des Site-Projekts gegenüber ähnlichen Diensten, um online ein falsches Integral mit einer detaillierten Lösung zu finden.

Sind Sie hier? =) Nein, ich habe nicht versucht, irgendjemanden einzuschüchtern, es ist nur so, dass das Thema uneigentliche Integrale ein sehr gutes Beispiel dafür ist, wie wichtig es ist, keine höhere Mathematik und andere exakte Wissenschaften zu betreiben. Um die Lektion auf der Website zu meistern, ist alles da - in einer detaillierten und zugänglichen Form würde es einen Wunsch geben ....

So lass uns anfangen. Bildlich gesprochen ist ein uneigentliches Integral ein „fortgeschrittenes“ bestimmtes Integral, und tatsächlich gibt es nicht so viele Schwierigkeiten damit, außerdem hat ein uneigentliches Integral eine sehr gute geometrische Bedeutung.

Was bedeutet es, ein uneigentliches Integral zu berechnen?

Berechnen Sie das uneigentliche Integral - es bedeutet, eine ZAHL zu finden(genauso wie im bestimmten Integral), oder beweisen, dass es divergiert(das heißt, am Ende unendlich statt einer Zahl).

Es gibt zwei Arten von uneigentlichen Integralen.

Uneigentliches Integral mit unendlicher Integrationsgrenze

Manchmal wird ein solches uneigentliches Integral aufgerufen unechtes Integral erster Art. Im Allgemeinen sieht ein uneigentliches Integral mit unendlichem Grenzwert meistens so aus: . Wie unterscheidet es sich von einem bestimmten Integral? An der oberen Grenze. Es ist endlos:

Weniger verbreitet sind Integrale mit unendlicher unterer Grenze oder mit zwei unendlichen Grenzen: , und wir werden sie später betrachten - wenn Sie auf den Geschmack kommen :)

Lassen Sie uns nun den beliebtesten Fall analysieren. In den allermeisten Beispielen die Integrand-Funktion kontinuierlich dazwischen und diese Wichtige Tatsache, die Sie zuerst überprüfen sollten! Denn wenn es Lücken gibt, dann gibt es zusätzliche Nuancen. Zur Eindeutigkeit gehen wir davon aus, dass auch dann das Typische krummliniges Trapez wird so aussehen:

Beachten Sie, dass es unendlich ist (rechts nicht begrenzt) und uneigentliche Integrale numerisch gleich seiner Fläche. In diesem Fall sind folgende Optionen möglich:

1) Der erste Gedanke, der mir in den Sinn kommt, ist: „Da die Figur also unendlich ist “, mit anderen Worten, die Fläche ist auch unendlich. So kann es sein. In diesem Fall spricht man vom uneigentlichen Integral weicht ab.

2) Aber. So paradox es auch klingen mag, die Fläche einer unendlichen Figur kann gleich ... einer endlichen Zahl sein! Zum Beispiel: . Könnte es sein? Leicht. Im zweiten Fall das uneigentliche Integral konvergiert.

3) Über die dritte Option etwas später.

Wann divergiert ein uneigentliches Integral und wann konvergiert es? Dies hängt vom Integranden ab, und wir werden uns sehr bald konkrete Beispiele ansehen.

Aber was passiert, wenn sich unterhalb der Achse ein unendliches krummliniges Trapez befindet? In diesem Fall das uneigentliche Integral (divergiert) oder gleich einer endlichen negativen Zahl ist.

Auf diese Weise, Uneigentliche Integrale können negativ sein.

Wichtig! Wenn Ihnen JEDES unpassende Integral zur Lösung angeboten wird, dann gilt im Allgemeinen: es ist keine Rede von einem Bereich und es besteht keine Notwendigkeit, eine Zeichnung zu erstellen. Ich habe die geometrische Bedeutung des uneigentlichen Integrals nur erklärt, um das Verständnis des Materials zu erleichtern.

Da das uneigentliche Integral dem bestimmten Integral sehr ähnlich ist, erinnern wir uns an die Newton-Leibniz-Formel: . Tatsächlich ist die Formel auch auf uneigentliche Integrale anwendbar, nur muss sie leicht modifiziert werden. Was ist der Unterschied? In der unendlichen oberen Integrationsgrenze: . Wahrscheinlich haben viele erraten, dass dies bereits nach der Anwendung der Theorie der Grenzen riecht, und die Formel wird wie folgt geschrieben: .

Wie unterscheidet es sich von einem bestimmten Integral? Ja, nichts besonderes! Wie bei einem bestimmten Integral müssen Sie in der Lage sein, die Stammfunktion (unbestimmtes Integral) zu finden und die Newton-Leibniz-Formel anwenden zu können. Neu hinzugekommen ist lediglich die Berechnung des Limits. Wer schlecht mit ihnen ist, lernt eine Lektion Grenzen der Funktionen. Lösungsbeispiele denn besser spät als in der Armee.

Betrachten Sie zwei klassische Beispiele:

Beispiel 1

Zur Verdeutlichung werde ich eine Zeichnung erstellen, obwohl ich noch einmal betone, auf die Praxis Bei dieser Aufgabe müssen keine Zeichnungen erstellt werden.

Der Integrand ist auf dem Halbintervall stetig, was bedeutet, dass alles in Ordnung ist und das uneigentliche Integral mit der „normalen“ Methode berechnet werden kann.

Anwendung unserer Formel und die Lösung sieht so aus:

Das heißt, das uneigentliche Integral divergiert und die Fläche des schattierten krummlinigen Trapezes ist gleich unendlich.

Im betrachteten Beispiel haben wir das einfachste Tabellenintegral und die gleiche Technik zur Anwendung der Newton-Leibniz-Formel wie beim bestimmten Integral. Aber diese Formel wird unter dem Zeichen des Grenzwerts angewendet. Anstelle des üblichen Buchstabens der "dynamischen" Variablen erscheint der Buchstabe "be". Dies sollte nicht verwirren oder verwirren, denn jeder Buchstabe ist nicht schlechter als das Standard „X“.

Wenn Sie nicht verstehen, warum wann , dann ist dies sehr schlecht, entweder Sie verstehen die einfachsten Grenzen nicht (und verstehen überhaupt nicht, was eine Grenze ist), oder Sie wissen nicht, was der Graph eines Logarithmus ist Funktion aussieht. Im zweiten Fall besuchen Sie die Lektion Graphen und Eigenschaften elementarer Funktionen.

Beim Lösen uneigentlicher Integrale ist es sehr wichtig zu wissen, wie die Graphen der wichtigsten Elementarfunktionen aussehen!

Ein sauberes Jobdesign sollte in etwa so aussehen:

“

! Beim Entwerfen eines Beispiels unterbrechen wir immer die Lösung und geben an, was mit dem Integranden passiert – Ist es im Integrationsintervall stetig oder nicht?. Damit identifizieren wir die Art des uneigentlichen Integrals und begründen weitere Aktionen.

Beispiel 2

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Machen wir eine Zeichnung:

Zunächst bemerken wir Folgendes: Der Integrand ist im Halbintervall stetig. Gut. Mit Formel lösen :

(1) Wir nehmen das einfachste Integral einer Potenzfunktion (dieser Sonderfall kommt in vielen Tabellen vor). Besser ist es, das Minus sofort über das Grenzzeichen hinaus zu verschieben, damit es bei weiteren Berechnungen nicht untergeht.

(2) Wir ersetzen die oberen und unteren Grenzen gemäß der Newton-Leibniz-Formel.

(3) Wir zeigen an, wann (Meine Herren, das ist seit langem verstanden) und vereinfachen die Antwort.

Hier ist die Fläche eines unendlichen krummlinigen Trapezes gleich einer endlichen Zahl! Unglaublich aber wahr.

Das cleane Design des Beispiels sollte etwa so aussehen:

“

Der Integrand ist kontinuierlich eingeschaltet

“

Was tun, wenn Sie auf ein Integral wie - mit stoßen? Bruchpunkt auf dem Integrationsintervall? Das bedeutet, dass sich im Beispiel ein Tippfehler eingeschlichen hat (am Wahrscheinlichsten) oder einen höheren Bildungsabschluss. Im letzteren Fall aufgrund von Additivitätseigenschaften, sollte man zwei uneigentliche Integrale über die Intervalle betrachten und sich dann mit der Summe befassen.

Manchmal ist dies aufgrund eines Tippfehlers oder der Absicht eines unzulässigen Integrals möglich gar nicht vorhanden Wenn also beispielsweise die Quadratwurzel von "x" in den Nenner des obigen Integrals gesetzt wird, tritt ein Teil des Integrationsintervalls überhaupt nicht in den Definitionsbereich des Integranden ein.

Darüber hinaus kann ein uneigentliches Integral auch bei allem "scheinbaren Wohlbefinden" nicht existieren. Klassisches Beispiel: . Trotz der Bestimmtheit und Stetigkeit des Kosinus existiert ein solches uneigentliches Integral nicht! Wieso den? Es ist ganz einfach, weil:
- existiert nicht entsprechende Grenze.

Und solche Beispiele, obwohl selten, findet man in der Praxis! Somit gibt es neben Konvergenz und Divergenz noch ein drittes Lösungsergebnis mit vollständiger Antwort: „es gibt kein uneigentliches Integral“.

Es sei auch darauf hingewiesen, dass die strenge Definition des uneigentlichen Integrals gerade durch den Grenzwert gegeben ist, und wer möchte, kann sich damit in der pädagogischen Literatur vertraut machen. Nun, wir setzen die praktische Lektion fort und gehen zu sinnvolleren Aufgaben über:

Beispiel 3

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Versuchen wir zunächst, die Stammfunktion (unbestimmtes Integral) zu finden. Tun wir das nicht, lösen wir natürlich auch das uneigentliche Integral nicht.

Welches der Tabellenintegrale sieht der Integrand aus? Es erinnert mich an den Arcustangens: . Aus diesen Überlegungen drängt sich der Gedanke auf, dass es schön wäre, ein Quadrat im Nenner zu bekommen. Dies geschieht durch Substitution.

Lassen Sie uns ersetzen:

Das unbestimmte Integral ist gefunden, es macht in diesem Fall keinen Sinn, eine Konstante hinzuzufügen.

Bei einem Entwurf ist es immer sinnvoll, eine Prüfung durchzuführen, also das Ergebnis zu differenzieren:

Der ursprüngliche Integrand wurde erhalten, was bedeutet, dass das unbestimmte Integral korrekt gefunden wurde.

Jetzt finden wir das uneigentliche Integral:

(1) Wir schreiben die Lösung gemäß der Formel . Es ist besser, die Konstante sofort über das Grenzzeichen hinaus zu verschieben, damit sie bei weiteren Berechnungen nicht stört.

(2) Wir ersetzen die oberen und unteren Grenzen gemäß der Newton-Leibniz-Formel. Wieso den beim ? Siehe Arcus-Tangens-Diagramm im bereits mehrfach empfohlenen Artikel.

(3) Wir erhalten die endgültige Antwort. Die Tatsache, dass es nützlich ist, es auswendig zu wissen.

Fortgeschrittene Schüler finden das unbestimmte Integral möglicherweise nicht separat und verwenden nicht die Ersetzungsmethode, sondern verwenden die Methode zum Summieren der Funktion unter dem Vorzeichen des Differentials und lösen das uneigentliche Integral "sofort". In diesem Fall sollte die Lösung in etwa so aussehen:

“

Der Integrand ist stetig auf .

“

Beispiel 4

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

! Dies ist ein typisches Beispiel, und ähnliche Integrale sind sehr verbreitet. Mach es gut! Die Stammfunktion wird hier durch die Methode der Auswahl eines ganzen Quadrats gefunden, mehr Details über die Methode finden Sie in der Lektion Integration einiger Brüche.

Beispiel 5

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Dieses Integral kann im Detail gelöst werden, d.h. zuerst das unbestimmte Integral finden, indem man die Variable ändert. Und Sie können es "sofort" lösen - indem Sie die Funktion unter dem Vorzeichen des Differentials zusammenfassen. Wer hat etwas mathematischen Hintergrund.

Vollständige Lösungen und Antworten am Ende der Lektion.

Beispiele für Lösungen von uneigentlichen Integralen mit unendlicher unterer Integrationsgrenze finden Sie auf der Seite Effiziente Methoden zur Lösung uneigentlicher Integrale. Dort wird auch der Fall betrachtet, dass beide Integrationsgrenzen unendlich sind.

Uneigentliche Integrale unbeschränkter Funktionen

Oder uneigentliche Integrale zweiter Art. Unechte Integrale der zweiten Art werden schlau unter das übliche bestimmte Integral "chiffriert" und sehen genauso aus: Anders als das bestimmte Integral erleidet der Integrand aber eine unendliche Diskontinuität (existiert nicht): 1) an der Stelle , 2) oder am Punkt , 3) ​​​​oder an beiden Punkten gleichzeitig, 4) oder sogar im Integrationsintervall. Wir werden die ersten beiden Fälle betrachten, für die Fälle 3-4 am Ende des Artikels gibt es einen Link zu einer zusätzlichen Lektion.

Nur ein Beispiel zur Verdeutlichung:. Es scheint ein bestimmtes Integral zu sein. Tatsächlich handelt es sich aber um ein uneigentliches Integral zweiter Art, wenn wir den Wert der unteren Grenze in den Integranden einsetzen, dann verschwindet der Nenner, dh der Integrand existiert an dieser Stelle einfach nicht!

Im Allgemeinen bei der Analyse des uneigentlichen Integrals es müssen immer beide Integrationsgrenzen in den Integranden eingesetzt werden. Dabei prüfen wir auch die Obergrenze: . Alles ist gut hier.

Das krummlinige Trapez für die betrachtete Variante des uneigentlichen Integrals sieht grundsätzlich so aus:

Hier ist fast alles gleich wie beim Integral erster Art.

Unser Integral ist numerisch gleich der Fläche des schattierten krummlinigen Trapezes, das nicht von oben begrenzt ist. In diesem Fall kann es zwei Möglichkeiten geben *: Das uneigentliche Integral divergiert (die Fläche ist unendlich) oder das uneigentliche Integral ist gleich einer endlichen Zahl (dh die Fläche einer unendlichen Figur ist endlich!).

* standardmäßig nehmen wir gewöhnlich an, dass das uneigentliche Integral existiert

Es bleibt nur die Newton-Leibniz-Formel zu modifizieren. Es wird auch mit Hilfe des Limits modifiziert, allerdings strebt das Limit nicht mehr nach Unendlich, sondern auf den rechten Wert. Es ist leicht, der Zeichnung zu folgen: Entlang der Achse müssen wir uns der Sollbruchstelle unendlich nahe nähern rechts.

Mal sehen, wie das in der Praxis umgesetzt wird.

Beispiel 6

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Der Integrand erleidet an einer Stelle einen unendlichen Bruch (Vergessen Sie nicht, mündlich oder auf einem Entwurf zu prüfen, ob mit der Obergrenze alles in Ordnung ist!)

Zuerst berechnen wir das unbestimmte Integral:

Ersatz:

Für diejenigen, die Schwierigkeiten mit dem Ersetzen haben, lesen Sie die Lektion Ersetzungsverfahren im unbestimmten Integral.

Wir berechnen das uneigentliche Integral:

(1) Was ist hier neu? Technisch praktisch nichts. Geändert hat sich lediglich der Eintrag unter dem Limit-Icon: . Die Addition bedeutet, dass wir den rechten Wert anstreben (was logisch ist – siehe Grafik). Eine solche Grenze wird in der Theorie der Grenzen genannt einseitige Begrenzung. In diesem Fall haben wir rechte Grenze.

(2) Wir ersetzen die oberen und unteren Grenzen gemäß der Newton-Leibniz-Formel.

(3) Umgang mit . Wie bestimmen Sie, wohin ein Ausdruck führt? Grob gesagt müssen Sie nur den Wert ersetzen, drei Viertel ersetzen und angeben, dass . Die Antwort kämmen.

In diesem Fall ist das uneigentliche Integral gleich einer negativen Zahl. Darin liegt kein Verbrechen, nur das entsprechende krummlinige Trapez befindet sich unter der Achse.

Und nun zwei Beispiele für eine eigenständige Entscheidung.

Beispiel 7

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Beispiel 8

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Wenn der Integrand an der Stelle nicht existiert

Ein unendliches krummliniges Trapez für solch ein uneigentliches Integral sieht im Grunde so aus.

Bestimmtes Integral

\[ I=\int_a^bf(x)dx \]

wurde unter der Annahme konstruiert, dass die Zahlen $a,\,b$ endlich sind und $f(x)$ eine stetige Funktion ist. Wird eine dieser Annahmen verletzt, spricht man von uneigentlichen Integralen.

10.1 Uneigentliche Integrale 1. Art

Ein uneigentliches Integral erster Art entsteht, wenn mindestens eine der Zahlen $a,\,b$ unendlich ist.

10.1.1 Definition und grundlegende Eigenschaften

Betrachten wir zunächst die Situation, wenn die untere Grenze der Integration endlich ist und die obere Grenze gleich $+\infty$ ist; andere Möglichkeiten werden später diskutiert. Betrachten Sie das Integral, damit $f(x)$ stetig für alle $x$ ist, die uns interessieren

\begin(gleichung) I=\int _a^(+\infty)f(x)dx. \quad(19) \label(inf1) \end(gleichung)

Zunächst ist es notwendig, die Bedeutung dieses Ausdrucks festzulegen. Dazu führen wir die Funktion ein

\[ I(N)=\int _a^(N)f(x)dx \]

und betrachte sein Verhalten als $N\rightarrow +\infty$.

Definition. Lass es eine Grenze geben

\[ A=\lim_(N\rightarrow+\infty)I(N)=\lim_(N\rightarrow+\infty)\int _a^(N)f(x)dx. \]

Dann heißt das uneigentliche Integral 1. Art (19) konvergieren und ihm wird der Wert $A$ zugewiesen, die Funktion selbst heißt integrierbar auf dem Intervall $\left[ a, \, +\infty \right)$ . Wenn die angegebene Grenze nicht existiert oder gleich $\pm \infty$ ist, sagt man, dass das Integral (19) divergiert.

Betrachten Sie das Integral

\[ I=\int _0^(+\infty) \frac(dx)(1+x^2). \]

\[ I(N)=\int _0^(N) \frac(dx)(1+x^2). \]

In diesem Fall ist die Stammfunktion des Integranden bekannt, so dass

\[ I(N)=\int _0^(N) \frac(dx)(1+x^2)=arctgx|_0^(N)=arctgN. \]

Es ist bekannt, dass $arctg N \rightarrow \pi /2 $ für $N \rightarrow +\infty$ gilt. Somit hat $I(N)$ einen endlichen Grenzwert, unser uneigentliches Integral konvergiert und ist gleich $\pi /2$.

Konvergierende uneigentliche Integrale der 1. Art haben alle Standardeigenschaften gewöhnlicher bestimmter Integrale.

1. Wenn $f(x)$, $g(x)$ auf dem Intervall $\left[ a, \, +\infty \right)$ integrierbar sind, dann ist ihre Summe $f(x)+g(x) $ ist auch auf diesem Intervall integrierbar, und \[ \int _a^(+\infty)\left(f(x)+g(x)\right)dx=\int _a^(+\infty)f(x )dx+\int _a^(+\infty)g(x)dx. \] 2. Wenn $f(x)$ auf dem Intervall $\left[ a, \, +\infty \right)$ integrierbar ist, dann ist für jede Konstante $C$ die Funktion $C\cdot f(x)$ ist auch auf diesem Intervall integrierbar, und \[ \int _a^(+\infty)C\cdot f(x)dx=C \cdot \int _a^(+\infty)f(x)dx. \] 3. Wenn $f(x)$ auf dem Intervall $\left[ a, \, +\infty \right)$ integrierbar ist und $f(x)>0$ auf diesem Intervall, dann \[ \int _a ^ (+\infty) f(x)dx\,>\,0. \] 4. Wenn $f(x)$ auf dem Intervall $\left[ a, \, +\infty \right)$ integrierbar ist, dann ist für jedes $b>a$ das Integral \[ \int _b^(+ \infty) f(x)dx \] konvergiert und \[ \int _a^(+\infty)f(x)dx=\int _a^(b) f(x)dx+\int _b^(+\infty ) f( x)dx \] (Additivität des Integrals über das Intervall).

Es gelten auch die Formeln für Variablenänderung, partielle Integration usw. (mit natürlichen Vorbehalten).

Betrachten Sie das Integral

\begin(gleichung) I=\int _1^(+\infty)\frac(1)(x^k)\,dx. \quad (20) \label(mod) \end(gleichung)

Wir führen die Funktion ein

\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx. \]

In diesem Fall ist die Stammfunktion bekannt, so dass

\[ I(N)=\int _1^(N)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k)|_1^N = \frac(N^(1-k))(1-k)-\frac(1)(1-k) \]

für $k \neq 1$,

\[ I(N)=\int _1^(N)\frac(1)(x)\,dx\,=lnx|_1^N= lnN \]

für $k = 1$. Betrachtet man das Verhalten für $N \rightarrow +\infty$, kommen wir zu dem Schluss, dass das Integral (20) für $k>1$ konvergiert und für $k \leq 1$ divergiert.

Betrachten wir nun den Fall, dass die untere Integrationsgrenze gleich $-\infty$ und die obere endlich ist, d.h. Betrachten Sie die Integrale

\[ I=\int _(-\infty)^af(x)dx. \]

Diese Variante lässt sich aber auf die vorherige zurückführen, wenn wir die Variablen $x=-s$ ändern und dann die Integrationsgrenzen vertauschen, so dass

\[ I=\int _(-a)^(+\infty)g(s)ds, \]

$g(s)=f(-s)$. Betrachten wir nun den Fall, dass es zwei unendliche Grenzen gibt, d.h. Integral-

\begin(equation) I=\int _(-\infty)^(+\infty)f(x)dx, \quad (21) \label(intr) \end(equation)

wobei $f(x)$ für alle $x \in \mathbb(R)$ stetig ist. Lassen Sie uns das Intervall in zwei Teile aufteilen: Nehmen Sie $c \in \mathbb(R)$ und betrachten Sie zwei Integrale,

\[ I_1=\int _(-\infty)^(c)f(x)dx, \quad I_2=\int _(c)^(+\infty)f(x)dx. \]

Definition. Konvergieren beide Integrale $I_1$, $I_2$, so heißt das Integral (21) konvergent, es erhält den Wert $I=I_1+I_2$ (nach der Intervalladditivität). Wenn mindestens eines der Integrale $I_1$, $I_2$ divergiert, heißt Integral (21) divergent.

Es lässt sich beweisen, dass die Konvergenz des Integrals (21) nicht von der Wahl des Punktes $c$ abhängt.

Unechte Integrale 1. Art mit Integrationsintervallen $\left(-\infty, \, c \right]$ oder $(-\infty, \, +\infty)$ haben ebenfalls alle Standardeigenschaften bestimmter Integrale (mit a entsprechende Umformulierung, die das Wahlintegrationsintervall berücksichtigt).

10.1.2 Kriterien für die Konvergenz uneigentlicher Integrale 1. Art

Theorem (das erste Vergleichszeichen). Seien $f(x)$, $g(x)$ stetig für $x>a$ und sei $0 a$. Dann

1. Wenn das Integral \[ \int _a^(+\infty)g(x)dx \] konvergiert, dann konvergiert auch das Integral \[ \int _a^(+\infty)f(x)dx. \] 2. Wenn das Integral \[ \int _a^(+\infty)f(x)dx \] divergiert, dann divergiert auch das Integral \[ \int _a^(+\infty)g(x)dx. \]

Theorem (das zweite Vergleichszeichen). Seien $f(x)$, $g(x)$ stetig und positiv für $x>a$, und es gebe einen endlichen Grenzwert

\[ \theta = \lim_(x \rightarrow +\infty) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Dann die Integrale

\[ \int _a^(+\infty)f(x)dx, \quad \int _a^(+\infty)g(x)dx \]

konvergieren oder gleichzeitig divergieren.

Betrachten Sie das Integral

\[ I=\int _1^(+\infty)\frac(1)(x+\sin x)\,dx. \]

Der Integrand ist eine positive Funktion auf dem Integrationsintervall. Weiterhin gilt für $x \rightarrow +\infty$:

$\sin x$ ist eine "kleine" Korrektur des Nenners. Genauer gesagt, wenn wir $f(x)=1/(x+\sin x)$, \, $g(x)=1/x$ nehmen, dann

\[ \lim _(x \rightarrow +\infty)\frac(f(x))(g(x))=\lim _(x \rightarrow +\infty)\frac(x)(x+\sin x) =1. \]

Wenden wir das zweite Vergleichskriterium an, kommen wir zu dem Schluss, dass unser Integral gleichzeitig mit dem Integral konvergiert oder divergiert

\[ \int _1^(+\infty)\frac(1)(x)\,dx . \]

Wie im vorherigen Beispiel gezeigt, divergiert dieses Integral ($k=1$). Daher divergiert das ursprüngliche Integral.

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Konvergenz (Divergenz) fest.

1. \[ \int _(0)^(+\infty)e^(-ax)\,dx. \] 2. \[ \int _(0)^(+\infty)xe^(-x^2)\,dx. \] 3. \[ \int _(-\infty)^(+\infty)\frac(2xdx)(x^2+1). \] 4. \[ \int _(0)^(+\infty)\frac(xdx)((x+2)^3). \] 5. \[ \int _(-\infty)^(+\infty)\frac(dx)(x^2+2x+2). \] 6. \[ \int _(1)^(+\infty)\frac(lnx)(x^2)\,dx. \] 7. \[ \int _(1)^(+\infty)\frac(dx)((1+x)\sqrt(x)). \] 8. \[ \int _(0)^(+\infty)e^(-\sqrt(x))\,dx. \] 9. \[ \int _(0)^(+\infty)e^(-ax)\cos x\,dx. \] 10. \[ \int _(0)^(+\infty)\frac(xdx)(x^3+1). \]

Uneigentliche Integrale erster Art: Erweiterung des Begriffs eines bestimmten Integrals auf die Fälle von Integralen mit unendlicher oberer oder unterer Integrationsgrenze, oder beide Integrationsgrenzen sind unendlich.

Uneigentliche Integrale zweiter Art: Erweiterung des Konzepts eines bestimmten Integrals auf die Fälle von Integralen unbeschränkter Funktionen existiert der Integrand nicht an einer endlichen Anzahl von Punkten des endlichen Integrationsintervalls, das sich gegen Unendlich wendet.

Zum Vergleich. Bei der Einführung des Konzepts bestimmtes Integral Es wurde angenommen, dass die Funktion f(x) ist stetig auf dem Segment [ a, b], und das Integrationsintervall ist endlich, das heißt, es ist durch Zahlen und nicht durch Unendlich begrenzt. Einige Aufgaben führen dazu, dass diese Einschränkungen aufgegeben werden müssen. So erscheinen uneigentliche Integrale.

Die geometrische Bedeutung des uneigentlichen Integrals stellt sich als recht einfach heraus. Wenn der Graph der Funktion j = f(x) liegt über der Achse Ochse, drückt das bestimmte Integral die Fläche eines krummlinigen Trapezes aus, das von einer Kurve begrenzt wird j = f(x) , Abszisse und Ordinaten x = a , x = b. Das uneigentliche Integral wiederum drückt die Fläche eines unbegrenzten (unendlichen) krummlinigen Trapezes aus, das zwischen den Linien eingeschlossen ist j = f(x) (unten in rot abgebildet) x = a und die Abszissenachse.

Uneigentliche Integrale werden ähnlich für andere unendliche Intervalle definiert:

Die Fläche eines unendlichen krummlinigen Trapezes kann eine endliche Zahl sein, in diesem Fall wird das uneigentliche Integral als konvergent bezeichnet. Die Fläche kann auch unendlich sein, in diesem Fall heißt das uneigentliche Integral divergent.

Verwenden der Grenze eines Integrals anstelle des uneigentlichen Integrals selbst. Um das uneigentliche Integral zu berechnen, müssen Sie den Grenzwert des bestimmten Integrals verwenden. Wenn dieser Grenzwert existiert und endlich ist (ungleich unendlich), dann heißt das uneigentliche Integral konvergent, andernfalls ist es divergent. Wohin die Variable unter dem Grenzzeichen strebt, hängt davon ab, ob es sich um ein uneigentliches Integral erster oder zweiter Art handelt. Finden wir es jetzt heraus.

Uneigentliche Integrale erster Art - mit unendlichen Grenzen und deren Konvergenz

Uneigentliche Integrale mit unendlicher Obergrenze

Die Aufzeichnung des uneigentlichen Integrals unterscheidet sich also vom üblichen bestimmten Integral dadurch, dass die obere Integrationsgrenze unendlich ist.

Definition. Ein uneigentliches Integral mit einer unendlichen oberen Integrationsgrenze aus einer stetigen Funktion f(x) zwischen a Vor ∞ heißt der Grenzwert des Integrals dieser Funktion mit der oberen Integrationsgrenze b und die untere Integrationsgrenze a vorausgesetzt, dass die obere Integrationsgrenze unendlich wächst, d.h.

.

Wenn diese Grenze existiert und gleich einer Zahl und nicht unendlich ist, dann das uneigentliche Integral heißt konvergent, und die Zahl, die der Grenze entspricht, wird als ihr Wert genommen. Sonst das uneigentliche Integral heißt divergent und ihm wird kein Wert beigemessen.

Beispiel 1. Uneigentliches Integral berechnen(wenn es konvergiert).

Entscheidung. Basierend auf der Definition des uneigentlichen Integrals finden wir

Da der Grenzwert existiert und gleich 1 ist, gilt das Gegebene unechtes Integral konvergiert und ist gleich 1.

Im folgenden Beispiel ist der Integrand fast derselbe wie in Beispiel 1, nur der Grad von x ist nicht zwei, sondern der Buchstabe Alpha, und die Aufgabe besteht darin, das uneigentliche Integral auf Konvergenz zu untersuchen. Das heißt, die Frage bleibt zu beantworten: Bei welchen Werten von Alpha konvergiert dieses uneigentliche Integral und bei welchen Werten divergiert es?

Beispiel 2. Untersuchen Sie die Konvergenz eines uneigentlichen Integrals(die untere Integrationsgrenze ist größer als Null).

Entscheidung. Nehmen Sie zuerst an, dass , dann

Im resultierenden Ausdruck gehen wir bis zur Grenze bei:

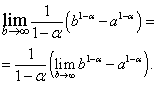
Es ist leicht zu sehen, dass die Grenze auf der rechten Seite existiert und gleich Null ist, wenn , d. h. , und nicht existiert, wenn , d.

Im ersten Fall, also wenn . Wenn, dann und existiert nicht.

Das Fazit unserer Studie lautet wie folgt: unechtes Integral konvergiert bei und weicht ab beim .

Anwendung der Newton-Leibniz-Formel auf den untersuchten Typ des uneigentlichen Integrals , können wir die folgende sehr ähnliche Formel ableiten:

.

Dies ist die verallgemeinerte Newton-Leibniz-Formel.

Beispiel 3. Unechtes Integral berechnen(wenn es konvergiert).

Der Grenzwert dieses Integrals besteht:

Das zweite Integral, das die Summe ist, die das ursprüngliche Integral ausdrückt:

Der Grenzwert dieses Integrals existiert auch:

.

Wir finden die Summe zweier Integrale, die auch der Wert des ursprünglichen uneigentlichen Integrals mit zwei unendlichen Grenzen ist:

Uneigentliche Integrale der zweiten Art - aus unbeschränkten Funktionen und ihrer Konvergenz

Lassen Sie die Funktion f(x) Setzen Sie auf das Segment aus a Vor b und unbegrenzt darauf. Angenommen, die Funktion geht an diesem Punkt gegen unendlich b , während sie an allen anderen Punkten des Segments stetig ist.

Definition. Uneigentliches Integral der Funktion f(x) auf dem Segment von a Vor b heißt der Grenzwert des Integrals dieser Funktion mit der oberen Integrationsgrenze c , wenn beim Streben c zu b die Funktion steigt unendlich, und an dem Punkt x = b Funktion nicht definiert, d.h.

.

Existiert dieser Grenzwert, so heißt das uneigentliche Integral zweiter Art konvergent, andernfalls divergent.

Unter Verwendung der Newton-Leibniz-Formel leiten wir ab.