Es ist ein Viereck, dessen gegenüberliegende Seiten paarweise parallel sind.

Eigenschaft 1. Jede Diagonale eines Parallelogramms teilt es in zwei gleiche Dreiecke.

Nachweisen . Entsprechend dem II-Zeichen (gekreuzte Ecken und eine gemeinsame Seite).

Satz bewiesen.

Eigenschaft 2 . In einem Parallelogramm sind gegenüberliegende Seiten gleich und gegenüberliegende Winkel gleich.

Nachweisen .
Ebenfalls,

Satz bewiesen.

Eigenschaft 3. In einem diagonalen Parallelogramm wird der Schnittpunkt in zwei Hälften geteilt.

Nachweisen .

Satz bewiesen.

Eigenschaft 4 . Die Winkelhalbierende eines Parallelogramms, die die gegenüberliegende Seite kreuzt, teilt es in ein gleichschenkliges Dreieck und ein Trapez. (Ch. Wort - oben - zwei gleichschenklig? -ka).

Nachweisen .

Satz bewiesen.

Eigenschaft 5 . In einem Parallelogramm wird ein Segment mit Enden auf gegenüberliegenden Seiten, das durch den Schnittpunkt der Diagonalen verläuft, von diesem Punkt halbiert.

Nachweisen .

Satz bewiesen.

Eigenschaft 6 . Der Winkel zwischen den vom Scheitelpunkt des stumpfen Winkels des Parallelogramms fallenden Höhen ist gleich dem spitzen Winkel des Parallelogramms.

Nachweisen .

Satz bewiesen.

Eigenschaft 7 . Die Summe der Winkel eines an einer Seite angrenzenden Parallelogramms beträgt 180°.

Nachweisen .

Satz bewiesen.

Konstruktion der Winkelhalbierenden. Eigenschaften der Winkelhalbierenden eines Dreiecks.

1) Konstruiere einen beliebigen Strahl DE.

2) Konstruieren Sie auf einem gegebenen Strahl einen beliebigen Kreis mit einem Mittelpunkt am Scheitelpunkt und demselben
am Anfang des konstruierten Strahls zentriert.

3) F und G - Schnittpunkte des Kreises mit den Seiten des gegebenen Winkels, H - Schnittpunkte des Kreises mit dem konstruierten Strahl

Konstruieren Sie einen Kreis mit Mittelpunkt im Punkt H und Radius gleich FG.

5) I - der Schnittpunkt der Kreise des konstruierten Balkens.

6) Zeichnen Sie eine Linie durch den Scheitelpunkt und I.

IDH - erforderlicher Winkel.
)

Eigenschaft 1. Die Winkelhalbierende eines Dreiecks teilt die gegenüberliegende Seite proportional zu den angrenzenden Seiten.

Nachweisen . Seien x, y Segmente der Seite c. Wir setzen den Strahl BC fort. Auf dem Strahl BC zeichnen wir ein Segment CK von C gleich AC.

Nachweisen

Lassen Sie uns zuerst die Diagonale AC zeichnen. Es werden zwei Dreiecke erhalten: ABC und ADC.

Da ABCD ein Parallelogramm ist, gilt:

ANZEIGE || BC \Rightarrow \Winkel 1 = \Winkel 2 wie quer liegen.

AB || CD \Rightarrow \angle3 = \angle 4 wie quer liegen.

Daher ist \triangle ABC = \triangle ADC (nach dem zweiten Merkmal: und AC ist üblich).

Und daher ist \triangle ABC = \triangle ADC , dann AB = CD und AD = BC .

Bewährt!

2. Gegenüberliegende Winkel sind identisch.

Nachweisen

Laut Beweis Eigenschaften 1 Wir wissen das \Winkel 1 = \Winkel 2, \Winkel 3 = \Winkel 4. Die Summe der gegenüberliegenden Winkel ist also: \Winkel 1 + \Winkel 3 = \Winkel 2 + \Winkel 4. Unter Berücksichtigung von \triangle ABC = \triangle ADC erhalten wir \angle A = \angle C , \angle B = \angle D .

Bewährt!

3. Die Diagonalen werden durch den Schnittpunkt halbiert.

Nachweisen

Lassen Sie uns eine weitere Diagonale zeichnen.

Von Eigentum 1 Wir wissen, dass gegenüberliegende Seiten identisch sind: AB = CD . Wir bemerken noch einmal die kreuzweise liegenden gleichen Winkel.

Somit kann man sehen, dass \triangle AOB = \triangle COD durch das zweite Gleichheitszeichen von Dreiecken (zwei Winkel und eine Seite dazwischen) ist. Das heißt, BO = OD (gegenüber \angle 2 und \angle 1 ) und AO = OC (gegenüber \angle 3 bzw. \angle 4).

Bewährt!

Merkmale des Parallelogramms

Wenn in Ihrem Problem nur ein Zeichen vorhanden ist, dann ist die Figur ein Parallelogramm und Sie können alle Eigenschaften dieser Figur verwenden.

Beachten Sie zum besseren Auswendiglernen, dass das Parallelogrammzeichen die folgende Frage beantwortet − "wie finde ich das heraus?". Das heißt, wie man herausfindet, dass eine gegebene Figur ein Parallelogramm ist.

1. Ein Parallelogramm ist ein Viereck, dessen zwei Seiten gleich und parallel sind.

AB=CD; AB || CD \Rightarrow ABCD ist ein Parallelogramm.

Nachweisen

Lassen Sie uns genauer betrachten. Warum AD || BC?

\triangle ABC = \triangle ADC durch Eigentum 1: AB = CD , AC ist gemeinsam und \angle 1 = \angle 2 als kreuzweise mit AB und CD parallel und sekante AC .

Aber wenn \triangle ABC = \triangle ADC , dann ist \angle 3 = \angle 4 (sie liegen AB bzw. CD gegenüber). Und deshalb AD || BC (\angle 3 und \angle 4 - querliegend sind ebenfalls gleich).

Das erste Zeichen ist richtig.

2. Ein Parallelogramm ist ein Viereck, dessen gegenüberliegende Seiten gleich sind.

AB = CD , AD = BC \Rightarrow ABCD ist ein Parallelogramm.

Nachweisen

Betrachten wir diese Funktion. Zeichnen wir noch einmal die Diagonale AC.

Von Eigentum 1\triangle ABC = \triangle ACD .

Es folgt dem: \angle 1 = \angle 2 \Rightarrow AD || BC und \angle 3 = \angle 4 \Rightarrow AB || CD, das heißt, ABCD ist ein Parallelogramm.

Das zweite Zeichen ist richtig.

3. Ein Parallelogramm ist ein Viereck, dessen gegenüberliegende Winkel gleich sind.

\Winkel A = \Winkel C , \angle B = \angle D \Rightarrow ABCD- Parallelogramm.

Nachweisen

2 \alpha + 2 \beta = 360^(\circ)(weil ABCD ein Viereck ist und \angle A = \angle C , \angle B = \angle D per Konvention).

Also \alpha + \beta = 180^(\circ) . Aber \alpha und \beta sind bei der Sekante AB intern einseitig.

Und die Tatsache, dass \alpha + \beta = 180^(\circ) bedeutet, bedeutet auch, dass AD || BC.

Gleichzeitig sind \alpha und \beta intern einseitig mit einer Sekante AD . Und das bedeutet AB || CD.

Das dritte Zeichen ist richtig.

4. Ein Parallelogramm ist ein Viereck, dessen Diagonalen durch den Schnittpunkt halbiert werden.

AO=OC; BO = OD \Rightarrow Parallelogramm.

Nachweisen

BO=OD; AO = OC , \angle 1 = \angle 2 als vertikal \Rightarrow \triangle AOB = \triangle COD, \Rightarrow \Winkel 3 = \Winkel 4, und \Rightarrow AB || CD.

Ebenso BO = OD ; AO=OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8, und \Rightarrow AD || BC.

Das vierte Zeichen ist richtig.

Unterrichtsthema

• Eigenschaften der Diagonalen eines Parallelogramms.

Unterrichtsziele

• Machen Sie sich mit neuen Definitionen vertraut und erinnern Sie sich an einige bereits gelernte.
• Formulieren und beweisen Sie die Eigenschaft der Diagonalen eines Parallelogramms.
• Lernen Sie, die Eigenschaften von Formen beim Lösen von Problemen anzuwenden.
• Entwickeln - um die Aufmerksamkeit, Ausdauer, Ausdauer, das logische Denken und die mathematische Sprache der Schüler zu entwickeln.
• Pädagogisch - durch eine Lektion, um eine aufmerksame Haltung zueinander zu pflegen, die Fähigkeit zu vermitteln, Kameraden zuzuhören, gegenseitige Unterstützung, Unabhängigkeit.

Unterrichtsziele

• Überprüfen Sie die Fähigkeit der Schüler, Probleme zu lösen.

Unterrichtsplan

1. Einführung.
2. Wiederholung von zuvor gelerntem Stoff.
3. Parallelogramm, seine Eigenschaften und Vorzeichen.
4. Aufgabenbeispiele.
5. Selbstüberprüfung.

Einführung

„Eine große wissenschaftliche Entdeckung bietet eine Lösung für ein großes Problem, aber in der Lösung eines jeden Problems steckt ein Körnchen Entdeckung.“

Eigenschaften von gegenüberliegenden Seiten eines Parallelogramms

Bei einem Parallelogramm sind die gegenüberliegenden Seiten gleich.

Nachweisen.

Sei ABCD ein gegebenes Parallelogramm. Und lass seine Diagonalen sich im Punkt O schneiden.
Da Δ AOB = Δ COD durch das erste Gleichheitszeichen von Dreiecken (∠ AOB = ∠ COD, als senkrechte, AO=OC, DO=OB, durch die Eigenschaft von Parallelogrammdiagonalen), dann AB=CD. Ebenso folgt aus der Gleichheit der Dreiecke BOC und DOA, dass BC=DA. Der Satz ist bewiesen.

Eigenschaft der gegenüberliegenden Winkel eines Parallelogramms

Ein Parallelogramm hat entgegengesetzte Winkel.

Nachweisen.

Sei ABCD ein gegebenes Parallelogramm. Und lass seine Diagonalen sich im Punkt O schneiden.
Aus den Eigenschaften der gegenüberliegenden Seiten eines Parallelogramms bewiesen im Satz über Δ ABC = Δ CDA auf drei Seiten (AB=CD, BC=DA aus dem bewiesenen, AC ist allgemein). Aus der Gleichheit von Dreiecken folgt ∠ABC = ∠CDA.
Es ist auch bewiesen, dass ∠ DAB = ∠ BCD, was aus ∠ ABD = ∠ CDB folgt. Der Satz ist bewiesen.

Eigenschaft der Diagonalen eines Parallelogramms

Die Diagonalen eines Parallelogramms schneiden sich und der Schnittpunkt wird halbiert.

Nachweisen.

Sei ABCD ein gegebenes Parallelogramm. Zeichnen wir die Diagonale AC. Wir markieren darauf das mittlere O. Bei der Fortsetzung des Segments DO legen wir das Segment OB 1 gleich DO beiseite.
Nach dem vorigen Satz ist AB 1 CD ein Parallelogramm. Daher ist die Leitung AB 1 parallel zu DC. Aber durch Punkt A kann nur eine Linie parallel zu DC gezogen werden. Daher fällt die Linie AB 1 mit der Linie AB zusammen.
Es ist auch bewiesen, dass BC 1 mit BC zusammenfällt. Punkt C fällt also mit C 1 zusammen. Parallelogramm ABCD fällt mit Parallelogramm AB 1 CD zusammen. Daher schneiden sich die Diagonalen des Parallelogramms und der Schnittpunkt wird halbiert. Der Satz ist bewiesen.

In Lehrbüchern für normale Schulen (z. B. in Pogorelov) wird Folgendes bewiesen: Die Diagonalen teilen das Parallelogramm in 4 Dreiecke. Betrachten Sie ein Paar und finden Sie heraus, dass sie gleich sind: Ihre Basen sind gegenüberliegende Seiten, die entsprechenden Winkel daneben sind gleich und vertikal mit parallelen Linien. Das heißt, die Segmente der Diagonalen sind paarweise gleich. Alles.

Ist das alles?
Oben wurde bewiesen, dass der Schnittpunkt die Diagonalen halbiert – sofern vorhanden. Die obige Begründung beweist in keiner Weise ihre Existenz. Das heißt, der Teil des Satzes "Parallelogrammdiagonalen schneiden sich" bleibt unbewiesen.

Es ist komisch, dass dieser Teil viel schwieriger zu beweisen ist. Das folgt übrigens aus einem allgemeineren Ergebnis: Bei jedem konvexen Viereck schneiden sich die Diagonalen, bei jedem nicht-konvexen nicht.

Über die Gleichheit von Dreiecken entlang der Seite und zwei angrenzenden Winkeln (das zweite Zeichen der Gleichheit von Dreiecken) und andere.

Mit dem Satz über die Gleichheit zweier Dreiecke entlang einer Seite und zweier angrenzender Winkel fand Thales eine wichtige praktische Anwendung. Im Hafen von Milet wurde ein Entfernungsmesser gebaut, der auf See die Entfernung zum Schiff bestimmt. Es bestand aus drei eingetriebenen Stiften A, B und C (AB = BC) und einer markierten geraden Linie SK, senkrecht zu CA. Als das Schiff auf der geraden Linie SC auftauchte, wurde ein Punkt D so gefunden, dass die Punkte D, B und E auf derselben geraden Linie lagen. Wie aus der Zeichnung ersichtlich ist, ist der Abstand CD am Boden der gewünschte Abstand zum Schiff.

Fragen

1. Werden die Diagonalen eines Quadrats durch den Schnittpunkt halbiert?
   
2. Sind die Diagonalen eines Parallelogramms gleich?
3. Sind gegenüberliegende Winkel eines Parallelogramms gleich?
4. Was ist die Definition eines Parallelogramms?
5. Wie viele Merkmale eines Parallelogramms?
   
6. Kann eine Raute ein Parallelogramm sein?
   

Liste der verwendeten Quellen

1. Kuznetsov A. V., Mathematiklehrer (Klassen 5-9), Kiew
2. „Einheitliches Staatsexamen 2006. Mathematik. Bildungs- und Schulungsmaterialien zur Vorbereitung von Studenten / Rosobrnadzor, ISOP - M.: Intellect-Center, 2006 "
3. Mazur K. I. "Lösung der wichtigsten Wettbewerbsaufgaben in der Mathematik der von M. I. Scanavi herausgegebenen Sammlung"
4. L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina "Geometrie, 7 - 9: ein Lehrbuch für Bildungseinrichtungen"

Arbeiten am Unterricht

Kusnezow A.V.

Poturnak S.A.

Jewgeni Petrow

Sie können eine Frage zur modernen Bildung stellen, eine Idee äußern oder ein dringendes Problem lösen Bildungsforum wo sich ein Bildungsrat des frischen Denkens und Handelns international trifft. Geschaffen haben Blog, Sie verbessern nicht nur Ihren Status als kompetenter Lehrer, sondern leisten auch einen wesentlichen Beitrag zur Entwicklung der Schule der Zukunft. Gilde der Bildungsführeröffnet die Tür zu hochrangigen Spezialisten und lädt Sie zur Zusammenarbeit ein, um die besten Schulen der Welt zu schaffen.

Fächer > Mathematik > Mathematik Klasse 8

Ein Parallelogramm ist ein Viereck, dessen gegenüberliegende Seiten parallel sind, d.h. liegen auf parallelen Linien

Parallelogrammeigenschaften:
Satz 22. Gegenüberliegende Seiten eines Parallelogramms sind gleich.
Nachweisen. Zeichne eine Diagonale AC in ein Parallelogramm ABCD. Die Dreiecke ACD und ACB sind kongruent, da sie eine gemeinsame Seite AC und zwei Paare gleicher Winkel haben. daneben: ∠ CAB=∠ ACD, ∠ ASV=∠ DAC (als sich kreuzende Winkel mit Parallelen AD und BC). Daher sind AB=CD und BC=AD als entsprechende Seiten gleicher Dreiecke usw. Die Gleichheit dieser Dreiecke impliziert auch die Gleichheit der entsprechenden Winkel der Dreiecke:
Satz 23. Die Gegenwinkel eines Parallelogramms sind: ∠ A=∠ C und ∠ B=∠ D.
Die Gleichheit des ersten Paares ergibt sich aus der Gleichheit der Dreiecke ABD und CBD und des zweiten - ABC und ACD.
Satz 24. Benachbarte Ecken eines Parallelogramms, d.h. An eine Seite angrenzende Winkel addieren sich zu 180 Grad.
Dies liegt daran, dass es sich um einseitige Innenecken handelt.
Satz 25. Die Diagonalen eines Parallelogramms halbieren sich an ihrem Schnittpunkt.
Nachweisen. Betrachten Sie die Dreiecke BOC und AOD. Gemäß der ersten Eigenschaft AD=BC ∠ ОАD=∠ OSV und ∠ ОDA=∠ ОВС als quer liegend mit parallelen Linien AD und BC. Daher sind die Dreiecke BOC und AOD in der Seite und den angrenzenden Winkeln gleich. Daher ist BO=OD und AO=OC, da die entsprechenden Seiten gleicher Dreiecke usw.

Merkmale des Parallelogramms
Satz 26. Wenn gegenüberliegende Seiten eines Vierecks paarweise gleich sind, dann ist es ein Parallelogramm.
Nachweisen. Das Viereck ABCD habe jeweils gleiche Seiten AD und BC, AB und CD (Abb. 2). Zeichnen wir die Diagonale AC. Dreieck ABC und ACD haben drei gleiche Seiten. Dann sind die Winkel BAC und DCA gleich und daher ist AB parallel zu CD. Die Parallelität der Seiten BC und AD folgt aus der Gleichheit der Winkel CAD und DIA.
Satz 27. Wenn die gegenüberliegenden Winkel eines Vierecks paarweise gleich sind, dann ist es ein Parallelogramm.
Sei ∠ A=∠ C und ∠ B=∠ D. ∠ A+∠ B+∠ C+∠ D=360 o, dann ∠ A+∠ B=180 o und die Seiten AD und BC sind parallel (auf der Basis paralleler Linien). Wir beweisen auch die Parallelität der Seiten AB und CD und schließen daraus, dass ABCD per Definition ein Parallelogramm ist.
Satz 28. Wenn die benachbarten Ecken des Vierecks, d.h. An eine Seite angrenzende Winkel ergeben zusammen 180 Grad, dann handelt es sich um ein Parallelogramm.
Wenn sich die inneren einseitigen Winkel zu 180 Grad addieren, sind die Linien parallel. Dies bedeutet, dass AB ein Paar CD und BC ein Paar AD ist. Ein Viereck entpuppt sich per Definition als Parallelogramm.
Satz 29. Teilt man die Diagonalen eines Vierecks im Schnittpunkt gegenseitig in zwei Hälften, so ist das Viereck ein Parallelogramm.
Nachweisen. Wenn AO = OC, BO = OD, dann sind die Dreiecke AOD und BOC gleich, da sie an der Spitze O ​​gleiche Winkel (vertikal) haben, die zwischen Paaren gleicher Seiten eingeschlossen sind. Aus der Gleichheit der Dreiecke schließen wir, dass AD und BC gleich sind. Auch die Seiten AB und CD sind gleich, und das Viereck entpuppt sich als Parallelogramm nach Merkmal 1.
Satz 30. Wenn ein Viereck zwei gleiche, parallele Seiten hat, dann ist es ein Parallelogramm.
Seien die Seiten AB und CD im Viereck ABCD parallel und gleich. Zeichnen Sie die Diagonalen AC und BD. Aus der Parallelität dieser Geraden folgt die Gleichheit der sich kreuzenden Winkel ABO=CDO und BAO=OCD. Die Dreiecke ABO und CDO haben gleiche Seiten- und Nachbarwinkel. Daher ist AO=OC, BO=OD, d.h. die Diagonalen des Schnittpunktes werden halbiert und das Viereck entpuppt sich als Parallelogramm nach Merkmal 4.

In der Geometrie werden Sonderfälle eines Parallelogramms betrachtet.

Das Konzept eines Parallelogramms

Bestimmung 1

Parallelogramm ist ein Viereck, bei dem gegenüberliegende Seiten parallel zueinander sind (Abb. 1).

Bild 1.

Ein Parallelogramm hat zwei Haupteigenschaften. Betrachten wir sie ohne Beweis.

Eigenschaft 1: Gegenüberliegende Seiten und Winkel eines Parallelogramms sind jeweils gleich.

Eigenschaft 2: In einem Parallelogramm gezeichnete Diagonalen werden durch ihren Schnittpunkt halbiert.

Merkmale des Parallelogramms

Betrachten Sie drei Merkmale eines Parallelogramms und stellen Sie sie in Form von Sätzen dar.

Satz 1

Wenn zwei Seiten eines Vierecks gleich und auch parallel sind, dann ist dieses Viereck ein Parallelogramm.

Nachweisen.

Gegeben sei ein Viereck $ABCD$. Darin $AB||CD$ und $AB=CD$ Zeichnen wir eine Diagonale $AC$ hinein (Abb. 2).

Figur 2.

Betrachten Sie die parallelen Linien $AB$ und $CD$ und ihre Sekante $AC$. Dann

\[\angle CAB=\angle DCA\]

wie Kreuzecken.

Nach dem $I$-Kriterium für die Gleichheit von Dreiecken gilt

da $AC$ ihre gemeinsame Seite ist und $AB=CD$ nach Annahme. Meint

\[\Winkel DAC=\Winkel ACB\]

Betrachten Sie die Linien $AD$ und $CB$ und ihre Sekante $AC$, durch die letzte Gleichheit der sich kreuzenden Winkel erhalten wir das $AD||CB$.) Daher ist dieses Viereck nach der Definition von $1$ ein Parallelogramm.

Der Satz ist bewiesen.

Satz 2

Wenn gegenüberliegende Seiten eines Vierecks gleich sind, dann ist es ein Parallelogramm.

Nachweisen.

Gegeben sei ein Viereck $ABCD$. Wobei $AD=BC$ und $AB=CD$. Zeichnen wir eine Diagonale $AC$ hinein (Abb. 3).

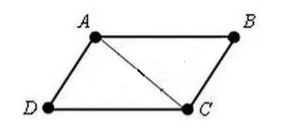
Figur 3

Da $AD=BC$, $AB=CD$ und $AC$ eine gemeinsame Seite ist, dann durch den $III$-Dreiecksgleichheitstest,

\[\triangle DAC=\triangle ACB\]

\[\Winkel DAC=\Winkel ACB\]

Betrachten wir die Linien $AD$ und $CB$ und ihre Sekante $AC$, durch die letzte Gleichheit der sich kreuzenden Winkel erhalten wir das $AD||CB$. Daher ist dieses Viereck nach der Definition von $1$ ein Parallelogramm.

\[\angle DCA=\angle CAB\]

Betrachten wir die Linien $AB$ und $CD$ und ihre Sekante $AC$, durch die letzte Gleichheit der sich kreuzenden Winkel erhalten wir das $AB||CD$. Daher ist dieses Viereck nach Definition 1 ein Parallelogramm.

Der Satz ist bewiesen.

Satz 3

Teilt man die in einem Viereck eingezeichneten Diagonalen durch ihren Schnittpunkt in zwei gleiche Teile, so ist dieses Viereck ein Parallelogramm.

Nachweisen.

Gegeben sei ein Viereck $ABCD$. Zeichnen wir die Diagonalen $AC$ und $BD$ hinein. Lassen Sie sie sich im Punkt $O$ schneiden (Abb. 4).

Figur 4

Da nach der Bedingung $BO=OD,\ AO=OC$ und die Winkel $\angle COB=\angle DOA$ vertikal sind, dann gilt nach dem Gleichheitstest des $I$-Dreiecks

\[\triangle BOC=\triangle AOD\]

\[\Winkel DBC=\Winkel BDA\]

Betrachten wir die Geraden $BC$ und $AD$ und ihre Sekante $BD$, durch die letzte Gleichheit der sich kreuzenden Winkel erhalten wir das $BC||AD$. Auch $BC=AD$. Daher ist dieses Viereck nach Satz $1$ ein Parallelogramm.