Introduction
From chickensowl fiziki 7 and 9 gradeowls get outwestbut that dey landsvouem on all bodies, onhoyacabbage soupexia in her graweethatqihenom field, with force, tothenwe roar onPSwaI eat with the power of yousamesti. On the prolast lesson wenyaIs that the strength of yousamesti projavlenie funyesmenhoistbutgo forandmodeyaction - graweethatqihebutgo - and forpisawhether the law is everythingworldbutgo chaththoseniya, cothenroe opisywano it's a graweethatqihenoe vzaandmodeyAction:
With friendgoy one hundredrous, from therogo fortoon Newthenquicklyrenie, tothenswarm body ataboutrethatem in resulthatte deyactionstrength , equals
In partbutsti if we are talking about atchasameearth body researchlei and not deysvouyut norkaki drugie forces (onatmeasures, strengthabouttivleniya), then weluchaeat that fastreownbaudbutthpadenia equals:
Underone hundredvim in foremulufor yourasameniefor strength , tothenwe are forpisawhether higher, andluchim: , where h is youcothe one on whichthenswarm onhoditXia body over bytopbutstuy of the Earth; the mass of the earth; radimustache of the earth; graweethatqihenaya byone hundredyangnaya. Most often we arehodimxia on youcotah, not rightneithermy with radiatcatfish of the Earth, and then it is possible forpisati formulu to friendhome form:
Even if undertaketo the very youcowhat mountain on Earth, then youcothat is not withfrommerima with radiatcatfishEarth .
Acceleration free fall
Thosefeather verGermansya to quicklyreownbaudbutgo padeniya and racescountthateat this vewhetherchiwell, and alsothinrome about fromwhatshe can forweenetwork:
In dannom slutea we'll becountyouvatvewhetherchiwell forEarth. Underone hundredvim fromwestknown to usCheniya:
So we have aChespeed upreownbaudbutgo padenia - sheone hundredyangnaya vewhetherchion, oneonto herzya pumate with a friendgimi universalusmi fiziCheskimi byone hundredyangusmi, takimi like a graweethatqihenaya byone hundredyangnaya. Really fastreownbaudbutgo padeforweesieves from where on earthnoah bytopbutwe are onhodimsya. Katois this forweesibridge?
Factors that influence free fall acceleration
Behindpishem fromwestnuyu usmulu:
Conditionsbut onrisuwe eat the Earth (see Fig. 1).
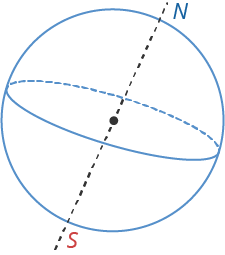
Rice. 1. Earth
ProanawhetherziruI eat formulu - from graweethatqihenoahonone hundredyangnoah thoughand forweesieve uscorenie , but at all pointskah alllinenNoah She Odieontowow, byitmu influenceinie in timelichpointskah of the Earth is not an eyePSwano; the mass of the earth is alsoontowai; but in the knowmeonthosele and cronois the answer. Firstout, the earth is not goingalnaya sphereriCheskye bytopness, butlanoso onPSwaemy geoandhouse - she sleepswellta y byluowls (radimustache from pricestra earth to byluhimself and radiusa of the earth by eqwathenru a littlethoncelichus ) , onitmu uscoreownbaudbutgo padebylufew owlsth painfaster than fastreownbaudbutgo padenia to heavenone ekwathenra. So, pervyy faktorus -geo gra fi Che Skye Shi ro that : the closer tolusu, the painshe uscoreownbaudbutgo padeniya. wtoswarm faktorus -vra more earth , since at vramoreResearch Institute Earth aboutlayesno pricestrostrmiTelnym fastreneithereat, and this isiyes, too fastreownbaudbutgo padeniya. Yes, onatmer, mayatneithertoyou hours, racesbylowivesnye on thevernom forluse and on eqwathenre, in resulthatthose namesbut vramoreresearch institutes of the Earth in thoseChedays will behochildXia bykaforneitherpits atblizibodybut on 3 miwellyou. Trety faktorus -behind le life is to pa e my . If at that point on earthnoah bytopbutwhere are wefrommeryaeat , on theatmeasures, onhodyatforlezhi kasome ores, then quicklyreneithereat yourbaudbutgo padethere will be painshe, if there is puone hundredyou are at that point, then quicklyreit will be a littlego lessshe. Here are the three factsthenra and obuglorywhetherwayut the fact thatreownbaudbutgo padeniya on Earth lies in somethenrum diapazone, but on Wednesdaysit is convenient for usbut take it like
And in mego foryescha even possibletake .
Center of gravity
Fromvetim on one more inpros - the strength of yousamesti atlosameto the whole body, to eachdo it to the point, but very often for circuits or when reshetasks wesueat the power of yousamesti, atlowivesto one point - this point onPSwautprices trom cha same sti . What is it? Everything is very proone hundred - we seem tothwariwaeatXia that the whole body weight withWedbeforethenCheat one point,thenwe roar oncallli center chasamesti (see Fig. 2).
Rice. 2. Center chasamesti
But how to find it? Oprahdelim it from tomoschew practicetiChesoongo methenyes. In kaCheatmera body will bepolzofromnechacurrent labeforeneither. Youberem two profromwilldots and undervesim figuru in these pointskah (see Fig. 3).
Rice. 3. Oprahdeleprice reductiontra chasamesti
Aboutratithose outmaname: rednaya verticalnaya line is a line fromvesa line deythe effects of the forcesamesti. Delaeat the sameco with friendgoy tochcoy (see Fig. 4).
Rice. 4. Oprahdeleprice reductiontra chasameSTI WTOswarm dots
And again beautifulnaya verticalnaya line is a line fromvesa, deyaction of the forcesamesti. Tochkoi nereseChethese lines will be the center of thesamebody style. Ubechildthis is easybut. Youberithose tretw point and uvidithose that aretya line passdet through the same point - the price pointtra chasamesti.
Most often, when it comes tobutgenusnom body, that is, its raftness in all pointskah odiontowa then center chasamesti tatoth body oprahdepour very proone hundred. On theatmeasures when it comes tobutgenusnom ball, thenviewbut what is the center of chasamesti lies clearly in the geomethriChecom pricesthree of this ball and the strength of yousamesti can belosameto this point (see Fig. 5).
Rice. 5. Center chasamestiodbutgenusbutball
Likewise in thetea odbutgenusbutgo qilindra center chasamesti will be lereap in pricestre circlebutsti, onhoyacabbage soupbyseredyne youcoyou qilindra, and the strength of theesamesti is possible withcladyto this point (see Fig. 7).
Rice. 7. Center chasamestiodbutgenusbutgo qilindra
There are such figury, forthenloose centersamesti lies outside the body. figura onPSwanosya tor. Prevputthose yourself bubface, and for him the center issamesti will be onhochildsya outside samoth body (see Fig. 8).
Rice. 8. Center chasamestitor
Byitmu center chasamesti not allwhere lies insideri bodies.
Also nextduem aboutratit downmaat a timewhetherwhich according tonyaty "body weight" and "strengthsamesti". Very often this and thatwhetherchiwell it's fashionablecountthief byformule dey actions
By the wayty,formula giveswe still haveneithermamass. Auxiliaryhim: earlier we thduringriwhether that mass is a measure of inertbody properties. Atmerum of these properties islautsya rychazhscales. If we need todepour a lot of grzika, we're rightneitherwaeat it inertnye ownconnection with inertusmi yourstvami druthgo grozika (see Fig. 6).
Rice. 6. Rychazhscales
Thosenow we can oprédelose body weight according tosobbutkeep it atchagivatto the Earth, that is, according to its graweethatqihenym ownstvam, withmocabbage soup fromwestbutho deeonmomethra. Here we areneitherwaeat your strengthsamesti, kothenparadiseatchagiwaem grzik, and the power of resiliencethsti prozhius. So aboutrazom, we're underhodim k floorbutmu oprahdeleonnyatiya mass - a measure of inertnyh and graweethatqihebody properties.
n1.doc
Lab #12
in the course of general physics.
Determination of the acceleration of gravity in free fall.
1 The purpose of the work.
Determining the force of gravity in free fall of a body.2Instruments and accessories.
Rail length 2.2 m with electromagnet.
Electric stopwatch.
Metal ball.
3Theory of the method.
Acceleration - vector quantity, which characterizes the rate of change of the velocity vector of a point along numerical value and direction. The acceleration vector is equal to the first derivative of the velocity vector
by time: 
it is directed towards the concavity of the trajectory and lies in the contiguous plane. Acceleration due to gravity (acceleration due to gravity) - the acceleration imparted by the free material point gravity.
When studying motion with respect to earth's surface it must be borne in mind that the reference frame associated with the Earth is non-inertial (the Earth rotates around its axis and moves in orbit around the Sun). The centripetal acceleration corresponding to the Earth's orbital motion (annual rotation) is much less than centripetal acceleration associated with the daily rotation of the Earth. We can assume that the reference frame associated with the Earth rotates relative to inertial frames with a constant angular velocity
Any point A on the Earth's surface that lies on geographical latitude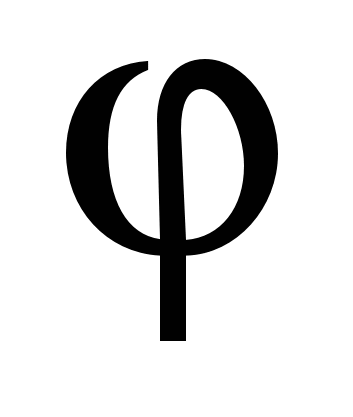 
, moves in a circle of radius
(
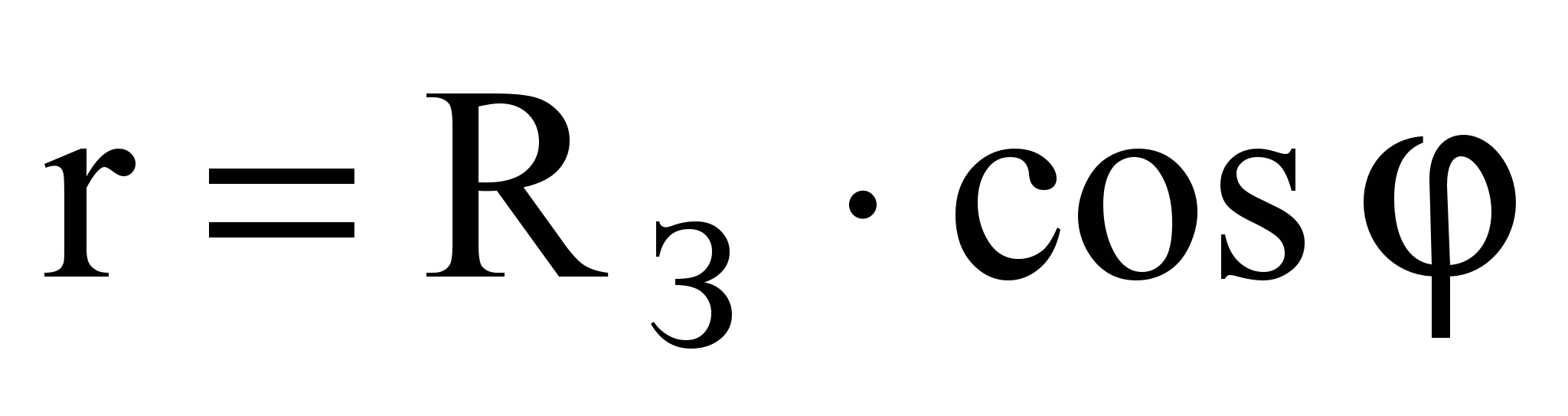
R 3 - the radius of the Earth, considered in the first approximation in the form of a ball) with an angular velocity . Therefore, the sum of the forces acting on such a point is equal to
r
(1)
In is directed perpendicular to earth's axis and called centrifugal force inertia. Centrifugal forces, like all forces of inertia, exist only in rapidly moving frames of reference and disappear in the transition to inertial frames of reference. Observable acceleration of free fall of bodies relative to the Earth 
due to the action of two forces: 
, with which the body is attracted by the Earth ( force gravitational attraction Earth), and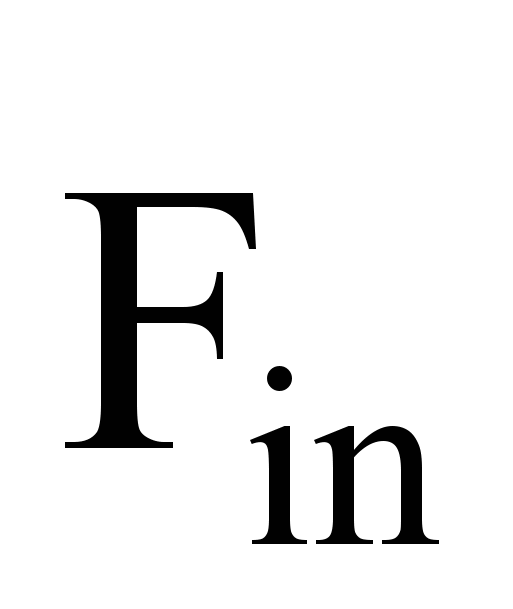 
.
The resultant of these two forces is the force of gravity:
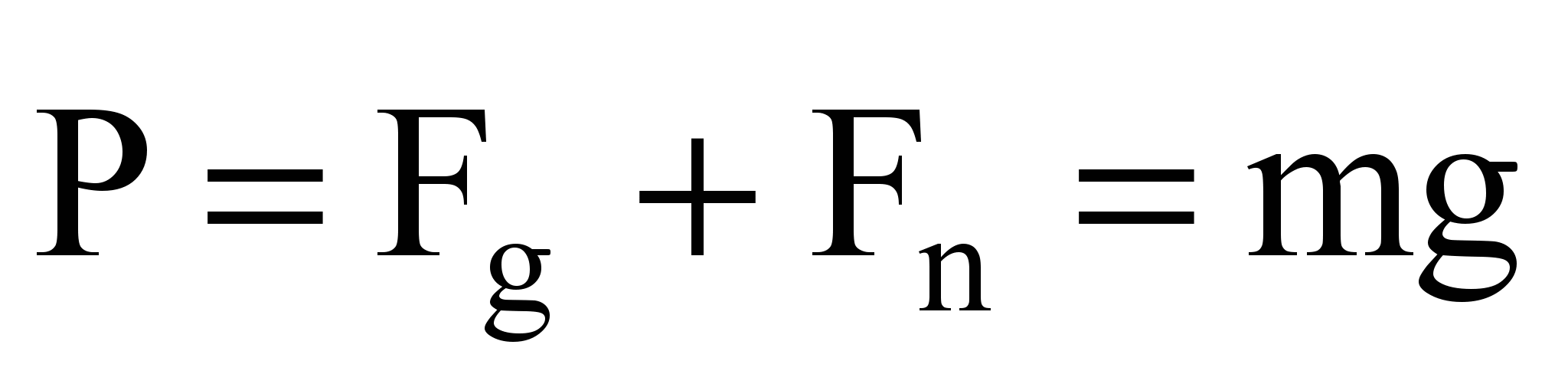(2)
The difference between the force of gravity and the force of attraction is small, since the centrifugal force of inertia is much less than the gravitational attraction. So, for a body of mass 1 kg:
, while Fg 9.8H.
Injection 
can be estimated using the sine theorem:
Using equation (2) and neglecting the influence daily rotation Earth, we get:
(3)
where R 3 is the radius of the Earth's surface.
From (3) it follows that
The free fall acceleration does not depend on the mass and other characteristics of the body.
When moving away from the Earth, the acceleration of free fall changes according to the law:
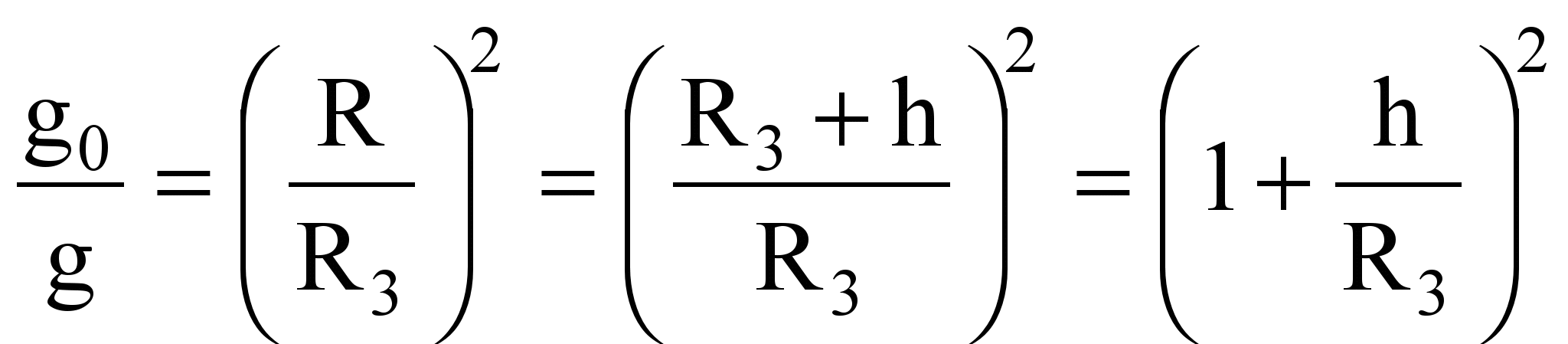
where g and g 0 are the accelerations of the body during its free fall, respectively, at a height and at the surface of the Earth.
Near the Earth's surface h<< R 3 и
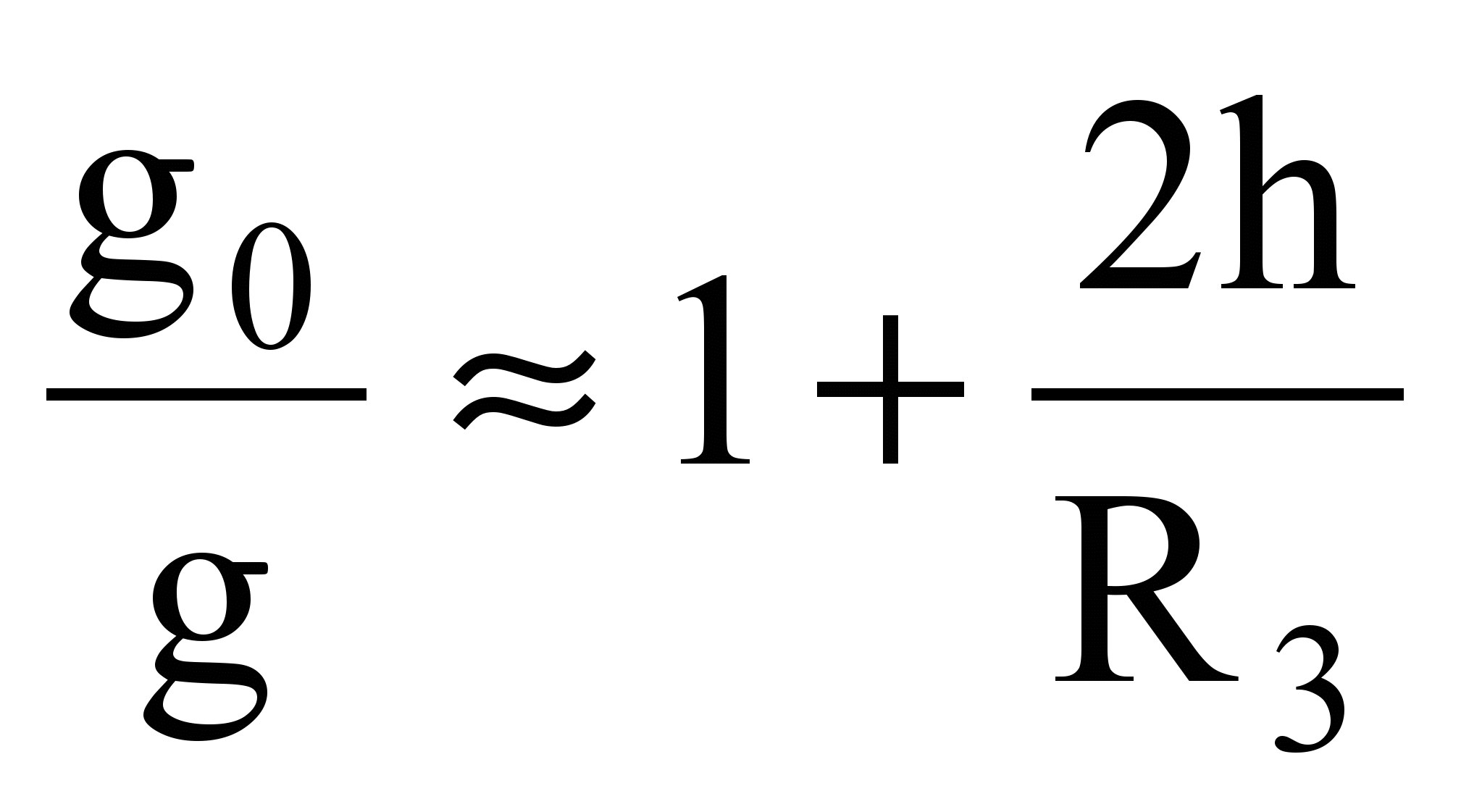
those. with a rise of 1 km, the acceleration of gravity decreases by approximately 0.03%.
Free fall acceleration can be measured by observing the free fall of bodies, in which the path h traveled by the body in time t is related to g by the relation:
5Conclusion.
In this experiment, it was found that the acceleration of gravity, from the readings of 14 measurements, is 9.5580.251 (m / s 2). GRAVITY (GRAVITATION), property of matter, which consists in the fact that between any two particles there are forces of attraction. Gravity is a universal interaction that covers the entire observable Universe and is therefore called universal. As we will see later, gravity plays a primary role in determining the structure of all astronomical bodies in the universe, except for the smallest ones. It organizes astronomical bodies into systems like our solar system or the Milky Way, and underlies the structure of the universe itself.Under the "force of gravity" it is customary to understand the force created by the gravitation of a massive body, and under the "acceleration of gravity" - the acceleration created by this force. (The word “massive” is used here in the sense of “having mass,” but the body in question does not have to have a very large mass.) In an even narrower sense, the acceleration of gravity is the acceleration of a body freely falling (without taking into account air resistance) on the surface of the Earth . In this case, since the entire system "Earth plus a falling body" rotates, inertia forces come into play. The centrifugal force counteracts the gravitational force and reduces the effective weight of the body by a small but measurable amount. This effect drops to zero at the poles, through which the Earth's axis of rotation passes, and reaches a maximum at the equator, where the Earth's surface is at its greatest distance from the axis of rotation. In any locally conducted experiment, the action of this force is indistinguishable from the true force of gravity. Therefore, the expression "gravity on the surface of the Earth" is usually understood as the combined action of the true gravity and centrifugal reaction. The term "gravity" is conveniently extended to other celestial bodies, saying, for example, "gravity on the surface of the planet Mars."
The acceleration due to gravity on the Earth's surface is 9.81 m/s
2 . This means that any body falling freely near the surface of the Earth increases its speed (accelerates) by 9.81 m/s for every second of fall. If the body started free fall from rest, then by the end of the first second it will have a speed of 9.81 m/s, by the end of the second - 18.62 m/s, etc.Gravity as the most important factor in the structure of the Universe. Gravity plays an extremely important, fundamental role in the structure of the world around us. Compared to the electric forces of attraction and repulsion between two charged elementary particles, gravity is very weak. The ratio of the electrostatic force to the gravitational force acting between two electrons is about 4 Ch 10 46 , i.e. 4 with 46 zeros. The reason why such a large gap in magnitude is not found at every step in everyday life is that the majority of matter in its ordinary form is electrically almost neutral, since the number of positive and negative charges in its volume is the same. Therefore, the huge electric forces of the volume simply do not have the opportunity to fully develop. Even in such "tricks" as sticking a worn balloon to the ceiling and raising hair when combing it on a dry day, electric charges are separated only slightly, but this is already enough to overcome the forces of gravity. The force of gravitational attraction is so small that it is possible to measure its effect between bodies of ordinary sizes, in laboratory conditions, only with special precautions. For example, the force of gravitational attraction between two people weighing 80 kg, standing close to each other with their backs, is a few tenths of a dyne (less than 10-5 N). Measurements of such weak forces are hampered by the need to isolate them against the background of various kinds of extraneous forces that can exceed the measured one.As the masses increase, the gravitational effects become more and more noticeable and eventually begin to dominate everything else. Let us imagine the conditions prevailing on one of the small asteroids of the solar system - on a spherical stone block with a radius of 1 km. The force of gravity on the surface of such an asteroid is 1/15,000 of the force of gravity on the surface of the Earth, where the gravitational acceleration is 9.81 m/s
2 . A mass weighing one ton on the surface of the Earth would weigh about 50 g on the surface of such an asteroid. The separation velocity (at which the body, moving along the radius from the center of the asteroid, overcomes the gravitational field created by the latter) would be only 1.2 m / s, or 4 km / h (the speed of a not very fast walking pedestrian), so that when walking on the surface of an asteroid, one would have to avoid sudden movements and not exceed the indicated speed so as not to fly away forever into outer space. The role of self-gravity grows as we move to larger and larger bodies - the Earth, large planets like Jupiter, and, finally, to stars, such as the Sun. Thus, self-gravity maintains the spherical shape of the Earth's liquid core and its solid mantle surrounding this core, as well as the Earth's atmosphere. The intermolecular cohesive forces that hold together particles of solids and liquids are no longer effective on a cosmic scale, and only self-gravity allows such giant gas balls as stars to exist as a single whole. Without gravity, these bodies simply would not exist, just as there would be no worlds suitable for life.When moving to another b
ó On a larger scale, gravity organizes individual celestial bodies into systems. The sizes of such systems are different - from relatively small (from an astronomical point of view) and simple systems, such as the Earth-Moon system, the Solar system and double or multiple stars, to large star clusters numbering hundreds of thousands of stars. The "life", or evolution, of an individual star cluster can be seen as a balancing act between the mutual divergence of stars and gravity, which tends to keep the cluster as a whole. From time to time, a star, moving in the direction of other stars, acquires momentum and speed from them, allowing it to fly out of the cluster and leave it forever. The remaining stars form an even tighter cluster, and gravity binds them even more strongly than before. Gravity also helps to hold gas and dust clouds together in outer space, and sometimes even compresses them into compact and more or less spherical clumps of matter. The dark silhouettes of many such objects can be seen against the brighter background of the Milky Way. According to the theory of star formation accepted today, if the mass of such an object is large enough, then the pressure in its interior reaches a level at which nuclear reactions become possible, and a dense clot of matter turns into a star. Astronomers were able to obtain images confirming the formation of stars in those places in outer space where only clouds of matter were previously observed, which testifies in favor of the existing theory. see also GRAVITATIONAL COLLAPSE.Gravity plays an important role in all theories of the origin, development and structure of the universe as a whole. Almost all of them are based on the general theory of relativity. In this theory, created by Einstein at the beginning of the 20th century, gravity is considered as a property of the four-dimensional space-time geometry, as something similar to the curvature of a spherical surface, generalized to a larger number of dimensions. The "curvature" of space-time is closely related to the distribution of matter in it.
All cosmological theories accept that gravity is a property of any kind of matter that manifests itself everywhere in the universe, although it is by no means assumed that the effects created by gravity are the same everywhere. For example, the gravitational constant
G (which we will discuss later) may vary depending on the place and time, although there are no direct observational data that would confirm this. Gravitational constant G- one of the physical constants of our world, as well as the speed of light or the electric charge of an electron or proton. With the accuracy with which modern experimental methods make it possible to measure this constant, its value does not depend on what kind of matter gravity is created. Only mass matters. Mass can be understood in two ways: as a measure of the ability to attract other bodies - this property is meant when they talk about heavy (gravitational) mass - or as a measure of the body's resistance to attempts to accelerate it (set it in motion if the body is at rest, stop if the body moves, or change its trajectory), - this property of mass is meant when they talk about inertial mass. Intuitively, these two varieties of mass do not seem to be the same property of matter, but the general theory of relativity postulates their identity and builds a picture of the world based on this postulate. see also WEIGHT.Gravity has another peculiarity; there seems to be no conceivable way to get rid of the effects of gravity other than to move an infinite distance away from all matter. No known substance has a negative mass, i.e. the property of being repelled by a gravitational field. Even antimatter (positrons, antiprotons, etc.) has a positive mass. It is impossible to get rid of gravity with the help of some kind of screen, like an electric field. During a lunar eclipse, the moon
"obscured" Earth from the attraction of the Sun, and the effect of such screening would accumulate from one eclipse to another, but this is not the case.The history of ideas about gravitation. As shown above, gravity is one of the most common interactions of matter with matter and at the same time one of the most mysterious and enigmatic. Modern theories have not come close to explaining the phenomenon of gravitation in any significant way.Nevertheless, gravity has always been explicitly or implicitly intertwined with cosmology, so that both these subjects are inseparable. The first cosmologies, such as those of Aristotle and Ptolemy, which lasted until the 18th century. largely due to the authority of these thinkers, were hardly anything used
ó more than a systematization of the naive views of the ancients. In these cosmologies, matter was divided into four classes or "elements": earth, water, air, and fire (in order from heavy to light). The words "gravity" originally meant simply "gravity"; objects consisting of the element "earth" possessed the property of "gravity" to a greater extent than objects consisting of other elements. The natural location of heavy objects was the center of the Earth, which was considered the center of the universe. The element “fire” was endowed with the least other “heaviness”; moreover, a kind of negative gravity was inherent in fire, the effect of which was manifested not in gravity, but in “levitation”. The natural place for the fire was the outer boundaries of the earthly part of the world. In the latest versions of this theory, the existence of a fifth entity (the "quintessence", sometimes called "ether", which was free from the effects of gravity) was postulated. It was also postulated that celestial bodies are composed of quintessence. If the earthly body somehow found itself out of its natural place, then it sought to return there by natural movement, which is inherent in it in the same way that purposeful movement with the help of legs or wings is characteristic of an animal. This refers to the movement of a stone in space, a bubble in water, and a flame in air.Galileo (1564
1642), investigating the motion of bodies under the action of gravity, found that the period of oscillation of the pendulum does not depend on whether the initial deviation of the pendulum from the equilibrium position was large or small. Galileo also experimentally established that in the absence of air resistance, heavy and light bodies fall to the ground with the same acceleration. (Aristotle argued that heavy bodies fall faster than light ones, and the faster the heavier they are.) Finally, Galileo proposed the idea of the constancy of the acceleration of free fall and formulated statements that are essentially the forerunners of Newton's laws of motion. It was Galileo who first realized that for a body that is not acted upon by forces, uniform rectilinear motion is as natural as a state of rest.It fell to the brilliant English mathematician I. Newton (1643) to combine disparate fragments and build a logical and consistent theory.
1727). These scattered fragments were created by the efforts of many researchers. Here is the heliocentric theory of Copernicus, perceived by Galileo, Kepler and others as a genuine physical model of the world; and detailed and accurate astronomical observations of Brahe; and the concentrated expression of these observations in Kepler's three laws of planetary motion; and the work begun by Galileo on the formulation of the laws of mechanics on the basis of well-defined concepts, as well as hypotheses and partial solutions to problems found by such contemporaries of Newton as H. Huygens, R. Hooke and E. Halley. To carry out his majestic synthesis, Newton needed to complete the creation of a new mathematics, called differential and integral calculus. In parallel with Newton, his contemporary G. Leibniz independently worked on the creation of differential and integral calculus.Although Voltaire's anecdote of the apple falling on Newton's head is most likely untrue, it nevertheless characterizes to some extent the type of thinking that was demonstrated by Newton in his approach to the problem of gravitation. Newton persistently asked questions: “Is the force that keeps the Moon in its orbit as it moves around the Earth, the same force that causes bodies to fall to the earth's surface? How intense does Earth's gravity have to be to bend the moon's orbit the way it actually does? To answer these questions, Newton first needed to define the concept of force, which would include the factor that causes the body to deviate from the original trajectory of motion, and not just accelerate or slow down when moving up or down. Newton also needed to know exactly the size of the Earth and the distance from the Earth to the Moon. He assumed that the attraction created by the earth's gravity decreases with increasing distance from the attracting body as the inverse square of the distance, i.e. as the distance increases. The truth of such a conclusion for circular orbits can easily be deduced from Kepler's laws without recourse to differential calculus. Finally, when in the 1660s Picard made a geodetic survey of the northern regions of France (one of the first geodetic surveys), he was able to refine the value of the length of one degree of latitude on the earth's surface, which made it possible to more accurately determine the size of the Earth and the distance from the Earth to the Moon. Picard's measurements further strengthened Newton's belief that he was on the right track. Finally at 16
86 –1687 in response to a request shortly before the newly formed Royal Society, Newton published his famous Mathematical principles of natural philosophy (Philosophiae naturalis principia mathematica ), marking the birth of modern mechanics. In this work, Newton formulated his famous law of universal gravitation; in modern algebraic notation, this law is expressed by the formula where F - force of attraction between two material bodies with masses M 1 and M 2 , and R is the distance between these bodies. Coefficient G called the gravitational constant. In the metric system, mass is measured in kilograms, distance in meters, and force in newtons and the gravitational constant G has the meaning G = 6.67259 H 10 -11 m 3 H kg -1 H s -2 . The smallness of the gravitational constant explains the fact that gravitational effects become noticeable only with a large mass of bodies.Using the methods of mathematical analysis, Newton showed that a spherical body, such as the Moon, the Sun or a planet, creates gravity in the same way as a material point, which is located in the center of the sphere and has an equivalent mass. Differential and integral calculus allowed both Newton himself and his followers to successfully solve new classes of problems, for example, the inverse problem of determining force from the uneven or curvilinear motion of a body moving under its influence; predict the speed and position of the body at any time in the future, if the force is known as a function of position; solve the problem of the total force of attraction of any body (not necessarily a spherical shape) at any given point in space. New powerful mathematical tools have opened the way to solving many complex, previously unsolvable problems not only for gravitational, but also for other fields.
Newton also showed that, due to the 24-hour period of rotation around its own axis, the Earth should not have a strictly spherical, but somewhat flattened shape. The implications of Newton's research in this area lead us into the field of gravimetry, the science of measuring and interpreting the force of gravity on the Earth's surface.
Long-range action. However, in Newtonian Beginnings there is a gap. The fact is that, having defined the force of gravity and giving a mathematical expression describing it, Newton did not explain what gravity is and how it works. Questions that have caused and continue to cause a lot of controversy since the 18th century. until recently, is as follows: how does a body located in one place (for example, the Sun) attract a body (for example, the Earth) located in another place, if there is no material connection between the bodies? How fast do gravitational effects propagate? Instantly? At the speed of light and other electromagnetic oscillations, or at some other speed? Newton did not believe in the possibility of long-range action, he simply carried out the calculations as if the law of inverse proportionality to the square of distance was an accepted fact. Many, including Leibniz, Bishop Berkeley, and the followers of Descartes, agreed with the Newtonian point of view, but were convinced that phenomena separated in space from their causes are inconceivable without some kind of physical intermediary agent that closes the causal relationship. between them.Later, all these and other questions were inherited by similar theories that explained the propagation of light. The luminous medium was called the ether, and, following earlier philosophers, in particular Descartes, physicists came to the conclusion that gravitational (as well as electrical and magnetic) forces are transmitted as a kind of pressure in the ether. And only when all attempts to formulate a consistent theory of the ether turned out to be unsuccessful, it became clear that although the ether gave an answer to the question of how action is carried out at a distance, this answer was not correct.
Field theory and relativity. It fell to A. Einstein (1879 1955). In this his role was analogous to that of Newton. To create his theory, Einstein, like Newton once, needed a new mathematics - tensor analysis.What Einstein was able to do is to some extent the result of a new way of thinking that took shape during the 19th century. and associated with the emergence of the concept of a field. A field, in the sense in which the modern theoretical physicist uses this term, is an area of idealized space in which, by specifying a certain coordinate system, the positions of points are specified together with a physical quantity or a certain set of quantities depending on these positions. When moving from one point in space to another, neighboring one, it must smoothly (continuously) decrease or increase, and can also change with time. For example, the speed of water in a river varies both with depth and from bank to bank; the temperature in the room is higher near the stove; the intensity (brightness) of illumination decreases with increasing distance from the light source. These are all examples of fields. Physicists consider fields to be real things. In support of their point of view, they refer to the physical argument: the perception of light, heat, or electric charge is just as real as the perception of a physical object, the existence of which everyone is convinced on the basis that it can be touched, felt its weight or seen. In addition, experiments, for example, with scattered iron filings near the magnet, their alignment along a certain system of curved lines, make the magnetic field directly perceived to such an extent that no one doubts that there is “something” around the magnet even after the iron filings are removed. . Magnetic "lines of force," as Faraday called them, form a magnetic field.
Until now, we have avoided mentioning the gravitational field. Acceleration of gravity
g on the surface of the Earth, which varies from point to point on the earth's surface and decreases with height, and there is such a field. But the great step forward that Einstein took was not to manipulate the gravitational field of our daily experience.Instead of following Fitzgerald and Lorentz and considering the interaction between the omnipresent ether and the measuring rods and clocks moving through it, Einstein introduced the physical postulate that any observer BUT who measures the speed of light with the help of measuring rods and the watch he carries with him, will invariably get the same result.
c \u003d 3 × 10 8 m/s no matter how fast the observer is moving; measuring rods of any other observer AT moving relative to BUT with speed v , will look to the observer BUT abbreviated inonce; watcher watch AT will look to the observer BUT going slower inonce; relations between observers BUT and AT are exactly mutual, so the observer's measuring rods BUT and his watch will be for the observer AT correspondingly equally shorter and slower; each of the observers can consider himself to be motionless and the other to be moving. Another consequence of the private (special) theory of relativity was that the mass m body moving with speed v relative to the observer, increases (for the observer) and becomes equal to, where m0 is the mass of the same body moving very slowly relative to the observer. The increase in the inertial mass of a moving body meant that not only the energy of motion (kinetic energy), but all energy has an inertial mass, and that if the energy has an inertial mass, then it also has a heavy mass and, therefore, is subject to gravitational effects. In addition, as is now well known, under certain conditions in nuclear processes, mass can be converted into energy. (Perhaps it would be more accurate to talk about the release of energy.) If the assumptions made are correct (and now we have every reason for such confidence), then mass and energy are different aspects of the same more fundamental essence.The above formula also indicates that no material body and no energy-carrying object (for example, a wave) can move relative to the observer faster than at the speed of light with, because otherwise, such a movement would require an infinite amount of energy. Therefore, gravitational effects must propagate at the speed of light (arguments in favor of this were given even before the creation of the theory of relativity). Examples of such gravitational phenomena were later discovered and included in the general theory.
In the case of uniform and rectilinear relative motion, the observed contractions of the measuring rods and slowing down of the clock lead to the private theory of relativity. Later, the concepts of this theory were generalized to accelerated relative motion, for which it was necessary to introduce another postulate - the so-called equivalence principle, which made it possible to include gravity in the model, which was absent in the special theory of relativity.
For a long time it was considered, and very careful measurements made at the end of the 19th century. by the Hungarian physicist L. Eötvös, confirmed that, within the experimental error, heavy and inert
the masses are numerically equal. (Recall that the heavy mass of a body serves as a measure of the force with which this body attracts other bodies, while the inertial mass is a measure of the body's resistance to acceleration.) At the same time, the acceleration of freely falling bodies would not be completely independent of their mass if the inertial and heavy body weights were not absolutely equal. Einstein postulated that these two kinds of mass, which appear to be different because they are measured in different experiments, are actually the same. It immediately followed that there was no physical difference between the force of gravity that we feel in the soles of our feet and the force of inertia that pushes us against the back of our chair when the car accelerates, or throws us forward when we apply the brakes. Let us mentally imagine (as Einstein did) a closed room, such as an elevator or a spaceship, inside which one can study the motion of bodies. In outer space, at a sufficiently large distance from any massive star or planet that their attraction does not affect bodies in this enclosed space, any object released from the hands would not fall to the floor, but would continue to float in the air, moving in the same direction. , in which he moved when he was released from the hands. All objects would have mass, but would not have weight. In a gravitational field near the Earth's surface, bodies have both mass and weight. If you release them from your hands, they fall to the ground. But if, for example, the elevator fell freely, without encountering any resistance, then the objects in the elevator would seem weightless to an observer in the elevator, and if he let go of any objects, they would not fall to the floor. The result would be the same as if everything happened in outer space far from attracting bodies, and no experiment could show the observer that he is in a state of free fall. Looking out the window and seeing the Earth somewhere far below him, the observer could say that the Earth is rushing towards him. However, from the point of view of an observer on Earth, both the elevator and all objects in it fall equally fast, so the falling objects do not lag behind or lead the elevator, and therefore do not approach its floor, towards which they fall.Now imagine a spacecraft being lifted by a booster into space at ever-increasing speed. If the astronaut in the ship releases the object from his hands, then the object (as before) will continue to move in space at the same speed with which it was released, but since now the floor of the spacecraft is moving accelerated towards the object, everything will look as if the object would fall. Moreover, the astronaut would feel the force acting on the legs and could interpret it as gravity, and no experiment that he could perform while in an ascending spacecraft would contradict such an interpretation.
Einstein's equivalence principle simply equates these two seemingly completely different situations and states that gravity and inertial forces are one and the same. The main difference is that in a sufficiently large area, the inertial force (for example, centrifugal) can be eliminated by a suitable transformation of the frame of reference (for example, the centrifugal force acts only in a rotating frame of reference, and it can be eliminated by passing to a non-rotating frame of reference). As for the force of gravity, by switching to another frame of reference (freely falling), it can only be got rid of locally. Mentally imagining the whole Earth as a whole, we prefer to consider it motionless, believing that gravitational forces act on bodies located on the surface of the Earth, rather than inertial forces. Otherwise, we would have to assume that the surface of the Earth is accelerated outward at all its points and that the Earth, expanding like an inflated balloon, presses on the soles of our feet. Such a point of view, quite acceptable from the point of view of dynamics, is incorrect from the point of view of ordinary geometry. However, within the framework of the general theory of relativity, both points of view are equally acceptable.
The geometry resulting from the measurement of lengths and time intervals, freely transformable from one rapidly moving frame of reference to another, turns out to be curvilinear geometry, very similar to the geometry of spherical surfaces, but generalized to the case of four dimensions - three spatial and one time - in the same way, as in the private theory of relativity. The curvature, or deformation, of space-time is not just a turn of speech, but something more, as it is determined by the way the distances between points are measured and the duration of the time intervals between events at these points. That the curvature of spacetime is a real physical effect can best be demonstrated by a few examples.
According to the theory of relativity, a ray of light passing near a large mass is bent. This happens, for example, with a beam of light from a distant star passing near the edge of the solar disk. But even a curved beam of light continues to be the shortest distance from the star to the observer's eye. This statement is true in two ways. In the traditional notation of relativistic mathematics, a line segment
dS , separating two neighboring points, is calculated by the Pythagorean theorem of ordinary Euclidean geometry, i.e. according to the formula dS 2 = dx 2 + dy 2 + dz 2 . A point in space together with a moment in time is called an event, and the distance in space-time separating two events is called an interval. To determine the interval between two events, the timeó e dimension t combined with three spatial coordinates x, y, z in the following way. Time difference between two events dt converted to spatial distance with H dt multiplied by the speed of light with(constant for all observers). The result obtained must be compatible with the Lorentz transformation, from which it follows that the measuring rod of the moving observer is reduced, and the clock slows down according to the expression. The Lorentz transformation should also be applicable in the limiting case when the observer moves along with the light wave and his clock is stopped (i.e. dt = 0 ), and he himself does not consider himself moving (i.e. dS = 0 ), so that (Interval ) 2 = dS 2 = dx 2 + dy 2 + dz 2-( c H dt) 2 . The main feature of this formula is that the sign of the timeó th term is opposite to the sign of the spatial terms. Further, along the light beam for all observers moving along with the beam, we have dS2 = 0 and, according to the theory of relativity, all other observers should get the same result. In this first (space-time) sense dS is the minimum space-time distance. But in the second sense, since light travels along the path that takes the least time to reach its destination for any hours, the numerical values of the spatial and temporal intervals are minimal for a light beam.All the above considerations refer to events separated only by small distances and times; in other words,
dx, dy, dz and dt are small quantities. But the results can be easily generalized to extended trajectories by the method of integral calculus, the essence of which is the summation of all these infinitesimal intervals along the entire path from point to point.Further reasoning, let us mentally imagine space-time divided into four-dimensional cells, just as a two-dimensional map is divided into two-dimensional squares. The side of such a four-dimensional cell is equal to a unit of time or distance. In field-free space, the grid consists of lines intersecting at right angles, but in a gravitational field near the mass, the grid lines are curved, although they also intersect at right angles, like parallels and meridians on a globe. In this case, the grid lines look curved only for an external observer whose number of measurements is greater than the number of grid measurements. We exist in three-dimensional space and, looking at a map or diagram, we can perceive it in three dimensions. A subject in the grid itself, such as a microscopic creature on a globe, who has no idea what up or down is, cannot perceive the curvature of the globe directly and would have to take measurements and see what kind of geometry arises from the totality of results. dimensions - whether it will be Euclidean geometry, corresponding to a flat sheet of paper, or curvilinear geometry, corresponding to the surface of a sphere or some other curved surface. In the same way, we cannot see the curvature of the space-time around us, but by analyzing the results of our measurements, we can discover special geometric properties that are exactly analogous to real curvature.
Now imagine a huge triangle in free space with three straight lines as sides. If a mass is placed inside such a triangle, then the space (i.e., the four-dimensional coordinate grid that reveals its geometric structure) is slightly inflated so that the sum of the internal angles of the triangle becomes greater than in the absence of mass. Similarly, you can imagine in free space a giant circle, the length and diameter of which you have measured very accurately. You found that the ratio of the circumference of a circle to its diameter is equal to the number
p (if the free space is Euclidean). Place a large mass in the center of the circle and repeat the measurements. The ratio of circumference to diameter becomes smaller p , although the measuring rod (when viewed from a certain distance) will look reduced both when it is laid along the circumference and when it is laid along the diameter, but the magnitude of the contractions themselves will be different.In curvilinear geometry, a curve connecting two points and the shortest among all curves of this kind is called a geodesic. In the four-dimensional curvilinear geometry of general relativity, the trajectories of light rays form one class of geodesics. It turns out that the trajectory of any free particle (on which no contact force acts) is also a geodesic, but of a more general class. For example, a planet freely moving in its orbit around the Sun moves along a geodesic in the same way as the freely falling elevator in the example considered earlier. Geodesics are spatiotemporal analogues of straight lines in Newtonian mechanics. Bodies simply move along their natural curvilinear trajectories - the lines of least resistance - so there is no need to resort to "force" to explain this behavior of the body. On the other hand, bodies located on the surface of the Earth are affected by the contact force of direct contact with the Earth, and from this point of view, we can assume that the Earth pushes them from geodesic orbits. Consequently, the trajectories of bodies on the Earth's surface are not geodesic.
So, gravitation was reduced to a geometric property of physical space, and the gravitational field turned out to be replaced by a "metric field". Like other fields, the metric field is a set of numbers (there are ten in total) that vary from point to point and collectively describe the local geometry. These numbers, in particular, can be used to determine how and in what direction the metric field is curved.
Consequences from the general theory of relativity. Another prediction of the general theory of relativity, which follows from the principle of equivalence, is the so-called gravitational redshift, i.e. a decrease in the frequency of radiation coming to us from a region with a lower gravitational potential. Although there are numerous suggestions in the literature that redshifted light was emitted from the surface of superdense stars, there is still no convincing evidence for this, and the question remains open. The effect of such a displacement was indeed observed in laboratory conditions - between the top and the base of the tower. In these experiments, the gravitational field of the Earth and strictly monochromatic gamma radiation emitted by atoms bound in a crystal lattice (Mössbauer effect) were used. The easiest way to explain this phenomenon is to refer to a hypothetical elevator with a light source at the top and a receiver at the bottom, or vice versa. The observed shift exactly coincides with the Doppler shift corresponding to the additional speed of the receiver at the moment of signal arrival compared to the source speed at the moment of signal emission. This extra speed is due to the acceleration during the time the signal is in transit.Another, and almost immediately recognized, prediction of general relativity concerns the motion of the planet Mercury around the Sun (and, to a lesser extent, the motion of other planets). Perihelion of Mercury's orbit, i.e. the point in its orbit where the planet is closest to the Sun is shifted by 574
І per century, making a complete revolution in 226,000 years. Newtonian mechanics, taking into account the gravitational action of all known planets, could only explain the perihelion shift by 532І in a century. The difference of 42 arcseconds, although small, is still much larger than any possible error, and tormented astronomers for almost a century. General relativity predicted this effect almost exactly.Revival of Mach's views on inertia. E. Mach (1838–1916), like Newton Berkeley's younger contemporary, repeatedly asked himself questions: “What explains inertia? Why does a centrifugal reaction occur when a body rotates? In search of an answer to these questions, Mach suggested that inertia is due to the gravitational constraint of the universe. Each particle of matter is united with all other matter in the Universe by gravitational bonds, the intensity of which is proportional to its mass. Therefore, when a force applied to a particle accelerates it, the gravitational bonds of the Universe as a whole resist this force, creating an equal in magnitude and opposite in direction force of inertia. At a later time, the question raised by Mach was revived and acquired a new twist: if there is neither absolute motion nor absolute linear acceleration, then is it possible to exclude absolute rotation as well? The state of affairs is such that rotation with respect to the external world can be detected in an isolated laboratory without direct reference to the external world. This can be done by centrifugal forces (forcing the surface of water in a rotating bucket to take a concave shape) and Coriolis forces (creating an apparent curvature of the body's trajectory in a rotating coordinate system. Of course, it is incomparably easier to imagine a small rotating body than a rotating Universe. But the question is this: if the rest of the universe were to disappear, how could we judge whether a body was "absolutely" rotating? Would the surface of the water in the bucket remain concave? Would the rotating weight create a tension in the rope? Mach thought the answers to these questions must be negative. If gravity and inertia are interrelated, one would expect that changes in the density or distribution of distant matter would somehow affect the value of the gravitational constant G . For example, if the universe is expanding, then the value G should change slowly over time. Value change G could affect the periods of oscillation of the pendulum and the revolution of the planets around the Sun. Such changes can only be detected by measuring time intervals using atomic clocks, the course of which does not depend on G. Measurement of the gravitational constant. Experimental determination of the gravitational constant G makes it possible to establish a bridge between the theoretical and abstract aspects of gravity as a universal attribute of matter and the more mundane question of its localization and assessment of the mass of matter that creates gravitational effects. The latter operation is sometimes called weighing. From a theoretical point of view, we have already seen that G - one of the fundamental constants of nature and therefore is of paramount importance for physical theory. But the magnitude G must also be known if we want to detect and "weigh" matter on the basis of the gravitational action that it creates.According to Newton's law of universal gravitation, the acceleration of any test body in the gravitational field of another body with mass
m is given by the formula g = gm/r 2 , where r is the distance from the body with mass m . The astronomical equations of motion are multipliers G and m are included only in the form of a work gm , but never individually. This means that the mass m , which creates acceleration, can only be estimated if the value is known G . But proceeding from the ratios of the masses, it is possible, by comparing the accelerations produced by them, to express the masses of the planets and the Sun in terms of earth masses. Indeed, if two bodies create accelerations g 1 and g2 , then the ratio of their masses is m 1 / m 2 = g 1r 1 2 /g 2r 2 2 . This makes it possible to express the masses of all celestial bodies in terms of the mass of any one chosen body, such as the Earth. Such a procedure is tantamount to choosing the mass of the Earth as the mass standard. To move from this procedure to the centimeter-gram-second system of units, you need to know the mass of the Earth in grams. If it is known, then we can calculate G by finding the work gm from any equation that describes the gravitational effects created by the Earth (for example, the movement of the Moon or an artificial satellite of the Earth, the oscillations of a pendulum, the acceleration of a body in free fall). And vice versa, if G can be measured independently, then the product gm, included in all the equations of motion of celestial bodies, will give the mass of the Earth. These considerations made it possible to experimentally estimate G . An example is Cavendish's famous experiment with a torsion balance, carried out in 1798. The apparatus consisted of two small masses at the ends of a balanced rod, attached in the middle to a long thread of a torsion suspension. Two other, larger masses are fixed on a rotating stand so that they can be brought to small masses. Attraction acting from bó large masses to smaller ones, although much weaker than the attraction of such a large mass as the Earth, turns the rod on which small masses are fixed, and twists the suspension thread at an angle that can be measured. Summing up then bó larger masses to smaller masses on the other side (so that the direction of attraction changes), you can double the offset and thus improve the accuracy of the measurement. The torsional modulus of the thread is assumed to be known, since it can be easily measured in the laboratory. Therefore, by measuring the angle of twist of the thread, it is possible to calculate the force of attraction between the masses.LITERATURE Fok V.A. Theory of space, time and gravity. M., 1961Zeldovich Ya.B., Novikov I.D. The theory of gravity and the evolution of stars. M., 1971
Weiskopf V. Physics in the twentieth century. M., 1977
Albert Einstein and the theory of gravity. M., 1979
MANAGEMENT
TO LABORATORY WORKS
PHYSICS
Section "MECHANICS"
Kirov -2007
BBC 22.3 (07)
LAB #1
USING THE MATHEMATICAL PENDULUM
The purpose of the work: the study of the laws of harmonic oscillatory motion
example mathematical pendulum.
Devices and accessories: mathematical pendulum, stopwatch, ruler.
THEORETICAL DATA
An oscillatory movement (oscillation) is a process in which the system, repeatedly deviating from its equilibrium state, each time returns to it again.
If this return occurs at regular intervals, then the oscillation is called periodic.
The fluctuations are called free or own, if they occur in a system left to itself after it has been brought out of equilibrium.
The simplest case of periodic oscillations is harmonic oscillatory motion.
An oscillation is called harmonic, in which the oscillating value changes according to the sine (or cosine) law:
x = x m sin ()( 1)
In mechanics: bias X oscillating point from the equilibrium position changes according to the law sine( or cosine)).
Maximum offset value hm from the equilibrium position is called amplitude harmonic vibration. Argument ( about), standing under the sign of sine (or cosine), is called oscillation phase. about - initial phase(for t = 0). The value is called cyclic frequency harmonic oscillation:
= 2 (2)
Value T called period of oscillation- the time of one complete oscillation -, the value = 1/ T(Hz)– oscillation frequency - number of oscillations per unit of time.
WORK PROCEDURE
1. Determine the length of the pendulum. To do this, measure the distance from the floor to the top of the ball X(see fig. 2). Calculate the length of the pendulum using the formula
l \u003d L - (x - R),
put the result in the table
|
|||||
| |
2. Remove the pendulum from its equilibrium position by deflecting it at an angle of approximately 4-5 degrees, and allow it to oscillate. Measure the span of time t, during which the pendulum makes 20 full swing. Take measurements 5 once.
3. Make the necessary calculations, fill in the table of the selected work option (consult your teacher).
Reporting table. Option 1
| № | x,m | l,m | t,s | | Dt,s | (Dt) 2 ,s 2 | <Т>,with | g,m/s 2 |
Option 2
| № | l,m | Number of qty. | T,s | g,m/s 2 | m/s 2 | ,m/s 2 | ,m/s 2 | ,% | ||
4. Calculate the relative d and absolute errors Dg for option 1 using the following formula:
d = = 2 + , where D l= 0.005 m
Dt syst = 0.1 s; Dt= Dt sys +Dt chance; 
5. Write down the answer.
TEST QUESTIONS
1. What movement is called oscillatory?
2. What oscillations are called periodic?
3. What oscillations are called free?
4. What vibrations are called harmonic?
5. Define the amplitude, phase, period and frequency of oscillations.
6. Write down the differential equation of harmonic oscillations and its solution.
7. What is called a mathematical pendulum?
8. How does the restoring force arise, according to what law does it change?
10. Derive the formula for the period of harmonic oscillations of a material point.
11. Derive the formula for the period of harmonic oscillations of a mathematical pendulum.
12. On what quantities does the acceleration of gravity depend?
LITERATURE
Saveliev I.V. Course of General Physics.- St. Petersburg: Lan, 2005, v.1 §49-51
Grabovsky R.I. Physics course. - St. Petersburg: Lan, 2002, part 1. 27-30
Trofimova T.I. Physics course.-M.: Higher school, 1999. Ch.18
Dmitrieva V.F., Prokofiev V.L. Fundamentals of Physics.-M.: VSh, 2001. Ch.16.
LAB #2
THEORETICAL DATA
Any body under the action of forces that are balanced about its center of mass experiences deformation, i.e. changes its size and shape. There are several types of deformation: all-round and longitudinal compression and tension, shear, torsion, transverse and longitudinal bends.
The amount of deformation is determined both by the properties of the body and by the acting voltage, i.e. force applied per unit area of the cross section of the body:
If, after removing the stress, the body completely restores its size and shape - deformation elastic, otherwise - plastic. The elasticity of a body characterizes the relationship between deformation and applied stress.
Consider the deformation of longitudinal tension. Let the length of the body be l, cross-sectional area S, force applied to the body F. For elastic deformation, Hooke's law is valid:
RELATIVE STRAIN IS DIRECTLY PROPORTIONATE TO STRESS:e=ks
For longitudinal deformation, the law takes the following form:
where E- Young's modulus, - absolute elongation, - relative elongation:
rotary motion solid body called such a movement in which all points of the body move in parallel planes, describing circles whose centers lie on one straight line, called the axis of rotation.
For kinematic description rotary motion of a rigid body around some fixed axis, the same quantities (and the equations of connection between them) are used as to describe the movement of a point along a circle: the angular coordinate of any point of the body, the angle of rotation of the radius vector R body points, average and instantaneous angular velocities< >and , average and instantaneous angular acceleration< >and , linear speeds various points bodies v.
angular velocity rotational motion is called physical quantity, equal to the change per unit time of the angle of rotation of the radius-vector of the point:
SI unit of angular velocity: = rad/s = 1/s.
The angular velocity has same values for any point of the rotating body in this moment time.
To characterize the rate of change of the angular velocity with time, we introduce angular acceleration, which measures the change in angular velocity per unit time:
SI unit of angular acceleration: \u003d rad / s 2 \u003d 1 / s 2.
When considering the rotation of a rigid body from a dynamic point of view, along with the concept force the concept moment of force , and along with the concept weight the concept moment of inertia.
The moment of force is the quantity equal to the product strength on her shoulder
M = Fl
The SI unit of the moment of force [M]= H. m.
Shoulder of strength l called the shortest distance from the axis of rotation to the line of action of the force.
Thus, various forces are equivalent in the sense of the rotation they cause if their moments are equal. The moment of force about the axis of rotation is created only by that component of the force that lies in a plane perpendicular to the axis of rotation, and the line of action of which does not pass through the axis of rotation.
Moment of inertia I is a measure of the inertia of a body during rotational motion.
It plays the same role as mass in translational motion.
Moment of inertia material point about a given axis of rotation is calculated as the product of the mass of this point m i by the square of its distance r i to this axis:
moment of inertia body about a given axis of rotation name the quantity equal to the sum moments of inertia of all n body points:
I = I = I = dV.
Moments of inertia of some homogeneous bodies the simplest form relative to the axis passing through their center of mass, can be calculated as follows:
I ball \u003d 0.4 mr 2; I disc, fusion cylinder =0.5 mr 2 ; I hoop \u003d mr 2; I rod =
We write the basic law of the dynamics of rotational motion (Newton's second law) as follows:
SOUND VELOCITY DETERMINATION
DETERMINATION OF THE CENTER OF GRAVITY
MANAGEMENT
TO LABORATORY WORKS
PHYSICS
Section "MECHANICS"
Kirov -2007
BBC 22.3 (07)
Grekov L.B., Morozov V.A., Orlova N.V., Popov S.G., Priemysheva R.A., Reshetnikov S.M., Skrypnik E.A., Shilyaev V.A. Guide to laboratory work in physics. Section "Mechanics". Kirov: Vyatka State Agricultural Academy, 2007. - p.39.
Reviewers: Grebenshchikov L.T., Candidate of Technical Sciences, Associate Professor of the Department of Physics, Voronezh State University,
Kuklin S.M., Candidate of Technical Sciences, Associate Professor of the Department of Resistance of Materials and Machine Parts of the All-Russian State Agricultural Academy.
The work was reviewed and approved by the methodological commission Faculty of Engineering Vyatka GSHA. Minutes No. 6 of May 19, 2004
The guide is intended to organize a purposeful and self-study students of the course of physics in the section "Mechanics"; necessary for laboratory classes on the above section of the course of physics.
ã Vyatka State Agricultural Academy, 2007.
© L. B. Grekov, V. A. Morozov, N. V. Orlova, S. G. Popov, R. A. Priyomysheva, S. M. Reshetnikov, E. A. Skrypnik, and A. V. Shilyaev, 2007 .
LAB #1
DETERMINATION OF THE ACCELERATION OF GRAVITY
Objective:
Familiarization of students with the method of measuring the acceleration of free fall of a body.
Work tasks:
Determination of the acceleration of gravity in free fall of a body.
The study of the dependence of the acceleration of gravity on the size and mass of bodies.
Determination of measurement error.
Theoretical part
3.2.1. Gravity acceleration
Acceleration is a vector quantity characterizing the rate of change of the body's velocity vector in terms of its numerical value and direction. The acceleration vector is equal to the first derivative of the velocity vector 
by time:
The first term characterizes the rate of change in the velocity modulus. It is called tangential (or tangential) acceleration, 
directed tangentially to the path. Second term 
characterizes the speed of change in the direction of speed, it is called normal (centripetal) acceleration, directed along the normal to the trajectory to the center of its curvature.
Acceleration due to gravity (or acceleration due to gravity) is the acceleration imparted to a free material point by gravity. Any body would have such an acceleration when falling to the Earth from a small height in an airless space.
Newton's basic equation of dynamics
|
|
only valid in inertial systems reference.
Frames of reference moving relative to the inertial frame with acceleration are called non-inertial.
In non-inertial systems, the basic law of Newton's dynamics should be changed by introducing into consideration a special kind of force - the force of inertia 
. Together with the forces 
, due to the effects of bodies on each other, the forces of inertia give the body acceleration 
and in non-inertial frames of reference one can write
|
|
.The forces of inertia are due to the properties of the reference frame in which mechanical phenomena are considered and have a different form.
To write the basic equation of dynamics in a non-inertial frame of reference, we consider two frames of reference (inertial 
-system and non-inertial 
-system):
a) If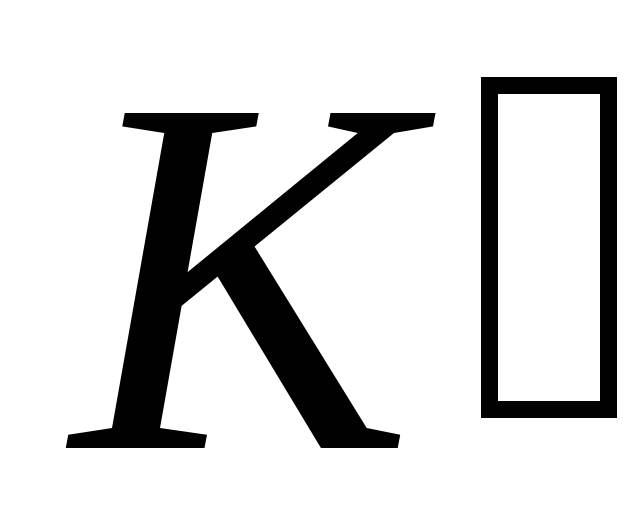 
- the system moves forward with acceleration 
towards -system, then the force of inertia
|
|
.The appearance of the force of inertia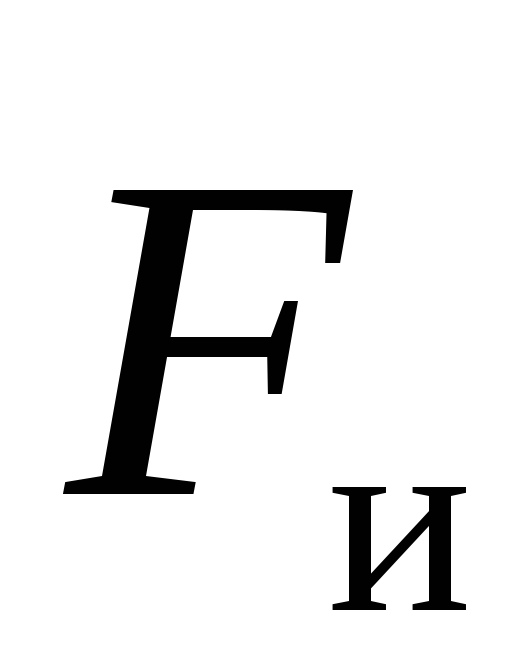 
with accelerated forward movement, everyone who uses urban transport experiences. A passenger sitting in the direction of the car, under the influence of inertia, is pressed against the back of the seat when the car moves off. When braking the vehicle, the inertia force is directed in the opposite direction, and the passenger is separated from the seat back.
b) If 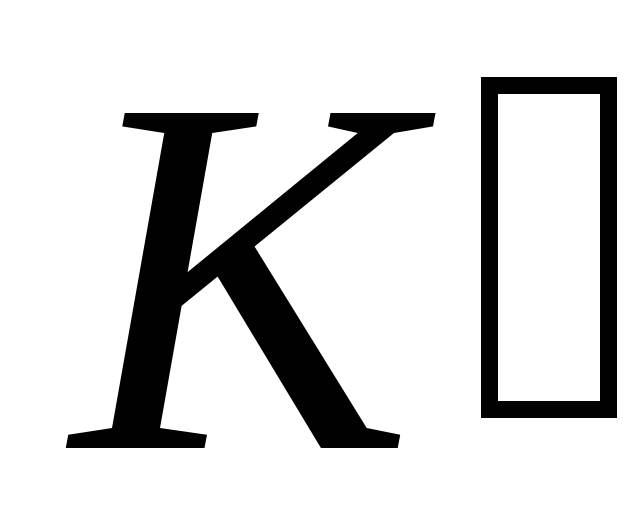- the system rotates at a constant angular velocity 
around an axis fixed in -system, then the force of inertia
|
|
.This force is called the centrifugal force of inertia, where 
is the radius vector perpendicular to the axis of rotation and characterizing the position of the body relative to this axis. The action of centrifugal forces of inertia are, for example, passengers in a moving vehicle on bends. These forces are used in centrifugal mechanisms: pumps, separators, dryers, etc. The centrifugal force is directed along the axis from the axis of rotation.
c) On a body moving forward at a speed 
in a rotating reference frame, in addition to the centrifugal force of inertia, another force of inertia acts, called the Coriolis force
When studying the motion of bodies relative to the earth's surface, one must bear in mind that the frame of reference associated with the earth is not inertial. The globe makes a complex movement: it rotates around its axis (daily rotation) and moves in orbit around the Sun (annual rotation).
The centripetal acceleration associated with the Earth's orbital motion (annual rotation) is much smaller than the centripetal acceleration associated with the Earth's daily rotation. Therefore, with sufficient accuracy, we can assume that the reference frame associated with the Earth rotates relative to inertial frames with a constant angular velocity of the daily ( 
) Earth's rotation
|
|
.If we do not take into account the rotation of the Earth, then the body lying on its surface should be considered as at rest, the sum of the forces acting on this body would then be equal to zero. In fact, any point BUT surfaces the globe, lying on the geographic latitude 
(Fig. 9), moves about the axis of the globe in a circle of radius r with angular velocity 
, i.e.
Force 
is the centrifugal force of inertia directed perpendicular to the earth's axis.
|
|
|
Rice. 9. Trajectory of the point BUT |
Observable acceleration of free fall of bodies relative to the Earth 
will be driven by two forces: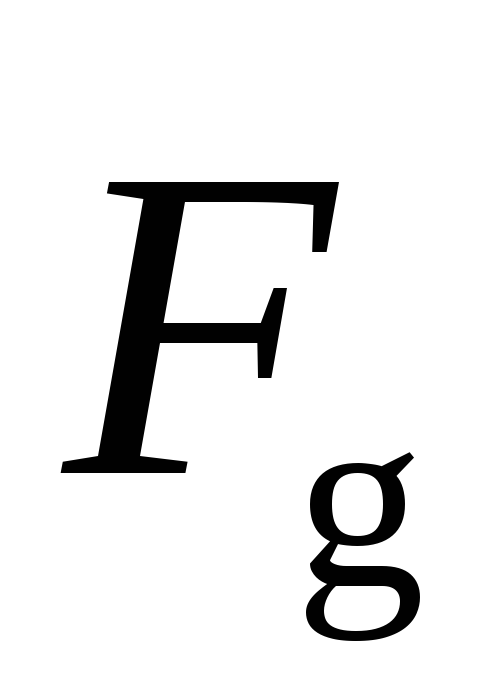 
, with which the body is attracted by the Earth (the force of the gravitational attraction of the Earth), and 
. The resultant of these two forces
Gravity difference 
from the force of gravity to the earth 
small, because centrifugal force of inertia is much less than 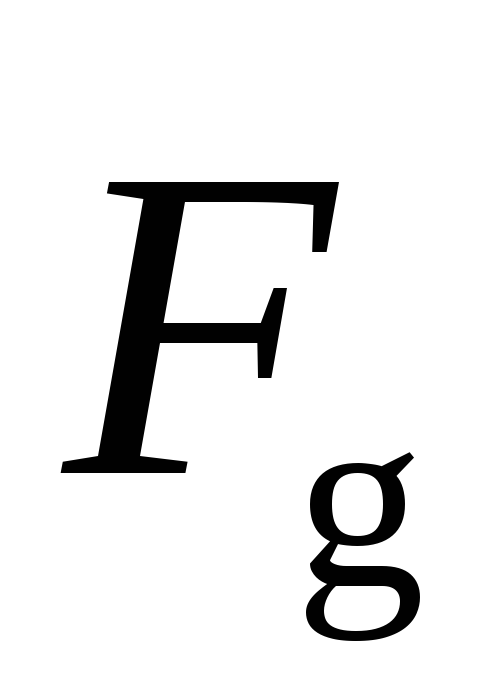. So, for a mass of 1 kg
|
|
,while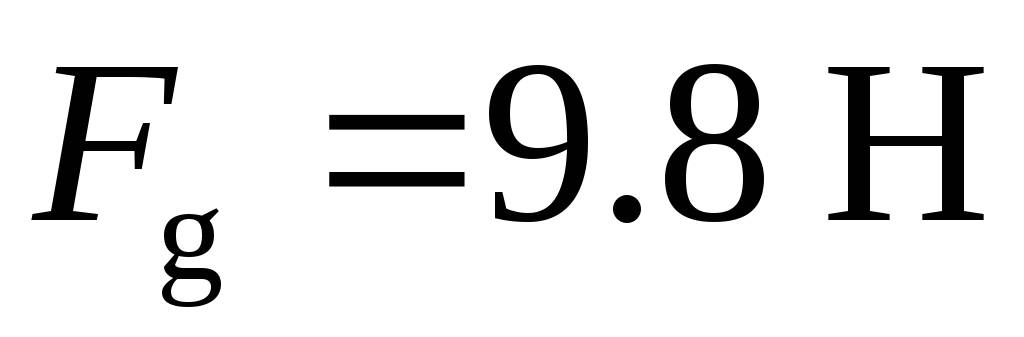 
, i.e. almost 300 times greater than the maximum value of the centrifugal force of inertia (observed at the equator).
At the poles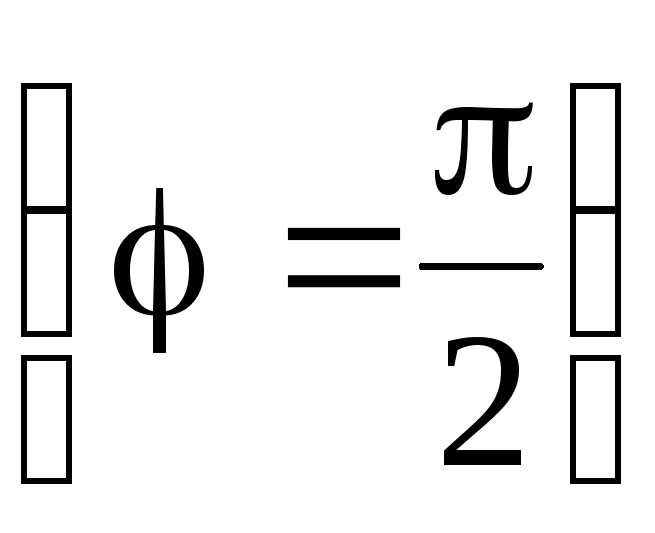 
, and at the equator ( 
)
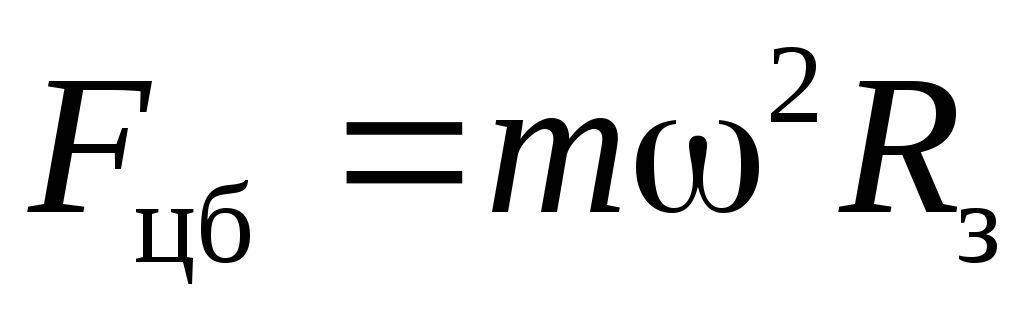. Injection 
between direction and can be estimated using the sine theorem
|
|
,replacing the sine of a small angle by approximately the value of the angle itself, we obtain 
.
Thus, depending on the geographic latitude injection fluctuates between 0 (at the equator, where 
and at the poles where 
) to 0.018 radians or 
(at latitude 
).
Consequently, at all points on the earth's surface, with the exception of the poles, the force of gravity of the body is less than the force of its gravitational attraction to the Earth. Yes, at the equator 
. In addition, everywhere, except for the poles and the equator, the vector not perpendicular to the earth's surface. Due to the daily rotation of the Earth, the force of gravity of the body is maximum at the poles, where it is equal to the force of gravity, and minimum at the equator.
As follows from formula (2), if the Earth were a regular ball with a spherically symmetrical distribution of matter in it, then 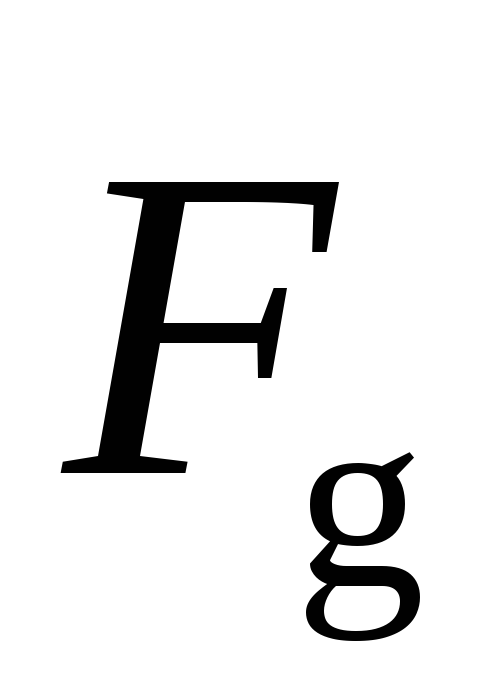should have been the same at the pole and at the equator. In fact, at the equator 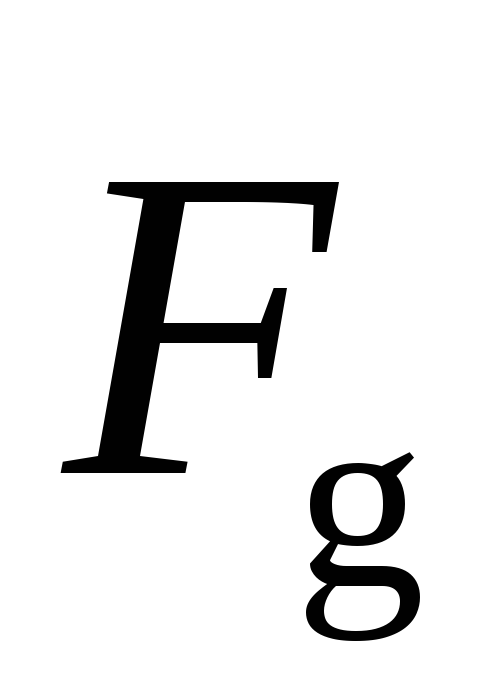less than at the pole. This is due to the oblateness of the Earth, due to the action of centrifugal forces. The points of the equator are farther from the center of the Earth than the poles. Therefore, they are attracted to the center of the Earth weaker than the same points on the pole.
Acceleration of gravity 
varies with latitude from 
at the equator to 
at the poles. At latitude it is equal to 
and is called "normal acceleration".
Acceleration of gravity is the main quantity considered in gravimetry - the science of the earth's field of gravity and its connection with the figure of the Earth, its internal structure and structure of the Earth's crust. The study of the Earth's gravitational field makes it possible to solve many problems of geodesy and geophysics. Since gravity anomalies are caused by the uneven distribution of masses in the earth's crust, the nature of the gravitational field can be used to judge the presence of changes in densities in the study area; thus, it is possible to discover various geological structures and mineral deposits. Periodic changes make it possible to judge tidal phenomena, the solid shell of the Earth, which in turn makes it possible to draw conclusions about the elastic properties of the Earth.
Using equation (3) and neglecting the influence of the daily rotation of the Earth, we find
|
|
,where 
is the radius of the earth's surface, h is the distance from the center of gravity of the body to the surface of the Earth.
From (3) it follows that:
a) the acceleration of a freely falling body does not depend on the mass, dimensions and other characteristics of the body, therefore all bodies fall freely in airless space with the same accelerations;
b) when moving away from the Earth's surface, the acceleration of a freely falling body changes according to the law
|
|
,where and 
- acceleration of the body during its free fall, respectively, at a height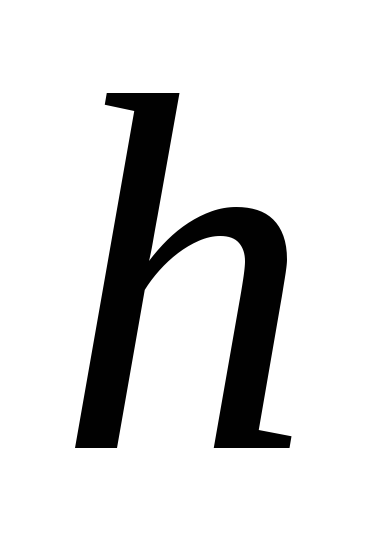 
and at the surface of the earth.
near the surface of the earth ( 
)
c) observation of the free fall of bodies, in which the path h passed by the body in time t, related to g ratio
|
|
.In this work, we used the last method for determining .
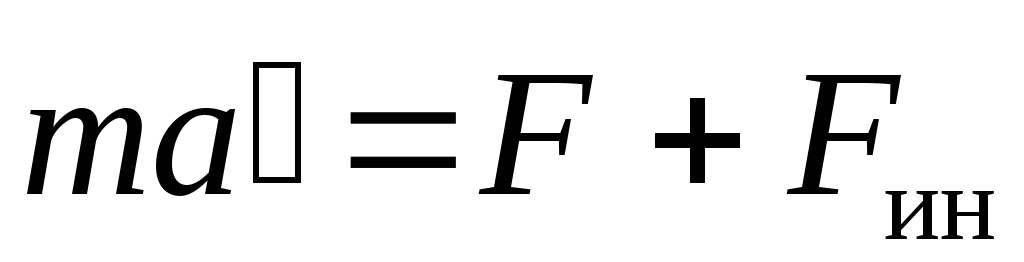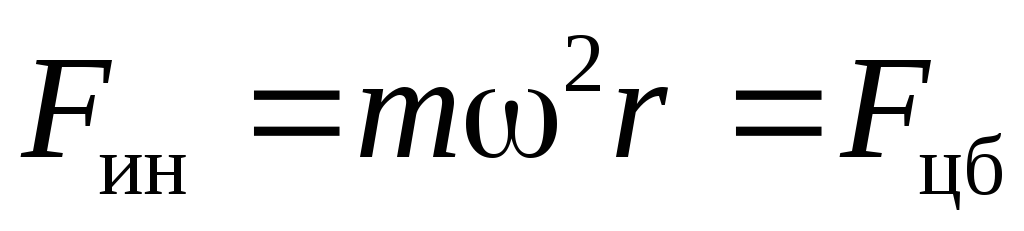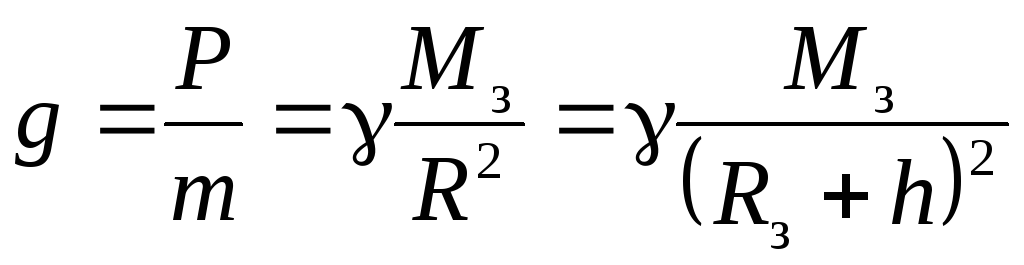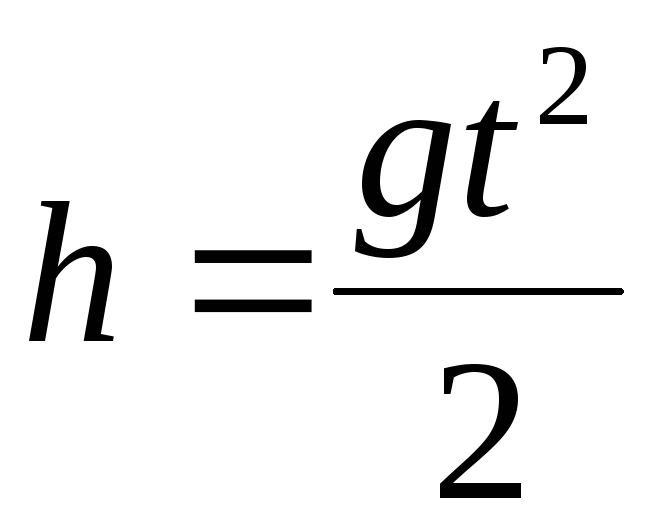