Joskus tällaisia ​​vääriä integraaleja kutsutaan toisen tyyppiset väärät integraalit. Toisen tyyppiset sopimattomat integraalit on salakavalasti "salattu" tavallisen määrätyn integraalin alle ja näyttävät täsmälleen samalta: .

Mutta toisin kuin määrätyllä integraalilla, integrandilla on ääretön epäjatkuvuus (ei ole olemassa):

1) kohdassa ,

2) piste,

3) molemmissa kohdissa kerralla,

4) tai jopa integrointivälillä.

Tarkastelemme kahta ensimmäistä tapausta, artikkelin lopussa on linkki lisäoppituntiin.

Katsotaanpa esimerkkiä sen selventämiseksi:

Se näyttää olevan selvä integraali. Mutta itse asiassa tämä on väärä toisen tyyppinen integraali, koska jos korvaamme integrandin, niin alarajan arvo

silloin nimittäjämme menee nollaan, eli integrandia ei yksinkertaisesti ole olemassa tässä vaiheessa!

Kun analysoidaan väärää integraalia sinun on aina korvattava molemmat integrointirajat integrandiin. Tässä suhteessa tarkistetaan yläraja:

Kaikki on hyvin täällä. Käyräviivainen puolisuunnikkaan tarkasteltavan virheellisen integraalin tyyppi näyttää pohjimmiltaan tältä:

Täällä kaikki on melkein sama kuin ensimmäisen tyypin integraalissa. Integraalimme on numeerisesti yhtä suuri kuin varjostetun kaarevan puolisuunnikkaan pinta-ala, jota ei ole rajoitettu ylhäältä. Tässä tapauksessa voi olla kaksi vaihtoehtoa: väärä integraali hajoaa (pinta-ala on ääretön) tai virheellinen integraali on yhtä suuri kuin äärellinen luku (kun äärettömän kuvion pinta-ala on äärellinen!).

Jäljelle jää vain Newton-Leibnizin kaavan muokkaaminen. Sitä muutetaan myös rajan avulla, mutta raja ei enää pyri äärettömyyteen, vaan arvostaa oikealla. Piirustuksesta on helppo jäljittää se akselia pitkin HÄRKÄ oikealla.

Katsotaan kuinka tämä toteutuu käytännössä.

Esimerkki 6

(älä unohda tarkistaa suullisesti tai luonnoksesta, onko kaikki kunnossa ylärajan kanssa!). Lasketaan ensin epämääräinen integraali:

Jos sinulla on vaikeuksia vaihtamisessa, katso oppitunti Korvausmenetelmä määrittelemättömässä integraalissa.

Lasketaan väärä integraali:

(1) Mitä uutta täällä on? Ratkaisutekniikassa ei ole käytännössä mitään. Ainoa asia, joka on muuttunut, on raja-kuvakkeen alla oleva merkintä:

+0:n lisääminen tarkoittaa, että pyrimme oikeanpuoleiseen arvoon ¾, mikä on loogista (katso kuvaaja). Tällaista rajaa rajojen teoriassa kutsutaan yksipuolinen raja. Tässä tapauksessa meillä on oikeanpuoleinen raja.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavalla.

(3) Käsitellään osoitteessa . Kuinka määrittää, mihin lauseke menee? Karkeasti sanottuna sinun tarvitsee vain korvata arvo siihen, korvata kolme neljäsosaa ja osoittaa, että . Kammataan vastaus.

Tässä tapauksessa väärä integraali on yhtä suuri kuin negatiivinen luku. Tässä ei ole rikollisuutta, vain vastaava kaareva puolisuunnikas sijaitsee akselin alla HÄRKÄ. Ja nyt esimerkkejä itsenäisistä ratkaisuista.

Esimerkki 7

Laske väärä integraali tai määritä sen ero.

Esimerkki 8

Laske väärä integraali tai määritä sen ero.

Jos integrandia ei ole pisteessä

Ääretön kaareva puolisuunnikas tällaiselle väärälle integraalille näyttää pohjimmiltaan tältä:

Täällä teemme kaiken täysin samoin, paitsi että rajamme pyrkii siihen arvostaa bvasemmalle. Akseli HÄRKÄ meidän on päästävä äärettömän lähelle murtumispistettä vasemmalle.

Esimerkki 9

Laske väärä integraali tai määritä sen ero.

Integrandi kärsii pisteessä äärettömästä epäjatkuvuudesta b = 3 (tarkistamme suullisesti, että kaikki on kunnossa toisella integrointirajalla!).

Vaihtelun vuoksi ratkaistaan ​​tämä raja heti - sisällyttämällä funktio erotusmerkin alle. Ne, joille se on vaikeaa, voivat ensin löytää määrittelemättömän integraalin käyttämällä jo käsiteltyä kaaviota.

Lisäys (-0) tarkoittaa, että meillä on raja vasenkätinen, ja asiaan b = 3 lähestymme akselia HÄRKÄ vasemmalle.

Selvitetään miksi murto-osa

(on parempi tehdä tämä suullisesti tai luonnoksessa).

Korvaamme raja-arvon juuren alle b = 3 - 0.

Lopuksi:

Väärä integraali hajoaa.

Miinusmerkki tarkoittaa, että vastaava kaareva puolisuunnikas sijaitsee akselin alla HÄRKÄ. Ole erittäin varovainen merkkien suhteen.

Kyllä, tietysti, väärä integraali eroaa, mutta molemmat ovat eri asioita, eri genrejä, ja jos et kiinnitä huomiota merkkeihin, teet tiukasti ottaen vakavan virheen.

Ja kaksi viimeistä esimerkkiä itsenäistä pohdintaa varten:

Esimerkki 10

Laske väärä integraali tai määritä sen ero.

Esimerkki 11

Laske väärä integraali tai määritä sen ero.

Analyysi tilanteesta, jossa molemmat integrointirajat ovat "huonoja" tai murtokohta sisältyy suoraan integrointisegmenttiin, löytyy artikkelista Tehokkaita menetelmiä määrällisten ja virheellisten integraalien ratkaisemiseen.

Ratkaisut ja vastaukset:

Esimerkki 4: Ratkaisu:

.

Esimerkki 5: Ratkaisu:

Integrand-toiminto on jatkuvasti päällä .

Esimerkki 7: Ratkaisu:

Integrandi kärsii pisteessä äärettömästä epäjatkuvuudesta

Väärä integraali hajoaa.

Huomautus: lausekerajoituksella

Ensimmäisen tyyppiset väärät integraalit. Pohjimmiltaan tämä on sama kiinteä integraali, mutta tapauksissa, joissa integraaleilla on äärettömät integroinnin ylä- tai alarajat tai molemmat integroinnin rajat ovat äärettömiä.

Toisen tyyppiset väärät integraalit. Pohjimmiltaan tämä on sama määrällinen integraali, mutta tapauksissa, joissa integraali otetaan rajoittamattomista funktioista, integrandilla ei äärellisessä määrässä pisteitä ole äärellistä integroinnin segmenttiä, joka kääntyy äärettömään.

Vertailun vuoksi. Kun otettiin käyttöön määrätyn integraalin käsite, oletettiin, että funktio f(x) on jatkuva aikavälillä [ a, b], ja integroinnin segmentti on äärellinen, eli sitä rajoittavat luvut, ei ääretön. Jotkut tehtävät johtavat tarpeeseen luopua näistä rajoituksista. Näin virheelliset integraalit näkyvät.

Väärän integraalin geometrinen merkitys Se osoittautuu melko yksinkertaisesti. Siinä tapauksessa, että funktion kuvaaja y = f(x) on akselin yläpuolella Härkä, määrätty integraali ilmaisee käyrän rajoittaman kaarevan puolisuunnikkaan alueen y = f(x) , x-akseli ja ordinaatit x = a , x = b. Väärä integraali puolestaan ​​ilmaisee rivien välissä olevan rajattoman (äärettömän) kaarevan puolisuunnikkaan alueen y = f(x) (alla olevassa kuvassa - punainen), x = a ja abskissa-akseli.

Väärät integraalit määritellään samalla tavalla muille äärettömille intervalleille:

Äärettömän kaarevan puolisuunnikkaan pinta-ala voi olla äärellinen luku, jolloin väärää integraalia kutsutaan konvergentiksi. Alue voi olla myös ääretön, ja tässä tapauksessa väärää integraalia kutsutaan divergentiksi.

Integraalin rajan käyttäminen väärän integraalin sijaan. Jotta voit arvioida väärän integraalin, sinun on käytettävä kiinteän integraalin rajaa. Jos tämä raja on olemassa ja on äärellinen (ei yhtä suuri kuin ääretön), niin väärää integraalia kutsutaan konvergentiksi ja muuten - divergentiksi. Se, mihin muuttuja pyrkii rajamerkin alle, riippuu siitä, onko kyseessä ensimmäisen vai toisen tyyppinen väärä integraali. Otetaan tämä nyt selvää.

Ensimmäisen tyyppiset väärät integraalit - äärettömillä rajoilla ja niiden lähentymisellä

Väärät integraalit, joilla on ääretön yläraja

Epäasianmukaisen integraalin kirjoittaminen eroaa siis tavallisesta kiinteästä integraalista siinä, että integroinnin yläraja on ääretön.

Määritelmä. Väärä integraali, jolla on jatkuvan funktion integroinnin yläraja f(x) välisenä aikana a ennen ∞ kutsutaan tämän funktion integraalin rajaa integroinnin ylärajan kanssa b ja integraation alaraja a edellyttäen, että integraation yläraja kasvaa rajattomasti, eli

.

Jos tämä raja on olemassa ja on yhtä suuri kuin jokin luku kuin ääretön, niin väärää integraalia kutsutaan konvergentiksi, ja sen arvoksi otetaan luku, jolla raja on yhtä suuri. Muuten väärää integraalia kutsutaan divergentiksi eikä sille anneta mitään merkitystä.

Esimerkki 1. Laske väärä integraali(jos se lähentyy).

Ratkaisu. Väärän integraalin määritelmän perusteella löydämme

Koska raja on olemassa ja on yhtä suuri kuin 1, niin tämä väärä integraali konvergoi ja on yhtä suuri kuin 1.

Seuraavassa esimerkissä integrandi on melkein sama kuin esimerkissä 1, vain aste x ei ole kaksi, vaan kirjain alfa, ja tehtävänä on tutkia epäsopivaa integraalia konvergenssin kannalta. Eli kysymys jää vastattavaksi: millä alfa-arvoilla tämä väärä integraali konvergoi ja millä arvoilla se eroaa?

Esimerkki 2. Tutki väärän integraalin konvergenssia(integroinnin alaraja on suurempi kuin nolla).

Ratkaisu. Oletetaan sitten ensin, että

Tuloksena olevassa lausekkeessa siirrymme rajaan osoitteessa:

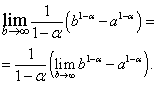
On helppo nähdä, että oikean puolen raja on olemassa ja on yhtä suuri kuin nolla, kun eli ja ei ole olemassa, kun eli .

Ensimmäisessä tapauksessa, eli kun . Jos sitten eikä ole olemassa.

Tutkimuksemme johtopäätös on seuraava: tämä väärä integraali konvergoi klo ja eroaa osoitteessa .

Newton-Leibnizin kaavan soveltaminen tutkittavaan väärän integraalin tyyppiin , voit johtaa seuraavan kaavan, joka on hyvin samanlainen kuin se:

.

Tämä on yleistetty Newton-Leibnizin kaava.

Esimerkki 3. Laske väärä integraali(jos se lähentyy).

Tämän integraalin raja on olemassa:

Toinen integraali, joka muodostaa alkuperäisen integraalin ilmaisevan summan:

Tämän integraalin raja on myös olemassa:

.

Löydämme kahden integraalin summan, joka on myös alkuperäisen virheellisen integraalin arvo kahdella äärettömällä rajalla:

Toisen tyyppiset väärät integraalit - rajoittamattomista funktioista ja niiden lähentymisestä

Anna toiminnon f(x) annettu segmentissä alkaen a ennen b ja se on rajaton. Oletetaan, että funktio menee pisteessä äärettömään b , kun taas segmentin kaikissa muissa kohdissa se on jatkuva.

Määritelmä. Väärä funktion integraali f(x) jaksolla alkaen a ennen b kutsutaan tämän funktion integraalin rajaa integroinnin ylärajan kanssa c , jos pyrittäessä c Vastaanottaja b funktio kasvaa ilman rajoitusta ja pisteessä x = b toimintoa ei ole määritelty, eli

.

Jos tämä raja on olemassa, niin toisen tyyppistä väärää integraalia kutsutaan konvergentiksi, muuten sitä kutsutaan divergentiksi.

Newton-Leibnizin kaavaa käyttäen johdetaan.

Tarkka integraali integraalisumman rajana

voi olla olemassa (eli sillä on tietty lopullinen arvo) vain, jos ehdot täyttyvät

Jos ainakin yksi näistä ehdoista rikotaan, määritelmä menettää merkityksensä. Todellakin, jos kyseessä on ääretön segmentti, esimerkiksi [ a; ) sitä ei voi jakaa P rajallisen pituiset osat
, joka lisäksi pyrkii nollaan segmenttien lukumäärän kasvaessa. Jos kyseessä on rajoittamaton jossain vaiheessa Kanssa[a; b] mielivaltaisen pisteen valinnan vaatimusta rikotaan osittaisilla segmenteillä – ei voi valita =Kanssa, koska funktion arvo tässä vaiheessa on määrittelemätön. Kuitenkin myös näissä tapauksissa on mahdollista yleistää määrätyn integraalin käsite ottamalla käyttöön toinen kulku rajaan. Integraaleja kutsutaan äärettömien intervallien ja epäjatkuvien (rajoittamattomien) funktioiden yli ei omaasi.

Määritelmä.

Anna toiminnon
on määritelty aikavälillä [ a; ) ja se on integroitavissa mille tahansa äärelliselle aikavälille [ a; b], eli olemassa
kenelle tahansa b > a. Tyyppirajoitus
nimeltään väärä integraali ensimmäinen laji (tai väärä integraali äärettömällä aikavälillä) ja merkitse
.

Siis määritelmän mukaan
=
.

Jos oikeanpuoleinen raja on olemassa ja on äärellinen, niin virheellinen integraali
nimeltään lähentyvä . Jos tämä raja on ääretön tai sitä ei ole ollenkaan, he sanovat, että väärä integraali eroaa .

Samalla tavalla voimme ottaa käyttöön funktion väärän integraalin käsitteen
intervallia pitkin (–; b]:

=
.

Ja funktion väärä integraali
intervallin yli (–; +) määritellään edellä esitettyjen integraalien summana:

=
+
,

Missä A- mielivaltainen piste. Tämä integraali konvergoi, jos molemmat termit konvergoivat, ja hajoaa, jos ainakin yksi termeistä poikkeaa.

Geometrialta katsottuna integraali
,
, määrittää funktion kaavion yläpuolella rajatun äärettömän kaarevan puolisuunnikkaan alueen numeerisen arvon
, vasen – suora
, alhaalta – OX-akselilla. Integraalin konvergenssi tarkoittaa tällaisen puolisuunnikkaan rajallisen alueen olemassaoloa ja sen yhtäläisyyttä kaarevan puolisuunnikkaan alueen rajaan, jossa on liikkuva oikea seinä.
.

Integraalin tapauksessa, jolla on ääretön raja, voimme yleistää Newton-Leibnizin kaava:

=
= F( + ) – F( a),

missä F( + ) =
. Jos tämä raja on olemassa, integraali konvergoi, muuten se hajoaa.

Tarkastelimme määrätyn integraalin käsitteen yleistämistä äärettömän intervallin tapaukseen.

Tarkastellaan nyt yleistystä rajoittamattoman funktion tapaukselle.

Määritelmä

Anna toiminnon
on määritelty aikavälillä [ a; b), on rajaton jossain pisteen alueella b, ja on jatkuva millä tahansa aikavälillä
, missä >0 (ja siksi integroitavissa tällä välillä, ts.
olemassa). Tyyppirajoitus
nimeltään toisen tyyppinen virheellinen integraali (tai rajoittamattoman funktion väärä integraali) ja on merkitty
.

Siten rajattoman integraali pisteessä b funktiot ovat olemassa määritelmän mukaan

=
.

Jos oikeanpuoleinen raja on olemassa ja on äärellinen, niin integraalia kutsutaan lähentyvä. Jos äärellistä rajaa ei ole, kutsutaan virheellistä integraalia poikkeava.

Samalla tavalla voimme määritellä funktion väärän integraalin
jossa on ääretön epäjatkuvuus pisteessä A:

=
.

Jos toiminto
sen sisäpisteessä on ääretön rako Kanssa
, niin väärä integraali määritellään seuraavasti

=
+
=
+
.

Tämä integraali konvergoi, jos molemmat termit konvergoivat, ja hajoaa, jos ainakin yksi termi hajoaa.

Geometrialta katsottuna rajoittamattoman funktion virheellinen integraali luonnehtii myös rajoittamattoman kaarevan puolisuunnikkaan aluetta:

Koska virheellinen integraali johdetaan siirtymällä rajalle määrätystä integraalista, kaikki määrätyn integraalin ominaisuudet voidaan siirtää (asianmukaisin tarkennuksin) ensimmäisen ja toisen tyyppisiin sopimattomiin integraaleihin.

Monissa virheellisiin integraaleihin johtavissa ongelmissa ei tarvitse tietää, mitä tämä integraali on yhtä suuri, riittää, kun varmistetaan sen konvergenssi tai hajaantuminen. Tätä varten he käyttävät lähentymisen merkkejä. Merkkejä väärien integraalien konvergenssista:

1) Vertailumerkki.

Olkoon se kaikille X

. Sitten jos
suppenee, sitten konvergoi
, ja

. Jos
poikkeaa, sitten hajoaa ja
.

2) Jos konvergoi
, sitten konvergoi ja
(tässä tapauksessa viimeistä integraalia kutsutaan täysin konvergoivaa).

Rajaamattomien funktioiden virheellisten integraalien konvergenssin ja hajaantumisen merkit ovat samanlaisia ​​kuin edellä muotoiltu.

Esimerkkejä ongelmanratkaisusta.

Esimerkki 1.

A)
; b)
; V)

G)
; d)
.

Ratkaisu.

a) Määritelmän mukaan meillä on:

.

b) Samoin

Siksi tämä integraali konvergoi ja on yhtä suuri kuin .

c) Määritelmän mukaan
=
+
, ja A– mielivaltainen numero. Laitetaanpa omaan tapaukseemme
, niin saamme:

Tämä integraali konvergoi.

Tämä tarkoittaa, että tämä integraali hajoaa.

e) Mietitään
. Integrandin antiderivaatan löytämiseksi on tarpeen soveltaa osittain integrointimenetelmää. Sitten saamme:

Koska ei kumpikaan
, ei myöskään
ei ole olemassa, sitten ei ole olemassa ja

Siksi tämä integraali hajoaa.

Esimerkki 2.

Tutki integraalin konvergenssia riippuen P.

Ratkaisu.

klo
meillä on:

Jos
, Tuo
Ja . Siksi integraali hajoaa.

Jos
, Tuo
, A
, Sitten

= ,

Siksi integraali konvergoi.

Jos
, Tuo

siksi integraali hajoaa.

Täten,

Esimerkki 3.

Laske väärä integraali tai määritä sen ero:

A)
; b)
; V)
.

Ratkaisu.

a) Integraali
on toisen tyyppinen virheellinen integraali, koska integrandi
ei ole rajoitettu jossain vaiheessa

. Sitten määritelmän mukaan

.

Integraali konvergoi ja on yhtä suuri kuin .

b) Harkitse
. Tässäkään integrandi ei ole rajoitettu pisteessä
. Siksi tämä integraali on väärä toisesta tyypistä ja määritelmän mukaan

Siksi integraali hajoaa.

c) Harkitse
. Integrand
kärsii äärettömästä aukosta kahdessa kohdassa:
Ja
, joista ensimmäinen kuuluu integrointiväliin
. Näin ollen tämä integraali on toisen tyyppinen sopimaton integraali. Siis määritelmän mukaan

=

=

.

Siksi integraali konvergoi ja on yhtä suuri kuin
.

Oletko täällä nyt? =) Ei, en yrittänyt pelotella ketään, vaan virheellisten integraalien aihe on erittäin hyvä esimerkki siitä, kuinka tärkeää on olla laiminlyömättä korkeampaa matematiikkaa ja muita tarkkoja tieteitä. Kaikki mitä tarvitset oppitunnin oppimiseen, on verkkosivuilla - yksityiskohtaisessa ja helposti saatavilla olevassa muodossa, jos haluat...

Joten aloitetaan. Kuvannollisesti sanottuna epäsopiva integraali on "edistynyt" määrätty integraali, eikä niissä itse asiassa ole niin paljon vaikeuksia, ja lisäksi väärällä integraalilla on erittäin hyvä geometrinen merkitys.

Mitä väärän integraalin arvioiminen tarkoittaa?

Laske väärä integraali - tämä tarkoittaa NUMERON löytämistä(täsmälleen sama kuin määrätyssä integraalissa), tai todistaa, että se eroaa(eli päädyt äärettömyyteen luvun sijaan).

On olemassa kahdenlaisia ​​vääriä integraaleja.

Väärä integraali, jolla on ääretön integrointiraja

Joskus tällaista väärää integraalia kutsutaan virheellinen ensimmäisen tyyppinen integraali. Yleensä väärä integraali, jolla on ääretön raja, näyttää useimmiten tältä: . Miten se eroaa määrätystä integraalista? Ylärajalla. Se on loputon: .

Vähemmän yleisiä ovat integraalit, joilla on ääretön alaraja tai kaksi ääretöntä rajaa: , ja tarkastelemme niitä myöhemmin - kun ymmärrät sen :)

No, katsotaanpa nyt suosituinta tapausta. Suurimmassa osassa esimerkeistä integrandi toimii jatkuva välissä ja tämä tärkeä tosiasia kannattaa tarkistaa ensin! Koska jos on aukkoja, on lisäviiveitä. Varmuuden vuoksi oletetaan, että silloinkin tyypillinen kaareva puolisuunnikkaan muotoinen näyttää tältä:

Huomaa, että se on ääretön (ei rajattu oikealla), ja väärä integraali numeerisesti yhtä suuri kuin sen pinta-ala. Seuraavat vaihtoehdot ovat mahdollisia:

1) Ensimmäinen ajatus, joka tulee mieleen: "Koska luku on ääretön, niin "Toisin sanoen alue on myös ääretön. Se voi olla niin. Tässä tapauksessa he sanovat, että väärä integraali eroaa.

2) Mutta. Niin paradoksaalista kuin se kuulostaakin, äärettömän hahmon pinta-ala voi olla yhtä suuri kuin... äärellinen luku! Esimerkiksi: . Voiko tämä olla totta? Helposti. Toisessa tapauksessa väärä integraali lähentyy.

3) Tietoja kolmannesta vaihtoehdosta hieman myöhemmin.

Missä tapauksissa väärä integraali hajoaa ja missä konvergoi? Tämä riippuu integrandista, ja tarkastelemme konkreettisia esimerkkejä pian.

Mitä tapahtuu, jos ääretön kaareva puolisuunnikas sijaitsee akselin alapuolella? Tässä tapauksessa väärä integraali (poikkeaa) tai on yhtä suuri kuin äärellinen negatiivinen luku.

Täten, väärä integraali voi olla negatiivinen.

Tärkeä! Kun sinulle annetaan MIKKI sopimaton integraali ratkaistavaksi, niin yleisesti ottaen mistään alueesta ei puhuta eikä piirustusta tarvitse rakentaa. Selitin väärän integraalin geometrisen merkityksen vain materiaalin ymmärtämisen helpottamiseksi.

Koska epäasianmukainen integraali on hyvin samanlainen kuin varma integraali, muistetaan Newton-Leibnizin kaava: . Itse asiassa kaava soveltuu myös vääriin integraaleihin, vain sitä on muutettava hieman. Mikä on ero? Integroinnin äärettömällä ylärajalla: . Luultavasti monet arvasivat, että tämä haisee jo rajojen teorian soveltamiselle, ja kaava kirjoitetaan näin: .

Mitä eroa on määrätystä integraalista? Ei mitään erityistä! Kuten määrätyssä integraalissa, sinun on kyettävä löytämään antiderivatiivinen funktio (epämääräinen integraali) ja osattava soveltaa Newton-Leibnizin kaavaa. Ainoa asia, joka on lisätty, on rajan laskeminen. Jolla on huono aika heidän kanssaan, ota oppia Toiminnan rajat. Esimerkkejä ratkaisuista, koska parempi myöhään kuin armeijassa.

Katsotaanpa kahta klassista esimerkkiä:

Esimerkki 1

Selvyyden vuoksi piirrän piirustuksen, vaikka korostan vielä kerran, käytännössä Tässä tehtävässä ei tarvitse rakentaa piirustuksia.

Integrandifunktio on jatkuva puolivälissä, mikä tarkoittaa, että kaikki on hyvin ja virheellinen integraali voidaan laskea "standardi"-menetelmällä.

Kaavamme soveltaminen ja ongelman ratkaisu näyttää tältä:

Eli väärä integraali hajoaa ja varjostetun kaarevan puolisuunnikkaan pinta-ala on yhtä suuri kuin ääretön.

Tarkastetussa esimerkissä meillä on yksinkertaisin taulukkointegraali ja sama tekniikka Newton-Leibnizin kaavan soveltamiseksi kuin määrätyssä integraalissa. Mutta tätä kaavaa sovelletaan rajamerkin alla. "Dynaamisen" muuttujan tavallisen kirjaimen sijaan ilmestyy kirjain "be". Tämän ei pitäisi hämmentää tai hämmentää, koska mikään kirjain ei ole huonompi kuin tavallinen "X".

Jos et ymmärrä miksi osoitteessa , tämä on erittäin huono, joko et ymmärrä yksinkertaisimpia rajoja (etkä yleensä ymmärrä mitä raja on), tai et tiedä miltä logaritmisen funktion kuvaaja näyttää. Toisessa tapauksessa osallistu oppitunnille Alkeisfunktioiden kuvaajat ja ominaisuudet.

Virheellisiä integraaleja ratkaistaessa on erittäin tärkeää tietää, miltä perusalkeisfunktioiden kuvaajat näyttävät!

Valmiin tehtävän pitäisi näyttää suunnilleen tältä:

“

! Kun valmistellaan esimerkkiä, keskeytämme aina ratkaisun ja osoitamme, mitä integrandille tapahtuu – onko se jatkuva integraatiovälillä vai ei?. Tämän avulla tunnistamme virheellisen integraalin tyypin ja oikeutamme jatkotoimenpiteet.

Esimerkki 2

Laske väärä integraali tai määritä sen ero.

Tehdään piirustus:

Ensin huomautetaan seuraavaa: integrandi on jatkuva puolivälissä. Huppu. Ratkaisemme kaavan avulla :

(1) Otetaan tehofunktion yksinkertaisin integraali (tämä erikoistapaus on monissa taulukoissa). On parempi sijoittaa miinus välittömästi rajamerkin ulkopuolelle, jotta se ei häiritse tulevissa laskelmissa.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavalla.

(3) Osoitamme, että (Herrat, tämä olisi pitänyt ymmärtää jo kauan sitten) ja yksinkertaistamme vastausta.

Tässä äärettömän kaarevan puolisuunnikkaan pinta-ala on äärellinen luku! Uskomatonta mutta totta.

Valmiin esimerkin pitäisi näyttää suunnilleen tältä:

“

Integrand-toiminto on jatkuvasti päällä

“

Mitä tehdä, jos törmäät integraaliin kuten - kanssa taukopiste integrointivälillä? Tämä tarkoittaa, että esimerkissä on kirjoitusvirhe. (Todennäköisimmin), tai edistyneestä koulutustasosta. Jälkimmäisessä tapauksessa johtuen additiivisuusominaisuudet, meidän pitäisi harkita kahta väärää integraalia intervalleilla ja käsitellä sitten summaa.

Joskus kirjoitusvirheen tai tarkoituksen vuoksi virheellinen integraali saattaa tulla ei ole olemassa ollenkaan, joten jos esimerkiksi laitat x:n neliöjuuren yllä olevan integraalin nimittäjään, osa integrointivälistä ei sisälly integrandin määritelmäalueeseen ollenkaan.

Lisäksi sopimatonta integraalia ei välttämättä ole olemassa edes kaiken "näennäisen hyvinvoinnin" kanssa. Klassinen esimerkki: . Huolimatta kosinin tarkkuudesta ja jatkuvuudesta, tällaista väärää integraalia ei ole olemassa! Miksi? Se on hyvin yksinkertaista, koska:
- ei ole olemassa sopiva raja.

Ja tällaisia ​​esimerkkejä, vaikkakin harvinaisia, esiintyy käytännössä! Siten konvergenssin ja divergenssin lisäksi ratkaisulla on myös kolmas tulos, jolla on pätevä vastaus: "ei ole sopimatonta integraalia".

On myös huomioitava, että epäsopivan integraalin tiukka määritelmä annetaan juuri rajan kautta, ja siihen voivat halukkaat tutustua oppikirjallisuudessa. No, jatkamme käytännön oppituntia ja siirrymme mielekkäämpiin tehtäviin:

Esimerkki 3

Laske väärä integraali tai määritä sen ero.

Ensin yritetään löytää antiderivatiivinen funktio (epämääräinen integraali). Jos emme tee tätä, emme luonnollisesti pysty ratkaisemaan myöskään väärää integraalia.

Mitä taulukon integraaleista integrandi on samanlainen? Tulee mieleen arktangentti: . Nämä näkökohdat viittaavat siihen, että olisi mukavaa, jos nimittäjässä olisi neliö. Tämä tehdään vaihtamalla.

Korvataan:

Epämääräinen integraali on löydetty tässä tapauksessa, vakion lisääminen ei ole järkevää.

Luonnos on aina hyödyllistä tarkistaa, eli erotella saatu tulos:

Alkuperäinen integraali on saatu, mikä tarkoittaa, että epämääräinen integraali on löydetty oikein.

Nyt löydämme väärän integraalin:

(1) Kirjoitamme ratkaisun kaavan mukaan . On parempi siirtää vakio välittömästi rajamerkin yli, jotta se ei häiritse jatkolaskutoimituksia.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavan mukaisesti. Miksi osoitteessa ? Katso arktangenttikaavio jo suositellusta artikkelista.

(3) Saamme lopullisen vastauksen. Fakta, joka on hyödyllistä tietää ulkoa.

Edistyneet opiskelijat eivät välttämättä löydä epämääräistä integraalia erikseen eivätkä käytä korvausmenetelmää, vaan käyttävät mieluummin menetelmää, jolla korvataan differentiaalimerkin alla oleva funktio ja ratkaistaan ​​virheellinen integraali "välittömästi". Tässä tapauksessa ratkaisun pitäisi näyttää suunnilleen tältä:

“

Integrand on jatkuva päällä.

“

Esimerkki 4

Laske väärä integraali tai määritä sen ero.

! Tämä on tyypillinen esimerkki, ja samanlaisia ​​integraaleja löytyy hyvin usein. Tee se hyvin! Tässä oleva antiderivatiivinen funktio löytyy täydellisen neliön valintamenetelmällä. Lisätietoja menetelmästä löytyy oppitunnista Joidenkin murtolukujen integrointi.

Esimerkki 5

Laske väärä integraali tai määritä sen ero.

Tämä integraali voidaan ratkaista yksityiskohtaisesti, eli löytää ensin epämääräinen integraali tekemällä muuttujan muutos. Tai voit ratkaista sen "välittömästi" - sisällyttämällä funktion erotusmerkin alle. Kenellä on matemaattinen koulutus?

Täydelliset ratkaisut ja vastaukset oppitunnin lopussa.

Esimerkkejä ratkaisuista vääriin integraaleihin, joilla on ääretön integroinnin alaraja, löytyy sivulta Tehokkaat menetelmät väärien integraalien ratkaisemiseen. Siellä analysoimme myös tapausta, jossa integraation molemmat rajat ovat äärettömät.

Virheelliset rajaamattomien funktioiden integraalit

Tai toisen tyyppiset väärät integraalit. Toisen tyyppiset sopimattomat integraalit "salataan" kavalasti tavanomaisen määrätyn integraalin alle ja näyttävät täsmälleen samalta: Mutta toisin kuin määrätty integraali, integrandi kärsii äärettömästä epäjatkuvuudesta (ei ole): 1) pisteessä , 2) tai kohdassa , 3) ​​tai molemmissa pisteissä kerralla, 4) tai jopa integrointisegmentissä. Tarkastelemme kahta ensimmäistä tapausta, artikkelin lopussa on linkki lisäoppituntiin.

Vain esimerkki selväksi: . Se näyttää olevan selvä integraali. Mutta itse asiassa tämä on toisen tyyppinen väärä integraali, jos korvaamme integrandin alarajan arvon, nimittäjämme menee nollaan, eli integrandia ei yksinkertaisesti ole olemassa tässä vaiheessa!

Yleensä, kun analysoidaan väärää integraalia sinun on aina korvattava molemmat integrointirajat integrandiin. Tässä suhteessa tarkistetaan yläraja: . Kaikki on hyvin täällä.

Käyräviivainen puolisuunnikkaan tarkasteltavan virheellisen integraalin tyyppi näyttää pohjimmiltaan tältä:

Täällä kaikki on melkein sama kuin ensimmäisen tyypin integraalissa.

Integraalimme on numeerisesti yhtä suuri kuin varjostetun kaarevan puolisuunnikkaan pinta-ala, jota ei ole rajoitettu ylhäältä. Tässä tapauksessa voi olla kaksi vaihtoehtoa*: väärä integraali hajoaa (pinta-ala on ääretön) tai väärä integraali on yhtä suuri kuin äärellinen luku (eli äärettömän kuvion pinta-ala on äärellinen!).

* oletuksena oletamme yleensä, että väärä integraali on olemassa

Jäljelle jää vain Newton-Leibnizin kaavan muokkaaminen. Sitä muutetaan myös rajan avulla, mutta raja ei enää pyri äärettömyyteen, vaan oikealla olevaan arvoon. Piirustuksesta on helppo seurata: akselia pitkin on lähestyttävä murtumiskohtaa äärettömän lähellä oikealla.

Katsotaan kuinka tämä toteutuu käytännössä.

Esimerkki 6

Laske väärä integraali tai määritä sen ero.

Integrandilla on ääretön epäjatkuvuus pisteessä (älä unohda tarkistaa suullisesti tai luonnoksesta, että kaikki on kunnossa ylärajan kanssa!)

Lasketaan ensin epämääräinen integraali:

Korvaus:

Jos sinulla on vaikeuksia vaihtamisessa, katso oppitunti Korvausmenetelmä määrittelemättömässä integraalissa.

Lasketaan väärä integraali:

(1) Mitä uutta täällä on? Ratkaisutekniikassa ei ole käytännössä mitään. Ainoa asia, joka on muuttunut, on raja-kuvakkeen alla oleva merkintä: . Lisäys tarkoittaa, että pyrimme oikeanpuoleiseen arvoon (mikä on loogista - katso kaavio). Tällaista rajaa rajojen teoriassa kutsutaan yksipuolinen raja. Tässä tapauksessa meillä on oikeanpuoleinen raja.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavalla.

(3) Käsitellään osoitteessa . Kuinka määrittää, mihin lauseke menee? Karkeasti sanottuna sinun tarvitsee vain korvata arvo siihen, korvata kolme neljäsosaa ja osoittaa, että . Kammataan vastaus.

Tässä tapauksessa väärä integraali on yhtä suuri kuin negatiivinen luku. Tässä ei ole rikollisuutta, vain vastaava kaareva puolisuunnikas sijaitsee akselin alla.

Ja nyt kaksi esimerkkiä itsenäisistä ratkaisuista.

Esimerkki 7

Laske väärä integraali tai määritä sen ero.

Esimerkki 8

Laske väärä integraali tai määritä sen ero.

Jos integrandia ei ole pisteessä

Ääretön kaareva puolisuunnikas tällaiselle väärälle integraalille näyttää pohjimmiltaan tältä.

Väärä integraali äärettömällä integrointirajalla

Joskus tällaista virheellistä integraalia kutsutaan myös ensimmäisen tyyppiseksi virheelliseksi integraaliksi..gif" width="49" height="19 src=">.

Vähemmän yleisiä ovat integraalit, joilla on ääretön alaraja tai kaksi ääretöntä rajaa: .

Harkitsemme suosituinta tapausta https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Ei ei aina. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Kuvataan piirustuksessa integrandifunktion kuvaaja. Tyypillinen kaavio ja kaareva puolisuunnikas tässä tapauksessa näyttää tältä:

Väärä integraalihttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", toisin sanoen alue on myös ääretön. Se voi olla niin. Tässä tapauksessa he sanovat, että väärä integraali eroaa.

2) Mutta. Niin paradoksaalista kuin se kuulostaakin, äärettömän hahmon pinta-ala voi olla yhtä suuri kuin... äärellinen luku! Esimerkiksi: .. Toisessa tapauksessa väärä integraali lähentyy.

Mitä tapahtuu, jos ääretön kaareva puolisuunnikas sijaitsee akselin alapuolella?.gif" width="217" height="51 src=">.

: .

Esimerkki 1

Integrandifunktio https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, mikä tarkoittaa, että kaikki on kunnossa ja virheellinen integraali voidaan laskea käyttämällä " standardi” menetelmä.

Kaavamme soveltaminen https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

Eli väärä integraali hajoaa ja varjostetun kaarevan puolisuunnikkaan pinta-ala on yhtä suuri kuin ääretön.

Virheellisiä integraaleja ratkaistaessa on erittäin tärkeää tietää, miltä perusalkeisfunktioiden kuvaajat näyttävät!

Esimerkki 2

Laske väärä integraali tai määritä sen ero.

Tehdään piirustus:

Ensin huomautetaan seuraavaa: integrandi on jatkuva puolivälissä. Hyvä..gif" width="327" height="53">

(1) Otetaan tehofunktion yksinkertaisin integraali (tämä erikoistapaus on monissa taulukoissa). On parempi sijoittaa miinus välittömästi rajamerkin ulkopuolelle, jotta se ei häiritse tulevissa laskelmissa.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavalla.

(3) Korostamme, että https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Hyvät herrat, tämä on ymmärrettävä pitkään aika sitten) ja yksinkertaista vastausta.

Tässä äärettömän kaarevan puolisuunnikkaan pinta-ala on äärellinen luku! Uskomatonta mutta totta.

Esimerkki 3

Laske väärä integraali tai määritä sen ero.

Integrand on jatkuva päällä.

Ensin yritetään löytää antiderivatiivinen funktio (epämääräinen integraali).

Mitä taulukon integraaleista integrandi on samanlainen? Tulee mieleen arktangentti: . Nämä näkökohdat viittaavat siihen, että olisi mukavaa, jos nimittäjässä olisi neliö. Tämä tehdään vaihtamalla.

Korvataan:

On aina hyödyllistä suorittaa tarkistus, eli erotella saatu tulos:

Nyt löydämme väärän integraalin:

(1) Kirjoitamme ratkaisun kaavan mukaan . On parempi siirtää vakio välittömästi rajamerkin yli, jotta se ei häiritse jatkolaskutoimituksia.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavan mukaisesti..gif" width="56" height="19 src=">? Katso arktangenttikaavio jo toistuvasti suositellusta artikkelista.

(3) Saamme lopullisen vastauksen. Fakta, joka on hyödyllistä tietää ulkoa.

Edistyneet opiskelijat eivät välttämättä löydä epämääräistä integraalia erikseen eivätkä käytä korvausmenetelmää, vaan käyttävät mieluummin menetelmää, jolla korvataan differentiaalimerkin alla oleva funktio ja ratkaistaan ​​virheellinen integraali "välittömästi". Tässä tapauksessa ratkaisun pitäisi näyttää suunnilleen tältä:

“

Integrand-toiminto on jatkuva osoitteessa https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“

Esimerkki 4

Laske väärä integraali tai määritä sen ero.

! Tämä on tyypillinen esimerkki, ja samanlaisia ​​integraaleja löytyy hyvin usein. Tee se hyvin! Antiderivatiivinen funktio löytyy tästä käyttämällä täydellisen neliön eristysmenetelmää.

Esimerkki 5

Laske väärä integraali tai määritä sen ero.

Tämä integraali voidaan ratkaista yksityiskohtaisesti, eli löytää ensin epämääräinen integraali tekemällä muuttujan muutos. Tai voit ratkaista sen "välittömästi" - sisällyttämällä funktion erotusmerkin alle.

Virheelliset rajaamattomien funktioiden integraalit

Joskus tällaisia ​​sopimattomia integraaleja kutsutaan toisen tyyppisiksi sopimattomiksi integraaleiksi. Toisen tyyppiset sopimattomat integraalit "salataan" salakavalasti tavallisen kiinteän integraalin alle ja näyttävät täsmälleen samalta: ..gif" width="39" height="15 src=">, 2) tai kohdassa , 3) tai molemmissa kohdissa kerralla, 4) tai jopa integrointisegmentissä. Tarkastellaan kahta ensimmäistä tapausta artikkelin lopussa.

Selvyyden vuoksi vain esimerkki: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, silloin nimittäjämme on nolla, eli integrandia ei yksinkertaisesti ole olemassa tässä vaiheessa!

Yleensä, kun analysoidaan väärää integraalia sinun on aina korvattava molemmat integrointirajat integrandiin..jpg" alt="Väärä integraali, epäjatkuvuuspiste integroinnin alarajassa" width="323" height="380">!}

Täällä kaikki on melkein sama kuin ensimmäisen tyypin integraalissa.
Integraalimme on numeerisesti yhtä suuri kuin varjostetun kaarevan puolisuunnikkaan pinta-ala, jota ei ole rajoitettu ylhäältä. Tässä tapauksessa voi olla kaksi vaihtoehtoa: väärä integraali hajoaa (pinta-ala on ääretön) tai väärä integraali on yhtä suuri kuin äärellinen luku (eli äärettömän kuvion pinta-ala on äärellinen!).

Jäljelle jää vain Newton-Leibnizin kaavan muokkaaminen. Sitä muutetaan myös rajan avulla, mutta raja ei enää pyri äärettömyyteen, vaan arvostaahttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> oikealla.

Esimerkki 6

Laske väärä integraali tai määritä sen ero.

Integrandilla on ääretön epäjatkuvuus pisteessä (älä unohda tarkistaa suullisesti tai luonnoksesta, että kaikki on kunnossa ylärajan kanssa!)

Lasketaan ensin epämääräinen integraali:

Korvaus:

Lasketaan väärä integraali:

(1) Mitä uutta täällä on? Ratkaisutekniikassa ei ole käytännössä mitään. Ainoa asia, joka on muuttunut, on merkintä raja-kuvakkeen alla: . Lisäys tarkoittaa, että pyrimme oikeanpuoleiseen arvoon (mikä on loogista - katso kaavio). Tällaista rajaa rajateoriassa kutsutaan yksipuoliseksi rajaksi. Tässä tapauksessa meillä on oikeakätisyysraja.

(2) Korvaamme ylä- ja alarajat Newton-Leibnizin kaavalla.

(3) Ymmärretään https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Miten määritetään, mihin lausekkeen tulisi mennä? Karkeasti sanottuna , sinun tarvitsee vain korvata arvo, korvata kolme neljäsosaa ja osoittaa, että kampa vastaus.

Tässä tapauksessa väärä integraali on yhtä suuri kuin negatiivinen luku.

Esimerkki 7

Laske väärä integraali tai määritä sen ero.

Esimerkki 8

Laske väärä integraali tai määritä sen ero.

Jos integrandia ei ole pisteessä

Ääretön kaareva puolisuunnikas tällaiselle väärälle integraalille näyttää pohjimmiltaan tältä:

Täällä kaikki on täysin sama, paitsi että rajamme pyrkii siihen arvostaahttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> meidän on päästävä äärettömän lähelle murtumispistettä vasemmalle.