समीकरणों का आलेखीय हल

सुनहरे दिन, 2009

परिचय

प्राचीन काल में द्विघात समीकरणों को हल करने की आवश्यकता एक सैन्य प्रकृति के भूमि और भूकंप के क्षेत्रों को खोजने के साथ-साथ खगोल विज्ञान और गणित के विकास से संबंधित समस्याओं को हल करने की आवश्यकता के कारण हुई थी। बेबीलोन के लोग लगभग 2000 ईसा पूर्व के द्विघात समीकरणों को हल करना जानते थे। बेबीलोन के ग्रंथों में वर्णित इन समीकरणों को हल करने का नियम अनिवार्य रूप से आधुनिक लोगों के साथ मेल खाता है, लेकिन यह ज्ञात नहीं है कि बेबीलोन के लोग इस नियम पर कैसे आए।

यूरोप में द्विघात समीकरणों को हल करने के सूत्र सबसे पहले 1202 में इतालवी गणितज्ञ लियोनार्डो फिबोनाची द्वारा लिखी गई पुस्तक अबेकस में निर्धारित किए गए थे। उनकी पुस्तक ने न केवल इटली में, बल्कि जर्मनी, फ्रांस और अन्य यूरोपीय देशों में भी बीजीय ज्ञान के प्रसार में योगदान दिया।

लेकिन गुणांक बी और सी के सभी संभावित संयोजनों के साथ द्विघात समीकरणों को हल करने के लिए सामान्य नियम, यूरोप में केवल 1544 में एम। स्टीफेल द्वारा तैयार किया गया था।

1591 में फ़्राँस्वा वियत द्विघात समीकरणों को हल करने के लिए सूत्र प्रस्तुत किए।

प्राचीन बेबीलोन में कुछ प्रकार के द्विघात समीकरणों को हल किया जा सकता था।

अलेक्जेंड्रिया के डायोफैंटस और यूक्लिड, अल-ख्वारिज्मीऔर उमर खय्यामज्यामितीय और चित्रमय तरीकों से हल किए गए समीकरण।

7वीं कक्षा में हमने कार्यों का अध्ययन किया वाई \u003d सी, वाई =केएक्स, वाई =केएक्स+ एम, वाई =एक्स 2,वाई = -एक्स 2, आठवीं कक्षा में - वाई =एक्स, वाई =|एक्स|, वाई =कुल्हाड़ी2 + बीएक्स+ सी, वाई =क/ एक्स. 9वीं कक्षा के बीजगणित पाठ्यपुस्तक में, मैंने ऐसे कार्य देखे जो अभी तक मुझे ज्ञात नहीं थे: वाई =एक्स 3, वाई =एक्स 4,वाई =एक्स 2एन, वाई =एक्स- 2एन, वाई = 3√एक्स, (एक्स– ए) 2 + (वाई -बी) 2 = आर 2 और अन्य। इन कार्यों के रेखांकन बनाने के नियम हैं। मैं सोच रहा था कि क्या ऐसे अन्य कार्य हैं जो इन नियमों का पालन करते हैं।

मेरा काम कार्यों के ग्राफ का अध्ययन करना और समीकरणों को ग्राफिक रूप से हल करना है।

1. कार्य क्या हैं

फ़ंक्शन का ग्राफ़ समन्वय विमान के सभी बिंदुओं का समूह है, जिनमें से एब्सिसास तर्कों के मूल्यों के बराबर होते हैं, और निर्देशांक फ़ंक्शन के संबंधित मानों के बराबर होते हैं।

रैखिक कार्य समीकरण द्वारा दिया गया है वाई =केएक्स+ बी, कहाँ पे कऔर बी- कुछ नंबर। इस फ़ंक्शन का आलेख एक सीधी रेखा है।

उलटा आनुपातिक कार्य वाई =क/ एक्स, जहाँ k 0. इस फलन के ग्राफ को अतिपरवलय कहते हैं।

समारोह (एक्स– ए) 2 + (वाई -बी) 2 = आर2 , कहाँ पे ए, बीऔर आर- कुछ नंबर। इस फलन का आलेख बिन्दु A पर केन्द्रित त्रिज्या r का एक वृत्त है। ए, बी).

द्विघात फंक्शन आप= कुल्हाड़ी2 + बीएक्स+ सीकहाँ पे ए,बी, साथ- कुछ नंबर और ए 0. इस फलन का आलेख एक परवलय है।

समीकरण पर2 (ए– एक्स) = एक्स2 (ए+ एक्स) . इस समीकरण का ग्राफ एक वक्र होगा जिसे स्ट्रोफॉइड कहा जाता है।

/>समीकरण (एक्स2 + आप2 ) 2 = ए(एक्स2 – आप2 ) . इस समीकरण के ग्राफ को बर्नौली लेम्निस्केट कहा जाता है।

समीकरण। इस समीकरण के ग्राफ को एस्ट्रोइड कहते हैं।

वक्र (एक्स2 आप2 - 2 एक्स)2 =4 ए2 (एक्स2 +y2 ) . इस वक्र को कार्डियोइड कहा जाता है।

कार्य: वाई =एक्स 3 - घन परवलय, वाई =एक्स 4, वाई = 1/एक्स 2.

2. एक समीकरण की अवधारणा, उसका आलेखीय हल

समीकरणएक चर युक्त अभिव्यक्ति है।

प्रश्न हल करें- इसका अर्थ है इसकी सभी जड़ों को खोजना, या यह साबित करना कि वे मौजूद नहीं हैं।

समीकरण का मूलएक संख्या है, जिसे समीकरण में प्रतिस्थापित करने पर सही संख्यात्मक समानता उत्पन्न होती है।

समीकरणों को आलेखीय रूप से हल करनाआपको जड़ों का सटीक या अनुमानित मूल्य खोजने की अनुमति देता है, आपको समीकरण की जड़ों की संख्या खोजने की अनुमति देता है।

ग्राफ़ बनाते समय और समीकरणों को हल करते समय, फ़ंक्शन के गुणों का उपयोग किया जाता है, इसलिए इस विधि को अक्सर कार्यात्मक-ग्राफ़िक कहा जाता है।

समीकरण को हल करने के लिए, हम इसे दो भागों में "विभाजित" करते हैं, दो कार्यों का परिचय देते हैं, उनके ग्राफ़ बनाते हैं, ग्राफ़ के प्रतिच्छेदन बिंदुओं के निर्देशांक पाते हैं। इन बिंदुओं के भुज समीकरण के मूल हैं।

3. किसी फलन का आलेख बनाने के लिए एल्गोरिथम

फलन का ग्राफ जानना वाई =एफ(एक्स) , आप कार्यों की साजिश कर सकते हैं वाई =एफ(एक्स+ एम) ,वाई =एफ(एक्स)+ मैंऔर वाई =एफ(एक्स+ एम)+ मैं. ये सभी ग्राफ़ फ़ंक्शन के ग्राफ़ से प्राप्त किए गए हैं वाई =एफ(एक्स) समानांतर अनुवाद परिवर्तन का उपयोग करना: on │ एम│ x-अक्ष के अनुदिश दाएँ या बाएँ स्केल इकाइयाँ और on │ मैं│ स्केल इकाइयों को अक्ष के साथ ऊपर या नीचे आप.

4. द्विघात समीकरण का आलेखीय हल

द्विघात फलन के उदाहरण का उपयोग करते हुए, हम द्विघात समीकरण के आलेखीय हल पर विचार करेंगे। द्विघात फलन का आलेख एक परवलय होता है।

प्राचीन यूनानियों को परवलय के बारे में क्या पता था?

आधुनिक गणितीय प्रतीकवाद की उत्पत्ति 16वीं शताब्दी में हुई थी।

प्राचीन यूनानी गणितज्ञों के पास न तो समन्वय विधि थी और न ही किसी फलन की अवधारणा। हालांकि, परवलय के गुणों का उनके द्वारा विस्तार से अध्ययन किया गया था। प्राचीन गणितज्ञों की आविष्कारशीलता बस आश्चर्यजनक है, क्योंकि वे केवल चित्र और निर्भरता के मौखिक विवरण का उपयोग कर सकते थे।

सबसे अधिक पूरी तरह से परवलय, अतिपरवलय और दीर्घवृत्त का पता लगाया पेर्गा का अपोलोनियस, जो तीसरी शताब्दी ईसा पूर्व में रहते थे। उन्होंने इन वक्रों को नाम भी दिए और संकेत दिया कि एक विशेष वक्र पर स्थित बिंदु किन स्थितियों को संतुष्ट करते हैं (आखिरकार, कोई सूत्र नहीं थे!)

एक परवलय के निर्माण के लिए एक एल्गोरिथ्म है:

परवलय A (x0; y0) के शीर्ष के निर्देशांक ज्ञात कीजिए: एक्स=- बी/2 ए;

y0=aho2+in0+s;

परवलय की सममिति का अक्ष ज्ञात कीजिए (सीधी रेखा x=x0);

पृष्ठ ब्रेक--

नियंत्रण बिंदुओं के निर्माण के लिए मूल्यों की एक तालिका संकलित करना;

हम प्राप्त बिंदुओं का निर्माण करते हैं और सममिति की धुरी के संबंध में उनके सममित बिंदुओं का निर्माण करते हैं।

1. आइए एल्गोरिथम के अनुसार एक परवलय का निर्माण करें आप= एक्स2 – 2 एक्स– 3 . अक्ष के साथ प्रतिच्छेदन बिंदुओं का भुज एक्सऔर द्विघात समीकरण के मूल हैं एक्स2 – 2 एक्स– 3 = 0.

इस समीकरण को आलेखीय रूप से हल करने के पाँच तरीके हैं।

2. आइए समीकरण को दो कार्यों में विभाजित करें: आप= एक्स2 और आप= 2 एक्स+ 3

3. आइए समीकरण को दो कार्यों में विभाजित करें: आप= एक्स2 –3 और आप=2 एक्स. समीकरण की जड़ें रेखा के साथ परवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

4. समीकरण को रूपांतरित करें एक्स2 – 2 एक्स– 3 = 0 फ़ंक्शन पर पूर्ण वर्ग का चयन करके: आप= (एक्स–1) 2 और आप=4. समीकरण की जड़ें रेखा के साथ परवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

5. हम पद को समीकरण के दोनों भागों से विभाजित करते हैं एक्स2 – 2 एक्स– 3 = 0 पर एक्स, हम पाते हैं एक्स– 2 – 3/ एक्स= 0 आइए इस समीकरण को दो कार्यों में विभाजित करें: आप= एक्स– 2, आप= 3/ एक्स. समीकरण की जड़ें रेखा और अतिपरवलय के प्रतिच्छेदन बिंदुओं के भुज हैं।

5. डिग्री समीकरणों का आलेखीय समाधानएन

उदाहरण 1प्रश्न हल करें एक्स5 = 3 – 2 एक्स.

आप= एक्स5 , आप= 3 – 2 एक्स.

जवाब:एक्स = 1.

उदाहरण 2प्रश्न हल करें 3 √ एक्स= 10 – एक्स.

इस समीकरण की जड़ें दो कार्यों के रेखांकन के प्रतिच्छेदन बिंदु का भुज है: आप= 3 √ एक्स, आप= 10 – एक्स.

जवाब:एक्स = 8।

निष्कर्ष

फ़ंक्शन ग्राफ़ को ध्यान में रखते हुए: वाई =कुल्हाड़ी2 + बीएक्स+ सी, वाई =क/ एक्स, वाई =एक्स, वाई =|एक्स|, वाई =एक्स 3, वाई =एक्स 4,वाई = 3√एक्स, मैंने देखा कि ये सभी ग्राफ अक्षों के सापेक्ष समानांतर अनुवाद के नियम के अनुसार बनाए गए हैं एक्सऔर आप.

द्विघात समीकरण को हल करने के उदाहरण का उपयोग करते हुए, हम यह निष्कर्ष निकाल सकते हैं कि आलेखीय विधि डिग्री n के समीकरणों पर भी लागू होती है।

समीकरणों को हल करने के लिए चित्रमय तरीके सुंदर और समझने योग्य हैं, लेकिन वे किसी भी समीकरण को हल करने की 100% गारंटी नहीं देते हैं। रेखांकन के प्रतिच्छेदन बिंदुओं के भुज अनुमानित हो सकते हैं।

9वीं कक्षा में और वरिष्ठ कक्षाओं में, मैं अभी भी अन्य कार्यों से परिचित होऊंगा। मुझे यह जानने में दिलचस्पी है कि क्या वे कार्य समानांतर अनुवाद के नियमों का पालन करते हैं, जब उनके रेखांकन की साजिश रचते हैं।

अगले साल मैं समीकरणों और असमानताओं की प्रणालियों के ग्राफिकल समाधान के मुद्दों पर भी विचार करना चाहता हूं।

साहित्य

1. बीजगणित। 7 वीं कक्षा। भाग 1. शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक / ए.जी. मोर्दकोविच। मॉस्को: मेनेमोसिन, 2007।

2. बीजगणित। 8 वीं कक्षा। भाग 1. शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक / ए.जी. मोर्दकोविच। मॉस्को: मेनेमोसिन, 2007।

3. बीजगणित। श्रेणी 9 भाग 1. शैक्षणिक संस्थानों के लिए पाठ्यपुस्तक / ए.जी. मोर्दकोविच। मॉस्को: मेनेमोसिन, 2007।

4. ग्लेज़र जी.आई. स्कूल में गणित का इतिहास। सातवीं-आठवीं कक्षा। - एम .: ज्ञानोदय, 1982।

5. जर्नल गणित 5 2009; नंबर 8 2007; नंबर 23 2008।

6. समीकरणों का ग्राफिक समाधान इंटरनेट साइट्स: Tol WIKI; स्टिमुल.बिज़/एन; wiki.iot.ru/images; berdsk.edu; पेग 3–6.htm।

विषय पर छात्रों का शोध कार्य:

"समस्याओं को हल करने में एक रैखिक कार्य का अनुप्रयोग"

"समस्या को हल करने के लिए एक रैखिक फ़ंक्शन ग्राफ़ का अनुप्रयोग"

MKOU "बोगुचार्स्काया माध्यमिक विद्यालय नंबर 1"

गणित में शोध कार्य।

विषय: "समस्याओं को हल करने के लिए एक रैखिक कार्य के ग्राफ का अनुप्रयोग"

7 "बी" वर्ग
प्रमुख: फोमेंको ओल्गा मिखाइलोवनास

बोगुचारी शहर

1. परिचय………………………………………………………… 2

2.मुख्य भाग………………………………………………………3-11

2.1 रैखिक फलन ग्राफ़ का उपयोग करके पाठ समस्याओं को हल करने की तकनीक

2.2 रेखांकन का उपयोग करके गति के लिए पाठ समस्याओं को हल करना

3. निष्कर्ष………………………………………………………… 11

4. साहित्य………………………………………………………………….12

परिचय

"बीजगणित। 7 वर्ग" उन कार्यों पर विचार करता है जिनमें, दिए गए कार्यक्रम के अनुसार, कई प्रश्नों का उत्तर देना आवश्यक है।

उदाहरण के लिए:

332 ग्रीष्मकालीन निवासी कार से घर से गांव गया था। उसने पहले राजमार्ग पर गाड़ी चलाई, और फिर एक देश की सड़क पर, धीमा करते हुए उसने ऐसा किया। ग्रीष्मकालीन निवासी के आंदोलन का कार्यक्रम चित्र में दिखाया गया है। प्रश्नों के उत्तर दें:

क) ग्रीष्मकालीन निवासी ने राजमार्ग के किनारे कितनी देर तक गाड़ी चलाई और उसने कितने किलोमीटर की दूरी तय की; सड़क के इस खंड पर कार की गति क्या थी;

बी) ग्रीष्मकालीन निवासी ने देश की सड़क पर कितनी देर तक गाड़ी चलाई और उसने कितने किलोमीटर की दूरी तय की; इस खंड में कार की गति क्या थी;

ग) ग्रीष्मकालीन निवासी ने घर से गाँव तक कितने समय तक यात्रा की?

साहित्य और इंटरनेट में इस विषय पर सामग्री की खोज के दौरान, मैंने अपने लिए पाया कि दुनिया में कई भौतिक, और यहां तक ​​​​कि सामाजिक और आर्थिक घटनाएं और प्रक्रियाएं एक रैखिक संबंध में हैं, लेकिन मैं आंदोलन पर बस गया, जैसा कि हमारे लिए सबसे परिचित और सभी के बीच लोकप्रिय। परियोजना में, मैंने शब्द समस्याओं का वर्णन किया और रैखिक फ़ंक्शन ग्राफ़ का उपयोग करके उन्हें कैसे हल किया जाए।

परिकल्पना:ग्राफ़ की सहायता से, आप न केवल किसी फ़ंक्शन के गुणों का एक दृश्य प्रतिनिधित्व प्राप्त कर सकते हैं, एक रैखिक फ़ंक्शन के गुणों और उसके विशेष रूप, प्रत्यक्ष आनुपातिकता से परिचित हो सकते हैं, बल्कि शब्द समस्याओं को भी हल कर सकते हैं।

मेरे शोध का उद्देश्यआंदोलन के लिए पाठ समस्याओं को हल करने में एक रैखिक फ़ंक्शन के ग्राफ़ के उपयोग का अध्ययन था। इन लक्ष्यों को प्राप्त करने के लिए निम्नलिखित कार्य:

रेखीय फलन ग्राफ़ का उपयोग करते हुए गति के लिए पाठ समस्याओं को हल करने के लिए कार्यप्रणाली का अध्ययन करना;

इस पद्धति का उपयोग करके गति की समस्याओं को हल करना सीखें;

रैखिक फलन ग्राफ़ का उपयोग करके समस्याओं को हल करने के फायदे और नुकसान के बारे में तुलनात्मक निष्कर्ष निकालें।

अध्ययन की वस्तु:रैखिक फ़ंक्शन ग्राफ।

शोध विधि:

सैद्धांतिक (अध्ययन और विश्लेषण), सिस्टम खोज, व्यावहारिक।

मुख्य हिस्सा।

अपने शोध में, मैंने अपनी पाठ्यपुस्तक में प्रस्तुत आंदोलन के कार्यों की एक चित्रमय व्याख्या देने का प्रयास करने का फैसला किया, फिर, अनुसूची के अनुसार, कार्य के प्रश्न का उत्तर दें। इस तरह के समाधान के लिए, मैंने पथ के एक हिस्से पर एक समान गति के साथ कार्य लिया। यह पता चला कि समीकरण का उपयोग करके सामान्य तरीके से कई समस्याओं को इस तरह हल किया जाता है। इस तकनीक का एकमात्र दोष यह है कि समस्या के प्रश्न का सही उत्तर प्राप्त करने के लिए, किसी को समन्वय अक्षों पर माप की इकाइयों के पैमाने का सही ढंग से चयन करने में सक्षम होना चाहिए। इस पैमाने के सही चुनाव में एक बड़ी भूमिका हल करने के अनुभव द्वारा निभाई जाती है। इसलिए, रेखांकन का उपयोग करके समस्याओं को हल करने की कला में महारत हासिल करने के लिए, मुझे उन पर बड़ी संख्या में विचार करना पड़ा।

एब्सिस्सा एक्सिस ओटी और ऑर्डिनेट एक्सिस ओएस के साथ कोऑर्डिनेट सिस्टम एसओटी सेट करें। ऐसा करने के लिए, समस्या की स्थिति के अनुसार, मूल का चयन करना आवश्यक है: वस्तु की गति की शुरुआत या कई वस्तुओं से, जो पहले चलना शुरू कर देती है या अधिक दूरी तय करती है, उसे चुना जाता है। भुज अक्ष पर, माप की इसकी इकाइयों में समय अंतराल को चिह्नित करें, और कोटि अक्ष पर, माप की इकाइयों के चयनित पैमाने में दूरी को चिह्नित करें।

समन्वय विमान पर बिंदुओं को कार्य के पैमाने के अनुसार चिह्नित किया जाना चाहिए, और रेखाएं सटीक रूप से खींची जानी चाहिए। समस्या के समाधान की सटीकता इस पर निर्भर करती है। इसलिए, समन्वय अक्षों पर विभाजनों के पैमाने को सफलतापूर्वक चुनना बहुत महत्वपूर्ण है: इसे इस तरह से चुना जाना चाहिए कि बिंदुओं के निर्देशांक अधिक सटीक रूप से निर्धारित किए जाते हैं और, यदि संभव हो तो, नोडल बिंदुओं पर स्थित होते हैं, अर्थात। निर्देशांक अक्षों के विभाजनों के चौराहों पर। कभी-कभी एब्सिस्सा अक्ष पर एक इकाई खंड के रूप में लेने के लिए उपयोगी होता है, कोशिकाओं की संख्या जो समय के संबंध में समस्या की स्थितियों का एक बहु है, और समन्वय अक्ष पर - कोशिकाओं की संख्या जो कई स्थितियों में से एक है दूरी के संबंध में समस्या का। उदाहरण के लिए, 12 मिनट के समय में 5 के गुणज में सेलों की संख्या चुनने की आवश्यकता होती है, क्योंकि 12 मिनट एक घंटे का पांचवां हिस्सा है।

ग्राफ़ का उपयोग करके आंदोलन के लिए पाठ समस्याओं को हल करना

उत्तर : 9 किमी.

समीकरण का उपयोग कर समाधान:

एक्स/12एच. - ए से बी तक का समय

एक्स/18एच. - पिछला समय

उत्तर: 9 किमी

कार्य 2. (यू.एन. मकरिचेव की पाठ्यपुस्तक "बीजगणित 7" में नंबर 156।)

हाईवे पर दो कारें समान गति से जा रही हैं। यदि पहला व्यक्ति गति को 10 किमी/घंटा बढ़ा देता है, और दूसरा उसे 10 किमी/घंटा कम कर देता है, तो पहला वाला 2 घंटे में उतना ही तय करेगा जितना कि दूसरा 3 घंटे में। कारें कितनी तेजी से जा रही हैं?

समीकरण का उपयोग कर समाधान:

मान लीजिए x किमी/घंटा कारों की गति है;

(x+10) और (x-10) क्रमशः वृद्धि और कमी के बाद गति;

2(x+10)=3(x-10)

उत्तर: 50 किमी/घंटा

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. आइए निर्देशांक तल sOt को भुज अक्ष Оt के साथ सेट करें, जिस पर हम गति के समय अंतराल को चिह्नित करते हैं, और निर्देशांक अक्ष Os, जिस पर हम वाहनों द्वारा तय की गई दूरी को चिह्नित करते हैं

2. चलो एब्सिस्सा अक्ष के साथ एक पैमाने पर विभाजन डालते हैं - 5 कोशिकाओं में एक घंटा (1 सेल में - 12 मिनट); हम y-अक्ष के अनुदिश विभाजन लागू करते हैं, लेकिन पैमाना निर्दिष्ट नहीं करते हैं।

3. आइए पहली कार I की गति की एक पंक्ति का निर्माण करें: एक बिंदु c . पर गति की शुरुआत

4. आइए दूसरी मशीन II की गति की रेखा का निर्माण करें: निर्देशांक के साथ बिंदु पर गति की शुरुआत (0; 0)। इसके बाद, हम तल पर एक मनमाना बिंदु (3;s 1) चिह्नित करते हैं, क्योंकि नई रफ्तार वाली कार 3 घंटे तक सड़क पर रही।

4. आइए कारों की गति निर्धारित करें v इसके परिवर्तन से पहले। आइए हम भुज 1 वाली रेखाओं पर स्थित बिंदुओं के निर्देशांकों के अंतर को चिह्न s द्वारा निरूपित करें। शर्त के अनुसार, यह खंड (10 + 10) किमी की लंबाई से मेल खाता है, क्योंकि उनमें से एक में गति कम हो गई, और दूसरे में गति में 10 किमी/घंटा की वृद्धि हुई। इसका मतलब यह है कि गति बदलने से पहले कारों की आवाजाही की रेखा I और II से समान दूरी पर होनी चाहिए और उनके बीच समन्वय विमान पर स्थित होनी चाहिए। अनुसूची के अनुसार, s \u003d 2cl। 20 किमी, v = 5 कोशिकाओं से मेल खाती है, इसलिए हम अनुपात v = 50 किमी / घंटा हल करते हैं।

उत्तर: 50 किमी/घंटा।

टास्क 3

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

संदर्भ बिंदु जेट्टी M . है

बिंदु N (0; 162) को चिह्नित करें।

उत्तर: 2 घंटे 20 मिनट।

समीकरण का उपयोग कर समाधान:

162 -45(x+0.75)-36x=0

162-45x - 33.75 -36x = 0

81x=128.25

2)

उत्तर: 2 घंटे 20 मिनट।

कार्य 4.

एक साइकिल चालक ने बिंदु A को छोड़ दिया। उसी समय, उसके बाद, एक मोटरसाइकिल चालक 16 किमी/घंटा बिंदु B को छोड़ देता है, जो A से 20 किमी दूर है। साइकिल सवार 12 किमी/घंटा की गति से यात्रा कर रहा था। बिंदु A से कितनी दूरी पर मोटरसाइकिल सवार साइकिल सवार से आगे निकल जाएगा?

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. आइए निर्देशांक विमान sOt को भुज अक्ष ओटी के साथ सेट करें, जिस पर हम गति के समय अंतराल को चिह्नित करते हैं, और y-अक्ष Os, जिस पर हम मोटरसाइकिल और साइकिल चालक द्वारा तय की गई दूरी को चिह्नित करेंगे

2. आइए एक पैमाने पर विभाजन बनाएं: y-अक्ष के साथ - 2 कोशिकाओं में 8 किमी; भुज के साथ - 2 कोशिकाओं में - 1h।

3. आइए मोटरसाइकिल चालक II के आंदोलन की एक पंक्ति बनाएं: हम निर्देशांक बी (0; 0) के मूल में उसके आंदोलन की शुरुआत को चिह्नित करते हैं। मोटरसाइकिल चालक 16 किमी/घंटा की गति से गाड़ी चला रहा था, जिसका अर्थ है कि सीधी रेखा II को निर्देशांक (1; 16) के साथ बिंदु से गुजरना होगा।

4. आइए एक साइकिल चालक I के लिए गति की एक रेखा बनाएं: इसकी शुरुआत बिंदु A (0; 20) पर होगी, क्योंकि बिंदु B, बिंदु A से 20 किमी की दूरी पर स्थित है, और वह उसी समय मोटरसाइकिल से चला गया। साइकिल चालक 12 किमी/घंटा की गति से यात्रा कर रहा था, जिसका अर्थ है कि रेखा I को निर्देशांक (1; 32) के साथ बिंदु से गुजरना होगा।

5. खोजें P (5; 80) - लाइनों I और II के चौराहे का बिंदु, एक मोटरसाइकिल और एक साइकिल चालक की गति को दर्शाता है: इसका कोटि बिंदु B से दूरी दिखाएगा, जिस पर मोटर साइकिल चालक साइकिल चालक के साथ पकड़ लेगा .

P(5; 80) |=s = 80, |=80 - 20 = 60(किमी) - बिंदु A से दूरी जिस पर मोटरसाइकिल साइकिल चालक के साथ पकड़ लेगी।

उत्तर : 60 किमी.

समीकरण का उपयोग कर समाधान:

मान लीजिए x किमी बिंदु A से बैठक बिंदु तक की दूरी है

x /12 साइकिल चालक समय

(x +20)/16 मोटरसाइकिल चालक का समय

एक्स /12=(एक्स +20)/16

16x=12x+240

4x=240

एक्स = 60

उत्तर: 60 किमी

कार्य 5.

शहरों के बीच की दूरी एक मोटर साइकिल चालक द्वारा 2 घंटे में और एक साइकिल चालक द्वारा 5 घंटे में तय की जाती है। एक साइकिल चालक की गति मोटरसाइकिल की गति से 18 किमी/घंटा कम है। साइकिल चालक और मोटरसाइकिल चालक की गति और शहरों के बीच की दूरी का पता लगाएं।

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. निर्देशांक विमान sOt को भुज अक्ष ओटी के साथ सेट करें, जिस पर हम गति के समय अंतराल और y-अक्ष Os को चिह्नित करते हैं, जिस पर हम दूरी को चिह्नित करते हैं।

2. 1 घंटे के लिए 2 कक्षों में भुज अक्ष के अनुदिश विभाजन करते हैं। आइए बिना विभाजन के दूरी को कोटि अक्ष के अनुदिश छोड़ दें।

3. आइए साइकिल चालक की गति I की रेखा 5 घंटे में और मोटरसाइकिल चालक II की गति की रेखा 2 घंटे में खींचते हैं। दोनों पंक्तियों के अंत में एक ही कोटि होनी चाहिए।

4. आइए रेखा I और II के बीच में भुज 1 वाला एक खंड बनाएं। इस खंड की लंबाई 18 किमी के बराबर दूरी को दर्शाती है। ड्राइंग से हमें पता चलता है कि 3 सेल 18 किमी के बराबर हैं, जिसका अर्थ है कि 1 सेल में 6 किमी हैं।

5. फिर, अनुसूची के अनुसार, हम निर्धारित करते हैं कि साइकिल चालक की गति 12 किमी / घंटा है, मोटरसाइकिल की गति 30 किमी / घंटा है, शहरों के बीच की दूरी 60 किमी है।

समीकरण का उपयोग कर समाधान:

मान लीजिए x किमी/घंटा साइकिल चालक की गति है, तो (x +18) किमी/घंटा मोटरसाइकिल की गति है

2(x+18)=5x

2x +36=5x

एक्स = 12

2) 12+18=30(किमी/घंटा) सवार गति

3) (किमी) शहरों के बीच की दूरी

उत्तर: 12 किमी/घंटा; 30 किमी/घंटा; 60 किमी

उत्तर : 60 किमी.

कार्य 6.

एक नाव नदी के किनारे 3 घंटे 20 मिनट में 30 किमी की दूरी तय करती है, और 4 घंटे में धारा के विपरीत 28 किमी की दूरी तय करती है। नाव 1.5 घंटे में झील को कितनी दूरी तय करेगी?

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. निर्देशांक तल sOt को भुज अक्ष ओटी के साथ सेट करें, जिस पर हम गति के समय अंतराल को चिह्नित करते हैं, और y-अक्ष Os, जिस पर हम नाव द्वारा तय की गई दूरी को चिह्नित करते हैं

2. आइए एक पैमाने पर विभाजन बनाएं: y-अक्ष के साथ - दो कोशिकाओं में 4 किमी; एब्सिस्सा अक्ष के साथ - 6 कोशिकाओं में - 1 घंटा (1 सेल में - 10 मिनट), क्योंकि समस्या की स्थिति के अनुसार मिनटों में समय दिया जाता है।

3. आइए नदी I के साथ नाव की गति की एक रेखा बनाएं: रेखा की शुरुआत निर्देशांक (0; 0) के साथ बिंदु पर होगी। नाव 3 घंटे और 20 मिनट में 30 किमी की दूरी तय करती है, जिसका अर्थ है कि रेखा को समन्वय (; 30) के साथ बिंदु से गुजरना होगा, क्योंकि 3 घंटे 20 मिनट। = एच.

4. आइए नदी II की धारा के विरुद्ध नाव की गति की एक रेखा बनाएँ: हम एक निर्देशांक (0; 0) के साथ एक बिंदु पर गति की शुरुआत करते हैं। नाव 4 घंटे में 28 किमी की दूरी तय करती है, जिसका अर्थ है कि गति की रेखा को निर्देशांक (4; 28) के साथ बिंदु से गुजरना होगा।

5. चलो झील पर नाव की गति की रेखा का निर्माण करें: हम बिंदु पर आंदोलन की शुरुआत निर्देशांक (0; 0) के साथ करेंगे। नाव की अपनी गति की रेखा नदी के किनारे नाव की गति की रेखाओं के बीच समान दूरी पर स्थित होनी चाहिए। इसका मतलब है कि हमें खंड को विभाजित करना होगा, जिसमें नदी के साथ आंदोलन की रेखाओं के बीच सभी बिंदुओं को एब्सिसा 1 के साथ आधा में विभाजित करना होगा और इसके मध्य को चिह्नित करना होगा। (0; 0) से इस चिह्नित बिंदु के माध्यम से हम एक किरण खींचेंगे, जो झील के साथ गति की रेखा होगी।

6. समस्या की स्थिति के अनुसार, झील पर नाव द्वारा 1.5 घंटे में तय की गई दूरी का पता लगाना आवश्यक है, जिसका अर्थ है कि हमें इस रेखा पर एब्सिसा टी \u003d 1.5 के साथ बिंदु की कोटि निर्धारित करनी चाहिए, | \u003d s \u003d 12, | \u003d 12 किमी 1,5 घंटा।

उत्तर : 12 किमी.

समीकरणों की एक प्रणाली का उपयोग कर समाधान:

मान लीजिए x किमी/घंटा झील की गति है और y किमी/घंटा नदी की गति है

उत्तर : 12 किमी.

टास्क 7.

नाव धारा के विपरीत 26 किमी के समान समय में नदी के किनारे 34 किमी की यात्रा करती है। नाव की स्वयं की गति 15 किमी/घंटा है। नदी की गति ज्ञात कीजिए।

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. निर्देशांक विमान sOt को भुज अक्ष ओटी के साथ सेट करें, जिस पर हम गति के समय अंतराल और y-अक्ष Os को चिह्नित करते हैं, जिस पर हम नाव द्वारा तय की गई दूरी को चिह्नित करते हैं।

2. आइए एक पैमाने पर विभाजन बनाएं: y-अक्ष के साथ - 1 सेल 1 किमी में; एब्सिस्सा अक्ष पर, हम बिना विभाजन के समय छोड़ते हैं।

3. आइए नदी के किनारे नाव की गति की रेखा I को 0 किमी से 34 किमी के बिंदु तक बनाएं: रेखा की शुरुआत निर्देशांक (0; 0) के साथ बिंदु पर होगी। दूसरा निर्देशांक होगा (x ; 34)।

4. नदी की धारा के विरुद्ध 0 किमी से 26 किमी के बिंदु तक नाव की गति की एक पंक्ति II का निर्माण करें: रेखा की शुरुआत निर्देशांक (0; 0) के साथ बिंदु पर होगी। दूसरा निर्देशांक होगा ( एक्स; 26)।

5. गति I और II की दो रेखाओं के बीच एक ही भुज के साथ सभी बिंदुओं से युक्त एक मनमाना खंड के मध्य से मूल (0; 0) के माध्यम से एक किरण III बनाएं। यह बीम नाव की अपनी गति को प्रतिबिंबित करेगा, जैसे नाव की अपनी गति नदी के अपस्ट्रीम और डाउनस्ट्रीम 2 गति का अंकगणितीय औसत है। परिणामी बीम पर, हम 15 के कोटि वाला एक बिंदु पाते हैं, क्योंकि नाव की अपनी गति 15 किमी/घंटा है। पाए गए बिंदु का भुज 1 घंटे के विभाजन के अनुरूप होगा।

6. नदी की गति ज्ञात करने के लिए, रेखा III से रेखा II तक भुज 1 वाले खंड की लंबाई ज्ञात करना पर्याप्त है। नदी की गति 2 किमी/घंटा है।

उत्तर: 2 किमी/घंटा

समीकरण का उपयोग कर समाधान:

नदी की गति x किमी/घंटा

34 / (15 + x) \u003d 26 / (15-x) अनुपात को हल करने पर, हम प्राप्त करते हैं:

उत्तर: 2 किमी/घंटा

निष्कर्ष।

लाभ:

कार्यों को संक्षेप में लिखा जा सकता है;

नुकसान:

साहित्य।

1. मकारिचेव यू। एन।, मिंड्युक एन। जी।, नेशकोव के। आई।, सुवोरोवा एस। बी।, बीजगणित: शैक्षणिक संस्थानों की 7 वीं कक्षा के लिए एक पाठ्यपुस्तक, "प्रोवेशचेनी", एम।, 2000।

2. बुलिनिन वी।, पाठ समस्याओं को हल करने में ग्राफिकल विधियों का उपयोग, शैक्षिक और पद्धतिगत समाचार पत्र "गणित", संख्या 14, 2005।

3. ज़्वाविच एल.आई. ग्रेड 7 के लिए बीजगणित पर उपदेशात्मक सामग्री।

दस्तावेज़ सामग्री देखें
"शब्द"

7वीं कक्षा में बीजगणित के पाठों में, मैं “रैखिक फलन” विषय से परिचित हुआ। रैखिक कार्यों के रेखांकन की पारस्परिक व्यवस्था। मैंने सीखा कि कैसे एक रेखीय फलन के रेखांकन का निर्माण किया जाता है, इसके गुणों को सीखा, यह सीखा कि दिए गए सूत्रों का उपयोग करके ग्राफ़ की सापेक्ष स्थिति कैसे निर्धारित की जाती है। मैंने देखा कि पाठ्यपुस्तक में यू.एन. मकर्यचेव द्वारा

"बीजगणित। 7 वर्ग" उन कार्यों पर विचार करता है जिनमें, दिए गए कार्यक्रम के अनुसार, कई प्रश्नों का उत्तर देना आवश्यक है। ऐसे कार्य का एक उदाहरण स्लाइड पर प्रस्तुत किया गया है।

दी गई अनुसूची के अनुसार, यह निर्धारित किया जा सकता है कि

और मेरे पास एक सवाल था, क्या आंदोलन के लिए समस्याओं को हल करना या समीकरणों का उपयोग करना संभव नहीं है, लेकिन इसके लिए एक रैखिक फ़ंक्शन के ग्राफिक्स का उपयोग करना संभव है?

स्लाइड पर परिकल्पना, लक्ष्य और उद्देश्य प्रस्तुत किए गए हैं

अपने शोध में, मैंने अपनी पाठ्यपुस्तक में प्रस्तुत आंदोलन के कार्यों की एक चित्रमय व्याख्या देने का प्रयास करने का फैसला किया, फिर, अनुसूची के अनुसार, कार्य के प्रश्न का उत्तर दें। इस तरह के समाधान के लिए, मैंने पथ के एक हिस्से पर एक समान गति के साथ कार्य लिया।

यह पता चला कि इस तरह से कई समस्याओं का समाधान किया जाता है। इस तकनीक का एकमात्र दोष यह है कि समस्या के प्रश्न का सही उत्तर प्राप्त करने के लिए, किसी को समन्वय अक्षों पर माप की इकाइयों के पैमाने का सही ढंग से चयन करने में सक्षम होना चाहिए। इस पैमाने के सही चुनाव में एक बड़ी भूमिका हल करने के अनुभव द्वारा निभाई जाती है। इसलिए, रेखांकन का उपयोग करके समस्याओं को हल करने की कला में महारत हासिल करने के लिए, मुझे उन पर बड़ी संख्या में विचार करना पड़ा।

रैखिक फ़ंक्शन ग्राफ़ का उपयोग करके पाठ समस्याओं को हल करने की एक तकनीक।

रैखिक फ़ंक्शन ग्राफ़ का उपयोग करके टेक्स्ट समस्या को हल करने के लिए, आपको यह करना होगा:

समन्वय प्रणाली सेट करें ऐसा करने के लिए, समस्या की स्थिति के अनुसार, मूल का चयन करना आवश्यक है: वस्तु की गति की शुरुआत या कई वस्तुओं से, जो पहले चलना शुरू कर दिया या अधिक दूरी तय की, उसे चुना जाता है . भुज अक्ष पर, माप की इसकी इकाइयों में समय अंतराल को चिह्नित करें, और कोटि अक्ष पर, माप की इकाइयों के चयनित पैमाने में दूरी को चिह्नित करें।

सीधी रेखाओं के कम से कम दो बिंदुओं के निर्देशांक के माध्यम से समस्या कथन में निर्दिष्ट प्रत्येक वस्तु की गति की रेखाएँ खींचिए। आमतौर पर किसी वस्तु की गति उसके आंदोलन की शुरुआत से एक इकाई समय में दूरी के पारित होने के बारे में जानकारी देती है। यदि वस्तु बाद में गति करना शुरू करती है, तो इसकी गति का प्रारंभिक बिंदु x-अक्ष के अनुदिश मूल बिंदु के दाईं ओर दी गई इकाइयों की संख्या द्वारा स्थानांतरित कर दिया जाता है। यदि वस्तु एक निश्चित दूरी से संदर्भ बिंदु से दूर किसी स्थान से गति करना शुरू कर देती है, तो उसके आंदोलन की शुरुआत का बिंदु y-अक्ष के साथ ऊपर की ओर विस्थापित हो जाता है।

समन्वय तल पर कई वस्तुओं का मिलन बिंदु उनके आंदोलन को दर्शाने वाली रेखाओं के प्रतिच्छेदन बिंदु द्वारा इंगित किया जाता है, जिसका अर्थ है कि इस बिंदु के निर्देशांक बैठक के समय और मूल स्थान से बैठक स्थान की दूरी के बारे में जानकारी प्रदान करते हैं।

दो वस्तुओं की गति की गति में अंतर खंड की लंबाई से निर्धारित होता है, जिसमें इन वस्तुओं की गति की रेखाओं के बीच स्थित एब्सिसा 1 के साथ सभी बिंदु शामिल होते हैं।

समन्वय विमान पर बिंदुओं को कार्य के पैमाने के अनुसार चिह्नित किया जाना चाहिए, और रेखाएं सटीक रूप से खींची जानी चाहिए। समस्या के समाधान की सटीकता इस पर निर्भर करती है।

समस्या 1. (यू.एन. मकारिचेव की पाठ्यपुस्तक "बीजगणित 7" में संख्या 673।)

एक साइकिल चालक ने पथ AB को 12 किमी/घंटा की गति से तय किया। वापस लौटते हुए, उसने 18 किमी/घंटा की गति विकसित की और वापस रास्ते में A से B के रास्ते की तुलना में 15 मिनट कम खर्च किया। A से B तक कितने किलोमीटर की दूरी तय की।

समीकरण का उपयोग कर समाधान:

मान लीजिए x किमी A से B की दूरी है।

एक्स/12एच. - ए से बी तक का समय

एक्स/18एच. - पिछला समय

चूंकि उसने वापसी में 15 मिनट कम समय बिताया, इसलिए हम समीकरण की रचना करेंगे

उत्तर: 9 किमी

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. आइए हम निर्देशांक तल sOtc को भुज अक्ष Ot के साथ सेट करें, जिस पर हम गति के समय अंतराल और y-अक्ष Os को चिह्नित करते हैं, जिस पर हम दूरी को चिह्नित करते हैं।

2. आइए एक पैमाने पर विभाजन बनाएं: y-अक्ष के साथ - एक सेल में 3 किमी; एब्सिस्सा अक्ष के साथ - 4 कोशिकाओं में एक घंटा (1 सेल में - 15 मिनट)।

3. आइए वहां आंदोलन की एक पंक्ति बनाएं: आंदोलन की शुरुआत को एक बिंदु (0; 0) के साथ चिह्नित करें। साइकिल चालक 12 किमी/घंटा की गति से यात्रा कर रहा था, जिसका अर्थ है कि सीधी रेखा को बिंदु (1; 12) से होकर गुजरना होगा।

4. चलो वापस आंदोलन की एक पंक्ति का निर्माण करें: रेखा के अंत को एक बिंदु (; 0) के साथ चिह्नित करें, क्योंकि साइकिल सवार ने वापसी यात्रा में 15 मिनट कम समय बिताया। वह 18 किमी/घंटा की गति से गाड़ी चला रहा था, जिसका अर्थ है कि रेखा के अगले बिंदु पर निर्देशांक (;18) है।

5. नोट (; 9) - रेखाओं का प्रतिच्छेदन बिंदु: इसकी कोटि दूरी दर्शाएगी: s = 9

उत्तर : 9 किमी.

टास्क 2 (यू.एन. मकारिचेव की पाठ्यपुस्तक "बीजगणित 7" में संख्या 757)

पियर्स एम और एन के बीच की दूरी 162 किमी है। एक मोटर जहाज घाट M से 45 किमी/घंटा की गति से प्रस्थान करता है। 45 मिनट के बाद, एक अन्य मोटर जहाज घाट N से उसकी ओर चला, जिसकी गति 36 किमी/घंटा है। वे पहले जहाज के प्रस्थान के कितने घंटे बाद मिलेंगे?

समीकरण का उपयोग कर समाधान:

माना x घंटे में एक मीटिंग है

162 -45(x+0.75)-36x=0

162-45x - 33.75 -36x = 0

81x=128.25

2)

उत्तर: 2 घंटे 20 मिनट।

रैखिक फ़ंक्शन ग्राफ़ के साथ हल करना:

1. निर्देशांक तल sOt को भुज अक्ष ओटी के साथ सेट करें, जिस पर हम गति के समय अंतराल को चिह्नित करते हैं, और y-अक्ष Os, जिस पर

घाट M से घाट N की दूरी 162 किमी के बराबर नोट करें। शुरुवात

संदर्भ बिंदु जेट्टी M . है

2. आइए एक पैमाने पर विभाजन बनाएं: y-अक्ष के साथ - दो कोशिकाओं में 18 किमी; एब्सिस्सा अक्ष के साथ - 6 कोशिकाओं में एक घंटा (1 सेल में - 10 मिनट।), चूंकि कार्य की स्थिति मिनटों में समय निर्दिष्ट करती है।

बिंदु N (0; 162) को चिह्नित करें।

3. आइए पहले जहाज I की गति की रेखा का निर्माण करें: इसकी गति की शुरुआत निर्देशांक (0; 0) के साथ बिंदु पर होगी। पहला जहाज 45 किमी / घंटा की गति से रवाना हुआ, जिसका अर्थ है कि सीधी रेखा को निर्देशांक (1; 45) के साथ बिंदु से गुजरना होगा।

4. आइए दूसरे जहाज II की गति की रेखा का निर्माण करें: आंदोलन की शुरुआत बिंदु c . पर होगी

निर्देशांक (; 162), क्योंकि वह बिंदु N से निकल गया, M से 162 किमी दूर, 45 मिनट। पहले की तुलना में बाद में, और 45 मि. \u003d ज। दूसरा जहाज 36 किमी / घंटा की गति से रवाना हुआ, जिसका अर्थ है कि सीधी रेखा को बिंदु (; 126) से गुजरना होगा, क्योंकि दूसरा जहाज बिंदु M: 162 - 36 \u003d की दिशा में चला गया था। 126 (किमी)।

5. रेखा I और II का प्रतिच्छेदन बिंदु बिंदु A (; 108) है। बिंदु का भुज उस समय को दर्शाता है जिसके बाद, पहले जहाज के प्रस्थान के बाद, वे मिले: t =, |=h = 2h20min। - पहले जहाज के जाने के बाद दो जहाजों के मिलने का समय।

उत्तर: 2 घंटे 20 मिनट।

निष्कर्ष।

अध्ययन के अंत में, मैं ग्राफिक रूप से समस्याओं को हल करने के फायदे और नुकसान की पहचान करने में सक्षम था।

लाभ:

कार्यों को संक्षेप में लिखा जा सकता है;

छोटी संख्याओं के साथ काम करना काफी आसान है।

नुकसान:

बड़ी संख्या के साथ काम करना मुश्किल है।

प्रस्तुति सामग्री देखें
"परियोजना"

प्रथम स्तर

फ़ंक्शन ग्राफ़ का उपयोग करके समीकरणों, असमानताओं, प्रणालियों को हल करना। विजुअल गाइड (2019)

कई कार्य जिनका उपयोग हम विशुद्ध रूप से बीजगणितीय रूप से गणना करने के लिए करते हैं, उन्हें बहुत आसान और तेज़ी से हल किया जा सकता है, फ़ंक्शन ग्राफ़ का उपयोग करने से हमें इसमें मदद मिलेगी। आप कहते हैं "ऐसा कैसे?" कुछ आकर्षित करने के लिए, और क्या आकर्षित करना है? मेरा विश्वास करो, कभी-कभी यह अधिक सुविधाजनक और आसान होता है। हम शुरू करें? आइए समीकरणों से शुरू करें!

समीकरणों का आलेखीय हल

रैखिक समीकरणों का आलेखीय हल

जैसा कि आप पहले से ही जानते हैं, एक रैखिक समीकरण का आलेख एक सीधी रेखा है, इसलिए इस प्रकार का नाम। रैखिक समीकरणों को बीजगणितीय रूप से हल करना काफी आसान है - हम सभी अज्ञात को समीकरण के एक तरफ स्थानांतरित करते हैं, जो कुछ भी हम जानते हैं - दूसरे को, और वॉयला! हमें जड़ मिल गई है। अब मैं आपको दिखाऊंगा कि यह कैसे करना है ग्राफिक तरीका।

तो आपके पास एक समीकरण है:

इसे कैसे हल करें?
विकल्प 1, और सबसे आम अज्ञात को एक तरफ ले जाना है, और दूसरे को जाना जाता है, हमें मिलता है:

और अब हम निर्माण कर रहे हैं। तुम्हें क्या मिला?

आपको क्या लगता है कि हमारे समीकरण की जड़ क्या है? यह सही है, रेखांकन के प्रतिच्छेदन बिंदु का समन्वय:

हमारा जवाब है

यही ग्राफिक समाधान का संपूर्ण ज्ञान है। जैसा कि आप आसानी से देख सकते हैं, हमारे समीकरण का मूल एक संख्या है!

जैसा कि मैंने ऊपर कहा, यह सबसे आम विकल्प है, बीजीय समाधान के करीब, लेकिन आप इसे दूसरे तरीके से हल कर सकते हैं। एक वैकल्पिक समाधान पर विचार करने के लिए, आइए अपने समीकरण पर वापस आते हैं:

इस बार हम किसी भी चीज़ को अगल-बगल से नहीं घुमाएंगे, बल्कि सीधे ग्राफ़ बनाएंगे, जैसे वे अभी हैं:

बनाया? नज़र!

इस बार क्या उपाय है? ठीक है। वही ग्राफ़ के प्रतिच्छेदन बिंदु का निर्देशांक है:

और, फिर से, हमारा जवाब है।

जैसा कि आप देख सकते हैं, रैखिक समीकरणों के साथ, सब कुछ बेहद सरल है। कुछ अधिक जटिल विचार करने का समय आ गया है... उदाहरण के लिए, द्विघात समीकरणों का ग्राफिक समाधान।

द्विघात समीकरणों का आलेखीय हल

तो, अब द्विघात समीकरण को हल करना शुरू करते हैं। मान लीजिए कि आपको इस समीकरण की जड़ें खोजने की जरूरत है:

बेशक, अब आप विवेचक के माध्यम से या विएटा प्रमेय के अनुसार गिनना शुरू कर सकते हैं, लेकिन कई तंत्रिकाएं गुणा या वर्ग करते समय गलती करती हैं, खासकर यदि उदाहरण बड़ी संख्या के साथ है, और, जैसा कि आप जानते हैं, आपके पास एक नहीं होगा परीक्षा में कैलकुलेटर ... इसलिए, आइए इस समीकरण को हल करते समय थोड़ा आराम करने और ड्रा करने का प्रयास करें।

आलेखीय रूप से, इस समीकरण के हल विभिन्न तरीकों से खोजे जा सकते हैं। विभिन्न विकल्पों पर विचार करें, और आप स्वयं चुनेंगे कि आपको कौन सा सबसे अच्छा लगता है।

विधि 1. सीधे

हम इस समीकरण के अनुसार सिर्फ एक परवलय बनाते हैं:

इसे जल्दी करने के लिए, मैं आपको एक छोटा सा संकेत दूंगा: परवलय के शीर्ष का निर्धारण करके निर्माण शुरू करना सुविधाजनक है।निम्नलिखित सूत्र परवलय के शीर्ष के निर्देशांक निर्धारित करने में मदद करेंगे:

आप कहते हैं "रुको! के लिए सूत्र विवेचक को खोजने के सूत्र के समान है "हाँ, यह है, और यह अपनी जड़ों को खोजने के लिए एक परवलय का निर्माण" प्रत्यक्ष "का एक बड़ा नुकसान है। हालांकि, चलिए अंत तक गिनती करते हैं, और फिर मैं आपको दिखाऊंगा कि इसे बहुत (बहुत!) आसान कैसे बनाया जाए!

क्या आपने गिनती की? परवलय के शीर्ष के निर्देशांक क्या हैं? आइए इसे एक साथ समझें:

बिल्कुल वही जवाब? बहुत अच्छा! और अब हम पहले से ही शीर्ष के निर्देशांक जानते हैं, और एक परवलय बनाने के लिए, हमें और अधिक ... अंक चाहिए। आपको क्या लगता है, हमें कितने न्यूनतम अंक चाहिए? सही ढंग से, .

आप जानते हैं कि एक परवलय अपने शीर्ष के प्रति सममित होता है, उदाहरण के लिए:

तदनुसार, हमें परवलय की बाईं या दाईं शाखा के साथ दो और बिंदुओं की आवश्यकता है, और भविष्य में हम इन बिंदुओं को विपरीत दिशा में सममित रूप से प्रतिबिंबित करेंगे:

हम अपने परवलय में लौटते हैं। हमारे मामले के लिए, बिंदु। हमें क्रमशः दो और अंक चाहिए, क्या हम सकारात्मक अंक ले सकते हैं, लेकिन क्या हम नकारात्मक ले सकते हैं? आपके लिए सबसे अच्छे अंक क्या हैं? मेरे लिए सकारात्मक लोगों के साथ काम करना अधिक सुविधाजनक है, इसलिए मैं और के साथ गणना करूंगा।

अब हमारे पास तीन बिंदु हैं, और हम अपने शीर्ष के बारे में अंतिम दो बिंदुओं को दर्शाकर आसानी से अपना परवलय बना सकते हैं:

आपको क्या लगता है कि समीकरण का हल क्या है? यह सही है, जिन बिंदुओं पर, वह है, और। क्योंकि।

और अगर हम ऐसा कहते हैं, तो इसका मतलब है कि यह भी बराबर होना चाहिए, या।

अभी-अभी? हमने आपके साथ समीकरण को एक जटिल चित्रमय तरीके से हल करना समाप्त कर दिया है, या और भी बहुत कुछ होगा!

बेशक, आप हमारे उत्तर को बीजगणितीय रूप से देख सकते हैं - आप वियत प्रमेय या विभेदक के माध्यम से जड़ों की गणना कर सकते हैं। तुम्हें क्या मिला? यह वही? आप समझ सकते हैं! आइए अब एक बहुत ही सरल आलेखीय समाधान देखते हैं, मुझे विश्वास है कि आपको यह बहुत पसंद आएगा!

विधि 2. कई कार्यों में विभाजित करें

आइए सब कुछ लेते हैं, हमारा समीकरण: , लेकिन हम इसे थोड़ा अलग तरीके से लिखते हैं, अर्थात्:

क्या हम इसे इस तरह लिख सकते हैं? हम कर सकते हैं, क्योंकि परिवर्तन समतुल्य है। आइए आगे देखें।

आइए दो कार्यों को अलग-अलग बनाएं:

1. - ग्राफ एक साधारण परवलय है, जिसे आप सूत्रों का उपयोग करके शीर्ष को परिभाषित किए बिना और अन्य बिंदुओं को निर्धारित करने के लिए एक तालिका बनाए बिना भी आसानी से बना सकते हैं।
2. - ग्राफ एक सीधी रेखा है, जिसे आप कैलकुलेटर का सहारा लिए बिना मूल्यों का अनुमान लगाकर और अपने सिर में आसानी से बना सकते हैं।

बनाया? मुझे जो मिला है उसकी तुलना करें:

क्या आपको लगता है कि में इस मामले मेंसमीकरण की जड़ें हैं? सही ढंग से! निर्देशांक जिसके द्वारा दो ग्राफों को पार करके प्राप्त किया जाता है, अर्थात्:

तदनुसार, इस समीकरण का हल है:

आपका क्या कहना है? सहमत हूँ, यह समाधान विधि पिछले एक की तुलना में बहुत आसान है और विवेचक के माध्यम से जड़ों की तलाश करने से भी आसान है! यदि ऐसा है, तो निम्न समीकरण को हल करने के लिए इस विधि का प्रयास करें:

तुम्हें क्या मिला? आइए हमारे चार्ट की तुलना करें:

रेखांकन दिखाते हैं कि उत्तर हैं:

क्या आप संभाल पाओगे? बहुत अच्छा! अब आइए समीकरणों को थोड़ा और जटिल देखें, अर्थात् मिश्रित समीकरणों का समाधान, अर्थात्, विभिन्न प्रकार के कार्यों वाले समीकरण।

मिश्रित समीकरणों का आलेखीय हल

आइए अब निम्नलिखित को हल करने का प्रयास करें:

बेशक, आप सब कुछ एक सामान्य हर में ला सकते हैं, परिणामी समीकरण की जड़ों का पता लगा सकते हैं, जबकि ओडीजेड को ध्यान में रखना नहीं भूलते हैं, लेकिन फिर से, हम इसे ग्राफिक रूप से हल करने का प्रयास करेंगे, जैसा कि हमने पिछले सभी मामलों में किया था।

इस बार आइए निम्नलिखित 2 ग्राफ़ बनाते हैं:

1. - ग्राफ एक अतिपरवलय है
2. - एक ग्राफ एक सीधी रेखा है जिसे आप कैलकुलेटर का सहारा लिए बिना भी मूल्यों का अनुमान लगाकर और अपने सिर में आसानी से बना सकते हैं।

समझना? अब निर्माण शुरू करें।

यहाँ मेरे साथ क्या हुआ है:

इस तस्वीर को देखकर, हमारे समीकरण की जड़ें क्या हैं?

यह सही है, और। यहाँ पुष्टि है:

हमारी जड़ों को समीकरण में जोड़ने का प्रयास करें। हो गई?

ठीक है! सहमत हूं, ऐसे समीकरणों को ग्राफिक रूप से हल करना खुशी की बात है!

समीकरण को रेखांकन द्वारा स्वयं हल करने का प्रयास करें:

मैं आपको एक संकेत देता हूं: समीकरण के हिस्से को दाईं ओर ले जाएं ताकि दोनों पक्षों के पास निर्माण करने के लिए सबसे सरल कार्य हों। संकेत मिला? कार्यवाही करना!

अब देखते हैं कि आपको क्या मिला:

क्रमश:

1. - घन परवलय।
2. - एक साधारण सीधी रेखा।

खैर, हम निर्माण कर रहे हैं:

जैसा कि आपने लंबे समय तक लिखा है, इस समीकरण का मूल है -।

इतनी बड़ी संख्या में उदाहरणों को हल करने के बाद, मुझे यकीन है कि आपने महसूस किया है कि आप कैसे आसानी से और जल्दी से समीकरणों को ग्राफिक रूप से हल कर सकते हैं। यह पता लगाने का समय है कि इस तरह से सिस्टम को कैसे हल किया जाए।

सिस्टम का ग्राफिक समाधान

सिस्टम का ग्राफिकल सॉल्यूशन अनिवार्य रूप से समीकरणों के ग्राफिकल सॉल्यूशन से अलग नहीं है। हम दो रेखांकन भी बनाएंगे, और उनके प्रतिच्छेदन बिंदु इस प्रणाली की जड़ें होंगे। एक ग्राफ एक समीकरण है, दूसरा ग्राफ एक और समीकरण है। सब कुछ बेहद सरल है!

आइए रैखिक समीकरणों की सरलतम - हल करने वाली प्रणालियों से शुरू करें।

रैखिक समीकरणों को हल करने वाली प्रणाली

मान लें कि हमारे पास निम्न प्रणाली है:

शुरू करने के लिए, हम इसे इस तरह से रूपांतरित करेंगे कि बाईं ओर सब कुछ है जो जुड़ा हुआ है, और दाईं ओर - जो जुड़ा हुआ है। दूसरे शब्दों में, हम इन समीकरणों को हमारे लिए सामान्य रूप में एक फ़ंक्शन के रूप में लिखते हैं:

और अब हम केवल दो सीधी रेखाएँ बनाते हैं। हमारे मामले में समाधान क्या है? सही ढंग से! उनके चौराहे का बिंदु! और यहां आपको बहुत सावधान रहने की जरूरत है! सोचो क्यों? मैं आपको एक संकेत देता हूँ: हम एक प्रणाली के साथ काम कर रहे हैं: सिस्टम में दोनों हैं, और... संकेत मिला?

ठीक है! सिस्टम को हल करते समय, हमें दोनों निर्देशांकों को देखना चाहिए, और न केवल समीकरणों को हल करते समय! एक और महत्वपूर्ण बिंदु यह है कि उन्हें सही ढंग से लिखें और भ्रमित न हों कि हमारे पास मूल्य कहाँ है और मूल्य कहाँ है! रिकॉर्ड किया गया? आइए अब सब कुछ क्रम में तुलना करें:

और उत्तर: मैं। एक जाँच करें - सिस्टम में मिली जड़ों को प्रतिस्थापित करें और सुनिश्चित करें कि हमने इसे ग्राफिकल तरीके से सही ढंग से हल किया है?

गैर-रेखीय समीकरणों की प्रणाली को हल करना

लेकिन क्या होगा अगर एक सीधी रेखा के बजाय, हमारे पास द्विघात समीकरण है? ठीक है! आप बस एक सीधी रेखा के बजाय एक परवलय का निर्माण करें! विश्वास नहीं करते? निम्नलिखित प्रणाली को हल करने का प्रयास करें:

हमारा अगला कदम क्या है? यह सही है, इसे लिख लें ताकि हमारे लिए रेखांकन बनाना सुविधाजनक हो:

और अब यह सब छोटी चीज़ों के बारे में है - मैंने इसे जल्दी से बनाया और यहाँ आपके लिए समाधान है! इमारत:

क्या ग्राफिक्स समान हैं? अब चित्र में सिस्टम के समाधानों को चिह्नित करें और प्रकट उत्तरों को सही ढंग से लिखें!

मैंने सब कुछ किया है? मेरे नोट्स के साथ तुलना करें:

ठीक है? बहुत अच्छा! आप पहले से ही पागल जैसे कार्यों पर क्लिक करते हैं! और यदि हां, तो आइए आपको एक अधिक जटिल प्रणाली प्रदान करते हैं:

हम क्या कर रहे हैं? सही ढंग से! हम सिस्टम लिखते हैं ताकि इसे बनाना सुविधाजनक हो:

मैं आपको थोड़ा संकेत दूंगा, क्योंकि सिस्टम बहुत जटिल दिखता है! रेखांकन बनाते समय, उन्हें "अधिक" बनाएं, और सबसे महत्वपूर्ण बात, चौराहे के बिंदुओं की संख्या पर आश्चर्य न करें।

तो चलते हैं! साँस छोड़ी? अब निर्माण शुरू करो!

कितनी अच्छी तरह से? सुन्दर है? आपको कितने चौराहे बिंदु मिले? मेरे पास तीन हैं! आइए हमारे रेखांकन की तुलना करें:

उसी तरह? अब हमारे सिस्टम के सभी समाधानों को ध्यान से लिखें:

अब सिस्टम को फिर से देखें:

क्या आप सोच सकते हैं कि आपने इसे केवल 15 मिनट में हल कर लिया? सहमत हूं, गणित अभी भी सरल है, खासकर जब एक अभिव्यक्ति को देखते हुए, आप गलती करने से डरते नहीं हैं, लेकिन आप इसे लेते हैं और निर्णय लेते हैं! तुम बड़े लड़के हो!

असमानताओं का चित्रमय समाधान

रैखिक असमानताओं का आलेखीय समाधान

अंतिम उदाहरण के बाद, आप कार्य पर निर्भर हैं! अब साँस छोड़ें - पिछले खंडों की तुलना में, यह बहुत, बहुत आसान होगा!

हम हमेशा की तरह, एक रैखिक असमानता के चित्रमय समाधान के साथ शुरू करते हैं। उदाहरण के लिए, यह एक:

आरंभ करने के लिए, हम सबसे सरल परिवर्तन करेंगे - हम पूर्ण वर्गों के कोष्ठक खोलेंगे और समान शब्द देंगे:

असमानता सख्त नहीं है, इसलिए - अंतराल में शामिल नहीं है, और समाधान सभी बिंदु होंगे जो दाईं ओर हैं, क्योंकि अधिक, अधिक, और इसी तरह:

जवाब:

बस इतना ही! सरलता? आइए दो चर के साथ एक साधारण असमानता को हल करें:

आइए समन्वय प्रणाली में एक फ़ंक्शन बनाएं।

क्या आपके पास ऐसा कोई चार्ट है? और अब हम ध्यान से देखें कि हमारे पास असमानता में क्या है? छोटा? इसलिए, हम अपनी सीधी रेखा के बाईं ओर की हर चीज़ पर पेंट करते हैं। क्या होगा अगर और भी थे? यह सही है, तब वे हमारी सीधी रेखा के दायीं ओर की हर चीज़ पर पेंट करेंगे। सब कुछ सरल है।

इस असमानता के सभी समाधान नारंगी रंग में छायांकित हैं। यही है, दो-चर असमानता हल हो गई है। इसका मतलब है कि निर्देशांक और छायांकित क्षेत्र से कोई भी बिंदु समाधान हैं।

द्विघात असमानताओं का आलेखीय समाधान

अब हम देखेंगे कि द्विघात असमानताओं को आलेखीय रूप से कैसे हल किया जाए।

लेकिन इससे पहले कि हम सीधे मुद्दे पर पहुँचें, चलिए वर्गाकार फलन के बारे में कुछ बातें फिर से समझते हैं।

भेदभाव करने वाला किसके लिए जिम्मेदार है? यह सही है, अक्ष के सापेक्ष ग्राफ की स्थिति के लिए (यदि आपको यह याद नहीं है, तो निश्चित रूप से द्विघात कार्यों के बारे में सिद्धांत पढ़ें)।

किसी भी मामले में, यहां आपके लिए एक छोटा सा अनुस्मारक है:

अब जब हमने अपनी स्मृति में सभी सामग्री को ताज़ा कर दिया है, तो चलिए व्यापार में उतरते हैं - हम असमानता को ग्राफिक रूप से हल करेंगे।

मैं आपको तुरंत बता दूंगा कि इसे हल करने के लिए दो विकल्प हैं।

विकल्प 1

हम अपने परवलय को एक फंक्शन के रूप में लिखते हैं:

सूत्रों का उपयोग करके, हम परवलय के शीर्ष के निर्देशांक निर्धारित करते हैं (उसी तरह जैसे द्विघात समीकरणों को हल करते समय):

क्या आपने गिनती की? तुम्हें क्या मिला?

अब दो और अलग-अलग बिंदु लेते हैं और उनके लिए गणना करते हैं:

हम परवलय की एक शाखा बनाना शुरू करते हैं:

हम परवलय की एक अन्य शाखा पर सममित रूप से अपनी बातों को प्रतिबिंबित करते हैं:

अब वापस हमारी असमानता पर।

हमें इसकी आवश्यकता है कि यह क्रमशः शून्य से कम हो:

चूंकि हमारी असमानता में एक संकेत सख्ती से कम है, हम अंतिम बिंदुओं को बाहर करते हैं - हम "बाहर निकलते हैं"।

जवाब:

लंबा रास्ता, है ना? अब मैं आपको एक उदाहरण के रूप में समान असमानता का उपयोग करके ग्राफिकल समाधान का एक सरल संस्करण दिखाऊंगा:

विकल्प 2

हम अपनी असमानता पर लौटते हैं और उन अंतरालों को चिह्नित करते हैं जिनकी हमें आवश्यकता होती है:

सहमत हूँ, यह बहुत तेज़ है।

आइए अब उत्तर लिखें:

आइए एक और समाधान विधि पर विचार करें जो बीजीय भाग को सरल करता है, लेकिन मुख्य बात भ्रमित नहीं होना है।

बाएँ और दाएँ पक्षों को इससे गुणा करें:

निम्नलिखित द्विघात असमानता को अपने आप किसी भी तरह से हल करने का प्रयास करें:

क्या आप संभाल पाओगे?

देखें कि मेरा चार्ट कैसा निकला:

जवाब: .

मिश्रित असमानताओं का आलेखीय समाधान

अब आइए अधिक जटिल असमानताओं की ओर बढ़ते हैं!

आपको यह कैसे लगता है:

भयानक, है ना? ईमानदारी से, मुझे नहीं पता कि इसे बीजगणितीय रूप से कैसे हल किया जाए ... लेकिन यह आवश्यक नहीं है। ग्राफिक रूप से, इसमें कुछ भी जटिल नहीं है! आंखें डरती हैं, लेकिन हाथ कर रहे हैं!

पहली चीज जो हम शुरू करते हैं वह है दो रेखांकन बनाना:

मैं हर किसी के लिए एक टेबल नहीं लिखूंगा - मुझे यकीन है कि आप इसे पूरी तरह से अपने दम पर कर सकते हैं (बेशक, हल करने के लिए बहुत सारे उदाहरण हैं!)

चित्रित? अब दो ग्राफ बनाएं।

आइए हमारे चित्र की तुलना करें?

क्या आपके पास वही है? बढ़िया! अब आइए चौराहे के बिंदुओं को रखें और एक रंग के साथ निर्धारित करें कि हमारे पास कौन सा ग्राफ होना चाहिए, सिद्धांत रूप में, बड़ा होना चाहिए, अर्थात। देखिए आखिर में क्या हुआ:

और अब हम देखते हैं कि हमारा चयनित चार्ट चार्ट से कहाँ ऊँचा है? बेझिझक एक पेंसिल लें और इस क्षेत्र पर पेंट करें! यह हमारी जटिल असमानता का समाधान होगा!

अक्ष के अनुदिश हम किस अंतराल से ऊपर हैं? सही, । यह उत्तर है!

ठीक है, अब आप किसी भी समीकरण, और किसी भी प्रणाली, और इससे भी अधिक किसी भी असमानता को संभाल सकते हैं!

संक्षेप में मुख्य के बारे में

फ़ंक्शन ग्राफ़ का उपयोग करके समीकरणों को हल करने के लिए एल्गोरिदम:

1. एक्सप्रेस के माध्यम से
2. फ़ंक्शन प्रकार को परिभाषित करें
3. आइए परिणामी कार्यों के रेखांकन बनाएं
4. ग्राफ़ के प्रतिच्छेदन बिंदु ज्ञात कीजिए
5. उत्तर को सही ढंग से लिखें (ODZ और असमानता के संकेतों को ध्यान में रखते हुए)
6. उत्तर की जाँच करें (समीकरण या प्रणाली में जड़ों को प्रतिस्थापित करें)

फ़ंक्शन ग्राफ़ प्लॉट करने के बारे में अधिक जानकारी के लिए, "" विषय देखें।

द्विघात समीकरण का आलेखीय समाधान विभिन्न कार्यों के ग्राफ़ बनाने की क्षमता को समेकित करना; द्विघात समीकरणों को आलेखीय रूप से हल करने की क्षमता का निर्माण करना। Brdsk 2009 नगर शैक्षणिक संस्थान - आर्थिक लिसेयुम "द्विघात समारोह" विषय पर पाठ का सामान्यीकरण, बीजगणित ग्रेड 8 शिक्षक फेडोसेवा टी.एम.

द्विघात फलन का आलेखन शाखाओं की दिशा निर्धारित करें: a>0 शाखाएँ ऊपर; ए 0 शाखाएं ऊपर; ए"> 0 शाखाएं ऊपर; ए"> 0 शाखाएं ऊपर; a" title="(!LANG:एक द्विघात फ़ंक्शन को प्लॉट करना शाखा दिशा निर्धारित करें: a>0 शाखाएं ऊपर; a"> title="द्विघात फलन का आलेखन शाखाओं की दिशा निर्धारित करें: a>0 शाखाएँ ऊपर; ए"> !}

0 शाखाएं ऊपर की ओर निर्देशित होती हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। बिंदु "शीर्षक ="(!LANG: आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। एक बिंदु ढूँढना" class="link_thumb"> 3 !}आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। हम OX अक्ष के साथ प्रतिच्छेदन बिंदु पाते हैं: x 1 \u003d -1; x 2 \u003d 3 1 समीकरण को हल करने का तरीका x 2 -2x-3 \u003d 0 y x समीकरण को हल करें x 2 +2x-3 \u003d 0 0 शाखाएं ऊपर की ओर निर्देशित होती हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। हम बिंदु पाते हैं "\u003e 0 शाखाएं ऊपर की ओर निर्देशित होती हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - अक्ष परवलय के नियंत्रण बिंदु: (0: -3) , (3; 0) और x = 1 अक्ष के बारे में सममित हम एक परवलय का निर्माण करते हैं। OX अक्ष के साथ चौराहे के बिंदु खोजें: x 1 \u003d -1; x 2 \u003d 3 1 समीकरण को हल करने का तरीका x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 समीकरण को हल करें x 2 + 2x-3 \u003d 0 "\u003e 0 शाखाएं ऊपर की ओर निर्देशित हैं; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। बिंदु "शीर्षक ="(!LANG: आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। एक बिंदु ढूँढना"> title="आइए एल्गोरिथ्म का उपयोग करके y=x 2 -2x-3 फ़ंक्शन का एक ग्राफ बनाएं: 1) a=1>0 शाखाओं को ऊपर की ओर निर्देशित किया जाता है; 2) शीर्ष y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - परवलय की धुरी नियंत्रण बिंदु: (0: -3), (3 ; 0) और x-अक्ष के सापेक्ष उनके सममित = 1 हम एक परवलय बनाते हैं। एक बिंदु ढूँढना"> !}

दूसरा तरीका: ए)। आइए समीकरण x 2 -2x-3=0 को भागों में विभाजित करें x 2 = 2x+3 आइए दो फलन y= x 2 लिखें; y \u003d 2x + 3 हम एक समन्वय प्रणाली में इन कार्यों के रेखांकन बनाते हैं। प्रतिच्छेदन बिंदुओं के भुज समीकरण के मूल हैं। 0 1 x y समीकरण को हल करें x 2 +2x-3=0

तीसरा तरीका: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x हम एक समन्वय प्रणाली में इन कार्यों के ग्राफ बनाते हैं। प्रतिच्छेदन बिंदुओं के भुज समीकरण के मूल हैं। 0 1 x y समीकरण को हल करें x 2 +2x-3=0

पेशेवर विकास के लिए दागिस्तान संस्थान

शैक्षणिक कर्मचारी

शारीरिक और गणितीय शिक्षा और आईसीटी विभाग

परियोजना

विषय पर:

« निर्माण और पी सुधारों

फ़ंक्शन ग्राफ़

स्कूल के गणित में »

रबाडानोवा पी.ए.

गणित शिक्षक

MBOU "कोचुबे सेकेंडरी स्कूल"

तारुमोव्स्की जिला

2015

1. परिचय……………………………………………………….3

2. अध्याय मैं. परियोजना के विषय पर साहित्य की समीक्षा……………………….….5

3. अध्याय द्वितीय. अनुभवजन्य भाग:

3.1. फ़ंक्शन ग्राफ़ को कनवर्ट करने के लिए मूल तरीके………..7

3.2. सम प्लॉटिंगऔरअजीब कार्य …………….. 10

3.3. व्युत्क्रम फलन प्लॉट करना ………………………… 11

3.4. ग्राफ़ का विरूपण (संपीड़न और तनाव)………………….12

3.5. स्थानांतरण, प्रतिबिंब और विरूपण का संयोजन ………………… 13

4. स्वतंत्र समाधान के लिए कार्य ………………………………14

5.निष्कर्ष………………………………………………………15

6. निष्कर्ष……………………………………………………………………17

परिचय

फ़ंक्शन ग्राफ़ का परिवर्तन सीधे व्यावहारिक गतिविधियों से संबंधित मूलभूत गणितीय अवधारणाओं में से एक है। रेखांकन वास्तविक दुनिया की परिवर्तनशीलता और गतिशीलता, वास्तविक वस्तुओं और घटनाओं के पारस्परिक संबंधों को दर्शाते हैं।

कार्यात्मक रेखा मूल और एकीकृत राज्य परीक्षाओं में शामिल मूल विषय है।साथ ही, कई गणितीय अवधारणाओं को आलेखीय विधियों द्वारा माना जाता है। उदाहरण के लिए, toद्विघातफ़ंक्शन को द्विघात समीकरणों और असमानताओं के साथ निकट संबंध में पेश और अध्ययन किया जाता है।इसलिए यह इस प्रकार है किछात्रों को किसी फ़ंक्शन के ग्राफ़ बनाने और बदलने का तरीका सिखाना स्कूल में गणित पढ़ाने के मुख्य कार्यों में से एक है।

फ़ंक्शन के अध्ययन से इसके बारे में पता लगाना संभव हो जाता हैपरिभाषा का क्षेत्र और कार्य का दायरा, दायराघटती या बढ़ती दरें, स्पर्शोन्मुख, अंतरालस्थिरता, आदि पर हस्ताक्षर करें। हालांकि, एक ग्राफ बनाने के लिएkov कई कार्य हो सकते हैंकई तरीकों का प्रयोग करेंइसे आसान बनाएंइमारत। अतः विद्यार्थियों में पद्धतिगत योजनाओं के अनुसार आलेख बनाने की योग्यता होनी चाहिए।

उपरोक्त परिभाषित करता हैप्रासंगिकता शोध के विषय।

अध्ययन की वस्तु स्कूली गणित में कार्यात्मक रेखा रेखांकन के परिवर्तन का अध्ययन है।

अध्ययन का विषय - माध्यमिक विद्यालय में फंक्शन ग्राफ बनाने और बदलने की प्रक्रिया।

अध्ययन का उद्देश्य: शैक्षिक - किसी फ़ंक्शन के ग्राफ़ के निर्माण और परिवर्तित करने के लिए एक कार्यप्रणाली योजना की पहचान करना शामिल है;विकसित होना - अमूर्त, एल्गोरिथम, तार्किक सोच, स्थानिक कल्पना का विकास;शिक्षात्मक - स्कूली बच्चों की ग्राफिक संस्कृति की शिक्षा, मानसिक कौशल का निर्माण।

लक्ष्यों ने निम्नलिखित के निर्णय का नेतृत्व कियाकार्य:

1. अध्ययन के तहत समस्या पर शैक्षिक और कार्यप्रणाली का विश्लेषण करें।

2. कार्यप्रणाली योजनाओं की पहचान करेंगणित के स्कूल पाठ्यक्रम में फ़ंक्शन ग्राफ़ का परिवर्तन।

3. सबसे प्रभावी तरीकों और साधनों का चयन करेंमाध्यमिक विद्यालय में फ़ंक्शन ग्राफ़ का निर्माण और परिवर्तनइसमें योगदान करना: शैक्षिक सामग्री का अर्थपूर्ण आत्मसात करना; छात्रों की संज्ञानात्मक गतिविधि में वृद्धि; उनकी रचनात्मक क्षमताओं का विकास।

परिकल्पनाअनुसंधान: छात्रों की ग्राफिक संस्कृति के कार्यों और शिक्षा का अध्ययन करने की प्रक्रिया में ग्राफिक कौशल का गठन होगा प्रभावी यदि छात्रों के पास स्कूल गणित पाठ्यक्रम में फ़ंक्शन ग्राफ़ बनाने और बदलने के लिए एक व्यवस्थित योजना है।

अध्याय मैं . परियोजना के विषय पर साहित्य की समीक्षा।

परियोजना की तैयारी में, हमने निम्नलिखित साहित्य का अध्ययन किया:

शिवशिंस्की, आई। ख। बीजगणित में प्रमेय और समस्याएं, प्राथमिक कार्य - एम।, 2002। - 115 पी।

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. कार्य और रेखांकन (मूल तकनीक) - M., 1985. - 120 s

वी.जेड.जैतसेव, वी.वी. रियाज़कोव, एम.आई. स्कैनवी। प्राथमिक गणित - एम।, 2010 (पुनः जारी)। - 590 पी।

कुज़मिन, एम. के. एक समारोह के ग्राफ का निर्माण - जे। स्कूल में गणित। - 2003. - नंबर 5। - एस 61-62।

शिलोव जी.ई. चार्ट कैसे बनाते हैं? - एम।, 1982।

इसहाक तनातार। कार्यों के रेखांकन के ज्यामितीय परिवर्तन - MTsNMO, 2012

परयह ध्यान दिया जाता है कि एक ग्राफ का उपयोग करके एक निश्चित सेट पर फ़ंक्शन के व्यवहार को "पढ़ने" की क्षमता का उपयोग न केवल गणित के पाठ्यक्रम में किया जाता है, बल्कि किसी व्यक्ति की किसी भी व्यावहारिक गतिविधि में भी किया जाता है जिसमें उसे कुछ ग्राफिक से निपटना होता है। निर्भरता का प्रतिनिधित्व। इसलिए, छात्रों को किसी फ़ंक्शन के ग्राफ़ से इसके कुछ गुणों को निर्धारित करने में सक्षम होना चाहिए।

रेखांकन के परिवर्तन के लिए सैद्धांतिक सामग्री में सख्ती से कहा गया है। तकनीक के साथ चित्र के साथ चित्र, अलग-अलग जटिलता के उदाहरण और उनके समाधान हैं, जो ज्ञान को गहरा करना और जटिल कार्यों की साजिश करना संभव बनाता है।

एक इलेक्ट्रॉनिक प्रशिक्षण पाठ्यक्रम का प्रतिनिधित्व करता है, जिसकी मात्रा और सामग्री हाई स्कूल गणित पाठ्यक्रम के लिए आवश्यकताओं को पूरा करती है। सैद्धांतिक सामग्री ग्राफिक एनीमेशन चित्रों द्वारा समर्थित है जो अध्ययन के तहत विषय का एक दृश्य प्रतिनिधित्व देते हैं। पाठ्यक्रम में तीन मॉड्यूल शामिल हैं: एक सैद्धांतिक सामग्री अध्ययन मॉड्यूल, एक आत्म-परीक्षा मॉड्यूल और एक ज्ञान नियंत्रण मॉड्यूल।

परियोजना के अनुभवजन्य भाग के लिए, पद्धतिगत चार्टिंग योजनाओं से, स्वतंत्र कार्य के उदाहरणों का उपयोग किया गया था।

अध्याय 1 के निष्कर्ष

शैक्षिक और पद्धतिगत साहित्य के अध्ययन की अनुमति है:

1. कार्यप्रणाली योजना की पहचान करेंस्कूल गणित पाठ्यक्रम में किसी फ़ंक्शन के ग्राफ़ का अध्ययन, निर्माण और रूपांतरण।

2. सबसे प्रभावी तरीकों और साधनों का चयन करेंस्कूली गणित में फलन ग्राफ का निर्माण और परिवर्तन,योगदान:

शैक्षिक सामग्री का सार्थक आत्मसात;

छात्रों की संज्ञानात्मक गतिविधि में वृद्धि;

उनकी रचनात्मक क्षमताओं का विकास।

3. दिखाओ कि गणित में विभिन्न अवधारणाओं के अध्ययन में कार्यात्मक रेखा का महत्वपूर्ण प्रभाव पड़ता है।

अध्याय 2. अनुभवजन्य भाग

इस अध्याय में, हम फ़ंक्शन ग्राफ़ को बदलने के लिए मुख्य विधियों पर विचार करेंगे, और विभिन्न कार्यों के लिए ग्राफ़ के विभिन्न संयोजनों के निर्माण के लिए पद्धतिगत योजनाएँ देंगे।

2.1. फंक्शन ग्राफ रूपांतरण के लिए बुनियादी तकनीक

y-अक्ष के अनुदिश अनुवाद

एफ ( एक्स ) एफ ( एक्स )+ बी .

के लिएएक समारोह की साजिश रचनेआप = एफ( एक्स) + बीपता लगानाउन्हें:

1. एक फंक्शन ग्राफ बनाएंआप= एफ( एक्स)

2. धुरी ले जाएँएब्सिस्सा ऑन| बी| इकाइयाँ ऊपरबी>0 या कि| बी| खाना खा लोनीचे की ओर झुकनाबी < 0. नई व्यवस्था में प्राप्तदीनाट ग्राफ एक फ़ंक्शन का ग्राफ हैआप = एफ( एक्स) + बी.

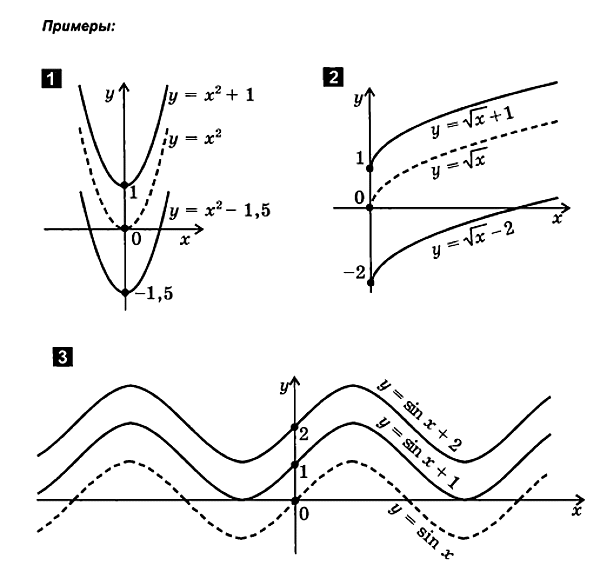
2. स्थानांतरण साथ में कुल्हाड़ियों सूच्याकार आकृति का भुज

एफ ( एक्स ) एफ ( एक्स + ए ) .

आप = एफ( एक्स+ ए) पता लगानाउन्हें:

3. फॉर्म का एक फंक्शन प्लॉट करना आप = एफ (- एक्स )

एफ (एक्स ) एफ (- एक्स ).

फ़ंक्शन प्लॉट करने के लिएआप = एफ( - एक्स) इस प्रकार है:

एक फ़ंक्शन प्लॉट करेंआप = एफ( एक्स)

इसे वापस प्रतिबिंबित करेंy-अक्ष के सापेक्ष

परिणामी ग्राफ हैफंक्शन ग्राफआप = एफ( - एक्स)।

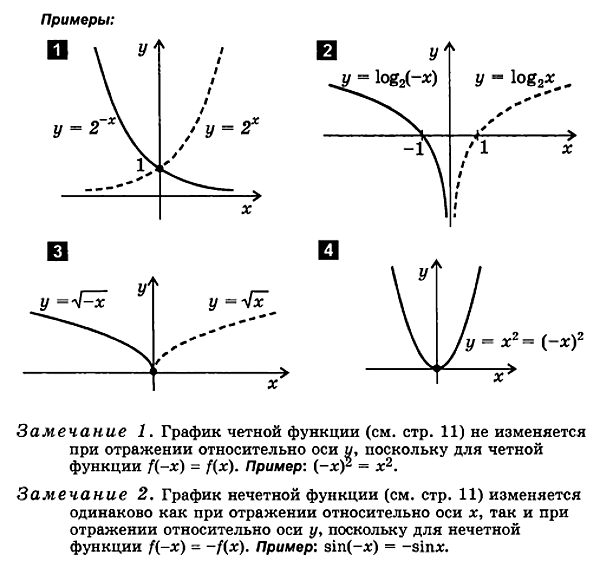
4. फॉर्म का एक फंक्शन प्लॉट करना वाई = - एफ ( एक्स )

एफ ( एक्स ) - एफ ( एक्स )

- एफ( एक्स) इस प्रकार है:

एक फ़ंक्शन प्लॉट करेंआप= एफ( एक्स)

इसे एक्स-अक्ष के बारे में प्रतिबिंबित करें

2.2. सम प्लॉटिंग और अजीब विशेषताएं

साजिश रचते समयसम और विषम कार्यों के लिए, निम्नलिखित गुणों का उपयोग करना सुविधाजनक है:

1. एक सम फलन का ग्राफ simmety-अक्ष के सापेक्ष उबड़-खाबड़।

2. एक विषम फलन का आलेख मूल के परितः सममित होता है।

सम और विषम फ़ंक्शन के ग्राफ़ बनाने के लिए, तर्क के सकारात्मक मूल्यों के लिए ग्राफ़ की केवल दाहिनी शाखा को प्लॉट करना पर्याप्त है। बाईं शाखा विषम फलन के मूल के बारे में और सम फलन के लिए y-अक्ष के बारे में सममित रूप से पूर्ण होती है।

सम फंक्शन प्लॉट करने के लिए आप = एफ ( एक्स ) बाद युगल:

केवल इस फलन के ग्राफ की एक शाखा की रचना करेंतर्क x≥0 के सकारात्मक मूल्यों की सीमा।

हेइस शाखा को y-अक्ष के परितः अनुरेखित कीजिए

एक अजीब समारोह की साजिश रचने के लिए आप = एफ ( एक्स ) इस प्रकार है:

इस फ़ंक्शन की केवल ग्राफ़ शाखा बनाएंतर्क के सकारात्मक मूल्यों का क्षेत्र (х≥0)।

हेमूल के संबंध में इस शाखा का पता लगाएंऋणात्मक x मानों के क्षेत्र में।

2.3. उलटा कार्य प्लॉट करना

जैसा कि पहले ही उल्लेख किया गया है, प्रत्यक्ष और उलटा कार्यचर के बीच समान संबंध दिखाएंx और y, केवल इस अंतर के साथ कि प्रतिलोम फलन में येचर ने भूमिकाएँ बदल दी हैं, जो बदलने के बराबर हैसमन्वय अक्षों का अंकन। इसलिए, ग्राफउलटा कार्य प्रत्यक्ष कार्य के ग्राफ के सममित हैद्विभाजक के बारे मेंमैंऔरतृतीयसमन्वय कोण,यानी अपेक्षाकृत सीधावाई = एक्स। इस प्रकार, हम प्राप्त करते हैंअगला नियम।

फलन y = . को आलेखित करने के लिए (एक्स) समारोह के विपरीतआप = एफ( एक्स), बनाया जाना चाहिएअनुसूचीआप = एफ( एक्स) और इसे सीधी रेखा y = x के सापेक्ष परावर्तित करें।

2.4. ग्राफ़ का विरूपण (संपीड़न और तनाव)

1. y-अक्ष के अनुदिश ग्राफ का संपीडन (विस्तार)

एफ ( एक्स ) ए ∙ एफ ( एक्स ).

फ़ंक्शन प्लॉट करने के लिएआप= ए∙ एफ( एक्स) इस प्रकार है:

8. x-अक्ष के अनुदिश ग्राफ का संपीडन (विस्तार)

एफ( एक्स)

फ़ंक्शन y . को प्लॉट करने के लिए= एफ( एक्स) इस प्रकार है:

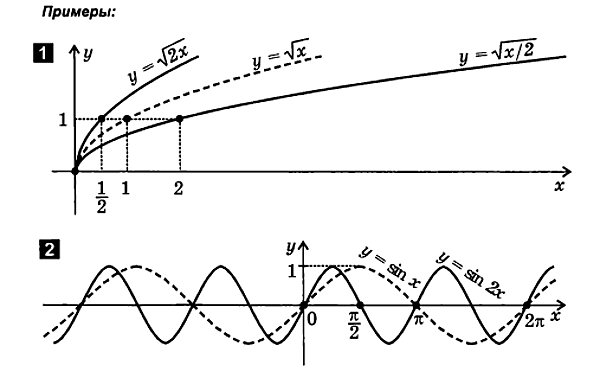
2.5. अनुवाद, प्रतिबिंब और विरूपण का संयोजन

बहुत बार जब के लिए फ़ंक्शन ग्राफ़ प्लॉट करते हैंसंयोजन बदलें.

ऐसी कई आसन तकनीकों का लगातार अनुप्रयोगका उपयोग करके ग्राफ के निर्माण को महत्वपूर्ण रूप से सरल बनाने की अनुमति देता हैचल रहा है और अक्सर इसे अंत में कम कर देता हैसबसे सरल प्राथमिक कार्यों में से एक का निर्माणबातें विचार करें कि, पूर्वगामी को ध्यान में रखते हुए, यह इस प्रकार हैफ़ंक्शन ग्राफ़ बनाएं।

आइए ध्यान दें कि यह समय हैअगले उत्तराधिकारी में सरलीकरण डॉक करना उचित हैनेस

समता का उपयोग करना orसमारोह विषमता।

अक्ष स्थानांतरण।

प्रतिबिंब और विरूपण।

ग्राफ का निर्माण उल्टे क्रम में किया जाता है।

उदाहरण। एक फ़ंक्शन प्लॉट करें

निर्माण निम्नलिखित चरणों में किया जाएगा:

1. प्राकृतिक लघुगणक की साजिश रचें:

2. निचोड़अक्ष के लिएओए2 बार:;
3. सममित रूप से प्रदर्शित करेंअक्ष के बारे मेंओए: ;
4. अक्ष के अनुदिश गति करेंबैलपर(!!!) दांई ओर::

5. अक्ष के बारे में सममित रूप से प्रदर्शित करेंबैल: ;
6. चालअक्ष के अनुदिशओए3 यूनिट ऊपर::

फंक्शन ग्राफ के निर्माण और रूपांतरण के उदाहरण

उदाहरण 1 एक फ़ंक्शन प्लॉट करें.

सबसे पहले, एक साइन ग्राफ बनाएं, इसकी अवधि बराबर है:

फंक्शन ग्राफग्राफ को संपीड़ित करके प्राप्त किया गयादो बार y-अक्ष के लिए।लॉग .

एक फ़ंक्शन प्लॉट करेंपर = 2 क्योंकिएक्स।

एक फ़ंक्शन प्लॉट करेंआप = पापएक्स .

निष्कर्ष

परियोजना कार्य पर काम के दौरान, इस मुद्दे पर विभिन्न शैक्षिक और पद्धति संबंधी साहित्य का विश्लेषण किया गया। अध्ययन के परिणामों ने अध्ययन के सबसे विशिष्ट सकारात्मक पहलुओं की पहचान करना संभव बना दियास्कूल गणित पाठ्यक्रम में एक समारोह के रेखांकन का निर्माण और परिवर्तन

परियोजना का मुख्य लक्ष्य स्वतंत्र गतिविधि के तर्कसंगत तरीकों के निर्माण में, चित्र पढ़ने और ड्राइंग में छात्रों के कौशल और क्षमताओं को विकसित करना है।

समग्र रूप से ग्राफिक शिक्षा में सुधार की आवश्यकता न केवल आधुनिक उत्पादन आवश्यकताओं से निर्धारित होती है, बल्कि छात्रों की तकनीकी सोच और संज्ञानात्मक क्षमताओं के विकास में ग्राफिक्स की भूमिका से भी निर्धारित होती है। किसी व्यक्ति की ग्राफिक जानकारी को संसाधित करने की क्षमता उसके मानसिक विकास के संकेतकों में से एक है। इसलिए, ग्राफिक प्रशिक्षण सामान्य शैक्षिक प्रशिक्षण का एक अभिन्न अंग बन जाना चाहिए।

जाँच - परिणाम

इस प्रकार, विकसित परियोजना "फ़ंक्शन ग्राफ़ का निर्माण और परिवर्तन", गणित की केंद्रीय अवधारणाओं में से एक को समर्पित है - कार्यात्मक निर्भरता, छात्रों के ज्ञान के व्यवस्थितकरण और विस्तार पर केंद्रित है। फ़ंक्शन ग्राफ़ को बदलने के लिए विशिष्ट तरीकों का अध्ययन सख्त कार्यप्रणाली योजनाओं के अनुसार विश्लेषणात्मक और चित्रमय तरीके से किया जाता है। एकत्रित सामग्री का उपयोग कक्षा में और छात्रों के स्व-प्रशिक्षण के लिए किया जा सकता है। कक्षाओं के संचालन के लिए संगठन और प्रशिक्षण के विभिन्न रूपों और विधियों का उपयोग किया जा सकता है।