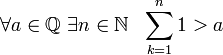Secara historis, yang pertama bilangan bulat$N$, sebagai hasil dari penghitungan ulang kentut. Himpunan bilangan-bilangan ini tak hingga dan membentuk deret alami $N=\(1, 2, 3, ..., n, ...\)$. Pada himpunan ini, operasi penjumlahan dan perkalian dapat dilakukan. Untuk melakukan operasi pengurangan, diperlukan angka-angka baru, yang menyebabkan munculnya satu set bilangan bulat: $Z$. $Z=N_+\cup N_- \cup \(0\)$. Jadi, dalam himpunan bilangan bulat, operasi penjumlahan, perkalian, pengurangan selalu dilakukan.
Angka rasional
Kebutuhan untuk melakukan pembagian menyebabkan himpunan bilangan rasional $Q$. $Q=\(\frac(m)(n), m\di Z, n\di N\)$.
Definisi. Dua bilangan rasional adalah sama: $\frac(m_1)(n_1)=\frac(m_2)(n_2)$ - jika $m_1\cdot n_2=n_1\cdot m_2$. Ini berarti bahwa setiap bilangan rasional dapat direpresentasikan secara unik sebagai pecahan tak tereduksi $\frac(m)(n)$. $gcd(m, n)=1$.
Sifat-sifat himpunan bilangan rasional
1. Akibatnya operasi aritmatika atas bilangan rasional (penjumlahan, perkalian, pengurangan, pembagian, kecuali pembagian dengan nol), diperoleh bilangan rasional.
2. Himpunan bilangan rasional terurut, yaitu untuk setiap pasangan bilangan rasional $a$ dan $b$ atau $a
3. Himpunan bilangan rasional rapat, yaitu, untuk setiap pasangan bilangan rasional $a$ dan $b$ terdapat bilangan rasional $c$ sehingga $a Setiap bilangan rasional positif selalu dapat direpresentasikan sebagai pecahan desimal: periodik terbatas atau tak terbatas. Misalnya: $\frac(3)(5)=0.6$, $\frac(1)(3)=0.333...=0,(3)$. $\frac(m)(n)=a_0,a_1a_1...a_kb_1b_2b_3...b_nb_1b_2b_3...b_n...$. $b_1b_2b_3...b_n...$ - disebut periode pecahan desimal, di mana tidak semua $b_i=0$. Perhatikan bahwa pecahan berhingga dapat ditulis sebagai pecahan periodik tak hingga dengan nol pada periode. $\frac(m)(n)=a_0,a_1a_1...a_k000000...$, $a_k\ne0$. Namun, representasi lain dari bilangan rasional sebagai pecahan desimal lebih umum: $\frac(m)(n)=a_0,a_1a_1...(a_k-1)999...$. Bilangan rasional negatif $-\frac(m)(n)$ ditulis sebagai perluasan desimal dari bilangan rasional berbentuk $\frac(m)(n)$ yang diambil dengan tanda yang berlawanan. Angka $0$ direpresentasikan sebagai $0,000...$. Jadi, bilangan rasional apa pun selalu dapat direpresentasikan sebagai pecahan periodik desimal tak terbatas yang tidak mengandung $0$ dalam periode tersebut, kecuali untuk bilangan $0$ itu sendiri. Pemandangan ini adalah satu-satunya. Himpunan bilangan rasional tertutup di bawah empat operasi aritmatika. Namun, dalam himpunan bilangan rasional, solusi dari persamaan paling sederhana dari bentuk $x^2-n=0$ tidak selalu terjadi. Oleh karena itu, ada kebutuhan untuk memperkenalkan nomor baru. Mari kita tunjukkan bahwa di antara bilangan rasional tidak ada bilangan yang kuadratnya sama dengan tiga. Pembuktian dilakukan dengan metode kontradiksi. Misalkan terdapat bilangan rasional $\frac(m)(n)$ sehingga kuadratnya adalah tiga: $\left(\frac(m)(n)\right)^2=3\;\;\;( 1 )$. $\frac(m^2)(n^2)=3$, $m^2=3n^2.\;\;\;(2)$ Ruas kanan persamaan (2) habis dibagi 3. Jadi, $m^2$ juga habis dibagi 3, maka $m$ habis dibagi 3, artinya $m=3k$. Substitusikan ke persamaan (2), kita peroleh: $3k^2=n^2.\;\;\;(3)$ Ruas kiri $(3)$ habis dibagi $3$, jadi ruas kanan juga habis dibagi $3$. Oleh karena itu $n^2$ habis dibagi $3$, maka $n$ juga habis dibagi $3$, dari mana $n=3p$. Hasilnya, kita mendapatkan: $\frac(m)(n)=\frac(3k)(3p)$, yaitu pecahan $\frac(m)(n)$ ternyata dapat direduksi, yang bertentangan dengan asumsi . Ini berarti bahwa di antara bilangan rasional tidak ada bilangan seperti itu, kuadratnya sama dengan tiga. Tetapi ada bilangan yang kuadratnya tiga. Ini dapat direpresentasikan sebagai fraksi non-periodik tak terbatas. Dan kami mendapat jenis nomor baru. Sebut saja mereka tidak rasional. Definisi. Bilangan irasional adalah setiap pecahan non-periodik tak terbatas. Himpunan semua pecahan non-periodik tak terbatas disebut himpunan bilangan irasional dan dilambangkan dengan $I$. Gabungan himpunan bilangan rasional $Q$ dan bilangan irasional $I$ menghasilkan himpunan bilangan real $R$: $Q\cup I=R$. Dengan demikian, setiap bilangan real dapat direpresentasikan sebagai pecahan desimal tak terbatas: periodik dalam kasus bilangan rasional dan non-periodik dalam kasus bilangan irasional. Untuk bilangan real $a=a_0,a_1a_2a_3\ldots a_n\ldots$, $b=b_0,b_1b_2b_3\ldots b_n\ldots$ perbandingannya adalah sebagai berikut: 1) Misalkan $a$ dan $b$ keduanya positif: $a>0$, $b>0$, maka: $a=b$ jika untuk $k$ $a_k=b_k$ apa saja; $a>b$ jika $\ada s$ $\forall k 2) Misalkan $a>0$, $b<0$, или иначе: $b<0 3) Misalkan $a$ dan $b$ keduanya negatif: $a<0$, $b<0$, тогда: $a=b$ jika untuk $-a=-b$; Ada angka-angka yang sifatnya berbeda - operasi mengekstrak akar kuadrat sering mengarah ke sana (dan bukan hanya itu, kita belum mengetahuinya). Jadi, kita perlu mengenal angka-angka baru secara lebih rinci. Tetapi pertama-tama, mari kita coba mensistematisasikan pengetahuan kita tentang angka "lama", yaitu rasional. 1. Beberapa simbol bahasa matematika
Ini adalah bilangan bulat, pecahan biasa, pecahan desimal. Untuk semua angka ini, Anda dapat menggunakan notasi yang sama, yang sekarang akan kita bahas. 5 = 50000... = 5,(0). Hal yang sama berlaku untuk angka 8.377: 8.377 = 8.377000... = 8.377(0). Untuk membuat semuanya rapi, mereka mengatakan ini: 8,377 adalah pecahan desimal hingga, dan 8,377000 ... adalah pecahan desimal tak terbatas. Secara umum, setiap bilangan rasional dapat ditulis sebagai pecahan periodik desimal tak terbatas. Komentar.
Kesimpulan ini cocok untuk teori, tetapi tidak terlalu nyaman untuk praktik. Lagi pula, jika pecahan desimal terakhir 8.377 diberikan, lalu mengapa perlu ditulis dalam bentuk 8.377 (0)? Oleh karena itu, mereka biasanya mengatakan ini: bilangan rasional apa pun dapat ditulis sebagai pecahan desimal hingga atau sebagai pecahan periodik desimal tak terbatas. Himpunan bilangan rasional dilambangkan dan dapat ditulis sebagai berikut: Ternyata entri yang berbeda dapat mewakili pecahan yang sama, misalnya, dan , (semua pecahan yang dapat diperoleh satu sama lain dengan mengalikan atau membagi dengan bilangan asli yang sama mewakili bilangan rasional yang sama). Karena dengan membagi pembilang dan penyebut suatu pecahan dengan pembagi persekutuan terbesarnya, seseorang dapat memperoleh satu-satunya representasi bilangan rasional yang tidak dapat direduksi, seseorang dapat menyebut himpunannya sebagai himpunan tidak dapat direduksi pecahan dengan pembilang bilangan bulat coprime dan penyebut alami: Berikut adalah pembagi persekutuan terbesar dari bilangan dan . Himpunan bilangan rasional adalah generalisasi alami dari himpunan bilangan bulat. Sangat mudah untuk melihat bahwa jika bilangan rasional memiliki penyebut , maka itu adalah bilangan bulat. Himpunan bilangan rasional di mana-mana padat pada sumbu bilangan: antara dua bilangan rasional yang berbeda setidaknya ada satu bilangan rasional (dan karenanya himpunan bilangan rasional tak terbatas). Namun, ternyata himpunan bilangan rasional memiliki kardinalitas yang dapat dihitung (yaitu, semua elemennya dapat dinomori ulang). Perhatikan, omong-omong, bahkan orang Yunani kuno pun yakin akan keberadaan bilangan yang tidak dapat dinyatakan sebagai pecahan (misalnya, mereka membuktikan bahwa tidak ada bilangan rasional yang kuadratnya adalah 2) Properti Sifat dasar Himpunan bilangan rasional memenuhi enam belas sifat dasar yang dapat dengan mudah diperoleh dari sifat-sifat bilangan bulat. Properti tambahan Semua sifat-sifat lain yang melekat pada bilangan rasional tidak dipilih sebagai sifat dasar, karena, secara umum, mereka tidak lagi didasarkan secara langsung pada sifat-sifat bilangan bulat, tetapi dapat dibuktikan berdasarkan sifat-sifat dasar yang diberikan atau langsung dengan definisi dari beberapa objek matematika. Ada banyak properti tambahan seperti itu. Masuk akal di sini untuk mengutip hanya beberapa dari mereka. 25..Set J bilangan irasional Contoh bilangan irasional: Himpunan bilangan irasional dilambangkan dengan huruf kapital bahasa Inggris [ai] - "I". Di antara himpunan bilangan, bilangan irasional menempati tempat khusus. Mereka tidak termasuk dalam bilangan rasional. Bilangan irasional(tidak seperti yang rasional) tidak dapat direpresentasikan sebagai pecahan a / b , di mana a Z (a termasuk bilangan bulat), b∈N (b termasuk bilangan asli). 26. Himpunan R bilangan real bilangan asli dari Wikipedia, ensiklopedia gratis Langsung ke: navigasi, cari Nyata, atau bilangan asli- abstraksi matematika yang muncul dari kebutuhan untuk mengukur kuantitas geometris dan fisik dunia sekitarnya, serta untuk melakukan operasi seperti mengekstraksi akar, menghitung logaritma, menyelesaikan persamaan aljabar. Nomor baris Jika bilangan asli muncul dalam proses penghitungan, bilangan rasional - dari kebutuhan untuk beroperasi dengan bagian-bagian dari keseluruhan, maka bilangan real dimaksudkan untuk mengukur kuantitas kontinu. Jadi, perluasan stok bilangan yang ditinjau telah menghasilkan himpunan bilangan real, yang, selain bilangan rasional, juga mencakup elemen lain yang disebut bilangan irasional. Konsep bilangan real dapat divisualisasikan menggunakan nomor baris. Jika Anda memilih arah pada garis lurus, titik awal dan satuan panjang untuk mengukur segmen, maka setiap bilangan real dapat dikaitkan dengan titik tertentu pada garis lurus ini, dan sebaliknya, setiap titik akan mewakili beberapa, dan terlebih lagi , hanya satu, bilangan real. Karena korespondensi ini, istilah garis bilangan biasanya digunakan sebagai sinonim untuk himpunan bilangan real. Konsep bilangan real telah berkembang jauh. Bahkan di Yunani kuno, di sekolah Pythagoras, yang menempatkan bilangan bulat dan hubungan mereka sebagai dasar untuk segala sesuatu, keberadaan jumlah yang tidak dapat dibandingkan(ketidaksebandingan sisi dan diagonal bujur sangkar), yaitu dalam terminologi modern, bilangan-bilangan yang tidak rasional. Setelah ini, Eudoxus dari Cnidus berusaha membangun teori umum bilangan yang mencakup besaran yang tidak dapat dibandingkan. Setelah itu, selama lebih dari dua ribu tahun, tidak ada yang merasa perlu definisi yang tepat dari konsep bilangan real, meskipun konsep ini berkembang secara bertahap. Hanya pada paruh kedua abad ke-19, ketika perkembangan analisis matematis membutuhkan restrukturisasi fondasinya pada tingkat ketelitian baru yang lebih tinggi, teori bilangan real yang ketat diciptakan dalam karya K. Weierstrass, R. Dedekind , G. Cantor, E. Heine, S. Mere . Dari sudut pandang matematika modern, himpunan bilangan real adalah bidang terurut yang kontinu. Definisi ini, atau sistem aksioma yang setara, secara tepat mendefinisikan konsep bilangan real dalam arti bahwa hanya ada satu, hingga isomorfisme, bidang berurutan yang kontinu. Himpunan bilangan real memiliki notasi standar - R("huruf tebal R"), atau (eng. papan tulis tebal"R") dari lat. nyata- sah. 27. Sistem bilangan Notasi- metode simbolis penulisan angka, mewakili angka menggunakan karakter tertulis. Notasi: Sistem bilangan dibagi menjadi: posisional, non-posisional dan Campuran.Bilangan irasional
Bilangan asli
Perbandingan bilangan real
Perhatikan, misalnya, bilangan bulat 5, pecahan biasa, dan desimal 8.377. Bilangan bulat 5 dapat ditulis sebagai desimal tak hingga: 5,0000... Desimal 8,377 juga dapat ditulis sebagai tak hingga pecahan desimal: 8.377000... Untuk bilangannya, mari kita gunakan metode "pembagian sudut":
Seperti yang Anda lihat, mulai dari digit kedua setelah titik desimal, kelompok angka yang sama diulang: 18, 18, 18, .... Jadi = 0,3181818... . Singkatnya, ditulis seperti ini: 0,3 (18). Sekelompok angka yang berulang setelah titik desimal disebut periode, dan pecahan desimal itu sendiri disebut pecahan periodik desimal tak terbatas.
pecahan periodik desimal tak terbatas. Untuk melakukan ini, tulis angka 0 pada periode:
Jadi, angka 5, dan angka, dan angka 8.377 ditulis sebagai pecahan periodik desimal tak hingga.![]()