Instrução
Use pi para encontrar o raio da área conhecida de um círculo. Esta constante especifica a proporção entre o diâmetro de um círculo e o comprimento de sua borda (círculo). A circunferência de um círculo é a área máxima do plano que é possível cobrir com sua ajuda, e o diâmetro é igual a dois raios, portanto, a área com o raio também se correlaciona entre si com uma proporção que pode ser expresso em termos de Pi. Esta constante (π) é definida como a área (S) e o raio quadrado (r) do círculo. Segue-se daí que o raio pode ser expresso como a raiz quadrada do quociente da divisão da área pelo número Pi: r=√(S/π).
Por muito tempo, Erastofen chefiou a Biblioteca de Alexandria, a biblioteca mais famosa do mundo antigo. Além de calcular o tamanho do nosso planeta, ele fez várias invenções e descobertas importantes. Inventou um método simples para determinar números primos, agora chamado de "peneira de Erastótenes".
Ele desenhou um "mapa do mundo", no qual mostrou todas as partes do mundo conhecidas na época pelos antigos gregos. O mapa foi considerado um dos melhores para a época. Ele desenvolveu um sistema de longitude e latitude e um calendário que incluía anos bissextos. Inventou a esfera armilar, um dispositivo mecânico usado pelos primeiros astrônomos para demonstrar e prever o movimento aparente das estrelas no céu. Ele também compilou um catálogo de estrelas, que incluiu 675 estrelas.
Origens:
- O cientista grego Eratóstenes de Cirene pela primeira vez no mundo calculou o raio da Terra
- Circunferência do "Cálculo da Terra" de Eratóstenes
- Eratóstenes
Como encontrar a área de um círculo? Primeiro encontre o raio. Aprenda a resolver problemas simples e complexos.
Um círculo é uma curva fechada. Qualquer ponto na linha do círculo estará à mesma distância do ponto central. Um círculo é uma figura plana, então é fácil resolver problemas para encontrar a área. Neste artigo, veremos como encontrar a área de um círculo inscrito em um triângulo, trapézio, quadrado e descrito em torno dessas figuras.
Para encontrar a área de uma determinada figura, você precisa saber quais são o raio, o diâmetro e o número π.
Raio Ré a distância limitada pelo centro do círculo. Os comprimentos de todos os raios R de um círculo serão iguais.
Diâmetro Dé uma linha entre quaisquer dois pontos em um círculo que passa pelo ponto central. O comprimento deste segmento é igual ao comprimento do raio R vezes 2.
Número πé um valor constante, que é igual a 3,1415926. Em matemática, esse número geralmente é arredondado para 3,14.
A fórmula para encontrar a área de um círculo usando o raio:


Exemplos de resolução de tarefas para encontrar a área S de um círculo através do raio R:
Tarefa: Encontre a área de um círculo se seu raio for 7 cm.
Decisão: S=πR², S=3,14*7², S=3,14*49=153,86 cm².
Responda: A área do círculo é 153,86 cm².
A fórmula para encontrar a área S de um círculo em termos do diâmetro D é:
Exemplos de resolução de tarefas para encontrar S, se D for conhecido:
————————————————————————————————————————-
Tarefa: Encontre o S do círculo se seu D for 10 cm.
Decisão: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 cm².
Responda: A área de uma figura redonda plana é de 78,5 cm².
Encontrando o círculo S se a circunferência for conhecida:
Primeiro, descubra qual é o raio. A circunferência é calculada pela fórmula: L=2πR, respectivamente, o raio R será igual a L/2π. Agora encontramos a área do círculo usando a fórmula por R.
Considere a solução no exemplo do problema:
———————————————————————————————————————-
Tarefa: Encontre a área de um círculo se a circunferência L for conhecida - 12 cm.
Decisão: Primeiro encontramos o raio: R=L/2π=12/2*3,14=12/6,28=1,91.
Agora encontramos a área através do raio: S=πR²=3,14*1,91²=3,14*3,65=11,46 cm².
Responda: A área de um círculo é 11,46 cm².


Encontrar a área de um círculo inscrito em um quadrado é fácil. O lado do quadrado é o diâmetro do círculo. Para encontrar o raio, você precisa dividir o lado por 2.
A fórmula para encontrar a área de um círculo inscrito em um quadrado é:
Exemplos de resolução de problemas para encontrar a área de um círculo inscrito em um quadrado:
———————————————————————————————————————
Tarefa nº 1: O lado de uma figura quadrada é conhecido, que é igual a 6 centímetros. Encontre a área S do círculo inscrito.
Decisão: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 cm².
Responda: A área de uma figura redonda plana é de 28,26 cm².
————————————————————————————————————————
Tarefa nº 2: Encontre S de um círculo inscrito em uma figura quadrada e seu raio se um lado é a = 4 cm.
Decida assim: Primeiro encontre R=a/2=4/2=2 cm.
Agora vamos encontrar a área do círculo S=3,14*2²=3,14*4=12,56 cm².
Responda: A área de uma figura redonda plana é de 12,56 cm².


É um pouco mais difícil encontrar a área de uma figura redonda circunscrita por um quadrado. Mas, conhecendo a fórmula, você pode calcular rapidamente esse valor.
A fórmula para encontrar S de um círculo circunscrito a uma figura quadrada:
Exemplos de resolução de tarefas para encontrar a área de um círculo descrito perto de uma figura quadrada:
Tarefa




Um círculo que está inscrito em uma figura triangular é um círculo que toca todos os três lados do triângulo. Um círculo pode ser inscrito em qualquer figura triangular, mas apenas em uma. O centro do círculo será o ponto de intersecção das bissetrizes dos ângulos do triângulo.
A fórmula para encontrar a área de um círculo inscrito em um triângulo isósceles é:


Quando o raio é conhecido, a área pode ser calculada usando a fórmula: S=πR².
A fórmula para encontrar a área de um círculo inscrito em um triângulo retângulo é:


Exemplos de resolução de tarefas:
Tarefa nº 1


Se neste problema você também precisa encontrar a área de um círculo com raio de 4 cm, isso pode ser feito usando a fórmula: S=πR²
Tarefa nº 2


Decisão:


Agora que você conhece o raio, pode encontrar a área do círculo em termos do raio. Veja a fórmula acima.
Tarefa nº 3


Área de um círculo circunscrito a um triângulo retângulo e isósceles: fórmula, exemplos de resolução de problemas
Todas as fórmulas para encontrar a área de um círculo se resumem ao fato de que primeiro você precisa encontrar seu raio. Quando o raio é conhecido, encontrar a área é simples, conforme descrito acima.
A área de um círculo circunscrito a um triângulo retângulo e isósceles é encontrada pela seguinte fórmula:


Exemplos de resolução de problemas:


Aqui está outro exemplo de solução de um problema usando a fórmula de Heron.


Resolver esses problemas é difícil, mas eles podem ser dominados se você conhecer todas as fórmulas. Os alunos resolvem esses problemas no 9º ano.
Área de um círculo inscrito em um trapézio retangular e isósceles: fórmula, exemplos de resolução de problemas
Um trapézio isósceles tem dois lados iguais. Um trapézio retangular tem um ângulo igual a 90º. Considere como encontrar a área de um círculo inscrito em um trapézio retangular e isósceles usando o exemplo de resolução de problemas.
Por exemplo, um círculo está inscrito em um trapézio isósceles, que no ponto de contato divide um lado em segmentos m e n.
Para resolver este problema, você precisa usar as seguintes fórmulas:


A área de um círculo inscrito em um trapézio retangular é encontrada usando a seguinte fórmula:


Se o lado lateral for conhecido, você poderá encontrar o raio através desse valor. A altura do lado do trapézio é igual ao diâmetro do círculo e o raio é metade do diâmetro. Assim, o raio é R=d/2.
Exemplos de resolução de problemas:


Um trapézio pode ser inscrito em um círculo quando a soma de seus ângulos opostos é 180º. Portanto, apenas um trapézio isósceles pode ser inscrito. O raio para calcular a área de um círculo circunscrito a um trapézio retangular ou isósceles é calculado usando as seguintes fórmulas:




Exemplos de resolução de problemas:


Decisão: A base grande neste caso passa pelo centro, pois um trapézio isósceles está inscrito em um círculo. O centro divide essa base exatamente pela metade. Se a base AB for 12, então o raio R pode ser encontrado da seguinte forma: R=12/2=6.
Responda: O raio é 6.
Em geometria, é importante conhecer as fórmulas. Mas é impossível lembrar de todos eles, então mesmo em muitos exames é permitido usar um formulário especial. No entanto, é importante ser capaz de encontrar a fórmula certa para resolver um problema específico. Pratique a resolução de diferentes problemas para encontrar o raio e a área de um círculo para poder substituir fórmulas corretamente e obter respostas precisas.
Vídeo: Matemática | Calculando a área de um círculo e suas partes
- Esta é uma figura plana, que é um conjunto de pontos equidistantes do centro. Todos eles estão à mesma distância e formam um círculo.
Um segmento de linha que liga o centro de um círculo com pontos em sua circunferência é chamado raio. Em cada círculo, todos os raios são iguais entre si. A linha que une dois pontos de uma circunferência e passa pelo centro chama-se diâmetro. A fórmula para a área de um círculo é calculada usando uma constante matemática - o número π ..
É interessante : O número pi. é a razão entre a circunferência de um círculo e o comprimento de seu diâmetro e é um valor constante. O valor π = 3,1415926 foi usado após o trabalho de L. Euler em 1737.
A área de um círculo pode ser calculada usando a constante π. e o raio do círculo. A fórmula para a área de um círculo em termos de raio é assim:
![]()
Considere um exemplo de cálculo da área de um círculo usando o raio. Seja dado um círculo com raio R = 4 cm. Vamos encontrar a área da figura.
A área do nosso círculo será igual a 50,24 metros quadrados. cm.
Existe uma fórmula a área de um círculo através do diâmetro. Também é amplamente utilizado para calcular os parâmetros necessários. Essas fórmulas podem ser usadas para encontrar .

Considere um exemplo de cálculo da área de um círculo através do diâmetro, conhecendo seu raio. Seja dado um círculo com um raio R = 4 cm Primeiro, vamos encontrar o diâmetro, que, como você sabe, é o dobro do raio.
Agora usamos os dados para o exemplo de cálculo da área de um círculo usando a fórmula acima:
Como você pode ver, como resultado, obtemos a mesma resposta que nos primeiros cálculos.
O conhecimento das fórmulas padrão para calcular a área de um círculo ajudará no futuro a determinar facilmente área do setor e é fácil encontrar as quantidades que faltam.
Já sabemos que a fórmula da área de um círculo é calculada pelo produto do valor constante π e o quadrado do raio do círculo. O raio pode ser expresso em termos da circunferência de um círculo e substituir a expressão na fórmula da área de um círculo em termos da circunferência:
Agora substituímos essa igualdade na fórmula para calcular a área de um círculo e obtemos a fórmula para encontrar a área do círculo, através da circunferência

Considere um exemplo de cálculo da área de um círculo através da circunferência. Seja um círculo com comprimento l = 8 cm. Vamos substituir o valor na fórmula derivada: 
A área total do círculo será de 5 metros quadrados. cm.
Área de um círculo circunscrito ao redor de um quadrado

É muito fácil encontrar a área de um círculo circunscrito em torno de um quadrado.
Isso exigirá apenas o lado do quadrado e o conhecimento de fórmulas simples. A diagonal do quadrado será igual à diagonal do círculo circunscrito. Conhecendo o lado a, ele pode ser encontrado usando o teorema de Pitágoras: daqui.
Depois de encontrarmos a diagonal, podemos calcular o raio: .
E então substituímos tudo na fórmula básica para a área de um círculo circunscrito ao redor de um quadrado:
Os círculos exigem uma abordagem mais cuidadosa e são muito menos comuns em tarefas B5. Ao mesmo tempo, o esquema geral de solução é ainda mais simples do que no caso de polígonos (consulte a lição " Áreas de polígonos em uma grade de coordenadas »).
Tudo o que é necessário em tais tarefas é encontrar o raio do círculo R . Então você pode calcular a área do círculo usando a fórmula S = πR 2 . Também segue desta fórmula que é suficiente encontrar R 2 para a solução.
Para encontrar os valores indicados, basta indicar no círculo um ponto situado na interseção das linhas da grade. E então use o teorema de Pitágoras. Considere exemplos específicos de cálculo do raio:
Tarefa. Encontre os raios dos três círculos mostrados na figura:
Vamos realizar construções adicionais em cada círculo:
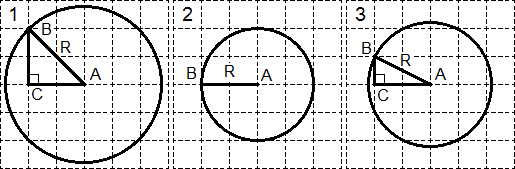
Em cada caso, o ponto B é escolhido no círculo para estar na interseção das linhas de grade. O ponto C nos círculos 1 e 3 completa a figura para um triângulo retângulo. Resta encontrar os raios:
Considere o triângulo ABC no primeiro círculo. De acordo com o teorema de Pitágoras: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.
Para o segundo círculo, tudo é óbvio: R = AB = 2.
O terceiro caso é semelhante ao primeiro. Do triângulo ABC de acordo com o teorema de Pitágoras: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 1 2 + 2 2 \u003d 5.
Agora sabemos como encontrar o raio de um círculo (ou pelo menos seu quadrado). Portanto, podemos encontrar a área. Existem tarefas em que é necessário encontrar a área de um setor, e não o círculo inteiro. Nesses casos, é fácil descobrir qual parte do círculo é esse setor e, assim, encontrar a área.
Tarefa. Encontre a área S do setor sombreado. Indique S / π em sua resposta.
Obviamente, o setor é um quarto do círculo. Portanto, S = 0,25 S do círculo.
Resta encontrar o S do círculo - a área do círculo. Para fazer isso, vamos realizar uma construção adicional:
O triângulo ABC é um triângulo retângulo. Pelo teorema de Pitágoras, temos: R 2 \u003d AB 2 \u003d AC 2 + BC 2 \u003d 2 2 + 2 2 \u003d 8.
Agora encontramos a área do círculo e o setor: S do círculo = πR 2 = 8π; S = 0,25 S círculo = 2π.
Finalmente, o valor desejado é igual a S /π = 2.
Área do setor com raio desconhecido
Este é um tipo de tarefa completamente novo, não havia nada parecido em 2010-2011. Por condição, nos é dado um círculo de uma certa área (ou seja, a área, não o raio!). Então, dentro desse círculo, é alocado um setor, cuja área deve ser encontrada.
A boa notícia é que esses problemas são os mais fáceis de todos os problemas do quadrado, que estão no exame de matemática. Além disso, o círculo e o setor são sempre colocados na grade de coordenadas. Portanto, para aprender a resolver esses problemas, basta dar uma olhada na imagem:

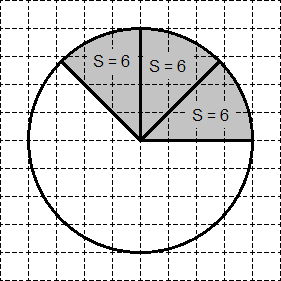
Deixe o círculo original ter área S do círculo = 80. Então ele pode ser dividido em dois setores de área S = 40 cada (veja o passo 2). Da mesma forma, cada um desses "meios" setores pode ser dividido pela metade novamente - obtemos quatro setores de área S = 20 cada (veja o passo 3). Finalmente, você pode dividir cada um desses setores em mais dois - obtemos 8 setores - "pequenos pedaços". A área de cada um desses "pedaços" será S = 10.
Observe: não há divisão menor em nenhuma tarefa USE em matemática! Assim, o algoritmo para resolver o problema B-3 é o seguinte:
- Corte o círculo original em 8 setores - "peças". A área de cada um deles é exatamente 1/8 da área de todo o círculo. Por exemplo, se de acordo com a condição o círculo tem a área S do círculo = 240, então os “grumos” têm a área S = 240: 8 = 30;
- Descubra quantos "grumos" cabem no setor original, cuja área você deseja encontrar. Por exemplo, se nosso setor contém 3 “grumos” com área de 30, então a área do setor desejado é S = 3 30 = 90. Esta será a resposta.
Isso é tudo! O problema é resolvido praticamente oralmente. Se você ainda não entendeu alguma coisa, compre uma pizza e corte-a em 8 pedaços. Cada uma dessas peças será o mesmo setor - "pedaço" que pode ser combinado em peças maiores.
E agora vamos ver exemplos do exame de teste:
Tarefa. Um círculo com área de 40 é desenhado em papel quadriculado. Encontre a área da figura sombreada.
Então, a área do círculo é 40. Divida-o em 8 setores - cada um com uma área de S = 40: 5 = 8. Obtemos:
Obviamente, o setor sombreado consiste em exatamente dois setores "pequenos". Portanto, sua área é 2 5 = 10. Essa é toda a solução!
Tarefa. Um círculo com área de 64 é desenhado em papel quadriculado. Encontre a área da figura sombreada.
Novamente, divida o círculo inteiro em 8 setores iguais. Obviamente, a área de um deles só precisa ser encontrada. Portanto, sua área é S = 64: 8 = 8.
Tarefa. Um círculo com área de 48 é desenhado em papel quadriculado. Encontre a área da figura sombreada.
Novamente, divida o círculo em 8 setores iguais. A área de cada um deles é igual a S = 48: 8 = 6. Exatamente três setores "pequenos" são colocados no setor desejado (veja a figura). Portanto, a área do setor desejado é 3 6 = 18.