Às vezes, essas integrais impróprias são chamadas integrais impróprias de segunda espécie. Integrais impróprias do segundo tipo são insidiosamente “criptografadas” sob a integral definida usual e têm exatamente a mesma aparência: .
Mas, ao contrário de uma integral definida, o integrando tem uma descontinuidade infinita (não existe):
1) no ponto ,
2) ponto,
3) em ambos os pontos ao mesmo tempo,
4) ou ainda no intervalo de integração.
Veremos os dois primeiros casos; para os casos 3-4, no final do artigo há um link para uma lição adicional.
Vejamos um exemplo para deixar claro:
Parece ser uma integral definida. Mas, na verdade, esta é uma integral imprópria de segundo tipo, pois se substituirmos no integrando, então o valor do limite inferior
então nosso denominador vai para zero, ou seja, o integrando simplesmente não existe neste ponto!
Ao analisar a integral imprópria você sempre precisa substituir ambos os limites de integração no integrando. A este respeito, vamos verificar o limite superior:
Está tudo bem aqui. O trapézio curvilíneo para o tipo de integral imprópria em consideração se parece fundamentalmente com isto:
Aqui tudo é quase igual à integral do primeiro tipo. Nossa integral é numericamente igual à área do trapézio curvo sombreado, que não é limitado por cima. Nesse caso, pode haver duas opções: a integral imprópria diverge (a área é infinita), ou a integral imprópria é igual a um número finito (quando a área de uma figura infinita é finita!).
Resta apenas modificar a fórmula de Newton-Leibniz. Também é modificado com a ajuda de um limite, mas o limite não tende mais ao infinito, mas dar valor na direita.É fácil traçar pelo desenho que ao longo do eixo BOI na direita.
Vamos ver como isso é implementado na prática.
Exemplo 6
(não se esqueça de verificar verbalmente ou em rascunho se está tudo bem com o limite superior!). Primeiro, vamos calcular a integral indefinida:
Se você tiver alguma dificuldade com a substituição, consulte a lição Método de substituição em integral indefinida.
Vamos calcular a integral imprópria:
(1) O que há de novo aqui? Não há praticamente nada em termos de tecnologia de solução. A única coisa que mudou foi a entrada abaixo do ícone de limite:
A adição de +0 significa que estamos buscando um valor de ¾ à direita, o que é lógico (ver gráfico). Tal limite na teoria dos limites é chamado limite unilateral. Neste caso temos limite à direita.
(2) Substituímos os limites superior e inferior usando a fórmula de Newton-Leibniz.
(3) Vamos lidar com em. Como determinar para onde vai uma expressão? Grosso modo, basta substituir o valor nele, substituir três quartos e indicar isso . Vamos pentear a resposta.
Neste caso, a integral imprópria é igual a um número negativo. Não há crime nisso, apenas o trapézio curvo correspondente está localizado sob o eixo BOI. E agora exemplos de soluções independentes.
Exemplo 7
Calcule a integral imprópria ou estabeleça sua divergência.
Exemplo 8
Calcule a integral imprópria ou estabeleça sua divergência.
Se o integrando não existir no ponto
Um trapézio curvo infinito para uma integral imprópria se parece fundamentalmente com isto:
Aqui fazemos tudo absolutamente igual, exceto que nosso limite tende a dar valor besquerda. Eixo BOI devemos chegar infinitamente perto do ponto de ruptura esquerda.
Exemplo 9
Calcule a integral imprópria ou estabeleça sua divergência.
O integrando sofre uma descontinuidade infinita no ponto b = 3 (verificamos verbalmente se está tudo bem com o outro limite de integração!).
Para variar, vamos resolver esse limite imediatamente - subsumindo a função sob o sinal diferencial. Aqueles que acharem difícil podem primeiro encontrar a integral indefinida usando o esquema já discutido.
A adição (-0) significa que temos um limite canhoto, e direto ao ponto b = 3 estamos nos aproximando do eixo BOI esquerda.
Vamos descobrir por que a fração
(é melhor fazer isso oralmente ou em rascunho).
Substituímos o valor limite na raiz b = 3 - 0.
Finalmente:
A integral imprópria diverge.
O sinal menos significa que o trapézio curvo correspondente está localizado sob o eixo BOI. Tenha muito cuidado com os sinais.
Sim, claro, a integral imprópria diverge, mas ambas são coisas diferentes, gêneros diferentes, e se você deixar de prestar atenção aos sinais, então, a rigor, você cometerá um erro grave.
E os dois exemplos finais para consideração independente:
Exemplo 10
Calcule a integral imprópria ou estabeleça sua divergência.
Exemplo 11
Calcule a integral imprópria ou estabeleça sua divergência.
Uma análise da situação quando ambos os limites de integração são “ruins”, ou o ponto de ruptura está contido diretamente no segmento de integração, pode ser encontrada no artigo Métodos eficientes para resolver integrais definidas e impróprias.
Soluções e respostas:
Exemplo 4: Solução:
.
Exemplo 5: Solução:
A função integrando é contínua em .
Exemplo 7: Solução:
O integrando sofre uma descontinuidade infinita no ponto
A integral imprópria diverge.
Nota: com limite de expressão
Integrais impróprias de primeiro tipo. Em essência, esta é a mesma integral definida, mas nos casos em que as integrais têm limites de integração superiores ou inferiores infinitos, ou ambos os limites de integração são infinitos.
Integrais impróprias de segundo tipo. Em essência, esta é a mesma integral definida, mas nos casos em que a integral é retirada de funções ilimitadas, o integrando em um número finito de pontos não possui um segmento finito de integração, voltando-se para o infinito.
Para comparação. Ao introduzir o conceito de integral definida, assumiu-se que a função f(x) é contínuo no intervalo [ a, b], e o segmento de integração é finito, ou seja, é limitado por números, e não pelo infinito. Algumas tarefas levam à necessidade de abandonar essas restrições. É assim que aparecem as integrais impróprias.
Significado geométrico da integral imprópria Acontece de forma bastante simples. No caso em que o gráfico de uma função sim = f(x) está acima do eixo Boi, a integral definida expressa a área de um trapézio curvilíneo delimitado por uma curva sim = f(x) , eixo x e ordenadas x = a , x = b. Por sua vez, a integral imprópria expressa a área de um trapézio curvilíneo ilimitado (infinito) encerrado entre as linhas sim = f(x) (na foto abaixo - vermelho), x = a e o eixo das abcissas.
Integrais impróprias são definidas de forma semelhante para outros intervalos infinitos:
A área de um trapézio curvo infinito pode ser um número finito, caso em que a integral imprópria é chamada convergente. A área também pode ser infinita e, neste caso, a integral imprópria é chamada de divergente.
Usando o limite de uma integral em vez da própria integral imprópria. Para calcular a integral imprópria, é necessário usar o limite da integral definida. Se esse limite existe e é finito (não igual ao infinito), então a integral imprópria é chamada de convergente, caso contrário - divergente. O que uma variável tende sob o sinal limite depende se estamos lidando com uma integral imprópria de primeiro tipo ou de segundo tipo. Vamos descobrir isso agora.
Integrais impróprias de primeiro tipo - com limites infinitos e sua convergência
Integrais impróprias com limite superior infinito
Assim, escrever uma integral imprópria difere da integral definida usual porque o limite superior da integração é infinito.
Definição. Uma integral imprópria com um limite superior infinito de integração de uma função contínua f(x) no intervalo de a antes ∞ o limite da integral desta função com o limite superior de integração é chamado b e o limite inferior de integração a desde que o limite superior de integração cresça sem limite, ou seja
.
Se este limite existir e for igual a algum número em vez de infinito, então uma integral imprópria é chamada convergente, e o número ao qual o limite é igual é considerado seu valor. De outra forma uma integral imprópria é chamada divergente e nenhum significado é atribuído a ele.
Exemplo 1. Calcular integral imprópria(se convergir).
Solução. Com base na definição da integral imprópria, encontramos
Como o limite existe e é igual a 1, então este Integrais impróprias convergem e é igual a 1.
No exemplo a seguir, o integrando é quase o mesmo do exemplo 1, apenas o grau x não é dois, mas a letra alfa, e a tarefa é estudar a integral imprópria para convergência. Ou seja, resta a questão a ser respondida: para quais valores de alfa essa integral imprópria converge e para quais valores ela diverge?
Exemplo 2. Examine a integral imprópria para convergência(o limite inferior de integração é maior que zero).
Solução. Vamos primeiro supor que , então
Na expressão resultante, passamos para o limite em:
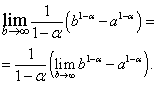
É fácil ver que o limite do lado direito existe e é igual a zero quando, isto é, e não existe quando, isto é.
No primeiro caso, isto é, quando . Se então 
e não existe.
A conclusão do nosso estudo é a seguinte: este Integrais impróprias convergem em e diverge no .
Aplicando a fórmula de Newton-Leibniz ao tipo de integral imprópria em estudo 
, você pode derivar a seguinte fórmula, que é muito semelhante a ela:
.
Esta é uma fórmula generalizada de Newton-Leibniz.
Exemplo 3. Calcular integral imprópria(se convergir).
O limite desta integral existe:
A segunda integral, constituindo a soma que expressa a integral original:
O limite desta integral também existe:
.
Encontramos a soma de duas integrais, que também é o valor da integral imprópria original com dois limites infinitos:
Integrais impróprias de segundo tipo - de funções ilimitadas e sua convergência
Deixe a função f(x) dado no segmento de a antes b e é ilimitado nele. Suponha que a função vá para o infinito no ponto b , enquanto em todos os outros pontos do segmento é contínuo.
Definição. Uma integral imprópria de uma função f(x) no segmento de a antes b o limite da integral desta função com o limite superior de integração é chamado c , se ao se esforçar c Para b a função aumenta sem limite, e no ponto x = b função não definida, ou seja
.
Se esse limite existir, então a integral imprópria de segundo tipo é chamada de convergente, caso contrário é chamada de divergente.
Usando a fórmula de Newton-Leibniz, derivamos.
Integral definida como o limite da soma integral
pode existir (ou seja, ter um determinado valor final) somente se as condições forem atendidas
Se pelo menos uma dessas condições for violada, a definição perde o significado. Na verdade, no caso de um segmento infinito, por exemplo [ a; ) não pode ser dividido em P partes de comprimento finito 
, que, aliás, tenderia a zero com o aumento do número de segmentos. No caso de ilimitado em algum momento Com[a;
b] o requisito para seleção arbitrária de pontos é violado 
em segmentos parciais – não pode ser selecionado 
=Com, já que o valor da função neste ponto é indefinido. Porém, mesmo para estes casos é possível generalizar o conceito de integral definida introduzindo outra passagem até o limite. Integrais sobre intervalos infinitos e sobre funções descontínuas (ilimitadas) são chamadas não é seu.
Definição.
Deixe a função 
é definido no intervalo [ a; ) e é integrável em qualquer intervalo finito [ a;
b], ou seja existe 
para qualquer um b
> a. Limite de tipo 
chamado totalmente inapropriado
primeiro tipo
(ou uma integral imprópria em um intervalo infinito) e denotam 
.
Assim, por definição, 
=
.
Se o limite à direita existe e é finito, então a integral imprópria 
chamado convergente
. Se este limite for infinito, ou não existir, então dizem que a integral imprópria diverge
.
Da mesma forma, podemos introduzir o conceito de integral imprópria da função 
ao longo do intervalo (–; b]:
=
.
E a integral imprópria da função 
no intervalo (–; +) é definido como a soma das integrais introduzidas acima:
=
+
,
Onde A– ponto arbitrário. Esta integral converge se ambos os termos convergirem e diverge se pelo menos um dos termos diverge.
Do ponto de vista geométrico, a integral 
,
, determina o valor numérico da área de um trapézio curvilíneo infinito limitado acima pelo gráfico da função 
, esquerda – direto 
, de baixo – pelo eixo OX. A convergência da integral significa a existência de uma área finita de tal trapézio e sua igualdade ao limite da área de um trapézio curvilíneo com parede direita móvel 
.
Para o caso de uma integral com limite infinito, podemos generalizar Fórmula de Newton-Leibniz:
=
=F( +
) – F( a),
onde F( +
)
=
. Se este limite existir, então a integral converge, caso contrário diverge.
Consideramos uma generalização do conceito de integral definida para o caso de um intervalo infinito.
Consideremos agora uma generalização para o caso de uma função ilimitada.
Definição
Deixe a função 
é definido no intervalo [ a;
b), é ilimitado em alguma vizinhança do ponto b, e é contínuo em qualquer intervalo 
, onde >0 (e, portanto, integrável neste intervalo, ou seja, 
existe). Limite de tipo 
chamado integral imprópria de segundo tipo
(ou uma integral imprópria de uma função ilimitada) e é denotado 
.
Assim, a integral imprópria do ilimitado no ponto b funções existem por definição
=
.
Se o limite à direita existe e é finito, então a integral é chamada convergente. Se não houver limite finito, então a integral imprópria é chamada divergente.
Da mesma forma, podemos definir a integral imprópria da função 
tendo uma descontinuidade infinita no ponto A:
=
.
Se a função 
tem uma descontinuidade infinita no ponto interior Com
, então a integral imprópria é definida como segue
=
+
=
+
.
Esta integral converge se ambos os termos convergirem e diverge se pelo menos um termo diverge.
Do ponto de vista geométrico, a integral imprópria de uma função ilimitada também caracteriza a área de um trapézio curvo ilimitado:
Como uma integral imprópria é derivada passando ao limite de uma integral definida, todas as propriedades de uma integral definida podem ser transferidas (com refinamentos apropriados) para integrais impróprias de primeiro e segundo tipo.
Em muitos problemas que levam a integrais impróprias, não é necessário saber a que é igual essa integral, basta apenas verificar sua convergência ou divergência. Para isso eles usam sinais de convergência. Sinais de convergência de integrais impróprias:
1) Sinal de comparação.
Que seja para todos X
. Então se 
converge, depois converge 
, e 
. Se 
diverge, depois diverge e 
.
2) Se converge 
, então converge e 
(a última integral neste caso é chamada absolutamente convergente).
Os sinais de convergência e divergência de integrais impróprias de funções ilimitadas são semelhantes aos formulados acima.
Exemplos de resolução de problemas.
Exemplo 1.
A) 
; b) 
; V) 
G) 
; e) 
.
Solução.
a) Por definição temos:
.
b) Da mesma forma
Portanto, esta integral converge e é igual a 
.
c) Por definição 
=
+
, e A– número arbitrário. Vamos colocar no nosso caso 
, então obtemos:
Esta integral converge.
Isso significa que esta integral diverge.
e) Considere 
. Para encontrar a antiderivada do integrando, é necessário aplicar o método de integração por partes. Então obtemos:
Já que nem 
, nem 
não existe, então não existe e
Portanto, esta integral diverge.
Exemplo 2.
Investigue a convergência da integral 
dependendo do P.
Solução.
No 
Nós temos:
Se 
, Que 
E . Portanto, a integral diverge.
Se 
, Que 
, A 
, Então
=
,
Portanto, a integral converge.
Se 
, Que
portanto, a integral diverge.
Por isso, 
Exemplo 3.
Calcule a integral imprópria ou estabeleça sua divergência:
A) 
; b) 
; V) 
.
Solução.
a) Integral 
é uma integral imprópria de segundo tipo, uma vez que o integrando 
não limitado em um ponto 
. Então, por definição,
.
A integral converge e é igual a 
.
b) Considere 
. Aqui também o integrando não está limitado no ponto 
. Portanto, esta integral é imprópria de segundo tipo e, por definição,
Portanto, a integral diverge.
c) Considere 
. Integrando 
sofre uma lacuna infinita em dois pontos: 
E 
, o primeiro dos quais pertence ao intervalo de integração 
. Consequentemente, esta integral é uma integral imprópria de segundo tipo. Então, por definição
=
=
.
Portanto, a integral converge e é igual a 
.
Você está aqui agora? =) Não, eu não estava tentando intimidar ninguém, só que o tópico das integrais impróprias é uma ilustração muito boa de como é importante não negligenciar a matemática superior e outras ciências exatas. Tudo o que você precisa para aprender a lição está no site - de forma detalhada e acessível, se desejar...
Então, vamos começar. Falando figurativamente, uma integral imprópria é uma integral definida “avançada” e, de fato, não há tantas dificuldades com elas e, além disso, a integral imprópria tem um significado geométrico muito bom.
O que significa avaliar uma integral imprópria?
Calcular integral imprópria - isso significa encontrar o NÚMERO(exatamente o mesmo que na integral definida), ou provar que diverge(ou seja, você acaba com o infinito em vez de um número).
Existem dois tipos de integrais impróprias.
Integral imprópria com limite(s) infinito(s) de integração
Às vezes, essa integral imprópria é chamada integral imprópria de primeiro tipo. Em geral, uma integral imprópria com limite infinito geralmente se parece com isto: . Como é diferente de uma integral definida? No limite superior. É infinito: .
Menos comuns são as integrais com um limite inferior infinito ou com dois limites infinitos: , e veremos elas mais tarde - quando você pegar o jeito :)
Bem, agora vamos dar uma olhada no caso mais popular. Na grande maioria dos exemplos, a função integrando contínuo no meio, e este fato importante deve ser verificado primeiro! Porque se houver lacunas, haverá nuances adicionais. Para ser definitivo, vamos supor que mesmo então o típico trapézio curvo ficará assim:
Observe que é infinito (não limitado à direita), e totalmente inapropriado numericamente igual à sua área. As seguintes opções são possíveis:
1) O primeiro pensamento que vem à mente: “já que a figura é infinita, então 
", ou seja, a área também é infinita. Pode ser que sim. Neste caso dizem que a integral imprópria diverge.
2) Mas. Por mais paradoxal que possa parecer, a área de uma figura infinita pode ser igual a... um número finito! Por exemplo: . Isso poderia ser verdade? Facilmente. No segundo caso, a integral imprópria converge.
3) Sobre a terceira opção um pouco mais tarde.
Em que casos uma integral imprópria diverge e em que casos converge? Isso depende do integrando e veremos exemplos específicos em breve.
O que acontece se um trapézio curvo infinito estiver localizado abaixo do eixo? Neste caso, a integral imprópria 
(diverge) ou é igual a um número negativo finito.
Por isso, integral imprópria pode ser negativa.
Importante! Quando você recebe QUALQUER integral imprópria para resolver, então, de modo geral, não se fala em nenhuma área e não há necessidade de fazer desenho. Expliquei o significado geométrico da integral imprópria apenas para facilitar a compreensão do material.
Como a integral imprópria é muito semelhante à integral definida, lembremos a fórmula de Newton-Leibniz: 
. Na verdade, a fórmula também é aplicável a integrais impróprias, mas precisa ser ligeiramente modificada. Qual é a diferença? No limite superior infinito de integração: . Provavelmente muitos adivinharam que isso já lembra a aplicação da teoria dos limites, e a fórmula será escrita assim: 
.
Qual é a diferença de uma integral definida? Nada especial! Como na integral definida, você precisa ser capaz de encontrar a função antiderivada (integral indefinida) e aplicar a fórmula de Newton-Leibniz. A única coisa que foi acrescentada é o cálculo do limite. Quem passa mal com eles, aprenda uma lição Limites de função. Exemplos de soluções, porque é melhor tarde do que no exército.
Vejamos dois exemplos clássicos:
Exemplo 1
Para maior clareza, farei um desenho, embora, enfatizo mais uma vez, na prática Não há necessidade de construir desenhos nesta tarefa.
A função integrando é contínua no meio intervalo, o que significa que está tudo bem e a integral imprópria pode ser calculada pelo método “padrão”.
Aplicação da nossa fórmula 
e a solução para o problema fica assim:
Ou seja, a integral imprópria diverge e a área do trapézio curvo sombreado é igual ao infinito.
No exemplo considerado, temos a integral de tabela mais simples e a mesma técnica de aplicação da fórmula de Newton-Leibniz da integral definida. Mas esta fórmula será aplicada sob o signo do limite. Em vez da letra usual de uma variável “dinâmica”, aparece a letra “ser”. Isso não deve confundir ou confundir, porque qualquer letra não é pior que o “X” padrão.
Se você não entende por que em , então isso é muito ruim, ou você não entende os limites mais simples (e geralmente não entende o que é um limite) ou não sabe como é o gráfico de uma função logarítmica. No segundo caso, assista a uma aula Gráficos e propriedades de funções elementares.
Ao resolver integrais impróprias, é muito importante saber como são os gráficos das funções elementares básicas!
A tarefa finalizada deve ser semelhante a esta:
“
! Ao preparar um exemplo, sempre interrompemos a solução e indicamos o que acontece com o integrando – é contínuo no intervalo de integração ou não?. Com isso identificamos o tipo de integral imprópria e justificamos ações posteriores.
Exemplo 2
Calcule a integral imprópria ou estabeleça sua divergência.
Vamos fazer o desenho: 
Primeiro, notamos o seguinte: o integrando é contínuo no meio intervalo. Capuz. Resolvemos usando a fórmula 
:
(1) Tomamos a integral mais simples de uma função potência (este caso especial está em muitas tabelas). É melhor mover imediatamente o sinal de menos além do sinal de limite para que não atrapalhe em cálculos posteriores.
(2) Substituímos os limites superior e inferior usando a fórmula de Newton-Leibniz.
(3) Indicamos que em (Senhores, isso já deveria ter sido entendido há muito tempo) e simplificamos a resposta.
Aqui a área de um trapézio curvo infinito é um número finito! Inacreditável, mas é verdade.
O exemplo finalizado deve ser parecido com isto:
“
A função integrando é contínua em
“
O que fazer se você encontrar uma integral como - com ponto de interrupção no intervalo de integração? Isso significa que há um erro de digitação no exemplo. (Provavelmente), ou sobre um nível avançado de treinamento. Neste último caso, devido propriedades de aditividade, devemos considerar duas integrais impróprias em intervalos e então lidar com a soma.
Às vezes, devido a um erro de digitação ou intenção, uma integral imprópria pode não existe de jeito nenhum, então, por exemplo, se você colocar a raiz quadrada de “x” no denominador da integral acima, então parte do intervalo de integração não será incluída no domínio de definição do integrando.
Além disso, a integral imprópria pode não existir mesmo com todo o “bem-estar aparente”. Exemplo clássico: . Apesar da definição e continuidade do cosseno, tal integral imprópria não existe! Por que? É muito simples porque:
- não existe limite apropriado.
E tais exemplos, embora raros, ocorrem na prática! Assim, além da convergência e da divergência, há também um terceiro resultado da solução com uma resposta válida: “não existe integral imprópria”.
Ressalta-se também que a definição estrita de integral imprópria se dá justamente através do limite, e quem desejar pode se familiarizar com ela na literatura educacional. Bem, continuamos a lição prática e passamos para tarefas mais significativas:
Exemplo 3
Calcule a integral imprópria ou estabeleça sua divergência.
Primeiro, vamos tentar encontrar a função antiderivada (integral indefinida). Se não conseguirmos fazer isto, naturalmente também não seremos capazes de resolver a integral imprópria.
A qual das integrais de tabela o integrando é semelhante? Isso me lembra um arco tangente: 
. Estas considerações sugerem que seria bom ter um quadrado no denominador. Isso é feito por substituição.
Vamos substituir:
A integral indefinida foi encontrada, neste caso não faz sentido adicionar uma constante;
É sempre útil verificar o rascunho, ou seja, diferenciar o resultado obtido:
O integrando original foi obtido, o que significa que a integral indefinida foi encontrada corretamente.
Agora encontramos a integral imprópria:
(1) Escrevemos a solução de acordo com a fórmula 
. É melhor mover imediatamente a constante além do sinal limite para que ela não interfira em cálculos posteriores.
(2) Substituímos os limites superior e inferior de acordo com a fórmula de Newton-Leibniz. Por que 
no ? Veja o gráfico arco tangente no artigo já recomendado.
(3) Obtemos a resposta final. Um fato que é útil saber de cor.
Os alunos avançados podem não encontrar a integral indefinida separadamente e não usar o método de substituição, mas sim usar o método de substituir a função sob o sinal diferencial e resolver a integral imprópria “imediatamente”. Neste caso, a solução deve ser mais ou menos assim:
“
O integrando é contínuo em . 
“
Exemplo 4
Calcule a integral imprópria ou estabeleça sua divergência.
! Este é um exemplo típico e integrais semelhantes são encontradas com muita frequência. Resolva bem! A função antiderivada aqui é encontrada usando o método de seleção de um quadrado completo. Mais detalhes sobre o método podem ser encontrados na lição; Integrando Algumas Frações.
Exemplo 5
Calcule a integral imprópria ou estabeleça sua divergência.
Esta integral pode ser resolvida detalhadamente, ou seja, primeiro encontre a integral indefinida fazendo uma mudança de variável. Ou você pode resolvê-lo “imediatamente” - subsumindo a função sob o sinal diferencial. Quem tem alguma formação matemática?
Soluções completas e respostas no final da lição.
Exemplos de soluções para integrais impróprias com limite inferior infinito de integração podem ser encontrados na página Métodos eficientes para resolver integrais impróprias. Lá também analisamos o caso em que ambos os limites de integração são infinitos.
Integrais impróprias de funções ilimitadas
Ou integrais impróprias de segunda espécie. Integrais impróprias do segundo tipo são insidiosamente “criptografadas” sob a integral definida usual e parecem exatamente iguais: Mas, ao contrário da integral definida, o integrando sofre uma descontinuidade infinita (não existe): 1) no ponto , 2) ou no ponto , 3) ou em ambos os pontos ao mesmo tempo, 4) ou mesmo no segmento de integração. Veremos os dois primeiros casos; para os casos 3-4, no final do artigo há um link para uma lição adicional.
Só um exemplo para deixar claro: . Parece ser uma integral definida. Mas, na verdade, esta é uma integral imprópria de segundo tipo; se substituirmos o valor do limite inferior no integrando, então nosso denominador vai para zero, ou seja, o integrando simplesmente não existe neste ponto!
Em geral, ao analisar uma integral imprópria você sempre precisa substituir ambos os limites de integração no integrando. A este respeito, vamos verificar o limite superior: 
. Está tudo bem aqui.
O trapézio curvilíneo para o tipo de integral imprópria em consideração se parece fundamentalmente com isto:
Aqui tudo é quase igual à integral do primeiro tipo.
Nossa integral é numericamente igual à área do trapézio curvo sombreado, que não é limitado por cima. Neste caso, pode haver duas opções*: a integral imprópria diverge (a área é infinita) ou a integral imprópria é igual a um número finito (ou seja, a área de uma figura infinita é finita!).
* por padrão, geralmente assumimos que a integral imprópria existe
Resta apenas modificar a fórmula de Newton-Leibniz. Também é modificado com a ajuda de um limite, mas o limite não tende mais ao infinito, mas para o valor à direita.É fácil acompanhar pelo desenho: ao longo do eixo devemos nos aproximar do ponto de ruptura infinitamente próximo na direita.
Vamos ver como isso é implementado na prática.
Exemplo 6
Calcule a integral imprópria ou estabeleça sua divergência.
O integrando tem uma descontinuidade infinita em um ponto (não se esqueça de verificar verbalmente ou em rascunho se está tudo bem com o limite superior!)
Primeiro, vamos calcular a integral indefinida: 
Substituição: 
Se você tiver alguma dificuldade com a substituição, consulte a lição Método de substituição em integral indefinida.
Vamos calcular a integral imprópria:
(1) O que há de novo aqui? Não há praticamente nada em termos de tecnologia de solução. A única coisa que mudou foi a entrada abaixo do ícone de limite: . A adição significa que estamos buscando o valor da direita (o que é lógico - veja o gráfico). Tal limite na teoria dos limites é chamado limite unilateral. Neste caso temos limite à direita.
(2) Substituímos os limites superior e inferior usando a fórmula de Newton-Leibniz.
(3) Vamos lidar com em. Como determinar para onde vai uma expressão? Grosso modo, basta substituir o valor nele, substituir três quartos e indicar isso . Vamos pentear a resposta.
Neste caso, a integral imprópria é igual a um número negativo. Não há crime nisso, apenas o trapézio curvo correspondente está localizado sob o eixo.
E agora dois exemplos de soluções independentes.
Exemplo 7
Calcule a integral imprópria ou estabeleça sua divergência.
Exemplo 8
Calcule a integral imprópria ou estabeleça sua divergência.
Se o integrando não existir no ponto
Um trapézio curvo infinito para uma integral imprópria se parece fundamentalmente com isto.
Integral imprópria com limite de integração infinito
Às vezes, essa integral imprópria também é chamada de integral imprópria de primeiro tipo..gif" width="49" height="19 src=">.
Menos comuns são as integrais com limite inferior infinito ou com dois limites infinitos: .
Consideraremos o caso mais popular https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Não, nem sempre. Integrandohttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">
Vamos representar no desenho o gráfico da função integrando. Um gráfico típico e um trapézio curvo para este caso se parece com isto:
Totalmente inapropriadohttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", ou seja, a área também é infinita. Pode ser que sim. Neste caso dizem que a integral imprópria diverge.
2) Mas. Por mais paradoxal que possa parecer, a área de uma figura infinita pode ser igual a... um número finito! Por exemplo: .. No segundo caso, a integral imprópria converge.
O que acontecerá se um trapézio curvo infinito estiver localizado abaixo do eixo?.gif" width="217" height="51 src=">.
: 
.
Exemplo 1
A função integrando https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, o que significa que está tudo bem e a integral imprópria pode ser calculada usando o “ método padrão”.
Aplicação de nossa fórmula https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">
Ou seja, a integral imprópria diverge e a área do trapézio curvo sombreado é igual ao infinito.
Ao resolver integrais impróprias, é muito importante saber como são os gráficos das funções elementares básicas!
Exemplo 2
Calcule a integral imprópria ou estabeleça sua divergência.
Vamos fazer o desenho: 
Primeiro, notamos o seguinte: o integrando é contínuo no meio intervalo. Bom..gif" width="327" height="53">
(1) Tomamos a integral mais simples de uma função potência (este caso especial está em muitas tabelas). É melhor mover imediatamente o sinal de menos além do sinal de limite para que não atrapalhe em cálculos posteriores.
(2) Substituímos os limites superior e inferior usando a fórmula de Newton-Leibniz.
(3) Ressaltamos que https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Senhores, isso precisa ser entendido há muito tempo há algum tempo) e simplifique a resposta.
Aqui a área de um trapézio curvo infinito é um número finito! Inacreditável, mas é verdade.
Exemplo 3
Calcule a integral imprópria ou estabeleça sua divergência.
O integrando é contínuo em .
Primeiro, vamos tentar encontrar a função antiderivada (integral indefinida).
A qual das integrais de tabela o integrando é semelhante? Isso me lembra um arco tangente: 
. Estas considerações sugerem que seria bom ter um quadrado no denominador. Isso é feito por substituição.
Vamos substituir:
É sempre útil realizar uma verificação, ou seja, diferenciar o resultado obtido:
Agora encontramos a integral imprópria:
(1) Escrevemos a solução de acordo com a fórmula 
. É melhor mover imediatamente a constante além do sinal limite para que ela não interfira em cálculos posteriores.
(2) Substituímos os limites superior e inferior de acordo com a fórmula de Newton-Leibniz..gif" width="56" height="19 src=">? Veja o gráfico arco tangente no artigo já recomendado repetidamente.
(3) Obtemos a resposta final. Um fato que é útil saber de cor.
Os alunos avançados podem não encontrar a integral indefinida separadamente e não usar o método de substituição, mas sim usar o método de substituir a função sob o sinal diferencial e resolver a integral imprópria “imediatamente”. Neste caso, a solução deve ser mais ou menos assim:
“
A função integrando é contínua em https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“
Exemplo 4
Calcule a integral imprópria ou estabeleça sua divergência.
! Este é um exemplo típico e integrais semelhantes são encontradas com muita frequência. Resolva bem! A função antiderivada é encontrada aqui usando o método de isolamento de um quadrado completo.
Exemplo 5
Calcule a integral imprópria ou estabeleça sua divergência.
Esta integral pode ser resolvida detalhadamente, ou seja, primeiro encontre a integral indefinida fazendo uma mudança de variável. Ou você pode resolvê-lo “imediatamente” - subsumindo a função sob o sinal diferencial.
Integrais impróprias de funções ilimitadas
Às vezes, essas integrais impróprias são chamadas de integrais impróprias de segundo tipo. Integrais impróprias do segundo tipo são insidiosamente “criptografadas” sob a integral definida usual e têm exatamente a mesma aparência: ..gif" width="39" height="15 src=">, 2) ou no ponto , 3) ou em ambos os pontos ao mesmo tempo, 4) ou mesmo no segmento de integração Consideraremos os dois primeiros casos para os casos 3-4 há um link para uma lição adicional no final do artigo;
Apenas um exemplo para deixar claro: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, então nosso denominador vai para zero, isto é, o integrando simplesmente não existe neste ponto!
Em geral, ao analisar uma integral imprópria você sempre precisa substituir ambos os limites de integração no integrando..jpg" alt="Integral impróprio, ponto de descontinuidade no limite inferior de integração" width="323" height="380">!}
Aqui tudo é quase igual à integral do primeiro tipo.
Nossa integral é numericamente igual à área do trapézio curvo sombreado, que não é limitado por cima. Nesse caso, pode haver duas opções: a integral imprópria diverge (a área é infinita) ou a integral imprópria é igual a um número finito (ou seja, a área de uma figura infinita é finita!).
Resta apenas modificar a fórmula de Newton-Leibniz. Também é modificado com a ajuda de um limite, mas o limite não tende mais ao infinito, mas dar valorhttps://pandia.ru/text/80/057/images/image052.gif" largura="28" altura="19"> na direita.
Exemplo 6
Calcule a integral imprópria ou estabeleça sua divergência.
O integrando tem uma descontinuidade infinita em um ponto (não se esqueça de verificar verbalmente ou em rascunho se está tudo bem com o limite superior!)
Primeiro, vamos calcular a integral indefinida: 
Substituição: 
Vamos calcular a integral imprópria:
(1) O que há de novo aqui? Não há praticamente nada em termos de tecnologia de solução. A única coisa que mudou foi a entrada abaixo do ícone de limite: . A adição significa que estamos buscando o valor da direita (o que é lógico - veja o gráfico). Tal limite na teoria dos limites é chamado de limite unilateral. Neste caso temos um limite para destros.
(2) Substituímos os limites superior e inferior usando a fórmula de Newton-Leibniz.
(3) Vamos entender https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Como determinar para onde a expressão deve ir? Grosso modo , basta substituir o valor, substituir três quartos e indicar aquele pente a resposta.
Neste caso, a integral imprópria é igual a um número negativo.
Exemplo 7
Calcule a integral imprópria ou estabeleça sua divergência.
Exemplo 8
Calcule a integral imprópria ou estabeleça sua divergência.
Se o integrando não existir no ponto
Um trapézio curvo infinito para uma integral imprópria se parece fundamentalmente com isto:
Aqui tudo é absolutamente igual, exceto que nosso limite tende a dar valorhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> devemos chegar infinitamente perto do ponto de ruptura esquerda.
