Acest articol continuă subiectul ecuației unei linii drepte pe un plan: luați în considerare un astfel de tip de ecuație ca ecuația generală a unei linii drepte. Să definim o teoremă și să dăm dovada acesteia; Să ne dăm seama ce este o ecuație generală incompletă a unei linii drepte și cum să facem tranziții de la o ecuație generală la alte tipuri de ecuații ale unei linii drepte. Vom consolida întreaga teorie cu ilustrații și rezolvarea problemelor practice.

Yandex.RTB R-A-339285-1

Fie dat un sistem de coordonate dreptunghiular O x y pe plan.

Teorema 1

Orice ecuație de gradul întâi, având forma A x + B y + C \u003d 0, unde A, B, C sunt numere reale (A și B nu sunt egale cu zero în același timp) definește o linie dreaptă în un sistem de coordonate dreptunghiular pe un plan. La rândul său, orice linie dintr-un sistem de coordonate dreptunghiular pe plan este determinată de o ecuație care are forma A x + B y + C = 0 pentru un anumit set de valori A, B, C.

Dovada

Această teoremă constă din două puncte, vom demonstra fiecare dintre ele.

1. Să demonstrăm că ecuația A x + B y + C = 0 definește o dreaptă pe plan.

Să existe un punct M 0 (x 0 , y 0) ale cărui coordonate corespund ecuației A x + B y + C = 0 . Astfel: A x 0 + B y 0 + C = 0 . Scădeți din partea stângă și dreaptă ale ecuațiilor A x + B y + C \u003d 0 laturile stânga și dreaptă ale ecuației A x 0 + B y 0 + C \u003d 0, obținem o nouă ecuație care arată ca A (x - x 0) + B (y - y 0) = 0 . Este echivalent cu A x + B y + C = 0 .

Ecuația rezultată A (x - x 0) + B (y - y 0) = 0 este o condiție necesară și suficientă pentru perpendicularitatea vectorilor n → = (A, B) și M 0 M → = (x - x) 0, y - y 0). Astfel, mulțimea punctelor M (x, y) definește într-un sistem de coordonate dreptunghiular o dreaptă perpendiculară pe direcția vectorului n → = (A, B) . Putem presupune că nu este așa, dar atunci vectorii n → = (A, B) și M 0 M → = (x - x 0, y - y 0) nu ar fi perpendiculari, iar egalitatea A (x - x 0 ) + B (y - y 0) = 0 nu ar fi adevărat.

Prin urmare, ecuația A (x - x 0) + B (y - y 0) \u003d 0 definește o linie într-un sistem de coordonate dreptunghiular pe plan și, prin urmare, ecuația echivalentă A x + B y + C \u003d 0 definește aceeași linie. Astfel am demonstrat prima parte a teoremei.

1. Să demonstrăm că orice dreaptă dintr-un sistem de coordonate dreptunghiular pe un plan poate fi dată printr-o ecuație de gradul I A x + B y + C = 0 .

Să stabilim o linie dreaptă a într-un sistem de coordonate dreptunghiular pe plan; punctul M 0 (x 0 , y 0) prin care trece această dreaptă, precum și vectorul normal al acestei drepte n → = (A , B) .

Să existe și un punct M (x , y) - un punct flotant al dreptei. În acest caz, vectorii n → = (A , B) și M 0 M → = (x - x 0 , y - y 0) sunt perpendiculari între ei, iar produsul lor scalar este zero:

n → , M 0 M → = A (x - x 0) + B (y - y 0) = 0

Să rescriem ecuația A x + B y - A x 0 - B y 0 = 0 , definim C: C = - A x 0 - B y 0 și în final obținem ecuația A x + B y + C = 0 .

Deci, am demonstrat a doua parte a teoremei și am demonstrat întreaga teoremă ca întreg.

Definiția 1

O ecuație care arată ca A x + B y + C = 0 - Acest ecuația generală a unei drepte pe un plan într-un sistem de coordonate dreptunghiularO x y .

Pe baza teoremei demonstrate, putem concluziona că o dreaptă dată pe un plan într-un sistem de coordonate dreptunghiular fix și ecuația sa generală sunt indisolubil legate. Cu alte cuvinte, linia originală corespunde ecuației sale generale; ecuația generală a unei drepte corespunde unei drepte date.

De asemenea, din demonstrarea teoremei rezultă că coeficienții A și B pentru variabilele x și y sunt coordonatele vectorului normal al dreptei, care este dat de ecuația generală a dreptei A x + B y + C = 0 .

Luați în considerare un exemplu specific de ecuație generală a unei linii drepte.

Să fie dată ecuația 2 x + 3 y - 2 = 0, care corespunde unei linii drepte într-un sistem de coordonate dreptunghiular dat. Vectorul normal al acestei linii este vectorul n → = (2, 3) ​​. Desenați o linie dreaptă dată în desen.

Se mai poate argumenta și următoarele: linia dreaptă pe care o vedem în desen este determinată de ecuația generală 2 x + 3 y - 2 = 0, deoarece coordonatele tuturor punctelor unei drepte date corespund acestei ecuații.

Putem obține ecuația λ · A x + λ · B y + λ · C = 0 înmulțind ambele părți ale ecuației generale drepte cu un număr diferit de zero λ. Ecuația rezultată este echivalentă cu ecuația generală inițială, prin urmare, va descrie aceeași dreaptă în plan.

Definiția 2

Ecuația generală completă a unei linii drepte- o astfel de ecuație generală a dreptei A x + B y + C \u003d 0, în care numerele A, B, C sunt diferite de zero. În caz contrar, ecuația este incomplet.

Să analizăm toate variațiile ecuației generale incomplete a dreptei.

1. Când A \u003d 0, B ≠ 0, C ≠ 0, ecuația generală devine B y + C \u003d 0. O astfel de ecuație generală incompletă definește o linie dreaptă într-un sistem de coordonate dreptunghiular O x y care este paralelă cu axa O x, deoarece pentru orice valoare reală a lui x, variabila y va lua valoarea - C B . Cu alte cuvinte, ecuația generală a liniei A x + B y + C \u003d 0, când A \u003d 0, B ≠ 0, definește locul punctelor (x, y) ale căror coordonate sunt egale cu același număr - C B .
2. Dacă A \u003d 0, B ≠ 0, C \u003d 0, ecuația generală devine y \u003d 0. O astfel de ecuație incompletă definește axa x O x .
3. Când A ≠ 0, B \u003d 0, C ≠ 0, obținem o ecuație generală incompletă A x + C \u003d 0, care definește o linie dreaptă paralelă cu axa y.
4. Fie A ≠ 0, B \u003d 0, C \u003d 0, atunci ecuația generală incompletă va lua forma x \u003d 0, iar aceasta este ecuația dreptei de coordonate O y.
5. În cele din urmă, când A ≠ 0, B ≠ 0, C \u003d 0, ecuația generală incompletă ia forma A x + B y \u003d 0. Și această ecuație descrie o linie dreaptă care trece prin origine. Într-adevăr, perechea de numere (0 , 0) corespunde egalității A x + B y = 0 , întrucât A · 0 + B · 0 = 0 .

Să ilustrăm grafic toate tipurile de mai sus ale ecuației generale incomplete a unei linii drepte.

Exemplul 1

Se știe că linia dreaptă dată este paralelă cu axa y și trece prin punctul 2 7 , - 11 . Este necesar să scrieți ecuația generală a unei linii drepte date.

Decizie

O linie dreaptă paralelă cu axa y este dată de o ecuație de forma A x + C \u003d 0, în care A ≠ 0. Condiția specifică și coordonatele punctului prin care trece linia, iar coordonatele acestui punct corespund condițiilor ecuației generale incomplete A x + C = 0 , adică. egalitatea este corectă:

A 2 7 + C = 0

Este posibil să se determine C din el dând lui A o valoare diferită de zero, de exemplu, A = 7 . În acest caz, obținem: 7 2 7 + C \u003d 0 ⇔ C \u003d - 2. Cunoaștem ambii coeficienți A și C, înlocuiți-i în ecuația A x + C = 0 și obținem ecuația necesară a dreptei: 7 x - 2 = 0

Răspuns: 7 x - 2 = 0

Exemplul 2

Desenul arată o linie dreaptă, este necesar să scrieți ecuația acesteia.

Decizie

Desenul dat ne permite să luăm cu ușurință datele inițiale pentru rezolvarea problemei. Vedem în desen că linia dată este paralelă cu axa O x și trece prin punctul (0 , 3) ​​​​.

Linia dreaptă, care este paralelă cu abscisa, este determinată de ecuația generală incompletă B y + С = 0. Aflați valorile lui B și C. Coordonatele punctului (0, 3), deoarece linia dreaptă dată trece prin el, vor satisface ecuația dreptei B y + С = 0, atunci egalitatea este valabilă: В · 3 + С = 0. Să setăm B la o altă valoare decât zero. Să spunem B \u003d 1, în acest caz, din egalitatea B · 3 + C \u003d 0 putem găsi C: C \u003d - 3. Folosind valorile cunoscute ale lui B și C, obținem ecuația necesară a dreptei: y - 3 = 0.

Răspuns: y - 3 = 0 .

Ecuația generală a unei drepte care trece printr-un punct dat al planului

Să treacă dreapta dată prin punctul M 0 (x 0, y 0), apoi coordonatele ei corespund ecuației generale a dreptei, adică. egalitatea este adevărată: A x 0 + B y 0 + C = 0 . Scădeți părțile stânga și dreaptă ale acestei ecuații din laturile stânga și dreapta ale ecuației generale complete a dreptei. Obținem: A (x - x 0) + B (y - y 0) + C \u003d 0, această ecuație este echivalentă cu cea generală inițială, trece prin punctul M 0 (x 0, y 0) și are o vector normal n → \u003d (A, B) .

Rezultatul pe care l-am obținut face posibilă scrierea ecuației generale a unei drepte pentru coordonatele cunoscute ale vectorului normal al dreptei și coordonatele unui anumit punct al acestei drepte.

Exemplul 3

Dat un punct M 0 (- 3, 4) prin care trece dreapta și vectorul normal al acestei drepte n → = (1 , - 2) . Este necesar să scrieți ecuația unei linii drepte date.

Decizie

Condițiile inițiale ne permit să obținem datele necesare pentru compilarea ecuației: A \u003d 1, B \u003d - 2, x 0 \u003d - 3, y 0 \u003d 4. Apoi:

A (x - x 0) + B (y - y 0) = 0 ⇔ 1 (x - (- 3)) - 2 y (y - 4) = 0 ⇔ ⇔ x - 2 y + 22 = 0

Problema ar fi putut fi rezolvată altfel. Ecuația generală a unei drepte are forma A x + B y + C = 0 . Vectorul normal dat vă permite să obțineți valorile coeficienților A și B, apoi:

A x + B y + C = 0 ⇔ 1 x - 2 y + C = 0 ⇔ x - 2 y + C = 0

Acum să găsim valoarea lui C, folosind punctul M 0 (- 3, 4) dat de condiția problemei, prin care trece dreapta. Coordonatele acestui punct corespund ecuației x - 2 · y + C = 0 , adică. - 3 - 2 4 + C \u003d 0. Prin urmare, C = 11. Ecuația necesară dreptei ia forma: x - 2 · y + 11 = 0 .

Răspuns: x - 2 y + 11 = 0 .

Exemplul 4

Având în vedere o dreaptă 2 3 x - y - 1 2 = 0 și un punct M 0 situat pe această dreaptă. Numai abscisa acestui punct este cunoscută și este egală cu - 3. Este necesar să se determine ordonata punctului dat.

Decizie

Să setăm desemnarea coordonatelor punctului M 0 ca x 0 și y 0 . Datele inițiale indică faptul că x 0 \u003d - 3. Deoarece punctul aparține unei linii date, atunci coordonatele sale corespund ecuației generale a acestei drepte. Atunci următoarea egalitate va fi adevărată:

2 3 x 0 - y 0 - 1 2 = 0

Definiți y 0: 2 3 (- 3) - y 0 - 1 2 = 0 ⇔ - 5 2 - y 0 = 0 ⇔ y 0 = - 5 2

Răspuns: - 5 2

Trecerea de la ecuația generală a unei linii drepte la alte tipuri de ecuații a unei linii drepte și invers

După cum știm, există mai multe tipuri de ecuații ale aceleiași drepte în plan. Alegerea tipului de ecuație depinde de condițiile problemei; se poate alege pe cea mai convenabila solutiei sale. Aici este foarte utilă abilitatea de a converti o ecuație de un fel într-o ecuație de alt fel.

Pentru început, luăm în considerare trecerea de la ecuația generală de forma A x + B y + C = 0 la ecuația canonică x - x 1 a x = y - y 1 a y .

Dacă A ≠ 0, atunci transferăm termenul B y în partea dreaptă a ecuației generale. În partea stângă, scoatem A din paranteze. Ca rezultat, obținem: A x + C A = - B y .

Această egalitate poate fi scrisă ca proporție: x + C A - B = y A .

Dacă B ≠ 0, lăsăm doar termenul A x în partea stângă a ecuației generale, le transferăm pe celelalte în partea dreaptă, obținem: A x \u003d - B y - C. Scoatem - B din paranteze, apoi: A x \u003d - B y + C B.

Să rescriem egalitatea ca proporție: x - B = y + C B A .

Desigur, nu este nevoie să memorezi formulele rezultate. Este suficient să cunoaștem algoritmul acțiunilor în timpul trecerii de la ecuația generală la cea canonică.

Exemplul 5

Este dată ecuația generală a dreptei 3 y - 4 = 0. Trebuie convertit într-o ecuație canonică.

Decizie

Scriem ecuația originală ca 3 y - 4 = 0 . În continuare, acționăm conform algoritmului: termenul 0 x rămâne în partea stângă; iar pe partea dreaptă scoatem - 3 din paranteze; obținem: 0 x = - 3 y - 4 3 .

Să scriem egalitatea rezultată ca proporție: x - 3 = y - 4 3 0 . Astfel, am obținut o ecuație a formei canonice.

Răspuns: x - 3 = y - 4 3 0.

Pentru a transforma ecuația generală a unei linii drepte în cele parametrice, se efectuează mai întâi trecerea la forma canonică, apoi trecerea de la ecuația canonică a dreptei la ecuațiile parametrice.

Exemplul 6

Linia dreaptă este dată de ecuația 2 x - 5 y - 1 = 0 . Notați ecuațiile parametrice ale acestei drepte.

Decizie

Să facem trecerea de la ecuația generală la cea canonică:

2 x - 5 y - 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Acum să luăm ambele părți ale ecuației canonice rezultate egale cu λ, atunci:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

Răspuns:x = 5 λ y = - 1 5 + 2 λ , λ ∈ R

Ecuația generală poate fi convertită în ecuația unei linii drepte cu panta y \u003d k x + b, dar numai atunci când B ≠ 0. Pentru trecerea pe partea stângă, lăsăm termenul B y , restul se transferă la dreapta. Se obține: B y = - A x - C . Să împărțim ambele părți ale egalității rezultate la B , care este diferit de zero: y = - A B x - C B .

Exemplul 7

Ecuația generală a unei drepte este dată: 2 x + 7 y = 0 . Trebuie să convertiți acea ecuație într-o ecuație a pantei.

Decizie

Să efectuăm acțiunile necesare conform algoritmului:

2 x + 7 y = 0 ⇔ 7 y - 2 x ⇔ y = - 2 7 x

Răspuns: y = - 2 7 x .

Din ecuația generală a unei linii drepte, este suficient să obțineți pur și simplu o ecuație în segmente de forma x a + y b \u003d 1. Pentru a face o astfel de tranziție, transferăm numărul C în partea dreaptă a egalității, împărțim ambele părți ale egalității rezultate cu - С și, în final, transferăm coeficienții pentru variabilele x și y la numitori:

A x + B y + C = 0 ⇔ A x + B y = - C ⇔ ⇔ A - C x + B - C y = 1 ⇔ x - C A + y - C B = 1

Exemplul 8

Este necesar să convertiți ecuația generală a dreptei x - 7 y + 1 2 = 0 în ecuația unei drepte în segmente.

Decizie

Să mutăm 1 2 în partea dreaptă: x - 7 y + 1 2 = 0 ⇔ x - 7 y = - 1 2 .

Împărțiți la -1/2 ambele părți ale ecuației: x - 7 y = - 1 2 ⇔ 1 - 1 2 x - 7 - 1 2 y = 1 .

Răspuns: x - 1 2 + y 1 14 = 1 .

În general, trecerea inversă este și ea ușoară: de la alte tipuri de ecuații la cea generală.

Ecuația unei drepte în segmente și ecuația cu o pantă pot fi ușor convertite într-una generală prin simpla colectare a tuturor termenilor din partea stângă a ecuației:

x a + y b ⇔ 1 a x + 1 b y - 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y - k x - b = 0 ⇔ A x + B y + C = 0

Ecuația canonică este convertită în cea generală după următoarea schemă:

x - x 1 a x = y - y 1 a y ⇔ a y (x - x 1) = a x (y - y 1) ⇔ ⇔ a y x - a x y - a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Pentru a trece de la parametric, se realizează mai întâi trecerea la canonic, apoi la cea generală:

x = x 1 + a x λ y = y 1 + a y λ ⇔ x - x 1 a x = y - y 1 a y ⇔ A x + B y + C = 0

Exemplul 9

Sunt date ecuațiile parametrice ale dreptei x = - 1 + 2 · λ y = 4. Este necesar să scrieți ecuația generală a acestei linii.

Decizie

Să facem tranziția de la ecuațiile parametrice la cele canonice:

x = - 1 + 2 λ y = 4 ⇔ x = - 1 + 2 λ y = 4 + 0 λ ⇔ λ = x + 1 2 λ = y - 4 0 ⇔ x + 1 2 = y - 4 0

Să trecem de la canonic la general:

x + 1 2 = y - 4 0 ⇔ 0 (x + 1) = 2 (y - 4) ⇔ y - 4 = 0

Răspuns: y - 4 = 0

Exemplul 10

Este dată ecuația unei drepte în segmente x 3 + y 1 2 = 1. Este necesar să se efectueze tranziția la forma generală a ecuației.

Decizie:

Să rescriem ecuația în forma necesară:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y - 1 = 0

Răspuns: 1 3 x + 2 y - 1 = 0 .

Întocmirea unei ecuații generale a unei linii drepte

Mai sus, am spus că ecuația generală poate fi scrisă cu coordonatele cunoscute ale vectorului normal și coordonatele punctului prin care trece dreapta. O astfel de dreaptă este definită de ecuația A (x - x 0) + B (y - y 0) = 0 . În același loc am analizat exemplul corespunzător.

Acum să ne uităm la exemple mai complexe în care, mai întâi, este necesar să se determine coordonatele vectorului normal.

Exemplul 11

Dată o dreaptă paralelă cu dreapta 2 x - 3 y + 3 3 = 0 . De asemenea, este cunoscut punctul M 0 (4 , 1) prin care trece linia dată. Este necesar să scrieți ecuația unei linii drepte date.

Decizie

Condițiile inițiale ne spun că dreptele sunt paralele, apoi, ca vector normal al dreptei a cărei ecuație trebuie scrisă, luăm vectorul de direcție al dreptei n → = (2, - 3) : 2 x - 3 y + 3 3 = 0. Acum cunoaștem toate datele necesare pentru a compune ecuația generală a unei linii drepte:

A (x - x 0) + B (y - y 0) = 0 ⇔ 2 (x - 4) - 3 (y - 1) = 0 ⇔ 2 x - 3 y - 5 = 0

Răspuns: 2 x - 3 y - 5 = 0 .

Exemplul 12

Linia dată trece prin originea perpendiculară pe dreapta x - 2 3 = y + 4 5 . Este necesar să scrieți ecuația generală a unei linii drepte date.

Decizie

Vectorul normal al dreptei date va fi vectorul de direcție al dreptei x - 2 3 = y + 4 5 .

Atunci n → = (3 , 5) . Linia dreaptă trece prin origine, adică. prin punctul O (0, 0) . Să compunem ecuația generală a unei drepte date:

A (x - x 0) + B (y - y 0) = 0 ⇔ 3 (x - 0) + 5 (y - 0) = 0 ⇔ 3 x + 5 y = 0

Răspuns: 3 x + 5 y = 0 .

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

În multe cazuri, trasarea unei funcții este mai ușoară dacă trasați mai întâi asimptotele curbei.

Definiție 1. Asimptotele sunt numite astfel de linii, de care graficul funcției se apropie cât se dorește atunci când variabila tinde spre plus infinit sau minus infinit.

Definiția 2. O linie dreaptă se numește asimptotă a graficului unei funcții dacă distanța de la punctul variabil M graficul funcției până la această dreaptă tinde spre zero pe măsură ce punctul se îndepărtează la infinit M de la originea coordonatelor de-a lungul oricărei ramuri a graficului funcției.

Există trei tipuri de asimptote: verticale, orizontale și oblice.

Asimptote verticale

Definiție. Drept X = A este o asimptotă verticală a graficului funcției dacă punct X = A este o punct de rupere de al doilea fel pentru această caracteristică.

Din definiție rezultă că linia X = A este asimptota verticală a graficului funcției f(X) dacă este îndeplinită cel puțin una dintre următoarele condiții:

În același timp, funcția f(X) poate să nu fie definită deloc, respectiv, pt X ≥ Ași X ≤ A .

Cometariu:

Exemplul 1 Graficul funcției y=ln X are o asimptotă verticală X= 0 (adică coincide cu axa Oi) la limita domeniului de definitie, deoarece limita functiei ca x tinde spre zero in dreapta este egala cu minus infinit:

(fig. mai sus).

pe cont propriu și apoi vezi soluțiile

Exemplul 2 Găsiți asimptotele graficului funcției.

Exemplul 3 Găsiți asimptotele graficului unei funcții

Asimptote orizontale

Dacă (limita funcției când argumentul tinde spre plus sau minus infinit este egală cu o anumită valoare b), apoi y = b – asimptotă orizontală strâmb y = f(X ) (dreapta când x tinde spre plus infinit, stânga când x tinde spre minus infinit și cu două fețe dacă limitele când x tinde spre plus sau minus infinit sunt egale).

Exemplul 5 Graficul funcției

la A> 1 are o asimptotă orizontală stângă y= 0 (adică coincide cu axa Bou), deoarece limita funcției când „x” tinde spre minus infinit este egală cu zero:

Curba nu are o asimptotă orizontală dreaptă, deoarece limita funcției ca x tinde spre plus infinit este egală cu infinit:

Asimptote oblice

Asimptotele verticale și orizontale pe care le-am considerat mai sus sunt paralele cu axele de coordonate, prin urmare, pentru a le construi, ne-a trebuit doar un anumit număr - un punct pe axa abscisă sau ordonată prin care trece asimptota. Este nevoie de mai mult pentru asimptota oblică - pantă k, care arată unghiul de înclinare a dreptei și interceptarea b, care arată cât de mult este linia deasupra sau sub origine. Cei care nu au avut timp să uite geometria analitică, iar din ea - ecuațiile unei linii drepte, vor observa că pentru o asimptotă oblică găsesc ecuația pantei. Existența unei asimptote oblice este determinată de următoarea teoremă, pe baza căreia se găsesc coeficienții tocmai numiți.

Teorema. Pentru a face o curbă y = f(X) avea o asimptotă y = kx + b , este necesar și suficient să existe limite finite kși b a funcției luate în considerare așa cum tinde variabila X la plus infinit și minus infinit:

(1)

(2)

Cifrele astfel găsite kși bși sunt coeficienții asimptotei oblice.

În primul caz (când x tinde spre plus infinit), se obține asimptota oblică dreaptă, în al doilea (când x tinde spre minus infinit), se obține asimptota stângă. Asimptota oblică dreaptă este prezentată în Fig. de desubt.

La găsirea ecuației asimptotei oblice, este necesar să se țină cont de tendința lui x atât la plus infinit, cât și la minus infinit. Pentru unele funcții, de exemplu, pentru raționalele fracționale, aceste limite coincid, dar pentru multe funcții aceste limite sunt diferite și doar una dintre ele poate exista.

Când limitele coincid cu x tinde spre plus infinit și minus infinit, linia dreaptă y = kx + b este o asimptotă cu două fețe a curbei.

Dacă cel puţin una dintre limitele care definesc asimptota y = kx + b , nu există, atunci graficul funcției nu are o asimptotă oblică (dar poate avea una verticală).

Este ușor de observat că asimptota orizontală y = b este un caz special de oblic y = kx + b la k = 0 .

Prin urmare, dacă o curbă are o asimptotă orizontală în orice direcție, atunci nu există nicio asimptotă oblică în acea direcție și invers.

Exemplul 6 Găsiți asimptotele graficului unei funcții

Decizie. Funcția este definită pe întreaga linie numerică, cu excepția X= 0, adică

Prin urmare, la punctul de rupere X= 0 curba poate avea o asimptotă verticală. Într-adevăr, limita funcției pe măsură ce x tinde spre zero din stânga este plus infinit:

Prin urmare, X= 0 este asimptota verticală a graficului acestei funcții.

Graficul acestei funcții nu are o asimptotă orizontală, deoarece limita funcției când x tinde spre plus infinit este egală cu plus infinit:

Să aflăm prezența unei asimptote oblice:

Am limite finite k= 2 și b= 0 . Drept y = 2X este o asimptotă oblică cu două fețe a graficului acestei funcții (fig. în interiorul exemplului).

Exemplul 7 Găsiți asimptotele graficului unei funcții

Decizie. Funcția are un punct de întrerupere X= −1 . Să calculăm limitele unilaterale și să determinăm tipul de discontinuitate:

Concluzie: X= −1 este un punct de discontinuitate de al doilea fel, deci linia X= −1 este asimptota verticală a graficului acestei funcții.

Caut asimptote oblice. Deoarece această funcție este fracționar rațională, limitele pentru și pentru vor coincide. Astfel, găsim coeficienții pentru înlocuirea dreptei - asimptotă oblică în ecuație:

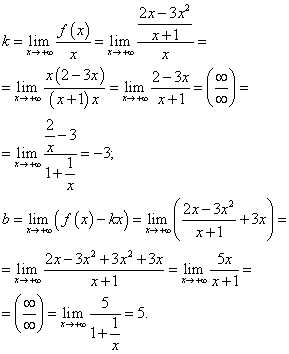
Înlocuind coeficienții găsiți în ecuația unei drepte cu pantă, obținem ecuația asimptotei oblice:

y = −3X + 5 .

În figură, graficul funcției este marcat cu visiniu, iar asimptotele sunt în negru.

Exemplul 8 Găsiți asimptotele graficului unei funcții

Decizie. Deoarece această funcție este continuă, graficul ei nu are asimptote verticale. Căutăm asimptote oblice:

.

Astfel, graficul acestei funcții are o asimptotă y= 0 la și nu are asimptotă la .

Exemplul 9 Găsiți asimptotele graficului unei funcții

Decizie. În primul rând, căutăm asimptotele verticale. Pentru a face acest lucru, găsim domeniul funcției. Funcția este definită atunci când inegalitatea este valabilă și . semn variabil X se potrivește cu semnul. Prin urmare, luați în considerare inegalitatea echivalentă. De aici obținem domeniul de aplicare al funcției: . Asimptota verticală poate fi doar la limita domeniului funcției. Dar X= 0 nu poate fi o asimptotă verticală, deoarece funcția este definită pentru X = 0 .

Luați în considerare limita din dreapta la (limita din stânga nu există):

.

Punct X= 2 este un punct de discontinuitate de al doilea fel, deci linia X= 2 - asimptota verticală a graficului acestei funcții.

Căutăm asimptote oblice:

Asa de, y = X+ 1 - asimptotă oblică a graficului acestei funcții la . Căutăm o asimptotă oblică pentru:

Asa de, y = −X − 1 - asimptotă oblică la .

Exemplul 10 Găsiți asimptotele graficului unei funcții

Decizie. Funcția are un domeniu de aplicare . Deoarece asimptota verticală a graficului acestei funcții poate fi doar la limita domeniului de definiție, vom găsi limitele unilaterale ale funcției la .

Proprietățile unei drepte în geometria euclidiană.

Există infinit de linii care pot fi trase prin orice punct.

Prin oricare două puncte care nu coincid, există o singură linie dreaptă.

Două drepte non-coincidente în plan fie se intersectează într-un singur punct, fie sunt

paralel (urmează din precedentul).

În spațiul tridimensional, există trei opțiuni pentru poziția relativă a două linii:

• liniile se intersectează;

• liniile drepte sunt paralele;

• linii drepte se intersectează.

Drept linia- curba algebrică de ordinul întâi: în sistemul de coordonate carteziene, o dreaptă

este dat pe plan de o ecuație de gradul I (ecuație liniară).

Ecuația generală a unei drepte.

Definiție. Orice dreaptă din plan poate fi dată printr-o ecuație de ordinul întâi

Ah + Wu + C = 0,

și constantă A, B nu este egal cu zero în același timp. Această ecuație de ordinul întâi se numește general

ecuație în linie dreaptă.În funcție de valorile constantelor A, Bși Cu Sunt posibile următoarele cazuri speciale:

. C = 0, A ≠ 0, B ≠ 0- linia trece prin origine

. A = 0, B ≠0, C ≠0 ( Prin + C = 0)- linie dreaptă paralelă cu axa Oh

. B = 0, A ≠ 0, C ≠ 0 ( Ax + C = 0)- linie dreaptă paralelă cu axa OU

. B = C = 0, A ≠ 0- linia coincide cu axa OU

. A = C = 0, B ≠ 0- linia coincide cu axa Oh

Ecuația unei linii drepte poate fi reprezentată în diferite forme în funcție de orice dat

condiții inițiale.

Ecuația unei drepte printr-un punct și un vector normal.

Definiție. Într-un sistem de coordonate dreptunghiular cartezian, un vector cu componente (A, B)

perpendicular pe dreapta dată de ecuație

Ah + Wu + C = 0.

Exemplu. Aflați ecuația unei drepte care trece printr-un punct A(1, 2) perpendicular pe vector (3, -1).

Decizie. Să compunem la A \u003d 3 și B \u003d -1 ecuația unei linii drepte: 3x - y + C \u003d 0. Pentru a găsi coeficientul C

înlocuim coordonatele punctului dat A în expresia rezultată. Obținem: 3 - 2 + C \u003d 0, prin urmare

C = -1. Total: ecuația dorită: 3x - y - 1 \u003d 0.

Ecuația unei drepte care trece prin două puncte.

Să fie date două puncte în spațiu M 1 (x 1 , y 1 , z 1)și M2 (x 2, y 2 , z 2), apoi ecuație în linie dreaptă,

trecând prin aceste puncte:

Dacă oricare dintre numitori este egal cu zero, numărătorul corespunzător trebuie setat egal cu zero. Pe

plan, ecuația unei drepte scrisă mai sus este simplificată:

dacă x 1 ≠ x 2și x = x 1, dacă x 1 = x 2 .

Fracțiune = k numit factor de pantă Drept.

Exemplu. Aflați ecuația unei drepte care trece prin punctele A(1, 2) și B(3, 4).

Decizie. Aplicând formula de mai sus, obținem:

Ecuația unei drepte după un punct și o pantă.

Dacă ecuația generală a unei drepte Ah + Wu + C = 0 aduce la forma:

și desemnează , atunci ecuația rezultată se numește

ecuația unei drepte cu panta k.

Ecuația unei drepte pe un punct și un vector de direcție.

Prin analogie cu punctul care are în vedere ecuația unei linii drepte prin vectorul normal, puteți intra în sarcină

o dreaptă printr-un punct și un vector de direcție al unei drepte.

Definiție. Fiecare vector diferit de zero (α 1 , α 2), ale căror componente satisfac condiția

Aα 1 + Bα 2 = 0 numit vector de direcție al dreptei.

Ah + Wu + C = 0.

Exemplu. Aflați ecuația unei drepte cu vector de direcție (1, -1) și care trece prin punctul A(1, 2).

Decizie. Vom căuta ecuația dreptei dorite sub forma: Ax + By + C = 0. Conform definiției,

coeficienții trebuie să îndeplinească condițiile:

1 * A + (-1) * B = 0, adică A = B.

Atunci ecuația unei drepte are forma: Ax + Ay + C = 0, sau x + y + C / A = 0.

la x=1, y=2 primim C/ A = -3, adică ecuația dorită:

x + y - 3 = 0

Ecuația unei drepte în segmente.

Dacă în ecuația generală a dreptei Ah + Wu + C = 0 C≠0, atunci, împărțind la -C, obținem:

sau unde

Sensul geometric al coeficienților este că coeficientul a este coordonata punctului de intersecție

drept cu ax Oh, A b- coordonata punctului de intersecție a dreptei cu axa OU.

Exemplu. Este dată ecuația generală a unei drepte x - y + 1 = 0. Găsiți ecuația acestei drepte în segmente.

C \u003d 1, , a \u003d -1, b \u003d 1.

Ecuația normală a unei linii drepte.

Dacă ambele părți ale ecuației Ah + Wu + C = 0împărțiți la număr , Care e numit

factor de normalizare, apoi primim

xcosφ + ysinφ - p = 0 -ecuația normală a unei linii drepte.

Semnul ± al factorului de normalizare trebuie ales astfel încât μ * C< 0.

R- lungimea perpendicularei coborâte de la origine la linie,

A φ - unghiul format de aceasta perpendiculara cu directia pozitiva a axei Oh.

Exemplu. Având în vedere ecuația generală a unei drepte 12x - 5y - 65 = 0. Necesar pentru a scrie diferite tipuri de ecuații

această linie dreaptă.

Ecuația acestei drepte în segmente:

Ecuația acestei drepte cu panta: (împarte la 5)

Ecuația unei linii drepte:

cos φ = 12/13; sin φ= -5/13; p=5.

Trebuie remarcat faptul că nu orice linie dreaptă poate fi reprezentată printr-o ecuație în segmente, de exemplu, linii drepte,

paralel cu axele sau trecând prin origine.

Unghiul dintre liniile unui plan.

Definiție. Dacă sunt date două rânduri y \u003d k 1 x + b 1, y \u003d k 2 x + b 2, apoi unghiul ascuțit dintre aceste linii

va fi definit ca

Două drepte sunt paralele dacă k 1 = k 2. Două drepte sunt perpendiculare

dacă k 1 \u003d -1 / k 2 .

Teorema.

Direct Ah + Wu + C = 0și A 1 x + B 1 y + C 1 \u003d 0 sunt paralele când coeficienții sunt proporționali

A 1 \u003d λA, B 1 \u003d λB. Dacă de asemenea С 1 \u003d λС, apoi liniile coincid. Coordonatele punctului de intersecție a două drepte

se găsesc ca soluție a sistemului de ecuații ale acestor drepte.

Ecuația unei drepte care trece printr-un punct dat este perpendiculară pe o dreaptă dată.

Definiție. Linie care trece printr-un punct M 1 (x 1, y 1)și perpendicular pe linie y = kx + b

reprezentată de ecuația:

Distanța de la un punct la o linie.

Teorema. Dacă se acordă un punct M(x 0, y 0), apoi distanța până la linie Ah + Wu + C = 0 definit ca:

Dovada. Lasă punctul M 1 (x 1, y 1)- baza perpendicularei coborâtă din punct M pentru un dat

direct. Apoi distanța dintre puncte Mși M 1:

(1)

Coordonatele x 1și 1 poate fi găsită ca soluție a sistemului de ecuații:

A doua ecuație a sistemului este ecuația unei drepte care trece perpendicular printr-un punct dat M 0

linie dată. Dacă transformăm prima ecuație a sistemului în forma:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

apoi, rezolvand, obtinem:

Înlocuind aceste expresii în ecuația (1), găsim:

Teorema a fost demonstrată.

Ecuația

Ah+Wu+C=0

(Unde A, B, C poate avea orice valoare, atâta timp cât coeficienții A, B nu au fost zero ambele deodată) reprezintă linie dreapta. Orice linie dreaptă poate fi reprezentată printr-o ecuație de acest tip. De aceea se numește ecuația generală a unei drepte.

În cazul în care un DAR X paralel cu axa x.

În cazul în care un LA=0, adică ecuația nu conține la, atunci reprezintă o linie, paralel cu axa OY.

Kogla LA nu este egal cu zero, atunci ecuația generală a unei linii drepte poate fi rezolvă relativ la ordonatăla , apoi este convertit în formular

(Unde a=-A/B; b=-C/B).

La fel, când DAR diferit de zero, ecuația generală a unei drepte poate fi rezolvată în raport cu X.

În cazul în care un Cu=0, adică ecuația generală a unei drepte nu conține un termen liber, atunci reprezintă o dreaptă care trece prin origine

5.

Ecuația unei drepte care trece printr-un punct dat A(X 1 , y 1) într-o direcție dată, determinată de pantă k,

y - y 1 = k(X - X 1). (1)

Această ecuație definește un creion de linii care trec printr-un punct A(X 1 , y 1), care se numește centrul fasciculului.

. Ecuația unei drepte care trece prin două puncte: A(X 1 , y 1) și B(X 2 , y 2) se scrie astfel:

Panta unei drepte care trece prin două puncte date este determinată de formula

7 Ecuația unei drepte în segmente

Dacă în ecuația generală a dreptei , atunci împărțind (1) la , obținem ecuația dreptei în segmente

Unde , . Linia intersectează axa în punct , axa în punct .

8Formulă: Unghiul dintre liniile unui plan

La Poartă α între două drepte date de ecuațiile: y=k 1 x+b 1 (prima linie) și y=k 2 x+b 2 (a doua linie), poate fi calculată prin formula (unghiul se măsoară de la prima linie la a doua în sens invers acelor de ceasornic ):

tg(α)=(k 2 -k 1 )/(1+k 1 k 2 )

9 Dispunerea reciprocă a două linii drepte pe un plan.

Lasă-le pe amândouă acum ecuații liniile drepte sunt scrise în formă generală.

Teorema. Lasa

- general ecuații două linii drepte coordona avion Oxy. Apoi

1) dacă , atunci Dreptși potrivire;

2) dacă , atunci liniile și

paralel;

3) dacă , atunci Drept se intersectează.

Dovada. Condiția este echivalentă cu coliniaritatea normalului vectori date directe:

Prin urmare, dacă , atunci Drept se intersectează.

Dacă , apoi , , și ecuația Drept ia forma:

Sau , adică Drept Meci. Rețineți că coeficientul de proporționalitate , altfel toți coeficienții totalului ecuații ar fi zero, ceea ce este imposibil.

Dacă Drept nu coincid si nu se intersecteaza, atunci ramane cazul, i.e. Drept sunt paralele.

Teorema a fost demonstrată.

Pentru a determina distanța de la un punct la o dreaptă, trebuie să cunoașteți ecuațiile dreptei și coordonatele punctului din sistemul de coordonate carteziene. Distanța de la un punct la o dreaptă este perpendiculara trasată de la acel punct la linie.

Instruire

Ecuația generală a unei drepte în coordonate carteziene este Ax+By+C=0, unde A, B și C sunt numere cunoscute. Fie punctul O să aibă coordonatele (x1, y1) în sistemul de coordonate carteziene.

În acest caz, abaterea acestui punct de la linia dreaptă este δ=(Ax1+By1+C)/sqrt((A^2)+(B^2)) dacă C<0, и δ=(Ax1+By1+C)/(-sqrt((A^2)+(B^2))), если C>0.

Distanța de la un punct la o dreaptă este abaterea absolută a unui punct de la o dreaptă, adică r=|(Ax1+By1+C)/sqrt((A^2)+(B^2))| , dacă C<0, и δ=|(Ax1+By1+C)/(-sqrt((A^2)+(B^2)))|, если C>0.

Acum să fie dat punctul cu coordonatele (x1, y1, z1) în spațiul tridimensional. Linia dreaptă poate fi definită parametric, printr-un sistem de trei ecuații: x = x0+ta, y = y0+tb, z = z0+tc, unde t este un număr real. Distanța de la un punct la o linie poate fi găsită ca distanța minimă de la acest punct la un punct arbitrar pe linie. Coeficientul t al acestui punct este tmin=(a(x1-x0)+b(y1-y0)+c(z1-z0))/((a^2)+(b^2)+(c^2) )

Distanța de la punctul (x1, y1) la linie dreaptă poate fi calculată și dacă dreapta este dată de o ecuație cu pantă: y = kx+b. Atunci ecuația dreptei perpendiculare pe aceasta va arăta astfel: y = (-1/k)x+a. În continuare, trebuie să țineți cont de faptul că această linie trebuie să treacă prin punctul (x1, y1). De aici se găsește numărul a. După transformări se găsește și distanța dintre punct și linie.

31 . Bazat pe plan și în spațiu

Definiție. Bazat pe avion se numesc oricare doi vectori liniar independenti.

oricare doi vectori necoliniari formează o bază. Lasa A orice vector din plan și vectorii bși c formează o bază. Deoarece oricare trei vectori sunt dependenți liniar de plan, vectorul A este exprimată liniar în termeni de vectori de bază, adică relația

Definiție. bază în spațiu se numesc oricare trei vectori liniar independenti. oricare trei vectori necoplanari formează o bază. Ca si in cazul planului, se stabileste ca orice vector A se descompune în vectori b, cși d

Definiție generală (pentru a fi clar pentru toată lumea) O bază pe un plan (în spațiu) este o pereche ordonată (triplu) de vectori necoliniari (necoplanari). Orice vector poate fi extins în mod unic în ceea ce privește baza. Coeficienții de expansiune se numesc coordonatele acestui vector în raport cu baza dată. Vectorii formează o bază în spațiul de coordonate carteziene Oxyz.