Introducere

Educația matematică primită într-o școală de învățământ general este o componentă esențială a educației generale și a culturii generale a unei persoane moderne. Aproape tot ceea ce înconjoară o persoană modernă este legat într-un fel sau altul de matematică. Iar cele mai recente realizări în fizică, inginerie și tehnologia informației nu lasă nicio îndoială că în viitor starea de lucruri va rămâne aceeași. Prin urmare, rezolvarea multor probleme practice se reduce la rezolvarea diferitelor tipuri de ecuații care trebuie învățate să le rezolve.

În matematica elementară se disting două tipuri de ecuații: algebrice și transcendentale.Ecuațiile algebrice includ:

liniar; pătrat; cub; biquad; ecuația de gradul al patrulea a unei forme generale; ecuație algebrică cu doi termeni de gradul al n-lea; algebrică de putere; - întoarcere (algebrică); – ecuația algebrică a gradului al treilea a unei forme generale;

10. ecuații algebrice fracționale, adică. ecuații care conțin polinoame și fracții algebrice (fracții de forma

, unde și sunt polinoame);

11. ecuații iraționale, adică. ecuații care conțin radicali sub care se află polinoamele și fracțiile algebrice;

12. ecuații care conțin un modul, sub modulul căruia sunt cuprinse polinoame și fracții algebrice.

Ecuațiile care conțin funcții transcendentale, cum ar fi funcțiile logaritmice, exponențiale sau trigonometrice, sunt numite transcendentale. În munca noastră, luăm în considerare ecuațiile algebrice mai detaliat.

În literatura educațională și metodică sunt considerate în mod tradițional metode speciale de rezolvare a ecuațiilor. Între timp, specificul rezolvării ecuațiilor fiecărei secțiuni este o chestiune secundară. Practic, există patru metode principale:

Înlocuirea ecuației h (f(x))=h (g(x)) cu ecuația f(x)=g(x);

Metoda de înlocuire variabilă;

Metoda de factoring;

Metoda funcțional-grafică și diversele modificări ale acestora.

Cea mai comună dintre acestea este metoda substituției variabile.

Pe baza acesteia, formulăm scopul lucrării noastre: studierea posibilităților metodei de înlocuire a necunoscutului în rezolvarea ecuațiilor algebrice și demonstrarea aplicării acestora în situații standard și nestandard. Pentru a atinge acest obiectiv, este necesar să se rezolve următoarele sarcini:

1. Extindeți conținutul principalelor concepte și enunțuri legate de teoria rezolvării ecuațiilor: rezolvarea unei ecuații, echivalență și consecință, metode generale de rezolvare a ecuațiilor.

2. Să identifice posibilităţile de utilizare a metodei de înlocuire a necunoscutului la rezolvarea ecuaţiilor algebrice în situaţii standard şi nestandard.

3. Să efectueze tipificarea metodelor de introducere de noi necunoscute la rezolvarea ecuațiilor algebrice și să identifice criteriile de aplicabilitate a acestora

4. Alcătuiește un set de probleme tipice care se rezumă la utilizarea metodei înlocuirii în rezolvarea ecuațiilor și demonstrează rezolvarea acestora.

1. Concepte de bază și enunțuri legate de teoria rezolvării ecuațiilor

În primul capitol al lucrării noastre, vom dezvălui conținutul principalelor concepte și enunțuri legate de teoria rezolvării ecuațiilor.

Ne familiarizăm cu conceptul de „ecuație” în lecțiile de matematică deja din școala elementară, iar sarcina de „rezolvare a unei ecuații” este probabil cea mai comună sarcină. Cu toate acestea, nu putem da o definiție precisă a conceptului de „ecuație”, defini cu precizie ce înseamnă „rezolvarea unei ecuații”, fără a depăși cu mult cadrul cursului de matematică elementară. Pentru a face acest lucru, este necesar să se implice categorii logice și chiar filozofice foarte serioase. Este suficient să ne familiarizăm cu aceste concepte la nivelul „bunului simț”.

Luați în considerare două ecuații A și B cu aceeași necunoscută. Vom spune că ecuația B este consecinţă ecuația A, dacă orice rădăcină a ecuației A este o rădăcină a ecuației B.

Ecuațiile sunt numite echivalent dacă vreo rădăcină a unuia dintre ele este o rădăcină a celuilalt și invers. Astfel, ecuațiile sunt echivalente dacă fiecare dintre ele este o consecință a celeilalte.

Din aceste definiții rezultă, de exemplu, că două ecuații care nu au soluții sunt echivalente. Dacă A nu are soluții, atunci B este consecinţă A, oricare ar fi ecuația B.

Să definim conceptul de „rezolvare a unei ecuații”. rezolva ecuatia- înseamnă a găsi toate astfel de valori ale necunoscutelor incluse în ea, care transformă ecuația într-o identitate. Aceste valori se numesc rădăcinile ecuației.

Procesul de rezolvare a ecuatiilor consta in principal in inlocuirea unei ecuatii date cu alta echivalenta acesteia.

După cum am menționat mai devreme, există patru metode cele mai comune utilizate în rezolvarea ecuațiilor de orice fel. Să aruncăm o privire mai atentă la fiecare metodă.

Metoda de înlocuire a ecuației h (f(x))=h (g(x)) cu ecuația f(x)=g(x) poate fi utilizată numai atunci când

este o funcție monotonă care își ia fiecare dintre valorile o dată. Dacă această funcție este nemonotonă, atunci metoda specificată nu poate fi aplicată, deoarece este posibilă pierderea rădăcinilor.

Esenţa metodei factorizării este următoarea: ecuaţia

poate fi inlocuit:

După ce ați rezolvat ecuațiile acestei mulțimi, trebuie să luați acele rădăcini care aparțin domeniului de definire a ecuației originale și să aruncați restul ca străine.Ideea unei metode grafice pentru rezolvarea ecuației

este după cum urmează: trebuie să construiți grafice ale funcțiilor și să găsiți punctele lor de intersecție. Rădăcinile ecuației sunt abscisele acestor puncte. Această metodă vă permite să determinați numărul de rădăcini ale ecuației, să ghiciți valoarea rădăcinii, să găsiți valori aproximative și, uneori, exacte ale rădăcinilor. În unele cazuri, construcția graficelor de funcții poate fi înlocuită cu o referire la unele proprietăți ale funcțiilor (de aceea nu vorbim despre o metodă grafică, ci despre o metodă funcțional-grafică de rezolvare a ecuațiilor). Dacă, de exemplu, una dintre funcții creste, iar celalalt scade, atunci ecuatia fie nu are radacini, fie are o singura radacina.Sa amintim o alta varietate destul de frumoasa a metodei functional-grafice: daca pe interval cea mai mare valoare a uneia dintre functii este egala cu si cea mai mică valoare a celeilalte funcții este de asemenea egală, atunci ecuația este echivalentă pe interval cu un sistem de ecuații.

Să dezvăluim esența metodei schimbării variabilei: dacă ecuația

Rezolvarea ecuațiilor prin modificarea variabilelor

Majoritatea sarcinilor vieții

se rezolvă sub formă de ecuații algebrice:

reducându-le la forma lor cea mai simplă.

L.N. Tolstoi.

Scopul lecției: să organizeze activităţile educaţionale ale elevilor în însuşirea metodelor de rezolvare a ecuaţiilor întregi de grade superioare prin metoda schimbării unei variabile; să prezinte elevilor conceptele, metodele de rezolvare a ecuaţiilor reciproce şi simetrice.

Sarcini:educational: continuă să dezvolte capacitatea de a aplica metoda de înlocuire

variabilă la rezolvarea ecuațiilor; formarea capacității de a vedea aceeași metodă de rezolvare a ecuațiilor în situații diferite; să-și facă o idee despre metodele și modalitățile de rezolvare a problemelor nestandardizate și a ecuațiilor algebrice la un nivel care depășește nivelul standardelor educaționale de stat;

în curs de dezvoltare: dezvoltarea gândirii elevilor; dezvoltarea memoriei; dezvoltare

gândire logică, capacitatea de a-și articula clar gândurile; dezvoltarea imaginației elevilor; dezvoltarea vorbirii orale.

educational: educația observației; educația acurateții

atunci când faceți notițe pe tablă și într-un caiet; educarea independenţei în efectuarea lucrărilor practice.

În timpul orelor

Organizarea timpului.

Actualizarea și sistematizarea cunoștințelor.

Sarcina numărul 1. Rezolvați cuvintele încrucișate. Scrieți răspunsurile dvs. numai în cazul nominativ.

Orizontal:

4. Care este expresia unei ecuații pătratice? (discriminant)

6. Valoarea variabilei la care ecuația se transformă într-o egalitate adevărată. (rădăcină)

8. Ecuația formei
, Unde
. (bi-pătrat)

9. Matematician francez legat de ecuațiile pătratice. (Viet)

10. O ecuație în care părțile din stânga și din dreapta sunt expresii întregi. (întreg)

11. Ecuații cu o variabilă având același set de rădăcini. (echivalent)

Vertical:

1. Mulțimea rădăcinilor ecuației. (soluţie)

2. Rezolvarea ecuației
. (zero)

3.Egalitatea care conține o variabilă. (ecuația)

5. O ecuație pătratică în care unul dintre coeficienții b sau c este egal cu 0. (incomplet)

7. O ecuație pătratică în care primul coeficient este egal cu unu. (redus)

Ceea ce ne vom dedica astăzi lecția? ( Rezolvarea ecuațiilor )

Sarcina numărul 2. Cum ați rezolva ecuațiile pentru fiecare grup?

RĂSPUNSURI: Exemplele din grupa 1) se rezolvă cel mai bine prin factorizare prin scoaterea factorului comun din paranteze sau prin utilizarea formulelor de înmulțire abreviate.

Exemplele din grupa 2) se rezolvă mai bine prin grupare și factorizare.

Exemplele din grupa 3) se rezolvă mai bine prin introducerea unei noi variabile și trecerea la o ecuație pătratică.

1 Ce multiplicator ați scoate dintre paranteze în exemplele grupului 1?

RĂSPUNSURI:

Cum ați grupa termenii din exemplele grupului 2?

RĂSPUNSURI:

Ce ați desemna printr-o nouă variabilă în exemplele grupului 3?

RĂSPUNSURI:

Cum poți factoriza un polinom
?

RĂSPUNSURI: .

Astăzi, în lecție, îți vei arăta cunoștințele despre subiectul „Rezolvarea ecuațiilor prin schimbarea variabilei”

Notați subiectul lecției în caiete.

Astăzi în lecție vom lua în considerare una dintre modalitățile de rezolvare a ecuațiilor de grade superioare - metoda de schimbare a unei variabile; ne vom familiariza cu conceptele, metodele de rezolvare a ecuatiilor reciproce si simetrice.

Arta substituirii variabilelor este de a vedea care substituție este mai rațională și mai probabil să conducă la succes.

Sarcina numărul 3.

Rezolvați ecuația.(Sarcina de la tablă este rezolvată simultan de 2 elevi.)

dar) (Primul elev decide la tablă cu o explicație.)

b) (Al doilea elev rezolvă ecuația în tăcere, apoi explică soluția, clasa ascultă și pune întrebări dacă ceva nu este clar.)

1 studentÎnlocuire:
.

2 elevÎnlocuire:
.

(Suplimentar pentru cei care s-au mai ocupat de ecuațiile anterioare).

. .

3 elev

(Elevii comentează de la fața locului evoluția deciziei.)

SOLUȚIE: Scoateți factorul comun: ,

Unde
sau
, adică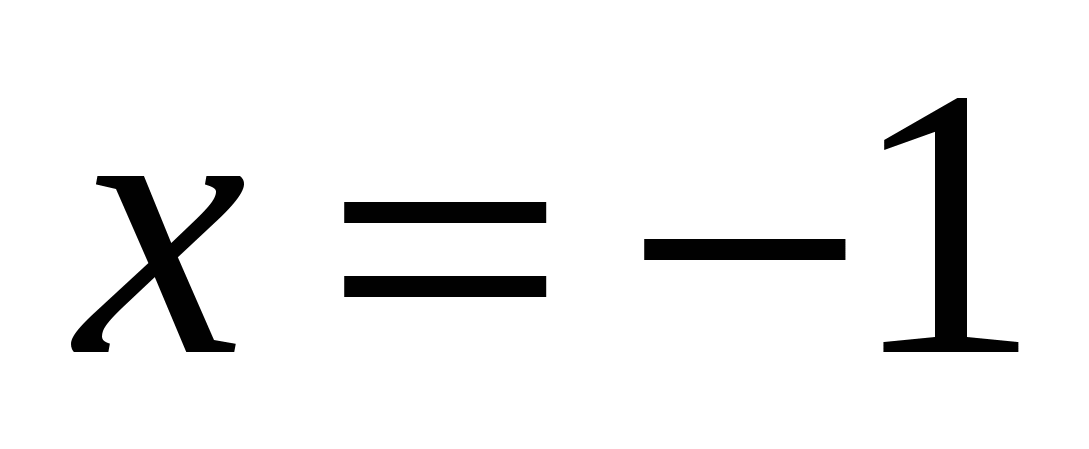

Răspuns:

Aprofundarea și extinderea cunoștințelor

Continuăm să lucrăm. Veți vedea ecuația pe diapozitiv: x 4 -5x 3 +6x 2 -5x + 1 = 0.

Cum ai propune să o rezolvi? Cum putem fi?

Este posibil să o rezolvi în cadrul programelor școlare de matematică? Poți răspunde nu. La urma urmei, metodele standard de rezolvare a ecuațiilor în școală prevăd rezolvarea ecuațiilor nu mai mari decât gradul doi. Dar ne putem aminti că ecuațiile individuale de grade superioare erau încă rezolvate la școală. Adevărat, metodele de rezolvare a acestora sunt aplicarea creativă a metodelor cunoscute, reducerea lor la soluția uneia sau mai multor ecuații de grad nu mai mari decât a doua.

Priviți foarte atent această ecuație? Ce ai observat ?(în această ecuație, coeficienții echidistanți de capete sunt egali)

Băieți, o ecuație de acest fel, când coeficienții echidistanți de la capete sunt aceiași, se numește returnabil. Această ecuație este redusă la una pătratică folosind substituție.

Vă ofer următorul algoritm pentru rezolvarea acestora:

Algoritm pentru rezolvarea ecuațiilor reciproce.

1. Împărțiți ambele părți ale ecuației la x 2.

2. Grupează termenii (primul cu ultimul, al doilea cu al patrulea).

Aduceți ecuația în formă dar + c = 0

3.Introduceți o nouă variabilă t = , apoi t 2 = , adică \u003d t 2 - 2.

4. Efectuați înlocuirea și rezolvați ecuația pătratică.

5. Reveniți la înlocuire și rezolvați ecuațiile rezultate.

6. Notează răspunsul.

Băieții învață algoritmul.

Elevul la tablă conform algoritmului și cu ajutorul profesorului rezolvă ecuația, restul scrie în caiete.

6x 4 – 5x 3 – 38x 2 – 5x + 6 = 0.

Soluţie.

6x 2 - 5x - 38 - 5 / x + 6 / x 2 \u003d 0.

6 (x 2 + 1 / x 2) - 5 (x + 1 / x) - 38 \u003d 0.

Introduceți t: substituție (x + 1/x) = t. Înlocuire: (x 2 + 1 / x 2) \u003d t 2 - 2, avem:

6t 2 – 5t – 50 = 0.

t = -5/2 sau t = 10/3.

Să revenim la x. După înlocuirea inversă, rezolvăm cele două ecuații rezultate:

1) x + 1/x = -5/2;

x 2 + 5/2 x +1 = 0;

x = -2 sau x = -1/2.

2) x + 1/x = 10/3;

x 2 - 10/3 x + 1 = 0;

x = 3 sau x = 1/3.

Răspuns: -2; -1/2; 1/3; 3.

Matematicienii italieni din secolul al XVI-lea N. Tartaglia, A. Fiore, D. Cardano și alții au adus o mare contribuție la problema ecuațiilor de gradul 3 și 4. În 1535, a avut loc un duel științific între A. Fiore și N. Tartaglia, la care acesta din urmă a câștigat. În 2 ore, a rezolvat 30 de probleme propuse de Fiore, iar Fiore însuși nu a putut rezolva nici una pe care i-a dat-o Tartaglia.

Băieți, și vreau să vă ofer încă o ecuație astăzi, am luat-o din colecția de sarcini pentru pregătirea pentru OGE.

. ((x + 1)(x + 4))((x + 2)(x + 3)) = 24,

(x 2 + 5x + 4) (x 2 + 5x + 6) = 24.

Făcând schimbarea x 2 + 5x + 4 = t, avem ecuația

t(t + 2) = 24, este pătrat:

t 2 + 2t - 24 = 0.

t = -6 sau t = 4.

După efectuarea înlocuirii inverse, putem găsi cu ușurință rădăcinile ecuației originale.

Răspuns: -5; 0.

Transfer creativ de cunoștințe și abilități în condiții noi.

La începutul lecției, am vorbit despre faptul că, dacă există elemente repetate în ecuație, atunci se poate folosi metoda înlocuirii variabilelor. Încă nu știm cum să rezolvăm ecuații trigonometrice și iraționale. Să vedem dacă le putem aplica această metodă dacă știm să rezolvăm cele mai simple ecuații trigonometrice și iraționale.

Exercitiul 1: Numiți modificarea variabilei în următoarele ecuații.

Sarcina 2: Scrieți mai multe ecuații bazate pe metoda schimbării variabilei.

Rezumând.

Deci, băieți, lecția noastră s-a încheiat. Să rezumam lecția noastră.

Ce obiective ne-am stabilit la începutul lecției?

Au fost atinse obiectivele noastre?

Ce nou am învățat la lecție?

Teme pentru acasă.

4x 4 - 8x 3 + 3x 2 - 8x + 4 = 0

(x+1)(x+2)(x+4)(x+5) = 40

. (o ecuație a matematicienilor italieni)

Și vreau să închei lecția cu cuvintele marelui om de știință Einstein A.:

„Trebuie să-mi împart timpul între politică și ecuații. Cu toate acestea, ecuația, după părerea mea, este mult mai importantă, pentru că politica există doar pentru acest moment, iar ecuația va exista pentru totdeauna.

Mulțumesc pentru lecție! La revedere!

Modificarea variabilei în integrala nedefinită. Formula pentru transformarea diferenţialelor. Exemple de integrare. Exemple de substituții liniare.

Metoda de înlocuire variabilă

Cu ajutorul unei schimbări de variabilă, puteți calcula integrale simple și, în unele cazuri, puteți simplifica calculul celor mai complexe.

Metoda de înlocuire a variabilei este că trecem de la variabila de integrare inițială, fie x , la o altă variabilă, pe care o notăm t . În același timp, presupunem că variabilele x și t sunt legate printr-o relație x = x (t), sau t = t (X). De exemplu x = log t, x = sin t, t = 2 x + 1, etc. Sarcina noastră este să alegem o astfel de relație între x și t, astfel încât integrala originală fie să se reducă la una tabelară, fie să devină mai simplă.

Formula de bază pentru modificarea variabilei

Luați în considerare expresia care se află sub semnul integral. Constă din produsul integrandului, pe care îl vom desemna f (X) si diferential dx : . Să trecem la o nouă variabilă t alegând o relație x = x (t). Atunci trebuie să exprimăm funcția f (X) iar diferenţialul dx în ceea ce priveşte variabila t .

Pentru a exprima integrandul f (X) prin variabila t, trebuie doar să înlocuiți raportul ales x = x în loc de variabila x (t).

Transformarea diferenţială se face astfel:
.
Adică diferența dx este egală cu produsul derivatei lui x față de t și diferența dt.

Apoi
.

În practică, cel mai frecvent caz este atunci când efectuăm o înlocuire prin alegerea unei variabile noi în funcție de cea veche: t = t (X). Dacă am ghici că integrandul poate fi reprezentat ca
,
unde t′ (X) este derivata lui t în raport cu x, atunci
.

Deci, formula de bază a schimbării variabilei poate fi reprezentată în două forme.
(1) ,
unde x este o funcție a lui t .
(2) ,
unde t este o funcție a lui x.

Notă importantă

În tabelele de integrale, variabila de integrare este cel mai adesea notă cu x . Cu toate acestea, merită luat în considerare faptul că variabila de integrare poate fi notată cu orice literă. Mai mult, orice expresie poate fi folosită ca variabilă de integrare.

Ca exemplu, luați în considerare integrala tabelului
.

Aici x poate fi înlocuit cu orice altă variabilă sau cu o funcție a unei variabile. Iată exemple de opțiuni posibile:
;
;
.

În ultimul exemplu, trebuie să țineți cont de faptul că la trecerea la variabila de integrare x , diferența este transformată după cum urmează:
.
Apoi
.

Acest exemplu este esența integrării substituției. Adică trebuie să ghicim asta
.
După aceea, integrala se reduce la una tabelară.
.

Puteți calcula această integrală folosind o schimbare de variabilă, aplicând formula (2) . Fie t = x 2+x. Apoi
;
;

.

Exemple de integrare prin schimbarea variabilei

1) Calculăm integrala
.
Observăm că (sin x)′ = cos x. Apoi

.
Aici am aplicat substituția t = sin x.

2) Calculăm integrala
.
Observăm că. Apoi

.
Aici am realizat integrarea prin modificarea variabilei t = arctg x.

3) Să ne integrăm
.
Observăm că. Apoi

. Aici, în timpul integrării, modificarea variabilei t = x 2 + 1 .

Substituții liniare

Poate că cele mai comune sunt substituțiile liniare. Aceasta este o înlocuire a variabilei de formă
t = ax + b
unde a și b sunt constante. Sub o astfel de schimbare, diferențele sunt legate prin relație
.

Exemple de integrare prin substituții liniare

A) Calculați integrala
.
Soluţie.
.

b) Găsiți integrala
.
Soluţie.
Să folosim proprietățile funcției exponențiale.
.
ln 2- este o constantă. Calculăm integrala.

.

c) Calculați integrala
.
Soluţie.
Aducem polinomul pătrat din numitorul unei fracții la suma pătratelor.
.
Calculăm integrala.

.

D) Găsiți integrala
.
Soluţie.
Transformăm polinomul sub rădăcină.

.
Integram folosind metoda schimbarii variabilei.

.
Am obținut anterior formula
.
De aici
.
Înlocuind această expresie, obținem răspunsul final.

Matematica este o gaură prin care mintea logică poate spiona lumea ideală.

Krotov Victor

La școală, primul loc în cursul de algebră este ocupat de ecuații raționale. Este dedicat mai mult timp studiului lor decât oricăror alte subiecte. Acest lucru se datorează în primul rând faptului că ecuațiile nu sunt doar de mare importanță teoretică, ci servesc și multor scopuri practice. Un număr mare de probleme din lumea reală se rezumă la rezolvarea diverselor ecuații și numai după ce stăpânești metodele de rezolvare a acestora, vei găsi răspunsuri la diferite întrebări ale științei și tehnologiei.

Pentru formarea capacității de a rezolva ecuații raționale, munca independentă a elevului este de mare importanță. Cu toate acestea, înainte de a trece la munca independentă, este necesar să cunoaștem clar și să fiți capabil să aplicați în practică toate metodele posibile de rezolvare a ecuațiilor raționale.

Să ne uităm la exemple în detaliu metoda de schimbare a variabilei pentru rezolvarea ecuațiilor raționale.

Exemplul 1

Rezolvați ecuația (2x 2 - 3x + 1) 2 = 22x 2 - 33x + 1.

Soluţie.

Rescriem ecuația sub forma

(2x 2 - 3x + 1) 2 = 11(2x 2 - 3x) + 1. Să facem o schimbare. Fie 2x 2 - 3x \u003d t, atunci ecuația va lua forma:

(t + 1) 2 = 11t + 1.

Acum deschidem parantezele și dăm altele similare, obținem:

t2 + 2t + 1 = 11t + 1;

În ecuația pătratică incompletă rezultată, scoatem factorul comun din paranteze, vom avea:

t = 0 sau t = 9.

Acum trebuie să faceți o înlocuire inversă și să rezolvați fiecare dintre ecuațiile rezultate:

2x 2 - 3x = 0 sau 2x 2 - 3x = 9

x(2x - 3) = 0 2x 2 - 3x - 9 = 0

x = 0 sau x = 3/2 x = 3 sau x = -3/2

Răspuns: -1,5; 0; 1,5; 3.

Exemplul 2

Rezolvați ecuația (x 2 - 6x) 2 - 2(x - 3) 2 = 81.

Soluţie.

Să aplicăm formula pătratului diferenței (a - b) 2 = a 2 - 2ab + b 2 . Scriem ecuația inițială în forma

(x 2 - 6x) 2 - 2(x 2 - 6x + 9) = 81. Acum puteți face o înlocuire.

Fie x 2 - 6x \u003d t, atunci ecuația va arăta astfel:

t 2 - 2 (t + 9) \u003d 81.

t 2 - 2t - 18 - 81 = 0;

t 2 - 2t - 99 = 0.

Conform teoremei Vieta, rădăcinile ecuației rezultate vor fi numerele -9 și 11.

Să facem înlocuirea inversă:

x 2 - 6x = -9 sau x 2 - 6x = 11

x 2 - 6x + 9 = 0 x 2 - 6x - 11 = 0

(x - 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 \u003d 3 - 2√5.

Răspuns: 3 - 2√5; 3; 3 + 2√5.

Exemplul 3

Rezolvați ecuația (x - 1)(x - 3)(x + 5)(x + 7) = 297 și găsiți produsul rădăcinilor sale.

Soluţie.

Să găsim o modalitate „profitabilă” de a grupa factorii și de a deschide perechile de paranteze:

((x - 1)(x + 5))((x - 3)(x + 7)) = 297;

(x 2 + 5x - x - 5) (x 2 + 7x - 3x - 21) = 297;

(x 2 + 4x - 5) (x 2 + 4x - 21) = 297.

Să facem schimbarea x 2 + 4x = t, atunci ecuația va arăta astfel:

(t - 5)(t - 21) = 297.

Să deschidem parantezele, dăm termeni similari:

t 2 - 21t - 5t + 105 = 297;

t 2 - 26t - 192 = 0.

Conform teoremei Vieta, determinăm că rădăcinile ecuației rezultate vor fi numerele -6 și 32.

După înlocuirea inversă vom avea:

x 2 + 4x = -6 sau x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x - 32 = 0

D = 16 - 24< 0 D = 16 + 128 > 0

Fără rădăcini x 1 = -8; x 2 = 4

Să aflăm produsul rădăcinilor: -8 4 = -32.

Răspuns: -32.

Exemplul 4

Aflați suma rădăcinilor ecuației (x 2 - 2x + 2) 2 + 3x(x 2 - 2x + 2) = 10x 2.

Soluţie.

Fie x 2 - 2x + 2 \u003d t, atunci ecuația va lua forma:

t 2 + 3xt - 10x 2 \u003d 0.

Considerați ecuația rezultată ca una pătratică în raport cu t.

D \u003d (3x) 2 - 4 (-10x 2) \u003d 9x 2 + 40x 2 \u003d 49x 2; ≥≤

t 1 = (-3x - 7x) / 2 și t 2 = (-3x + 7x) / 2;

t 1 = -5x și t 2 = 2x.

Deoarece t \u003d x 2 - 2x + 2, atunci

x 2 - 2x + 2 = -5x sau x 2 - 2x + 2 = 2x. Să rezolvăm fiecare dintre ecuațiile obținute.

x 2 + 3x + 2 = 0 sau x 2 - 4x + 2 = 0.

Ambele ecuații au rădăcini, deoarece D > 0.

Folosind teorema Vieta, putem concluziona că suma rădăcinilor primei ecuații este -3, iar a doua ecuație este 4. Obținem că suma rădăcinilor ecuației inițiale este -3 + 4 = 1

Raspunsul 1.

Exemplul 5

Aflați rădăcina ecuației (x + 1) 4 + (x + 5) 4 = 32 aparținând intervalului [-5; 10].

Soluţie.

Fie x = t - 3, apoi x + 1 = t - 2; x + 5 = t + 2 și ecuația inițială devine:

(t - 2) 4 + (t + 2) 4 \u003d 32. Pentru a ridica expresiile la a patra putere, puteți folosi triunghiul lui Pascal (Fig. 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4 .

După reducerea termenilor similari, obținem:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t 4 + 6t 2 2 2 + 2 4 = 16;

t 4 + 24t 2 + 16 = 16;

t4 + 24t2 = 0;

t2 (t2 + 24) = 0;

t \u003d 0 sau t 2 \u003d -24.

A doua ecuație nu are rădăcini, ceea ce înseamnă că t = 0 și după înlocuirea inversă

x \u003d t - 3 \u003d 0 - 3 \u003d -3. Rădăcina ecuației -3 aparține intervalului [-5; 10].

Răspuns: -3.

După cum puteți vedea, atunci când rezolvați ecuații raționale, trebuie să cunoașteți formulele de mai sus și să puteți număra corect. Erorile apar cel mai adesea la alegerea unui înlocuitor și la înlocuirea înapoi. Pentru a evita acest lucru, trebuie să descrieți în detaliu fiecare acțiune, apoi nu vor exista greșeli în deciziile dvs.

site, cu copierea integrală sau parțială a materialului, este necesară un link către sursă.

Matematica este o gaură prin care mintea logică poate spiona lumea ideală.

Krotov Victor

La școală, primul loc în cursul de algebră este ocupat de ecuații raționale. Este dedicat mai mult timp studiului lor decât oricăror alte subiecte. Acest lucru se datorează în primul rând faptului că ecuațiile nu sunt doar de mare importanță teoretică, ci servesc și multor scopuri practice. Un număr mare de probleme din lumea reală se rezumă la rezolvarea diverselor ecuații și numai după ce stăpânești metodele de rezolvare a acestora, vei găsi răspunsuri la diferite întrebări ale științei și tehnologiei.

Pentru formarea capacității de a rezolva ecuații raționale, munca independentă a elevului este de mare importanță. Cu toate acestea, înainte de a trece la munca independentă, este necesar să cunoaștem clar și să fiți capabil să aplicați în practică toate metodele posibile de rezolvare a ecuațiilor raționale.

Să ne uităm la exemple în detaliu metoda de schimbare a variabilei pentru rezolvarea ecuațiilor raționale.

Exemplul 1

Rezolvați ecuația (2x 2 - 3x + 1) 2 = 22x 2 - 33x + 1.

Soluţie.

Rescriem ecuația sub forma

(2x 2 - 3x + 1) 2 = 11(2x 2 - 3x) + 1. Să facem o schimbare. Fie 2x 2 - 3x \u003d t, atunci ecuația va lua forma:

(t + 1) 2 = 11t + 1.

Acum deschidem parantezele și dăm altele similare, obținem:

t2 + 2t + 1 = 11t + 1;

În ecuația pătratică incompletă rezultată, scoatem factorul comun din paranteze, vom avea:

t = 0 sau t = 9.

Acum trebuie să faceți o înlocuire inversă și să rezolvați fiecare dintre ecuațiile rezultate:

2x 2 - 3x = 0 sau 2x 2 - 3x = 9

x(2x - 3) = 0 2x 2 - 3x - 9 = 0

x = 0 sau x = 3/2 x = 3 sau x = -3/2

Răspuns: -1,5; 0; 1,5; 3.

Exemplul 2

Rezolvați ecuația (x 2 - 6x) 2 - 2(x - 3) 2 = 81.

Soluţie.

Să aplicăm formula pătratului diferenței (a - b) 2 = a 2 - 2ab + b 2 . Scriem ecuația inițială în forma

(x 2 - 6x) 2 - 2(x 2 - 6x + 9) = 81. Acum puteți face o înlocuire.

Fie x 2 - 6x \u003d t, atunci ecuația va arăta astfel:

t 2 - 2 (t + 9) \u003d 81.

t 2 - 2t - 18 - 81 = 0;

t 2 - 2t - 99 = 0.

Conform teoremei Vieta, rădăcinile ecuației rezultate vor fi numerele -9 și 11.

Să facem înlocuirea inversă:

x 2 - 6x = -9 sau x 2 - 6x = 11

x 2 - 6x + 9 = 0 x 2 - 6x - 11 = 0

(x - 3) 2 = 0 D = 80

x = 3 x 1 = 3 + 2√5; x 2 \u003d 3 - 2√5.

Răspuns: 3 - 2√5; 3; 3 + 2√5.

Exemplul 3

Rezolvați ecuația (x - 1)(x - 3)(x + 5)(x + 7) = 297 și găsiți produsul rădăcinilor sale.

Soluţie.

Să găsim o modalitate „profitabilă” de a grupa factorii și de a deschide perechile de paranteze:

((x - 1)(x + 5))((x - 3)(x + 7)) = 297;

(x 2 + 5x - x - 5) (x 2 + 7x - 3x - 21) = 297;

(x 2 + 4x - 5) (x 2 + 4x - 21) = 297.

Să facem schimbarea x 2 + 4x = t, atunci ecuația va arăta astfel:

(t - 5)(t - 21) = 297.

Să deschidem parantezele, dăm termeni similari:

t 2 - 21t - 5t + 105 = 297;

t 2 - 26t - 192 = 0.

Conform teoremei Vieta, determinăm că rădăcinile ecuației rezultate vor fi numerele -6 și 32.

După înlocuirea inversă vom avea:

x 2 + 4x = -6 sau x 2 + 4x = 32

x 2 + 4x + 6 = 0 x 2 + 4x - 32 = 0

D = 16 - 24< 0 D = 16 + 128 > 0

Fără rădăcini x 1 = -8; x 2 = 4

Să aflăm produsul rădăcinilor: -8 4 = -32.

Răspuns: -32.

Exemplul 4

Aflați suma rădăcinilor ecuației (x 2 - 2x + 2) 2 + 3x(x 2 - 2x + 2) = 10x 2.

Soluţie.

Fie x 2 - 2x + 2 \u003d t, atunci ecuația va lua forma:

t 2 + 3xt - 10x 2 \u003d 0.

Considerați ecuația rezultată ca una pătratică în raport cu t.

D \u003d (3x) 2 - 4 (-10x 2) \u003d 9x 2 + 40x 2 \u003d 49x 2; ≥≤

t 1 = (-3x - 7x) / 2 și t 2 = (-3x + 7x) / 2;

t 1 = -5x și t 2 = 2x.

Deoarece t \u003d x 2 - 2x + 2, atunci

x 2 - 2x + 2 = -5x sau x 2 - 2x + 2 = 2x. Să rezolvăm fiecare dintre ecuațiile obținute.

x 2 + 3x + 2 = 0 sau x 2 - 4x + 2 = 0.

Ambele ecuații au rădăcini, deoarece D > 0.

Folosind teorema Vieta, putem concluziona că suma rădăcinilor primei ecuații este -3, iar a doua ecuație este 4. Obținem că suma rădăcinilor ecuației inițiale este -3 + 4 = 1

Raspunsul 1.

Exemplul 5

Aflați rădăcina ecuației (x + 1) 4 + (x + 5) 4 = 32 aparținând intervalului [-5; 10].

Soluţie.

Fie x = t - 3, apoi x + 1 = t - 2; x + 5 = t + 2 și ecuația inițială devine:

(t - 2) 4 + (t + 2) 4 \u003d 32. Pentru a ridica expresiile la a patra putere, puteți folosi triunghiul lui Pascal (Fig. 1);

(t – 2) 4 = t 4 – 4t 3 2 + 6t 2 2 2 – 4t 2 3 + 2 4 ;

(t + 2) 4 = t 4 + 4t 3 2 + 6t 2 2 2 + 4t 2 3 + 2 4 .

După reducerea termenilor similari, obținem:

2t 4 – 2 6t 2 2 2 + 2 2 4 = 32;

t 4 + 6t 2 2 2 + 2 4 = 16;

t 4 + 24t 2 + 16 = 16;

t4 + 24t2 = 0;

t2 (t2 + 24) = 0;

t \u003d 0 sau t 2 \u003d -24.

A doua ecuație nu are rădăcini, ceea ce înseamnă că t = 0 și după înlocuirea inversă

x \u003d t - 3 \u003d 0 - 3 \u003d -3. Rădăcina ecuației -3 aparține intervalului [-5; 10].

Răspuns: -3.

După cum puteți vedea, atunci când rezolvați ecuații raționale, trebuie să cunoașteți formulele de mai sus și să puteți număra corect. Erorile apar cel mai adesea la alegerea unui înlocuitor și la înlocuirea înapoi. Pentru a evita acest lucru, trebuie să descrieți în detaliu fiecare acțiune, apoi nu vor exista greșeli în deciziile dvs.

blog.site, cu copierea integrală sau parțială a materialului, este necesar un link către sursă.