Valorea estimata. așteptări matematice variabilă aleatoare discretă X, care ia un număr finit de valori Xi cu probabilităţi Ri, se numește suma:

așteptări matematice variabilă aleatoare continuă X se numește integrala produsului valorilor sale X asupra densității distribuției de probabilitate f(X):

(6b)

Integrală necorespunzătoare (6 b) se presupune că este absolut convergent (altfel spunem că așteptarea M(X) nu exista). Aşteptarea matematică caracterizează Rău variabilă aleatorie X. Dimensiunea sa coincide cu dimensiunea unei variabile aleatoare.

Proprietățile așteptărilor matematice:

Dispersia. dispersie variabilă aleatorie X numarul se numeste:

Dispersia este caracteristică de împrăștiere valorile unei variabile aleatoare X raportat la valoarea sa medie M(X). Dimensiunea varianței este egală cu dimensiunea variabilei aleatoare la pătrat. Pe baza definițiilor varianței (8) și așteptărilor matematice (5) pentru o variabilă aleatoare discretă și (6) pentru o variabilă aleatoare continuă, obținem expresii similare pentru varianță:

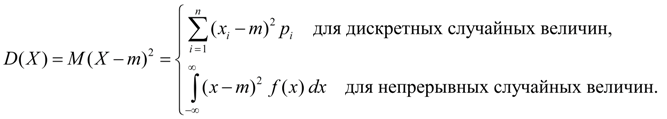(9)

Aici m = M(X).

Proprietăți de dispersie:

Deviație standard:

(11)

Deoarece dimensiunea abaterii standard este aceeași cu cea a unei variabile aleatoare, este mai des decât varianța utilizată ca măsură de dispersie.

momentele de distribuție. Conceptele de așteptare și varianță matematică sunt cazuri speciale ale unui concept mai general pentru caracteristicile numerice ale variabilelor aleatoare - momentele de distribuție. Momentele de distribuție ale unei variabile aleatoare sunt introduse ca așteptări matematice ale unor funcții simple ale unei variabile aleatoare. Deci, momentul comenzii k relativ la punct X 0 se numește așteptare M(X–X 0 )k. Momente relativ la origine X= 0 sunt numite momentele inițialeși sunt marcate:

(12)

Momentul inițial de ordinul întâi este centrul de distribuție al variabilei aleatoare considerate:

(13)

Momente relativ la centrul de distribuție X= m numit punctele centraleși sunt marcate:

(14)

Din (7) rezultă că momentul central de ordinul întâi este întotdeauna egal cu zero:

Momentele centrale nu depind de originea valorilor variabilei aleatoare, deoarece cu o deplasare cu o valoare constantă Cu centrul său de distribuție este deplasat cu aceeași valoare Cu, iar abaterea de la centru nu se modifică: X – m = (X – Cu) – (m – Cu).
Acum este evident că dispersie- Acest moment central de ordinul doi:

Asimetrie. Momentul central al ordinului al treilea:

(17)

serveste la evaluare asimetrie de distribuție. Dacă distribuția este simetrică față de punct X= m, atunci momentul central al ordinului al treilea va fi egal cu zero (precum și toate momentele centrale ale ordinelor impare). Prin urmare, dacă momentul central de ordinul trei este diferit de zero, atunci distribuția nu poate fi simetrică. Mărimea asimetriei este estimată folosind un adimensional coeficient de asimetrie:

(18)

Semnul coeficientului de asimetrie (18) indică asimetria din dreapta sau din stânga (Fig. 2).

Orez. 2. Tipuri de asimetrie a distribuţiilor.

Exces. Momentul central al ordinului al patrulea:

(19)

serveşte la evaluarea aşa-numitelor curtoză, care determină gradul de abrupție (punctură) al curbei de distribuție în apropierea centrului de distribuție în raport cu curba de distribuție normală. Deoarece pentru o distribuție normală, cantitatea luată ca curtoză este:

(20)

Pe fig. 3 prezintă exemple de curbe de distribuție cu diferite valori de curtoză. Pentru o distribuție normală E= 0. Curbele care au vârfuri mai mari decât în ​​mod normal au curtoză pozitivă, iar curbele cu vârfuri mai plate au kurtoză negativă.

Orez. 3. Curbe de distribuție cu diferite grade de abruptitate (kurtoză).

Momentele de ordin superior în aplicațiile de inginerie ale statisticii matematice nu sunt de obicei utilizate.

Modă discret variabila aleatoare este valoarea sa cea mai probabilă. Modă continuu o variabilă aleatorie este valoarea sa la care densitatea de probabilitate este maximă (Fig. 2). Dacă curba de distribuție are un maxim, atunci distribuția este numită unimodal. Dacă curba de distribuție are mai mult de un maxim, atunci distribuția este numită polimodal. Uneori există distribuții ale căror curbe nu au un maxim, ci un minim. Astfel de distribuții sunt numite antimodal. În cazul general, modul și așteptarea matematică a unei variabile aleatoare nu coincid. Într-un caz anume, pentru modal, adică având un mod, o distribuție simetrică și cu condiția să existe o așteptare matematică, aceasta din urmă coincide cu modul și centrul de simetrie al distribuției.

Median variabilă aleatorie X este sensul lui Pe mine, pentru care egalitatea este valabilă: i.e. este la fel de probabil ca variabila aleatoare X va fi mai putin sau mai mult Pe mine. Geometric median este abscisa punctului în care aria de sub curba de distribuție este împărțită la jumătate (fig. 2). În cazul unei distribuții modale simetrice, mediana, modul și media sunt aceleași.

Modul este cea mai probabilă valoare a unei variabile aleatorii. Cu o distribuție simetrică față de medie, modul coincide cu așteptarea matematică. Dacă valorile variabilei aleatoare nu se repetă, nu există mod.

Punctul de pe axa x care corespunde maximului curbei densității distribuției se numește mod, adică modul este valoarea cea mai probabilă a variabilei aleatoare. Cu toate acestea, modul nu există pentru toate distribuțiile. Un exemplu este distribuția uniformă. În acest caz, definirea centrului de distribuție ca mod este imposibilă. Moda este de obicei denumită Mo.

Există concepte de mod și mediană ale unei variabile aleatorii.

Este evident că în cazul unei mediane simetrice coincide cu modul și așteptarea matematică.

Pe baza faptului că modul nu se bazează pe măsurători unice, ci pe un volum mare de observații, nu poate fi considerat o variabilă aleatorie. Amploarea modului nu este afectată de diferitele tipuri de întârzieri în lucru și de pierderea ratelor normale.

Uneori, în analiza distribuțiilor empirice, se folosesc conceptele de mod și mediană a distribuției, „...Modul este valoarea cea mai probabilă a unei variabile aleatoare,

O interpretare probabilistică extinsă a fenomenului loteriei este conceptul de distribuție probabilistică a unei variabile aleatoare. Este folosit pentru a determina probabilitățile ca o variabilă aleatoare să ia una sau alta dintre valorile sale posibile. Notați cu y variabila aleatoare și cu y valorile ei posibile. Apoi, pentru o variabilă aleatorie discretă, care poate lua valori posibile Y, y2, US,. .., yn o formă convenabilă de distribuție a probabilității ar trebui considerată dependența P(y = y), care se numește de obicei o serie de probabilități, n serie de distribuție. În practică, pentru o evaluare operațională generalizată a distribuției de probabilitate a valorilor de risc, se folosesc adesea așa-numitele caracteristici numerice și alte caracteristici ale distribuției rezultatelor aleatoare: așteptare matematică, varianță, abatere standard, coeficient de variație, mod, mediană, etc. (vezi, de exemplu, și altele.). Cu alte cuvinte, pentru o percepție rapidă și holistică, antreprenorul te caută (sau pur și simplu pe tine

Pe baza datelor Comitetului de Stat de Statistică al URSS privind distribuția populației în funcție de venitul total pe cap de locuitor, vom încerca să comparăm indicatorii veniturilor medii, mediane și modale (Tabelul 1). Tabelul arată că venitul mediu în termeni absoluti depășește veniturile mediane și modale, iar creșterea acestuia se produce în principal datorită creșterii proporției persoanelor cu venituri mari, adică utilizarea indicatorului venitului mediu duce la o supraestimare semnificativă. a nivelului veniturilor majorului populaţiei şi ascunde în mare măsură procesul de diferenţiere a acestora. Valorile venitului modal gravitează către grupurile de distribuție inferioare și se abat de la venitul median în jos. Cu toate acestea, lovitura unui mod într-unul sau altul interval este adesea de natură aleatorie, o schimbare destul de mică a distribuției - iar modul va fi deja în intervalul vecin. De exemplu, în 1989, cel mai frecvent nivel de venit a fost de la 100 la 125 de ruble (16,1% din populație a primit un astfel de venit), dar din cauza schimbărilor minore ale veniturilor care au avut loc în 1989-1990, intervalul cel mai frecvent s-a dovedit a fi următorul interval (125-150 ruble): , iar valoarea modei în sine a crescut cu 15,6 ruble. În plus, ponderea populației în intervalul venitului modal poate depăși foarte puțin alte ponderi.

Pentru a caracteriza centrul de distribuție al unei variabile aleatoare normale logaritmic a, se poate folosi, alături de așteptarea matematică deja calculată Ma, modul

Mod - modă. Cea mai probabilă valoare a unei variabile aleatoare.

MODA - concept

Pe lângă așteptările și dispersia matematică, în teoria probabilității sunt utilizate o serie de caracteristici numerice, care reflectă anumite caracteristici ale distribuției.

Definiție. Modul Mo(X) al unei variabile aleatoare X este valoarea sa cea mai probabilă(pentru care probabilitatea r r sau densitatea de probabilitate

Dacă probabilitatea sau densitatea de probabilitate atinge un maxim nu în unul, ci în mai multe puncte, distribuția se numește polimodal(Fig. 3.13).

Modă Mușchi), la care probabilitatea R ( sau densitatea de probabilitate (p(x) atinge un maxim global, se numește valoarea cel mai probabil variabilă aleatoare (în Fig. 3.13 aceasta Mo(X) 2).

Definiție. Mediana Me(X) a unei variabile aleatoare continue X este valoarea acesteia, pentru care

acestea. probabilitatea ca variabila aleatoare X ia o valoare mai mică decât mediana Blană) sau mai mare decât acesta, la fel și egal cu 1/2. Linie verticală geometric X = Blană) trecând printr-un punct cu o abscisă egală cu Blană), împarte aria figurii curbei de distribuție în două părți egale (Fig. 3.14). Evident, la punct X = Blană) functia de distributie este egala cu 1/2, i.e. P(Me(X))= 1/2 (Fig. 3.15).

Observați o proprietate importantă a medianei unei variabile aleatoare: așteptarea matematică a valorii absolute a abaterii variabilei aleatoare X de la valoarea constantă C este minimă atunci, când această constantă C este egală cu mediana Me(X) = m, adică

(proprietatea este similară cu proprietatea (3,10") a minimalității pătratului mediu al abaterii unei variabile aleatoare de la așteptarea ei matematică).

O Exemplul 3.15. Găsiți modul, mediana și media unei variabile aleatoare X s densitatea de probabilitate φ(x) = 3x 2 pentru xx.

Decizie. Curba de distribuție este prezentată în fig. 3.16. Evident, densitatea de probabilitate φ(x) este maximă la X= Mo(X) = 1.

Median Blană) = b găsim din condiția (3.28):

Unde

Așteptările matematice se calculează prin formula (3.25):

Aranjarea reciprocă a punctelor M(X) > Eu(X) și Mușchi) în ordinea crescătoare a absciselor este prezentată în fig. 3.16. ?

Alături de caracteristicile numerice menționate mai sus, conceptul de cuantile și puncte procentuale este folosit pentru a descrie o variabilă aleatorie.

Definiție. Cuantila de nivel y-quantila )

se numește o astfel de valoare x q a unei variabile aleatoare , la care funcţia sa de distribuţie ia o valoare egală cu a muri.

Unele cuantile au primit un nume special. Evident, cele de mai sus median variabila aleatoare este cuantila de nivel 0,5, adică Eu (X) \u003d x 05. Cuantilele dg 0 2 5 și x 075 sunt denumite respectiv inferior și quartila superioarăK

Strâns legat de conceptul de cuantilă este conceptul punct procentual. Sub YuOuHo-noi dot cuantilă implicită x x (( , acestea. o astfel de valoare a unei variabile aleatoare X, sub care

0 Exemplul 3.16. Conform exemplului 3.15 găsiți cuantila x 03 și 30% punct variabil aleatoriu X.

Decizie. Conform formulei (3.23), funcţia de distribuţie

Găsim cuantila r 0 z din ecuația (3.29), adică. x $ 3 \u003d 0,3, de unde L "oz -0,67. Găsiți punctul de 30% al variabilei aleatoare X, sau cuantila x 0 7, din ecuație x$ 7 = 0,7, de unde x 0 7 "0,89. ?

Dintre caracteristicile numerice ale unei variabile aleatoare, momentele - inițiale și centrale - au o importanță deosebită.

Definiție. Moment de pornireOrdinul k al unei variabile aleatoare X este așteptarea matematică a puterii k a acestei variabile :

Definiție. Punctul centralordinul k al unei variabile aleatoare X este așteptarea matematică a gradului k de abatere al variabilei aleatoare X de la așteptarea sa matematică:

Formule pentru calcularea momentelor pentru variabile aleatoare discrete (luând valorile x 1 cu probabilități p,) și continue (cu densitate de probabilitate cp(x)) sunt date în tabel. 3.1.

Tabelul 3.1

Este ușor să vezi că atunci când k = 1 primul moment inițial al variabilei aleatoare X este așteptarea sa matematică, adică h x \u003d M [X) \u003d a, la la= 2 al doilea moment central este dispersia, i.e. p 2 = T)(X).

Momentele centrale p A pot fi exprimate în termeni de momente inițiale folosind formulele:

etc.

De exemplu, c 3 \u003d M (X-a) * \u003d M (X * -ZaX 2 + Za 2 X-a-\u003e) \u003d M (X *) ~ -ZaM (X 2) + Za 2 M (X) ~ a3 \u003d y 3 -Zy ^ + Zy (y, -y ^ \u003d y 3 - Zy ^ + 2y ^ (la derivare, am luat în considerare faptul că A = M(X)= V, - valoare non-aleatorie). ?

După cum sa menționat mai sus, așteptările matematice M(X), sau primul moment inițial, caracterizează valoarea sau poziția medie, centrul de distribuție al unei variabile aleatorii X pe linia numerică; dispersie OH), sau al doilea moment central p 2 , - s t s - împrăștierea distribuției X relativ M(X). Momentele de ordin superior servesc pentru o descriere mai detaliată a distribuției.

Al treilea moment central p 3 servește la caracterizarea asimetriei distribuției (asimetrie). Are dimensiunea unui cub al unei variabile aleatorii. Pentru a obține o valoare adimensională, aceasta este împărțită la aproximativ 3, unde a este abaterea standard a variabilei aleatoare X. Valoare primită DAR numit coeficientul de asimetrie al unei variabile aleatoare.

Dacă distribuția este simetrică față de așteptările matematice, atunci coeficientul de asimetrie este A = 0.

Pe fig. 3.17 prezintă două curbe de distribuție: I și II. Curba I are o asimetrie pozitivă (pe partea dreaptă) (L > 0), iar curba II are o asimetrie negativă (pe partea stângă) (L

Al patrulea moment central p 4 servește la caracterizarea abruptului (vârful vârfului sau vârf plat - stâlp) distribuției.

Modă- valoarea din setul de observatii care apare cel mai des

Mo \u003d X Mo + h Mo * (f Mo - f Mo-1) : ((f Mo - f Mo-1) + (f Mo - f Mo + 1)),

aici X Mo este marginea din stânga a intervalului modal, h Mo este lungimea intervalului modal, f Mo-1 este frecvența intervalului premodal, f Mo este frecvența intervalului modal, f Mo+1 este frecvența intervalului postmodal.

Modul unei distribuții absolut continue este orice punct al maximului local al densității distribuției. Pentru distribuțiile discrete, un mod este orice valoare a i a cărei probabilitate p i este mai mare decât probabilitățile valorilor învecinate

median variabilă aleatoare continuă X valoarea sa Me se numește astfel, pentru care este la fel de probabil dacă variabila aleatoare va fi mai mică sau mai mare Pe mine, adică

M e \u003d (n + 1) / 2 P(X < Eu) = P(X > Pe mine)

Distribuit uniform NOU

Distribuție uniformă. O variabilă aleatoare continuă se numește distribuită uniform pe segmentul () dacă funcția sa de densitate de distribuție (Fig. 1.6, A) se pare ca:

Denumire: - SW este distribuit uniform pe .

În consecință, funcția de distribuție pe segment (Fig. 1.6, b):

Orez. 1.6. Funcții ale unei variabile aleatoare distribuite uniform pe [ A,b]: A– densități de probabilitate f(X); b– distribuții F(X)

Așteptările matematice și varianța acestui RV sunt determinate de expresiile:

Datorită simetriei funcției de densitate, aceasta coincide cu mediana. Moda nu are o distribuție uniformă

Exemplul 4 Timpul de așteptare pentru un răspuns la un apel telefonic este o variabilă aleatorie care se supune unei legi de distribuție uniformă în intervalul de la 0 la 2 minute. Găsiți funcțiile de distribuție integrală și diferențială ale acestei variabile aleatoare.

27. Legea normală a distribuției probabilităților

O variabilă aleatoare continuă x are o distribuție normală cu parametrii: m,s > 0, dacă densitatea distribuției de probabilitate are forma:

unde: m este așteptarea matematică, s este abaterea standard.

Distribuția normală este numită și Gauss după matematicianul german Gauss. Faptul că o variabilă aleatoare are o distribuţie normală cu parametrii: m, , se notează astfel: N (m, s), unde: m=a=M[X];

Destul de des, în formule, așteptarea matematică este notă cu A . Dacă o variabilă aleatoare este distribuită conform legii N(0,1), atunci se numește valoare normală normalizată sau standardizată. Funcția de distribuție a acesteia are forma:

Graficul densității distribuției normale, care se numește curbă normală sau curbă Gauss, este prezentat în Fig. 5.4.

Orez. 5.4. Densitatea normală de distribuție

proprietăți o variabilă aleatoare cu o lege de distribuție normală.

1. Dacă , atunci pentru a găsi probabilitatea ca această valoare să se încadreze într-un interval dat ( x 1; x 2) se utilizează formula:

2. Probabilitatea ca abaterea unei variabile aleatoare de la așteptările ei matematice să nu depășească valoarea (în valoare absolută) este egală cu:

3. „Regula celor trei sigma”. Dacă este o variabilă aleatoare, atunci este practic sigur că valorile sale sunt conținute în intervalul (). (Probabilitatea de a depăși aceste limite este de 0,0027.) Regula permite, cunoscând parametrii ( și ), să se determine aproximativ intervalul valorilor practice ale unei variabile aleatorii.

distribuție exponențială

O variabilă aleatoare X are o distribuție exponențială cu un parametru dacă densitatea sa are forma

Integrând densitatea, obținem funcția de distribuție exponențială:

Principalele caracteristici ale distribuției exponențiale:

Diagrame de densitate și funcții ale distribuției exponențiale rezultate