Articolul vorbește despre găsirea unghiului dintre planuri. După ce aducem definiția, vom stabili o ilustrare grafică, vom lua în considerare o metodă detaliată pentru găsirea coordonatelor prin metodă. Obținem o formulă pentru planurile care se intersectează, care include coordonatele vectorilor normali.

Yandex.RTB R-A-339285-1

Materialul va folosi date și concepte care au fost studiate anterior în articole despre avion și linia în spațiu. Pentru început, este necesar să trecem la raționament care să permită o anumită abordare pentru a determina unghiul dintre două plane care se intersectează.

Sunt date două plane care se intersectează γ 1 și γ 2. Intersecția lor va lua denumirea c . Construcția planului χ este legată de intersecția acestor plane. Planul χ trece prin punctul M ca o dreaptă c. Planele γ 1 și γ 2 vor fi intersectate folosind planul χ. Acceptăm denumirile dreptei care intersectează γ 1 și χ pentru dreapta a și care intersectează γ 2 și χ pentru dreapta b. Obținem că intersecția dreptelor a și b dă punctul M .

Locația punctului M nu afectează unghiul dintre liniile care se intersectează a și b, iar punctul M este situat pe dreapta c prin care trece planul χ.

Este necesar să se construiască un plan χ 1 perpendicular pe dreapta c și diferit de planul χ . Intersecția planelor γ 1 și γ 2 cu ajutorul lui χ 1 va lua denumirea dreptelor a 1 și b 1 .

Se poate observa că la construirea χ și χ 1, dreptele a și b sunt perpendiculare pe dreapta c, apoi a 1, b 1 sunt perpendiculare pe dreapta c. Găsind drepte a și a 1 în planul γ 1 cu perpendicularitate pe dreapta c, atunci pot fi considerate paralele. În același mod, locația lui b și b 1 în planul γ 2 cu perpendicularitatea dreptei c indică paralelismul lor. Aceasta înseamnă că este necesar să facem un transfer paralel al planului χ 1 la χ, unde obținem două drepte care coincid a și a 1 , b și b 1 . Obținem că unghiul dintre liniile care se intersectează a și b 1 este egal cu unghiul dreptelor care se intersectează a și b.

Luați în considerare figura de mai jos.

Această judecată este dovedită de faptul că între dreptele care se intersectează a și b există un unghi care nu depinde de locația punctului M, adică de punctul de intersecție. Aceste drepte sunt situate în planurile γ 1 și γ 2 . De fapt, unghiul rezultat poate fi considerat ca fiind unghiul dintre două plane care se intersectează.

Să trecem la determinarea unghiului dintre planele de intersectare existente γ 1 și γ 2 .

Definiția 1

Unghiul dintre două plane care se intersectează γ 1 și γ 2 numiți unghiul format de intersecția dreptelor a și b, unde planele γ 1 și γ 2 se intersectează cu planul χ perpendicular pe dreapta c.

Luați în considerare figura de mai jos.

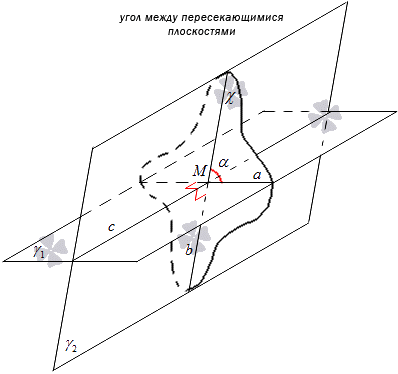
Definiția poate fi transmisă sub altă formă. La intersecția planurilor γ 1 și γ 2, unde c este dreapta pe care se intersectează, marcați punctul M, prin care se trasează drepte a și b, perpendiculare pe dreapta c și situate în planele γ 1 și γ 2 , atunci unghiul dintre dreptele a și b va fi unghiul dintre plane. În practică, acest lucru este aplicabil pentru construirea unui unghi între planuri.

La intersecție se formează un unghi care are o valoare mai mică de 90 de grade, adică măsura gradului unghiului este valabilă pe un interval de acest tip (0, 90] . În același timp, aceste plane sunt numite perpendiculare dacă la intersecţie se formează un unghi drept.Unghiul dintre plane paralele este considerat egal cu zero.

Modul obișnuit de a găsi unghiul dintre planurile care se intersectează este de a efectua construcții suplimentare. Acest lucru ajută la determinarea cu acuratețe, iar acest lucru se poate face folosind semnele de egalitate sau similaritate ale triunghiului, sinusurilor, cosinusului unghiului.

Luați în considerare rezolvarea problemelor folosind un exemplu din problemele Examenului de stat unificat din blocul C 2.

Exemplul 1

Este dat un paralelipiped dreptunghic A B C D A 1 B 1 C 1 D 1, unde latura A B \u003d 2, A D \u003d 3, A A 1 \u003d 7, punctul E separă latura A A 1 într-un raport de 4: 3. Aflați unghiul dintre planele A B C și B E D 1 .

Decizie

Pentru claritate, trebuie să faceți un desen. Înțelegem asta

O reprezentare vizuală este necesară pentru a face mai convenabil lucrul cu unghiul dintre planuri.

Facem definirea unei drepte de-a lungul căreia se intersectează planele A B C și B E D 1. Punctul B este un punct comun. Ar trebui găsit un alt punct comun de intersecție. Se consideră dreptele D A și D 1 E , care sunt situate în același plan A D D 1 . Locația lor nu indică paralelism, ceea ce înseamnă că au un punct de intersecție comun.

Cu toate acestea, linia DA este situată în planul A B C, iar D 1 E în B E D 1 . Prin urmare, obținem că liniile D Ași D 1 E au un punct comun de intersecție, care este comun și pentru planele A B C și B E D 1 . Indică punctul de intersecție al liniilor D Ași D 1 E litera F. De aici obținem că B F este o dreaptă de-a lungul căreia se intersectează planele A B C și B E D 1.

Luați în considerare figura de mai jos.

Pentru a obține un răspuns este necesar să construim drepte situate în planele A B C și B E D 1 cu trecerea printr-un punct situat pe dreapta B F și perpendicular pe acesta. Atunci unghiul rezultat dintre aceste drepte este considerat unghiul dorit dintre planele A B C și B E D 1.

Din aceasta se poate observa că punctul A este proiecția punctului E pe planul A B C. Este necesar să se traseze o dreaptă care să intersecteze dreapta B F în unghi drept în punctul M. Se poate observa că linia A M este proiecția dreptei E M pe planul A B C, pe baza teoremei despre acele perpendiculare A M ⊥ B F . Luați în considerare figura de mai jos.

∠ A M E este unghiul dorit format din planele A B C și B E D 1 . Din triunghiul rezultat A E M putem găsi sinusul, cosinusul sau tangenta unghiului, după care unghiul însuși, numai cu cele două laturi cunoscute ale sale. Prin condiție, avem că lungimea lui A E se găsește în acest fel: linia A A 1 este împărțită la punctul E într-un raport de 4: 3, ceea ce înseamnă că lungimea totală a liniei este de 7 părți, apoi A E \u003d 4 părți. Îl găsim pe A.M.

Este necesar să luăm în considerare un triunghi dreptunghic A B F. Avem un unghi drept A cu înălțimea A M. Din condiția A B \u003d 2, atunci putem găsi lungimea A F prin asemănarea triunghiurilor D D 1 F și A E F. Obținem că A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Este necesar să găsim lungimea laturii B F din triunghiul A B F folosind teorema lui Pitagora. Obținem că B F   = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Lungimea laturii A M se găsește prin aria triunghiului A B F. Avem că aria poate fi egală atât cu S A B C = 1 2 · A B · A F , cât și cu S A B C = 1 2 · B F · A M .

Obținem că A M = A B A F B F = 2 4 2 5 = 4 5 5

Atunci putem afla valoarea tangentei unghiului triunghiului A E M. Se obtine:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Unghiul dorit obținut prin intersecția planelor A B C și B E D 1 este egal cu a r c t g 5, apoi, la simplificare, se obține a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Răspuns: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Unele cazuri de găsire a unghiului dintre liniile care se intersectează sunt date folosind planul de coordonate O x y z și metoda coordonatelor. Să luăm în considerare mai detaliat.

Dacă este dată o problemă în care este necesar să se găsească unghiul dintre planele care se intersectează γ 1 și γ 2, notăm unghiul dorit cu α.

Atunci sistemul de coordonate dat arată că avem coordonatele vectorilor normali ai planurilor care se intersectează γ 1 și γ 2 . Atunci notăm că n 1 → = n 1 x , n 1 y , n 1 z este un vector normal al planului γ 1 , iar n 2 → = (n 2 x , n 2 y , n 2 z) - pentru planul γ 2 . Luați în considerare o constatare detaliată a unghiului situat între aceste plane în funcție de coordonatele vectorilor.

Este necesar să se desemneze linia dreaptă de-a lungul căreia planele γ 1 și γ 2 se intersectează cu litera c. Pe dreapta cu avem un punct M, prin care trasăm un plan χ, perpendicular pe c. Planul χ de-a lungul dreptelor a și b intersectează planele γ 1 și γ 2 în punctul M . Din definiție rezultă că unghiul dintre planele de intersectare γ 1 și γ 2 este egal cu unghiul dreptelor de intersectare a și, respectiv, b aparținând acestor plane.

În planul χ, punem deoparte vectorii normali din punctul M și îi notăm n 1 → și n 2 →. Vectorul n 1 → este situat pe o dreaptă perpendiculară pe dreapta a, iar vectorul n 2 → pe o dreaptă perpendiculară pe dreapta b. De aici rezultă că planul dat χ are un vector normal al dreptei a egal cu n 1 → iar pentru dreapta b egal cu n 2 → . Luați în considerare figura de mai jos.

De aici obținem o formulă prin care putem calcula sinusul unghiului dreptelor care se intersectează folosind coordonatele vectorilor. Am constatat că cosinusul unghiului dintre dreptele a și b este același cu cosinusul dintre planele care se intersectează γ 1 și γ 2 este derivat din formula cos α = cos n 1 → , n 2 → ^ = n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2 , unde avem că n 1 → = (n 1 x , n 1 y , n 1 z) și n 2 → = (n 2 x , n 2 y , n 2 z) sunt coordonatele vectorilor planurilor reprezentate.

Unghiul dintre liniile care se intersectează se calculează folosind formula

α = a r c cos n 1 x n 2 x + n 1 y n 2 y + n 1 z n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 n 2 x 2 + n 2 y 2 + n 2 z 2

Exemplul 2

Prin condiție, este dat un paralelipiped А В С D A 1 B 1 C 1 D 1 , unde A B \u003d 2, A D \u003d 3, A A 1 \u003d 7 și punctul E separă latura A A 1 4: 3. Aflați unghiul dintre planele A B C și B E D 1 .

Decizie

Se poate observa din condiția ca laturile sale să fie perpendiculare perechi. Aceasta înseamnă că este necesar să se introducă un sistem de coordonate O x y z cu un vârf în punctul C și axe de coordonate O x, O y, O z. Este necesar să puneți direcția pe părțile corespunzătoare. Luați în considerare figura de mai jos.

Planuri care se intersectează A B Cși B E D 1 formează un unghi, care poate fi găsit prin formula 2 x 2 + n 2 y 2 + n 2 z 2 , unde n 1 → = (n 1 x , n 1 y , n 1 z) și n 2 → = (n 2 x , n 2 y , n 2 z ) sunt vectori normali ai acestor plane. Este necesar să se determine coordonatele. Din figură, vedem că axa de coordonate O x y coincide în planul A B C, ceea ce înseamnă că coordonatele vectorului normal k → egale cu valoarea n 1 → = k → = (0, 0, 1) .

Vectorul normal al planului B E D 1 este produsul vectorial B E → și B D 1 → , unde coordonatele lor se găsesc prin coordonatele punctelor extreme B, E, D 1 , care sunt determinate pe baza stării problemei.

Obținem că B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Deoarece A E E A 1 = 4 3 , din coordonatele punctelor A 2 , 3 , 0 , A 1 2 , 3 , 7 găsim E 2 , 3 , 4 . Obținem că B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 i → - 6 j → - 6 k → ⇔ n 2 → = (12, - 6, - 6)

Este necesar să înlocuiți coordonatele găsite în formula pentru calcularea unghiului prin arc cosinus. Primim

α = a r c cos 0 12 + 0 (- 6) + 1 (- 6) 0 2 + 0 2 + 1 2 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Metoda coordonatelor dă un rezultat similar.

Răspuns: a r c cos 6 6 .

Problema finală este luată în considerare pentru a găsi unghiul dintre planele care se intersectează cu ecuațiile disponibile cunoscute ale planelor.

Exemplul 3

Calculați sinusul, cosinusul unghiului și valoarea unghiului format din două drepte care se intersectează, care sunt definite în sistemul de coordonate O x y z și date de ecuațiile 2 x - 4 y + z + 1 = 0 și 3 y - z - 1 = 0 .

Decizie

La studierea subiectului ecuației generale a dreptei de forma A x + B y + C z + D = 0, s-a relevat că A, B, C sunt coeficienți egali cu coordonatele vectorului normal. Prin urmare, n 1 → = 2 , - 4 , 1 și n 2 → = 0 , 3 , - 1 sunt vectori normali ai dreptelor date.

Este necesar să înlocuiți coordonatele vectorilor normali ai planurilor în formula de calcul al unghiului dorit al planurilor care se intersectează. Atunci obținem asta

α = a r c cos 2 0 + - 4 3 + 1 (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Avem deci că cosinusul unghiului ia forma cos α = 13 210 . Atunci unghiul liniilor care se intersectează nu este obtuz. Înlocuind în identitatea trigonometrică, obținem că valoarea sinusului unghiului este egală cu expresia. Calculăm și obținem asta

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Răspuns: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .

Dacă observați o greșeală în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter

Unghiul dintre două planuri diferite poate fi determinat pentru orice poziție relativă a planurilor.

Cazul banal este dacă planurile sunt paralele. Atunci unghiul dintre ele este considerat egal cu zero.

Caz non-trivial dacă planurile se intersectează. Acest caz face obiectul unor discuții ulterioare. Mai întâi avem nevoie de conceptul de unghi diedru.

9.1 Unghiul diedric

Un unghi diedru sunt două semiplane cu o linie dreaptă comună (care se numește marginea unui unghi diedru). Pe fig. 50 prezintă un unghi diedru format din semiplane şi; muchia acestui unghi diedric este dreapta a comună semiplanurilor date.

Orez. 50. Unghiul diedric

Unghiul diedrului poate fi măsurat în grade sau radiani într-un cuvânt, introduceți valoarea unghiulară a unghiului diedric. Acest lucru se face în felul următor.

Pe marginea unghiului diedric format din semiplane și, luăm un punct arbitrar M. Să desenăm razele MA și MB, situate respectiv în aceste semiplane și perpendicular pe muchie (Fig. 51).

Orez. 51. Unghi liniar unghi diedru

Unghiul rezultat AMB este unghiul liniar al unghiului diedru. Unghiul " = \AMB este exact valoarea unghiulară a unghiului nostru diedru.

Definiție. Mărimea unghiulară a unui unghi diedru este mărimea unghiului liniar al unui unghi diedru dat.

Toate unghiurile liniare ale unui unghi diedru sunt egale între ele (la urma urmei, ele sunt obținute unul de celălalt printr-o deplasare paralelă). Prin urmare, această definiție este corectă: valoarea „nu depinde de alegerea specifică a punctului M de pe marginea unghiului diedrului.

9.2 Determinarea unghiului dintre planuri

Când două plane se intersectează, se obțin patru unghiuri diedrice. Dacă toate au aceeași valoare (90 fiecare), atunci planurile se numesc perpendiculare; unghiul dintre plane este atunci 90 .

Dacă nu toate unghiurile diedrice sunt la fel (adică sunt două acute și două obtuze), atunci unghiul dintre plane este valoarea unghiului diedric acut (Fig. 52).

Orez. 52. Unghiul dintre plane

9.3 Exemple de rezolvare a problemelor

Să luăm în considerare trei sarcini. Primul este simplu, al doilea și al treilea sunt aproximativ la nivelul C2 la examenul de matematică.

Sarcina 1. Găsiți unghiul dintre două fețe ale unui tetraedru obișnuit.

Decizie. Fie ABCD un tetraedru regulat. Să desenăm medianele AM ​​și DM ale fețelor corespunzătoare, precum și înălțimea tetraedrului DH (Fig. 53).

Orez. 53. La problema 1

Fiind mediane, AM și DM sunt și înălțimile triunghiurilor echilaterale ABC și DBC. Prin urmare, unghiul " = \AMD este unghiul liniar al unghiului diedric format din fețele ABC și DBC. Îl găsim din triunghiul DHM:

			1AM

Raspuns: arccos 1 3 .

Problema 2. Într-o piramidă pătrangulară regulată SABCD (cu vârful S), muchia laterală este egală cu latura bazei. Punctul K este punctul de mijloc al muchiei SA. Găsiți unghiul dintre planuri

Decizie. Linia BC este paralelă cu AD și deci paralelă cu planul ADS. Prin urmare, planul KBC intersectează planul ADS de-a lungul liniei drepte KL paralelă cu BC (Fig. 54).

Orez. 54. La problema 2

În acest caz, KL va fi și paralel cu linia AD; prin urmare, KL este linia mediană a triunghiului ADS, iar punctul L este punctul de mijloc al DS.

Desenați înălțimea piramidei SO. Fie N punctul de mijloc al lui DO. Atunci LN este linia mediană a triunghiului DOS și, prin urmare, LN k SO. Deci LN este perpendicular pe planul ABC.

Din punctul N coborâm perpendiculara NM pe dreapta BC. Linia dreaptă NM va fi proiecția oblicului LM pe planul ABC. Din teorema celor trei perpendiculare rezultă că LM este, de asemenea, perpendicular pe BC.

Astfel, unghiul " = \LMN este un unghi liniar al unghiului diedric format din semiplanele KBC și ABC. Vom căuta acest unghi din triunghiul dreptunghic LMN.

Fie marginea piramidei a. Mai întâi, găsiți înălțimea piramidei:

SO=p

Decizie. Fie L punctul de intersecție al dreptelor A1 K și AB. Apoi planul A1 KC intersectează planul ABC de-a lungul dreptei CL (Fig.55).

A C

Orez. 55. Problema 3

Triunghiurile A1 B1 K și KBL sunt egale în catete și unghi ascuțit. Prin urmare, celelalte catete sunt și ele egale: A1 B1 = BL.

Luați în considerare triunghiul ACL. În ea BA = BC = BL. Unghiul CBL este de 120 ; deci \BCL = 30 . De asemenea, \BCA = 60 . Prin urmare \ACL = \BCA + \BCL = 90 .

Deci LC? AC. Dar linia AC este proiecția dreptei A1 C pe planul ABC. Prin teorema celor trei perpendiculare, concluzionăm că LC ? A1C.

Astfel, unghiul A1 CA este unghiul liniar al unghiului diedru format din semiplanele A1 KC și ABC. Acesta este unghiul necesar. Din triunghiul dreptunghic isoscel A1 AC vedem că este egal cu 45 .

Acest articol este despre unghiul dintre avioane și despre cum să-l găsiți. În primul rând, este dată definiția unghiului dintre două plane și este dată o ilustrare grafică. După aceea, a fost analizat principiul găsirii unghiului dintre două plane care se intersectează prin metoda coordonatelor, s-a obținut o formulă care permite calcularea unghiului dintre planele care se intersectează folosind coordonatele cunoscute ale vectorilor normali ai acestor plane. În concluzie, sunt prezentate soluții detaliate ale problemelor tipice.

Navigare în pagină.

Unghiul dintre planuri - definiție.

Să oferim argumente care ne vor permite să ne apropiem treptat de definiția unghiului dintre două plane care se intersectează.

Să ni se dea două plane care se intersectează și . Aceste planuri se intersectează într-o linie dreaptă, pe care o notăm cu litera c. Să construim un plan care trece prin punctul M al dreptei c și perpendicular pe dreapta c. În acest caz, planul va intersecta planele și . Să notăm drepta de-a lungul căreia planele se intersectează și ca a și linia de-a lungul căreia se intersectează planele și ca b. Evident, liniile a și b se intersectează în punctul M.

Este ușor de arătat că unghiul dintre dreptele care se intersectează a și b nu depinde de locația punctului M pe dreapta c prin care trece planul.

Să construim un plan perpendicular pe dreapta c și diferit de planul . Planul este intersectat de plane și de-a lungul unor drepte, pe care le notăm cu a 1 și, respectiv, b 1.

Din metoda de construire a planurilor rezultă că dreptele a și b sunt perpendiculare pe dreapta c, iar dreptele a 1 și b 1 sunt perpendiculare pe dreapta c. Deoarece dreptele a și a 1 se află în același plan și sunt perpendiculare pe dreapta c, ele sunt paralele. În mod similar, dreptele b și b 1 se află în același plan și sunt perpendiculare pe dreapta c, prin urmare sunt paralele. Astfel, este posibil să se efectueze un transfer paralel al planului în plan, în care linia a 1 coincide cu linia a, iar linia b cu linia b 1. Prin urmare, unghiul dintre două drepte care se intersectează a 1 și b 1 este egal cu unghiul dintre liniile care se intersectează a și b .

Aceasta dovedește că unghiul dintre liniile de intersectare a și b aflate în planurile de intersectare și nu depinde de alegerea punctului M prin care trece planul. Prin urmare, este logic să luăm acest unghi ca unghi între două plane care se intersectează.

Acum puteți exprima definiția unghiului dintre două plane care se intersectează și .

Definiție.

Unghiul dintre două plane care se intersectează în linie dreaptă și este unghiul dintre două drepte care se intersectează a și b, de-a lungul cărora planele și se intersectează cu planul perpendicular pe dreapta c.

Definiția unghiului dintre două plane poate fi dată puțin diferit. Dacă pe dreapta c, de-a lungul căreia se intersectează planele, marcați punctul M și trasați prin el drepte a și b, perpendiculare pe dreapta c și situate în planuri și, respectiv, atunci unghiul dintre liniile a și b este unghiul dintre plane şi. De obicei, în practică, astfel de construcții se realizează pentru a obține unghiul dintre plane.

Deoarece unghiul dintre liniile care se intersectează nu depășește, din definiția vocală rezultă că gradul de măsură a unghiului dintre două plane care se intersectează este exprimat printr-un număr real din interval. În acest caz, se numesc planuri care se intersectează perpendicular dacă unghiul dintre ele este de nouăzeci de grade. Unghiul dintre planele paralele fie nu este determinat deloc, fie este considerat egal cu zero.

Aflarea unghiului dintre două plane care se intersectează.

De obicei, atunci când găsiți unghiul dintre două plane care se intersectează, mai întâi trebuie să efectuați construcții suplimentare pentru a vedea liniile care se intersectează, unghiul dintre care este egal cu unghiul dorit, apoi conectați acest unghi cu datele originale folosind semne egale, semne de asemănare, teorema cosinusului sau definițiile sinusului, cosinusului și tangentei unghiului. La cursul de geometrie din liceu sunt probleme similare.

De exemplu, să dăm o soluție problemei C2 de la examenul unificat de stat la matematică pentru 2012 (condiția este schimbată intenționat, dar acest lucru nu afectează principiul soluției). În ea, era doar necesar să se găsească unghiul dintre două plane care se intersectează.

Exemplu.

Decizie.

Mai întâi, să facem un desen.

Să realizăm construcții suplimentare pentru a „vedea” unghiul dintre avioane.

Mai întâi, să definim o dreaptă de-a lungul căreia se intersectează planele ABC și BED 1. Punctul B este unul dintre punctele lor comune. Găsiți al doilea punct comun al acestor planuri. Dreptele DA și D 1 E se află în același plan ADD 1 și nu sunt paralele și, prin urmare, se intersectează. Pe de altă parte, linia DA se află în planul ABC, iar linia D 1 E se află în planul BED 1, prin urmare, punctul de intersecție al dreptelor DA și D 1 E va fi un punct comun al planurilor ABC și PATUL 1. Deci, să continuăm liniile DA și D 1 E până când se intersectează, notăm punctul de intersecție cu litera F. Atunci BF este linia de-a lungul căreia se intersectează planele ABC și BED 1.

Rămâne să construim două drepte situate în planurile ABC și respectiv BED 1, care trec printr-un punct de pe dreapta BF și perpendicular pe dreapta BF - unghiul dintre aceste linii, prin definiție, va fi egal cu unghiul dorit între avioane ABC şi BED 1 . S-o facem.

Punct A este proiecția punctului E pe planul ABC. Să desenăm o dreaptă care intersectează linia BF în unghi drept în punctul M. Atunci linia AM este proiecția dreptei EM pe planul ABC și după teorema celor trei perpendiculare.

Astfel, unghiul dorit între planele ABC și BED 1 este .

Putem determina sinusul, cosinusul sau tangenta acestui unghi (și, prin urmare, unghiul însuși) dintr-un triunghi dreptunghic AEM dacă știm lungimile celor două laturi ale sale. Din condiție este ușor de găsit lungimea AE: deoarece punctul E împarte latura AA 1 în raport cu 4 la 3, numărând din punctul A, iar lungimea laturii AA 1 este 7, atunci AE \u003d 4. Să aflăm lungimea AM.

Pentru a face acest lucru, luați în considerare un triunghi dreptunghic ABF cu unghi drept A, unde AM este înălțimea. Prin condiția AB=2. Putem afla lungimea laturii AF din asemanarea triunghiurilor dreptunghic DD 1 F si AEF :

După teorema lui Pitagora, din triunghiul ABF găsim . Găsim lungimea AM prin aria triunghiului ABF: pe o parte, aria triunghiului ABF este egală cu , pe cealaltă parte , Unde .

Astfel, din triunghiul dreptunghic AEM avem .

Atunci unghiul dorit dintre planurile ABC și BED 1 este (rețineți că ).

Răspuns:

În unele cazuri, pentru a găsi unghiul dintre două plane care se intersectează, este convenabil să specificați Oxyz și să utilizați metoda coordonatelor. Să ne oprim asupra ei.

Să stabilim sarcina: să găsim unghiul dintre două plane care se intersectează și . Să notăm unghiul dorit ca .

Vom presupune că într-un sistem de coordonate dreptunghiular dat Oxyz cunoaștem coordonatele vectorilor normali ai planurilor care se intersectează și sau este posibil să le găsim. Lasa este vectorul normal al planului și este vectorul normal al planului. Să arătăm cum să găsim unghiul dintre planele care se intersectează și prin coordonatele vectorilor normali ai acestor plane.

Să notăm dreapta de-a lungul căreia planele se intersectează și ca c . Prin punctul M de pe dreapta c trasăm un plan perpendicular pe dreapta c. Planul intersectează planele și de-a lungul dreptelor a și, respectiv, b, liniile a și b se intersectează în punctul M. Prin definiție, unghiul dintre planele care se intersectează și este egal cu unghiul dintre liniile care se intersectează a și b.

Să lăsăm deoparte din punctul M din plan vectorii normali și ai planurilor și . În acest caz, vectorul se află pe o dreaptă perpendiculară pe linia a, iar vectorul se află pe o dreaptă perpendiculară pe linia b. Astfel, în plan, vectorul este vectorul normal al dreptei a, este vectorul normal al dreptei b.

În articolul Găsirea unghiului dintre liniile care se intersectează, am obținut o formulă care vă permite să calculați cosinusul unghiului dintre liniile care se intersectează folosind coordonatele vectorilor normali. Astfel, cosinusul unghiului dintre liniile a și b și, în consecință, și cosinusul unghiului dintre planele care se intersecteazăși se găsește prin formula , unde și sunt vectorii normali ai planelor și, respectiv. Apoi se calculează ca .

Să rezolvăm exemplul anterior folosind metoda coordonatelor.

Exemplu.

Este dat un paralelipiped dreptunghic ABCDA 1 B 1 C 1 D 1, în care AB \u003d 2, AD \u003d 3, AA 1 \u003d 7 și punctul E împarte latura AA 1 într-un raport de la 4 la 3, numărând din punct A. Aflați unghiul dintre planele ABC și BED 1.

Decizie.

Deoarece laturile unui paralelipiped dreptunghiular la un vârf sunt perpendiculare pe perechi, este convenabil să se introducă un sistem de coordonate dreptunghiular Oxyz astfel: începutul este aliniat cu vârful C, iar axele de coordonate Ox, Oy și Oz sunt direcționate de-a lungul laturilor. CD, CB și respectiv CC 1.

Unghiul dintre planele ABC și BED 1 poate fi găsit prin coordonatele vectorilor normali ai acestor plane folosind formula , unde și sunt vectorii normali ai planurilor ABC și respectiv BED 1. Să determinăm coordonatele vectorilor normali.

\(\blacktriangleright\) Un unghi diedru este unghiul format din două semiplane și dreapta \(a\) , care este limita lor comună.

\(\blacktriangleright\) Pentru a găsi unghiul dintre planele \(\xi\) și \(\pi\) , trebuie să găsiți unghiul liniar picant sau Drept) a unghiului diedric format de planele \(\xi\) si \(\pi\) :

Pasul 1: fie \(\xi\cap\pi=a\) (linia de intersecție a planurilor). În planul \(\xi\) marchem un punct arbitrar \(F\) și desenăm \(FA\perp a\) ;

Pasul 2: desenați \(FG\perp \pi\) ;

Pasul 3: conform TTP (\(FG\) - perpendicular, \(FA\) - oblic, \(AG\) - proiecție) avem: \(AG\perp a\) ;

Pasul 4: Unghiul \(\angle FAG\) se numește unghiul liniar al unghiului diedric format din planele \(\xi\) și \(\pi\) .

Rețineți că triunghiul \(AG\) este un triunghi dreptunghic.
De asemenea, rețineți că planul \(AFG\) construit în acest fel este perpendicular atât pe planurile \(\xi\) cât și pe \(\pi\) . Prin urmare, se poate spune și în alt mod: unghiul dintre planuri\(\xi\) și \(\pi\) este unghiul dintre două drepte care se intersectează \(c\in \xi\) și \(b\in\pi\), formând un plan perpendicular pe și \(\xi\) \ ) și \(\pi\) .

Sarcina 1 #2875

Nivel de sarcină: Mai dificil decât examenul

Având în vedere o piramidă patruunghiulară, ale cărei toate marginile sunt egale, iar baza este un pătrat. Găsiți \(6\cos \alpha\) , unde \(\alpha\) este unghiul dintre fețele sale laterale adiacente.

Fie \(SABCD\) o piramidă dată (\(S\) este un vârf) ale cărei muchii sunt egale cu \(a\) . Prin urmare, toate fețele laterale sunt triunghiuri echilaterale egale. Găsiți unghiul dintre fețele \(SAD\) și \(SCD\) .

Să desenăm \(CH\perp SD\) . La fel de \(\triunghi SAD=\triunghi SCD\), atunci \(AH\) va fi, de asemenea, o înălțime de \(\triunghi SAD\) . Prin urmare, prin definiție, \(\angle AHC=\alpha\) este unghiul diedric liniar dintre fețele \(SAD\) și \(SCD\) .
Deoarece baza este un pătrat, atunci \(AC=a\sqrt2\) . De asemenea, rețineți că \(CH=AH\) este înălțimea unui triunghi echilateral cu latura \(a\) , deci \(CH=AH=\frac(\sqrt3)2a\) .
Apoi, după teorema cosinusului din \(\triunghiul AHC\): \[\cos \alpha=\dfrac(CH^2+AH^2-AC^2)(2CH\cdot AH)=-\dfrac13 \quad\Rightarrow\quad 6\cos\alpha=-2.\]

Raspuns: -2

Sarcina 2 #2876

Nivel de sarcină: Mai dificil decât examenul

Planele \(\pi_1\) și \(\pi_2\) se intersectează la un unghi al cărui cosinus este egal cu \(0,2\) . Planele \(\pi_2\) și \(\pi_3\) se intersectează în unghi drept, iar linia de intersecție a planurilor \(\pi_1\) și \(\pi_2\) este paralelă cu linia de intersecție a lui. avioanele \(\pi_2\) și \(\ pi_3\) . Aflați sinusul unghiului dintre planele \(\pi_1\) și \(\pi_3\) .

Fie linia de intersecție a lui \(\pi_1\) și \(\pi_2\) să fie linia \(a\), iar linia de intersecție a lui \(\pi_2\) și \(\pi_3\) să fie linia \ (b\) , iar linia de intersecție \(\pi_3\) și \(\pi_1\) sunt linia dreaptă \(c\) . Deoarece \(a\parallel b\) , atunci \(c\parallel a\parallel b\) (conform teoremei din secțiunea referinței teoretice „Geometrie în spațiu” \(\rightarrow\) „Introducere în stereometrie, paralelism").

Marcați punctele \(A\in a, B\in b\) astfel încât \(AB\perp a, AB\perp b\) (acest lucru este posibil deoarece \(a\parallel b\) ). Observați \(C\in c\) astfel încât \(BC\perp c\), deci \(BC\perp b\) . Apoi \(AC\perp c\) și \(AC\perp a\) .
Într-adevăr, deoarece \(AB\perp b, BC\perp b\) , atunci \(b\) este perpendicular pe planul \(ABC\) . Deoarece \(c\parallel a\parallel b\) , atunci dreptele \(a\) și \(c\) sunt, de asemenea, perpendiculare pe planul \(ABC\) și, prin urmare, pe orice dreaptă din acest plan, în special , la linia \ (AC\) .

De aici rezultă că \(\angle BAC=\angle (\pi_1, \pi_2)\), \(\angle ABC=\angle (\pi_2, \pi_3)=90^\circ\), \(\angle BCA=\angle (\pi_3, \pi_1)\). Se pare că \(\triunghiul ABC\) este dreptunghiular, ceea ce înseamnă \[\sin \angle BCA=\cos \angle BAC=0,2.\]

Răspuns: 0,2

Sarcina 3 #2877

Nivel de sarcină: Mai dificil decât examenul

Dreptele date \(a, b, c\) care se intersectează într-un punct, iar unghiul dintre oricare dintre ele este egal cu \(60^\circ\) . Aflați \(\cos^(-1)\alpha\) , unde \(\alpha\) este unghiul dintre planul format din dreptele \(a\) și \(c\) și planul format de drepte \(b\ ) și \(c\) . Dați răspunsul în grade.

Fie ca liniile să se intersecteze în punctul \(O\) . Deoarece unghiul dintre oricare dintre ele este egal cu \(60^\circ\), atunci toate cele trei drepte nu pot fi situate în același plan. Să marchem un punct \(A\) pe dreapta \(a\) și să desenăm \(AB\perp b\) și \(AC\perp c\) . Apoi \(\triunghi AOB=\triunghi AOC\) dreptunghiular în ipotenuză și unghi ascuțit. Prin urmare, \(OB=OC\) și \(AB=AC\) .
Să facem \(AH\perp (BOC)\) . Apoi, după teorema celor trei perpendiculare \(HC\perp c\) , \(HB\perp b\) . Din moment ce \(AB=AC\) , atunci \(\triunghi AHB=\triunghi AHC\) dreptunghiular de-a lungul ipotenuzei și catetei. Prin urmare, \(HB=HC\) . Prin urmare, \(OH\) ​​​​este bisectoarea unghiului \(BOC\) (deoarece punctul \(H\) este echidistant de laturile unghiului).

Rețineți că în acest fel am construit și unghiul liniar al unghiului diedru format din planul format din dreptele \(a\) și \(c\) și planul format din dreptele \(b\) și \( c\) . Acesta este unghiul \(ACH\) .

Să găsim acest colț. Deoarece am ales punctul \(A\) în mod arbitrar, atunci să-l alegem astfel încât \(OA=2\) . Apoi, în dreptunghiular \(\triunghi AOC\): \[\sin 60^\circ=\dfrac(AC)(OA) \quad\Rightarrow\quad AC=\sqrt3 \quad\Rightarrow\quad OC=\sqrt(OA^2-AC^2)=1.\ ] Deoarece \(OH\) ​​​​este o bisectoare, atunci \(\angle HOC=30^\circ\), prin urmare, într-un dreptunghiular \(\triunghi HOC\): \[\mathrm(tg)\,30^\circ=\dfrac(HC)(OC)\quad\Rightarrow\quad HC=\dfrac1(\sqrt3).\] Apoi din dreptunghiular \(\triunghi ACH\): \[\cos\angle \alpha=\cos\angle ACH=\dfrac(HC)(AC)=\dfrac13 \quad\Rightarrow\quad \cos^(-1)\alpha=3.\]

Raspuns: 3

Sarcina 4 #2910

Nivel de sarcină: Mai dificil decât examenul

Planele \(\pi_1\) și \(\pi_2\) se intersectează de-a lungul dreptei \(l\) , care conține punctele \(M\) și \(N\) . Segmentele \(MA\) și \(MB\) sunt perpendiculare pe dreapta \(l\) și se află în planurile \(\pi_1\) și, respectiv, \(\pi_2\), și \(MN = 15). \) , \(AN = 39\) , \(BN = 17\) , \(AB = 40\) . Găsiți \(3\cos\alpha\) , unde \(\alpha\) este unghiul dintre planele \(\pi_1\) și \(\pi_2\) .

Triunghiul \(AMN\) este dreptunghic, \(AN^2 = AM^2 + MN^2\) , de unde \ Triunghiul \(BMN\) este dreptunghic, \(BN^2 = BM^2 + MN^2\) , de unde \ Scriem teorema cosinusului pentru triunghiul \(AMB\): \ Apoi \ Deoarece unghiul \(\alpha\) dintre plane este un unghi ascuțit și \(\angle AMB\) sa dovedit a fi obtuz, atunci \(\cos\alpha=\dfrac5(12)\) . Apoi \

Răspuns: 1,25

Sarcina 5 #2911

Nivel de sarcină: Mai dificil decât examenul

\(ABCDA_1B_1C_1D_1\) este un paralelipiped, \(ABCD\) este un pătrat cu latura \(a\) , punctul \(M\) este baza perpendicularei coborâte din punctul \(A_1\) în plan \ ((ABCD)\) , în plus, \(M\) este punctul de intersecție al diagonalelor pătratului \(ABCD\) . Se știe că \(A_1M = \dfrac(\sqrt(3))(2)a\). Aflați unghiul dintre planele \((ABCD)\) și \((AA_1B_1B)\) . Dați răspunsul în grade.

Construim \(MN\) perpendicular pe \(AB\) așa cum se arată în figură.

Deoarece \(ABCD\) este un pătrat cu latura \(a\) și \(MN\perp AB\) și \(BC\perp AB\) , atunci \(MN\parallel BC\) . Deoarece \(M\) este punctul de intersecție al diagonalelor pătratului, atunci \(M\) este punctul de mijloc al lui \(AC\) , prin urmare, \(MN\) este linia mediană și \(MN=\frac12BC=\frac(1)(2)a\).
\(MN\) este proiecția lui \(A_1N\) pe planul \((ABCD)\) și \(MN\) este perpendicular pe \(AB\) , apoi, după teorema celor trei perpendiculare, \( A_1N\) este perpendicular pe \(AB \) iar unghiul dintre planele \((ABCD)\) și \((AA_1B_1B)\) este \(\angle A_1NM\) .
\[\mathrm(tg)\, \angle A_1NM = \dfrac(A_1M)(NM) = \dfrac(\frac(\sqrt(3))(2)a)(\frac(1)(2)a) = \sqrt(3)\qquad\Rightarrow\qquad\angle A_1NM = 60^(\circ)\]

Raspuns: 60

Sarcina 6 #1854

Nivel de sarcină: Mai dificil decât examenul

În pătratul \(ABCD\) : \(O\) este punctul de intersecție al diagonalelor; \(S\) nu este în planul pătratului, \(SO \perp ABC\) . Aflați unghiul dintre planele \(ASD\) și \(ABC\) dacă \(SO = 5\) și \(AB = 10\) .

Triunghiurile dreptunghiulare \(\triunghi SAO\) și \(\triunghi SDO\) sunt egale în două laturi și unghiul dintre ele (\(SO \perp ABC\) \(\Rightarrow\) \(\angle SOA = \angle SOD = 90^\circ\); \(AO = DO\) , deoarece \(O\) este punctul de intersecție al diagonalelor pătratului, \(SO\) este latura comună) \(\Rightarrow\) \(AS = SD\) \(\Rightarrow\) \(\triangle ASD\) este isoscel. Punctul \(K\) este mijlocul lui \(AD\) , atunci \(SK\) este înălțimea în triunghi \(\triangle ASD\) și \(OK\) este înălțimea în triunghi \ (AOD\) \(\Rightarrow\) plan \(SOK\) este perpendicular pe planurile \(ASD\) și \(ABC\) \(\Rightarrow\) \(\angle SKO\) este un unghi liniar egal la unghiul diedric necesar.

În \(\triunghi SKO\): \(OK = \frac(1)(2)\cdot AB = \frac(1)(2)\cdot 10 = 5 = SO\)\(\Rightarrow\) \(\triangle SOK\) este un triunghi dreptunghic isoscel \(\Rightarrow\) \(\angle SKO = 45^\circ\) .

Raspuns: 45

Sarcina 7 #1855

Nivel de sarcină: Mai dificil decât examenul

În pătratul \(ABCD\) : \(O\) este punctul de intersecție al diagonalelor; \(S\) nu este în planul pătratului, \(SO \perp ABC\) . Aflați unghiul dintre planele \(ASD\) și \(BSC\) dacă \(SO = 5\) și \(AB = 10\) .

Triunghiuri dreptunghiulare \(\triangle SAO\) , \(\triangle SDO\) , \(\triangle SOB\) și \(\triangle SOC\) sunt egale în două laturi și unghiul dintre ele (\(SO \perp ABC \) \(\Săgeată la dreapta\) \(\angle SOA = \angle SOD = \angle SOB = \angle SOC = 90^\circ\); \(AO = OD = OB = OC\) , deoarece \(O\) este punctul de intersecție al diagonalelor pătratului, \(SO\) este latura comună) \(\Rightarrow\) \(AS = DS = BS = CS\) \(\Rightarrow\) \(\triunghiul ASD\) și \(\triunghiul BSC\) sunt isoscele. Punctul \(K\) este mijlocul lui \(AD\) , atunci \(SK\) este înălțimea în triunghi \(\triangle ASD\) și \(OK\) este înălțimea în triunghi \ (AOD\) \(\ Săgeată la dreapta\) planul \(SOK\) este perpendicular pe planul \(ASD\) . Punctul \(L\) este mijlocul lui \(BC\) , atunci \(SL\) este înălțimea în triunghi \(\triangle BSC\) și \(OL\) este înălțimea în triunghi \ (BOC\) \(\ Săgeată la dreapta\) planul \(SOL\) (alias planul \(SOK\) ) este perpendicular pe planul \(BSC\) . Astfel, obținem că \(\angle KSL\) este un unghi liniar egal cu unghiul diedric dorit.

\(KL = KO + OL = 2\cdot OL = AB = 10\)\(\Rightarrow\) \(OL = 5\) ; \(SK = SL\) - înălțimi în triunghiuri isoscele egale, care pot fi găsite folosind teorema lui Pitagora: \(SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50\). Se vede că \(SK^2 + SL^2 = 50 + 50 = 100 = KL^2\)\(\Rightarrow\) pentru un triunghi \(\triangle KSL\), teorema inversă a lui Pitagora este valabilă \(\Rightarrow\) \(\triangle KSL\) este un triunghi dreptunghic \(\Rightarrow\) \(\angle KSL = 90^\ circ\) .

Raspuns: 90

Pregătirea elevilor pentru examenul de matematică, de regulă, începe cu o repetare a formulelor de bază, inclusiv a celor care vă permit să determinați unghiul dintre planuri. În ciuda faptului că această secțiune de geometrie este acoperită suficient de detaliat în cadrul programului școlar, mulți absolvenți trebuie să repete materialul de bază. Înțelegând cum să găsească unghiul dintre avioane, elevii de liceu vor putea calcula rapid răspunsul corect în cursul rezolvării problemei și vor putea conta pe obținerea de scoruri decente pe baza examenului de stat unificat.

Nuanțe principale

Pentru ca întrebarea cum să găsiți unghiul diedric să nu creeze dificultăți, vă recomandăm să urmați algoritmul de soluție care vă va ajuta să faceți față sarcinilor examenului.

Mai întâi trebuie să determinați linia de-a lungul căreia se intersectează planurile.

Apoi pe această linie trebuie să alegeți un punct și să desenați două perpendiculare pe acesta.

Următorul pas este găsirea funcției trigonometrice a unghiului diedric, care este format de perpendiculare. Cel mai convenabil este să faceți acest lucru cu ajutorul triunghiului rezultat, din care colțul face parte.

Răspunsul va fi valoarea unghiului sau a funcției sale trigonometrice.

Pregătirea pentru examenul împreună cu Shkolkovo este cheia succesului tău

În procesul de studiu în ajunul promovării examenului, mulți studenți se confruntă cu problema găsirii definițiilor și formulelor care vă permit să calculați unghiul dintre 2 plane. Un manual școlar nu este întotdeauna la îndemână exact când este necesar. Și pentru a găsi formulele și exemplele necesare pentru aplicarea lor corectă, inclusiv pentru găsirea online a unghiului dintre avioane pe Internet, uneori trebuie să petreceți mult timp.

Portalul matematic „Shkolkovo” oferă o nouă abordare a pregătirii pentru examenul de stat. Cursurile de pe site-ul nostru web îi vor ajuta pe studenți să identifice cele mai dificile secțiuni pentru ei înșiși și să umple golurile în cunoștințe.

Am pregătit și am prezentat clar tot materialul necesar. Definițiile și formulele de bază sunt prezentate în secțiunea „Referință teoretică”.

Pentru a asimila mai bine materialul, vă sugerăm și practicarea exercițiilor corespunzătoare. O selecție largă de sarcini de diferite grade de complexitate, de exemplu, pe, este prezentată în secțiunea Catalog. Toate sarcinile conțin un algoritm detaliat pentru găsirea răspunsului corect. Lista de exerciții de pe site este completată și actualizată în mod constant.

Exersând în rezolvarea problemelor în care se cere găsirea unghiului dintre două planuri, elevii au posibilitatea de a salva orice sarcină online la „Favorite”. Datorită acestui lucru, ei vor putea să se întoarcă la el de numărul necesar de ori și să discute progresul soluției sale cu un profesor sau un tutore.

Luați în considerare două avioane R 1 și R 2 cu vectori normali n 1 și n 2. Unghiul φ dintre plane R 1 și R 2 se exprimă în termeni de unghi ψ = \(\widehat((n_1; n_2))\) după cum urmează: dacă ψ < 90°, apoi φ = ψ (Fig. 202, a); dacă ψ > 90°, atunci ψ = 180° - ψ (Fig. 202.6).

Evident, în orice caz, egalitatea

cos φ = |cos ψ|

Deoarece cosinusul unghiului dintre vectorii nenuli este egal cu produsul scalar al acestor vectori împărțit la produsul lungimilor lor, avem

$$ cos\psi=cos\widehat((n_1; n_2))=\frac(n_1\cdot n_2)(|n_1|\cdot |n_2|) $$

și deci cosinusul unghiului φ dintre plane R 1 și R 2 poate fi calculat prin formula

$$ cos\phi=\frac(n_1\cdot n_2)(|n_1|\cdot |n_2|) (1)$$

Dacă planurile sunt date de ecuaţiile generale

A 1 X+B1 y+C1 z+ D 1 \u003d 0 și A 2 X+ B2 y+C2 z+ D2 = 0,

atunci pentru vectorii lor normali putem lua vectorii n 1 \u003d (A 1; B 1; C 1) și n 2 \u003d (A 2; B 2; C 2).

Scriind partea dreaptă a formulei (1) în termeni de coordonate, obținem

$$ cos\phi=\frac(|A_1 A_2 + B_1 B-2 + C_1 C_2|)(\sqrt((A_1)^2+(B_1)^2+(C_1)^2)\sqrt((A_2) ^2+(B_2)^2+(C_2)^2)) $$

Sarcina 1. Calculați unghiul dintre planuri

X - √2 y + z- 2 = 0 și x+ √2 y - z + 13 = 0.

În acest caz, A 1 .=1, B 1 = - √2, C 1 = 1, A 2 = 1, B 2 = √2, C 2 = - 1.

Prin formula (2) obținem

$$ cos\phi=\frac(|1\cdot 1 - \sqrt2 \cdot \sqrt2 - 1 \cdot 1|)(\sqrt(1^2+(-\sqrt2)^2+1^2)\sqrt (1^2+(\sqrt2)^2+(-1)^2))=\frac(1)(2) $$

Prin urmare, unghiul dintre aceste planuri este de 60°.

Avioane cu vectori normali n 1 și n 2:

a) sunt paralele dacă și numai dacă vectorii n 1 și n 2 sunt coliniare;

b) sunt perpendiculare dacă şi numai dacă vectorii n 1 și n 2 sunt perpendiculare, adică când n 1 n 2 = 0.

Din aceasta obținem condițiile necesare și suficiente pentru paralelismul și perpendicularitatea a două plane date prin ecuații generale.

Randul de sus

A 1 X+B1 y+C1 z+ D 1 \u003d 0 și A 2 X+ B2 y+C2 z+ D2 = 0

sunt paralele, este necesar și suficient ca egalitățile

$$ \frac(A_1)(A_2)=\frac(B_1)(B_2)=\frac(C_1)(C_2) \;\; (3)$$

Dacă oricare dintre coeficienții A 2 , B 2 , C 2 este egal cu zero, se înțelege că este egal cu zero și coeficientul corespunzător A 1 , B 1 , C 1

Neîndeplinirea a cel puțin una dintre aceste două egalități înseamnă că planurile nu sunt paralele, adică se intersectează.

Pentru planuri perpendiculare

A 1 X+B1 y+C1 z+ D 1 \u003d 0 și A 2 X+ B2 y+C2 z+ D2 = 0

necesare si suficiente pentru egalitate

A 1 A 2 + B 1 B 2 + C 1 C 2 = 0. (4)

Sarcina 2. Dintre următoarele perechi de avioane:

2X + 5la + 7z- 1 = 0 și 3 X - 4la + 2z = 0,

la - 3z+ 1 = 0 și 2 la - 6z + 5 = 0,

4X + 2la - 4z+ 1 = 0 și 2 X + la + 2z + 3 = 0

specificați paralel sau perpendicular. Pentru prima pereche de avioane

A 1 A 2 + B 1 B 2 + C 1 C 2 \u003d 2 3 + 5 (- 4) + 7 2 \u003d 0,

adică condiția de perpendicularitate este îndeplinită. Planurile sunt perpendiculare.

Pentru a doua pereche de avioane

\(\frac(B_1)(B_2)=\frac(C_1)(C_2)\) deoarece \(\frac(1)(2)=\frac(-3)(-6) \)

iar coeficienţii A 1 şi A 2 sunt egali cu zero. Prin urmare, planurile celei de-a doua perechi sunt paralele. Pentru a treia pereche

\(\frac(B_1)(B_2)\neq\frac(C_1)(C_2)\) deoarece \(\frac(2)(1)\neq\frac(-4)(2) \)

și A 1 A 2 + B 1 B 2 + C 1 C 2 \u003d 4 2 + 2 1 - 4 2 \u003d/= 0, adică planurile celei de-a treia perechi nu sunt paralele și nu sunt perpendiculare.