Rezolvarea grafică a unei ecuații pătratice Pentru a consolida capacitatea de a construi grafice ale diferitelor funcții; Pentru a forma capacitatea de a rezolva grafic ecuații pătratice. Proiect pe tema „Transformarea graficelor unei funcții”

Rezolvarea grafică a unei ecuații pătratice Pentru a consolida capacitatea de a construi grafice ale diferitelor funcții; Pentru a forma capacitatea de a rezolva grafic ecuații pătratice. Brdsk 2009 Instituție de învățământ municipală - Liceul Economic Lecție de generalizare pe tema „Funcția cadranică”, profesoară de algebră clasa a VIII-a Fedoseeva T.M.

Trasarea unei funcţii pătratice Determinaţi direcţia ramurilor: a>0 ramuri în sus; A 0 ramuri în sus; a"> 0 ramuri în sus; a"> 0 ramuri în sus; a" title="(!LANG:Reprezentarea unei funcții pătratice Determinați direcția ramificației: a>0 ramuri în sus; a"> title="Trasarea unei funcţii pătratice Determinaţi direcţia ramurilor: a>0 ramuri în sus; A"> !}

0 ramuri sunt îndreptate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsiți punctul „title="(!LANG: Să construim un grafic al funcției y=x 2 -2x-3 folosind algoritmul: 1) a=1>0 ramurile sunt îndreptate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsirea unui punct" class="link_thumb"> 3 !} Să construim un grafic al funcției y=x 2 -2x-3 folosind algoritmul: 1) a=1>0 ramuri sunt direcționate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsim punctele de intersecție cu axa OX: x 1 \u003d -1; x 2 \u003d 3 1 mod de a rezolva ecuația x 2 -2x-3 \u003d 0 y x Rezolvați ecuația x 2 +2x-3 \u003d 0 0 ramuri sunt îndreptate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsim punctul „\u003e 0 ramurile sunt îndreptate în sus; 2) partea de sus y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa al parabolei Puncte de control: (0: -3) , (3; 0) și simetric față de axa x = 1 Construim o parabolă.Găsiți punctele de intersecție cu axa OX: x 1 \u003d -1; x 2 \u003d 3 1 mod de a rezolva ecuația x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Rezolvați ecuația x 2 + 2x-3 \u003d 0 "\u003e 0 ramuri sunt îndreptate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsiți punctul „title="(!LANG: Să construim un grafic al funcției y=x 2 -2x-3 folosind algoritmul: 1) a=1>0 ramurile sunt îndreptate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsirea unui punct"> title="Să construim un grafic al funcției y=x 2 -2x-3 folosind algoritmul: 1) a=1>0 ramuri sunt direcționate în sus; 2) vârf y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - axa parabolei Puncte de control: (0: -3), (3) ; 0) și simetric față de ele față de axa x = 1 Construim o parabolă. Găsirea unui punct"> !}

A doua cale: a). Să împărțim ecuația x 2 -2x-3=0 în părți x 2 = 2x+3 Să scriem două funcții y= x 2 ; y \u003d 2x + 3 Construim grafice ale acestor funcții într-un singur sistem de coordonate. Abcisele punctelor de intersecție sunt rădăcinile ecuației. 0 1 x y Rezolvați ecuația x 2 +2x-3=0

A treia cale: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Construim grafice ale acestor funcții într-un singur sistem de coordonate. Abcisele punctelor de intersecție sunt rădăcinile ecuației. 0 1 x y Rezolvați ecuația x 2 +2x-3=0

Rezolvarea grafică a ecuațiilor

Ziua de glorie, 2009

Introducere

Necesitatea rezolvării ecuațiilor pătratice din antichitate a fost cauzată de necesitatea rezolvării problemelor legate de găsirea zonelor de pământ și de terasamente cu caracter militar, precum și de dezvoltarea astronomiei și matematicii în sine. Babilonienii au știut să rezolve ecuații patratice pentru aproximativ 2000 î.Hr. Regula de rezolvare a acestor ecuații, enunțată în textele babiloniene, coincide în esență cu cele moderne, dar nu se știe cum au ajuns babilonienii la această regulă.

Formulele pentru rezolvarea ecuațiilor pătratice din Europa au fost prezentate pentru prima dată în Cartea Abacului, scrisă în 1202 de matematicianul italian Leonardo Fibonacci. Cartea sa a contribuit la răspândirea cunoștințelor algebrice nu numai în Italia, ci și în Germania, Franța și alte țări europene.

Dar regula generală pentru rezolvarea ecuațiilor pătratice, cu toate combinațiile posibile de coeficienți b și c, a fost formulată în Europa abia în 1544 de M. Stiefel.

În 1591 François Viet a introdus formule de rezolvare a ecuaţiilor pătratice.

Unele tipuri de ecuații pătratice ar putea fi rezolvate în Babilonul antic.

Diofantul Alexandriei și Euclid , Al-Khwarizmiși Omar Khayyam ecuații rezolvate în moduri geometrice și grafice.

În clasa a VII-a am studiat funcțiile y \u003d C, y= kx , y = kx + m , y = X 2 ,y = - X 2 , in clasa a VIII-a - y = √ X , y = |X |, y= topor 2 + bx + c , y = k / X. În manualul de algebră de clasa a IX-a, am văzut funcții care nu îmi erau încă cunoscute: y= X 3 , y= X 4 ,y= X 2 n , y= X - 2 n , y= 3 √X , ( X – A ) 2 + (y - b ) 2 = r 2 si altele. Există reguli pentru construirea graficelor acestor funcții. Mă întrebam dacă există și alte funcții care respectă aceste reguli.

Sarcina mea este să studiez grafice ale funcțiilor și să rezolv ecuații grafic.

1. Care sunt funcțiile

Graficul unei funcții este mulțimea tuturor punctelor planului de coordonate, ale căror abscise sunt egale cu valorile argumentelor, iar ordonatele sunt egale cu valorile corespunzătoare ale funcției.

Funcția liniară este dată de ecuație y= kx + b, Unde kși b- unele numere. Graficul acestei funcții este o linie dreaptă.

Funcția inversă proporțională y= k / X, unde k¹ 0. Graficul acestei funcții se numește hiperbolă.

Funcţie ( X – A ) 2 + (y – b ) 2 = r 2 , Unde A , bși r- unele numere. Graficul acestei funcții este un cerc cu raza r centrat în punctul A ( A , b).

funcţie pătratică y = topor 2 + bx + c Unde A, b , cu- niște numere și A¹ 0. Graficul acestei funcții este o parabolă.

Ecuația y 2 ( A – X ) = X 2 ( A + X ) . Graficul acestei ecuații va fi o curbă numită strofoid.

Ecuația ( X 2 + y 2 ) 2 = A ( X 2 – y 2 ) . Graficul acestei ecuații se numește lemniscata Bernoulli.

Ecuația. Graficul acestei ecuații se numește astroid.

Curba (x 2 y 2 - 2 a x) 2 \u003d 4 a 2 (x 2 + y 2). Această curbă se numește cardioid.

Functii: y= X 3 - parabolă cubică, y= X 4 , y = 1/ X 2 .

2. Conceptul de ecuație, soluția sa grafică

Ecuația este o expresie care conține o variabilă.

rezolva ecuatia- asta înseamnă să-i găsești toate rădăcinile, sau să dovedești că acestea nu există.

Rădăcina ecuației este un număr care, atunci când este substituit în ecuație, produce egalitatea numerică corectă.

Rezolvarea grafică a ecuațiilor vă permite să găsiți valoarea exactă sau aproximativă a rădăcinilor, vă permite să găsiți numărul de rădăcini ale ecuației.

Când se trasează grafice și se rezolvă ecuații, se folosesc proprietățile unei funcții, așa că metoda este adesea numită grafic funcțional.

Pentru a rezolva ecuația, o „împărțim” în două părți, introducem două funcții, construim graficele lor, găsim coordonatele punctelor de intersecție ale graficelor. Abcisele acestor puncte sunt rădăcinile ecuației.

3. Algoritm pentru construirea unui grafic al unei funcții

Cunoașterea graficului funcției y= f ( X ) , puteți reprezenta funcții y= f ( X + m ) ,y= f ( X )+ lși y= f ( X + m )+ l. Toate aceste grafice sunt obținute din graficul funcției y= f ( X ) folosind transformarea de translație paralelă: on │ m │ scala unități la dreapta sau la stânga de-a lungul axei x și mai departe │ l │ scalați unitățile în sus sau în jos de-a lungul axei y .

4. Rezolvarea grafică a ecuației pătratice

Folosind exemplul unei funcții pătratice, vom lua în considerare o soluție grafică a unei ecuații pătratice. Graficul unei funcții pătratice este o parabolă.

Ce știau grecii antici despre parabolă?

Simbolismul matematic modern a apărut în secolul al XVI-lea.

Vechii matematicieni greci nu aveau nici metoda coordonatelor, nici conceptul de funcție. Cu toate acestea, proprietățile parabolei au fost studiate de ei în detaliu. Inventivitatea matematicienilor antici este pur și simplu uimitoare, deoarece aceștia nu puteau folosi decât desene și descrieri verbale ale dependențelor.

Cel mai pe deplin a explorat parabola, hiperbola și elipsa Apollonius din Perga, care a trăit în secolul al III-lea î.Hr. De asemenea, a dat nume acestor curbe și a indicat ce condiții le îndeplinesc punctele aflate pe o anumită curbă (la urma urmei, nu existau formule!).

Există un algoritm pentru construirea unei parabole:

Găsim coordonatele vârfului parabolei A (x 0; y 0): x 0 =- b /2 A ;

Y 0 \u003d ax aproximativ 2 + în 0 + c;

Găsim axa de simetrie a parabolei (linie dreaptă x \u003d x 0);

Alcătuirea unui tabel de valori pentru construirea punctelor de control;

Construim punctele obținute și construim puncte simetrice față de ele față de axa de simetrie.

1. Să construim o parabolă conform algoritmului y = X 2 – 2 X – 3 . Abscisele punctelor de intersecție cu axa Xși sunt rădăcinile ecuației pătratice X 2 – 2 X – 3 = 0.

Există cinci moduri de a rezolva grafic această ecuație.

2. Să despărțim ecuația în două funcții: y = X 2 și y = 2 X + 3

3. Să despărțim ecuația în două funcții: y = X 2 –3 și y =2 X. Rădăcinile ecuației sunt abscisele punctelor de intersecție ale parabolei cu dreapta.

4. Transformați ecuația X 2 – 2 X – 3 = 0 selectând pătratul complet pe funcție: y = ( X –1) 2 și y =4. Rădăcinile ecuației sunt abscisele punctelor de intersecție ale parabolei cu dreapta.

5. Împărțim termen cu termen ambele părți ale ecuației X 2 – 2 X – 3 = 0 pe X, primim X – 2 – 3/ X = 0 Să împărțim această ecuație în două funcții: y = X – 2, y = 3/ X . Rădăcinile ecuației sunt abscisele punctelor de intersecție ale dreptei și hiperbolei.

5. Rezolvarea grafică a ecuațiilor de grade n

Exemplul 1 rezolva ecuația X 5 = 3 – 2 X .

y = X 5 , y = 3 – 2 X .

Răspuns: x = 1.

Exemplul 2 rezolva ecuația 3 √ X = 10 – X .

Rădăcinile acestei ecuații sunt abscisa punctului de intersecție a graficelor a două funcții: y = 3 √ X , y = 10 – X .

Răspuns: x=8.

Concluzie

Luând în considerare graficele funcțiilor: y= topor 2 + bx + c , y = k / X , y = √ X , y = |X |, y= X 3 , y= X 4 ,y= 3 √X , Am observat că toate aceste grafice sunt construite după regula translației paralele în raport cu axele Xși y .

Folosind exemplul de rezolvare a unei ecuații pătratice, putem concluziona că metoda grafică este aplicabilă și ecuațiilor de gradul n.

Metodele grafice de rezolvare a ecuațiilor sunt frumoase și de înțeles, dar nu oferă o garanție de 100% a rezolvării vreunei ecuații. Abcisele punctelor de intersecție ale graficelor pot fi aproximative.

În clasa a IX-a și la clasele mari mă voi familiariza în continuare cu alte funcții. Sunt interesat să știu dacă acele funcții respectă regulile translației paralele atunci când își trasează graficele.

Anul viitor vreau să iau în considerare și problemele rezolvării grafice a sistemelor de ecuații și inegalități.

Literatură

1. Algebră. clasa a 7-a. Partea 1. Manual pentru instituţiile de învăţământ / A.G. Mordkovici. Moscova: Mnemosyne, 2007.

2. Algebră. clasa a 8-a. Partea 1. Manual pentru instituţiile de învăţământ / A.G. Mordkovici. Moscova: Mnemosyne, 2007.

3. Algebră. Clasa a 9-a Partea 1. Manual pentru instituţiile de învăţământ / A.G. Mordkovici. Moscova: Mnemosyne, 2007.

4. Glazer G.I. Istoria matematicii la scoala. clasele VII-VIII. – M.: Iluminismul, 1982.

5. Jurnal Matematică №5 2009; nr. 8 2007; Nr. 23 2008.

6. Rezolvarea grafică a ecuațiilor Site-uri Internet: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

Rezolvarea grafică a ecuațiilor

Ziua de glorie, 2009

Introducere

Dar regula generală pentru rezolvarea ecuațiilor pătratice, cu toate combinațiile posibile de coeficienți b și c, a fost formulată în Europa abia în 1544 de M. Stiefel.

În 1591 François Viet a introdus formule de rezolvare a ecuaţiilor pătratice.

Unele tipuri de ecuații pătratice ar putea fi rezolvate în Babilonul antic.

Diofantul Alexandriei și Euclid, Al-Khwarizmiși Omar Khayyam ecuații rezolvate în moduri geometrice și grafice.

În clasa a VII-a am studiat funcțiile y \u003d C, y=kx, y =kx+ m, y =X 2,y = -X 2, in clasa a VIII-a - y = √X, y =|X|, y=topor2 + bx+ c, y =k/ X. În manualul de algebră de clasa a IX-a, am văzut funcții care nu îmi erau încă cunoscute: y=X 3, y=X 4,y=X 2n, y=X- 2n, y= 3√X, (X– A) 2 + (y -b) 2 = r 2 si altele. Există reguli pentru construirea graficelor acestor funcții. Mă întrebam dacă există și alte funcții care respectă aceste reguli.

Sarcina mea este să studiez grafice ale funcțiilor și să rezolv ecuații grafic.

1. Care sunt funcțiile

Funcția liniară este dată de ecuație y=kx+ b, Unde kși b- unele numere. Graficul acestei funcții este o linie dreaptă.

Funcția inversă proporțională y=k/ X, unde k ¹ 0. Graficul acestei funcții se numește hiperbolă.

Funcţie (X– A) 2 + (y -b) 2 = r2 , Unde A, bși r- unele numere. Graficul acestei funcții este un cerc cu raza r centrat în punctul A ( A, b).

funcţie pătratică y= topor2 + bx+ c Unde A,b, cu- niște numere și A¹ 0. Graficul acestei funcții este o parabolă.

Ecuația la2 (A– X) = X2 (A+ X) . Graficul acestei ecuații va fi o curbă numită strofoid.

/>Ecuația (X2 + y2 ) 2 = A(X2 – y2 ) . Graficul acestei ecuații se numește lemniscata Bernoulli.

Ecuația. Graficul acestei ecuații se numește astroid.

Curba (X2 y2 – 2 a x)2 =4 a2 (X2 +y2 ) . Această curbă se numește cardioid.

Functii: y=X 3 - parabolă cubică, y=X 4, y = 1/X 2.

2. Conceptul de ecuație, soluția sa grafică

Ecuația este o expresie care conține o variabilă.

rezolva ecuatia- asta înseamnă să-i găsești toate rădăcinile, sau să dovedești că acestea nu există.

Rădăcina ecuației este un număr care, atunci când este substituit în ecuație, produce egalitatea numerică corectă.

Rezolvarea grafică a ecuațiilor vă permite să găsiți valoarea exactă sau aproximativă a rădăcinilor, vă permite să găsiți numărul de rădăcini ale ecuației.

Când se trasează grafice și se rezolvă ecuații, se folosesc proprietățile unei funcții, așa că metoda este adesea numită grafic funcțional.

3. Algoritm pentru construirea unui grafic al unei funcții

Cunoașterea graficului funcției y=f(X) , puteți reprezenta funcții y=f(X+ m) ,y=f(X)+ lși y=f(X+ m)+ l. Toate aceste grafice sunt obținute din graficul funcției y=f(X) folosind transformarea de translație paralelă: on │ m│ scala unități la dreapta sau la stânga de-a lungul axei x și mai departe │ l│ scalați unitățile în sus sau în jos de-a lungul axei y.

4. Rezolvarea grafică a ecuației pătratice

Folosind exemplul unei funcții pătratice, vom lua în considerare o soluție grafică a unei ecuații pătratice. Graficul unei funcții pătratice este o parabolă.

Ce știau grecii antici despre parabolă?

Simbolismul matematic modern a apărut în secolul al XVI-lea.

Există un algoritm pentru construirea unei parabole:

Aflați coordonatele vârfului parabolei A (x0; y0): X=- b/2 A;

y0=aho2+in0+s;

Aflați axa de simetrie a parabolei (dreaptă x=x0);

PAGE_BREAK--

Alcătuirea unui tabel de valori pentru construirea punctelor de control;

Construim punctele obținute și construim puncte simetrice față de ele față de axa de simetrie.

1. Să construim o parabolă conform algoritmului y= X2 – 2 X– 3 . Abscisele punctelor de intersecție cu axa Xși sunt rădăcinile ecuației pătratice X2 – 2 X– 3 = 0.

Există cinci moduri de a rezolva grafic această ecuație.

2. Să despărțim ecuația în două funcții: y= X2 și y= 2 X+ 3

3. Să despărțim ecuația în două funcții: y= X2 –3 și y=2 X. Rădăcinile ecuației sunt abscisele punctelor de intersecție ale parabolei cu dreapta.

4. Transformați ecuația X2 – 2 X– 3 = 0 selectând pătratul complet pe funcție: y= (X–1) 2 și y=4. Rădăcinile ecuației sunt abscisele punctelor de intersecție ale parabolei cu dreapta.

5. Împărțim termen cu termen ambele părți ale ecuației X2 – 2 X– 3 = 0 pe X, primim X– 2 – 3/ X= 0 Să împărțim această ecuație în două funcții: y= X– 2, y= 3/ X. Rădăcinile ecuației sunt abscisele punctelor de intersecție ale dreptei și hiperbolei.

5. Rezolvarea grafică a ecuațiilor de graden

Exemplul 1 rezolva ecuația X5 = 3 – 2 X.

y= X5 , y= 3 – 2 X.

Răspuns: x = 1.

Exemplul 2 rezolva ecuația 3 √ X= 10 – X.

Rădăcinile acestei ecuații sunt abscisa punctului de intersecție a graficelor a două funcții: y= 3 √ X, y= 10 – X.

Răspuns: x=8.

Concluzie

Luând în considerare graficele funcțiilor: y=topor2 + bx+ c, y =k/ X, y = √X, y =|X|, y=X 3, y=X 4,y= 3√X, Am observat că toate aceste grafice sunt construite după regula translației paralele în raport cu axele Xși y.

Folosind exemplul de rezolvare a unei ecuații pătratice, putem concluziona că metoda grafică este aplicabilă și ecuațiilor de gradul n.

Anul viitor vreau să iau în considerare și problemele rezolvării grafice a sistemelor de ecuații și inegalități.

Literatură

1. Algebră. clasa a 7-a. Partea 1. Manual pentru instituţiile de învăţământ / A.G. Mordkovici. Moscova: Mnemosyne, 2007.

2. Algebră. clasa a 8-a. Partea 1. Manual pentru instituţiile de învăţământ / A.G. Mordkovici. Moscova: Mnemosyne, 2007.

3. Algebră. Clasa a 9-a Partea 1. Manual pentru instituţiile de învăţământ / A.G. Mordkovici. Moscova: Mnemosyne, 2007.

4. Glazer G.I. Istoria matematicii la scoala. clasele VII-VIII. – M.: Iluminismul, 1982.

5. Jurnal Matematică №5 2009; nr. 8 2007; Nr. 23 2008.

6. Rezolvarea grafică a ecuațiilor Site-uri Internet: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm.

În această lecție video, subiectul „Funcția y \u003d x 2. Rezolvarea grafică a ecuațiilor. În cadrul acestei lecții, elevii vor putea să se familiarizeze cu o nouă modalitate de rezolvare a ecuațiilor - grafică, care se bazează pe cunoașterea proprietăților graficelor de funcții. Profesorul vă va arăta cum să rezolvați grafic funcția y=x 2 .

Subiect:Funcţie

Lecţie:Funcţie. Rezolvarea grafică a ecuațiilor

Rezolvarea grafică a ecuațiilor se bazează pe cunoașterea graficelor de funcții și a proprietăților acestora. Enumerăm funcțiile ale căror grafice le cunoaștem:

1), graficul este o linie dreaptă paralelă cu axa x, care trece printr-un punct de pe axa y. Luați în considerare un exemplu: y=1:

Pentru valori diferite, obținem o familie de linii drepte paralele cu axa x.

2) Funcția de proporționalitate directă graficul acestei funcții este o dreaptă care trece prin origine. Luați în considerare un exemplu:

Am construit deja aceste grafice în lecțiile anterioare, amintiți-vă că pentru a construi fiecare linie, trebuie să selectați un punct care o satisface și să luați originea ca al doilea punct.

Reamintim rolul coeficientului k: pe măsură ce funcția crește, unghiul dintre dreapta și direcția pozitivă a axei x este acut; când funcția scade, unghiul dintre linia dreaptă și direcția pozitivă a axei x este obtuz. În plus, există următoarea relație între doi parametri k de același semn: pentru k pozitiv, cu cât este mai mare, cu atât funcția crește mai repede, iar pentru negativ, funcția scade mai repede pentru valori mari ale k modulo.

3) Funcția liniară. Când - obținem punctul de intersecție cu axa y și toate liniile de acest fel trec prin punctul (0; m). În plus, pe măsură ce funcția crește, unghiul dintre linie și direcția pozitivă a axei x este acut; când funcția scade, unghiul dintre linia dreaptă și direcția pozitivă a axei x este obtuz. Și, desigur, valoarea lui k afectează rata de modificare a valorii funcției.

4). Graficul acestei funcții este o parabolă.

Luați în considerare exemple.

Exemplul 1 - rezolvați grafic ecuația:

Nu cunoaștem funcții de acest tip, așa că trebuie să transformăm ecuația dată pentru a lucra cu funcții cunoscute:

Avem funcții familiare în ambele părți ale ecuației:

Să construim grafice ale funcțiilor:

Graficele au două puncte de intersecție: (-1; 1); (2; 4)

Să verificăm dacă soluția este găsită corect, înlocuiți coordonatele în ecuație:

Primul punct este găsit corect.

, , , , , ,

Al doilea punct este de asemenea găsit corect.

Deci, soluțiile ecuației sunt și

Acționăm similar cu exemplul anterior: transformăm ecuația dată în funcțiile cunoscute de noi, trasăm graficele acestora, găsim curenții de intersecție și de aici indicăm soluțiile.

Obtinem doua functii:

Să construim grafice:

Aceste grafice nu au puncte de intersecție, ceea ce înseamnă că ecuația dată nu are soluții

Concluzie: în această lecție, am trecut în revistă funcțiile cunoscute nouă și graficele lor, ne-am amintit proprietățile lor și am considerat o modalitate grafică de rezolvare a ecuațiilor.

1. Dorofeev G.V., Suvorova S.B., Bunimovici E.A. et al. Algebra 7. Ediţia a VI-a. M.: Iluminismul. 2010

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. si altele.Algebra 7 .M .: Educatie. 2006

Sarcina 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et al., Algebra 7, nr.494, p. 110;

Sarcina 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. şi altele.Algebra 7, Nr. 495, poz. 110;

Sarcina 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et al., Algebra 7, nr.496, p. 110;

INSTITUTUL DE DEZVOLTARE PROFESIONALĂ DAGESTAN

PERSONAL PEDAGOGIC

DEPARTAMENTUL EDUCAȚIE FIZICĂ ȘI MATEMATICĂ ȘI TIC

Proiect

pe subiect:

« Construcție și p reforme

grafice de funcții

la matematica scolara »

Rabadanova P.A.

profesor de matematică

MBOU „Școala secundară Kochubey”

raionul Tarumovski

2015

1. Introducere……………………………………………………………………………….….3

2. Capitolul eu. Revizuirea literaturii de specialitate pe tema proiectului………………………………………….5

3. Capitolul II. Partea empirică:

3.1. Metode de bază pentru conversia graficelor de funcții……….….7

3.2. Complotează un egalșifuncții ciudate……….. 10

3.3. Trasarea unei funcții inverse……………………………… 11

3.4. Deformarea (compresia și tensiunea) graficelor………………….12

3.5.Combinație de transfer, reflexie și deformare…………………………………13

4. Sarcini pentru soluție independentă……………..……14

5.Concluzie…………………………………………………………………15

6. Concluzii…………………………………………………………………..………17

INTRODUCERE

Transformarea graficelor de funcții este unul dintre conceptele matematice fundamentale legate direct de activitățile practice. Graficele reflectă variabilitatea și dinamismul lumii reale, relațiile reciproce ale obiectelor și fenomenelor reale.

Linia funcțională este subiectul de bază abordat în examenele de stat de bază și unificate.De asemenea, multe concepte matematice sunt luate în considerare prin metode grafice. De exemplu, săpătraticăfuncţia este introdusă şi studiată în strânsă legătură cu ecuaţiile pătratice şi inegalităţile.De aici rezultă căPredarea elevilor cum să construiască și să transforme graficele unei funcții este una dintre sarcinile principale ale predării matematicii la școală.

Studiul funcției face posibilă aflarea despredomeniul de definire și domeniul de aplicare al funcției, domeniul de aplicareRate în scădere sau în creștere, asimptote, intervaleconstanța semnului etc. Cu toate acestea, pentru a construi un grafickov multe funcții pot fiutilizați o serie de metodefa-o mai usorclădire. Prin urmare, elevii ar trebui să aibă competența de a construi grafice după scheme metodologice.

Cele de mai sus definescrelevanţă teme de cercetare.

Obiect de studiu este studiul transformării graficelor cu linii funcționale în matematica școlară.

Subiect de studiu - procesul de construire și transformare a graficelor de funcții într-o școală secundară.

Scopul studiului: educativ - constă în identificarea unei scheme metodologice de construire şi conversie a graficelor unei funcţii;în curs de dezvoltare - dezvoltarea gândirii abstracte, algoritmice, logice, a imaginației spațiale;educational - educarea culturii grafice a şcolarilor, formarea deprinderilor mentale.

Scopurile au condus la decizia următoarelorsarcini:

1. Analizați aspectul educațional și metodologic asupra problemei studiate.

2. Identificați scheme metodologicetransformarea graficelor de funcţii în cursul şcolar de matematică.

3. Selectați cele mai eficiente metode și mijloaceconstruirea și transformarea graficelor de funcții într-o școală secundarăcontribuind la: asimilarea semnificativă a materialului educațional; creșterea activității cognitive a elevilor; dezvoltarea abilităților lor creative.

IPOTEZĂ cercetare: formarea deprinderilor grafice în procesul studierii funcţiilor şi educarea culturii grafice a elevilor va eficient dacă elevii au o schemă metodică de construire și transformare a graficelor de funcții într-un curs de matematică școlar.

CAPITOL eu . REVISTA LITERATURII PE TEMA PROIECTULUI.

În pregătirea proiectului, am studiat următoarea literatură:

Sivashinsky, I. Kh. Teoreme și probleme în algebră, funcții elementare - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Funcții și grafice (tehnici de bază) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Matematică elementară - M., 2010 (reeditare). - 590 p.

Kuzmin, M. K. Construcția unui grafic al unei funcții - J. Matematică la școală. - 2003. - Nr. 5. - S. 61-62.

Shilov G.E. Cum se construiesc diagrame? - M., 1982.

Isaac Tanatar. Transformări geometrice ale graficelor funcțiilor - MTsNMO, 2012

LASe remarcă faptul că capacitatea de a „citi” comportamentul unei funcții pe o anumită mulțime folosind un grafic este folosită nu numai în cursul matematicii, ci și în orice activitate practică a unei persoane în care trebuie să se ocupe de anumite grafice. reprezentări ale dependenţelor. Prin urmare, elevii ar trebui să fie capabili să determine unele dintre proprietățile sale din graficul unei funcții.

Materialul teoretic pentru transformarea graficelor este strict precizat în. Tehnica este însoțită de ilustrații cu desene, exemple de complexitate variată și soluțiile acestora, ceea ce face posibilă aprofundarea cunoștințelor și trasarea funcțiilor complexe.

Reprezintă un curs de pregătire electronic, al cărui volum și conținut îndeplinesc cerințele pentru un curs de matematică de liceu. Materialul teoretic este susținut de ilustrații grafice de animație care oferă o reprezentare vizuală a temei studiate. Cursul include trei module: un modul de studiu a materialelor teoretice, un modul de autoexaminare și un modul de control al cunoștințelor.

Din , , scheme de grafice metodice, exemple de lucru independent au fost folosite pentru partea empirică a proiectului.

Concluzii la capitolul 1

Studiul literaturii educaționale și metodice a permis:

1. Identificați schema metodologicăstudierea, construirea și transformarea graficelor unei funcții într-un curs de matematică școlar.

2. Selectați cele mai eficiente metode și mijloaceconstruirea și transformarea graficelor de funcții în matematică școlară,contribuind:

asimilarea semnificativă a materialului educațional;

creșterea activității cognitive a elevilor;

dezvoltarea abilităților lor creative.

3. arata ca linia funcţională are un impact semnificativ în studiul diferitelor concepte din matematică.

Capitolul 2. PARTEA EMPIRICA

În acest capitol, vom lua în considerare principalele metode de transformare a graficelor de funcții și vom oferi scheme metodologice pentru construirea diferitelor combinații de grafice pentru diferite funcții.

2.1. TEHNICI DE BAZĂ PENTRU CONVERSIUNEA GRAFURILOR FUNCȚIILOR

Translația de-a lungul axei y

f ( X ) f ( X )+ b .

Pentrutrasarea unei funcțiiy = f( X) + burmăei:

1. construiți un grafic al funcțieiy= f( X)

2. deplasare axaabscisă pe| b| unități până lab>0 sau la| b| mâncase prosternează lab < 0. Obținut în noul sistemdinat graph este graficul unei funcțiiy = f( X) + b.

2. Transfer de-a lungul topoare abscisă

f ( X ) f ( X + A ) .

y = f( X+ A) urmăei:

3. Trasarea unei funcții a formei y = f (- X )

f (X ) f (- X ).

Pentru a reprezenta o funcțiey = f( - x) urmează:

trasează o funcțiey = f( X)

reflectă-l înapoiraportat la axa y

graficul rezultat estegraficul funcțieiy = f( - X).

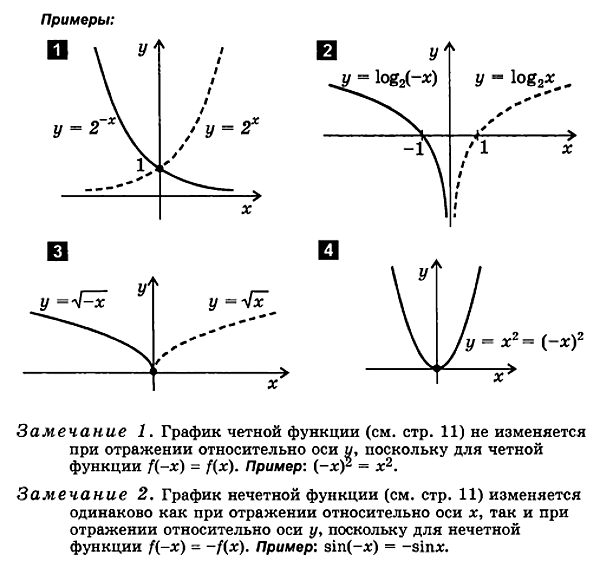
4. Trasarea unei funcții a formei y= - f ( X )

f ( X ) - f ( X )

- f( X) urmează:

trasează o funcțiey= f( X)

reflectați-l în jurul axei x

2.2. Complotează un egal și caracteristici ciudate

La complotPentru funcțiile pare și impare, este convenabil să utilizați următoarele proprietăți:

1. Graficul unei funcții par simmetrecen în raport cu axa y.

2. Graficul unei funcții impare este simetric față de origine.

Pentru a construi grafice ale unei funcții pare și impare, este suficient să reprezentați numai ramura dreaptă a graficului pentru valorile pozitive ale argumentului. Ramura din stânga este completată simetric față de originea pentru o funcție impară și față de axa y pentru o funcție pară.

Pentru a reprezenta o funcție pară y = f ( X ) după duet:

construiți o ramură a graficului acestei funcții numai înintervalul de valori pozitive ale argumentului x≥0.

Otrasează această ramură în jurul axei y

Pentru a reprezenta o funcție ciudată y = f ( X ) urmează:

construiți o ramură grafică a acestei funcții numai înzona valorilor pozitive ale argumentului (х≥0).

Otrasează această ramură în raport cu origineala regiunea valorilor negative x.

2.3. Reprezentarea grafică a funcției inverse

După cum sa menționat deja, funcțiile directe și inversearată aceeași relație între variabilex și y, cu singura diferență că în funcție inversă acesteavariabilele și-au schimbat rolurile, ceea ce echivalează cu schimbareanotarea axelor de coordonate. Prin urmare, graficulfuncția inversă este simetrică cu graficul funcției directedespre bisectoareeușiIIIunghiuri de coordonate,adică relativ drepty = x. Astfel, primimurmătoarea regulă.

Pentru a reprezenta grafic funcția y = (x) inversă funcțieiy = f( X), ar trebui construitprogramay = f( X) și reflectați-l în raport cu dreapta y = x.

2.4. Deformarea (compresia și tensiunea) graficelor

1. Comprimarea (extinderea) graficului de-a lungul axei y

f ( X ) A ∙ f ( X ).

Pentru a reprezenta o funcțiey= A∙ f( X) urmează:

8. Comprimarea (extinderea) graficului de-a lungul axei x

f( X)

Pentru a reprezenta grafic funcția y= f( X) urmează:

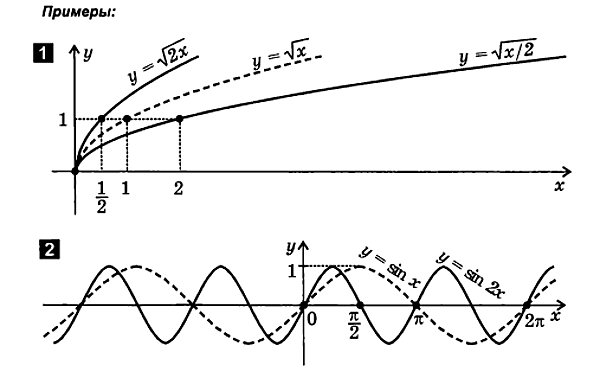
2.5. Combinație de translație, reflexie și deformare

Foarte des atunci când trasează grafice de funcții pentruschimba combinatia.

Aplicarea consecventă a unui număr de astfel de tehnici de posturăpermite simplificarea semnificativă a construcției unui grafic folosindfuncția de rulare și deseori o reduc în cele din urmă laconstruirea uneia dintre cele mai simple funcţii elementarețiuni. Luați în considerare cum, având în vedere cele de mai sus, rezultăconstruiți grafice de funcții.

Să observăm că este timpuleste recomandabil să se efectueze docul de simplificare în următorul succesorness.

Folosind paritatea sauciudățenia funcției.

Transferul axelor.

Reflecție și deformare.

Construcția graficului se realizează în ordine inversă.

Exemplu. Trasează o funcție

Construcția se va realiza în următoarele etape:

1. reprezentați grafic logaritmul natural:

2. stoarcela axaOYde 2 ori:;
3. afișați simetricdespre axaOY: ;
4. se deplasează de-a lungul axeiBOUpe(!!!) La dreapta::

5. afisare simetric fata de axaBOU: ;
6. mutarede-a lungul axeiOY3 unitati in sus::

EXEMPLE DE CONSTRUCȚIE ȘI CONVERSIE DE GRAFICE DE FUNCȚII

Exemplul 1 Trasează o funcție.

Mai întâi, desenați un grafic sinus, perioada sa este egală cu:

graficul funcțieiobtinut prin comprimarea graficuluide două ori către axa y. Buturuga .

Trasează o funcțiela = 2 cosX.

Trasează o funcțiey = păcatX .

CONCLUZIE

Pe parcursul lucrărilor de proiect au fost analizate diverse literaturi educaționale și metodologice pe această temă. Rezultatele studiului au făcut posibilă identificarea celor mai caracteristice aspecte pozitive ale studiului, construirea și transformarea graficelor unei funcții într-un curs școlar de matematică

Scopul principal al proiectului este de a dezvolta abilitățile și abilitățile elevilor în citirea și desenul desenelor, în formarea unor metode raționale de activitate independentă.

Necesitatea îmbunătățirii educației grafice în ansamblu este dictată nu numai de cerințele moderne de producție, ci și de rolul graficii în dezvoltarea gândirii tehnice și a abilităților cognitive ale elevilor. Capacitatea unei persoane de a procesa informații grafice este unul dintre indicatorii dezvoltării sale mentale. Prin urmare, pregătirea grafică ar trebui să devină un element integral al pregătirii educaționale generale.

constatări

Astfel, proiectul dezvoltat „Construcția și transformarea graficelor de funcții”, dedicat unuia dintre conceptele centrale ale matematicii – dependența funcțională, este axat pe sistematizarea și extinderea cunoștințelor elevilor. Studiul metodelor specifice de transformare a graficelor de funcții se realizează în mod analitic și grafic după scheme metodologice stricte. Materialul colectat poate fi folosit în sala de clasă și pentru autoformarea elevilor. O varietate de forme și metode de organizare și instruire pot fi folosite pentru a conduce cursurile.

Portal pentru student. Autoinstruire

ARTICOLE SIMILARE