DAGESTAN INSTITUTE FOR PROFESSIONAL DEVELOPMENT

PEDAGOGICAL STAFF

DEPARTMENT OF PHYSICAL AND MATHEMATICAL EDUCATION AND ICT

Proyekto

Naaayon sa paksa:

« Konstruksyon at p mga reporma

mga function graph

sa matematika ng paaralan »

Rabadanova P.A.

guro sa matematika

MBOU "Kochubey secondary school"

distrito ng Tarumovsky

2015

1. Panimula………………………………………………………………….3

2. Kabanata ako. Pagsusuri ng panitikan sa paksa ng proyekto………………………………………….5

3. Kabanata II. Empirical na bahagi:

3.1. Pangunahing pamamaraan para sa pag-convert ng mga function graph...........7

3.2. Nagpaplano ng pantayatkakaibang pag-andar…………………… 10

3.3. Pag-plot ng inverse function………………………………………… 11

3.4. Deformation (compression at tension) ng mga graph………………….12

3.5 Kumbinasyon ng paglilipat, pagmuni-muni at pagpapapangit………………….13

4. Mga gawain para sa independiyenteng solusyon…………………………………..14

5. Konklusyon…………………………………………………………………………15

6. Mga Konklusyon……………………………………………………………………..………17

PANIMULA

Ang pagbabago ng mga function graph ay isa sa mga pangunahing konsepto ng matematika na direktang nauugnay sa mga praktikal na aktibidad. Ang mga graph ay sumasalamin sa pagkakaiba-iba at dynamism ng totoong mundo, ang magkaparehong relasyon ng mga tunay na bagay at phenomena.

Ang functional line ay ang pangunahing paksa na sakop sa Basic at Unified State Examinations.Gayundin, maraming mga konsepto sa matematika ang isinasaalang-alang ng mga graphical na pamamaraan. Halimbawa, saparisukatang pagpapaandar ay ipinakilala at pinag-aralan na may malapit na koneksyon sa mga quadratic equation at hindi pagkakapantay-pantay.Kaya naman sinusunod iyonpagtuturo sa mga mag-aaral kung paano bumuo at mag-transform ng mga graph ng isang function ay isa sa mga pangunahing gawain ng pagtuturo ng matematika sa paaralan.

Ginagawang posible ng pag-aaral ng function na mahanap ang tungkol sadomain ng kahulugan at saklaw ng function, saklawPagbaba o pagtaas ng mga rate, asymptotes, agwatmag-sign constancy, atbp. Gayunpaman, upang bumuo ng isang graphkov maraming mga pag-andar ay maaaring maginggumamit ng ilang pamamaraangawing mas madaligusali. Samakatuwid, ang mga mag-aaral ay dapat magkaroon ng kakayahan na bumuo ng mga graph ayon sa pamamaraang pamamaraan.

Tinutukoy ng nasa itaaskaugnayan mga paksa ng pananaliksik.

Layunin ng pag-aaral ay ang pag-aaral ng pagbabago ng functional line graphs sa matematika ng paaralan.

Paksa ng pag-aaral - ang proseso ng pagbuo at pagbabago ng mga function graph sa isang sekondaryang paaralan.

Layunin ng pag-aaral: pang-edukasyon - binubuo sa pagtukoy ng pamamaraang pamamaraan para sa pagbuo at pag-convert ng mga graph ng isang function;umuunlad - pagbuo ng abstract, algorithmic, lohikal na pag-iisip, spatial na imahinasyon;pang-edukasyon - edukasyon ng graphic na kultura ng mga mag-aaral, ang pagbuo ng mga kasanayan sa pag-iisip.

Ang mga layunin ay humantong sa desisyon ng mga sumusunodmga gawain:

1. Suriin ang pang-edukasyon at metodolohikal sa problemang pinag-aaralan.

2. Tukuyin ang mga pamamaraang pamamaraanpagbabago ng mga function graph sa kursong paaralan ng matematika.

3. Piliin ang pinakamabisang paraan at paraanpagbuo at pagbabago ng mga function graph sa isang sekondaryang paaralannag-aambag sa: makabuluhang asimilasyon ng materyal na pang-edukasyon; pagtaas ng aktibidad ng nagbibigay-malay ng mga mag-aaral; pag-unlad ng kanilang mga malikhaing kakayahan.

HIPOTESIS pananaliksik: ang pagbuo ng mga graphic na kasanayan sa proseso ng pag-aaral ng mga function at ang edukasyon ng graphic na kultura ng mga mag-aaral ay epektibo kung ang mga mag-aaral ay may pamamaraang pamamaraan para sa pagbuo at pagbabago ng mga function graph sa isang kurso sa matematika ng paaralan.

KABANATA ako . REVIEW NG LITERATURA SA PAKSA NG PROYEKTO.

Bilang paghahanda para sa proyekto, pinag-aralan namin ang sumusunod na literatura:

Sivashinsky, I. Kh. Theorems at mga problema sa algebra, elementarya function - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. Mga function at graph (pangunahing diskarte) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. Scanavi. Elementarya Mathematics - M., 2010 (reissue). - 590 p.

Kuzmin, M. K. Konstruksyon ng isang graph ng isang function - J. Mathematics sa paaralan. - 2003. - Hindi. 5. - S. 61-62.

Shilov G.E. Paano bumuo ng mga tsart? - M., 1982.

Isaac Tanatar. Mga pagbabagong geometriko ng mga graph ng mga function - MTsNMO, 2012

ATNabanggit na ang kakayahang "basahin" ang pag-uugali ng isang function sa isang tiyak na hanay gamit ang isang graph ay ginagamit hindi lamang sa kurso ng matematika, kundi pati na rin sa anumang praktikal na aktibidad ng isang tao kung saan kailangan niyang harapin ang ilang graphic. representasyon ng mga dependency. Samakatuwid, dapat na matukoy ng mga mag-aaral ang ilan sa mga katangian nito mula sa graph ng isang function.

Ang teoretikal na materyal para sa pagbabago ng mga graph ay mahigpit na nakasaad sa. Ang pamamaraan ay sinamahan ng mga guhit na may mga guhit, mga halimbawa ng iba't ibang pagiging kumplikado at ang kanilang mga solusyon, na ginagawang posible upang palalimin ang kaalaman at magplano ng mga kumplikadong pag-andar.

Kumakatawan sa isang elektronikong kurso sa pagsasanay, ang dami at nilalaman nito ay nakakatugon sa mga kinakailangan para sa isang kurso sa matematika sa mataas na paaralan. Ang teoretikal na materyal ay sinusuportahan ng mga graphic na animation na ilustrasyon na nagbibigay ng visual na representasyon ng paksang pinag-aaralan. Kasama sa kurso ang tatlong module: isang theoretical material study module, isang self-examination module at isang knowledge control module.

Mula sa , , mga pamamaraan ng pag-chart ng mga pamamaraan, mga halimbawa para sa independiyenteng gawain ay ginamit para sa empirikal na bahagi ng proyekto.

Mga konklusyon sa kabanata 1

Ang pag-aaral ng pang-edukasyon at pamamaraang panitikan ay pinapayagan:

1. Tukuyin ang pamamaraang pamamaraanpag-aaral, pagbuo at pagbabago ng mga graph ng isang function sa isang kurso sa matematika ng paaralan.

2. Piliin ang pinaka-epektibong paraan at paraanpagbuo at pagbabago ng mga function graph sa matematika ng paaralan,nag-aambag:

makabuluhang asimilasyon ng materyal na pang-edukasyon;

pagtaas ng aktibidad ng nagbibigay-malay ng mga mag-aaral;

pag-unlad ng kanilang mga malikhaing kakayahan.

3. ipakita mo na ang functional line ay may malaking epekto sa pag-aaral ng iba't ibang konsepto sa matematika.

Kabanata 2. EMPIRIKAL NA BAHAGI

Sa kabanatang ito, isasaalang-alang namin ang mga pangunahing pamamaraan para sa pagbabago ng mga function graph, at magbibigay ng mga pamamaraan ng pamamaraan para sa pagbuo ng iba't ibang kumbinasyon ng mga graph para sa iba't ibang mga function.

2.1. MGA BATAYANG TEKNIK PARA SA FUNCTION GRAPH CONVERSION

Pagsasalin sa kahabaan ng y-axis

f ( x ) f ( x )+ b .

Para sanagpaplano ng isang functiony = f( x) + bbakasem:

1. bumuo ng isang function graphy= f( x)

2. ilipat axisabscissa on| b| mga unit sab>0 o sa| b| kumainmagpatirapa sab < 0. Nakuha sa bagong sistemaAng dinat graph ay ang graph ng isang functiony = f( x) + b.

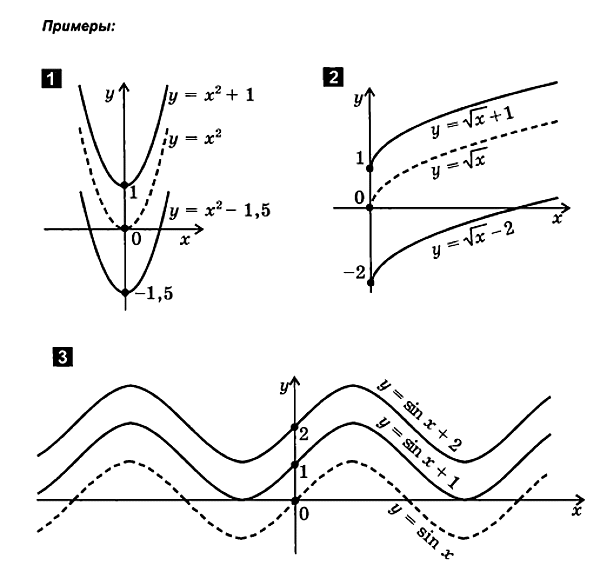
2. Paglipat kasama mga palakol abscissa

f ( x ) f ( x + a ) .

y = f( x+ a) bakasem:

3. Pag-plot ng function ng form y = f (- x )

f (x ) f (- x ).

Upang magplano ng isang functiony = f( - x) sumusunod:

magplano ng isang functiony = f( x)

sumasalamin ito pabalikmay kaugnayan sa y-axis

ang resultang graph ayfunction graphy = f( - X).

4. Pag-plot ng isang function ng form y= - f ( x )

f ( x ) - f ( x )

- f( x) sumusunod:

magplano ng isang functiony= f( x)

ipakita ito tungkol sa x-axis

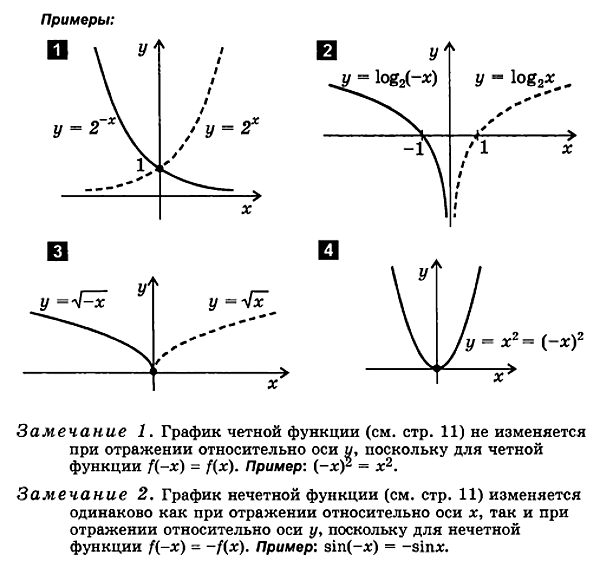
2.2. Nagpaplano ng pantay at kakaibang katangian

Kapag nagpaplanoPara sa pantay at kakaibang mga pag-andar, maginhawang gamitin ang mga sumusunod na katangian:

1. Graph ng isang even function na simmetricen na may kaugnayan sa y-axis.

2. Ang graph ng isang kakaibang function ay simetriko tungkol sa pinagmulan.

Upang makabuo ng mga graph ng pantay at kakaibang function, sapat na upang i-plot lamang ang tamang sangay ng graph para sa mga positibong halaga ng argumento. Ang kaliwang sangay ay nakumpleto nang simetriko tungkol sa pinagmulan para sa isang kakaibang function at tungkol sa y-axis para sa isang even na function.

Upang magplano ng isang pantay na function y = f ( x ) pagkatapos duet:

bumuo ng isang sangay ng graph ng function na ito lamang sahanay ng mga positibong halaga ng argumento x≥0.

Osubaybayan ang sangay na ito tungkol sa y-axis

Upang mag-plot ng kakaibang function y = f ( x ) sumusunod:

bumuo ng isang sangay ng graph ng function na ito lamang salugar ng mga positibong halaga ng argumento (х≥0).

Osubaybayan ang sangay na ito tungkol sa pinagmulansa rehiyon ng mga negatibong halaga ng x.

2.3. Pag-plot ng inverse function

Tulad ng nabanggit na, ang direkta at kabaligtaran ay gumaganaipakita ang parehong relasyon sa pagitan ng mga variablex at y, na may pagkakaiba lamang na sa kabaligtaran na pag-andar ang mga itoang mga variable ay nagbago ng mga tungkulin, na katumbas ng pagbabagonotasyon ng mga coordinate axes. Samakatuwid, ang iskedyulang inverse function ay simetriko sa graph ng direktang functiontungkol sa bisectorakoatIIImga anggulo ng coordinate,ibig sabihin, medyo tuwidy = x. Kaya, nakukuha naminsusunod na tuntunin.

Upang i-plot ang function y = (x) kabaligtaran sa functiony = f( x), dapat itayoiskedyuly = f( x) at ipakita ito sa tuwid na linya y = x.

2.4. Deformation (compression at tension) ng mga graph

1. Compression (expansion) ng graph sa kahabaan ng y-axis

f ( x ) A ∙ f ( x ).

Upang magplano ng isang functiony= A∙ f( x) sumusunod:

8. Compression (expansion) ng graph sa kahabaan ng x-axis

f( x)

Upang i-plot ang function na y= f( x) sumusunod:

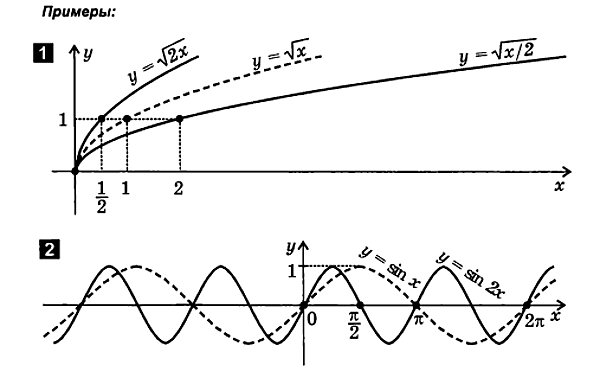
2.5. Kumbinasyon ng pagsasalin, pagmuni-muni at pagpapapangit

Kadalasan kapag nagpaplano ng mga function graph para sabaguhin ang kumbinasyon.

Ang pare-parehong aplikasyon ng isang bilang ng naturang mga diskarte sa pusturanagbibigay-daan upang makabuluhang pasimplehin ang pagbuo ng isang graph gamit angtumatakbo function at madalas na bawasan ito sa dulo sapagbuo ng isa sa pinakasimpleng elementarya na pag-andartions. Isaalang-alang kung paano, sa pagtingin sa nabanggit, ito ay sumusunodbumuo ng mga function graph.

Tandaan natin na oras naipinapayong isagawa ang dock ng pagpapasimple sa susunod na kapalitness.

Gamit ang parity opagiging kakaiba ng function.

Paglipat ng mga axes.

Pagninilay at pagpapapangit.

Ang pagbuo ng graph ay isinasagawa sa reverse order.

Halimbawa. Mag-plot ng function

Ang pagtatayo ay isasagawa sa mga sumusunod na hakbang:

1. balangkasin ang natural logarithm:

2. pisilinsa axisOY2 beses:;
3. ipakita ang simetrikotungkol sa axisOY: ;
4. gumalaw sa kahabaan ng axisOXsa(!!!) sa kanan::

5. magpakita ng simetriko tungkol sa axisOX: ;
6. gumalawkasama ang axisOY3 units up::

MGA HALIMBAWA NG CONSTRUCTION AT CONVERSION OF FUNCTION GRAPHS

Halimbawa 1 Mag-plot ng function.

Una, gumuhit ng sine graph, ang panahon nito ay katumbas ng:

function graphnakuha sa pamamagitan ng pag-compress ng graphdalawang beses sa y-axis. log .

Mag-plot ng functionsa = 2 cosX.

Mag-plot ng functiony = kasalananx .

KONGKLUSYON

Sa panahon ng trabaho sa gawaing proyekto, nasuri ang iba't ibang literatura na pang-edukasyon at pamamaraan sa isyung ito. Ang mga resulta ng pag-aaral ay naging posible upang matukoy ang pinaka-katangiang positibong aspeto ng pag-aaral, pagbuo at pagbabago ng mga graph ng isang function sa isang kurso sa matematika ng paaralan

Ang pangunahing layunin ng proyekto ay upang bumuo ng mga kasanayan at kakayahan ng mga mag-aaral sa pagbabasa at pagguhit ng mga guhit, sa pagbuo ng mga makatuwirang pamamaraan ng independiyenteng aktibidad.

Ang pangangailangan upang mapabuti ang graphic na edukasyon sa kabuuan ay idinidikta hindi lamang ng mga modernong kinakailangan sa produksyon, kundi pati na rin ng papel ng mga graphic sa pagbuo ng teknikal na pag-iisip at nagbibigay-malay na kakayahan ng mga mag-aaral. Ang kakayahan ng isang tao na magproseso ng graphic na impormasyon ay isa sa mga tagapagpahiwatig ng kanyang pag-unlad ng kaisipan. Samakatuwid, ang graphic na pagsasanay ay dapat maging isang mahalagang elemento ng pangkalahatang pagsasanay sa edukasyon.

natuklasan

Kaya, ang binuo na proyekto na "Konstruksyon at pagbabago ng mga function graph", na nakatuon sa isa sa mga sentral na konsepto ng matematika - functional dependence, ay nakatuon sa systematization at pagpapalawak ng kaalaman ng mga mag-aaral. Ang pag-aaral ng mga tiyak na pamamaraan para sa pagbabago ng mga function graph ay isinasagawa sa isang analytical at graphical na paraan ayon sa mahigpit na pamamaraan ng pamamaraan. Ang nakolektang materyal ay maaaring gamitin sa silid-aralan at para sa self-training ng mga mag-aaral. Ang iba't ibang anyo at pamamaraan ng organisasyon at pagsasanay ay maaaring gamitin sa pagsasagawa ng mga klase.

Graphical na solusyon ng isang quadratic equation Upang pagsama-samahin ang kakayahang bumuo ng mga graph ng iba't ibang function; Upang mabuo ang kakayahang lutasin ang mga quadratic equation sa graphical na paraan. Brdsk 2009 Municipal educational institution - Economic Lyceum Generalizing lesson sa paksang "Quadratic function", algebra grade 8 teacher Fedoseeva T.M.

Pag-plot ng quadratic function Tukuyin ang direksyon ng mga sanga: a>0 sanga pataas; a 0 sanga pataas; a"> 0 sanga pataas; a"> 0 sanga pataas; a" title="(!LANG:Pag-plot ng quadratic function Tukuyin ang direksyon ng branch: a>0 branches up; a"> title="Pag-plot ng quadratic function Tukuyin ang direksyon ng mga sanga: a>0 sanga pataas; a"> !}

0 sanga ay nakadirekta paitaas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Hanapin ang puntong "title="(!LANG: Bumuo tayo ng graph ng function na y=x 2 -2x-3 gamit ang algorithm: 1) a=1>0 ang mga sanga ay nakadirekta pataas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Paghanap ng punto" class="link_thumb"> 3 !} Bumuo tayo ng graph ng function na y=x 2 -2x-3 gamit ang algorithm: 1) a=1>0 na mga sanga ay nakadirekta pataas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Nahanap namin ang mga punto ng intersection sa axis ng OX: x 1 \u003d -1; x 2 \u003d 3 1 paraan upang malutas ang equation x 2 -2x-3 \u003d 0 y x Solve ang equation x 2 +2x-3 \u003d 0 0 sanga ay nakadirekta paitaas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Nahanap namin ang punto "\u003e 0 ang mga sanga ay nakadirekta paitaas; 2) ang tuktok y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3) , (3; 0) at simetriko tungkol sa x = 1 axis Bumubuo kami ng parabola.Hanapin ang mga punto ng intersection sa OX axis: x 1 \u003d -1; x 2 \u003d 3 1 paraan upang malutas ang equation x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 Lutasin ang equation x 2 + 2x-3 \u003d 0 "\u003e 0 sanga ay nakadirekta paitaas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Hanapin ang puntong "title="(!LANG: Bumuo tayo ng graph ng function na y=x 2 -2x-3 gamit ang algorithm: 1) a=1>0 ang mga sanga ay nakadirekta pataas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Paghanap ng punto"> title="Bumuo tayo ng graph ng function na y=x 2 -2x-3 gamit ang algorithm: 1) a=1>0 na mga sanga ay nakadirekta pataas; 2) vertex y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - ang axis ng parabola Control point: (0: -3), (3 ; 0) at simetriko sa kanila tungkol sa x-axis = 1 Bumubuo kami ng parabola. Paghanap ng punto"> !}

Ang pangalawang paraan: a). Hatiin natin ang equation x 2 -2x-3=0 sa mga bahagi x 2 = 2x+3 Isulat natin ang dalawang function y= x 2 ; y \u003d 2x + 3 Bumubuo kami ng mga graph ng mga function na ito sa isang coordinate system. Ang abscissas ng mga intersection point ay ang mga ugat ng equation. 0 1 x y Lutasin ang equation x 2 +2x-3=0

Ang ikatlong paraan: x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x Bumubuo kami ng mga graph ng mga function na ito sa isang coordinate system. Ang abscissas ng mga intersection point ay ang mga ugat ng equation. 0 1 x y Lutasin ang equation x 2 +2x-3=0

Graphical na solusyon ng mga equation

Kaarawan, 2009

- Panimula -

Ang pangangailangang lutasin ang mga quadratic equation noong sinaunang panahon ay dulot ng pangangailangang lutasin ang mga problemang may kaugnayan sa paghahanap ng mga lugar ng lupain at mga gawaing lupa ng kalikasang militar, gayundin ang pag-unlad ng astronomiya at matematika mismo. Alam ng mga Babylonians kung paano lutasin ang mga quadratic equation para sa mga 2000 BC. Ang tuntunin para sa paglutas ng mga equation na ito, na nakasaad sa mga teksto ng Babylonian, ay talagang kasabay ng mga makabago, ngunit hindi alam kung paano napunta ang mga Babylonians sa panuntunang ito.

Ang mga formula para sa paglutas ng mga quadratic equation sa Euroᴨȇ ay unang itinakda sa Book of the Abacus, na isinulat noong 1202 ng Italyano na matematiko na si Leonardo Fibonacci. Ang kanyang libro ay nag-ambag sa paglaganap ng algebraic na kaalaman hindi lamang sa Italya, kundi pati na rin sa Alemanya, Pransya at iba pang mga bansa sa Europa.

Ngunit ang pangkalahatang tuntunin para sa paglutas ng mga quadratic equation, kasama ang lahat ng posibleng kumbinasyon ng mga coefficient b at c, ay binuo sa Euroᴨȇ lamang noong 1544 ni M. Stiefel.

Noong 1591 François Viet ipinakilala ang mga formula para sa paglutas ng mga quadratic equation.

Ang ilang mga uri ng quadratic equation ay maaaring malutas sa sinaunang Babylon.

Diophantus ng Alexandria at Euclid, Al-Khawarizmi at Omar Khayyam nalutas ang mga equation sa geometric at graphical na paraan.

Sa ika-7 baitang pinag-aralan namin ang mga function y \u003d C, y=kx, y = kx+ m, y =x 2 ,y=- x 2 , sa ika-8 baitang - y = vx, y =|x|, sa = palakol 2 + bx+ c, y =k / x. Sa 9th grade algebra textbook, nakakita ako ng mga function na hindi ko pa alam: y=x 3 , sa = x 4 ,y=x 2 n , sa = x - 2 n , sa = 3v x, (x - a) 2 + (y -b) 2 = r 2 at iba pa. May mga panuntunan para sa pagbuo ng mga graph ng mga function na ito. Iniisip ko kung may iba pang function na sumusunod sa mga patakarang ito.

Ang aking trabaho ay pag-aralan ang mga graph ng mga function at lutasin ang mga equation nang grapiko.

1. Ano ang mga function

Ang graph ng isang function ay ang hanay ng lahat ng mga punto ng coordinate plane, ang abscissas kung saan ay katumbas ng mga halaga ng mga argumento, at ang mga ordinate ay katumbas ng kaukulang mga halaga ng function.

Ang linear function ay ibinibigay ng equation y=kx + b, saan k at b- ilang mga numero. Ang graph ng function na ito ay isang tuwid na linya.

Inverse Proportional Function y=k/ x, kung saan k 0. Ang graph ng function na ito ay tinatawag na giᴨȇrbola.

Function (x - a) 2 + (y -b) 2 = r 2 , saan a, b at r- ilang mga numero. Ang graph ng function na ito ay isang bilog ng radius r na nakasentro sa punto A ( a, b).

quadratic function y = palakol 2 + bx + c saan a,b, kasama- ilang mga numero at a 0. Ang graph ng function na ito ay isang parabola.

Ang equation sa 2 (a - x) = x 2 (a+ x) . Ang graph ng equation na ito ay magiging isang curve na tinatawag na strophoid.

Ang equation (x 2 + y 2 ) 2 = a (x 2 - y 2 ) . Ang graph ng equation na ito ay tinatawag na Bernoulli lemma.

Ang equation. Ang graph ng equation na ito ay tinatawag na astroid.

Kurba (x 2 y 2 - 2ax) 2 =4 a 2 (x 2 + y 2 ) . Ang kurba na ito ay tinatawag na cardioid.

Mga function: y=x 3 - kubiko parabola, y=x 4 , y = 1/x 2 .

2. Ang konsepto ng isang equation, ang graphical na solusyon nito

Ang equation- isang expression na naglalaman ng ᴨȇ.

lutasin ang equation- nangangahulugan ito na hanapin ang lahat ng pinagmulan nito, o patunayan na hindi sila umiiral.

Root ng equation- ito ay isang numero, kapag pinapalitan ito sa equation, ang tamang pagkakapantay-pantay ng numero ay makukuha.

Paglutas ng mga Equation nang Grapiko nagbibigay-daan sa iyo upang mahanap ang eksaktong o tinatayang halaga ng mga ugat, nagbibigay-daan sa iyo upang mahanap ang bilang ng mga ugat ng equation.

Kapag gumagawa ng mga graph at paglutas ng mga equation, ginagamit ang mga katangian ng isang function; sa bagay na ito, ang pamamaraan ay mas madalas na tinatawag na functional-graphic.

Upang malutas ang equation, "hatiin" namin ito sa dalawang bahagi, ipinakilala ang dalawang function, bumuo ng kanilang mga graph, hanapin ang mga coordinate ng mga intersection point ng mga graph. Ang abscissas ng mga puntong ito ay ang mga ugat ng equation.

3. Algorithm para sa pag-plot ng isang function graph

Pag-alam sa graph ng function y=f(x) , maaari kang mag-plot ng mga function y=f (x+ m) ,y=f(x)+ l at y=f (x+ m)+ l. Ang lahat ng mga graph na ito ay nakuha mula sa graph ng function y=f(x) gamit ang pagbabago ng parallel ᴨȇrenos: on ¦ m¦ scale unit sa kanan o kaliwa sa kahabaan ng x-axis at sa ¦ l¦ scale unit pataas o pababa sa kahabaan ng axis y.

4. Graphical na solusyon ng isang quadratic equation

Gamit ang halimbawa ng isang quadratic function, isasaalang-alang namin ang isang graphical na solusyon ng isang quadratic equation. Ang graph ng isang quadratic function ay isang parabola.

Ano ang alam ng mga sinaunang Griyego tungkol sa parabola?

Ang makabagong simbolismong matematikal ay nagmula noong ika-16 na siglo.

Ang mga sinaunang Greek mathematician ay walang coordinate method o konsepto ng isang function. Gayunpaman, ang mga katangian ng parabola ay pinag-aralan nila nang detalyado. Ang pagiging mapag-imbento ng mga sinaunang mathematician ay kahanga-hanga lamang, dahil maaari lamang silang gumamit ng mga guhit at pandiwang paglalarawan ng mga dependency.

Ganap niyang ginalugad ang parabola, giᴨȇrbola at ellipse Apollonius ng Perga, na nabuhay noong ika-3 siglo BC. Binigyan din niya ng mga pangalan ang mga kurbadang ito at ipinahiwatig kung anong mga kundisyon ang natutugunan ng mga puntong nakahiga sa isang partikular na kurba (pagkatapos ng lahat, walang mga formula!).

Mayroong isang algorithm para sa pagbuo ng isang parabola:

Nahanap namin ang mga coordinate ng vertex ng parabola A (x 0; y 0): X 0 =- b/2 a;

Y 0 \u003d palakol tungkol sa 2 + sa 0 + c;

Nahanap namin ang axis ng simetrya ng parabola (tuwid na linya x \u003d x 0);

Pag-compile ng isang talahanayan ng mga halaga para sa pagbuo ng mga control point;

Binubuo namin ang nakuha na mga puntos at itinayo ang mga puntos na simetriko sa kanila na may paggalang sa axis ng simetrya.

1. Bumuo tayo ng parabola ayon sa algorithm y = x 2 - 2 x - 3 . Abscissas ng mga punto ᴨȇintersections sa axis x at ang mga ugat ng quadratic equation x 2 - 2 x - 3 = 0.

Mayroong limang paraan upang graphical na malutas ang equation na ito.

2. Hatiin natin ang equation sa dalawang function: y= x 2 at y= 2 x + 3

3. Hatiin natin ang equation sa dalawang function: y= x 2 -3 at y =2 x. Ang mga ugat ng equation ay ang abscissas ng mga punto sa intersection ng parabola sa linya.

4. Ibahin ang anyo ng equation x 2 - 2 x - 3 = 0 sa pamamagitan ng pagpili ng buong parisukat sa function: y= (x -1) 2 at y=4 . Ang mga ugat ng equation ay ang abscissas ng mga punto sa intersection ng parabola sa linya.

5. Hinahati namin ang term sa termino sa parehong bahagi ng equation x 2 - 2 x - 3 = 0 sa x, nakukuha namin x - 2 - 3/ x = 0 Hatiin natin ang equation na ito sa dalawang function: y = x - 2, y = 3/ x. Ang mga ugat ng equation ay ang abscissas ng mga punto ng intersection ng tuwid na linya at ang giᴨȇrbola.

5. Graphic na solusyonmga equation ng degreen

Halimbawa 1 lutasin ang equation x 5 = 3 - 2 x.

y = x 5 , y = 3 - 2 x.

Sagot: x = 1.

Halimbawa 2 lutasin ang equation 3 vx = 10 - x.

Ang mga ugat ng equation na ito ay ang abscissa ng intersection point ng mga graph ng dalawang function: y = 3 vx, y = 10 - x.

Sagot: x=8.

- Konklusyon -

Isinasaalang-alang ang mga function graph: sa = palakol 2 + bx+ c, y =k / x, y = vx, y =|x|, y=x 3 , y=x 4 ,y= 3v x, Napansin ko na ang lahat ng mga graph na ito ay binuo ayon sa panuntunan ng parallel ᴨȇrenos na may paggalang sa mga axes x at y.

Gamit ang halimbawa ng paglutas ng isang quadratic equation, maaari nating tapusin na ang graphical na paraan ay naaangkop din sa mga equation ng degree n.

Ang mga graphical na pamamaraan para sa paglutas ng mga equation ay maganda at naiintindihan, ngunit hindi sila nagbibigay ng 100% na garantiya ng paglutas ng anumang equation. Ang abscissas ng ᴨȇ intersection point ng mga graph ay maaaring tantiyahin.

Sa ika-9 na baitang at sa mga senior na klase, makikilala ko pa rin ang iba pang mga tungkulin. Interesado akong malaman kung ang mga function na iyon ay sumusunod sa mga alituntunin ng parallel ᴨȇrenos kapag nag-plot ng kanilang mga graph.

Sa susunod na taon gusto ko ring isaalang-alang ang mga isyu ng graphical na solusyon ng mga sistema ng mga equation at hindi pagkakapantay-pantay.

Panitikan

1. Algebra. ika-7 baitang. Bahagi 1. Teksbuk para sa mga institusyong pang-edukasyon / A.G. Mordkovich. Moscow: Mnemosyne, 2007.

2. Algebra. ika-8 baitang. Bahagi 1. Teksbuk para sa mga institusyong pang-edukasyon / A.G. Mordkovich. Moscow: Mnemosyne, 2007.

3. Algebra. Baitang 9 Bahagi 1. Teksbuk para sa mga institusyong pang-edukasyon / A.G. Mordkovich. Moscow: Mnemosyne, 2007.

4. Glazer G.I. Kasaysayan ng matematika sa paaralan. VII-VIII na mga klase. - M.: Enlightenment, 1982.

5. Journal Mathematics №5 2009; 8 2007; No. 23 2008.

6. Graphic na solusyon ng mga equation na mga site sa Internet: Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3-6.htm.

Ang isang paraan upang malutas ang mga equation ay isang graphical na pamamaraan. Ito ay batay sa paglalagay ng mga function at pagtukoy ng kanilang mga intersection point. Isaalang-alang ang isang graphical na paraan upang malutas ang quadratic equation na a*x^2+b*x+c=0.

Unang paraan upang malutas

Ibahin natin ang equation na a*x^2+b*x+c=0 sa anyo na a*x^2 =-b*x-c. Bumubuo kami ng mga graph ng dalawang function na y= a*x^2 (parabola) at y=-b*x-c (tuwid na linya). Naghahanap ng mga intersection point. Ang abscissas ng mga intersection point ang magiging solusyon ng equation.

Ipakita natin sa isang halimbawa: lutasin ang equation na x^2-2*x-3=0.

Ibahin natin ito sa x^2 =2*x+3. Bumubuo kami ng mga graph ng mga function y= x^2 at y=2*x+3 sa isang coordinate system.

Ang mga graph ay nagsalubong sa dalawang punto. Ang kanilang mga abscissas ang magiging ugat ng ating equation.

Solusyon sa formula

Upang maging kapani-paniwala, sinusuri namin ang solusyon na ito nang analytical. Malutas namin ang quadratic equation sa pamamagitan ng formula:

D = 4-4*1*(-3) = 16.

X1= (2+4)/2*1 = 3.

X2 = (2-4)/2*1 = -1.

Ibig sabihin, magkatugma ang mga solusyon.

Ang graphical na paraan ng paglutas ng mga equation ay mayroon ding disbentaha nito, sa tulong nito ay hindi laging posible na makakuha ng eksaktong solusyon ng equation. Subukan nating lutasin ang equation na x^2=3+x.

Bumuo tayo ng parabola y=x^2 at isang tuwid na linya y=3+x sa parehong coordinate system.

Muli ay nakakuha ng katulad na larawan. Ang isang linya at isang parabola ay nagsalubong sa dalawang punto. Ngunit hindi namin masasabi ang eksaktong mga halaga ng abscissas ng mga puntong ito, mga tinatayang lamang: x≈-1.3 x≈2.3.

Kung nasiyahan tayo sa mga sagot ng gayong katumpakan, maaari nating gamitin ang pamamaraang ito, ngunit bihirang mangyari ito. Karaniwan ang mga eksaktong solusyon ay kailangan. Samakatuwid, ang graphical na paraan ay bihirang ginagamit, at higit sa lahat upang suriin ang mga umiiral na solusyon.

Kailangan mo ng tulong sa iyong pag-aaral?

Nakaraang paksa:

Pananaliksik ng mga mag-aaral sa paksa:

"Paglalapat ng isang linear function sa paglutas ng mga problema"

"Paglalapat ng Linear Function Graph sa Paglutas ng Problema"

MKOU "Bogucharskaya secondary school No. 1"

Mga gawaing pananaliksik sa matematika.

Paksa: "Paglalapat ng isang graph ng isang linear na function upang malutas ang mga problema"

7 "B" na klase
Pinuno: Fomenko Olga Mikhailovna

lungsod ng Boguchar

1. Panimula………………………………………………………………………… 2

2. Pangunahing bahagi…………………………………………………………………………3-11

2.1 Pamamaraan para sa paglutas ng mga problema sa teksto gamit ang mga linear function graph

2.2Paglutas ng mga problema sa teksto para sa paggalaw gamit ang mga graph

3. Konklusyon………………………………………………………………………… 11

4. Panitikan………………………………………………………………………….12

PANIMULA

Isinasaalang-alang ng "klase ng Algebra.7" ang mga gawain kung saan, ayon sa isang naibigay na iskedyul, kinakailangan upang sagutin ang isang bilang ng mga tanong.

Halimbawa:

№332 Ang residente ng tag-araw ay umalis sa bahay sakay ng kotse patungo sa nayon. Nagmaneho muna siya sa highway, at pagkatapos ay sa isang country road, bumagal habang ginagawa niya iyon. Ang iskedyul ng paggalaw ng residente ng tag-init ay ipinapakita sa figure. Sagutin ang mga tanong:

a) gaano katagal nagmaneho ang residente ng tag-araw sa kahabaan ng highway at kung gaano karaming kilometro ang kanyang pagmamaneho; ano ang bilis ng sasakyan sa bahaging ito ng kalsada;

b) gaano katagal nagmaneho ang residente ng tag-araw sa kalsada ng bansa at ilang kilometro ang kanyang pagmamaneho; ano ang bilis ng sasakyan sa seksyong ito;

c) gaano katagal naglakbay ang residente ng tag-araw mula sa bahay hanggang sa nayon?

Sa kurso ng paghahanap ng materyal sa paksang ito sa panitikan at sa Internet, natuklasan ko sa aking sarili na maraming pisikal, at maging ang panlipunan at pang-ekonomiyang mga phenomena at proseso ay nasa isang linear na relasyon sa mundo, ngunit nanirahan ako sa kilusan, bilang ang pinaka-pamilyar sa amin at sikat sa lahat. Sa proyekto, inilarawan ko ang mga problema sa salita at kung paano lutasin ang mga ito gamit ang mga linear function graph.

Hypothesis: sa tulong ng mga graph, hindi ka lamang makakakuha ng visual na representasyon ng mga katangian ng isang function, makilala ang mga katangian ng isang linear function at ang partikular na anyo nito, direktang proporsyonalidad, ngunit malutas din ang mga problema sa salita.

Ang layunin ng aking pananaliksik ay ang pag-aaral ng paggamit ng mga graph ng isang linear function sa paglutas ng mga problema sa teksto para sa paggalaw. Upang makamit ang mga layuning ito, ang mga sumusunod mga gawain:

Upang pag-aralan ang pamamaraan para sa paglutas ng mga problema sa teksto para sa paggalaw gamit ang mga linear function graph;

Alamin kung paano lutasin ang mga problema sa paggalaw gamit ang paraang ito;

Gumawa ng mga paghahambing na konklusyon tungkol sa mga pakinabang at disadvantages ng paglutas ng mga problema gamit ang mga linear function graph.

Layunin ng pag-aaral: linear function graph.

Paraan ng Pananaliksik:

Teoretikal (pag-aaral at pagsusuri), paghahanap ng system, praktikal.

Pangunahing bahagi.

Sa aking pananaliksik, nagpasya akong subukang magbigay ng isang graphical na interpretasyon ng mga gawain para sa paggalaw na ipinakita sa aming aklat-aralin, pagkatapos, ayon sa iskedyul, sagutin ang tanong ng gawain. Para sa gayong solusyon, kumuha ako ng mga gawain na may pare-parehong paggalaw ng rectilinear sa isang seksyon ng landas. Ito ay lumabas na maraming mga problema ang nalutas sa ganitong paraan nang mas simple kaysa sa karaniwang paraan gamit ang isang equation. Ang tanging disbentaha ng diskarteng ito ay upang tumpak na makakuha ng isang sagot sa tanong ng problema, dapat na magawa ng isa na tama na piliin ang sukat ng mga yunit ng pagsukat sa mga coordinate axes. Ang isang malaking papel sa tamang pagpili ng sukat na ito ay nilalaro ng karanasan sa paglutas. Samakatuwid, upang makabisado ang sining ng paglutas ng mga problema gamit ang mga graph, kailangan kong isaalang-alang ang mga ito sa malalaking numero.

itakda ang coordinate system sOt na may abscissa axis Ot at ang ordinate axis Os . Upang gawin ito, ayon sa kondisyon ng problema, kinakailangang piliin ang pinagmulan: ang simula ng paggalaw ng bagay o mula sa ilang mga bagay, ang isa na nagsimulang gumalaw nang mas maaga o naglakbay ng mas malaking distansya ay napili. Sa abscissa axis, markahan ang mga agwat ng oras sa mga yunit ng pagsukat nito, at sa ordinate axis, markahan ang distansya sa napiling sukat ng mga yunit ng pagsukat nito.

Ang mga punto sa coordinate plane ay dapat markahan ayon sa sukat ng gawain, at ang mga linya ay dapat na iguguhit nang tumpak. Ang katumpakan ng solusyon ng problema ay nakasalalay dito. Samakatuwid, napakahalaga na matagumpay na piliin ang sukat ng mga dibisyon sa mga coordinate axes: dapat itong mapili sa paraang mas tumpak na matukoy ang mga coordinate ng mga punto at, kung maaari, na matatagpuan sa mga nodal point, i.e. sa mga intersection ng mga dibisyon ng coordinate axes. Minsan kapaki-pakinabang na kunin bilang isang segment ng yunit sa abscissa axis ang bilang ng mga cell na isang maramihang mga kondisyon ng problema na may paggalang sa oras, at sa ordinate axis - ang bilang ng mga cell na isang maramihang mga kundisyon. ng problema tungkol sa distansya. Halimbawa, ang 12 minuto sa oras ay nangangailangan ng pagpili ng bilang ng mga cell sa multiple ng 5, dahil Ang 12 minuto ay isang ikalimang bahagi ng isang oras.

Paglutas ng mga problema sa teksto para sa paggalaw gamit ang mga graph

Sagot: 9 km.

Solusyon gamit ang equation:

x/12h. - oras mula A hanggang B

x/18h. - oras sa likod

Sagot: 9 km

Gawain 2. (Blg. 156 sa aklat-aralin ni Yu.N. Makarychev na "Algebra 7".)

Dalawang kotse ang nagmamaneho sa highway sa parehong bilis. Kung ang una ay nagdaragdag ng bilis ng 10 km / h, at ang pangalawa ay binabawasan ito ng 10 km / h, kung gayon ang una ay sasaklaw ng mas maraming sa loob ng 2 oras gaya ng pangalawa sa loob ng 3 oras. Gaano kabilis ang takbo ng mga sasakyan?

Solusyon gamit ang equation:

Hayaang x km/h ang bilis ng mga sasakyan;

(x+10) at (x-10) ayon sa pagkakasunod-sunod na bilis pagkatapos ng pagtaas at pagbaba;

2(x+10)=3(x-10)

Sagot: 50km/h

Paglutas gamit ang Linear Function Graph:

1. Itakda natin ang coordinate plane sOt na may abscissa axis Оt, kung saan minarkahan natin ang mga agwat ng oras ng paggalaw, at ang ordinate axis Os, kung saan minarkahan natin ang distansya na nilakbay ng mga sasakyan.

2. Maglagay tayo ng mga dibisyon sa isang sukat sa kahabaan ng abscissa axis - isang oras sa 5 cell (sa 1 ​​cell - 12 minuto); inilalapat namin ang mga dibisyon sa kahabaan ng y-axis, ngunit hindi tinukoy ang sukat.

3. Bumuo tayo ng isang linya ng paggalaw ng unang kotse I: ang simula ng paggalaw sa isang punto c

4. Buuin natin ang linya ng paggalaw ng pangalawang makina II: ang simula ng paggalaw sa punto na may coordinate (0; 0). Susunod, markahan namin ang isang arbitrary na punto (3;s 1) sa eroplano, dahil ang kotse na may bagong bilis ay nasa kalsada sa loob ng 3 oras.

4. Tukuyin natin ang bilis ng mga kotse v bago ito magbago. Tukuyin natin ang pagkakaiba ng mga ordinate ng mga puntong nakahiga sa mga linyang may abscissa 1 sa pamamagitan ng tanda ∆s . Ayon sa kondisyon, ang segment na ito ay tumutugma sa haba na (10 + 10) km, dahil sa isa sa kanila ang bilis ay nabawasan, at sa iba pang bilis ay tumaas ng 10 km / h. Nangangahulugan ito na ang linya ng paggalaw ng mga kotse bago baguhin ang bilis ay dapat na katumbas ng mga linya I at II at matatagpuan sa coordinate plane sa pagitan nila .. Ayon sa iskedyul, Δs \u003d 2cl. tumutugma sa 20 km, v = 5 mga cell, kaya't nalutas namin ang proporsyon v = 50 km / h.

Sagot: 50km/h.

Gawain 3

Paglutas gamit ang Linear Function Graph:

reference point ay jetty M

markahan ang puntong N (0; 162).

Sagot: 2 oras 20 minuto.

Solusyon gamit ang equation:

162 -45(x+0.75)-36x=0

162-45x - 33.75 -36x = 0

81x=128.25

2)

Sagot: 2 oras 20 minuto.

Gawain 4.

Isang siklista ang umalis sa punto A. Kasabay nito, pagkatapos niya, isang nakamotorsiklo na 16 km/h ang umalis sa punto B, na 20 km ang layo mula sa A. Naglalakbay ang siklista sa bilis na 12 km/h. Sa anong distansya mula sa punto A maaabutan ng nakamotorsiklo ang nagbibisikleta?

Paglutas gamit ang Linear Function Graph:

1. Itakda natin ang coordinate plane sOt na may abscissa axis Ot, kung saan minarkahan natin ang mga agwat ng oras ng paggalaw, at ang y-axis Os, kung saan markahan natin ang distansyang nilakbay ng nakamotorsiklo at nagbibisikleta.

2. Gumuhit tayo ng mga dibisyon sa isang sukat: kasama ang y-axis - sa 2 mga cell 8 km; kasama ang abscissa - sa 2 mga cell - 1h.

3. Bumuo tayo ng linya ng paggalaw ng isang nakamotorsiklo II: minarkahan natin ang simula ng kanyang paggalaw sa pinanggalingan ng mga coordinate B (0; 0). Ang nakamotorsiklo ay nagmamaneho sa bilis na 16 km/h, na nangangahulugan na ang tuwid na linya II ay dapat dumaan sa puntong may mga coordinate (1; 16).

4. Bumuo tayo ng linya ng paggalaw para sa isang siklista I: ang simula nito ay sa punto A (0; 20), dahil Ang punto B ay matatagpuan sa layong 20 km mula sa punto A, at siya ay umalis kasabay ng nakamotorsiklo. Ang siklista ay naglalakbay sa bilis na 12 km/h, na nangangahulugan na ang linya na dapat kong lampasan sa puntong may mga coordinate (1; 32).

5. Hanapin ang P (5; 80) - ang punto ng intersection ng mga linya I at II, na sumasalamin sa paggalaw ng isang nakamotorsiklo at isang siklista: ang ordinate nito ay magpapakita ng distansya mula sa punto B, kung saan ang nakamotorsiklo ay makakahabol sa siklista .

P(5; 80) |=s = 80, |=80 - 20 = 60(km) - ang distansya mula sa punto A kung saan maaabutan ng nakamotorsiklo ang nagbibisikleta..

Sagot: 60 km.

Solusyon gamit ang equation:

Hayaang x km ang distansya mula sa punto A hanggang sa tagpuan

x /12 oras ng siklista

(x +20)/16 oras ng nakamotorsiklo

x /12=(x +20)/16

16x=12x+240

4x=240

x=60

Sagot: 60 km

Gawain 5.

Ang distansya sa pagitan ng mga lungsod ay sakop ng isang nakamotorsiklo sa loob ng 2 oras, at ng isang siklista sa loob ng 5 oras. Ang bilis ng isang siklista ay 18 km/h na mas mababa kaysa sa bilis ng isang nakamotorsiklo. Hanapin ang bilis ng siklista at nagmomotorsiklo at ang distansya sa pagitan ng mga lungsod.

Paglutas gamit ang Linear Function Graph:

1. Itakda ang coordinate plane sOt na may abscissa axis Ot, kung saan minarkahan namin ang mga agwat ng oras ng paggalaw, at ang y-axis Os, kung saan minarkahan namin ang distansya.

2. Maglagay tayo ng dibisyon kasama ang abscissa axis sa 2 cell sa loob ng 1 oras. Iwanan natin ang distansya nang walang mga dibisyon kasama ang ordinate axis.

3. Iguhit natin ang linya ng paggalaw I ng siklista sa loob ng 5 oras at ang linya ng paggalaw ng nakamotorsiklo II sa loob ng 2 oras. Ang dulo ng parehong linya ay dapat magkaroon ng parehong ordinate.

4. Gumuhit tayo ng isang segment na may abscissa 1 sa pagitan ng mga linya I at II. Ang haba ng segment na ito ay sumasalamin sa isang distansya na katumbas ng 18 km. Mula sa pagguhit ay nakuha namin na ang 3 mga cell ay katumbas ng 18 km, na nangangahulugang mayroong 6 na km sa 1 cell.

5. Pagkatapos, ayon sa iskedyul, tinutukoy namin ang bilis ng siklista ay 12 km / h, ang bilis ng nagmomotorsiklo ay 30 km / h, ang distansya sa pagitan ng mga lungsod ay 60 km.

Solusyon gamit ang equation:

Hayaan ang x km/h ang bilis ng siklista, pagkatapos ay (x +18) km/h ang bilis ng nakamotorsiklo

2(x+18)=5x

2x +36=5x

x=12

2) 12+18=30(km/h) bilis ng rider

3) (km) distansya sa pagitan ng mga lungsod

Sagot: 12 km/h; 30 km/h; 60 km

Sagot: 60 km.

Gawain 6.

Ang isang bangka ay naglalakbay sa layong 30 km sa loob ng 3 oras at 20 minuto sa kahabaan ng ilog, at 28 km laban sa agos sa loob ng 4 na oras. Gaano kalayo tatatakpan ng bangka ang lawa sa loob ng 1.5 oras?

Paglutas gamit ang Linear Function Graph:

1. Itakda ang coordinate plane sOt na may abscissa axis Ot, kung saan minarkahan namin ang mga agwat ng oras ng paggalaw, at ang y-axis Os, kung saan minarkahan namin ang distansya na nilakbay ng bangka

2. Gumuhit tayo ng mga dibisyon sa isang sukat: kasama ang y-axis - sa dalawang mga cell 4 km; kasama ang abscissa axis - sa 6 na cell - 1 oras (sa 1 ​​cell - 10 minuto), dahil ayon sa kondisyon ng problema, ang oras ay ibinibigay sa ilang minuto.

3. Bumuo tayo ng isang linya ng paggalaw ng bangka sa tabi ng ilog I: ang simula ng linya ay nasa punto na may coordinate (0; 0). Ang bangka ay naglalayag ng 30 km sa loob ng 3 oras at 20 minuto, na nangangahulugan na ang linya ay dapat dumaan sa punto na may coordinate (; 30), dahil 3h 20min. = h.

4. Bumuo tayo ng linya ng paggalaw ng bangka laban sa agos ng ilog II: kinukuha natin ang simula ng paggalaw sa isang puntong may coordinate (0; 0). Ang bangka ay naglalayag ng 28 km sa loob ng 4 na oras, na nangangahulugan na ang linya ng paggalaw ay dapat dumaan sa punto na may coordinate (4; 28).

5. Buuin natin ang linya ng paggalaw ng bangka sa lawa: kukunin natin ang simula ng paggalaw sa punto na may coordinate (0; 0). Ang linya ng sariling paggalaw ng bangka ay kailangang matatagpuan nang pantay-pantay sa pagitan ng mga linya ng paggalaw ng bangka sa tabi ng ilog. Nangangahulugan ito na dapat nating hatiin ang segment, na binubuo ng lahat ng mga punto na may abscissa 1 sa pagitan ng mga linya ng paggalaw sa kahabaan ng ilog, sa kalahati at markahan ang gitna nito. Mula sa (0; 0) hanggang sa minarkahang puntong ito ay gumuhit tayo ng sinag, na siyang magiging linya ng paggalaw sa lawa.

6. Ayon sa kondisyon ng problema, kinakailangan upang mahanap ang distansya na nilakbay ng bangka sa lawa sa loob ng 1.5 na oras, na nangangahulugan na dapat nating matukoy sa linyang ito ang ordinate ng punto na may abscissa t \u003d 1.5, | \u003d s \u003d 12, | \u003d 12 km 1,5 oras.

Sagot: 12 km.

Solusyon gamit ang isang sistema ng mga equation:

Hayaang x km/h ang bilis ng lawa at y km/h ang bilis ng ilog

Sagot: 12 km.

Gawain 7.

Ang bangka ay naglalakbay sa kahabaan ng ilog ng 34 km kasabay ng 26 km laban sa agos. Ang sariling bilis ng bangka ay 15 km/h. Hanapin ang bilis ng ilog.

Paglutas gamit ang Linear Function Graph:

1. Itakda ang coordinate plane sOt na may abscissa axis Ot, kung saan minarkahan namin ang mga agwat ng oras ng paggalaw, at ang y-axis Os, kung saan minarkahan namin ang distansya na nilakbay ng bangka.

2. Gumuhit tayo ng mga dibisyon sa isang sukat: kasama ang y-axis - sa 1 cell 1 km; sa abscissa axis, iniiwan namin ang oras nang walang mga dibisyon.

3. Bumuo tayo ng linya I ng paggalaw ng bangka sa tabi ng ilog mula 0 km hanggang sa puntong 34 km: ang simula ng linya ay nasa puntong may coordinate (0; 0). Ang pangalawang coordinate ay (x). ; 34).

4. Bumuo tayo ng linya II ng paggalaw ng bangka laban sa agos ng ilog mula 0 km hanggang sa puntong 26 km: ang simula ng linya ay nasa puntong may coordinate (0; 0). Ang pangalawang coordinate ay ( x; 26).

5. Gumuhit ng ray III mula sa pinanggalingan (0; 0) hanggang sa gitna ng isang arbitrary na segment na binubuo ng lahat ng mga punto na may parehong abscissa sa pagitan ng dalawang linya ng paggalaw I at II. Sinasalamin ng sinag na ito ang sariling paggalaw ng bangka, bilang ang sariling bilis ng bangka ay ang arithmetic average ng 2 bilis upstream at downstream ng ilog. Sa resultang sinag, nakita namin ang isang punto na may ordinate na 15, dahil sariling bilis ng bangka ay 15 km/h. Ang abscissa ng nahanap na punto ay tumutugma sa isang dibisyon ng 1 oras.

6. Upang mahanap ang bilis ng ilog, sapat na upang mahanap ang haba ng segment na may abscissa 1 mula sa linya III hanggang sa linya II. Ang bilis ng ilog ay 2 km / h.

Sagot: 2km/h

Solusyon gamit ang equation:

Bilis ng ilog x km/h

34 / (15 + x) \u003d 26 / (15-x) Ang paglutas ng proporsyon, nakukuha namin:

Sagot: 2km/h

Konklusyon.

Mga kalamangan:

Maaaring maisulat nang maikli ang mga gawain;

Mga disadvantages:

PANITIKAN.

1. Makarychev Yu. N., Mindyuk N. G., Neshkov K. I., Suvorova S. B., Algebra: Isang aklat-aralin para sa ika-7 baitang ng mga institusyong pang-edukasyon, "Prosveshchenie", M., 2000.

2.Bulynin V., Ang paggamit ng mga graphical na pamamaraan sa paglutas ng mga problema sa teksto, pang-edukasyon at pamamaraan na pahayagan na "Mathematics", No. 14, 2005.

3. Zvavich L.I. Didactic na materyales sa algebra para sa grade 7.

Tingnan ang nilalaman ng dokumento
"ang mga salita"

Sa mga aralin sa algebra sa ika-7 baitang, nakilala ko ang paksang "Linear function. Mutual na pag-aayos ng mga graph ng mga linear na function. Natutunan ko kung paano bumuo ng mga graph ng isang linear na function, natutunan ang mga katangian nito, natutunan kung paano matukoy ang relatibong posisyon ng mga graph gamit ang mga ibinigay na formula. Napansin ko iyon sa aklat-aralin ni Yu.N. Makarychev

Isinasaalang-alang ng "klase ng Algebra.7" ang mga gawain kung saan, ayon sa isang naibigay na iskedyul, kinakailangan upang sagutin ang isang bilang ng mga tanong. Ang isang halimbawa ng naturang gawain ay ipinakita sa slide.

Ayon sa ibinigay na iskedyul, maaari itong matukoy

At mayroon akong tanong, posible bang malutas ang mga problema para sa paggalaw hindi sa pamamagitan ng mga aksyon o paggamit ng mga equation, ngunit gamitin ang mga graphics ng isang linear function para dito?

Ang hypothesis, layunin at layunin ay ipinakita sa slide

Sa aking pananaliksik, nagpasya akong subukang magbigay ng isang graphical na interpretasyon ng mga gawain para sa paggalaw na ipinakita sa aming aklat-aralin, pagkatapos, ayon sa iskedyul, sagutin ang tanong ng gawain. Para sa gayong solusyon, kumuha ako ng mga gawain na may pare-parehong paggalaw ng rectilinear sa isang seksyon ng landas.

Lumalabas na maraming problema ang nareresolba sa ganitong paraan. Ang tanging disbentaha ng diskarteng ito ay upang tumpak na makakuha ng isang sagot sa tanong ng problema, dapat na magawa ng isa na tama na piliin ang sukat ng mga yunit ng pagsukat sa mga coordinate axes. Ang isang malaking papel sa tamang pagpili ng sukat na ito ay nilalaro ng karanasan sa paglutas. Samakatuwid, upang makabisado ang sining ng paglutas ng mga problema gamit ang mga graph, kailangan kong isaalang-alang ang mga ito sa malalaking numero.

Isang pamamaraan para sa paglutas ng mga problema sa teksto gamit ang mga linear na function graph.

Upang malutas ang isang problema sa teksto gamit ang mga linear na function graph, kailangan mong:

itakda ang coordinate system Upang gawin ito, ayon sa kondisyon ng problema, kinakailangang piliin ang pinagmulan: ang simula ng paggalaw ng bagay o mula sa ilang mga bagay, ang isa na nagsimulang gumalaw nang mas maaga o naglakbay ng mas malaking distansya ay pinili . Sa abscissa axis, markahan ang mga agwat ng oras sa mga yunit ng pagsukat nito, at sa ordinate axis, markahan ang distansya sa napiling sukat ng mga yunit ng pagsukat nito.

Iguhit ang mga linya ng paggalaw ng bawat isa sa mga bagay na tinukoy sa kondisyon ng problema sa pamamagitan ng mga coordinate ng hindi bababa sa dalawang punto ng mga tuwid na linya. Karaniwan ang bilis ng isang bagay ay nagbibigay ng impormasyon tungkol sa pagdaan ng isang distansya sa isang yunit ng oras mula sa simula ng paggalaw nito. Kung ang bagay ay magsisimulang gumalaw sa ibang pagkakataon, ang panimulang punto ng paggalaw nito ay inilipat ng isang naibigay na bilang ng mga yunit sa kanan ng pinanggalingan sa kahabaan ng x-axis. Kung ang bagay ay nagsimulang gumalaw mula sa isang lugar na malayo mula sa reference point sa isang tiyak na distansya, kung gayon ang punto ng simula ng paggalaw nito ay inilipat paitaas sa kahabaan ng y-axis.

Ang punto ng pagpupulong ng ilang mga bagay sa coordinate plane ay ipinahiwatig ng intersection point ng mga linya na naglalarawan ng kanilang paggalaw, na nangangahulugang ang mga coordinate ng puntong ito ay nagbibigay ng impormasyon tungkol sa oras ng pagpupulong at ang distansya ng lugar ng pagpupulong mula sa pinanggalingan.

Ang pagkakaiba sa mga bilis ng paggalaw ng dalawang bagay ay tinutukoy ng haba ng segment, na binubuo ng lahat ng mga punto na may abscissa 1, na matatagpuan sa pagitan ng mga linya ng paggalaw ng mga bagay na ito.

Ang mga puntos sa coordinate plane ay dapat markahan ayon sa sukat ng gawain, at ang mga linya ay dapat na iguguhit nang tumpak. Ang katumpakan ng solusyon ng problema ay nakasalalay dito.

Problema 1. (Blg. 673 sa aklat-aralin ni Yu.N. Makarychev na "Algebra 7".)

Isang siklista ang naglakbay sa landas na AB sa bilis na 12 km/h. Sa pagbabalik, nakagawa siya ng bilis na 18 km / h at gumugol ng 15 minutong mas kaunti sa pagbabalik kaysa sa daan mula A hanggang B. Ilang kilometro mula A hanggang B.

Solusyon gamit ang equation:

Hayaan ang x km ang distansya mula A hanggang B.

x/12h. - oras mula A hanggang B

x/18h. - oras sa likod

Dahil mas kaunti ang ginugol niya sa pagbabalik, bubuo kami ng equation

Sagot: 9 km

Paglutas gamit ang Linear Function Graph:

1. Itinakda namin ang coordinate plane sOtc na may abscissa axis Оt, kung saan minarkahan namin ang mga agwat ng oras ng paggalaw, at ang ordinate axis Os, kung saan minarkahan namin ang distansya.

2. Gumuhit tayo ng mga dibisyon sa isang sukat: kasama ang y-axis - sa isang cell 3 km; kasama ang abscissa axis - isang oras sa 4 na mga cell (sa 1 ​​cell - 15 min).

3. Bumuo tayo ng isang linya ng paggalaw doon: markahan ang simula ng paggalaw ng isang tuldok (0; 0). Ang siklista ay naglalakbay sa bilis na 12 km/h, na nangangahulugan na ang tuwid na linya ay dapat dumaan sa punto (1; 12).

4. Bumuo tayo ng isang linya ng paggalaw pabalik: markahan ang dulo ng linya ng isang tuldok (; 0), dahil ang siklista ay gumugol ng 15 minutong mas kaunti sa paglalakbay pabalik. Siya ay nagmamaneho sa bilis na 18km/h, na nangangahulugan na ang susunod na punto ng linya ay may coordinate (;18).

5. Tandaan (; 9) - ang punto ng intersection ng mga linya: ang ordinate nito ay magpapakita ng distansya: s = 9

Sagot: 9 km.

Gawain 2 (Blg. 757 sa aklat-aralin ni Yu.N. Makarychev na "Algebra 7")

Ang distansya sa pagitan ng mga pier M at N ay 162 km. Isang motor na barko ang umalis mula sa pier M sa bilis na 45 km/h. Pagkaraan ng 45 minuto, isa pang motor na barko ang umalis mula sa pier N patungo sa kanya, ang bilis nito ay 36 km/h. Ilang oras pagkatapos ng pag-alis ng unang barko sila magkikita?

Solusyon gamit ang equation:

Hayaang magkaroon ng pulong sa loob ng x oras

162 -45(x+0.75)-36x=0

162-45x - 33.75 -36x = 0

81x=128.25

2)

Sagot: 2 oras 20 minuto.

Paglutas gamit ang Linear Function Graph:

1. Itakda ang coordinate plane sOt sa abscissa axis Ot, kung saan minarkahan namin ang mga agwat ng oras ng paggalaw, at ang y-axis Os, kung saan

tandaan ang distansya mula sa pier M hanggang pier N, katumbas ng 162 km. ang simula

reference point ay jetty M

2. Gumuhit tayo ng mga dibisyon sa isang sukat: kasama ang y-axis - sa dalawang cell na 18 km; kasama ang abscissa axis - isang oras sa 6 na mga cell (sa 1 ​​cell - 10 min.), mula noong Tinutukoy ng kondisyon ng gawain ang oras sa minuto.

markahan ang puntong N (0; 162).

3. Buuin natin ang linya ng paggalaw ng unang barko I: ang simula ng paggalaw nito ay nasa punto na may mga coordinate (0; 0). Ang unang barko ay naglayag sa bilis na 45 km / h, na nangangahulugang ang tuwid na linya ay dapat dumaan sa punto na may mga coordinate (1; 45).

4. Buuin natin ang linya ng paggalaw ng pangalawang barko II: ang simula ng paggalaw ay nasa punto c

mga coordinate (; 162), mula noong umalis siya sa puntong N, 162 km ang layo mula sa M, 45 min. mamaya kaysa sa una, at 45 min. \u003d h. Ang pangalawang barko ay naglayag sa bilis na 36 km / h, na nangangahulugang ang tuwid na linya ay dapat dumaan sa punto (; 126), dahil ang pangalawang barko ay umalis sa direksyon ng punto M: 162 - 36 \u003d 126 (km).

5. Ang punto ng intersection ng mga linya I at II ay punto A (; 108). Ang abscissa ng punto ay nagpapakita ng oras pagkatapos nito, pagkatapos ng pag-alis ng unang barko, nakilala nila: t =, |=h = 2h20min. - ang oras ng pagpupulong ng dalawang barko pagkatapos ng pag-alis ng unang barko.

Sagot: 2 oras 20 minuto.

Konklusyon.

Sa pagtatapos ng pag-aaral, natukoy ko ang mga pakinabang at disadvantage ng paglutas ng mga problema sa grapikong paraan.

Mga kalamangan:

Maaaring maisulat nang maikli ang mga gawain;

Ito ay medyo madali upang gumana sa mga maliliit na numero.

Mga disadvantages:

Mahirap magtrabaho sa malalaking numero.

Tingnan ang nilalaman ng pagtatanghal
"proyekto"