Gumuhit ng polygon sa may checkered na papel. Halimbawa, tulad ng ipinapakita sa Figure 1.

Subukan nating kalkulahin ang lawak nito ngayon. Paano ito gagawin? Marahil ang pinakamadaling paraan ay hatiin ito sa mga right-angled na tatsulok at parihaba, ang mga lugar kung saan madali nang kalkulahin at idagdag ang mga resulta. Ang paraan na ginamit ko ay simple, ngunit napakahirap, at bukod pa, hindi ito angkop para sa lahat ng polygons.

Isaalang-alang ang isang di-degenerate na simpleng integer polygon (iyon ay, ito ay konektado - alinman sa dalawa sa mga punto nito ay maaaring konektado sa pamamagitan ng isang tuluy-tuloy na curve na ganap na nakapaloob dito, at lahat ng mga vertices nito ay may mga integer na coordinate, ang hangganan nito ay isang konektadong polyline na walang mga intersection sa sarili, at mayroon itong non-zero square). Upang kalkulahin ang lugar ng naturang polygon, maaari mong gamitin ang sumusunod na theorem:

Teorama ni Pick. Hayaan ang bilang ng mga integer na puntos sa loob ng polygon, ang bilang ng mga integer na puntos sa hangganan nito, at ang lugar nito. Pagkatapos Ang formula ni Pick:

Halimbawa. Para sa polygon sa Figure 1 (mga dilaw na tuldok), (mga asul na tuldok, huwag kalimutan ang mga vertices!), Kaya mga square unit.

Katibayan ng Teorama ng Pick. Una, tandaan na ang formula ng Pick ay totoo para sa square unit. Sa katunayan, sa kasong ito mayroon tayo

Isaalang-alang ang isang parihaba na may mga gilid na nakahiga sa mga linya ng sala-sala. Hayaang ang haba ng mga gilid nito ay katumbas ng at. Mayroon kaming sa kasong ito at, ayon sa formula ng Pick,

Isaalang-alang ngayon ang isang kanang tatsulok na may mga binti na nakahiga sa mga coordinate axes. Ang ganitong tatsulok ay nakuha mula sa isang rektanggulo na may mga gilid at, isinasaalang-alang sa nakaraang kaso, sa pamamagitan ng pagputol nito nang pahilis. Hayaang nakahiga ang mga integer na puntos sa dayagonal. Pagkatapos para sa kasong ito, nakukuha natin iyon

Ngayon isaalang-alang ang isang arbitrary na tatsulok. Maaari itong makuha sa pamamagitan ng pagputol ng ilang mga right-angled na triangles at, posibleng, isang parihaba mula sa isang parihaba (tingnan ang mga figure 2 at 3). Dahil ang formula ng Pick ay totoo para sa parehong isang parihaba at isang right-angled na tatsulok, nakuha namin na ito ay magiging totoo din para sa isang arbitrary na tatsulok.

Ito ay nananatiling gawin ang huling hakbang: lumipat mula sa mga tatsulok patungo sa mga polygon. Anumang polygon ay maaaring hatiin sa mga tatsulok (halimbawa, sa pamamagitan ng mga dayagonal). Samakatuwid, kailangan lang nating patunayan na kapag nagdaragdag ng anumang tatsulok sa isang arbitrary na polygon, ang formula ng Pick ay nananatiling totoo.

Hayaan ang polygon at ang tatsulok na magkaroon ng isang karaniwang panig. Ipagpalagay na ang formula ng Pick ay wasto para sa, at papatunayan namin na ito ay magiging totoo din para sa polygon na nakuha mula sa karagdagan. Dahil at may isang karaniwang panig, ang lahat ng mga integer point na nakahiga sa gilid na ito, maliban sa dalawang vertices, ay nagiging mga panloob na punto ng bagong polygon. Ang mga vertices ay magiging mga boundary point. Tukuyin natin ang bilang ng mga karaniwang puntos sa pamamagitan ng at makuha

Ang bilang ng mga interior integer point ng bagong polygon,

Ang bilang ng mga boundary point para sa bagong polygon.

Mula sa mga pagkakapantay-pantay na ito ay nakukuha natin

Dahil ipinapalagay namin na ang teorama ay totoo para sa at para sa hiwalay, kung gayon

Kaya, ang pormula ng Pick ay napatunayan.

Ang formula na ito ay natuklasan ng Austrian mathematician na si Peak Georg Aleksandrov (1859 - 1943) noong 1899. Bilang karagdagan sa formula na ito, natuklasan ni Georg Pick ang Pick, Pick - Julia, Pick - Nevalina theorems, pinatunayan ang Schwarz - Pick inequality. AT Appendix 1 makikita mo ang mga hindi karaniwang gawain na aking isinasaalang-alang para sa paglalapat ng formula ng Pick.

Peak Formula

1. Panimula

2. Peak formula. Patunay I.

Patunay II.

Ang patunay ni Sh.

3. Mga gawain.

4. Ang formula para sa lugar ng isang polygon sa mga tuntunin ng mga coordinate ng vertices.

5. Mga gawain.

6. Panitikan

Peak na formula.

1. Panimula.

Humugot tayo ng karunungan sa kasaysayan,

sa tula - talino,

sa matematika - pananaw.

F. Bacon

Ang balangkas ay magbubukas sa isang regular na piraso ng checkered na papel.

Ang mga linya na dumaraan sa mga gilid ng mga cell ay bumubuo ng isang grid, at ang mga vertices ng mga cell ay ang mga node ng grid na ito. Gumuhit tayo ng polygon sa sheet na may mga vertex sa mga node at hanapin ang lugar nito.

Maaari mong hanapin ito sa iba't ibang paraan. Halimbawa, maaari mong gupitin ang isang polygon sa medyo simpleng mga hugis, hanapin ang kanilang mga lugar at idagdag ang mga ito.

Ngunit narito tayo para sa maraming problema. Ang pigura ay madaling masira sa mga parihaba, trapezoid, at tatsulok, at ang lugar nito ay kinakalkula nang walang kahirap-hirap.

Kahit na ang polygon ay mukhang sapat na simple, kakailanganin ng maraming trabaho upang makalkula ang lugar nito. Paano kung ang polygon ay mukhang mas maganda? Lumalabas na ang mga lugar ng mga polygon na ang mga vertice ay matatagpuan sa mga node ng grid ay maaaring kalkulahin nang mas simple: mayroong isang formula na nauugnay ang kanilang lugar sa bilang ng mga node na nakahiga sa loob at sa hangganan ng polygon. Ang kahanga-hanga at simpleng formula na ito ay tinatawag na Pick's formula.

2. Peak formula.

Ang mga vertices ng isang polygon (hindi kinakailangang convex) ay matatagpuan sa mga node ng isang integer na sala-sala. Sa loob nito ay matatagpuan ang mga B node ng sala-sala, at sa hangganan ng mga G node. Patunayan natin na ang lugar nito ay B + – 1 (pormula ng Peak).

Patunay I.

Isaalang-alang ang isang polygon na ang mga vertice ay nasa mga node ng isang integer na sala-sala, iyon ay, mayroon silang mga integer na coordinate.

Hinahati namin ang polygon sa mga tatsulok na may mga vertice sa mga node ng sala-sala, na hindi naglalaman ng mga node sa loob o sa mga gilid.

Ipahiwatig:

n ay ang bilang ng mga gilid ng polygon,

m ay ang bilang ng mga tatsulok na may mga vertice sa mga node ng sala-sala na hindi naglalaman ng mga node sa loob o sa mga gilid,

Ang B ay ang bilang ng mga node sa loob ng polygon,

Ang Г ay ang bilang ng mga node sa mga gilid, kabilang ang mga vertex.

Ang mga lugar ng lahat ng mga tatsulok na ito ay pareho at pantay.

Samakatuwid, ang lugar ng polygon ay
.

180 0 m .

Ngayon, hanapin natin ang kabuuan na ito sa ibang paraan.

Ang kabuuan ng mga anggulo na may vertex sa anumang panloob na node ay 360 0 .

Pagkatapos ang kabuuan ng mga anggulo na may mga vertice sa lahat ng mga panloob na node ay katumbas ng 360 0 V.

Ang kabuuang kabuuan ng mga anggulo sa mga node sa mga gilid, ngunit hindi sa mga vertices, ay 180 0 (G - n).

Ang kabuuan ng mga anggulo sa vertices ng polygon ay 180 0 ( n – 2) .

Ang kabuuang kabuuan ng mga anggulo ng lahat ng mga tatsulok ay 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

Kaya 1800 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,

180 0 m\u003d 360 0 V + 180 0 G– 360 0,

= B + – 1 ,

kung saan nakuha namin ang expression para sa lugar S ng polygon:

S= B + – 1 ,

kilala bilang formula ng Pick.

Sa figure: V = 24, D = 9, samakatuwid,S = 24 + – 1 = 27,5.

Hanapin ang lugar ng unang polygon gamit ang Peak formula:

B = 28 (berdeng tuldok);

D = 20 (asul na tuldok).

Nakukuha namin, S =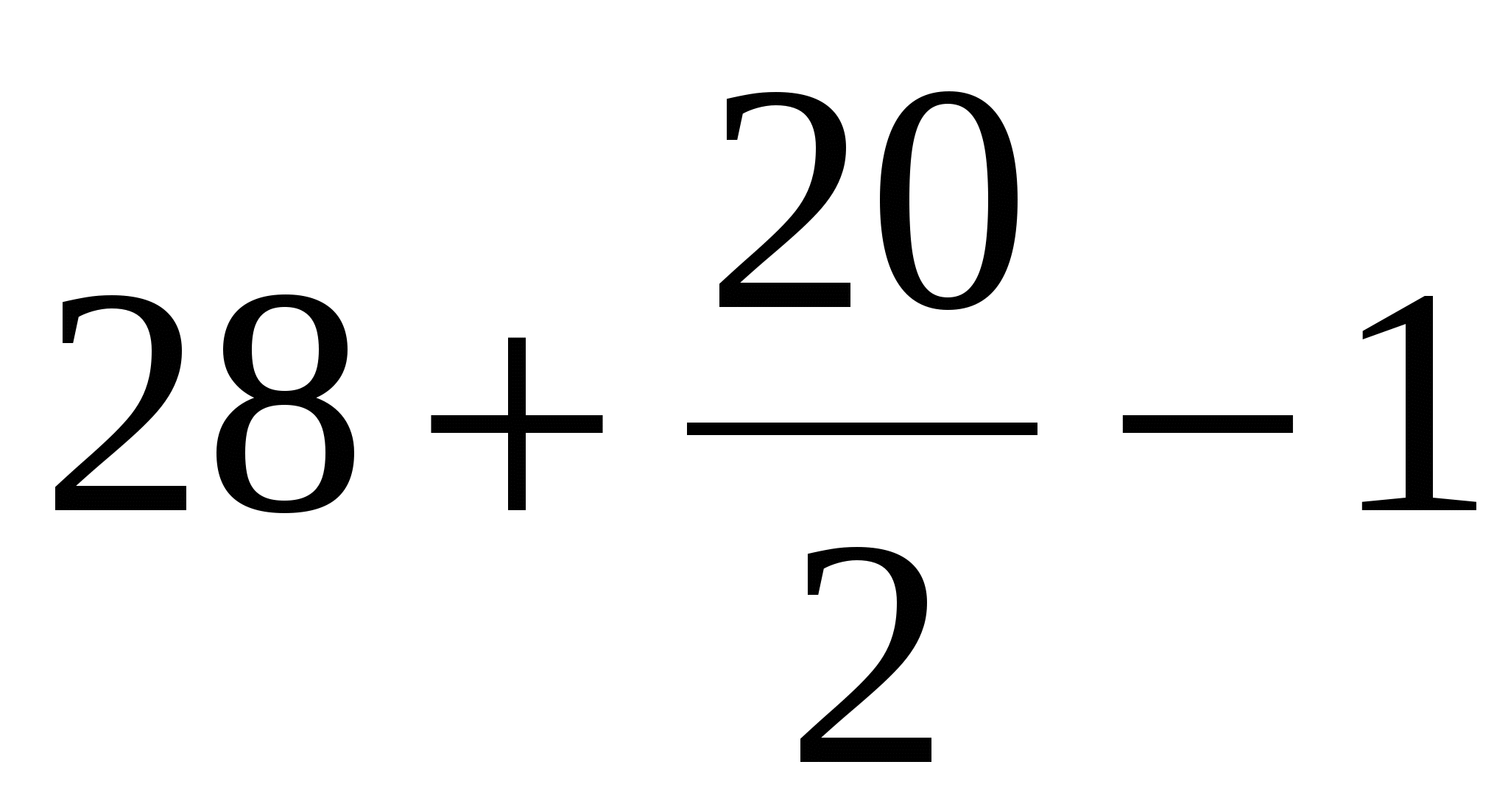
= 37 square units

Patunay II.

Sa bawat polygon M na may mga vertice sa mga node ng isang integer na sala-sala ay itinalaga namin ang bilang na f (M) =
, kung saan ang summation ay nasa lahat ng lattice node na kabilang sa M, at ang anggulo ay tinukoy bilang mga sumusunod: =
para sa isang panloob na punto ng isang polygon, =
para sa isang boundary point maliban sa isang vertex, at – anggulo sa vertex, kung ang ibinigay na node ay isang vertex. Madaling makita na f (M) =
+
= B + – 1. Ito ay nananatiling suriin na ang numero f (M) ay katumbas ng lugar ng polygon M.

Hayaang putulin ang polygon M sa mga polygon M 1 at M 2 na may mga vertices sa mga node ng sala-sala. Pagkatapos f(M) = f(M 1) + f(M 2), dahil para sa bawat node ang mga anggulo ay nagdaragdag. Samakatuwid, kung ang formula ng Pick ay totoo para sa dalawa sa mga polygon na M, M 1 at M 2 , kung gayon ito ay totoo para sa pangatlo.

Kung ang M ay isang parihaba na may mga gilid p at q, nakadirekta sa mga linya ng sala-sala, pagkatapos

f (M) = (p – 1)(q – 1) +
= pq.

Sa kasong ito, valid ang formula ng Pick. Sa pamamagitan ng pagputol ng rektanggulo M nang pahilis sa mga tatsulok na M 1 at M 2 at gamit ang katotohanan na f (M) = f (M 1) + f (M 2) at f (M 1) = f (M 2), ito ay madali. upang patunayan ang bisa ng formula ng Pick para sa anumang kanang tatsulok na may mga binti na nakadirekta sa mga linya ng sala-sala. Sa pamamagitan ng pagputol ng ilang tulad na tatsulok mula sa isang parihaba, anumang tatsulok ay maaaring makuha.

Upang makumpleto ang patunay ng formula ng Pick, nananatili itong tandaan na ang anumang polygon ay maaaring gupitin sa mga tatsulok sa pamamagitan ng mga di-intersecting na diagonal.

Ang patunay ni Sh.

Ang koneksyon sa pagitan ng lugar ng isang figure at ang bilang ng mga node na nahuhulog sa figure na ito ay lalong malinaw sa kaso ng isang rektanggulo.

Hayaan A B C D- isang parihaba na may mga vertice sa mga node at gilid na dumadaan sa mga linya ng grid.

Tukuyin ng AT ang bilang ng mga node na nakahiga sa loob ng parihaba, at sa pamamagitan ng G ay ang bilang ng mga node sa hangganan nito. Ilipat ang grid kalahating cell sa kanan at kalahating cell pababa.

Pagkatapos ang teritoryo ng rektanggulo ay maaaring "ibinahagi" sa pagitan ng mga node tulad ng sumusunod: bawat isa AT"Kinokontrol" ng mga node ang buong cell ng shifted grid, bawat isa G- 4 na hangganan na hindi sulok na mga node - kalahati ng cell, at bawat isa sa mga sulok na punto - isang quarter ng cell. Samakatuwid, ang lugar ng rektanggulo S ay

Kaya, para sa mga parihaba na may mga vertice sa mga node at gilid na sumasabay sa mga linya ng grid, naitatag namin ang formula

Patunayan natin na ang formula na ito ay totoo hindi lamang para sa mga parihaba, kundi pati na rin para sa mga arbitrary na polygon na may mga vertice sa mga grid node.

Tukuyin ng S m polygon areaM na may mga vertex sa mga node, at sa pamamagitan ngP m - halaga
, saanAT m ay ang bilang ng mga node sa loobM, a G m ay ang bilang ng mga node sa hangganan. Pagkatapos ay ang Pick formula ay maaaring isulat bilang
.

Hinahati namin ang patunay ng formula sa ilang hakbang.

Hakbang 1.

Kung polygonM na may mga vertice sa mga grid node na pinutol sa 2 polygonsM 1 at M 2 , mayroon ding mga vertices lamang sa mga grid node, kung gayon
. Hayaan ang polygonM gupitin sa mga polygonM 1 at M 2 na may mga vertice sa mga node sa pamamagitan ng isang segment AB. Lahat ng mga node, maliban sa mga nahuhulog sa segmentAB, magbigay ng parehong kontribusyon sa kaliwa at kanang bahagi ng formula. Isaalang-alang ang mga node na nakahiga sa segment AB.

Kung ang naturang node ay nasa pagitan ng A at B (halimbawa, C), pagkatapos ay para sa isang polygonM ito ay panloob, at para sa mga polygonM 1 at M 2 - hangganan. Samakatuwid, ang kanyang kontribusyon saP m katumbas ng 1, at sa bawat isa sa mga expression
at
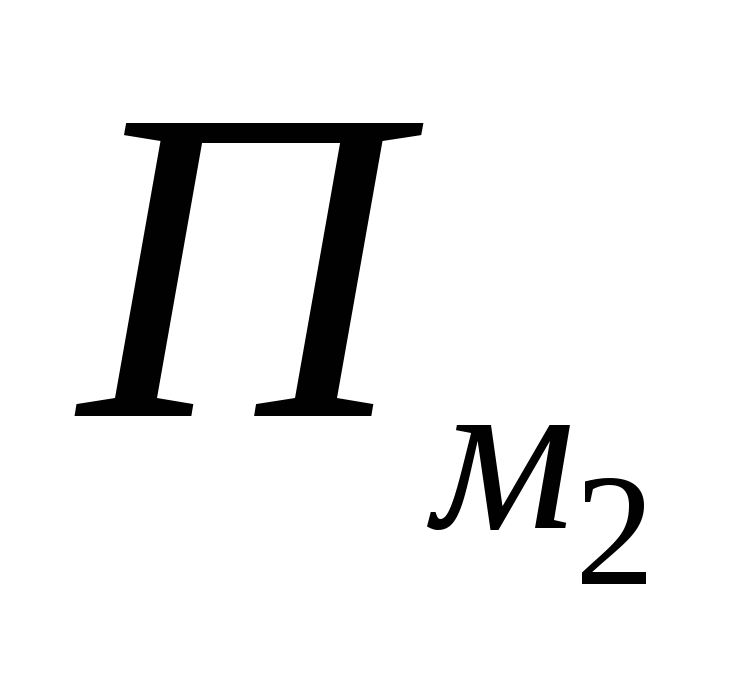– 0.5 bawat isa, iyon ay, ang mga kontribusyon ng naturang node saP m at
ay pantay-pantay.

Isaalang-alang ang mga node A at B. Pareho silang hangganan para sa M, at para sa M 1 , M 2 .

Samakatuwid, ang kontribusyon ng bawat isa sa mga node na ito saP m ay 0.5 a
- yunit. Nangangahulugan ito na ang kabuuang kontribusyon ng mga node A at B saP m katumbas ng 1, na 1 mas mababa sa kanilang kontribusyon sa
. Pero
, isang .

Mula sa kabuuang "kontribusyon" ng lahat ng node P m 1 ay ibinabawas sa
2 ay ibinabawas, at binabayaran nito ang pagkakaiba sa mga kontribusyon ng mga node A at B.

Kaya,
.

Hakbang 2

Kung polygon M na may mga vertice sa mga grid node na pinutol sa dalawang polygon M 1 at M 2 (kasama rin ang mga vertices sa mga node) at ang formula ay totoo para sa ilang dalawang polygon MM 1 , M 2 , pagkatapos ay totoo rin ito para sa ikatlong polygon.

Hayaan, halimbawa, ito ay totoo para saM 1 at M 2 , i.e
. Pagkatapos (sa unang hakbang), ngunit sa unang hakbang), ang huling expression ay katumbas ngP m , at pagkakapantay-pantay
at mayroong formula ng Pick.

Hakbang 3

Patunayan natin ang formula ng Pick para sa isang tamang tatsulok na may mga vertex sa mga grid node at mga binti na nakahiga sa mga linya ng grid.

Tatsulok ABC bumuo sa isang parihaba A B C D .

Para sa mga parihaba, tama ang formula ng Pick: S A B C D = P A B C D . Ayon sa unang hakbang P A B C D = P ABC + P ACD , P ABC = P ACD , kaya P A B C D = 2P ABC . Pero S A B C D = 2 S ABC . Kaya S ABC = P ABC .

Hakbang 4

Tama ang formula ng Pick para sa isang arbitrary na tatsulok na may mga vertex sa mga grid node.

Ang pagkakaroon ng pagsusuri sa figure, madaling maunawaan: ang anumang naturang tatsulok ay maaaring makuha sa pamamagitan ng "pagputol" mula sa ilang parihaba na may mga gilid na tumatakbo kasama ang mga linya ng grid, maraming mga parihaba at mga tatsulok na may tamang anggulo na may mga binti sa mga linya ng grid. At dahil totoo ang formula ng Pick para sa mga parihaba at right-angled na tatsulok, kung gayon (tandaan ang hakbang 2) totoo rin ito para sa orihinal na tatsulok.

Napatunayan namin na kung ang isang polygon ay maaaring gupitin sa mga tatsulok na may mga vertex sa mga node ng grid, kung gayon ang formula ng Pick ay totoo para dito.

3. Mga gawain.

Hanapin ang lugar ng mga figure:

1
.

B=9

G = 4

B=9

G = 5

Pagkalkula ng lugar ng isang figure.

Pumili ng paraan

Ang gawain ng isang mag-aaral ng klase 5B MBOU sekundaryong paaralan No. 23 sa Irkutsk

Balsukova Alexandra

Pinuno: Khodyreva T.G.

2014

Pagkalkula ng lugar ng isang figure. Pumili ng paraan

Layunin ng pag-aaral : mga gawain sa checkered na papel

Paksa ng pag-aaral : mga problema para sa pagkalkula ng lugar ng isang polygon sa checkered na papel, mga pamamaraan at pamamaraan para sa paglutas ng mga ito.

Mga pamamaraan ng pananaliksik Mga keyword: paghahambing, paglalahat, pagkakatulad, pag-aaral ng literatura at mga mapagkukunan sa Internet, pagsusuri ng impormasyon.

Layunin ng pag-aaral:

piliin ang pangunahing, kawili-wili, naiintindihan na impormasyon

Suriin at ayusin ang impormasyong natanggap

Maghanap ng iba't ibang pamamaraan at pamamaraan para sa paglutas ng mga problema sa checkered na papel

suriin ang mga formula para sa pagkalkula ng mga lugar ng mga geometric na hugis gamit ang Peak formula

Gumawa ng isang elektronikong presentasyon ng gawain upang ipakita ang nakolektang materyal

Ang geometry ay ang pinakamakapangyarihang tool para sa pagpipino ng ating mga kakayahan sa pag-iisip at nagbibigay-daan sa atin na makapag-isip at mangatuwiran nang tama.

(G. Galileo)

Kaugnayan ng paksa

Ang hilig sa matematika ay madalas na nagsisimula sa pag-iisip tungkol sa isang problema. Kaya, kapag pinag-aaralan ang paksang "Mga Lugar ng polygons", ang tanong ay lumitaw kung mayroong mga gawain na naiiba sa mga gawain na isinasaalang-alang sa aklat-aralin. Kasama sa mga naturang gawain ang mga gawain sa checkered na papel. Ano ang kakaiba ng mga naturang problema, mayroon bang mga espesyal na pamamaraan at pamamaraan para sa paglutas ng mga problema sa checkered na papel. Sa isang klase sa matematika, ipinakilala sa amin ng guro ang isang kawili-wiling paraan para sa pagkalkula ng mga polygon. Nagsimula akong mag-aral ng panitikan, mga mapagkukunan sa Internet sa paksang ito. Tila ang mga kamangha-manghang bagay ay matatagpuan sa isang checkered na eroplano, iyon ay, sa isang walang katapusang piraso ng papel, na may linya sa magkatulad na mga parisukat. Lumalabas na ang mga gawain na nauugnay sa checkered na papel ay medyo magkakaibang. Natutunan ko kung paano kalkulahin ang mga lugar ng mga polygon na iginuhit sa isang checkered na piraso ng papel. Para sa maraming mga gawain sa papel sa isang hawla walang pangkalahatang tuntunin para sa paglutas, mga tiyak na pamamaraan at pamamaraan. Ito ang kanilang pag-aari na tumutukoy sa kanilang halaga para sa pag-unlad ng hindi isang tiyak na kasanayan sa edukasyon o kasanayan, ngunit sa pangkalahatan ang kakayahang mag-isip, magmuni-muni, mag-analisa, maghanap ng mga pagkakatulad, iyon ay, ang mga gawaing ito ay bumuo ng mga kasanayan sa pag-iisip sa kanilang pinakamalawak na kahulugan.

At nalaman ko rin na ang mga naturang gawain ay isinasaalang-alang sa kontrol at pagsukat ng mga materyales ng GIA at ng Pinag-isang Estado na Pagsusuri. Samakatuwid, isinasaalang-alang ko ang pag-aaral ng materyal na ito na kapaki-pakinabang para sa aplikasyon nito hindi lamang sa karagdagang proseso ng edukasyon, kundi pati na rin para sa paglutas ng mga hindi karaniwang problema sa Olympiad.

2.Ang konsepto ng lugar

parisukat- numerical na katangian ng isang two-dimensional geometric figure, na nagpapakita ng laki ng figure na ito. Sa kasaysayan, tinawag ang pagkalkula ng lugar . Ang pigura na may lawak ay tinatawag parisukat .

Ang lugar ng isang patag na pigura sa mga tuntunin ng geometry

1. parisukat- ang sukat ng isang flat figure na may kaugnayan sa karaniwang figure, na isang parisukat na may gilid na katumbas ng isang haba.

2. parisukat- isang numerical na katangian na iniuugnay sa mga flat figure ng isang partikular na klase (halimbawa, polygons). Ang lugar ng isang parisukat na may gilid na katumbas ng isang yunit ng haba, kinuha katumbas ng isang yunit ng lugar

3. parisukat- isang positibong halaga, ang numerical na halaga nito ay may mga sumusunod na katangian:

 Ang mga pantay na numero ay may pantay na lugar;

 Kung ang isang figure ay nahahati sa mga bahagi na simpleng figure (iyon ay, ang mga maaaring nahahati sa isang may hangganan na bilang ng mga flat triangle), kung gayon ang lugar ng figure na ito ay katumbas ng kabuuan ng mga lugar nito. mga bahagi;

 Ang lugar ng isang parisukat na may gilid na katumbas ng yunit ng pagsukat ay katumbas ng isa.

Kaya, maaari nating tapusin na ang lugar ay hindi isang tiyak na halaga, ngunit nagbibigay lamang ng ilang kondisyon na katangian ng isang flat figure. Upang mahanap ang lugar ng isang di-makatwirang figure, kinakailangan upang matukoy kung gaano karaming mga parisukat na may gilid na katumbas ng isang haba, naglalaman ito. Halimbawa, kumuha tayo ng isang parihaba kung saan ang isang parisukat na sentimetro ay magkasya nang eksaktong 6 na beses. Nangangahulugan ito na ang lugar ng parihaba ay 6 cm2.

Ang pagpili ng lugar ng isang parisukat na may gilid na katumbas ng yunit ng pagsukat bilang pinakamababang yunit ng pagsukat para sa lahat ng mga lugar ay hindi sinasadya. Ito ang resulta ng isang kasunduan sa pagitan ng mga tao na lumitaw sa kurso ng "natural" na mga siglo na gulang na pagpili. Bilang karagdagan, mayroong iba pang mga panukala para sa isang yunit ng panukala. Kaya, halimbawa, iminungkahi na kunin ang lugar ng isang equilateral triangle bilang isang unit (i.e., anumang flat figure ay maaaring katawanin bilang isang "sum" ng isang tiyak na bilang ng equilateral triangles), na hahantong sa isang pagbabago sa numerical na representasyon ng mga lugar.

Kaya, ang mga formula para sa pagkalkula ng mga lugar ay lumitaw sa matematika at hindi agad natanto ng isang tao - ito maraming mga siyentipiko na naninirahan sa iba't ibang panahon at iba't ibang bansa. (Ang mga maling formula ay hindi nakahanap ng lugar sa agham at napunta sa limot). Ang mga tunay na pormula ay dinagdagan, itinuwid at pinatunayan sa loob ng libu-libong taon, hanggang sa maabot nila tayo sa kanilang modernong anyo.

Syempre pagsukat ng lugar ay binubuo sa paghahambing ng lugar ng isang naibigay na figure sa lugar ng isang figure na kinuha bilang isang yunit ng pagsukat. Bilang resulta ng paghahambing, ang isang tiyak na numero ay nakuha - ang numerical na halaga ng lugar ng ibinigay na figure. Ang numerong ito ay nagpapakita kung gaano karaming beses ang lugar ng isang naibigay na figure ay mas malaki (o mas kaunti) kaysa sa lugar ng figure, na kinuha bilang isang yunit ng lugar.

T Kaya, maaari nating tapusin na ang lugar ay isang artipisyal na dami, na makasaysayang ipinakilala ng tao upang sukatin ang ilang ari-arian ng isang patag na pigura. Ang pangangailangan na magpasok ng ganoong halaga ay dahil sa lumalaking pangangailangan na malaman kung gaano kalaki ito o ang teritoryong iyon, kung gaano karaming butil ang kailangan upang maghasik ng isang patlang o kalkulahin ang lugar sa ibabaw ng sahig para sa dekorasyon ng mga pandekorasyon na tile.

Peak Formula

Upang matantya ang lugar ng isang polygon sa checkered na papel, sapat na upang kalkulahin kung gaano karaming mga cell ang sakop ng polygon na ito (kinuha namin ang lugar ng cell bilang isang yunit). Mas tiyak, kungS ay ang lugar ng polygon, ang B ay ang bilang ng mga cell na ganap na nasa loob ng polygon, at ang G ay ang bilang ng mga cell na may panloob. Isasaalang-alang lamang namin ang gayong mga polygon, ang lahat ng mga vertices na kung saan ay nasa mga node ng checkered na papel - sa mga kung saan ang mga linya ng grid ng polygon ay nagsalubong ng hindi bababa sa isang karaniwang punto.

Ang lugar ng anumang tatsulok na iginuhit sa checkered na papel ay madaling makalkula sa pamamagitan ng pagrepresenta nito bilang kabuuan o pagkakaiba ng mga lugar ng right-angled triangles at rectangles na ang mga gilid ay sumusunod sa mga linya ng grid na dumadaan sa mga vertices ng iginuhit na tatsulok.

Upang kalkulahin ang lugar ng naturang polygon, maaari mong gamitin ang sumusunod na theorem:

Teorama . Hayaan - ang bilang ng mga integer point sa loob ng polygon, - ang bilang ng mga integer na puntos sa hangganan nito, - ang lugar nito. PagkataposAng formula ni Pick:

Halimbawa. Para sa polygon sa figureL = 7 (mga pulang tuldok), 9 (mga berdeng tuldok), kayaS = 7+ 9/2 -1 = 10,5 square units.

Teorama ni Pick- klasikong resulta at .

Ang lugar ng isang tatsulok na may mga vertice sa mga node at walang mga node sa loob o sa mga gilid (maliban sa mga vertices) ay katumbas ng 1/2. Itong katotohanan.

3. Kasaysayan

Ang pormula ni Pick ay natuklasan ng Austrian mathematician na si Georg Alexander (1859-1942) noong . Sa edad na 16, nakatapos ng pag-aaral si Georg at pumasok. Sa edad na 20 natanggap niya ang karapatang magturo ng pisika at matematika. Noong 1884 nagpunta si Peak sa sa . Doon niya nakilala ang isa pang estudyante ng Klein,. Nang maglaon, noong 1885, bumalik siya sakung saan ginugol niya ang natitirang bahagi ng kanyang pang-agham na karera.

Si Georg Pick ay kaibigan ni Einstein. Sina Pick at Einstein ay hindi lamang nagbahagi ng mga siyentipikong interes, ngunit mahilig din sa musika. Si Pick, na naglaro sa isang quartet na binubuo ng mga propesor sa unibersidad, ay nagpakilala kay Einstein sa mga pang-agham at musikal na lipunan ng Prague.

Ang bilog ng mga interes sa matematika ng Peak ay napakalawak. Sa partikular, mayroon siyang higit sa 50 siyentipikong papel. Ang theorem ni Pick, na natuklasan niya noong 1899, ay malawak na kilala para sa pagkalkula ng lugar ng isang polygon. Sa Alemanya, ang teorama na ito ay kasama sa mga aklat-aralin sa paaralan.

4.Mga aplikasyon ng formula ng Pick

Ang Pick formula ay ginagamit hindi lamang upang kalkulahin ang mga lugar ng polygons, ngunit din upang malutas ang maraming mga problema sa antas ng Olympiad.

Ilang halimbawa ng paggamit ng formula ng Pick kapag nilulutas ang mga problema:

1) Ang hari ng chess ay naglibot sa board ng 8 × 8 na mga cell, na binisita ang bawat isa

eksaktong isang beses at sa huling paglipat ay bumalik sa orihinal

patlang. Isang putol na linya na kumukonekta sa serye sa mga sentro ng mga patlang na

ang hari ay lumipas, walang sariling intersection. Anong area pwede

limitahan itong sirang linya? (Ang gilid ng cell ay 1.)

Kaagad itong sumusunod mula sa pormula ng Pick na ang lugar na napapaligiran ng lo-

ang mana ay 64/2 − 1 = 31; dito ang mga lattice node ay ang mga sentro 64

mga field at, sa pag-aakalang, lahat sila ay nasa hangganan ng polygon. Kaya

Kaya, kahit na mayroong maraming mga tulad ng "trajectory" ng hari, ngunit lahat ng mga ito

limitahan ang mga polygon ng pantay na lugar.

Mga gawain mula sa kontrol at pagsukat ng mga materyales ng GIA at ang Pinag-isang Estado na Pagsusuri

Gawain B3

Hanapin ang lugar ng figure na inilalarawan sa checkered na papel na may laki ng cell na 1 cm 1 cm (tingnan ang Fig.). Ibigay ang iyong sagot sa square centimeters.

4. Konklusyon

Sa proseso ng pananaliksik, nag-aral ako ng sanggunian, popular na literatura sa agham. Nalaman ko na ang problema sa paghahanap ng lugar ng polygon na may vertices sa mga node ng grid ay nagbigay inspirasyon sa Austrian mathematician Pick noong 1899 upang patunayan ang kahanga-hangang Pick formula.

Bilang resulta ng aking trabaho, pinalawak ko ang aking kaalaman sa paglutas ng mga problema sa checkered na papel, natukoy para sa aking sarili ang klasipikasyon ng mga problemang pinag-aaralan, at naging kumbinsido sa pagkakaiba-iba ng mga ito.

Natutunan ko kung paano kalkulahin ang mga lugar ng mga polygon na iginuhit sa isang checkered sheet. Ang mga itinuturing na gawain ay may ibang antas ng kahirapan - mula sa simple hanggang sa Olympiad. Ang bawat tao'y makakahanap sa kanila ng mga gawain ng isang magagawa na antas ng pagiging kumplikado, simula kung saan, magiging posible na magpatuloy sa paglutas ng mga mas mahirap.

Nakarating ako sa konklusyon na ang paksa na interesado sa akin ay medyo multifaceted, ang mga gawain sa checkered na papel ay magkakaiba, ang mga pamamaraan at pamamaraan para sa paglutas ng mga ito ay magkakaiba din. Samakatuwid, nagpasya kaming magpatuloy sa pagtatrabaho sa direksyon na ito.

5. Literatura na ginamit:

1. N. B. Vasil'ev, "Sa paligid ng pormula ng Pick," Kvant. - 1974. - Hindi. 12

2. Kokse Prasolov VV Mga Gawain sa planimetry. - M.: MTsNMO, 2006.t e r G.S.M. Panimula sa geometry. - M.: Nauka, 1966

3. Roslova L.O., Sharygin I.F. Mga sukat. - M.: Ed. "Open World", 2005.

Mga mapagkukunan sa internet:

:

Feedback sa trabaho

"Pagkalkula ng mga lugar ng mga numero ng eroplano. Piliin ang Paraan"

Ang pagsasaalang-alang sa paksang ito ay magpapataas sa aktibidad ng pag-iisip ng mag-aaral, na sa mga aralin sa geometry ay magsisimulang makita ang pagkakatugma ng pagguhit at titigil na makita ang geometry (at matematika sa pangkalahatan) bilang isang nakakainip na agham.

Sinuri ng guro sa matematika

Khodyreva Tatyana Georgievna

Mayroong isang kahanga-hangang formula na nagbibigay-daan sa iyo upang mabilang polygon area sa coordinate grid halos walang mga error. Ito ay hindi kahit isang formula, ito ay totoo teorama. Sa unang tingin, maaaring mukhang kumplikado. Ngunit ito ay sapat na upang malutas ang isang pares ng mga gawain - at mauunawaan mo kung gaano kahusay ang tampok na ito. Mauna ka na!

Magsimula tayo sa isang bagong kahulugan:

Ang coordinate stack node ay anumang punto na nasa intersection ng patayo at pahalang na mga linya ng grid na ito.

pagtatalaga:

Sa unang larawan, ang mga node ay hindi minarkahan sa lahat. Ang pangalawa ay may 4 na node. Sa wakas, sa ikatlong larawan, lahat ng 16 na node ay minarkahan.

Ano ang kinalaman nito sa problemang B5? Ang katotohanan ay ang mga vertices ng polygon sa naturang mga problema palagi humiga sa mga node ng grid. Bilang kinahinatnan, ang sumusunod na theorem ay gumagana para sa kanila:

Teorama. Isaalang-alang ang isang polygon sa isang coordinate grid na ang mga vertice ay nasa mga node ng grid na ito. Kung gayon ang lugar ng polygon ay:

kung saan ang n ay ang bilang ng mga node sa loob ng ibinigay na polygon, ang k ay ang bilang ng mga node na nasa hangganan nito (mga boundary node).

Bilang halimbawa, isaalang-alang ang isang ordinaryong tatsulok sa isang coordinate grid at subukang markahan ang panloob at hangganan na mga node.

Ang unang larawan ay nagpapakita ng isang ordinaryong tatsulok. Sa pangalawang larawan, ang mga panloob na node nito ay minarkahan, ang bilang nito ay n = 10. Sa ikatlong larawan, ang mga node na nakahiga sa hangganan ay minarkahan, mayroong k = 6 sa kanila sa kabuuan.

Marahil maraming mambabasa ang hindi nakakaunawa kung paano bilangin ang mga numero n at k. Magsimula sa mga panloob na node. Ang lahat ay malinaw dito: nagpinta kami sa ibabaw ng tatsulok gamit ang isang lapis at nakikita kung gaano karaming mga node ang may kulay.

Sa mga boundary node, medyo mas kumplikado ito. hangganan ng polygon - saradong putol na linya, na nag-intersect sa coordinate grid sa maraming punto. Ang pinakamadaling paraan ay markahan ang ilang "pagsisimula" na punto, at pagkatapos ay umikot sa iba pa.

Ang mga boundary node ay ang mga punto lamang sa polyline kung saan sila ay sabay na nagsa-intersect tatlong linya:

1. Sa totoo lang, isang putol na linya;
2. Pahalang na linya ng grid;
3. patayong linya.

Tingnan natin kung paano gumagana ang lahat sa mga totoong problema.

Gawain. Hanapin ang lugar ng isang tatsulok kung ang laki ng cell ay 1 x 1 cm:

Una, markahan natin ang mga node na nasa loob ng tatsulok, pati na rin sa hangganan nito:

Ito ay lumiliko na mayroon lamang isang panloob na node: n = 1. Mayroong anim na boundary node: tatlo ang nag-tutugma na may tatsulok na vertex, at tatlo pang nakahiga sa mga gilid. Kabuuang k = 6.

Ngayon kalkulahin namin ang lugar gamit ang formula:

Iyon lang! Nalutas ang problema.

Gawain. Hanapin ang lugar ng quadrangle na iginuhit sa checkered na papel na may cell size na 1 cm by 1 cm. Ibigay ang iyong sagot sa square centimeters.

Muli, minarkahan namin ang panloob at hangganan na mga node. Mayroong n = 2 panloob na node. Boundary node: k = 7, kung saan 4 ay vertex ng quadrilateral, at 3 pang nakahiga sa mga gilid.

Ito ay nananatiling palitan ang mga numero n at k sa pormula ng lugar:

Bigyang-pansin ang huling halimbawa. Ang problemang ito ay aktwal na iminungkahi sa diagnostic work noong 2012. Kung nagtatrabaho ka ayon sa karaniwang pamamaraan, kakailanganin mong gumawa ng maraming karagdagang mga konstruksyon. At sa pamamagitan ng paraan ng mga buhol, ang lahat ay nalutas halos pasalita.

Mahalagang tala sa mga lugar

Ngunit ang formula ay hindi lahat. Isulat muli natin ang formula nang kaunti, na dinadala ang mga termino sa kanang bahagi sa isang common denominator. Nakukuha namin:

Ang mga numero n at k ay ang bilang ng mga node, palagi silang integer. Kaya ang buong numerator ay isa ring integer. Hinahati namin ito sa 2, na nagpapahiwatig ng isang mahalagang katotohanan:

Ang lugar ay palaging ipinahayag buong bilang o fraction. Bukod dito, sa dulo ng fraction ay palaging may "limang ikasampu": 10.5; 17.5 atbp.

Kaya, ang lugar sa problema B5 ay palaging ipinapakita bilang isang integer o isang fraction ng form ***.5. Kung iba ang sagot, nangangahulugan ito na nagkamali sa isang lugar. Isaisip ito kapag kumuha ka ng tunay na pagsusulit sa matematika!

Upang gamitin ang preview ng mga presentasyon, lumikha ng isang Google account (account) at mag-sign in: https://accounts.google.com

Mga slide caption:

Nakumpleto ng isang mag-aaral ng sekondaryang paaralan No. 7 8 "A" na klase Yunosheva Ksenia Instruktor: Babina Natalya Alekseevna Salsk 2011 "Peak Formula"

Mga layunin ng gawain: Pag-alam sa pagkakaroon ng isa pa, naiiba sa kurikulum ng paaralan, pormula para sa paghahanap ng lugar ng isang lattice polygon. Mga lugar ng aplikasyon ng nais na formula.

Panimula. Ang edukasyong matematikal na natanggap sa mga paaralan ng pangkalahatang edukasyon ay isang mahalagang bahagi ng pangkalahatang edukasyon at pangkalahatang kultura ng modernong tao. Sa yugtong ito, ang sistema ng paaralan ay idinisenyo para sa labing-isang taon ng edukasyon. Ang lahat ng mga mag-aaral sa pagtatapos ng ikalabing-isang baitang ay kailangang kumuha ng Pinag-isang Pagsusulit ng Estado, na magpapakita ng antas ng kaalaman na natamo habang nag-aaral sa paaralan. Ngunit ang kurikulum ng paaralan ay hindi palaging nagbibigay ng pinaka makatwirang paraan upang malutas ang anumang mga problema. Halimbawa, kung titingnan ang resulta ng USE noong 2010, makikita na maraming estudyante ang nawalan ng puntos dahil sa gawain B6. Itinakda ko upang malaman kung paano makatipid ng oras at malutas nang tama ang problemang ito.

Gawain B6. Ang mga figure ay inilalarawan sa checkered na papel na may mga cell na may sukat na 1 cm sa 1 cm (tingnan ang figure). Hanapin ang kanilang lugar sa square centimeters.

Kaya, upang malutas pa rin ang gawaing ito, kailangan kong ilapat ang mga pormula para sa paghahanap ng lugar, na pinag-aaralan namin sa grade 8. Ngunit kakailanganin ng maraming oras, at kailangan kong sagutin ang tanong sa lalong madaling panahon, dahil ang oras para sa pagsusulit ay mahigpit na limitado. Samakatuwid, pagkatapos ng pagsasaliksik, nalaman ko na mayroong Pick's theorem, na hindi pinag-aralan sa kurikulum ng paaralan, ngunit makakatulong sa akin na makayanan ang gawain nang mas mabilis.

Sanggunian sa kasaysayan. Si Georg Alexander Pick (Agosto 10, 1859 - Hulyo 26, 1942) ay isang Austrian mathematician. Namatay siya sa kampong konsentrasyon ng Terezin. Ito ay kilala ngayon dahil sa pormula ng Pick para sa pagtukoy ng lugar ng isang sala-sala ng mga polygon. Inilathala niya ang kanyang formula sa isang papel noong 1899, naging tanyag ito nang isama ito ni Hugo Steinhaus sa isang 1969 na edisyon ng Mathematical Pictures. Nag-aral si Pick sa Unibersidad ng Vienna at natapos ang kanyang PhD noong 1880. Matapos matanggap ang kanyang titulo ng doktor, siya ay hinirang na katulong ni Ernest Mach sa Scherl-Ferdinand University sa Prague. Naging guro siya doon noong 1881. Pagkuha ng leave of absence mula sa unibersidad noong 1884, nagsimula siyang magtrabaho kasama si Felix Klein sa Unibersidad ng Leipzig. Nanatili siya sa Prague hanggang sa kanyang pagreretiro noong 1927, nang bumalik siya sa Vienna. Pinuno ni Pick ang komite sa (noon) German University of Prague na nagtalaga kay Albert Einstein na propesor ng mathematical physics noong 1911. Nahalal si Pick bilang miyembro ng Czech Academy of Sciences and Arts, ngunit pinatalsik pagkatapos ng pagkuha ng Nazi sa Prague. Pagkatapos magretiro noong 1927, bumalik si Pick sa Vienna, ang lungsod kung saan siya ipinanganak. Pagkatapos ng Anschluss, nang pumasok ang mga Nazi sa Austria noong Marso 12, 1938, bumalik si Pieck sa Prague. Noong Marso 1939, sinalakay ng mga Nazi ang Czechoslovakia. Si Georg ay ipinadala sa kampong piitan ng Terezin noong Hulyo 13, 1942. Namatay siya pagkaraan ng dalawang linggo.

Teorama ni Pick. Ang theorem ng Pick ay isang klasikal na resulta ng combinatorial geometry at ang geometry ng mga numero. Ang lugar ng polygon na may integer vertices ay katumbas ng sum B + D/2 - 1, kung saan ang B ay ang bilang ng mga integer point sa loob ng polygon, at ang D ay ang bilang ng mga integer point sa hangganan ng polygon.

Isang nakakabigay-puri na patunay ng teorama ni Pick. Anumang ganoong polygon ay madaling mahahati sa mga tatsulok na may mga vertice sa mga node ng sala-sala, na walang mga node sa loob o sa mga gilid. Maaari itong ipakita na ang mga lugar ng lahat ng mga tatsulok na ito ay pareho at katumbas ng 1/2, at, samakatuwid, ang lugar ng polygon ay katumbas ng kalahati ng kanilang numerong T. Upang mahanap ang numerong ito, tinutukoy namin ng n ang bilang ng mga gilid ng polygon, sa pamamagitan ng i - ang bilang ng mga node sa loob nito at sa pamamagitan ng b - ang bilang ng mga node sa mga gilid, kabilang ang mga vertices. Ang kabuuang kabuuan ng mga anggulo ng lahat ng mga tatsulok ay πТ. Ngayon, hanapin natin ang kabuuan na ito sa ibang paraan. Ang kabuuan ng mga anggulo na may vertex sa anumang panloob na node ay 2 π, ibig sabihin, ang kabuuang kabuuan ng naturang mga anggulo ay 2 π i; ang kabuuang kabuuan ng mga anggulo sa mga node sa mga gilid, ngunit hindi sa vertices, ay (b - n) π, at ang kabuuan ng mga anggulo sa vertices ng polygon ay (n - 2) π. Kaya, π T \u003d 2i π + (b - n) π + (n - 2) π, kung saan nakakuha tayo ng expression para sa lugar S ng isang polygon, na kilala bilang formula ng Pick. Halimbawa, sa figure b = 9, i = 24, at samakatuwid ang lugar ng polygon ay 27.5.

Aplikasyon. Kaya, bumalik sa gawain B6. Ngayon, alam ang bagong formula, madali nating mahahanap ang lugar ng quadrilateral na ito. Dahil ang B ay 5; D - 14, pagkatapos ay 5 + 14: 2-1 \u003d 11 (cm squared) Ang lugar ng quadrangle na ito ay 11 cm squared.

Gamit ang parehong formula, mahahanap natin ang lugar ng isang tatsulok. Dahil B-14, G-10, pagkatapos ay 14+10:2-1=18 (square cm) Ang lugar ng tatsulok na ito ay 18 cm squared.

Kung B-9, D-12, kung gayon: 9+12:2-1=14 (cm squared) Ang lugar ng quadrilateral na ito ay 14 cm squared.

Saklaw ng formula. Bilang karagdagan sa katotohanan na ang formula ay ginagamit sa iba't ibang uri ng pagsusulit, takdang-aralin, at iba pa, sinasamahan nito ang buong mundo sa paligid natin.

Ayon sa formula ng Peak S = B + ½ G-1 1) katawan B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) buntot B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

Ayon sa formula ng Peak S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10.5-1 \u003d 45.5

Konklusyon. Bilang isang resulta, ako ay dumating sa konklusyon na mayroong maraming iba't ibang mga paraan upang malutas ang mga problema sa lugar na hindi pinag-aralan sa kurikulum ng paaralan, at ipinakita ang mga ito gamit ang Pick formula bilang isang halimbawa.

Direktoryo. Ang polygon na walang self-intersections ay tinatawag na lattice polygon kung ang lahat ng vertices nito ay nasa mga puntong may integer coordinates (sa Cartesian coordinate system). Ang isang punto sa coordinate plane ay tinatawag na integer kung ang parehong mga coordinate nito ay integer.