Manchmal werden solche uneigentlichen Integrale aufgerufen unechte Integrale zweiter Art. Unechte Integrale der zweiten Art werden heimtückisch unter dem üblichen bestimmten Integral „verschlüsselt“ und sehen genauso aus: .

Aber im Gegensatz zu einem bestimmten Integral hat der Integrand eine unendliche Diskontinuität (existiert nicht):

1) am Punkt ,

2) Punkt,

3) an beiden Punkten gleichzeitig,

4) oder sogar auf dem Integrationsintervall.

Wir werden uns die ersten beiden Fälle ansehen; für die Fälle 3-4 gibt es am Ende des Artikels einen Link zu einer zusätzlichen Lektion.

Schauen wir uns zur Verdeutlichung ein Beispiel an:

Es scheint ein bestimmtes Integral zu sein. Tatsächlich handelt es sich jedoch um ein uneigentliches Integral zweiter Art, denn wenn wir es in den Integranden einsetzen, dann ist der Wert die untere Grenze

dann geht unser Nenner auf Null, das heißt, der Integrand existiert zu diesem Zeitpunkt einfach nicht!

Bei der Analyse des unechten Integrals Sie müssen immer beide Integrationsgrenzen in den Integranden einsetzen. Lassen Sie uns in diesem Zusammenhang die Obergrenze überprüfen:

Alles ist gut hier. Das krummlinige Trapez für den betrachteten Typ des uneigentlichen Integrals sieht grundsätzlich so aus:

Hier ist fast alles das Gleiche wie beim Integral erster Art. Unser Integral ist numerisch gleich der Fläche des schattierten gekrümmten Trapezes, das von oben nicht begrenzt ist. In diesem Fall gibt es zwei Möglichkeiten: Das unechte Integral divergiert (die Fläche ist unendlich) oder das unechte Integral ist gleich einer endlichen Zahl (wenn die Fläche einer unendlichen Figur endlich ist!).

Es bleibt nur noch, die Newton-Leibniz-Formel zu modifizieren. Es wird auch mit Hilfe einer Grenze modifiziert, allerdings strebt die Grenze nicht mehr gegen Unendlich, sondern schätzen rechts. Aus der Zeichnung lässt sich leicht erkennen, dass dies entlang der Achse der Fall ist OCHSE rechts.

Schauen wir mal, wie das in der Praxis umgesetzt wird.

Beispiel 6

(Vergessen Sie nicht, mündlich oder auf einem Entwurf zu prüfen, ob mit der Obergrenze alles in Ordnung ist!). Berechnen wir zunächst das unbestimmte Integral:

Wenn Sie Schwierigkeiten mit dem Austausch haben, lesen Sie bitte die Lektion Substitutionsmethode im unbestimmten Integral.

Berechnen wir das unechte Integral:

(1) Was ist hier neu? Lösungstechnisch gibt es praktisch nichts. Das einzige, was sich geändert hat, ist der Eintrag unter dem Limit-Symbol:

Die Addition von +0 bedeutet, dass wir rechts einen Wert von ¾ anstreben, was logisch ist (siehe Grafik). Ein solcher Grenzwert wird in der Grenzwerttheorie genannt einseitige Grenze. In diesem Fall haben wir rechte Grenze.

(2) Wir ersetzen die Ober- und Untergrenzen mithilfe der Newton-Leibniz-Formel.

(3) Befassen wir uns mit . Wie kann festgestellt werden, wohin ein Ausdruck führt? Grob gesagt müssen Sie nur den Wert hineinsetzen, drei Viertel ersetzen und das angeben. Lassen Sie uns die Antwort durchkämmen.

In diesem Fall ist das unechte Integral gleich einer negativen Zahl. Darin liegt kein Verbrechen, lediglich das entsprechende gebogene Trapez befindet sich unter der Achse OCHSE. Und nun Beispiele für eigenständige Lösungen.

Beispiel 7

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Beispiel 8

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Wenn der Integrand an der Stelle nicht existiert

Ein unendlich gekrümmtes Trapez für ein solches uneigentliches Integral sieht grundsätzlich so aus:

Hier machen wir alles absolut gleich, außer dass unsere Grenze dazu tendiert schätzen Blinks. Achse OCHSE wir müssen dem Bruchpunkt unendlich nahe kommen links.

Beispiel 9

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Der Integrand weist an diesem Punkt eine unendliche Diskontinuität auf B = 3 (Wir prüfen mündlich, ob mit der anderen Integrationsgrenze alles in Ordnung ist!).

Zur Abwechslung lösen wir diese Grenze gleich – indem wir die Funktion unter dem Differentialzeichen subsumieren. Wem das schwer fällt, kann zunächst das unbestimmte Integral nach dem bereits besprochenen Schema ermitteln.

Der Zusatz (-0) bedeutet, dass wir ein Limit haben linkshändig, und zwar auf den Punkt B = 3 wir nähern uns der Achse OCHSE links.

Lassen Sie uns herausfinden, warum der Bruch

(es ist besser, dies mündlich oder im Entwurf zu tun).

Wir ersetzen den Grenzwert unter der Wurzel B = 3 - 0.

Endlich:

Das uneigentliche Integral divergiert.

Das Minuszeichen bedeutet, dass sich das entsprechende gebogene Trapez unter der Achse befindet OCHSE. Seien Sie sehr vorsichtig mit den Schildern.

Ja, natürlich geht das unechte Integral auseinander, aber beides sind unterschiedliche Dinge, unterschiedliche Gattungen, und wenn man die Zeichen nicht beachtet, dann macht man streng genommen einen schweren Fehler.

Und die letzten beiden Beispiele zur unabhängigen Betrachtung:

Beispiel 10

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Beispiel 11

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Eine Analyse der Situation, wenn beide Integrationsgrenzen „schlecht“ sind oder die Bruchstelle direkt auf dem Integrationssegment liegt, finden Sie im Artikel Effiziente Methoden zur Lösung bestimmter und uneigentlicher Integrale.

Lösungen und Antworten:

Beispiel 4: Lösung:

.

Beispiel 5: Lösung:

Die Integrandenfunktion ist stetig .

Beispiel 7: Lösung:

Der Integrand weist an diesem Punkt eine unendliche Diskontinuität auf

Das uneigentliche Integral divergiert.

Hinweis: mit Ausdrucksbegrenzung

Uneigentliche Integrale erster Art. Im Wesentlichen ist dies dasselbe bestimmte Integral, jedoch in Fällen, in denen die Integrale unendliche obere oder untere Integrationsgrenzen haben oder beide Integrationsgrenzen unendlich sind.

Uneigentliche Integrale zweiter Art. Im Wesentlichen ist dies dasselbe bestimmte Integral, aber in Fällen, in denen das Integral aus unbegrenzten Funktionen entnommen wird, hat der Integrand an einer endlichen Anzahl von Punkten kein endliches Integrationssegment und wendet sich ins Unendliche.

Zum Vergleich. Bei der Einführung des Konzepts eines bestimmten Integrals wurde davon ausgegangen, dass die Funktion F(X) ist stetig im Intervall [ A, B], und das Integrationssegment ist endlich, das heißt, es ist durch Zahlen und nicht durch Unendlichkeit begrenzt. Einige Aufgaben führen dazu, dass diese Einschränkungen aufgegeben werden müssen. So entstehen unechte Integrale.

Geometrische Bedeutung des uneigentlichen Integrals Es stellt sich ganz einfach heraus. Im Fall des Graphen einer Funktion j = F(X) liegt oberhalb der Achse Ochse, das bestimmte Integral drückt die Fläche eines krummlinigen Trapezes aus, das von einer Kurve begrenzt wird j = F(X) , x-Achse und Ordinaten X = A , X = B. Das uneigentliche Integral wiederum drückt die Fläche eines unbegrenzten (unendlichen) krummlinigen Trapezes aus, das zwischen den Linien eingeschlossen ist j = F(X) (im Bild unten - rot), X = A und die Abszissenachse.

Uneigentliche Integrale werden auf ähnliche Weise für andere unendliche Intervalle definiert:

Die Fläche eines unendlich gekrümmten Trapezes kann eine endliche Zahl sein. In diesem Fall wird das unechte Integral als konvergent bezeichnet. Die Fläche kann auch unendlich sein, und in diesem Fall heißt das uneigentliche Integral divergent.

Verwendung des Grenzwerts eines Integrals anstelle des uneigentlichen Integrals selbst. Um das uneigentliche Integral auszuwerten, müssen Sie den Grenzwert des bestimmten Integrals verwenden. Wenn dieser Grenzwert existiert und endlich ist (ungleich unendlich), dann heißt das uneigentliche Integral konvergent und andernfalls divergent. Wozu eine Variable unter dem Grenzzeichen tendiert, hängt davon ab, ob es sich um ein uneigentliches Integral erster oder zweiter Art handelt. Lassen Sie uns das jetzt herausfinden.

Uneigentliche Integrale erster Art – mit unendlichen Grenzen und deren Konvergenz

Uneigentliche Integrale mit unendlicher Obergrenze

Das Schreiben eines uneigentlichen Integrals unterscheidet sich also vom üblichen bestimmten Integral dadurch, dass die Obergrenze der Integration unendlich ist.

Definition. Ein uneigentliches Integral mit einer unendlichen oberen Integrationsgrenze einer stetigen Funktion F(X) im Intervall von A Vor ∞ die Grenze des Integrals dieser Funktion mit der oberen Integrationsgrenze wird aufgerufen B und die untere Integrationsgrenze A vorausgesetzt, dass die Obergrenze der Integration unbegrenzt wächst, d.h.

.

Wenn diese Grenze existiert und einer Zahl und nicht einer Unendlichkeit entspricht, dann Ein uneigentliches Integral heißt konvergent, und die Zahl, der der Grenzwert entspricht, wird als Wert genommen. Sonst Ein uneigentliches Integral heißt divergent und ihm wird keine Bedeutung zugeschrieben.

Beispiel 1. Berechnen Sie unechte Integrale(falls es konvergiert).

Lösung. Basierend auf der Definition des uneigentlichen Integrals finden wir

Da der Grenzwert existiert und gleich 1 ist, dann ist dies der Fall uneigentliches Integral konvergiert und ist gleich 1.

Im folgenden Beispiel ist der Integrand fast derselbe wie in Beispiel 1, nur ist der Grad x nicht zwei, sondern der Buchstabe Alpha, und die Aufgabe besteht darin, das unechte Integral auf Konvergenz zu untersuchen. Das heißt, die Frage muss noch beantwortet werden: Bei welchen Alpha-Werten konvergiert dieses uneigentliche Integral und bei welchen Werten divergiert es?

Beispiel 2. Untersuchen Sie das uneigentliche Integral auf Konvergenz(die untere Integrationsgrenze ist größer als Null).

Lösung. Nehmen wir also zunächst an, dass

Im resultierenden Ausdruck bewegen wir uns zum Grenzwert bei:

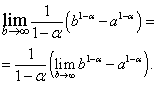
Es ist leicht zu erkennen, dass der Grenzwert auf der rechten Seite existiert und gleich Null ist, wenn das heißt, und nicht existiert, wenn das heißt.

Im ersten Fall, also wenn . Wenn, dann und existiert nicht.

Das Fazit unserer Studie lautet wie folgt: Dies uneigentliches Integral konvergiert bei und divergiert bei .

Anwendung der Newton-Leibniz-Formel auf den Typ des untersuchten uneigentlichen Integrals , können Sie die folgende Formel ableiten, die dieser sehr ähnlich ist:

.

Dies ist eine verallgemeinerte Newton-Leibniz-Formel.

Beispiel 3. Berechnen Sie unechte Integrale(falls es konvergiert).

Der Grenzwert dieses Integrals besteht:

Das zweite Integral, das die Summe bildet, die das ursprüngliche Integral ausdrückt:

Der Grenzwert dieses Integrals existiert auch:

.

Wir finden die Summe zweier Integrale, die auch der Wert des ursprünglichen unechten Integrals mit zwei unendlichen Grenzen ist:

Uneigentliche Integrale zweiter Art – aus unbeschränkten Funktionen und deren Konvergenz

Lassen Sie die Funktion F(X) angegeben auf dem Segment von A Vor B und ist darauf unbegrenzt. Angenommen, die Funktion geht an diesem Punkt ins Unendliche B , während es an allen anderen Punkten des Segments kontinuierlich ist.

Definition. Ein uneigentliches Integral einer Funktion F(X) auf dem Segment von A Vor B die Grenze des Integrals dieser Funktion mit der oberen Integrationsgrenze wird aufgerufen C , wenn beim Streben C Zu B Die Funktion wächst unbegrenzt und am Punkt X = B Funktion nicht definiert, d.h.

.

Wenn dieser Grenzwert existiert, heißt das uneigentliche Integral zweiter Art konvergent, andernfalls heißt es divergent.

Mit der Newton-Leibniz-Formel leiten wir ab.

Bestimmtes Integral als Grenzwert der Integralsumme

kann nur existieren (d. h. einen bestimmten Endwert haben), wenn die Bedingungen erfüllt sind

Wird mindestens eine dieser Bedingungen verletzt, verliert die Definition ihre Bedeutung. Im Fall eines unendlichen Segments, zum Beispiel [ A; ) es kann nicht unterteilt werden P Teile endlicher Länge
, die zudem mit zunehmender Segmentanzahl gegen Null tendieren würde. Im Falle einer unbegrenzten irgendwann Mit[A; B] wird die Anforderung einer willkürlichen Punktauswahl verletzt auf Teilsegmenten – nicht auswählbar =Mit, da der Wert der Funktion zu diesem Zeitpunkt undefiniert ist. Aber auch für diese Fälle ist es möglich, den Begriff eines bestimmten Integrals zu verallgemeinern, indem man einen weiteren Grenzübergang einführt. Man nennt Integrale über unendliche Intervalle und über diskontinuierliche (unbeschränkte) Funktionen nicht dein eigenes.

Definition.

Lassen Sie die Funktion
ist auf dem Intervall [ definiert A; ) und ist in jedem endlichen Intervall integrierbar [ A; B], d.h. existiert
für jeden B > A. Typbeschränkung
angerufen uneigentliches Integral erste Art (oder ein uneigentliches Integral über ein unendliches Intervall) und bezeichnen
.

Somit ist per Definition
=
.

Wenn der Grenzwert rechts existiert und endlich ist, dann ist das uneigentliche Integral
angerufen konvergent . Wenn diese Grenze unendlich ist oder überhaupt nicht existiert, spricht man vom unechten Integral divergiert .

Ebenso können wir das Konzept eines uneigentlichen Integrals der Funktion einführen
entlang des Intervalls (–; B]:

=
.

Und das uneigentliche Integral der Funktion
über das Intervall (–; +) ist definiert als die Summe der oben eingeführten Integrale:

=
+
,

Wo A– willkürlicher Punkt. Dieses Integral konvergiert, wenn beide Terme konvergieren, und divergiert, wenn mindestens einer der Terme divergiert.

Aus geometrischer Sicht ist das Integral
,
, bestimmt den numerischen Wert der Fläche eines unendlichen krummlinigen Trapezes, das oben durch den Funktionsgraphen begrenzt wird
, links – geradeaus
, von unten – an der OX-Achse. Die Konvergenz des Integrals bedeutet die Existenz einer endlichen Fläche eines solchen Trapezes und ihre Gleichheit mit der Grenze der Fläche eines krummlinigen Trapezes mit einer beweglichen rechten Wand
.

Auf den Fall eines Integrals mit unendlichem Grenzwert können wir verallgemeinern Newton-Leibniz-Formel:

=
= F( + ) – F( A),

wo F( + ) =
. Wenn dieser Grenzwert existiert, konvergiert das Integral, andernfalls divergiert es.

Wir haben eine Verallgemeinerung des Konzepts eines bestimmten Integrals auf den Fall eines unendlichen Intervalls betrachtet.

Betrachten wir nun eine Verallgemeinerung für den Fall einer unbeschränkten Funktion.

Definition

Lassen Sie die Funktion
ist auf dem Intervall [ definiert A; B), ist in einer Umgebung des Punktes unbegrenzt B und ist in jedem Intervall stetig
, wobei >0 (und daher in diesem Intervall integrierbar ist, d. h.
existiert). Typbeschränkung
angerufen uneigentliches Integral zweiter Art (oder ein uneigentliches Integral einer unbeschränkten Funktion) und wird bezeichnet
.

Somit ist das uneigentliche Integral des Unbeschränkten am Punkt B Funktionen existieren per Definition

=
.

Wenn der Grenzwert rechts existiert und endlich ist, heißt das Integral konvergent. Gibt es keinen endlichen Grenzwert, so heißt das uneigentliche Integral abweichend.

Ebenso können wir das uneigentliche Integral der Funktion definieren
an dem Punkt eine unendliche Diskontinuität haben A:

=
.

Wenn die Funktion
hat im inneren Punkt eine unendliche Diskontinuität Mit
, dann ist das uneigentliche Integral wie folgt definiert

=
+
=
+
.

Dieses Integral konvergiert, wenn beide Terme konvergieren, und divergiert, wenn mindestens ein Term divergiert.

Aus geometrischer Sicht charakterisiert das uneigentliche Integral einer unbeschränkten Funktion auch die Fläche eines unbeschränkten gekrümmten Trapezes:

Da ein uneigentliches Integral durch Grenzübergang von einem bestimmten Integral abgeleitet wird, können alle Eigenschaften eines bestimmten Integrals (mit entsprechenden Verfeinerungen) auf unechte Integrale erster und zweiter Art übertragen werden.

Bei vielen Problemen, die zu unechten Integralen führen, ist es nicht notwendig zu wissen, was dieses Integral ist, es reicht aus, nur seine Konvergenz oder Divergenz zu überprüfen. Dafür verwenden sie Zeichen der Konvergenz. Konvergenzzeichen uneigentlicher Integrale:

1) Vergleichszeichen.

Lass es für alle sein X

. Dann wenn
konvergiert, dann konvergiert
, Und

. Wenn
divergiert, dann divergiert und
.

2) Wenn konvergiert
, dann konvergiert und
(Das letzte Integral heißt in diesem Fall absolut konvergent).

Die Konvergenz- und Divergenzzeichen uneigentlicher Integrale unbeschränkter Funktionen ähneln den oben formulierten.

Beispiele für Problemlösungen.

Beispiel 1.

A)
; B)
; V)

G)
; D)
.

Lösung.

a) Per Definition gilt:

.

b) Ebenso

Daher konvergiert dieses Integral und ist gleich .

c) Per Definition
=
+
, Und A- willkürliche Nummer. Lassen Sie uns in unseren Fall eintreten
, dann erhalten wir:

Dieses Integral konvergiert.

Das bedeutet, dass dieses Integral divergiert.

e) Betrachten wir
.

Um die Stammfunktion des Integranden zu finden, ist es notwendig, die Methode der partiellen Integration anzuwenden. Dann erhalten wir:
Da weder
, weder

nicht existieren, dann existiert nicht und

Daher divergiert dieses Integral.

Beispiel 2. Untersuchen Sie die Konvergenz des Integrals P.

Lösung.

abhängig von
Bei

wir haben:
Wenn
, Das

wir haben:
Wenn
Und . Daher divergiert das Integral.
, Dann

= ,

Daher konvergiert das Integral.

wir haben:
, Das

daher divergiert das Integral.

Auf diese Weise,

Beispiel 3.

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest:

A)
;
B)
.

Lösung.

;
V)
a) Integral

ist ein uneigentliches Integral zweiter Art, da der Integrand

.

nicht auf einen Punkt begrenzt .

. Dann ist per Definition
Das Integral konvergiert und ist gleich
b) Überlegen Sie

. Auch hier ist der Integrand nicht auf den Punkt beschränkt

. Daher ist dieses Integral uneigentlich zweiter Art und per Definition
Daher divergiert das Integral.
c) Überlegen Sie
. Integrand
weist an zwei Stellen eine unendliche Lücke auf:
Und

=

=

.

, von denen das erste zum Integrationsintervall gehört
.

. Daher ist dieses Integral ein uneigentliches Integral zweiter Art. Dann per Definition

Daher konvergiert das Integral und ist gleich

Bist du jetzt hier? =) Nein, ich wollte niemanden einschüchtern, das Thema der unechten Integrale ist nur ein sehr gutes Beispiel dafür, wie wichtig es ist, die höhere Mathematik und andere exakte Wissenschaften nicht zu vernachlässigen. Alles, was Sie zum Erlernen der Lektion benötigen, finden Sie auf der Website – auf Wunsch auch in detaillierter und zugänglicher Form ...

Also, fangen wir damit an. Im übertragenen Sinne ist ein uneigentliches Integral ein „fortgeschrittenes“ bestimmtes Integral, und tatsächlich gibt es bei ihnen nicht so viele Schwierigkeiten, und außerdem hat das uneigentliche Integral eine sehr gute geometrische Bedeutung. Was bedeutet es, ein uneigentliches Integral auszuwerten? Berechnen Sie unechte Integrale - das bedeutet, die NUMMER zu finden(genau das Gleiche wie im bestimmten Integral),

oder beweisen Sie, dass es divergiert

(das heißt, am Ende erhält man Unendlich statt einer Zahl).

Es gibt zwei Arten uneigentlicher Integrale. Uneigentliches Integral mit unendlicher(n) Integrationsgrenze(n). Manchmal wird ein solches uneigentliches Integral aufgerufen

uneigentliches Integral erster Art

. Im Allgemeinen sieht ein uneigentliches Integral mit einem unendlichen Grenzwert am häufigsten so aus: . Wie unterscheidet es sich von einem bestimmten Integral? An der Obergrenze. Es ist endlos: . Seltener sind Integrale mit einer unendlichen unteren Grenze oder mit zwei unendlichen Grenzen: , und wir werden sie später betrachten – wenn Sie den Dreh raus haben :) Schauen wir uns nun den beliebtesten Fall an. In den allermeisten Beispielen die Integrandenfunktion kontinuierlich dazwischen und dieses hier Wichtige Tatsache sollte zuerst überprüft werden! Denn wenn es Lücken gibt, dann gibt es zusätzliche Nuancen. Der Sicherheit halber gehen wir davon aus, dass auch dann das Typische gilt

gebogenes Trapez wird so aussehen: numerisch gleich seiner Fläche. Folgende Optionen sind möglich:

1) Der erste Gedanke, der mir in den Sinn kommt: „Da die Zahl also unendlich ist ", mit anderen Worten, die Fläche ist ebenfalls unendlich. Es kann so sein. In diesem Fall spricht man vom unechten Integral divergiert.

2) Aber. So paradox es auch klingen mag, die Fläche einer unendlichen Figur kann gleich sein... einer endlichen Zahl! Zum Beispiel: . Könnte das wahr sein? Leicht. Im zweiten Fall das unechte Integral konvergiert.

3) Mehr zur dritten Option etwas später.

In welchen Fällen divergiert ein uneigentliches Integral und in welchen Fällen konvergiert es? Dies hängt vom Integranden ab und wir werden uns bald konkrete Beispiele ansehen.

Was passiert, wenn sich unterhalb der Achse ein unendlich gekrümmtes Trapez befindet? In diesem Fall das unechte Integral (divergiert) oder gleich einer endlichen negativen Zahl ist.

Auf diese Weise, Unechte Integrale können negativ sein.

Wichtig! Wenn Ihnen irgendein uneigentliches Integral zur Lösung gegeben wird, dann gilt im Allgemeinen: Es wird nicht über einen Bereich gesprochen und es besteht keine Notwendigkeit, eine Zeichnung zu erstellen. Ich habe die geometrische Bedeutung des uneigentlichen Integrals nur erklärt, um das Verständnis des Materials zu erleichtern.

Da das uneigentliche Integral dem bestimmten Integral sehr ähnlich ist, erinnern wir uns an die Newton-Leibniz-Formel: . Tatsächlich ist die Formel auch auf unechte Integrale anwendbar, nur muss sie geringfügig modifiziert werden. Was ist der Unterschied? An der unendlichen oberen Integrationsgrenze: . Wahrscheinlich haben viele vermutet, dass dies bereits nach der Anwendung der Grenzwerttheorie riecht, und die Formel wird wie folgt geschrieben: .

Was ist der Unterschied zu einem bestimmten Integral? Nichts Besonderes! Wie beim bestimmten Integral müssen Sie in der Lage sein, die Stammfunktion (unbestimmtes Integral) zu finden und die Newton-Leibniz-Formel anzuwenden. Das Einzige, was hinzugefügt wurde, ist die Berechnung des Limits. Wer eine schlechte Zeit damit hat, der lernt eine Lektion Funktionsgrenzen. Beispiele für Lösungen, weil es spät besser ist als in der Armee.

Schauen wir uns zwei klassische Beispiele an:

Beispiel 1

Der Übersichtlichkeit halber werde ich eine Zeichnung zeichnen, obwohl ich noch einmal betone: zur Praxis Für diese Aufgabe ist es nicht erforderlich, Zeichnungen zu erstellen.

Die Integrandenfunktion ist im halben Intervall stetig, was bedeutet, dass alles in Ordnung ist und das uneigentliche Integral mit der „Standard“-Methode berechnet werden kann.

Anwendung unserer Formel und die Lösung des Problems sieht so aus:

Das heißt, das uneigentliche Integral divergiert und die Fläche des schattierten gekrümmten Trapezes ist gleich unendlich.

Im betrachteten Beispiel haben wir das einfachste Tabellenintegral und die gleiche Technik zur Anwendung der Newton-Leibniz-Formel wie beim bestimmten Integral. Diese Formel wird jedoch unter dem Vorzeichen des Grenzwerts angewendet. Anstelle des üblichen Buchstabens einer „dynamischen“ Variablen erscheint der Buchstabe „be“. Dies sollte nicht verwirren oder verwirren, denn jeder Buchstabe ist nicht schlechter als das Standard-„X“.

Wenn Sie nicht verstehen, warum bei , dann ist das sehr schlecht, entweder verstehen Sie die einfachsten Grenzwerte nicht (und verstehen im Allgemeinen nicht, was ein Grenzwert ist), oder Sie wissen nicht, wie der Graph einer logarithmischen Funktion aussieht. Im zweiten Fall besuchen Sie eine Unterrichtsstunde Graphen und Eigenschaften elementarer Funktionen.

Bei der Lösung uneigentlicher Integrale ist es sehr wichtig zu wissen, wie die Graphen grundlegender Elementarfunktionen aussehen!

Die fertige Aufgabe sollte etwa so aussehen:

“

! Bei der Vorbereitung eines Beispiels unterbrechen wir immer die Lösung und geben an, was mit dem Integranden passiert – Ist es im Integrationsintervall stetig oder nicht?. Damit identifizieren wir die Art des uneigentlichen Integrals und begründen weitere Maßnahmen.

Beispiel 2

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Machen wir die Zeichnung:

Zunächst stellen wir Folgendes fest: Der Integrand ist auf dem Halbintervall stetig. Haube. Wir lösen mit der Formel :

(1) Wir nehmen das einfachste Integral einer Potenzfunktion (dieser Sonderfall kommt in vielen Tabellen vor). Es ist besser, das Minuszeichen sofort über das Grenzzeichen hinaus zu verschieben, damit es bei weiteren Berechnungen nicht stört.

(2) Wir ersetzen die Ober- und Untergrenzen mithilfe der Newton-Leibniz-Formel.

(3) Wir weisen darauf hin (Meine Herren, das hätte schon vor langer Zeit verstanden werden müssen) und vereinfachen die Antwort.

Hier ist die Fläche eines unendlich gekrümmten Trapezes eine endliche Zahl! Unglaublich, aber wahr.

Das fertige Beispiel sollte etwa so aussehen:

“

Die Integrandenfunktion ist stetig

“

Was tun, wenn Sie auf ein Integral wie - mit stoßen? Bruchpunkt auf dem Integrationsintervall? Das bedeutet, dass im Beispiel ein Tippfehler vorliegt. (am Wahrscheinlichsten), oder über ein fortgeschrittenes Ausbildungsniveau. Im letzteren Fall aufgrund Additivitätseigenschaften, sollten wir zwei uneigentliche Integrale über Intervalle betrachten und uns dann mit der Summe befassen.

Manchmal kann es aufgrund eines Tippfehlers oder einer Absicht zu einem falschen Integral kommen existieren überhaupt nicht Wenn Sie also beispielsweise die Quadratwurzel von „x“ in den Nenner des obigen Integrals setzen, wird ein Teil des Integrationsintervalls überhaupt nicht in den Definitionsbereich des Integranden einbezogen.

Darüber hinaus kann es sein, dass das uneigentliche Integral selbst bei allem „scheinbaren Wohlergehen“ nicht existiert. Klassisches Beispiel: . Trotz der Eindeutigkeit und Stetigkeit des Kosinus existiert ein solches uneigentliches Integral nicht! Warum? Es ist ganz einfach, weil:
- existiert nicht angemessene Grenze.

Und solche Beispiele kommen zwar selten vor, kommen aber in der Praxis vor! Somit gibt es neben Konvergenz und Divergenz auch ein drittes Ergebnis der Lösung mit einer gültigen Antwort: „Es gibt kein uneigentliches Integral.“

Es ist auch zu beachten, dass die strenge Definition eines uneigentlichen Integrals gerade durch den Grenzwert gegeben ist und wer möchte, kann sich damit in der Lehrliteratur vertraut machen. Nun, wir setzen die praktische Lektion fort und gehen zu sinnvolleren Aufgaben über:

Beispiel 3

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Versuchen wir zunächst, die Stammfunktion (unbestimmtes Integral) zu finden. Wenn wir dies nicht tun, können wir natürlich auch das uneigentliche Integral nicht lösen.

Welchem ​​der Tabellenintegrale ähnelt der Integrand? Es erinnert mich an einen Arcustangens: . Diese Überlegungen legen nahe, dass es schön wäre, ein Quadrat im Nenner zu haben. Dies geschieht durch Austausch.

Ersetzen wir:

Das unbestimmte Integral wurde gefunden; in diesem Fall macht es keinen Sinn, eine Konstante hinzuzufügen.

Es ist immer sinnvoll, den Entwurf zu überprüfen, d. h. das erzielte Ergebnis zu differenzieren:

Der ursprüngliche Integrand wurde erhalten, was bedeutet, dass das unbestimmte Integral korrekt gefunden wurde.

Jetzt finden wir das uneigentliche Integral:

(1) Wir schreiben die Lösung gemäß der Formel . Es ist besser, die Konstante sofort über das Grenzzeichen hinaus zu verschieben, damit sie weitere Berechnungen nicht beeinträchtigt.

(2) Wir ersetzen die Ober- und Untergrenzen gemäß der Newton-Leibniz-Formel. Warum bei ? Siehe den Arcustangens-Graph im bereits empfohlenen Artikel.

(3) Wir erhalten die endgültige Antwort. Eine Tatsache, die man auswendig wissen sollte.

Fortgeschrittene Schüler finden das unbestimmte Integral möglicherweise nicht separat und verwenden nicht die Ersetzungsmethode, sondern verwenden stattdessen die Methode, die Funktion unter dem Differentialzeichen zu ersetzen und das uneigentliche Integral „sofort“ zu lösen. In diesem Fall sollte die Lösung etwa so aussehen:

“

Der Integrand ist stetig auf .

“

Beispiel 4

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

! Dies ist ein typisches Beispiel, und ähnliche Integrale werden sehr oft gefunden. Mach es gut! Die Stammfunktion wird hier mithilfe der Methode der Auswahl eines vollständigen Quadrats ermittelt. Weitere Einzelheiten zur Methode finden Sie in der Lektion Einige Brüche integrieren.

Beispiel 5

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Dieses Integral kann im Detail gelöst werden, das heißt, man findet zunächst das unbestimmte Integral, indem man eine Variable ändert. Oder Sie lösen es „sofort“ – indem Sie die Funktion unter dem Differentialvorzeichen subsumieren. Wer hat eine mathematische Ausbildung?

Vollständige Lösungen und Antworten am Ende der Lektion.

Beispiele für Lösungen uneigentlicher Integrale mit unendlicher unterer Integrationsgrenze finden Sie auf der Seite Effiziente Methoden zur Lösung uneigentlicher Integrale. Dort haben wir auch den Fall analysiert, dass beide Integrationsgrenzen unendlich sind.

Uneigentliche Integrale unbeschränkter Funktionen

Oder unechte Integrale zweiter Art. Uneigentliche Integrale der zweiten Art werden heimtückisch unter dem üblichen bestimmten Integral „verschlüsselt“ und sehen genau gleich aus: Aber im Gegensatz zum bestimmten Integral weist der Integrand eine unendliche Diskontinuität auf (existiert nicht): 1) am Punkt , 2) oder am Punkt , 3) ​​​​oder an beiden Punkten gleichzeitig, 4) oder sogar am Integrationssegment. Wir werden uns die ersten beiden Fälle ansehen; für die Fälle 3-4 gibt es am Ende des Artikels einen Link zu einer zusätzlichen Lektion.

Nur ein Beispiel zur Verdeutlichung: . Es scheint ein bestimmtes Integral zu sein. Tatsächlich handelt es sich jedoch um ein uneigentliches Integral zweiter Art; wenn wir den Wert der unteren Grenze in den Integranden einsetzen, geht unser Nenner auf Null, das heißt, der Integrand existiert an dieser Stelle einfach nicht!

Im Allgemeinen bei der Analyse eines unechten Integrals Sie müssen immer beide Integrationsgrenzen in den Integranden einsetzen. Lassen Sie uns in diesem Zusammenhang die Obergrenze überprüfen: . Alles ist gut hier.

Das krummlinige Trapez für den betrachteten Typ des uneigentlichen Integrals sieht grundsätzlich so aus:

Hier ist fast alles das Gleiche wie beim Integral erster Art.

Unser Integral ist numerisch gleich der Fläche des schattierten gekrümmten Trapezes, das von oben nicht begrenzt ist. In diesem Fall gibt es zwei Möglichkeiten*: Das unechte Integral divergiert (die Fläche ist unendlich) oder das unechte Integral ist gleich einer endlichen Zahl (d. h. die Fläche einer unendlichen Figur ist endlich!).

* Standardmäßig gehen wir normalerweise davon aus, dass das uneigentliche Integral existiert

Es bleibt nur noch, die Newton-Leibniz-Formel zu modifizieren. Es wird auch mit Hilfe einer Grenze modifiziert, allerdings strebt die Grenze nicht mehr gegen Unendlich, sondern auf den Wert rechts. Aus der Zeichnung ist es leicht zu erkennen: Entlang der Achse müssen wir uns der Bruchstelle unendlich nahe nähern rechts.

Schauen wir mal, wie das in der Praxis umgesetzt wird.

Beispiel 6

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Der Integrand hat an einem Punkt eine unendliche Diskontinuität (vergessen Sie nicht, mündlich oder auf einem Entwurf zu überprüfen, ob mit der Obergrenze alles in Ordnung ist!)

Berechnen wir zunächst das unbestimmte Integral:

Ersatz:

Wenn Sie Schwierigkeiten mit dem Austausch haben, lesen Sie bitte die Lektion Substitutionsmethode im unbestimmten Integral.

Berechnen wir das unechte Integral:

(1) Was ist hier neu? Lösungstechnisch gibt es praktisch nichts. Das einzige, was sich geändert hat, ist der Eintrag unter dem Limit-Symbol: . Der Zusatz bedeutet, dass wir den Wert rechts anstreben (was logisch ist – siehe Grafik). Ein solcher Grenzwert wird in der Grenzwerttheorie genannt einseitige Grenze. In diesem Fall haben wir rechte Grenze.

(2) Wir ersetzen die Ober- und Untergrenzen mithilfe der Newton-Leibniz-Formel.

(3) Befassen wir uns mit . Wie kann festgestellt werden, wohin ein Ausdruck führt? Grob gesagt müssen Sie nur den Wert hineinsetzen, drei Viertel ersetzen und das angeben. Lassen Sie uns die Antwort durchkämmen.

In diesem Fall ist das unechte Integral gleich einer negativen Zahl. Darin liegt kein Verbrechen, lediglich das entsprechende gebogene Trapez befindet sich unter der Achse.

Und nun zwei Beispiele für eigenständige Lösungen.

Beispiel 7

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Beispiel 8

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Wenn der Integrand an der Stelle nicht existiert

Ein unendlich gekrümmtes Trapez für ein solches uneigentliches Integral sieht grundsätzlich so aus.

Uneigentliches Integral mit unendlicher Integrationsgrenze

Manchmal wird ein solches uneigentliches Integral auch als uneigentliches Integral erster Art bezeichnet..gif" width="49" height="19 src=">.

Seltener sind Integrale mit einer unendlichen Untergrenze oder mit zwei unendlichen Grenzen: .

Wir betrachten den beliebtesten Fall https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Nein nicht immer. Integrandhttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Lassen Sie uns in der Zeichnung den Graphen der Integrandenfunktion darstellen. Ein typischer Graph und ein gekrümmtes Trapez für diesen Fall sieht so aus:

Falsches Integralhttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", mit anderen Worten, die Fläche ist auch unendlich. Es kann so sein. In diesem Fall spricht man vom unechten Integral divergiert.

2) Aber. So paradox es auch klingen mag, die Fläche einer unendlichen Figur kann gleich sein... einer endlichen Zahl! Zum Beispiel: .. Im zweiten Fall das unechte Integral konvergiert.

Was passiert, wenn sich unterhalb der Achse ein unendlich gekrümmtes Trapez befindet?.gif" width="217" height="51 src=">.

: .

Beispiel 1

Die Integrandenfunktion https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, was bedeutet, dass alles in Ordnung ist und das unechte Integral mit der Funktion „ „Standard“-Methode.

Anwendung unserer Formel https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

Das heißt, das uneigentliche Integral divergiert und die Fläche des schattierten gekrümmten Trapezes ist gleich unendlich.

Bei der Lösung uneigentlicher Integrale ist es sehr wichtig zu wissen, wie die Graphen grundlegender Elementarfunktionen aussehen!

Beispiel 2

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Machen wir die Zeichnung:

Zunächst stellen wir Folgendes fest: Der Integrand ist auf dem Halbintervall stetig. Gut..gif" width="327" height="53">

(1) Wir nehmen das einfachste Integral einer Potenzfunktion (dieser Sonderfall kommt in vielen Tabellen vor). Es ist besser, das Minuszeichen sofort über das Grenzzeichen hinaus zu verschieben, damit es bei weiteren Berechnungen nicht stört.

(2) Wir ersetzen die Ober- und Untergrenzen mithilfe der Newton-Leibniz-Formel.

(3) Wir weisen darauf hin, dass https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Meine Herren, das muss schon lange verstanden werden ) und vereinfachen Sie die Antwort.

Hier ist die Fläche eines unendlich gekrümmten Trapezes eine endliche Zahl! Unglaublich, aber wahr.

Beispiel 3

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Der Integrand ist stetig auf .

Versuchen wir zunächst, die Stammfunktion (unbestimmtes Integral) zu finden.

Welchem ​​der Tabellenintegrale ähnelt der Integrand? Es erinnert mich an einen Arcustangens: . Diese Überlegungen legen nahe, dass es schön wäre, ein Quadrat im Nenner zu haben. Dies geschieht durch Austausch.

Ersetzen wir:

Es ist immer sinnvoll, eine Überprüfung durchzuführen, d. h. das erhaltene Ergebnis zu differenzieren:

Jetzt finden wir das uneigentliche Integral:

(1) Wir schreiben die Lösung gemäß der Formel . Es ist besser, die Konstante sofort über das Grenzzeichen hinaus zu verschieben, damit sie weitere Berechnungen nicht beeinträchtigt.

(2) Wir ersetzen die Ober- und Untergrenzen gemäß der Newton-Leibniz-Formel..gif" width="56" height="19 src=">? Siehe den Graphen des Arkustangens im bereits mehrfach empfohlenen Artikel.

(3) Wir erhalten die endgültige Antwort. Eine Tatsache, die man auswendig wissen sollte.

Fortgeschrittene Schüler finden das unbestimmte Integral möglicherweise nicht separat und verwenden nicht die Ersetzungsmethode, sondern verwenden stattdessen die Methode, die Funktion unter dem Differentialzeichen zu ersetzen und das uneigentliche Integral „sofort“ zu lösen. In diesem Fall sollte die Lösung etwa so aussehen:

“

Die Integrandenfunktion ist kontinuierlich unter https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“

Beispiel 4

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

! Dies ist ein typisches Beispiel, und ähnliche Integrale werden sehr oft gefunden. Mach es gut! Die Stammfunktion wird hier mithilfe der Methode der Isolierung eines vollständigen Quadrats ermittelt.

Beispiel 5

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Dieses Integral kann im Detail gelöst werden, das heißt, man findet zunächst das unbestimmte Integral, indem man eine Variable ändert. Oder Sie lösen es „sofort“ – indem Sie die Funktion unter dem Differentialvorzeichen subsumieren.

Uneigentliche Integrale unbeschränkter Funktionen

Manchmal werden solche uneigentlichen Integrale auch uneigentliche Integrale zweiter Art genannt. Unechte Integrale der zweiten Art werden heimtückisch unter dem üblichen bestimmten Integral „verschlüsselt“ und sehen genauso aus: ..gif" width="39" height="15 src=">, 2) oder am Punkt , 3) ​​​​​​oder an beiden Punkten gleichzeitig, 4) oder sogar zum Integrationssegment. Für die Fälle 3-4 gibt es einen Link zu einer zusätzlichen Lektion.

Nur ein Beispiel zur Verdeutlichung: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, dann geht unser Nenner auf Null, das heißt, der Integrand existiert zu diesem Zeitpunkt einfach nicht!

Im Allgemeinen bei der Analyse eines unechten Integrals Sie müssen immer beide Integrationsgrenzen in den Integranden einsetzen..jpg" alt="Uneigentliches Integral, Unstetigkeitspunkt an der unteren Integrationsgrenze" width="323" height="380">!}

Hier ist fast alles das Gleiche wie beim Integral erster Art.
Unser Integral ist numerisch gleich der Fläche des schattierten gekrümmten Trapezes, das von oben nicht begrenzt ist. In diesem Fall gibt es zwei Möglichkeiten: Das unechte Integral divergiert (die Fläche ist unendlich) oder das unechte Integral ist gleich einer endlichen Zahl (d. h. die Fläche einer unendlichen Figur ist endlich!).

Es bleibt nur noch, die Newton-Leibniz-Formel zu modifizieren. Es wird auch mit Hilfe einer Grenze modifiziert, allerdings strebt die Grenze nicht mehr gegen Unendlich, sondern schätzenhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> rechts.

Beispiel 6

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Der Integrand hat an einem Punkt eine unendliche Diskontinuität (vergessen Sie nicht, mündlich oder auf einem Entwurf zu überprüfen, ob mit der Obergrenze alles in Ordnung ist!)

Berechnen wir zunächst das unbestimmte Integral:

Ersatz:

Berechnen wir das unechte Integral:

(1) Was ist hier neu? Lösungstechnisch gibt es praktisch nichts. Das einzige, was sich geändert hat, ist der Eintrag unter dem Limit-Symbol: . Der Zusatz bedeutet, dass wir den Wert rechts anstreben (was logisch ist – siehe Grafik). Eine solche Grenze wird in der Grenzwerttheorie als einseitige Grenze bezeichnet. In diesem Fall haben wir einen rechtshändigen Grenzwert.

(2) Wir ersetzen die Ober- und Untergrenzen mithilfe der Newton-Leibniz-Formel.

(3) Lassen Sie uns https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src="> verstehen. Wie kann man bestimmen, wohin der Ausdruck gehen soll? Grob gesagt , in müssen Sie nur den Wert ersetzen, drei Viertel ersetzen und angeben, dass die Lösung die Antwort ist.

In diesem Fall ist das unechte Integral gleich einer negativen Zahl.

Beispiel 7

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Beispiel 8

Berechnen Sie das uneigentliche Integral oder stellen Sie seine Divergenz fest.

Wenn der Integrand an der Stelle nicht existiert

Ein unendlich gekrümmtes Trapez für ein solches uneigentliches Integral sieht grundsätzlich so aus:

Hier ist alles absolut gleich, außer dass unsere Grenze dazu tendiert schätzenhttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> Wir müssen dem Bruchpunkt unendlich nahe kommen links.