Terkadang integral tak wajar seperti itu disebut integral tak wajar jenis kedua. Integral tak wajar jenis kedua secara diam-diam “dienkripsi” di bawah integral tentu biasa dan terlihat persis sama: .

Namun, berbeda dengan integral tertentu, integran memiliki diskontinuitas tak terhingga (tidak ada):

1) pada titik ,

2) titik,

3) di kedua titik sekaligus,

4) atau bahkan pada interval integrasi.

Kita akan melihat dua kasus pertama; untuk kasus 3-4 di akhir artikel terdapat link ke pelajaran tambahan.

Mari kita lihat contoh untuk memperjelasnya:

Tampaknya menjadi satu kesatuan yang pasti. Namun nyatanya ini merupakan integral tak wajar jenis kedua, karena jika kita substitusikan ke dalam integran, maka nilai batas bawahnya

maka penyebut kita menjadi nol, artinya integran tidak ada pada saat ini!

Saat menganalisis integral tak wajar Anda selalu perlu mengganti kedua batas integrasi ke dalam integrand. Dalam hal ini, mari kita periksa batas atas:

Semua baik-baik saja disini. Trapesium lengkung untuk jenis integral tak wajar yang dibahas pada dasarnya terlihat seperti ini:

Di sini semuanya hampir sama seperti pada integral jenis pertama. Integral kita secara numerik sama dengan luas trapesium lengkung yang diarsir, yang tidak dibatasi dari atas. Dalam hal ini, terdapat dua pilihan: integral tak wajar divergen (luasnya tak terhingga), atau integral tak wajar sama dengan bilangan berhingga (jika luas suatu bangun tak hingga berhingga!).

Yang tersisa hanyalah memodifikasi rumus Newton-Leibniz. Ia juga dimodifikasi dengan bantuan suatu limit, namun limitnya tidak lagi cenderung tak terhingga, melainkan untuk menilai di sebelah kanan. Dari gambar, mudah untuk melacak apa yang ada di sepanjang sumbu SAPI di sebelah kanan.

Mari kita lihat bagaimana hal ini diterapkan dalam praktik.

Contoh 6

(jangan lupa cek secara lisan atau draft apakah semuanya baik-baik saja dengan batas atas!). Pertama, mari kita hitung integral tak tentu:

Jika Anda mengalami kesulitan dalam penggantian, silakan lihat pelajarannya Metode substitusi dalam integral tak tentu.

Mari kita hitung integral tak wajar:

(1) Apa yang baru di sini? Praktis tidak ada apa pun dalam hal teknologi solusi. Satu-satunya hal yang berubah adalah entri di bawah ikon batas:

Penambahan +0 berarti kita mengupayakan nilai ¾ di sebelah kanan, yang logis (lihat grafik). Batasan seperti itu dalam teori limit disebut batas sepihak. Dalam hal ini kita punya batas sebelah kanan.

(2) Kita substitusikan batas atas dan batas bawah menggunakan rumus Newton-Leibniz.

(3) Mari kita bahas di . Bagaimana cara menentukan ke mana arah ekspresi? Secara kasar, Anda hanya perlu mengganti nilainya, mengganti tiga perempat dan menunjukkannya. Mari kita sisir jawabannya.

Dalam hal ini, integral tak wajar sama dengan bilangan negatif. Tidak ada kejahatan dalam hal ini, hanya trapesium melengkung yang sesuai terletak di bawah sumbu SAPI. Dan sekarang contoh solusi independen.

Contoh 7

Hitung integral tak wajar atau tentukan divergensinya.

Contoh 8

Hitung integral tak wajar atau tentukan divergensinya.

Jika integran tidak ada pada titik tersebut

Trapesium lengkung tak hingga untuk integral tak wajar pada dasarnya terlihat seperti ini:

Di sini kami melakukan semuanya dengan cara yang persis sama, hanya saja batas kami cenderung demikian untuk menilai Bkiri. Sumbu SAPI kita harus sangat dekat dengan titik puncaknya kiri.

Contoh 9

Hitung integral tak wajar atau tentukan divergensinya.

Integran mengalami diskontinuitas tak terhingga pada titik tersebut B = 3 (kami memeriksa secara lisan bahwa semuanya baik-baik saja dengan batas integrasi lainnya!).

Untuk variasinya, mari kita selesaikan limit ini segera - dengan memasukkan fungsi tersebut ke dalam tanda diferensial. Bagi yang kesulitan dapat mencari integral tak tentu terlebih dahulu menggunakan skema yang telah dibahas.

Penambahan (-0) berarti kita mempunyai batas kidal, dan langsung pada intinya B = 3 kita mendekati porosnya SAPI kiri.

Mari kita cari tahu mengapa pecahan

(lebih baik melakukannya secara lisan atau dalam bentuk draf).

Kami mengganti nilai batas di bawah root B = 3 - 0.

Akhirnya:

Integral tak wajarnya divergen.

Tanda minus berarti trapesium lengkung yang bersangkutan terletak di bawah sumbu SAPI. Berhati-hatilah dengan tanda-tandanya.

Ya, tentu saja, integral tak wajar itu berbeda, tetapi keduanya adalah hal yang berbeda, genre yang berbeda, dan jika Anda gagal memperhatikan tanda-tandanya, maka sebenarnya Anda akan membuat kesalahan yang serius.

Dan dua contoh terakhir untuk pertimbangan independen:

Contoh 10

Hitung integral tak wajar atau tentukan divergensinya.

Contoh 11

Hitung integral tak wajar atau tentukan divergensinya.

Analisis situasi ketika kedua batas integrasi “buruk”, atau titik puncaknya terdapat langsung pada segmen integrasi, dapat ditemukan di artikel Metode yang efisien untuk menyelesaikan integral tertentu dan integral tak wajar.

Solusi dan jawaban:

Contoh 4: Solusi:

.

Contoh 5: Solusi:

Fungsi integral terus menerus aktif .

Contoh 7: Solusi:

Integran mengalami diskontinuitas tak terhingga pada titik tersebut

Integral tak wajarnya divergen.

Catatan: dengan batas ekspresi

Integral tak wajar jenis pertama. Intinya, ini adalah integral tertentu yang sama, tetapi dalam kasus di mana integral memiliki batas atas atau batas bawah integrasi yang tak terbatas, atau kedua batas integrasi tersebut tidak terbatas.

Integral tak wajar jenis kedua. Intinya, ini adalah integral tertentu yang sama, tetapi dalam kasus di mana integral diambil dari fungsi tak terbatas, integran pada sejumlah titik berhingga tidak memiliki segmen integrasi berhingga, yang berubah menjadi tak terhingga.

Untuk perbandingan. Ketika memperkenalkan konsep integral tertentu, diasumsikan bahwa fungsinya F(X) kontinu pada interval [ A, B], dan segmen integrasinya berhingga, yaitu dibatasi oleh bilangan, dan bukan oleh tak terhingga. Beberapa tugas menyebabkan perlunya mengabaikan pembatasan ini. Ini adalah bagaimana integral tak wajar muncul.

Arti geometris dari integral tak wajar Ternyata cukup sederhana. Dalam kasus ketika grafik suatu fungsi kamu = F(X) berada di atas sumbu Sapi, integral tertentu menyatakan luas trapesium lengkung yang dibatasi oleh suatu kurva kamu = F(X) , sumbu x dan ordinat X = A , X = B. Pada gilirannya, integral tak wajar menyatakan luas trapesium lengkung tak berhingga (tak terhingga) yang diapit di antara garis-garisnya kamu = F(X) (pada gambar di bawah - merah), X = A dan sumbu absis.

Integral tak wajar didefinisikan dengan cara yang sama untuk interval tak hingga lainnya:

Luas trapesium lengkung tak hingga dapat berupa bilangan berhingga, dalam hal ini integral tak wajar disebut konvergen. Luasnya juga bisa tak terhingga, dan dalam hal ini integral tak wajar disebut divergen.

Menggunakan limit suatu integral dan bukan integral tak wajar itu sendiri. Untuk menghitung integral tak wajar, kita perlu menggunakan limit integral tertentu. Jika limit ini ada dan berhingga (tidak sama dengan tak terhingga), maka integral tak wajar disebut konvergen, dan sebaliknya - divergen. Kecenderungan suatu variabel di bawah tanda limit bergantung pada apakah kita berhadapan dengan integral tak wajar jenis pertama atau jenis kedua. Mari kita cari tahu tentang ini sekarang.

Integral tak wajar jenis pertama - dengan limit tak terhingga dan konvergensinya

Integral tak wajar dengan batas atas tak terhingga

Jadi, penulisan integral tak wajar berbeda dengan integral tentu biasa karena batas atas integrasinya tidak terhingga.

Definisi. Integral tak wajar dengan batas atas integrasi fungsi kontinu yang tak terhingga F(X) dalam interval dari A sebelum ∞ batas integral fungsi ini dengan batas atas integrasi disebut B dan batas bawah integrasi A asalkan batas atas integrasi tumbuh tanpa batas, yaitu

.

Jika batas ini ada dan sama dengan suatu bilangan, bukannya tak terhingga, maka integral tak wajar disebut konvergen, dan bilangan yang sama dengan limitnya diambil sebagai nilainya. Jika tidak integral tak wajar disebut divergen dan tidak ada arti yang dikaitkan dengannya.

Contoh 1. Hitung integral tak wajar(jika konvergen).

Larutan. Berdasarkan definisi integral tak wajar, kita temukan

Karena limitnya ada dan sama dengan 1, maka ini integral tak wajar konvergen dan sama dengan 1.

Pada contoh berikut integrannya hampir sama dengan contoh 1, hanya saja derajat x bukan dua, melainkan huruf alpha, dan tugasnya mempelajari integral tak wajar untuk konvergensi. Artinya, pertanyaannya masih harus dijawab: pada nilai alfa manakah integral tak wajar ini bertemu, dan pada nilai apa ia menyimpang?

Contoh 2. Periksa integral tak wajar untuk konvergensi(batas bawah integrasi lebih besar dari nol).

Larutan. Kalau begitu, mari kita asumsikan dulu

Dalam ekspresi yang dihasilkan, kita berpindah ke batas di:

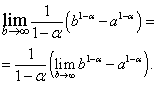
Sangat mudah untuk melihat bahwa limit di ruas kanan ada dan sama dengan nol ketika , yaitu , dan tidak ada ketika , yaitu .

Dalam kasus pertama, yaitu ketika . Jika kemudian dan tidak ada.

Kesimpulan dari penelitian kami adalah sebagai berikut: ini integral tak wajar konvergen di dan menyimpang pada .

Menerapkan rumus Newton-Leibniz pada jenis integral tak wajar yang sedang dipelajari , Anda dapat memperoleh rumus berikut, yang sangat mirip dengannya:

.

Ini adalah rumus umum Newton-Leibniz.

Contoh 3. Hitung integral tak wajar(jika konvergen).

Batas integral ini ada:

Integral kedua, yang merupakan jumlah yang menyatakan integral asal:

Limit integral ini juga ada:

.

Kita cari jumlah dua integral, yang juga merupakan nilai integral tak wajar asli dengan dua limit tak terhingga:

Integral tak wajar jenis kedua - dari fungsi tak terbatas dan konvergensinya

Biarkan fungsinya F(X) diberikan pada segmen dari A sebelum B dan tidak terbatas padanya. Misalkan fungsi tersebut menuju tak terhingga pada suatu titik B , sedangkan di semua titik lain pada segmen tersebut kontinu.

Definisi. Integral tak wajar suatu fungsi F(X) pada segmen dari A sebelum B batas integral fungsi ini dengan batas atas integrasi disebut C , jika saat berusaha C Ke B fungsinya bertambah tanpa batas, dan pada titik X = B fungsi tidak ditentukan, yaitu

.

Jika limit ini ada, maka integral tak wajar jenis kedua disebut konvergen, jika tidak maka disebut divergen.

Dengan menggunakan rumus Newton-Leibniz, kita peroleh.

Integral pasti sebagai limit jumlah integral

dapat ada (yaitu memiliki nilai akhir tertentu) hanya jika kondisinya terpenuhi

Jika setidaknya salah satu dari kondisi ini dilanggar, maka definisi tersebut kehilangan maknanya. Memang benar, dalam kasus segmen tak hingga, misalnya [ A; ) tidak dapat dibagi lagi P bagian yang panjangnya terbatas
, yang, terlebih lagi, akan cenderung nol seiring bertambahnya jumlah segmen. Dalam hal tidak terbatas pada suatu saat Dengan[A; B] persyaratan pemilihan titik sewenang-wenang dilanggar pada sebagian segmen – tidak dapat dipilih =Dengan, karena nilai fungsi pada titik ini tidak terdefinisi. Namun, bahkan untuk kasus-kasus ini, konsep integral tertentu dapat digeneralisasi dengan memperkenalkan bagian lain ke limitnya. Integral pada interval tak terhingga dan fungsi terputus-putus (tak terbatas) disebut bukan milikmu sendiri.

Definisi.

Biarkan fungsinya
didefinisikan pada interval [ A; ) dan dapat diintegralkan pada sembarang interval berhingga [ A; B], yaitu ada
untuk siapa pun B > A. Batas jenis
ditelepon integral tak wajar jenis pertama (atau integral tak wajar pada interval tak hingga) dan tunjukkan
.

Jadi, menurut definisi,
=
.

Jika limit di sebelah kanan ada dan berhingga, maka integral tak wajar
ditelepon konvergen . Jika limit ini tidak terhingga, atau tidak ada sama sekali, maka dikatakan integral tak wajar menyimpang .

Demikian pula, kita dapat memperkenalkan konsep integral tak wajar dari suatu fungsi
sepanjang interval (–; B]:

=
.

Dan integral tak wajar dari fungsi tersebut
pada interval (–; +) didefinisikan sebagai jumlah integral yang diperkenalkan di atas:

=
+
,

Di mana A– titik sewenang-wenang. Integral ini konvergen jika kedua suku konvergen, dan divergen jika paling sedikit salah satu sukunya divergen.

Dari sudut pandang geometris, integral
,
, menentukan nilai numerik luas trapesium lengkung tak hingga yang dibatasi di atasnya oleh grafik fungsi
, kiri – lurus
, dari bawah - sumbu OX. Konvergensi integral berarti adanya luas berhingga pada trapesium tersebut dan persamaannya dengan batas luas trapesium lengkung dengan dinding siku-siku yang dapat digerakkan.
.

Untuk kasus integral yang limitnya tak terhingga, kita dapat menggeneralisasikannya Rumus Newton-Leibniz:

=
= F( + ) – F( A),

di mana F( + ) =
. Jika limit ini ada, maka integralnya konvergen, jika tidak maka integralnya divergen.

Kami mempertimbangkan generalisasi konsep integral tertentu pada kasus interval tak hingga.

Sekarang mari kita pertimbangkan generalisasi untuk kasus fungsi tak terbatas.

Definisi

Biarkan fungsinya
didefinisikan pada interval [ A; B), tidak terbatas pada lingkungan tertentu pada titik tersebut B, dan kontinu pada interval apa pun
, di mana >0 (dan, oleh karena itu, dapat diintegrasikan pada interval ini, yaitu.
ada). Batas jenis
ditelepon integral tak wajar jenis kedua (atau integral tak wajar dari fungsi tak terbatas) dan dilambangkan
.

Jadi, integral tak wajar dari tak terbatas pada suatu titik B fungsi ada menurut definisi

=
.

Jika limit di sebelah kanan ada dan berhingga, maka disebut integral konvergen. Jika tidak ada limit berhingga, maka disebut integral tak wajar berbeda.

Demikian pula, kita dapat mendefinisikan integral tak wajar dari suatu fungsi
mempunyai diskontinuitas tak terhingga pada titik tersebut A:

=
.

Jika fungsinya
mempunyai celah tak terhingga pada titik interiornya Dengan
, maka integral tak wajar didefinisikan sebagai berikut

=
+
=
+
.

Integral ini konvergen jika kedua suku konvergen, dan divergen jika paling sedikit satu suku menyimpang.

Dari sudut pandang geometris, integral tak wajar dari fungsi tak terbatas juga mencirikan luas trapesium lengkung tak terbatas:

Karena integral tak wajar diturunkan dengan meneruskan ke limit integral tertentu, semua sifat integral tertentu dapat dipindahkan (dengan penyempurnaan yang sesuai) ke integral tak wajar jenis pertama dan kedua.

Dalam banyak soal yang mengarah pada integral tak wajar, tidak perlu mengetahui integral tersebut sama dengan apa, cukup dengan memverifikasi konvergensi atau divergensinya. Untuk ini mereka menggunakan tanda-tanda konvergensi. Tanda-tanda konvergensi integral tak wajar:

1) Tanda perbandingan.

Biarlah itu untuk semua orang X

. Lalu jika
menyatu, lalu menyatu
, Dan

. Jika
menyimpang, lalu menyimpang dan
.

2) Jika konvergen
, lalu konvergen dan
(integral terakhir dalam hal ini disebut benar-benar konvergen).

Tanda-tanda konvergensi dan divergensi integral tak wajar fungsi tak terbatas serupa dengan yang dirumuskan di atas.

Contoh pemecahan masalah.

Contoh 1.

A)
; B)
; V)

G)
; D)
.

Larutan.

a) Menurut definisi kita mempunyai:

.

b) Demikian pula

Oleh karena itu, integral ini konvergen dan sama dengan .

c) Menurut definisi
=
+
, Dan A– nomor sewenang-wenang. Mari kita bahas kasus kita
, maka kita mendapatkan:

Integral ini konvergen.

Artinya integral ini divergen.

e) Mari kita pertimbangkan
.

Untuk mencari antiturunan dari integrand, perlu diterapkan metode integrasi per bagian. Kemudian kita mendapatkan:
Sejak keduanya
, juga tidak

tidak ada, maka tidak ada dan

Oleh karena itu, integral ini divergen.

Contoh 2. Selidiki konvergensi integral P.

Larutan.

tergantung pada
Pada

kita punya:
Jika
, Itu

kita punya:
Jika
Dan . Oleh karena itu, integralnya divergen.
, Kemudian

= ,

Oleh karena itu, integralnya konvergen.

kita punya:
, Itu

oleh karena itu, integralnya divergen.

Dengan demikian,

Contoh 3.

Hitung integral tak wajar atau tentukan divergensinya:

A)
;
B)
.

Larutan.

;
V)
a) Integral

merupakan integral tak wajar jenis kedua, sejak integran

.

tidak terbatas pada satu titik .

. Kemudian, menurut definisi,
Integralnya konvergen dan sama dengan
b) Pertimbangkan

. Disini juga integran tidak dibatasi pada titiknya

. Oleh karena itu, integral ini merupakan integral jenis kedua dan, menurut definisi,
Oleh karena itu, integralnya divergen.
c) Pertimbangkan
. Integrasi
mengalami kesenjangan tak terbatas di dua titik:
Dan

=

=

.

, yang pertama termasuk dalam interval integrasi
.

. Oleh karena itu, integral ini merupakan integral tak wajar jenis kedua. Kemudian, menurut definisi

Oleh karena itu, integralnya konvergen dan sama dengan

Apakah kamu di sini sekarang? =) Tidak, saya tidak bermaksud mengintimidasi siapa pun, hanya saja topik integral tak wajar merupakan ilustrasi yang sangat baik tentang betapa pentingnya untuk tidak mengabaikan matematika tingkat tinggi dan ilmu eksakta lainnya. Semua yang Anda perlukan untuk mempelajari pelajaran ini ada di situs web - dalam bentuk yang terperinci dan dapat diakses, jika Anda mau...

Jadi, mari kita mulai. Secara kiasan, integral tak wajar adalah integral tentu “lanjutan”, dan sebenarnya tidak banyak kesulitan yang dihadapinya, dan selain itu, integral tak wajar mempunyai arti geometri yang sangat baik. Apa yang dimaksud dengan mengevaluasi integral tak wajar? Hitung integral tak wajar - ini berarti menemukan NOMORnya(persis sama dengan integral tertentu),

atau buktikan bahwa itu berbeda

(yaitu, Anda berakhir dengan tak terhingga, bukan angka).

Ada dua jenis integral tak wajar. Integral tak wajar dengan batas integrasi tak terhingga Kadang-kadang integral tak wajar disebut

integral tak wajar jenis pertama

. Secara umum, integral tak wajar dengan limit tak hingga paling sering terlihat seperti ini: . Apa bedanya dengan integral tertentu? Di batas atas. Tidak ada habisnya: . Yang kurang umum adalah integral dengan batas bawah tak hingga atau dengan dua batas tak hingga: , dan kita akan membahasnya nanti - setelah Anda sudah terbiasa :) Nah, sekarang mari kita lihat kasus yang paling populer. Dalam sebagian besar contoh, fungsi integrand kontinu di antaranya, dan yang ini fakta penting harus diperiksa dulu! Karena jika ada gap, maka ada tambahan nuansa. Untuk lebih pastinya, mari kita asumsikan bahwa itu pun tipikal

trapesium melengkung akan terlihat seperti ini: secara numerik sama dengan luasnya. Opsi berikut ini dimungkinkan:

1) Pikiran pertama yang terlintas dalam pikiran: “karena angkanya tidak terbatas, maka ", dengan kata lain luasnya juga tidak terbatas. Mungkin saja demikian. Dalam hal ini mereka mengatakan bahwa integral tak wajar menyimpang.

2) Tetapi. Meski terdengar paradoks, luas suatu bangun tak terhingga bisa sama dengan... bilangan berhingga! Misalnya: . Mungkinkah ini benar? Dengan mudah. Dalam kasus kedua, integral tak wajar menyatu.

3) Tentang opsi ketiga nanti.

Dalam kasus apa integral tak wajar menyimpang dan dalam kasus apa integral tak wajar itu konvergen? Ini bergantung pada integran, dan kita akan segera melihat contoh spesifiknya.

Apa yang terjadi jika trapesium lengkung tak hingga terletak di bawah sumbu? Dalam hal ini, integral tak wajar (divergen) atau sama dengan bilangan negatif berhingga.

Dengan demikian, integral tak wajar dapat bernilai negatif.

Penting! Ketika Anda diberikan integral tak wajar APAPUN untuk diselesaikan, maka, secara umum, tidak ada pembicaraan tentang area mana pun dan tidak perlu membuat gambar. Pengertian geometri integral tak wajar telah saya jelaskan hanya untuk memudahkan pemahaman materi.

Karena integral tak wajar sangat mirip dengan integral tentu, mari kita ingat rumus Newton-Leibniz: . Sebenarnya rumus tersebut juga berlaku untuk integral tak wajar, hanya saja perlu sedikit dimodifikasi. Apa bedanya? Pada batas atas integrasi yang tak terhingga: . Mungkin banyak yang menduga ini sudah berbau penerapan teori limit, dan rumusnya akan ditulis seperti ini: .

Apa perbedaannya dengan integral tertentu? Tidak ada yang spesial! Seperti pada integral tentu, Anda harus bisa mencari fungsi antiturunannya (integral tak tentu), dan bisa menerapkan rumus Newton-Leibniz. Yang ditambahkan hanya perhitungan limitnya saja. Siapa pun yang mengalami saat-saat buruk bersama mereka, ambillah pelajaran Batasan fungsi. Contoh solusi, karena lebih baik terlambat daripada wajib militer.

Mari kita lihat dua contoh klasik:

Contoh 1

Untuk lebih jelasnya, saya akan menggambarnya, meskipun saya tekankan sekali lagi, pada latihan Tidak perlu membuat gambar dalam tugas ini.

Fungsi integran kontinu pada setengah interval, artinya semuanya baik-baik saja dan integral tak wajar dapat dihitung dengan metode “standar”.

Penerapan formula kami dan solusi untuk masalahnya terlihat seperti ini:

Artinya, integral tak wajar menyimpang, dan luas trapesium lengkung yang diarsir sama dengan tak terhingga.

Dalam contoh yang dibahas, kita memiliki integral tabel paling sederhana dan teknik penerapan rumus Newton-Leibniz yang sama seperti pada integral tertentu. Namun rumus ini akan diterapkan di bawah tanda limit. Alih-alih huruf biasa dari variabel “dinamis”, huruf “menjadi” muncul. Hal ini tidak boleh membingungkan atau membingungkan, karena huruf apa pun tidak lebih buruk dari huruf “X” standar.

Jika Anda tidak mengerti mengapa di , maka ini sangat buruk, entah Anda tidak memahami limit yang paling sederhana (dan umumnya tidak memahami apa itu limit), atau Anda tidak tahu seperti apa grafik fungsi logaritma. Dalam kasus kedua, hadiri pelajaran Grafik dan sifat-sifat fungsi dasar.

Saat menyelesaikan integral tak wajar, sangat penting untuk mengetahui seperti apa grafik fungsi dasar dasar!

Tugas yang sudah selesai akan terlihat seperti ini:

“

! Saat menyiapkan contoh, kami selalu menginterupsi solusi dan menunjukkan apa yang terjadi pada integran – apakah kontinu pada interval integrasi atau tidak?. Dengan ini kami mengidentifikasi jenis integral tak wajar dan membenarkan tindakan selanjutnya.

Contoh 2

Hitung integral tak wajar atau tentukan divergensinya.

Mari kita membuat gambarnya:

Pertama, kita perhatikan hal berikut: integran kontinu pada setengah interval. Tudung. Kami menyelesaikannya menggunakan rumus :

(1) Kita mengambil integral paling sederhana dari fungsi pangkat (kasus khusus ini ada di banyak tabel). Sebaiknya segera pindahkan tanda minus melampaui tanda batas agar tidak mengganggu perhitungan selanjutnya.

(2) Kita substitusikan batas atas dan batas bawah menggunakan rumus Newton-Leibniz.

(3) Kami menunjukkan bahwa di (Tuan-tuan, ini seharusnya sudah dipahami sejak lama) dan menyederhanakan jawabannya.

Di sini luas trapesium lengkung tak hingga adalah bilangan berhingga! Sulit dipercaya tapi benar.

Contoh yang sudah selesai akan terlihat seperti ini:

“

Fungsi integral terus menerus aktif

“

Apa yang harus dilakukan jika Anda menemukan integral seperti - dengan titik istirahat pada interval integrasi? Artinya ada kesalahan ketik pada contoh. (Yang paling disukai), atau tentang pelatihan tingkat lanjut. Dalam kasus terakhir, karena sifat aditif, kita harus mempertimbangkan dua integral tak wajar pada interval dan kemudian menangani jumlahnya.

Terkadang, karena kesalahan ketik atau kesengajaan, dapat terjadi integral tak wajar tidak ada sama sekali, jadi, misalnya, jika Anda memasukkan akar kuadrat dari “x” ke dalam penyebut integral di atas, maka bagian dari interval integrasi tidak akan termasuk dalam domain definisi integral sama sekali.

Selain itu, integral tak wajar mungkin tidak ada bahkan dengan semua “kesejahteraan nyata”. Contoh klasik: . Meskipun kosinus mempunyai kepastian dan kontinuitas, integral tak wajar seperti itu tidak ada! Mengapa? Ini sangat sederhana karena:
- tidak ada batas yang sesuai.

Dan contoh-contoh seperti itu, meskipun jarang, memang terjadi dalam praktiknya! Jadi, selain konvergensi dan divergensi, ada juga hasil ketiga dari penyelesaian dengan jawaban yang valid: “tidak ada integral tak wajar”.

Perlu juga dicatat bahwa definisi ketat dari integral tak wajar diberikan secara tepat melalui limit, dan mereka yang ingin dapat membiasakan diri dengannya dalam literatur pendidikan. Baiklah, kita lanjutkan pelajaran praktis dan beralih ke tugas yang lebih bermakna:

Contoh 3

Hitung integral tak wajar atau tentukan divergensinya.

Pertama, mari kita coba mencari fungsi antiturunan (integral tak tentu). Jika kita gagal melakukan hal ini, maka tentu saja kita juga tidak akan dapat menyelesaikan integral tak wajar tersebut.

Integral tabel manakah yang serupa dengan integran? Ini mengingatkan saya pada garis singgung busur: . Pertimbangan ini menunjukkan bahwa akan lebih baik jika ada persegi sebagai penyebutnya. Hal ini dilakukan dengan penggantian.

Mari kita ganti:

Integral tak tentu telah ditemukan; dalam hal ini, tidak masuk akal untuk menambahkan konstanta.

Selalu berguna untuk memeriksa draf, yaitu membedakan hasil yang diperoleh:

Integran asal telah diperoleh, artinya integral tak tentu telah ditemukan dengan benar.

Sekarang kita cari integral tak wajarnya:

(1) Kita tuliskan penyelesaiannya sesuai dengan rumus . Sebaiknya segera pindahkan konstanta tersebut melampaui tanda batas agar tidak mengganggu perhitungan selanjutnya.

(2) Kita substitusikan batas atas dan batas bawah sesuai dengan rumus Newton-Leibniz. Mengapa pada ? Lihat grafik arctangent di artikel yang sudah direkomendasikan.

(3) Kami mendapatkan jawaban akhir. Sebuah fakta yang berguna untuk dihafal.

Siswa tingkat lanjut tidak boleh mencari integral tak tentu secara terpisah dan tidak menggunakan metode penggantian, melainkan menggunakan metode mensubstitusi fungsi di bawah tanda diferensial dan menyelesaikan integral tak wajar “segera”. Dalam hal ini, solusinya akan terlihat seperti ini:

“

Integran terus menerus pada .

“

Contoh 4

Hitung integral tak wajar atau tentukan divergensinya.

! Ini adalah contoh tipikal, dan integral serupa sangat sering ditemukan. Kerjakan dengan baik! Fungsi antiturunan di sini ditemukan dengan menggunakan metode pemilihan kuadrat lengkap; rincian lebih lanjut tentang metode tersebut dapat ditemukan dalam pelajaran Mengintegrasikan Beberapa Pecahan.

Contoh 5

Hitung integral tak wajar atau tentukan divergensinya.

Integral ini dapat diselesaikan secara detail, yaitu mencari terlebih dahulu integral tak tentu dengan melakukan perubahan variabel. Atau Anda dapat menyelesaikannya “segera” - dengan memasukkan fungsi tersebut ke dalam tanda diferensial. Siapa yang memiliki pelatihan matematika?

Solusi dan jawaban lengkap di akhir pelajaran.

Contoh solusi integral tak wajar dengan batas bawah integrasi tak terhingga dapat ditemukan di halaman Metode yang efisien untuk menyelesaikan integral tak wajar. Di sana kami juga menganalisis kasus ketika kedua batas integrasi tidak terbatas.

Integral tak wajar dari fungsi tak terbatas

Atau integral tak wajar jenis kedua. Integral tak wajar jenis kedua secara diam-diam “dienkripsi” di bawah integral pasti biasa dan terlihat persis sama: Namun, tidak seperti integral tentu, integran mengalami diskontinuitas tak terhingga (tidak ada): 1) pada titik , 2) atau pada titik , 3) ​​​​atau pada kedua titik sekaligus, 4) atau genap pada ruas integrasi. Kita akan melihat dua kasus pertama; untuk kasus 3-4 di akhir artikel terdapat link ke pelajaran tambahan.

Sekadar contoh untuk memperjelas: . Tampaknya menjadi satu kesatuan yang pasti. Namun kenyataannya, ini adalah integral tak wajar jenis kedua; jika kita mensubstitusikan nilai batas bawah ke dalam integran, maka penyebut kita menjadi nol, yaitu integran tidak ada pada saat ini!

Secara umum, ketika menganalisis integral tak wajar Anda selalu perlu mengganti kedua batas integrasi ke dalam integrand. Dalam hal ini, mari kita periksa batas atas: . Semua baik-baik saja disini.

Trapesium lengkung untuk jenis integral tak wajar yang dibahas pada dasarnya terlihat seperti ini:

Di sini semuanya hampir sama seperti pada integral jenis pertama.

Integral kita secara numerik sama dengan luas trapesium lengkung yang diarsir, yang tidak dibatasi dari atas. Dalam hal ini, terdapat dua pilihan*: integral tak wajar divergen (luasnya tak terhingga) atau integral tak wajar sama dengan bilangan berhingga (yaitu, luas suatu bangun tak hingga berhingga!).

* secara default kita biasanya berasumsi bahwa integral tak wajar itu ada

Yang tersisa hanyalah memodifikasi rumus Newton-Leibniz. Ia juga dimodifikasi dengan bantuan suatu limit, namun limitnya tidak lagi cenderung tak terhingga, melainkan ke nilai di sebelah kanan. Hal ini mudah untuk diikuti dari gambarnya: sepanjang sumbu kita harus mendekati titik puncaknya dengan jarak yang sangat dekat di sebelah kanan.

Mari kita lihat bagaimana hal ini diterapkan dalam praktik.

Contoh 6

Hitung integral tak wajar atau tentukan divergensinya.

Integran tersebut mempunyai diskontinuitas tak terhingga pada suatu titik (jangan lupa untuk mengecek secara verbal atau pada draft bahwa semuanya baik-baik saja dengan batas atasnya!)

Pertama, mari kita hitung integral tak tentu:

Penggantian:

Jika Anda mengalami kesulitan dalam penggantian, silakan lihat pelajarannya Metode substitusi dalam integral tak tentu.

Mari kita hitung integral tak wajar:

(1) Apa yang baru di sini? Praktis tidak ada apa pun dalam hal teknologi solusi. Satu-satunya hal yang berubah adalah entri di bawah ikon batas: . Penambahan berarti kita mengupayakan nilai di sebelah kanan (yang logis - lihat grafik). Batasan seperti itu dalam teori limit disebut batas sepihak. Dalam hal ini kita punya batas sebelah kanan.

(2) Kita substitusikan batas atas dan batas bawah menggunakan rumus Newton-Leibniz.

(3) Mari kita bahas di . Bagaimana cara menentukan ke mana arah ekspresi? Secara kasar, Anda hanya perlu mengganti nilainya, mengganti tiga perempat dan menunjukkannya. Mari kita sisir jawabannya.

Dalam hal ini, integral tak wajar sama dengan bilangan negatif. Tidak ada kejahatan dalam hal ini, hanya trapesium melengkung yang sesuai terletak di bawah sumbu.

Dan sekarang dua contoh solusi independen.

Contoh 7

Hitung integral tak wajar atau tentukan divergensinya.

Contoh 8

Hitung integral tak wajar atau tentukan divergensinya.

Jika integran tidak ada pada titik tersebut

Trapesium lengkung tak hingga untuk integral tak wajar pada dasarnya terlihat seperti ini.

Integral tak wajar dengan limit integrasi tak hingga

Terkadang integral tak wajar seperti itu disebut juga integral tak wajar jenis pertama..gif" width="49" height="19 src=">.

Yang kurang umum adalah integral dengan batas bawah tak hingga atau dengan dua batas tak hingga: .

Kami akan mempertimbangkan kasus paling populer https://pandia.ru/text/80/057/images/image005_1.gif" width="63" height="51"> ? Tidak, tidak selalu. Integrasihttps://pandia.ru/text/80/057/images/image007_0.gif" width="47" height="23 src=">

Mari kita gambarkan grafik fungsi integran pada gambar. Grafik tipikal dan trapesium lengkung untuk kasus ini terlihat seperti ini:

Integral tak wajarhttps://pandia.ru/text/80/057/images/image009_0.gif" width="100" height="51">", dengan kata lain luasnya juga tidak terbatas. Mungkin saja demikian. Dalam hal ini mereka mengatakan bahwa integral tak wajar menyimpang.

2) Tetapi. Meski terdengar paradoks, luas suatu bangun tak terhingga bisa sama dengan... bilangan berhingga! Misalnya: .. Dalam kasus kedua, integral tak wajar menyatu.

Apa yang terjadi jika trapesium lengkung tak hingga terletak di bawah sumbu?.gif" width="217" height="51 src=">.

: .

Contoh 1

Fungsi integran https://pandia.ru/text/80/057/images/image017_0.gif" width="43" height="23">, yang berarti semuanya baik-baik saja dan integral tak wajar dapat dihitung menggunakan “ metode standar”.

Penerapan rumus kami https://pandia.ru/text/80/057/images/image018_0.gif" width="356" height="49">

Artinya, integral tak wajar menyimpang, dan luas trapesium lengkung yang diarsir sama dengan tak terhingga.

Saat menyelesaikan integral tak wajar, sangat penting untuk mengetahui seperti apa grafik fungsi dasar dasar!

Contoh 2

Hitung integral tak wajar atau tentukan divergensinya.

Mari kita membuat gambarnya:

Pertama, kita perhatikan hal berikut: integran kontinu pada setengah interval. Bagus..gif" width="327" height="53">

(1) Kita mengambil integral paling sederhana dari fungsi pangkat (kasus khusus ini ada di banyak tabel). Sebaiknya segera pindahkan tanda minus melampaui tanda batas agar tidak mengganggu perhitungan selanjutnya.

(2) Kita substitusikan batas atas dan batas bawah menggunakan rumus Newton-Leibniz.

(3) Kami menunjukkan bahwa https://pandia.ru/text/80/057/images/image024.gif" width="56" height="19 src="> (Tuan-tuan, ini sudah lama perlu dipahami ) dan sederhanakan jawabannya.

Di sini luas trapesium lengkung tak hingga adalah bilangan berhingga! Sulit dipercaya tapi benar.

Contoh 3

Hitung integral tak wajar atau tentukan divergensinya.

Integran terus menerus pada .

Pertama, mari kita coba mencari fungsi antiturunan (integral tak tentu).

Integral tabel manakah yang serupa dengan integran? Ini mengingatkan saya pada garis singgung busur: . Pertimbangan ini menunjukkan bahwa akan lebih baik jika ada persegi sebagai penyebutnya. Hal ini dilakukan dengan penggantian.

Mari kita ganti:

Melakukan pemeriksaan selalu berguna, yaitu membedakan hasil yang diperoleh:

Sekarang kita cari integral tak wajarnya:

(1) Kita tuliskan penyelesaiannya sesuai dengan rumus . Sebaiknya segera pindahkan konstanta tersebut melampaui tanda batas agar tidak mengganggu perhitungan selanjutnya.

(2) Kita substitusikan batas atas dan bawah sesuai dengan rumus Newton-Leibniz..gif" width="56" height="19 src=">? Lihat grafik arctangent di artikel yang sudah berulang kali direkomendasikan.

(3) Kami mendapatkan jawaban akhir. Sebuah fakta yang berguna untuk dihafal.

Siswa tingkat lanjut tidak boleh mencari integral tak tentu secara terpisah dan tidak menggunakan metode penggantian, melainkan menggunakan metode mensubstitusi fungsi di bawah tanda diferensial dan menyelesaikan integral tak wajar “segera”. Dalam hal ini, solusinya akan terlihat seperti ini:

“

Fungsi integrand berkelanjutan di https://pandia.ru/text/80/057/images/image041.gif" width="337" height="104">
“

Contoh 4

Hitung integral tak wajar atau tentukan divergensinya.

! Ini adalah contoh tipikal, dan integral serupa sangat sering ditemukan. Kerjakan dengan baik! Fungsi antiturunan ditemukan di sini menggunakan metode mengisolasi kuadrat lengkap.

Contoh 5

Hitung integral tak wajar atau tentukan divergensinya.

Integral ini dapat diselesaikan secara detail, yaitu mencari terlebih dahulu integral tak tentu dengan melakukan perubahan variabel. Atau Anda dapat menyelesaikannya "segera" - dengan memasukkan fungsi tersebut ke dalam tanda diferensial..

Integral tak wajar dari fungsi tak terbatas

Terkadang integral tak wajar seperti itu disebut integral tak wajar jenis kedua. Integral tak wajar jenis kedua secara diam-diam “dienkripsi” di bawah integral pasti biasa dan terlihat persis sama: ..gif" width="39" height="15 src=">, 2) atau pada titik , 3) ​​​​atau di kedua titik sekaligus, 4) atau bahkan pada segmen integrasi. Kami akan mempertimbangkan dua kasus pertama; untuk kasus 3-4 terdapat tautan ke pelajaran tambahan di akhir artikel.

Sekadar contoh untuk memperjelas: https://pandia.ru/text/80/057/images/image048.gif" width="65 height=41" height="41">, maka penyebut kita menjadi nol, artinya, integrand sama sekali tidak ada pada saat ini!

Secara umum, ketika menganalisis integral tak wajar Anda selalu perlu mengganti kedua batas integrasi ke dalam integrand..jpg" alt="Integral tak wajar, titik diskontinuitas di batas bawah integrasi" width="323" height="380">!}

Di sini semuanya hampir sama seperti pada integral jenis pertama.
Integral kita secara numerik sama dengan luas trapesium lengkung yang diarsir, yang tidak dibatasi dari atas. Dalam hal ini, terdapat dua pilihan: integral tak wajar divergen (luasnya tak terhingga) atau integral tak wajar sama dengan bilangan berhingga (yaitu, luas suatu bangun tak hingga berhingga!).

Yang tersisa hanyalah memodifikasi rumus Newton-Leibniz. Ia juga dimodifikasi dengan bantuan suatu limit, namun limitnya tidak lagi cenderung tak terhingga, melainkan untuk menilaihttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> di sebelah kanan.

Contoh 6

Hitung integral tak wajar atau tentukan divergensinya.

Integran tersebut mempunyai diskontinuitas tak terhingga pada suatu titik (jangan lupa untuk mengecek secara verbal atau pada draft bahwa semuanya baik-baik saja dengan batas atasnya!)

Pertama, mari kita hitung integral tak tentu:

Penggantian:

Mari kita hitung integral tak wajar:

(1) Apa yang baru di sini? Praktis tidak ada apa pun dalam hal teknologi solusi. Satu-satunya hal yang berubah adalah entri di bawah ikon batas: . Penambahan berarti kita mengupayakan nilai di sebelah kanan (yang logis - lihat grafik). Batasan seperti itu dalam teori batas disebut batas satu sisi. Dalam hal ini kita mempunyai limit tangan kanan.

(2) Kita substitusikan batas atas dan batas bawah menggunakan rumus Newton-Leibniz.

(3) Mari kita pahami https://pandia.ru/text/80/057/images/image058.gif" width="69" height="41 src=">. Bagaimana cara menentukan ke mana ekspresi harus pergi? Secara kasar , di dalamnya Anda hanya perlu mengganti nilainya, mengganti tiga perempat dan menunjukkan sisir jawabannya.

Dalam hal ini, integral tak wajar sama dengan bilangan negatif.

Contoh 7

Hitung integral tak wajar atau tentukan divergensinya.

Contoh 8

Hitung integral tak wajar atau tentukan divergensinya.

Jika integran tidak ada pada titik tersebut

Trapesium lengkung tak hingga untuk integral tak wajar pada dasarnya terlihat seperti ini:

Di sini semuanya sama persis, hanya saja batas kita cenderung untuk menilaihttps://pandia.ru/text/80/057/images/image052.gif" width="28" height="19"> kita harus mendekati titik puncaknya secara tak terhingga kiri.