Fungsi y=f(x) disebut terdiferensiasi di suatu titik x 0 jika mempunyai turunan tertentu di titik tersebut, yaitu. jika limit hubungan itu ada dan terbatas.

Jika suatu fungsi terdiferensiasi pada setiap titik pada segmen tertentu [a; b] atau interval (a; b), maka dikatakan terdiferensiasi pada interval [a; b] atau, masing-masing, dalam interval (a; b).

Teorema berikut ini valid, yang menetapkan hubungan antara fungsi terdiferensiasi dan fungsi kontinu.

Dalil. Jika fungsi y=f(x) terdiferensialkan di suatu titik x 0, maka fungsi tersebut kontinu di titik tersebut.

Jadi, dari diferensiasi suatu fungsi, kontinuitasnya mengikuti.

Bukti. Jika kemudian

di mana b adalah kuantitas yang sangat kecil, mis. besaran yang cenderung nol jika Dx>0. Tapi kemudian

Dy=f "(x 0) Dx+bDx=> Dy>0 di Dx>0, yaitu f(x) - f(x 0)>0 di x>x 0,

dan ini berarti fungsi f(x) kontinu di titik x 0 . Q.E.D.

Jadi, fungsi tersebut tidak dapat mempunyai turunan pada titik diskontinuitas. Kebalikannya tidak benar: ada fungsi kontinu yang tidak terdiferensiasi di beberapa titik (yaitu, tidak memiliki turunan di titik-titik tersebut).

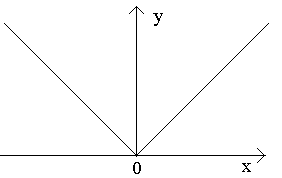
Perhatikan titik a,b,c pada gambar.

Pada titik a untuk Dx>0, rasionya tidak mempunyai batas (karena batas satu sisinya berbeda untuk Dx>0-0 dan Dx>0+0). Di titik A pada grafik tidak terdapat garis singgung tertentu, namun terdapat dua garis singgung satu arah yang berbeda dengan kemiringan 1 dan 2. Titik seperti ini disebut titik sudut.

Di titik b untuk Dx>0, rasionya bertanda konstan dan besarnya tak terhingga. Fungsi tersebut memiliki turunan tak terhingga. Pada titik ini grafik mempunyai garis singgung vertikal. Jenis titik - “titik belok” dengan garis singgung vertikal.

Di titik c, turunan satu sisinya adalah sejumlah besar tanda yang berbeda-beda. Pada titik ini grafik mempunyai dua garis singgung vertikal yang digabungkan. Ketik - "titik kembali" dengan garis singgung vertikal - kasus khusus dari titik sudut.

1. Perhatikan fungsi y=|x|. Fungsi ini kontinu pada suatu titik

Mari kita tunjukkan bahwa ia tidak mempunyai turunan pada saat ini.

f(0+Dx) = f(Dx) = |Dx|. Oleh karena itu, Дy = f(Дx) - f(0) = |Дx|

Tapi kemudian di Dx< 0 (т.е. при Дx стремящемся к 0 слева)

Dan ketika Dx > 0

Jadi perbandingan Dx > 0 di kanan dan kiri mempunyai batas yang berbeda, artinya perbandingan tersebut tidak mempunyai batas, yaitu. turunan dari fungsi y=|x| tidak ada di titik x= 0. Secara geometris, ini berarti bahwa pada titik x = 0 “kurva” ini tidak mempunyai garis singgung tertentu (pada titik ini ada dua).

2. Fungsi tersebut terdefinisi dan kontinu pada seluruh garis bilangan. Mari kita cari tahu apakah fungsi ini memiliki turunan di x= 0.

Oleh karena itu, fungsi yang ditinjau tidak terdiferensiasi di titik tersebut x= 0. Garis singgung kurva di titik ini membentuk sudut p/2 dengan sumbu absis, yaitu. bertepatan dengan sumbu Oy.

3 Definisi turunan suatu fungsi di suatu titik Misalkan fungsi f(x) terdefinisi di lingkungan titik x 0. DEFINISI. Jika terdapat limit (hingga) dari relasi tersebut, maka f(x) disebut titik terdiferensiasi x 0, dan limit itu sendiri disebut turunan dari fungsi f(x) di titik x 0 dan dilambangkan dengan f" (x 0), yaitu, mari kita nyatakan x = x – x 0 adalah pertambahan argumen ketika berpindah dari titik x 0 ke titik x, dan y = f(x 0 + x) – f(x 0) adalah kenaikan fungsi yang sesuai, maka turunan fungsi f(x) di titik x 0 adalah limit rasio kenaikan fungsi terhadap kenaikan argumen yang menyebabkannya, ketika kenaikan argumen cenderung nol.

4 Contoh 1. Mari kita berikan contoh penghitungan turunan dari beberapa fungsi dasar paling sederhana, berdasarkan definisi turunannya. y = a x (0 0. Dengan asumsi | x | 0 adalah titik sembarang, maka 0.Dengan asumsi bahwa | x | 0 adalah titik sembarang, maka">

0.Dengan asumsi bahwa | x | 0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung kenaikan fungsi pada titik ini: Jadi (sinx) = cosx, x R." title=" 5 Contoh 3. Misalkan x 0 > 0. Misalkan |x|0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung pertambahan fungsi pada titik ini: Jadi ( sinx) = cosx, xR." class="link_thumb"> 5 !} 5 Contoh 3. Ambil x 0 > 0. Asumsikan | x | 0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung kenaikan fungsi pada titik ini: Jadi (sinx) = cosx, x R. 0.Dengan asumsi bahwa | x | 0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung kenaikan fungsi pada titik ini: Jadi (sinx) = cosx, x R."> 0. Dengan asumsi bahwa | x | 0 – titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung kenaikan fungsi pada titik ini: Jadi (sinx) = cosx, x R."> 0. Dengan asumsi bahwa | x | 0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung kenaikan fungsi pada titik ini: Jadi (sinx) = cosx, x R." title=" 5 Contoh 3. Misalkan x 0 > 0. Misalkan |x|0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung pertambahan fungsi pada titik ini: Jadi ( sinx) = cosx, xR."> title="5 Contoh 3. Ambil x 0 > 0. Asumsikan | x | 0 adalah titik sembarang, maka Contoh 4. y = sinx, x R. Ambil x 0 R dan hitung kenaikan fungsi pada titik ini: Jadi (sinx) = cosx, x R."> !}

6 TEOREMA. Jika suatu fungsi f(x) terdiferensialkan di suatu titik x 0, maka fungsi tersebut kontinu di titik tersebut. Bukti. Misalkan ada Maka Dari sini kita peroleh bahwa f (x) – f (x 0) = f "(x 0) (x – x 0) + (x – x 0)α(x) untuk x x 0. Artinya, f( x) kontinu di titik x 0. Kontinuitas fungsi terdiferensiasi (1)

7 CATATAN. Kontinuitas suatu fungsi di suatu titik bukanlah syarat yang cukup bagi adanya turunan di titik tersebut. Contoh 5. f(x) = x. Mari kita pelajari perilaku f (x) di sekitar x 0 = 0. Di sini f (x) f (0) = 0 di x 0. Yaitu fungsinya kontinu di titik x 0 = 0. Misalkan x y 0 Limitnya tidak ada, karena Jadi, fungsi f (x) = x tidak mempunyai turunan di titik x = 0, meskipun kontinu di titik ini titik

8 Contoh x y 0 pada x 0. pada x 0. Yaitu f(x) kontinu di titik x = 0. Artinya, f(x) tidak mempunyai turunan di titik x = 0 dan oleh karena itu, tidak terdiferensiasi di titik ini. Mari kita pelajari perilaku f(x) di sekitar titik x = 0.

9 Misalkan fungsi y = f(x) terdiferensialkan di titik x 0. Maka, menurut (1), kenaikannya di titik x 0 dapat ditulis sebagai y = f(x 0 + x) – f(x 0) = f ( x 0) x + o(x) di x. Diferensial fungsi f (x 0) x adalah linier utama relatif terhadap x bagian kenaikan fungsi y = f(x) di titik x 0 disebut diferensial fungsi di titik x 0 dengan kenaikan x dan dilambangkan df(x 0 ; x) atau df(x 0 ) atau df atau dу. kamu = f(x 0 + x) – f(x 0) = df(x 0; x) + o(x) di x. DEFINISI. Bagian utama dari kenaikan, linier terhadap x. Sangat kecil dari orde yang lebih tinggi dari x. Sekarang kenaikan fungsi dapat ditulis seperti ini:

10 CATATAN. Kenaikan x sering dilambangkan dengan simbol dx dan disebut diferensial variabel bebas. Jadi, diferensial suatu fungsi di suatu titik x 0 dapat ditulis sebagai df (x 0) \u003d f "(x 0) dx. Jika suatu fungsi terdiferensiasi di setiap titik pada interval tertentu, maka diferensialnya dy adalah a fungsi x dan dx: dy \u003d f "(x)dx. Dari sini, secara khusus, kita memperoleh ekspresi untuk turunannya, yaitu turunan dapat dianggap sebagai rasio diferensial suatu fungsi terhadap diferensial variabel bebas.

11 Arti Geometris Turunan dan Diferensial Misalkan fungsi y = f(x) terdefinisi pada U(x 0) dan terdiferensiasi di titik x 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + y 0 L – garis potong L 0 – garis singgung x y = f(x 0 + x) – f(x 0) di x karena kontinuitas fungsi. Garis singgung grafik fungsi y = f(x) di titik M 0 adalah posisi batas garis potong L di x. y Jika fungsinya terdiferensiasi di titik x 0, maka pada persamaan garis potong y/ x f (x 0) di x dan persamaan tangennya berbentuk y = y 0 + f (x 0) (x – x 0).

12 М0М0 М x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) untuk x 0 L0L0 tg = f (x 0) Jika y/ x untuk x, maka garis lurus x = x 0 yang dihasilkan persamaan garis potong disebut garis singgung vertikal grafik fungsi di titik M 0. Dari persamaan tangen diperoleh y – y 0 = f (x 0) (x – x 0) = df (x 0) – pertambahan ordinat garis singgung ketika berpindah dari titik x 0 ke titik x. Garis normal suatu fungsi di titik M 0 adalah garis lurus yang tegak lurus garis singgung yang melalui titik M 0. Persamaannya berbentuk y = y 0 – 1/f (x 0) (x – x 0). L 1 - biasa

13 Penerapan fisika turunan dan diferensial Jika S(t) adalah lintasan yang dilalui suatu titik material dalam waktu t, maka S"(t) adalah kecepatan sesaat titik material tersebut, dan dS = S"(t)dt adalah jarak yang ditempuh titik material selama periode waktu dari t ke t + dt, jika titik tersebut bergerak dengan kecepatan yang sama dengan kecepatan sesaat pada saat t. Jika Q(t) adalah banyaknya listrik yang mengalir melalui penampang penghantar pada waktu t, maka Q”(t) = I adalah kuat arus. Jika N(t) adalah banyaknya zat yang terbentuk pada waktu t selama reaksi kimia, maka N "(t) – laju reaksi kimia.

Jika fungsinya kamu = F(X) dapat terdiferensiasi pada titik tertentu X = X 0, maka kontinu pada titik ini.

Jadi, fungsi tersebut tidak dapat mempunyai turunan pada titik diskontinuitas. Kesimpulan sebaliknya salah, yaitu. dari kenyataan bahwa pada suatu saat X = X 0 fungsi kamu = F(X) kontinu bukan berarti dapat terdiferensiasi pada saat ini. Misalnya saja fungsinya kamu = |X| berkelanjutan untuk semua orang X (–< X < ), но в точке X= 0 tidak mempunyai turunan. Pada titik ini tidak ada garis singgung pada grafik. Ada garis singgung kanan dan garis singgung kiri, tetapi keduanya tidak berhimpitan.

21 Menemukan aturan produksi jumlah

Aturan 1. Jika fungsi y = f(x) dan y = g(x) mempunyai turunan di titik x, maka jumlahnya juga mempunyai turunan di titik x, dan turunan dari jumlah tersebut sama dengan jumlah dari turunannya:
(f(x) + 8(x))" =f (x)+ (x).
Dalam praktiknya, aturan ini dirumuskan lebih singkat: turunan suatu penjumlahan sama dengan jumlah turunannya.
Misalnya,
Aturan 2. Jika fungsi y = f(x) mempunyai turunan di titik x, maka fungsi y = kf(x) juga mempunyai turunan di titik x, dan:

Dalam praktiknya, aturan ini dirumuskan lebih singkat: faktor konstanta dapat dikeluarkan dari tanda turunannya. Misalnya,

Aturan 3 Jika fungsi y=f(x) dan y =g(x) mempunyai turunan di titik x, maka hasil kali keduanya juga mempunyai turunan di titik x, dan:

Dalam prakteknya aturan ini dirumuskan sebagai berikut: turunan hasil kali dua fungsi sama dengan jumlah kedua sukunya. Suku pertama merupakan hasil kali turunan fungsi pertama dan fungsi kedua, dan suku kedua merupakan hasil kali fungsi pertama dan turunan fungsi kedua.
Misalnya:
Aturan 4. Jika fungsi y = f(x) dan y=g(x) mempunyai turunan di maka hasil bagi mempunyai turunan di titik x, dan:

Tabel turunan kompleks

22 Perbedaan. fungsional pada intinya

Fungsi kamu=F(X) dikatakan terdiferensiasi pada titik tersebut X 0 jika kenaikannya adalah Δ kamu(X 0,Δ X) dapat direpresentasikan sebagai

Δ kamu(X 0,Δ X)=AΔ X+Hai(Δ X).

Bagian linier utama AΔ X kenaikan Δ kamu disebut diferensial fungsi ini di titik X 0, sesuai dengan kenaikan Δ X, dan dilambangkan dengan simbol mati(X 0,Δ X).

Agar fungsinya kamu=F(X) dapat dibedakan pada saat itu X 0, maka perlu dan cukup turunannya F′( X 0), sedangkan persamaan A=F′( X 0).

Ekspresi diferensial mempunyai bentuk

mati(X 0,dx)=F′( X 0)dx,

Di mana dx=Δ X.

23 Produk. Kompleks Fungsi

Turunan dari fungsi kompleks. Turunan dari suatu fungsi yang didefinisikan secara parametrik

Membiarkan kamu – fungsi kompleks X, yaitu. kamu = F(kamu), kamu = G(X), atau

Jika G(X) Dan F(kamu) adalah fungsi terdiferensiasi dari argumennya, masing-masing, pada titiknya X Dan kamu = G(X), maka fungsi kompleksnya juga terdiferensiasi pada suatu titik X dan ditemukan dengan rumus

Turunan dari suatu fungsi yang diberikan secara parametrik.

24 Prod.dan diff. Urutan tertinggi

Sekarang biarkan turunan orde ke-th terdefinisi pada lingkungan titik tertentu dan terdiferensiasi. Kemudian

Jika suatu fungsi mempunyai turunan parsial terhadap salah satu variabel di suatu daerah D, maka turunan tersebut, yang merupakan fungsi dari, dapat mempunyai turunan parsial terhadap variabel yang sama atau variabel lain pada suatu saat. Untuk fungsi aslinya, turunan ini akan menjadi turunan parsial orde kedua (atau turunan parsial kedua).

Turunan parsial orde kedua atau lebih tinggi yang diambil terhadap variabel berbeda disebut turunan parsial campuran. Misalnya,

Diferensial pesanan N, Di mana n > 1, suatu fungsi di suatu titik disebut diferensial pada titik ini dari diferensial orde (n - 1), itu adalah

Untuk fungsi yang bergantung pada satu variabel, perbedaan kedua dan ketiga terlihat seperti ini:

Dari sini kita dapat memperoleh gambaran umum tentang diferensial N urutan ke-th dari fungsi:

25 Teorema Fermat, Rolle, Langrange

ay Teorema Fermat: Biarkan fungsi tersebut didefinisikan dan mencapai nilai maksimum dan minimumnya ( M Dan M) di beberapa . Jika ada turunan pada , maka turunannya harus sama dengan 0.

Bukti: Ada. Ada dua kemungkinan kasus:

1) , => , => .

2) , => , => .

Dari 1) dan 2) berikut ini

ay Teorema Rolle (tentang akar turunan): Biarkan fungsi tersebut kontinu dan terdiferensialkan dan ambil nilai yang sama di ujung segmen: . Maka terdapat sedikitnya satu titik dari , turunan di mana .

v Bukti: Jangkauan terus menerus M Dan M. Maka ada dua kasus yang mungkin terjadi:

2) nilai terbesar dicapai dalam interval menurut teorema Fermat.

ay teorema Langrage (tentang kenaikan akhir): Biarkan fungsinya kontinu dan terdiferensiasi pada . Maka terdapat setidaknya satu yang persamaan berikut berlaku: .

Bukti: Mari kita perkenalkan fungsinya. (terus menerus dan terdiferensiasi pada ).

Suatu fungsi memenuhi Teorema Rolle ada , yang mana: , , , .

· fungsi dipanggil meningkat secara ketat pada jika

· fungsi dipanggil menurun pada jika

· fungsi dipanggil sangat menurun pada jika

Definisi: Turunan suatu fungsi di suatu titik adalah batas di mana rasio kenaikannya pada titik tersebut terhadap kenaikan argumen yang bersangkutan cenderung ketika argumen tersebut cenderung nol:

Artinya, jika didefinisikan dalam, maka

Teorema 1:

Grafik suatu fungsi mempunyai garis singgung nonvertikal jika dan hanya jika terdapat nilai berhingga dari turunan fungsi tersebut pada suatu titik tertentu.

Bukti:

Misalkan ada nilai f'()-terbatas

Misalkan ada garis singgung nonvertikal => ada garis singgung yang berhingga.

Garis potong cenderung bersinggungan.

Teorema tersebut telah terbukti.

Tiket 2 Kontinuitas suatu fungsi yang mempunyai turunan.

Suatu fungsi f(x) yang didefinisikan di suatu lingkungan suatu titik a disebut kontinu di titik ini jika

Dalil: (kondisi yang diperlukan untuk keberadaan turunan)

Jika suatu fungsi berhingga di suatu titik, maka fungsi tersebut tidak kontinu di titik tersebut.

Bukti:

Oleh karena itu, kontinu pada suatu titik.

Teorema tersebut telah terbukti.

Komentar : tidak berlaku sebaliknya, jika suatu fungsi kontinu di suatu titik, maka tidak berarti fungsi tersebut mempunyai turunan di titik tersebut.

Penyataan : jika suatu fungsi mempunyai turunan kanan dan kiri di suatu titik, maka fungsi tersebut kontinu di kanan dan kiri.

Tiket 3

Turunan dari jumlah, hasil kali, hasil bagi.

Turunan dari fungsi invers.

Definisi fungsi terdiferensiasi. Kondisi yang diperlukan dan cukup untuk diferensiasi.

Misalkan fungsi tersebut mempunyai turunan di suatu titik (berhingga): .

Kemudian, untuk cukup kecil, dapat ditulis sebagai penjumlahan dari suatu fungsi, yang dilambangkan dengan, yang cenderung nol dengan :,

dan pertambahan suatu titik dapat dituliskan sebagai:

atau (1) ,

lagi pula, ekspresi tersebut dipahami sebagai fungsi yang rasionya cenderung nol bersama-sama.

Penjelasan:

Definisi .

Suatu fungsi dikatakan terdiferensiasi pada suatu titik jika pertambahannya dapat direpresentasikan sebagai: (2),

dimana A tidak bergantung pada, tetapi umumnya bergantung pada.

Teorema 1:

Agar suatu fungsi dapat terdiferensiasi di suatu titik, fungsi tersebut perlu dan cukup mempunyai turunan berhingga di titik tersebut.

Bukti:

Kecukupan kondisi telah dibuktikan di atas: dari adanya turunan berhingga maka kemungkinan representasi dalam bentuk (1) dapat kita letakkan.

Kondisi kebutuhan . Biarkan fungsinya terdiferensiasi pada suatu titik. Kemudian dari (2), dengan asumsi, kita peroleh.

Limit ruas kanan di ada dan sama dengan A:.

Artinya ada turunannya. Teorema tersebut telah terbukti.

Tiket 6 Diferensial suatu fungsi, makna geometrisnya.

Jika fungsinya F memiliki turunan f΄(x Hai ) pada intinya X Hai, maka ada batas dimana Δ f=f(x Hai + Δ x)-f(x Hai ) ,,atau dimana SEBUAH=f΄(x Hai ) .

Definisi:

Fungsi F dapat dibedakan pada intinya X Hai, jika kenaikannya dapat direpresentasikan sebagai:

Di mana AΔ x=df. (*)

Diferensial adalah bagian linier utama dari kenaikan fungsi.

Jika ada turunan berhingga f΄(x Hai ) pada intinya X Hai, lalu fungsinya f(x) dapat dibedakan pada saat ini.

Kebalikannya juga benar: jika fungsinya F dapat dibedakan pada intinya X Hai, yaitu. pertambahannya dapat direpresentasikan dalam bentuk (*), kemudian mempunyai turunan di titik tersebut X Hai, sama dengan A:

Arti geometris dari diferensial:

A Dan B– titik grafik f(x), sesuai dengan nilainya X Hai Dan (X Hai + Δ X) variabel bebas. Ordinat poin A Dan B masing-masing sama f(x Hai ) Dan f(x Hai + Δ X). Kenaikan fungsi Δ f=f(x Hai + Δ x)-f(x Hai ) pada intinya X Hai sama dengan panjang segmen tersebut BD dan dapat direpresentasikan sebagai jumlah Δ f=BD=DC+CB, Di mana DC=tgαΔ x=f΄(x Hai ) Δ X Dan α adalah sudut antara garis singgung pada suatu titik A terhadap grafik dan arah sumbu positif X. Dari sini jelas bahwa DC ada fungsi diferensial F pada intinya X Hai :

DC=df=f΄(x Hai ) Δ X.

Apalagi bagian anggota kedua C.B. kenaikan Δ F memperhitungkan nilai. Nilai ini, pada umumnya Δ X, bahkan mungkin lebih dari suku utamanya, tetapi tingkatannya jauh lebih tinggi daripada Δ X, ketika Δ x→0.

SIFAT-SIFAT FUNGSI TERUS MENERUS PADA WAWANCARA

Mari kita perhatikan beberapa sifat fungsi kontinu pada suatu interval. Kami menyajikan properti ini tanpa bukti.

Fungsi kamu = f(x) ditelepon kontinu pada segmen tersebut [A, B], jika kontinu di semua titik dalam segmen ini, dan di ujungnya, yaitu. di poin A Dan B, berturut-turut di kanan dan kiri.

Teorema 1. Suatu fungsi kontinu pada interval [ A, B], setidaknya pada satu titik segmen ini mengambil nilai terbesar dan setidaknya pada satu titik - yang terkecil.

Teorema menyatakan bahwa jika suatu fungsi kamu = f(x) kontinu pada interval [ A, B], maka setidaknya ada satu poin x 1 Î [ A, B] sedemikian rupa sehingga nilai fungsinya f(x) pada titik ini akan menjadi nilai terbesar dari semua nilainya di segmen ini: f(x 1) ≥ f(x). Demikian pula, ada hal seperti itu x 2, yang nilai fungsinya akan menjadi nilai terkecil dari semua nilai pada segmen: f(x 1) ≤ f(x).

Jelas bahwa ada beberapa titik seperti itu, misalnya, gambar menunjukkan fungsi f(x) mengambil nilai terkecil pada dua titik x 2 Dan X 2 ".

Komentar. Pernyataan teorema bisa menjadi salah jika kita memperhitungkan nilai fungsi pada interval ( A, B). Memang jika kita mempertimbangkan fungsinya kamu = x pada (0, 2), maka kontinu pada interval ini, tetapi tidak mencapai nilai maksimum atau minimum di dalamnya: ia mencapai nilai-nilai ini di ujung interval, tetapi ujung-ujungnya bukan milik kita wilayah.

Selain itu, teorema tersebut tidak lagi berlaku untuk fungsi diskontinyu. Berikan contoh.

Konsekuensi. Jika fungsinya f(x) terus menerus pada [ A, B], maka dibatasi pada segmen ini.

Teorema 2. Biarkan fungsinya kamu = f(x) kontinu pada interval [ A, B] dan mengambil nilai tanda yang berbeda di ujung segmen ini, maka setidaknya ada satu titik di dalam segmen tersebut x = C, yang fungsinya menjadi nol: f(C)= 0, dimana a< C< b

Teorema ini mempunyai arti geometri sederhana: jika titik-titik pada grafik suatu fungsi kontinu kamu = f(x), sesuai dengan ujung segmen [ A, B] terletak pada sisi berlawanan dari sumbu Sapi, maka grafik ini memotong sumbu paling sedikit satu titik pada segmen tersebut Sapi. Fungsi terputus-putus mungkin tidak memiliki properti ini.

Teorema ini mengakui generalisasi berikut.

Teorema 3 (teorema nilai antara). Biarkan fungsinya kamu = f(x) kontinu pada interval [ A, B] Dan f(a) = SEBUAH, f(b) = B. Lalu untuk nomor berapa pun C, menyimpulkan antara A Dan B, ada titik seperti itu di dalam segmen ini CÎ [ A, B], Apa f(c) = C.

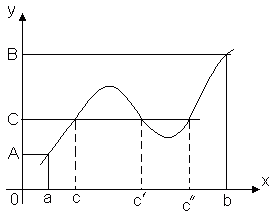
Teorema ini jelas secara geometris. Perhatikan grafik fungsinya kamu = f(x). Membiarkan f(a) = SEBUAH, f(b) = B. Lalu garis lurus apa pun kamu = C, Di mana C– nomor apa pun di antaranya A Dan B, akan memotong grafik fungsi setidaknya di satu titik. Absis titik potongnya akan menjadi nilai tersebut x = C, di mana f(c) = C.

Jadi, suatu fungsi kontinu, yang berpindah dari satu nilai ke nilai lainnya, harus melewati semua nilai perantara. Secara khusus:

Konsekuensi. Jika fungsinya kamu = f(x) kontinu dalam selang waktu tertentu dan mengambil nilai terbesar dan terkecil, maka pada interval tersebut dibutuhkan paling sedikit satu kali nilai apa pun yang terdapat di antara nilai terkecil dan terbesarnya.

DERIVATIF DAN APLIKASINYA. DEFINISI TURUNAN

Mari kita memiliki beberapa fungsi kamu=f(x), ditentukan pada interval tertentu. Untuk setiap nilai argumen X dari interval ini fungsinya kamu=f(x) mempunyai arti tertentu.

Pertimbangkan dua nilai argumen: awal X 0 dan baru X.

Perbedaan x–x 0 dipanggil dengan menambah argumen x pada intinya X 0 dan dilambangkan Δx. Dengan demikian, Δx = x – x 0 (peningkatan argumen bisa positif atau negatif). Dari persamaan ini dapat disimpulkan bahwa x=x 0 +Δx, yaitu. nilai awal variabel telah menerima beberapa kenaikan. Lalu, jika pada intinya X 0 nilai fungsi tadinya f(x 0 ), lalu pada titik baru X fungsi akan mengambil nilainya f(x) = f(x 0 +Δx).

Perbedaan Y y 0 = f(x) – f(x 0 ) ditelepon peningkatan fungsi kamu = f(x) pada intinya X 0 dan ditandai dengan simbol Δy. Dengan demikian,

Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) .

(1)

Biasanya nilai awal argumen X 0 dianggap tetap, dan nilai baru X- variabel. Kemudian kamu 0 = f(x 0 ) ternyata konstan, dan kamu = f(x)- variabel. Peningkatan Δy Dan Δx juga akan menjadi variabel dan rumus (1) menunjukkan hal itu Mati adalah fungsi dari variabel Δx.

Mari kita buat rasio pertambahan fungsi dengan pertambahan argumen

Mari kita cari batas rasio ini di Δx→0. Jika limit ini ada, maka disebut turunan dari fungsi tersebut f(x) pada intinya X 0 dan menunjukkan F "(X 0). Jadi,

Turunan fungsi ini kamu = f(x) pada intinya X 0 disebut batas rasio kenaikan fungsi Δ kamu dengan kenaikan argumen Δ X, ketika yang terakhir secara sewenang-wenang cenderung nol.

Perhatikan bahwa untuk fungsi yang sama turunannya pada titik yang berbeda X dapat mengambil nilai yang berbeda, mis. turunannya dapat dianggap sebagai fungsi argumen X. Fungsi ini ditunjuk F "(X)

Turunannya dilambangkan dengan simbol F "(x),y", . Nilai spesifik turunan di x = sebuah dilambangkan dengan F "(A) atau kamu "| x=sebuah.

Operasi mencari turunan suatu fungsi f(x) disebut diferensiasi fungsi ini.

Untuk mencari turunan menurut definisi secara langsung, Anda dapat menggunakan cara berikut: aturan praktis:

Contoh.

RASA MEKANIK DERIVATIF

Dari ilmu fisika diketahui bahwa hukum gerak beraturan mempunyai bentuk s = vt, Di mana S– jalur yang ditempuh ke momen waktu T, ay adalah kecepatan gerak seragam.

Namun karena sebagian besar pergerakan yang terjadi di alam tidak merata, maka secara umum kecepatannya, dan akibatnya, jaraknya S akan bergantung pada waktu T, yaitu. akan menjadi fungsi waktu.

Jadi, biarkan titik material bergerak lurus ke satu arah sesuai hukum s=s(t).

Catatlah suatu saat T 0 . Pada titik ini, titik tersebut telah melewati jalurnya s=s(t 0 ). Mari kita tentukan kecepatannya ay titik material pada saat itu T 0 .

Untuk melakukan ini, pertimbangkan momen lain T 0 + Δ T. Ini sesuai dengan jarak yang ditempuh s =s(t 0 + Δ T). Kemudian untuk selang waktu Δ T titik tersebut telah menempuh lintasan Δs =s(t 0 + Δ T)–s(t).

Mari kita pertimbangkan sikapnya. Disebut kecepatan rata-rata dalam selang waktu Δ T. Kecepatan rata-rata tidak dapat secara akurat mengkarakterisasi kecepatan pergerakan suatu titik saat ini T 0 (karena pergerakannya tidak merata). Untuk menyatakan kecepatan sebenarnya ini dengan lebih akurat menggunakan kecepatan rata-rata, Anda perlu mengambil interval waktu yang lebih kecil Δ T.

Jadi, kecepatan gerak pada waktu tertentu T 0 (kecepatan sesaat) adalah batas kecepatan rata-rata dalam selang waktu dari T 0 sampai T 0 +Δ T, ketika Δ T→0:

,

itu. kecepatan gerakan yang tidak merata adalah turunan jarak yang ditempuh terhadap waktu.

MAKNA GEOMETRIS DARI TURUNAN

Mari kita kenalkan terlebih dahulu definisi garis singgung kurva pada suatu titik tertentu.

Misalkan kita mempunyai sebuah kurva dan sebuah titik tetap di atasnya M 0(lihat gambar) Pertimbangkan hal lain M kurva ini dan gambar garis potong M 0 M. Jika intinya M mulai bergerak sepanjang kurva, dan titik M 0 tetap diam, garis potong tersebut berubah posisinya. Jika, dengan perkiraan titik yang tidak terbatas M sepanjang kurva menuju suatu titik M 0 di sisi manapun, garis potong cenderung mengambil posisi garis lurus tertentu M 0 T, lalu lurus M 0 T disebut garis singgung kurva pada titik tertentu M 0.

Itu., garis singgung ke kurva pada suatu titik tertentu M 0 disebut posisi batas garis potong M 0 M kapan titik M cenderung sepanjang kurva menuju suatu titik M 0.

Sekarang mari kita perhatikan fungsi kontinu kamu=f(x) dan kurva yang sesuai dengan fungsi ini. Pada nilai tertentu X 0 fungsi mengambil nilai kamu0=f(x0). Nilai-nilai ini X 0 dan kamu 0 pada kurva berhubungan dengan suatu titik M 0 (x 0; kamu 0). Mari kita berikan argumennya x 0 kenaikan Δ X. Nilai argumen yang baru sesuai dengan nilai fungsi yang bertambah kamu 0 +Δ kamu=f(x 0 –Δ X). Kami mengerti maksudnya M(x 0+Δ X; kamu 0+Δ kamu). Mari menggambar garis potong M 0 M dan dilambangkan dengan φ sudut yang dibentuk oleh garis potong dengan arah sumbu positif Sapi. Mari buat relasi dan perhatikan itu.

Jika sekarang Δ X→0, maka karena kontinuitas fungsi Δ pada→0, dan karena itu intinya M, bergerak sepanjang kurva, mendekati titik tanpa batas M 0. Kemudian garis potong M 0 M akan cenderung mengambil posisi bersinggungan dengan kurva di titik tersebut M 0, dan sudut φ→α di Δ X→0, di mana α menunjukkan sudut antara garis singgung dan arah positif sumbu Sapi. Karena fungsi tan φ bergantung terus menerus pada φ untuk φ≠π/2, maka untuk φ→α tan φ → tan α dan, oleh karena itu, kemiringan garis singgungnya adalah:

itu. f "(x)= tg α .

Jadi, secara geometris kamu "(x 0) mewakili kemiringan garis singgung grafik fungsi ini di titik tersebut x 0, yaitu. untuk nilai argumen tertentu X, turunannya sama dengan garis singgung sudut yang dibentuk oleh garis singgung grafik fungsi tersebut f(x) pada titik yang sesuai M 0 (x; y) dengan arah sumbu positif Sapi.

Contoh. Temukan kemiringan garis singgung kurva kamu = x 2 pada titik M(-1; 1).

Kita telah melihat sebelumnya bahwa ( X 2)" = 2X. Tetapi koefisien sudut garis singgung kurva adalah tan α = kamu"| x=-1 = – 2.

DIFERENTIABILITAS FUNGSI. KONTINUITAS FUNGSI YANG DAPAT DIBEDAKAN

Fungsi kamu=f(x) ditelepon dapat dibedakan dalam beberapa kasus X 0 jika memiliki turunan tertentu pada titik ini, mis. jika limit hubungan itu ada dan terbatas.

Jika suatu fungsi terdiferensiasi pada setiap titik pada segmen tertentu [ A; B] atau interval ( A; B), lalu mereka mengatakan bahwa dia dapat dibedakan di segmen [ A; B] atau, masing-masing, dalam interval ( A; B).

Teorema berikut ini valid, yang menetapkan hubungan antara fungsi terdiferensiasi dan fungsi kontinu.

Dalil. Jika fungsinya kamu=f(x) dapat dibedakan pada suatu saat x 0, maka kontinu pada saat ini.

Jadi, dari diferensiasi suatu fungsi, kontinuitasnya mengikuti.

Bukti. Jika , Itu

,

di mana α adalah kuantitas yang sangat kecil, mis. besaran yang cenderung nol sebagai Δ X→0. Tapi kemudian

Δ kamu=F "(x 0) Δ X+αΔ X=> Δ kamu→0 pada Δ X→0, yaitu f(x) – f(x 0)→0 jam X→X 0 , yang berarti fungsinya f(x) kontinu pada suatu titik X 0 . Q.E.D.

Jadi, fungsi tersebut tidak dapat mempunyai turunan pada titik diskontinuitas. Kebalikannya tidak benar: ada fungsi kontinu yang tidak terdiferensiasi di beberapa titik (yaitu, tidak memiliki turunan di titik-titik tersebut).

Perhatikan poin-poin pada gambar a, b, c.

Pada intinya A di Δ X→0 rasio tidak memiliki batas (karena batas satu sisi berbeda untuk Δ X→0–0 dan Δ X→0+0). Pada intinya A grafik tidak ada garis singgung yang pasti, tetapi ada dua garis singgung satu arah yang berbeda dengan kemiringan Ke 1 dan Ke 2. Titik seperti ini disebut titik sudut.

Pada intinya B di Δ X Rasio →0 adalah tanda konstanta kuantitas yang sangat besar. Fungsi tersebut memiliki turunan tak terhingga. Pada titik ini grafik mempunyai garis singgung vertikal. Tipe titik – “titik belok” dari garis singgung vertikal.

Pada intinya C turunan satu sisi adalah sejumlah besar tanda yang berbeda-beda. Pada titik ini grafik mempunyai dua garis singgung vertikal yang digabungkan. Ketik – “titik kembali” dengan garis singgung vertikal – kasus khusus dari titik sudut.