និយមន័យ ៩.៣.វ៉ិចទ័រ X បានហៅ វ៉ិចទ័រផ្ទាល់ខ្លួនម៉ាទ្រីស ប៉ុន្តែប្រសិនបើមានលេខបែបនេះ λ, ដែលសមភាពទទួលបាន៖ ប៉ុន្តែ X= λ X, នោះគឺជាលទ្ធផលនៃការអនុវត្តទៅ X ការបំប្លែងលីនេអ៊ែរដែលផ្តល់ដោយម៉ាទ្រីស ប៉ុន្តែ, គឺជាគុណនៃវ៉ិចទ័រនេះដោយចំនួន λ . លេខខ្លួនឯង λ បានហៅ លេខផ្ទាល់ខ្លួនម៉ាទ្រីស ប៉ុន្តែ.

ការជំនួសរូបមន្ត (៩.៣) x` j = λx j ,យើងទទួលបានប្រព័ន្ធនៃសមីការសម្រាប់កំណត់កូអរដោនេនៃ eigenvector:

. (9.5)

ប្រព័ន្ធលីនេអ៊ែរដូចគ្នានេះនឹងមានដំណោះស្រាយមិនសំខាន់ លុះត្រាតែកត្តាកំណត់សំខាន់របស់វាគឺ 0 (ច្បាប់របស់ Cramer)។ ដោយសរសេរលក្ខខណ្ឌនេះក្នុងទម្រង់៖

យើងទទួលបានសមីការសម្រាប់កំណត់ eigenvalues λ បានហៅ សមីការលក្ខណៈ. ដោយសង្ខេប វាអាចត្រូវបានតំណាងដូចខាងក្រោមៈ

| អេ-ល | = 0, (9.6)

ដោយសារផ្នែកខាងឆ្វេងរបស់វាគឺជាកត្តាកំណត់នៃម៉ាទ្រីស អេ-ល. ពហុនាមទាក់ទងនឹង λ | អេ-ល| បានហៅ ពហុនាមលក្ខណៈម៉ាទ្រីស ក

លក្ខណៈសម្បត្តិនៃពហុនាមលក្ខណៈ៖

1) ពហុនាមលក្ខណៈនៃការផ្លាស់ប្តូរលីនេអ៊ែរមិនអាស្រ័យលើជម្រើសនៃមូលដ្ឋាននោះទេ។ ភស្តុតាង។ (សូមមើល (៩.៤)) ប៉ុន្តែ ជាលទ្ធផល, ។ ដូច្នេះមិនអាស្រ័យលើជម្រើសនៃមូលដ្ឋាន។ ដូច្នេះហើយ | អេ-ល| មិនផ្លាស់ប្តូរនៅពេលផ្លាស់ប្តូរទៅមូលដ្ឋានថ្មី។

2) ប្រសិនបើម៉ាទ្រីស ប៉ុន្តែការផ្លាស់ប្តូរលីនេអ៊ែរគឺ ស៊ីមេទ្រី(ទាំងនោះ។ a ij = a ji) បន្ទាប់មកឫសទាំងអស់នៃសមីការលក្ខណៈ (9.6) គឺជាចំនួនពិត។

លក្ខណៈសម្បត្តិនៃ eigenvalues ​​និង eigenvectors:

1) ប្រសិនបើយើងជ្រើសរើសមូលដ្ឋានពី eigenvectors x 1, x 2, x 3 ដែលត្រូវគ្នាទៅនឹង eigenvalues λ 1 , λ 2 , λ ៣ម៉ាទ្រីស ប៉ុន្តែបន្ទាប់មកនៅក្នុងមូលដ្ឋាននេះ ការបំលែងលីនេអ៊ែរ A មានម៉ាទ្រីសអង្កត់ទ្រូង៖

(9.7) ភស្តុតាងនៃទ្រព្យសម្បត្តិនេះធ្វើតាមនិយមន័យនៃ eigenvectors ។

2) ប្រសិនបើការផ្លាស់ប្តូរ eigenvalues ប៉ុន្តែមានភាពខុសប្លែកគ្នា បន្ទាប់មក eigenvectors ដែលត្រូវគ្នានឹងពួកវាគឺឯករាជ្យលីនេអ៊ែរ។

3) ប្រសិនបើពហុនាមលក្ខណៈនៃម៉ាទ្រីស ប៉ុន្តែមានឫសបីផ្សេងគ្នា បន្ទាប់មកក្នុងមូលដ្ឋានខ្លះ ម៉ាទ្រីស ប៉ុន្តែមានរាងអង្កត់ទ្រូង។

ចូរយើងស្វែងរក eigenvalues ​​និង eigenvectors នៃ matrix ចូរយើងបង្កើតសមីការលក្ខណៈ៖ (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - ៧ λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

ស្វែងរកកូអរដោនេនៃ eigenvectors ដែលត្រូវគ្នានឹងតម្លៃដែលបានរកឃើញនីមួយៗ λ. ពី (9.5) វាធ្វើតាមថាប្រសិនបើ X (1) ={x 1 , x 2 , x 3) គឺជា eigenvector ដែលត្រូវគ្នានឹង λ 1 = -2 បន្ទាប់មក

គឺជាប្រព័ន្ធសហការ ប៉ុន្តែមិនអាចកំណត់បាន។ ដំណោះស្រាយរបស់វាអាចត្រូវបានសរសេរជា X (1) ={ក,0,-ក) ដែល a ជាលេខណាមួយ។ ជាពិសេសប្រសិនបើអ្នកទាមទារនោះ | x (1) |=1, X (1) =

ការជំនួសប្រព័ន្ធ (៩.៥) λ 2 =3 យើងទទួលបានប្រព័ន្ធសម្រាប់កំណត់កូអរដោនេនៃ eigenvector ទីពីរ - x (2) ={y1,y2,y3}:

កន្លែងណា X (2) ={b,-b, ខ) ឬផ្តល់ | x (2) |=1, x (2) =

សម្រាប់ λ 3 = 6 ស្វែងរក eigenvector x (3) ={z1, z2, z3}:

, x (3) ={គ,2c, គ) ឬនៅក្នុងកំណែធម្មតា។

x (3) = វាអាចត្រូវបានគេមើលឃើញថា X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. ដូច្នេះ eigenvectors នៃ matrix នេះ គឺ​ជា​គូ​ orthogonal ។

ធម្មទេសនា ១០

ទម្រង់បួនជ្រុង និងការភ្ជាប់របស់ពួកគេជាមួយម៉ាទ្រីសស៊ីមេទ្រី។ លក្ខណៈសម្បត្តិនៃ eigenvectors និង eigenvalues ​​នៃម៉ាទ្រីសស៊ីមេទ្រី។ ការកាត់បន្ថយទម្រង់បួនជ្រុងទៅជាទម្រង់ Canonical ។

និយមន័យ 10.1 ។ទម្រង់បួនជ្រុងអថេរពិតប្រាកដ x 1, x 2,…, x nគឺជាពហុនាមនៃសញ្ញាបត្រទីពីរទាក់ទងនឹងអថេរទាំងនេះ ដែលមិនមានពាក្យឥតគិតថ្លៃ និងលក្ខខណ្ឌនៃសញ្ញាបត្រទីមួយ។

ឧទាហរណ៍នៃទម្រង់ការ៉េ៖

(ន = 2),

(ន = 3). (10.1)

រំលឹកឡើងវិញនូវនិយមន័យនៃម៉ាទ្រីសស៊ីមេទ្រីដែលបានផ្តល់ឱ្យនៅក្នុងការបង្រៀនចុងក្រោយនេះ៖

និយមន័យ 10.2 ។ម៉ាទ្រីសការ៉េត្រូវបានគេហៅថា ស៊ីមេទ្រីប្រសិនបើ នោះគឺប្រសិនបើធាតុម៉ាទ្រីសស៊ីមេទ្រីទាក់ទងនឹងអង្កត់ទ្រូងសំខាន់គឺស្មើគ្នា។

លក្ខណៈសម្បត្តិនៃ eigenvalues ​​និង eigenvectors នៃម៉ាទ្រីសស៊ីមេទ្រី៖

1) eigenvalues ​​ទាំងអស់នៃម៉ាទ្រីសស៊ីមេទ្រីគឺពិតប្រាកដ។

ភស្តុតាង (សម្រាប់ ន = 2).

អនុញ្ញាតឱ្យម៉ាទ្រីស ប៉ុន្តែមើល​ទៅ​ដូច​ជា: . ចូរយើងបង្កើតសមីការលក្ខណៈ៖

(១០.២) ស្វែងរកអ្នករើសអើង៖

ដូច្នេះ សមីការ​មាន​ឫស​ពិត​តែ​ប៉ុណ្ណោះ។

2) eigenvectors នៃម៉ាទ្រីសស៊ីមេទ្រីគឺ orthogonal ។

ភស្តុតាង (សម្រាប់ ន= 2).

កូអរដោនេនៃ eigenvectors និងត្រូវតែបំពេញសមីការ។

ម៉ាទ្រីសប្រភេទអង្កត់ទ្រូងត្រូវបានរៀបចំយ៉ាងសាមញ្ញបំផុត។ សំណួរកើតឡើងថាតើវាអាចទៅរួចក្នុងការស្វែងរកមូលដ្ឋានដែលម៉ាទ្រីសនៃប្រតិបត្តិករលីនេអ៊ែរនឹងមានទម្រង់អង្កត់ទ្រូងដែរឬទេ។ មូលដ្ឋានបែបនេះមាន។
អនុញ្ញាតឱ្យចន្លោះលីនេអ៊ែរ R n និងប្រតិបត្តិករលីនេអ៊ែរ A ដើរតួនៅក្នុងវាត្រូវបានផ្តល់ឱ្យ; ក្នុងករណីនេះ ប្រតិបត្តិករ A យក R n ចូលទៅក្នុងខ្លួនវា នោះគឺ A: R n → R n ។

និយមន័យ។ វ៉ិចទ័រដែលមិនមែនជាសូន្យត្រូវបានគេហៅថា eigenvector នៃប្រតិបត្តិករ A ប្រសិនបើប្រតិបត្តិករ A បកប្រែទៅជាវ៉ិចទ័រ collinear ទៅវា នោះគឺ . លេខ λ ត្រូវបានគេហៅថា eigenvalue ឬ eigenvalue របស់ប្រតិបត្តិករ A ដែលត្រូវគ្នានឹង eigenvector ។
យើងកត់សំគាល់លក្ខណៈសម្បត្តិមួយចំនួននៃ eigenvalues ​​និង eigenvectors ។
1. ការរួមបញ្ចូលគ្នាលីនេអ៊ែរនៃ eigenvectors នៃប្រតិបត្តិករ A ដែលត្រូវគ្នាទៅនឹង eigenvalue ដូចគ្នា λ គឺជា eigenvector ដែលមាន eigenvalue ដូចគ្នា។
2. Eigenvectors ប្រតិបត្តិករ A ដែលមាន eigenvalues ​​​​ λ 1 , λ 2 , … , λ m ដាច់ដោយឡែកពីគ្នាជាគូ។
3. ប្រសិនបើ eigenvalues ​​λ 1 =λ 2 = λ m = λ នោះ eigenvalue λ ត្រូវគ្នាទៅនឹង eigenvectors ឯករាជ្យលីនេអ៊ែរមិនលើសពី m ។

ដូច្នេះប្រសិនបើមាន eigenvectors ឯករាជ្យលីនេអ៊ែរ ដែលត្រូវគ្នាទៅនឹង eigenvalues ​​​​ផ្សេងគ្នា λ 1 , λ 2 , … , λ n បន្ទាប់មកពួកវាគឺឯករាជ្យលីនេអ៊ែរ ដូច្នេះពួកគេអាចត្រូវបានគេយកជាមូលដ្ឋាននៃលំហ R n ។ ចូរយើងស្វែងរកទម្រង់ម៉ាទ្រីសនៃប្រតិបត្តិករលីនេអ៊ែរ A ដោយផ្អែកលើ eigenvectors របស់វា ដែលយើងធ្វើសកម្មភាពជាមួយប្រតិបត្តិករ A លើវ៉ិចទ័រមូលដ្ឋាន៖ បន្ទាប់មក .
ដូច្នេះម៉ាទ្រីសនៃប្រតិបត្តិករលីនេអ៊ែរ A នៅក្នុងមូលដ្ឋាននៃ eigenvectors របស់វាមានទម្រង់អង្កត់ទ្រូង ហើយ eigenvalues ​​នៃប្រតិបត្តិករ A គឺស្ថិតនៅលើអង្កត់ទ្រូង។
តើមានមូលដ្ឋានមួយផ្សេងទៀតដែលម៉ាទ្រីសមានទម្រង់អង្កត់ទ្រូងទេ? ចម្លើយចំពោះសំណួរនេះត្រូវបានផ្តល់ដោយទ្រឹស្តីបទខាងក្រោម។

ទ្រឹស្តីបទ។ ម៉ាទ្រីស​នៃ​ប្រតិបត្តិករ​លីនេអ៊ែរ A ក្នុង​មូលដ្ឋាន (i = 1..n) មាន​ទម្រង់​អង្កត់ទ្រូង ប្រសិន​បើ​វ៉ិចទ័រ​ទាំងអស់​នៃ​មូលដ្ឋាន​ជា eigenvectors របស់​ប្រតិបត្តិករ A។

ច្បាប់សម្រាប់ការស្វែងរក eigenvalues ​​និង eigenvectors

អនុញ្ញាតឱ្យវ៉ិចទ័រ , ដែល x 1 , x 2 , … , x n - កូអរដោនេនៃវ៉ិចទ័រទាក់ទងទៅនឹងមូលដ្ឋាន និងជា eigenvector នៃប្រតិបត្តិករលីនេអ៊ែរ A ដែលត្រូវគ្នានឹង eigenvalue λ ពោលគឺ . ទំនាក់ទំនងនេះអាចត្រូវបានសរសេរជាទម្រង់ម៉ាទ្រីស

. (*)

សមីការ (*) អាចត្រូវបានចាត់ទុកថាជាសមីការសម្រាប់ការស្វែងរក ហើយនោះមានន័យថា យើងចាប់អារម្មណ៍លើដំណោះស្រាយដែលមិនសំខាន់ ដោយសារ eigenvector មិនអាចជាសូន្យ។ វាត្រូវបានគេដឹងថាដំណោះស្រាយ nontrivial នៃប្រព័ន្ធដូចគ្នានៃសមីការលីនេអ៊ែរមានប្រសិនបើ និងលុះត្រាតែ det(A - λE) = 0។ ដូច្នេះសម្រាប់ λ ទៅជា eigenvalue របស់ប្រតិបត្តិករ A វាចាំបាច់ និងគ្រប់គ្រាន់ដែល det(A - λE ) = 0 ។
ប្រសិនបើសមីការ (*) ត្រូវបានសរសេរលម្អិតក្នុងទម្រង់កូអរដោណេ នោះយើងទទួលបានប្រព័ន្ធនៃសមីការដូចគ្នាលីនេអ៊ែរ៖

(1)
កន្លែងណា គឺជាម៉ាទ្រីសរបស់ប្រតិបត្តិករលីនេអ៊ែរ។

ប្រព័ន្ធ (1) មានដំណោះស្រាយមិនសូន្យ ប្រសិនបើកត្តាកំណត់ D របស់វាស្មើនឹងសូន្យ

យើងទទួលបានសមីការសម្រាប់ការស្វែងរក eigenvalues ​​។
សមីការនេះត្រូវបានគេហៅថាសមីការលក្ខណៈ ហើយផ្នែកខាងឆ្វេងរបស់វាត្រូវបានគេហៅថាពហុនាមលក្ខណៈនៃម៉ាទ្រីស (ប្រតិបត្តិករ) A. ប្រសិនបើពហុនាមលក្ខណៈមិនមានឫសពិតទេ នោះម៉ាទ្រីស A មិនមាន eigenvectors ហើយមិនអាចកាត់បន្ថយទៅជាទម្រង់អង្កត់ទ្រូងបានទេ។
អនុញ្ញាតឱ្យ λ 1 , λ 2 , … , λ n ជាឫសពិតនៃសមីការលក្ខណៈ ហើយវាអាចមានពហុគុណក្នុងចំណោមពួកគេ។ ការជំនួសតម្លៃទាំងនេះនៅក្នុងវេនចូលទៅក្នុងប្រព័ន្ធ (1) យើងរកឃើញ eigenvectors ។

ឧទាហរណ៍ 12 ។ ប្រតិបត្តិករលីនេអ៊ែរ A ដើរតួក្នុង R 3 យោងទៅតាមច្បាប់ដែល x 1 , x 2 , .., x n គឺជាកូអរដោនេនៃវ៉ិចទ័រនៅក្នុងមូលដ្ឋាន , , . ស្វែងរក eigenvalues ​​និង eigenvectors នៃប្រតិបត្តិករនេះ។
ដំណោះស្រាយ។ យើងបង្កើតម៉ាទ្រីសនៃប្រតិបត្តិករនេះ៖
.
យើងបង្កើតប្រព័ន្ធសម្រាប់កំណត់កូអរដោនេនៃ eigenvectors៖

យើងបង្កើតសមីការលក្ខណៈ និងដោះស្រាយវា៖

.
λ 1,2 = −1, λ 3 = 3 ។
ការជំនួស λ = -1 ទៅក្នុងប្រព័ន្ធ យើងមាន៖
ឬ
ដោយសារតែ បន្ទាប់មកមានអថេរពឹងផ្អែកពីរ និងអថេរឥតគិតថ្លៃមួយ។
អនុញ្ញាតឱ្យ x 1 ជាមិនស្គាល់ឥតគិតថ្លៃ យើងដោះស្រាយប្រព័ន្ធនេះតាមមធ្យោបាយណាមួយ ហើយស្វែងរកដំណោះស្រាយទូទៅនៃប្រព័ន្ធនេះ៖ ប្រព័ន្ធមូលដ្ឋាននៃដំណោះស្រាយមានដំណោះស្រាយមួយចាប់តាំងពី n - r = 3 - 2 = 1 ។
សំណុំនៃ eigenvectors ដែលត្រូវគ្នានឹង eigenvalue λ = -1 មានទម្រង់៖ , ដែល x 1 ជាលេខណាមួយក្រៅពីសូន្យ។ ចូរយើងជ្រើសរើសវ៉ិចទ័រមួយពីសំណុំនេះ ឧទាហរណ៍ ដោយកំណត់ x 1 = 1៖ .
ប្រកែកស្រដៀងគ្នានេះ យើងរកឃើញ eigenvector ដែលត្រូវគ្នានឹង eigenvalue λ = 3: .
នៅក្នុងលំហ R 3 មូលដ្ឋានមានវ៉ិចទ័រឯករាជ្យចំនួនបី ប៉ុន្តែយើងទទួលបាន eigenvectors ឯករាជ្យលីនេអ៊ែរតែពីរប៉ុណ្ណោះ ដែលមូលដ្ឋាននៅក្នុង R 3 មិនអាចបង្កើតបាន។ ដូច្នេះម៉ាទ្រីស A នៃប្រតិបត្តិករលីនេអ៊ែរមិនអាចកាត់បន្ថយទៅជាទម្រង់អង្កត់ទ្រូងបានទេ។

ឧទាហរណ៍ 13 បានផ្តល់ម៉ាទ្រីស .
1. បញ្ជាក់ថាវ៉ិចទ័រ គឺជា eigenvector នៃម៉ាទ្រីស A. ស្វែងរក eigenvalue ដែលត្រូវគ្នានឹង eigenvector នេះ។
2. ស្វែងរកមូលដ្ឋានដែលម៉ាទ្រីស A មានទម្រង់អង្កត់ទ្រូង។
ដំណោះស្រាយ។
1. ប្រសិនបើ នោះគឺជា eigenvector

.
វ៉ិចទ័រ (1, 8, -1) គឺជា eigenvector ។ Eigenvalue λ = -1 ។
ម៉ាទ្រីស​មាន​ទម្រង់​អង្កត់ទ្រូង​ក្នុង​មូលដ្ឋាន​ដែល​មាន eigenvectors ។ មួយក្នុងចំណោមពួកគេគឺល្បីល្បាញ។ តោះរកសល់។
យើងកំពុងស្វែងរក eigenvectors ពីប្រព័ន្ធ៖

សមីការលក្ខណៈ៖ ;
(3+λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 − 1) = 0
λ 1 = −3, λ 2 = 1, λ 3 = −1 ។
ស្វែងរក eigenvector ដែលត្រូវគ្នានឹង eigenvalue λ = -3:

ចំណាត់ថ្នាក់នៃម៉ាទ្រីសនៃប្រព័ន្ធនេះគឺស្មើនឹងពីរ និងស្មើនឹងចំនួនមិនស្គាល់ ដូច្នេះប្រព័ន្ធនេះមានតែដំណោះស្រាយសូន្យ x 1 = x 3 = 0. x 2 នៅទីនេះអាចជាអ្វីផ្សេងក្រៅពីសូន្យឧទាហរណ៍។ x 2 = 1. ដូច្នេះវ៉ិចទ័រ (0 ,1,0) គឺជា eigenvector ដែលត្រូវគ្នានឹង λ = -3 ។ តោះពិនិត្យ៖
.
ប្រសិនបើ λ = 1 នោះយើងទទួលបានប្រព័ន្ធ
ចំណាត់ថ្នាក់នៃម៉ាទ្រីសគឺពីរ។ ឆ្លងកាត់សមីការចុងក្រោយ។
អនុញ្ញាតឱ្យ x 3 ជាមិនស្គាល់ឥតគិតថ្លៃ។ បន្ទាប់មក x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3 ។
សន្មត់ x 3 = 1 យើងមាន (-3,-9,1) - eigenvector ដែលត្រូវគ្នានឹង eigenvalue λ = 1. ពិនិត្យ៖

.
ដោយសារតម្លៃ eigenvalues ​​គឺពិតប្រាកដ និងខុសគ្នា វ៉ិចទ័រដែលត្រូវគ្នានឹងពួកវាគឺឯករាជ្យលីនេអ៊ែរ ដូច្នេះពួកគេអាចត្រូវបានគេយកជាមូលដ្ឋាននៅក្នុង R 3 ។ ដូច្នេះនៅក្នុងមូលដ្ឋាន , , ម៉ាទ្រីស A មានទម្រង់៖
.
មិនមែនគ្រប់ម៉ាទ្រីសនៃប្រតិបត្តិករលីនេអ៊ែរ A:R n → R n អាចត្រូវបានកាត់បន្ថយទៅជាទម្រង់អង្កត់ទ្រូងទេ ព្រោះសម្រាប់ប្រតិបត្តិករលីនេអ៊ែរមួយចំនួនអាចមានតិចជាង n អ៊ីហ្សែនវ៉ិចទ័រឯករាជ្យ។ ទោះយ៉ាងណាក៏ដោយ ប្រសិនបើម៉ាទ្រីសគឺស៊ីមេទ្រី នោះពិតជា m វ៉ិចទ័រឯករាជ្យ លីនេអ៊ែរ ត្រូវគ្នាទៅនឹងឫសនៃសមីការលក្ខណៈនៃគុណ m ។

និយមន័យ។ ម៉ាទ្រីស​ស៊ីមេទ្រី​គឺ​ជា​ម៉ាទ្រីស​ការ៉េ​ដែល​ធាតុ​ដែល​ស៊ីមេទ្រី​ទាក់ទង​នឹង​អង្កត់ទ្រូង​មេ​គឺ​ស្មើ​គ្នា នោះ​គឺ​ក្នុង​នោះ​។
សុន្ទរកថា។ 1. eigenvalues ​​ទាំងអស់នៃម៉ាទ្រីសស៊ីមេទ្រីគឺពិតប្រាកដ។
2. Eigenvectors នៃម៉ាទ្រីសស៊ីមេទ្រីដែលត្រូវគ្នានឹងតម្លៃ eigenvalues ​​ផ្សេងគ្នាជាគូគឺ orthogonal ។
ក្នុងនាមជាកម្មវិធីមួយក្នុងចំណោមកម្មវិធីជាច្រើននៃបរិធានដែលបានសិក្សា យើងពិចារណាពីបញ្ហានៃការកំណត់ទម្រង់នៃខ្សែកោងលំដាប់ទីពីរ។

ជាមួយនឹងម៉ាទ្រីស A ប្រសិនបើមានលេខ l នោះ AX = lX ។

ក្នុងករណីនេះលេខ l ត្រូវបានហៅ eigenvalueប្រតិបត្តិករ (ម៉ាទ្រីស A) ដែលត្រូវគ្នានឹងវ៉ិចទ័រ X ។

ម្យ៉ាងវិញទៀត eigenvector គឺជាវ៉ិចទ័រដែលនៅក្រោមសកម្មភាពរបស់ប្រតិបត្តិករលីនេអ៊ែរ បំប្លែងទៅជាវ៉ិចទ័រ collinear i.e. គ្រាន់តែគុណនឹងចំនួនមួយចំនួន។ ផ្ទុយ​ទៅ​វិញ វ៉ិចទ័រ​មិន​ត្រឹមត្រូវ​គឺ​ពិបាក​ក្នុង​ការ​បំប្លែង​ជាង។

យើងសរសេរនិយមន័យនៃ eigenvector ជាប្រព័ន្ធនៃសមីការ៖

ចូរផ្លាស់ទីលក្ខខណ្ឌទាំងអស់ទៅផ្នែកខាងឆ្វេង៖

ប្រព័ន្ធចុងក្រោយអាចត្រូវបានសរសេរជាទម្រង់ម៉ាទ្រីសដូចខាងក្រោមៈ

(A - lE)X \u003d O

ប្រព័ន្ធលទ្ធផលតែងតែមានដំណោះស្រាយសូន្យ X = O ។ ប្រព័ន្ធបែបនេះដែលលក្ខខណ្ឌឥតគិតថ្លៃទាំងអស់ស្មើនឹងសូន្យត្រូវបានគេហៅថា ដូចគ្នា. ប្រសិនបើម៉ាទ្រីសនៃប្រព័ន្ធបែបនេះគឺការ៉េហើយកត្តាកំណត់របស់វាមិនស្មើនឹងសូន្យទេនោះយោងទៅតាមរូបមន្តរបស់ Cramer យើងនឹងទទួលបានដំណោះស្រាយតែមួយគត់ - សូន្យ។ វាអាចត្រូវបានបង្ហាញថាប្រព័ន្ធមានដំណោះស្រាយ nonzero ប្រសិនបើ និងលុះត្រាតែកត្តាកំណត់នៃម៉ាទ្រីសនេះគឺស្មើនឹងសូន្យ ពោលគឺឧ។

|A - lE| = = 0

សមីការនេះជាមួយ l មិនស្គាល់ត្រូវបានគេហៅថា សមីការលក្ខណៈ (ពហុនាមលក្ខណៈ) ម៉ាទ្រីស A (ប្រតិបត្តិករលីនេអ៊ែរ) ។

វាអាចត្រូវបានបង្ហាញថាពហុនាមលក្ខណៈនៃប្រតិបត្តិករលីនេអ៊ែរមិនអាស្រ័យលើជម្រើសនៃមូលដ្ឋានទេ។

ឧទាហរណ៍ ចូរយើងស្វែងរក eigenvalues ​​និង eigenvectors នៃ linear operator ដែលផ្តល់ដោយ matrix A = .

ដើម្បីធ្វើដូចនេះយើងបង្កើតសមីការលក្ខណៈ |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; ឃ \u003d 4 + 140 \u003d 144; eigenvalues ​​​​l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d ៧.

ដើម្បីស្វែងរក eigenvectors យើងដោះស្រាយប្រព័ន្ធសមីការពីរ

(A + 5E) X = O

(A - 7E) X = O

សម្រាប់ទីមួយនៃពួកគេ ម៉ាទ្រីសដែលបានពង្រីកនឹងយកទម្រង់

,

ពេលណា x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s) ។

សម្រាប់ទីពីរនៃពួកគេ ម៉ាទ្រីសពង្រីកនឹងយកទម្រង់

,

ពេលណា x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1) ។

ដូច្នេះ eigenvectors នៃប្រតិបត្តិករលីនេអ៊ែរនេះគឺជាវ៉ិចទ័រទាំងអស់នៃទម្រង់ (-(2/3)c; c) ជាមួយ eigenvalue (-5) និងវ៉ិចទ័រទាំងអស់នៃទម្រង់ ((2/3)c 1 ; c 1) ជាមួយ eigenvalue ៧.

វាអាចត្រូវបានបង្ហាញថាម៉ាទ្រីសនៃប្រតិបត្តិករ A នៅក្នុងមូលដ្ឋានដែលមាន eigenvectors របស់វាគឺអង្កត់ទ្រូងហើយមានទម្រង់:

,

ដែលជាកន្លែងដែលខ្ញុំគឺជា eigenvalues ​​នៃម៉ាទ្រីសនេះ។

ការសន្ទនាក៏ពិតដែរ៖ ប្រសិនបើម៉ាទ្រីស A ក្នុងមូលដ្ឋានខ្លះជាអង្កត់ទ្រូង នោះវ៉ិចទ័រទាំងអស់នៃមូលដ្ឋាននេះនឹងក្លាយជា eigenvectors នៃម៉ាទ្រីសនេះ។

វាក៏អាចបញ្ជាក់បានថា ប្រសិនបើប្រតិបត្តិករលីនេអ៊ែរមាន eigenvalues ​​ខុសគ្នាជាគូ នោះ eigenvectors ដែលត្រូវគ្នាគឺឯករាជ្យលីនេអ៊ែរ ហើយម៉ាទ្រីសនៃប្រតិបត្តិករនេះក្នុងមូលដ្ឋានដែលត្រូវគ្នាមានទម្រង់អង្កត់ទ្រូង។

ចូរយើងពន្យល់រឿងនេះជាមួយឧទាហរណ៍មុន។ អនុញ្ញាតឱ្យយើងយកតម្លៃមិនសូន្យតាមអំពើចិត្ត c និង c 1 ប៉ុន្តែដូចជាវ៉ិចទ័រ X (1) និង X (2) គឺឯករាជ្យលីនេអ៊ែរ ឧ។ នឹងបង្កើតជាមូលដ្ឋាន។ ឧទាហរណ៍ អនុញ្ញាតឱ្យ c \u003d c 1 \u003d 3 បន្ទាប់មក X (1) \u003d (-2; 3), X (2) \u003d (2; 3) ។

អនុញ្ញាតឱ្យយើងផ្ទៀងផ្ទាត់ឯករាជ្យលីនេអ៊ែរនៃវ៉ិចទ័រទាំងនេះ:

12 ≠ 0. ក្នុងមូលដ្ឋានថ្មីនេះ ម៉ាទ្រីស A នឹងយកទម្រង់ A * = ។

ដើម្បីផ្ទៀងផ្ទាត់នេះយើងប្រើរូបមន្ត A * = C -1 AC ។ តោះរក C-1 ជាមុនសិន។

គ −1 = ;

ទម្រង់បួនជ្រុង

ទម្រង់បួនជ្រុង f (x 1, x 2, x n) ពីអថេរ n ត្រូវបានគេហៅថាផលបូក ដែលពាក្យនីមួយៗគឺជាការ៉េនៃអថេរមួយ ឬផលគុណនៃអថេរពីរផ្សេងគ្នា ដែលយកដោយមេគុណជាក់លាក់មួយ៖ f (x 1 , x 2, x n) = (a ij = a ji) ។

ម៉ាទ្រីស A ដែលផ្សំឡើងដោយមេគុណទាំងនេះត្រូវបានគេហៅថា ម៉ាទ្រីសទម្រង់បួនជ្រុង។ វាតែងតែ ស៊ីមេទ្រីម៉ាទ្រីស (ឧ. ស៊ីមេទ្រីម៉ាទ្រីសអំពីអង្កត់ទ្រូងសំខាន់ a ij = a ji) ។

នៅក្នុងសញ្ញាណម៉ាទ្រីស ទម្រង់បួនជ្រុងមានទម្រង់ f(X) = X T AX ដែលជាកន្លែងដែល

ជា​ការ​ពិត

ឧទាហរណ៍ ចូរយើងសរសេរទម្រង់ quadratic ក្នុងទម្រង់ម៉ាទ្រីស។

ដើម្បីធ្វើដូចនេះយើងរកឃើញម៉ាទ្រីសនៃទម្រង់បួនជ្រុង។ ធាតុអង្កត់ទ្រូងរបស់វាគឺស្មើនឹងមេគុណនៅការ៉េនៃអថេរ ហើយធាតុដែលនៅសល់គឺស្មើនឹងពាក់កណ្តាលនៃមេគុណដែលត្រូវគ្នានៃទម្រង់ការ៉េ។ នោះ​ហើយ​ជា​មូល​ហេតុ​ដែល

អនុញ្ញាតឱ្យ​ជួរ​ឈរ​ម៉ាទ្រីស​នៃ​អថេរ X ត្រូវ​បាន​ទទួល​ដោយ​ការ​បំប្លែង​លីនេអ៊ែរ​ដែល​មិន​កើត​ចេញ​នៃ​ជួរ​ឈរ​ម៉ាទ្រីស Y, i.e. X = CY ដែល C ជាម៉ាទ្រីសមិន degenerate នៃលំដាប់ n ។ បន្ទាប់មកទម្រង់ការ៉េ f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y ។

ដូច្នេះនៅក្រោមការបំលែងលីនេអ៊ែរដែលមិន degenerate C ម៉ាទ្រីសនៃទម្រង់បួនជ្រុងយកទម្រង់៖ A * = C T AC ។

ឧទាហរណ៍ ចូរយើងស្វែងរកទម្រង់ការ៉េ f(y 1, y 2) ដែលទទួលបានពីទម្រង់រាងចតុកោណ f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 ដោយការបំលែងលីនេអ៊ែរ។

ទម្រង់បួនជ្រុងត្រូវបានគេហៅថា Canonical(វា​មាន ទិដ្ឋភាព Canonical) ប្រសិនបើមេគុណរបស់វា a ij = 0 សម្រាប់ i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 = ។

ម៉ាទ្រីសរបស់វាគឺអង្កត់ទ្រូង។

ទ្រឹស្តីបទ(ភស្តុតាងមិនត្រូវបានផ្តល់ឱ្យនៅទីនេះ) ។ ទម្រង់បួនជ្រុងណាមួយអាចត្រូវបានកាត់បន្ថយទៅជាទម្រង់ Canonical ដោយប្រើការបំប្លែងលីនេអ៊ែរដែលមិន degenerate ។

ជាឧទាហរណ៍ អនុញ្ញាតឱ្យយើងកាត់បន្ថយទៅជាទម្រង់ Canonical ទម្រង់បួនជ្រុង
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 ។

ដើម្បីធ្វើដូចនេះដំបូងត្រូវជ្រើសរើសការ៉េពេញសម្រាប់អថេរ x 1៖

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 − 5x 2 2 − x 2 x 3 ។

ឥឡូវនេះយើងជ្រើសរើសការ៉េពេញសម្រាប់អថេរ x 2៖

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2 ។

បន្ទាប់មកការផ្លាស់ប្តូរលីនេអ៊ែរមិន degenerate y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 និង y 3 \u003d x 3 នាំទម្រង់ការ៉េនេះទៅជាទម្រង់ Canonical f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 ។

ចំណាំថាទម្រង់ Canonical នៃទម្រង់បួនជ្រុងត្រូវបានកំណត់មិនច្បាស់លាស់ (ទម្រង់ការ៉េដូចគ្នាអាចត្រូវបានកាត់បន្ថយទៅជាទម្រង់ Canonical ក្នុងវិធីផ្សេងគ្នា)។ ទោះជាយ៉ាងណាក៏ដោយទម្រង់ Canonical ដែលទទួលបានដោយវិធីសាស្រ្តផ្សេងៗមានលក្ខណៈសម្បត្តិទូទៅមួយចំនួន។ ជាពិសេស ចំនួននៃពាក្យដែលមានមេគុណវិជ្ជមាន (អវិជ្ជមាន) នៃទម្រង់បួនជ្រុងមិនអាស្រ័យលើរបៀបដែលទម្រង់ត្រូវបានកាត់បន្ថយទៅជាទម្រង់នេះទេ (ឧទាហរណ៍ ក្នុងឧទាហរណ៍ដែលបានពិចារណា វាតែងតែមានមេគុណអវិជ្ជមានពីរ និងមេគុណវិជ្ជមានមួយ)។ ទ្រព្យសម្បត្តិនេះត្រូវបានគេហៅថាច្បាប់នៃនិចលភាពនៃទម្រង់បួនជ្រុង។

អនុញ្ញាតឱ្យយើងផ្ទៀងផ្ទាត់វាដោយកាត់បន្ថយទម្រង់បួនជ្រុងដូចគ្នាទៅជាទម្រង់ Canonical ក្នុងវិធីផ្សេងគ្នា។ ចូរចាប់ផ្តើមការបំប្លែងដោយអថេរ x 2៖

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 − (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2 ដែល y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) ) x 3 និង y 3 = x 1 ។ នៅទីនេះ មេគុណអវិជ្ជមាន -3 នៅ y 1 និងមេគុណវិជ្ជមានពីរ 3 និង 2 នៅ y 2 និង y 3 (ហើយដោយប្រើវិធីមួយផ្សេងទៀត យើងទទួលបានមេគុណអវិជ្ជមាន (-5) នៅ y 2 និងមេគុណវិជ្ជមានពីរ៖ 2 នៅ y 1 និង 1/20 សម្រាប់ y ​​3) ។

វាគួរតែត្រូវបានគេកត់សម្គាល់ផងដែរថាចំណាត់ថ្នាក់នៃម៉ាទ្រីសនៃទម្រង់រាងបួនជ្រុងត្រូវបានគេហៅថា ចំណាត់ថ្នាក់នៃទម្រង់បួនជ្រុង, គឺស្មើនឹងចំនួនមេគុណមិនសូន្យនៃទម្រង់ Canonical និងមិនផ្លាស់ប្តូរក្រោមការបំប្លែងលីនេអ៊ែរ។

ទម្រង់បួនជ្រុង f(X) ត្រូវបានគេហៅថា ជាវិជ្ជមាន (អវិជ្ជមាន) ជាក់លាក់, ប្រសិនបើសម្រាប់តម្លៃទាំងអស់នៃអថេរដែលមិនក្នុងពេលដំណាលគ្នាស្មើនឹងសូន្យនោះវាវិជ្ជមាន, i.e. f(X) > 0 (អវិជ្ជមាន, i.e.
f(X)< 0).

ឧទាហរណ៍ ទម្រង់រាងបួនជ្រុង f 1 (X) \u003d x 1 2 + x 2 2 ត្រូវបានកំណត់ជាវិជ្ជមាន ពីព្រោះ គឺជាផលបូកនៃការ៉េ ហើយទម្រង់ចតុកោណ f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 គឺជានិយមន័យអវិជ្ជមាន ពីព្រោះ តំណាងវាអាចត្រូវបានតំណាងជា f 2 (X) \u003d - (x 1 - x 2) 2 ។

នៅក្នុងស្ថានភាពជាក់ស្តែងភាគច្រើន វាមានការលំបាកជាងក្នុងការកំណត់សញ្ញា-កំណត់នៃទម្រង់បួនជ្រុង ដូច្នេះទ្រឹស្តីបទមួយក្នុងចំណោមទ្រឹស្តីបទខាងក្រោមត្រូវបានប្រើសម្រាប់ការនេះ (យើងបង្កើតពួកវាដោយគ្មានភស្តុតាង)។

ទ្រឹស្តីបទ. ទម្រង់បួនជ្រុងគឺវិជ្ជមាន (អវិជ្ជមាន) កំណត់ប្រសិនបើ និងលុះត្រាតែតម្លៃ eigenvalue ទាំងអស់នៃម៉ាទ្រីសរបស់វាគឺវិជ្ជមាន (អវិជ្ជមាន)។

ទ្រឹស្តីបទ(លក្ខណៈវិនិច្ឆ័យរបស់ Sylvester) ។ ទម្រង់ quadratic គឺវិជ្ជមានកំណត់ប្រសិនបើ និងលុះត្រាតែអនីតិជនសំខាន់ៗទាំងអស់នៃម៉ាទ្រីសនៃទម្រង់នេះគឺវិជ្ជមាន។

ធំ (ជ្រុង) អនីតិជនលំដាប់ k-th នៃម៉ាទ្រីស A នៃលំដាប់ n-th ត្រូវបានគេហៅថា កត្តាកំណត់នៃម៉ាទ្រីស ដែលផ្សំឡើងពីជួរ k ដំបូង និងជួរឈរនៃម៉ាទ្រីស A () ។

ចំណាំថាសម្រាប់ទម្រង់រាងចតុកោណដែលកំណត់និយមន័យអវិជ្ជមាន សញ្ញានៃអនីតិជនចម្បងឆ្លាស់គ្នា ហើយអនីតិជនលំដាប់ទីមួយត្រូវតែអវិជ្ជមាន។

ឧទាហរណ៍ យើងពិនិត្យទម្រង់រាងការ៉េ f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 សម្រាប់ការកំណត់សញ្ញា។

= (2 - លីត្រ)*
*(3 - លីត្រ) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; ឃ = 25 - 8 = 17;
. ដូច្នេះទម្រង់ quadratic គឺវិជ្ជមានកំណត់។

វិធីសាស្រ្ត 2. អនីតិជនសំខាន់នៃលំដាប់ទីមួយនៃម៉ាទ្រីស A D 1 = a 11 = 2 > 0. អនីតិជនសំខាន់នៃលំដាប់ទីពីរ D 2 = = 6 - 4 = 2 > 0. ដូច្នេះយោងទៅតាមលក្ខណៈវិនិច្ឆ័យរបស់ Sylvester ។ ទម្រង់​បួន​ជ្រុង​គឺ​ជា​ការ​កំណត់​វិជ្ជមាន។

យើងពិនិត្យមើលទម្រង់បួនជ្រុងផ្សេងទៀតសម្រាប់ការកំណត់សញ្ញា f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2 ។

វិធីសាស្រ្ត 1. ចូរយើងបង្កើតម៉ាទ្រីសនៃទម្រង់បួនជ្រុង А = ។ សមីការលក្ខណៈនឹងមានទម្រង់ = (-2 - លីត្រ)*
*(−3 − l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; ឃ = 25 - 8 = 17;
. ដូច្នេះទម្រង់ quadratic គឺអវិជ្ជមានកំណត់។

វិធីសាស្រ្ត 2. អនីតិជនសំខាន់នៃលំដាប់ទីមួយនៃម៉ាទ្រីស A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. ដូច្នេះយោងទៅតាមលក្ខណៈវិនិច្ឆ័យរបស់ Sylvester ទម្រង់រាងចតុកោណគឺអវិជ្ជមានកំណត់ (សញ្ញានៃអនីតិជនចម្បងឆ្លាស់គ្នា ចាប់ផ្តើមពីដក)។

ហើយជាឧទាហរណ៍មួយទៀត យើងពិនិត្យមើលទម្រង់ការ៉េ f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 សម្រាប់ការកំណត់សញ្ញា។

វិធីសាស្រ្ត 1. ចូរយើងបង្កើតម៉ាទ្រីសនៃទម្រង់បួនជ្រុង А = ។ សមីការលក្ខណៈនឹងមានទម្រង់ = (2 - លីត្រ)*
*(−3 − l) - 4 = (−6 − 2l + 3l + l 2) - 4 = l 2 + l − 10 = 0; ឃ = 1 + 40 = 41;
.

លេខមួយក្នុងចំណោមលេខទាំងនេះគឺអវិជ្ជមាន ហើយមួយទៀតគឺវិជ្ជមាន។ សញ្ញានៃ eigenvalues ​​គឺខុសគ្នា។ ដូច្នេះ ទម្រង់​រាង​បួនជ្រុង​មិន​អាច​កំណត់​បាន​ទាំង​អវិជ្ជមាន ឬ​វិជ្ជមាន​ទេ ឧ. ទម្រង់​ការ៉េ​នេះ​មិន​មាន​សញ្ញា​កំណត់​ទេ (វា​អាច​យក​តម្លៃ​នៃ​សញ្ញា​ណាមួយ)។

វិធីសាស្រ្ត 2. អនីតិជនសំខាន់នៃលំដាប់ទីមួយនៃម៉ាទ្រីស A D 1 = a 11 = 2 > 0. អនីតិជនសំខាន់នៃលំដាប់ទីពីរ D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

ប្រព័ន្ធនៃសមីការលីនេអ៊ែរដូចគ្នា។

ប្រព័ន្ធនៃសមីការលីនេអ៊ែរដូចគ្នា គឺជាប្រព័ន្ធនៃទម្រង់

វាច្បាស់ណាស់ថាក្នុងករណីនេះ , ដោយសារតែ ធាតុទាំងអស់នៃជួរឈរមួយក្នុងកត្តាកំណត់ទាំងនេះគឺស្មើនឹងសូន្យ។

ចាប់តាំងពីមិនស្គាល់ត្រូវបានរកឃើញដោយរូបមន្ត បន្ទាប់មកក្នុងករណី Δ ≠ 0 ប្រព័ន្ធមានដំណោះស្រាយសូន្យតែមួយគត់ x = y = z= 0. ទោះយ៉ាងណាក៏ដោយ នៅក្នុងបញ្ហាជាច្រើន សំណួរថាតើប្រព័ន្ធដូចគ្នាមានដំណោះស្រាយក្រៅពីសូន្យ គឺជាការចាប់អារម្មណ៍។

ទ្រឹស្តីបទ។ដើម្បីឱ្យប្រព័ន្ធនៃសមីការលីនេអ៊ែរមានដំណោះស្រាយមិនសូន្យ វាចាំបាច់ និងគ្រប់គ្រាន់ដែល Δ ≠ 0 ។

ដូច្នេះ ប្រសិនបើកត្តាកំណត់គឺ Δ ≠ 0 នោះប្រព័ន្ធមានដំណោះស្រាយតែមួយគត់។ ប្រសិនបើ Δ ≠ 0 នោះប្រព័ន្ធនៃសមីការលីនេអ៊ែរមានដំណោះស្រាយគ្មានកំណត់។

ឧទាហរណ៍។

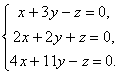
Eigenvectors និង Matrix Eigenvalues

សូមឱ្យម៉ាទ្រីសការ៉េត្រូវបានផ្តល់ឱ្យ , Xគឺ​ជា​ជួរ​ឈរ​ម៉ាទ្រីស​មួយ​ចំនួន​ដែល​កម្ពស់​ស្រប​នឹង​លំដាប់​នៃ​ម៉ាទ្រីស ក. .

នៅក្នុងបញ្ហាជាច្រើន មនុស្សម្នាក់ត្រូវពិចារណាសមីការសម្រាប់ X

ដែល λ គឺជាលេខមួយចំនួន។ វាច្បាស់ណាស់ថាសម្រាប់ λ សមីការនេះមានដំណោះស្រាយសូន្យ។

លេខ λ ដែលសមីការនេះមានដំណោះស្រាយមិនសូន្យត្រូវបានគេហៅថា eigenvalueម៉ាទ្រីស ក, ក Xសម្រាប់ λ បែបនេះត្រូវបានគេហៅថា វ៉ិចទ័រផ្ទាល់ខ្លួនម៉ាទ្រីស ក.

ចូរយើងស្វែងរក eigenvector នៃម៉ាទ្រីស ក. ដោយសារតែ អ៊ី∙X=Xបន្ទាប់មកសមីការម៉ាទ្រីសអាចត្រូវបានសរសេរឡើងវិញជា ឬ . នៅក្នុងទម្រង់ពង្រីក សមីការនេះអាចត្រូវបានសរសេរឡើងវិញជាប្រព័ន្ធនៃសមីការលីនេអ៊ែរ។ ពិត .

ហើយ​ដូច្នេះ

ដូច្នេះ យើងទទួលបានប្រព័ន្ធនៃសមីការលីនេអ៊ែរដូចគ្នាសម្រាប់កំណត់កូអរដោនេ x ១, x2, x ៣វ៉ិចទ័រ X. ដើម្បីឱ្យប្រព័ន្ធមានដំណោះស្រាយមិនសូន្យ វាចាំបាច់ និងគ្រប់គ្រាន់ដែលកត្តាកំណត់នៃប្រព័ន្ធស្មើនឹងសូន្យ i.e.

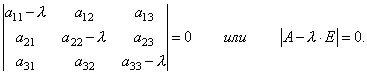
នេះគឺជាសមីការដឺក្រេទី 3 ទាក់ទងនឹង λ ។ វាត្រូវបានគេហៅថា សមីការលក្ខណៈម៉ាទ្រីស កនិងបម្រើដើម្បីកំណត់ eigenvalues ​​λ ។

eigenvalue λ នីមួយៗត្រូវគ្នាទៅនឹង eigenvector Xដែលកូអរដោនេរបស់វាត្រូវបានកំណត់ពីប្រព័ន្ធនៅតម្លៃដែលត្រូវគ្នានៃ λ ។

ឧទាហរណ៍។

Vector ALGEBRA ។ គំនិតវ៉ិចទ័រ

នៅពេលសិក្សាផ្នែកផ្សេងៗនៃរូបវិទ្យា វាមានបរិមាណដែលត្រូវបានកំណត់ទាំងស្រុងដោយការកំណត់តម្លៃលេខរបស់ពួកគេ ឧទាហរណ៍ ប្រវែង តំបន់ ម៉ាស សីតុណ្ហភាព។ល។ តម្លៃបែបនេះត្រូវបានគេហៅថា scalar ។ ទោះយ៉ាងណាក៏ដោយ បន្ថែមពីលើពួកវា វាក៏មានបរិមាណផងដែរ សម្រាប់ការកំណត់ដែលបន្ថែមពីលើតម្លៃលេខ វាក៏ចាំបាច់ផងដែរ ដើម្បីដឹងពីទិសដៅរបស់ពួកគេក្នុងលំហ ឧទាហរណ៍ កម្លាំងដែលធ្វើសកម្មភាពលើរាងកាយ ល្បឿន និងការបង្កើនល្បឿន។ នៃរាងកាយនៅពេលដែលវាផ្លាស់ទីក្នុងលំហ កម្លាំងនៃដែនម៉ាញេទិកនៅចំណុចដែលបានផ្តល់ឱ្យក្នុងលំហ។ល។ បរិមាណបែបនេះត្រូវបានគេហៅថាបរិមាណវ៉ិចទ័រ។

ចូរយើងណែនាំនិយមន័យដ៏តឹងរឹងមួយ។

ផ្នែកទិសដៅចូរ​ហៅ​ផ្នែក​មួយ​ទាក់ទង​នឹង​ចុង​ដែល​គេ​ដឹង​ថា​មួយ​ណា​ជា​ផ្នែក​ទីមួយ និង​មួយ​ណា​ជា​ទីពីរ។

វ៉ិចទ័រផ្នែកដែលដឹកនាំត្រូវបានគេហៅថា ដែលមានប្រវែងជាក់លាក់ ពោលគឺឧ។ នេះគឺជាផ្នែកនៃប្រវែងជាក់លាក់មួយ ដែលចំណុចមួយក្នុងចំនោមចំណុចកំណត់វាត្រូវបានយកជាការចាប់ផ្តើម និងទីពីរ - ជាចុងបញ្ចប់។ ប្រសិនបើ ក កគឺជាការចាប់ផ្តើមនៃវ៉ិចទ័រ ខជាចុងបញ្ចប់របស់វា បន្ទាប់មកវ៉ិចទ័រត្រូវបានតាងដោយនិមិត្តសញ្ញា លើសពីនេះ វ៉ិចទ័រត្រូវបានតំណាងដោយអក្សរតែមួយ។ នៅក្នុងរូបភាព វ៉ិចទ័រត្រូវបានចង្អុលបង្ហាញដោយផ្នែកមួយ និងទិសដៅរបស់វាដោយព្រួញមួយ។

ម៉ូឌុលឬ វែងវ៉ិចទ័រត្រូវបានគេហៅថាប្រវែងនៃផ្នែកដឹកនាំដែលកំណត់វា។ តំណាងដោយ || ឬ || ។

អ្វី​ដែល​ហៅ​ថា​វ៉ិចទ័រ​សូន្យ ដែល​ការចាប់ផ្តើម​និង​ចុង​ត្រូវគ្នា​នឹង​ត្រូវ​បាន​គេ​ហៅថា​វ៉ិចទ័រ​ផងដែរ។ វាត្រូវបានសម្គាល់។ វ៉ិចទ័រសូន្យមិនមានទិសដៅច្បាស់លាស់ទេ ហើយម៉ូឌុលរបស់វាស្មើនឹងសូន្យ ||=0 ។

វ៉ិចទ័រនិងត្រូវបានគេហៅថា collinearប្រសិនបើពួកវាស្ថិតនៅលើបន្ទាត់ដូចគ្នា ឬនៅលើបន្ទាត់ប៉ារ៉ាឡែល។ ក្នុងករណីនេះ ប្រសិនបើវ៉ិចទ័រ និងត្រូវបានដឹកនាំស្មើៗគ្នា យើងនឹងសរសេរ ផ្ទុយគ្នា។

វ៉ិចទ័រដែលស្ថិតនៅលើបន្ទាត់ត្រង់ស្របទៅនឹងយន្តហោះដូចគ្នាត្រូវបានគេហៅថា coplanar.

វ៉ិចទ័រពីរហើយត្រូវបានគេហៅថា ស្មើប្រសិនបើពួកវាជាគូ មានទិសដៅដូចគ្នា និងមានប្រវែងស្មើគ្នា។ ក្នុងករណីនេះសូមសរសេរ។

វាធ្វើតាមនិយមន័យនៃភាពស្មើគ្នានៃវ៉ិចទ័រ ដែលវ៉ិចទ័រអាចផ្លាស់ទីស្របទៅនឹងខ្លួនវាដោយដាក់ប្រភពដើមរបស់វានៅចំណុចណាមួយក្នុងលំហ។

ឧទាហរណ៍.

ប្រតិបត្តិការលីនេអ៊ែរលើវ៉ិចទ័រ

1. គុណវ៉ិចទ័រដោយលេខ។

   ផលិតផលនៃវ៉ិចទ័រដោយលេខ λ គឺជាវ៉ិចទ័រថ្មីដូចជា៖

   ផលិតផលនៃវ៉ិចទ័រ និងលេខ λ ត្រូវបានតំណាងដោយ .

   

   ឧទាហរណ៍,គឺ​ជា​វ៉ិចទ័រ​ដែល​ចង្អុល​ទៅ​ទិស​ដូច​គ្នា​នឹង​វ៉ិចទ័រ ហើយ​មាន​ប្រវែង​ពាក់​កណ្តាល​នៃ​វ៉ិចទ័រ។

   ប្រតិបត្តិការដែលបានបញ្ចូលមានដូចខាងក្រោម លក្ខណៈសម្បត្តិ:

2. ការបន្ថែមវ៉ិចទ័រ។

   អនុញ្ញាតឱ្យនិងជាវ៉ិចទ័របំពានពីរ។ យកចំណុចបំពាន អូនិងបង្កើតវ៉ិចទ័រ។ បន្ទាប់ពីនោះពីចំណុច កទុកវ៉ិចទ័រមួយឡែក។ វ៉ិចទ័រដែលភ្ជាប់ការចាប់ផ្តើមនៃវ៉ិចទ័រទីមួយជាមួយចុងបញ្ចប់នៃទីពីរត្រូវបានគេហៅថា ផលបូកនៃវ៉ិចទ័រទាំងនេះ និងត្រូវបានតំណាង .

   

   និយមន័យដែលបានបង្កើតនៃការបន្ថែមវ៉ិចទ័រត្រូវបានគេហៅថា ក្បួន​ប៉ារ៉ាឡែលចាប់តាំងពីផលបូកដូចគ្នានៃវ៉ិចទ័រអាចទទួលបានដូចខាងក្រោម។ ដាក់មួយឡែកពីចំណុច អូវ៉ិចទ័រ និង។ សង់ប្រលេឡូក្រាមលើវ៉ិចទ័រទាំងនេះ OABC. ចាប់តាំងពីវ៉ិចទ័រ បន្ទាប់មកវ៉ិចទ័រ ដែលជាអង្កត់ទ្រូងនៃប្រលេឡូក្រាមដែលដកចេញពីកំពូល អូច្បាស់ជាផលបូកនៃវ៉ិចទ័រ។

   

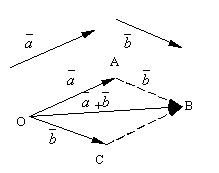
   វាងាយស្រួលក្នុងការត្រួតពិនិត្យដូចខាងក្រោម លក្ខណៈសម្បត្តិបន្ថែមវ៉ិចទ័រ.

3. ភាពខុសគ្នានៃវ៉ិចទ័រ។

   វ៉ិចទ័រ collinear ទៅវ៉ិចទ័រដែលបានផ្តល់ឱ្យ ប្រវែងស្មើគ្នា និងតម្រង់ផ្ទុយគ្នាត្រូវបានគេហៅថា ទល់មុខវ៉ិចទ័រ​សម្រាប់​វ៉ិចទ័រ ហើយ​ត្រូវ​បាន​តំណាង​ដោយ . វ៉ិចទ័រផ្ទុយអាចត្រូវបានចាត់ទុកថាជាលទ្ធផលនៃគុណវ៉ិចទ័រដោយលេខ λ = –1: ។