ចូរយើងពិចារណាកាំរស្មីបី a, b, c ដែលចេញមកពីចំណុចតែមួយ ហើយមិនស្ថិតនៅលើយន្តហោះតែមួយ។ មុំត្រីកោណ (abc) គឺជាតួរលេខដែលផ្សំឡើងដោយ "មុំសំប៉ែតបី (ab), (bc) និង (ac) (រូបភាពទី 2)) មុំទាំងនេះត្រូវបានគេហៅថាមុខនៃមុំត្រីកោណ ហើយជ្រុងរបស់ពួកគេគឺជាគែម។ ចំនុចកំពូលទូទៅនៃមុំសំប៉ែតត្រូវបានគេហៅថា មុំ dihedral ដែលបង្កើតឡើងដោយមុខនៃមុំត្រីកោណត្រូវបានគេហៅថាមុំ dihedral នៃមុំ trihedral ។

គោលគំនិតនៃមុំពហុកែងត្រូវបានកំណត់ស្រដៀងគ្នា (រូបភាពទី 3) ។
Polyhedron
នៅក្នុង stereometric តួលេខនៅក្នុងលំហ ហៅថាសាកសពត្រូវបានសិក្សា។ ដោយមើលឃើញ រូបកាយ (ធរណីមាត្រ) ត្រូវតែស្រមៃថាជាផ្នែកនៃលំហដែលកាន់កាប់ដោយរូបកាយ និងត្រូវបានចងដោយផ្ទៃ។

ពហុកោណគឺជាតួដែលផ្ទៃរបស់វាមានចំនួនកំណត់នៃពហុកោណរាបស្មើ (រូបភាពទី 4) ។ ពហុកោណត្រូវបានគេហៅថាប៉ោង ប្រសិនបើវាស្ថិតនៅផ្នែកម្ខាងនៃយន្តហោះនៃពហុកោណផ្ទះល្វែងទាំងអស់លើផ្ទៃរបស់វា។ ផ្នែកទូទៅនៃយន្តហោះបែបនេះ និងផ្ទៃនៃប៉ោងប៉ោងត្រូវបានគេហៅថា មុខ។ មុខនៃពហុកោណប៉ោងគឺជាពហុកោណប៉ោង។ ជ្រុងនៃមុខត្រូវបានគេហៅថា គែមនៃ polyhedron ហើយកំពូលត្រូវបានគេហៅថា vertices នៃ polyhedron ។
ចូរយើងពន្យល់ពីអ្វីដែលបាននិយាយនៅលើឧទាហរណ៍នៃគូបដែលធ្លាប់ស្គាល់ (រូបភាពទី 5)។ គូបគឺជាពហុកោណប៉ោង។ ផ្ទៃរបស់វាមានប្រាំមួយការ៉េ: ABCD, BEFC, .... ពួកវាជាមុខរបស់វា។ គែមនៃគូបគឺជាជ្រុងនៃការ៉េទាំងនេះ៖ AB, BC, BE, .... ចំនុចកំពូលនៃគូបគឺជាចំនុចកំពូលនៃការ៉េ៖ A, B, C, D, E, .... គូបមានមុខប្រាំមួយ គែមដប់ពីរ និង កំពូលប្រាំបី។

polyhedra សាមញ្ញបំផុត - ព្រីស និងពីរ៉ាមីត ដែលនឹងក្លាយជាវត្ថុសំខាន់នៃការសិក្សារបស់យើង - យើងនឹងផ្តល់និយមន័យថា ជាខ្លឹមសារ មិនត្រូវប្រើគំនិតនៃរូបកាយទេ។ ពួកវានឹងត្រូវបានកំណត់ជាតួលេខធរណីមាត្រជាមួយនឹងការចង្អុលបង្ហាញពីចំណុចទាំងអស់នៃលំហដែលជាកម្មសិទ្ធិរបស់ពួកគេ។ គំនិតនៃតួធរណីមាត្រ និងផ្ទៃរបស់វានៅក្នុងករណីទូទៅនឹងត្រូវបានផ្តល់ឱ្យនៅពេលក្រោយ។
មុំប៉ូលីហេដរ៉ាល់
មុំពហុកោណគឺជាអាណាឡូកលំហនៃពហុកោណ។ សូមចាំថាពហុកោណនៅលើយន្តហោះគឺជាតួរលេខដែលបង្កើតឡើងដោយបន្ទាត់ដែលខូចដែលបិទជិតធម្មតា ហើយតំបន់ខាងក្នុងដែលជាប់នឹងវា។ យើងនឹងពិចារណាកាំរស្មីក្នុងលំហជាអាណាឡូកនៃចំណុចនៅលើយន្តហោះ និងមុំរាបស្មើក្នុងលំហ ជាអាណាឡូកនៃផ្នែកមួយនៅលើយន្តហោះ។ បន្ទាប់មក analogue នៃបន្ទាត់ដែលខូចបិទធម្មតានៅក្នុងយន្តហោះគឺជាផ្ទៃដែលបង្កើតឡើងដោយសំណុំកំណត់នៃមុំយន្តហោះក 1 អេស 2 , ក 2 អេស 3 , …, ក ន -1 SA n, A n SA 1 ជាមួយនឹងកំពូលធម្មតា។ស ។ តួរលេខដែលបង្កើតឡើងដោយផ្ទៃដែលបានបញ្ជាក់ និងផ្នែកមួយក្នុងចំនោមផ្នែកទាំងពីរនៃលំហដែលជាប់នឹងវាត្រូវបានគេហៅថា មុំ polyhedral. កំពូលធម្មតា។សបានហៅ កិច្ចប្រជុំកំពូលមុំពហុមុខ។ កាំរស្មីអេស 1 , …, SA nបានហៅ ឆ្អឹងជំនីមុំ polyhedral និងមុំផ្ទះល្វែងដោយខ្លួនឯង។ក 1 អេស 2 , ក 2 អេស 3 , …, ក ន -1 SA n, A n SA 1 – មុខមុំពហុមុខ។ មុំពហុកោណត្រូវបានតាងដោយអក្សរអេស 1 … ក នចង្អុលបង្ហាញចំនុចកំពូល និងចំនុចនៅលើគែមរបស់វា។ អាស្រ័យលើចំនួនមុខ មុំពហុកែងត្រូវបានគេហៅថា trihedral, tetrahedral, pentahedral (រូបភាព 2) ។ល។

មុំ polyhedral ត្រូវបានគេហៅថា ប៉ោងប្រសិនបើវាជាតួលេខប៉ោង ឧ។ មាន រួមជាមួយនឹងចំណុចទាំងពីររបស់វា ការតភ្ជាប់ផ្នែកបន្ទាត់។ ក្នុងរូបភាពទី 2 មុំត្រីកោណ និង tetrahedral គឺប៉ោង ប៉ុន្តែមុំ pentahedral គឺមិនមែនទេ។
ពិចារណាអំពីលក្ខណៈសម្បត្តិមួយចំនួននៃត្រីកោណ និងលក្ខណៈសម្បត្តិស្រដៀងគ្នានៃមុំត្រីកោណ។
ទ្រព្យ ១(វិសមភាពត្រីកោណ) ។ ជ្រុងនីមួយៗនៃត្រីកោណមួយគឺតិចជាងផលបូកនៃភាគីទាំងពីរផ្សេងទៀត។
ទ្រព្យសម្បត្តិស្រដៀងគ្នាសម្រាប់មុំត្រីកោណគឺជាទ្រព្យសម្បត្តិដូចខាងក្រោម។
ទ្រព្យ ១"។ មុំសំប៉ែតនីមួយៗនៃមុំបីគឺតិចជាងផលបូកនៃមុំរាបស្មើពីរផ្សេងទៀតរបស់វា។
ភស្តុតាង។
ពិចារណាមុំត្រីកោណ SABC
.
សូមឱ្យមុំធំជាងគេបំផុតរបស់វាគឺជាមុំ ASC. បន្ទាប់មកវិសមភាព
ASB ASC< ASC + BSC ;BSC ASC< ASC + ASB .
ដូច្នេះហើយ វានៅសល់ដើម្បីបញ្ជាក់អំពីវិសមភាព ASC< ASB+ BSC.
ចូរយើងដាក់វានៅលើគែម ASCការចាក់ថ្នាំ ASD, ស្មើនឹង ASB
,
និងចំណុច ខជ្រើសរើសដូច្នេះ SB=SD(រូបទី 3) ។ បន្ទាប់មកត្រីកោណ ASBនិង ASDគឺស្មើគ្នា (នៅសងខាង និងមុំរវាងពួកវា) ហើយដូច្នេះ AB=AD. ចូរយើងប្រើវិសមភាពត្រីកោណ AC< AB + BC
. ដកពីផ្នែកទាំងពីរ AD=ABយើងទទួលបានវិសមភាព ឌី.ស៊ី< BC.
នៅក្នុងត្រីកោណ DSCនិង BSCម្ខាងជារឿងធម្មតា SC), SD=SBនិង ឌី.ស៊ី< BC.
ក្នុងករណីនេះ មុំធំជាងស្ថិតនៅទល់មុខផ្នែកធំជាង ហើយដូច្នេះ DSC< BSC
. ការបន្ថែមទៅភាគីទាំងពីរនៃវិសមភាពនេះ មុំ ASD
,
ស្មើ ASBយើងទទួលបានវិសមភាពដែលត្រូវការ ASC< ASB+ BSC.

លទ្ធផល ១.ផលបូកនៃមុំយន្តហោះនៃមុំត្រីកោណគឺតិចជាង 360°
.
ភស្តុតាង។
អនុញ្ញាតឱ្យមាន SABCគឺជាមុំបីហ្វារដែលបានផ្តល់ឱ្យ។ ពិចារណាមុំបីជ្រុងជាមួយចំនុចកំពូល កបង្កើតឡើងដោយមុខ ABS, ACSនិងមុំ BAC. ដោយសារទ្រព្យសម្បត្តិដែលបានបង្ហាញ យើងមានវិសមភាព BAC< បាស+ CAS. ស្រដៀងគ្នានេះដែរ សម្រាប់មុំបីបួនជ្រុងជាមួយកំពូល ខនិង ជាមួយមានភាពមិនស្មើគ្នា៖ ABS< ABS+ ស៊ី.ប៊ី.អេស, ACB< ACS+ ប៊ី.ស៊ី. ការបន្ថែមវិសមភាពទាំងនេះ ហើយពិចារណាថាផលបូកនៃមុំនៃត្រីកោណមួយ។ ABCស្មើនឹង 180° យើងទទួលបាន 180 ° < BAS + CAS+ ABS+CBS+BCS+ ACS= 180
°
- ASB+ 180°- BSC+180° - ASC. អាស្រ័យហេតុនេះ ASB + BSC + ASC<
360
°
.
លទ្ធផល ២.ផលបូកនៃមុំយន្តហោះនៃមុំពហុកែងប៉ោងគឺតិចជាង 360 ។
ភស្តុតាងគឺស្រដៀងនឹងឯកសារមុនដែរ។
លទ្ធផល ៣.ផលបូកនៃមុំ dihedral នៃមុំ trihedral គឺធំជាង 180°
.
ភស្តុតាង។
អនុញ្ញាតឱ្យមាន SABC- មុំ trihedral ។ ចូរយើងជ្រើសរើសចំណុចមួយ។ ទំនៅខាងក្នុងវាហើយទម្លាក់កាត់កែងពីវា។ ប៉ា
1 ,
PB 1 ,
កុំព្យូទ័រ 1 នៅលើគែម (រូបភាព 4) ។

ជ្រុងរាបស្មើ ខ
1 កុំព្យូទ័រ 1 ,
ក 1 កុំព្យូទ័រ 1 ,
ក 1 PB 1 បំពេញមុំ dihedral ដែលត្រូវគ្នាជាមួយឆ្អឹងជំនី SA, SB, SCរហូតដល់ 180°
. ដូច្នេះផលបូកនៃមុំ dihedral ទាំងនេះគឺ 540°
- ( ខ
1 កុំព្យូទ័រ 1 + ក 1 កុំព្យូទ័រ 1 + ក
1 PB 1 ) ពិចារណាថាផលបូកនៃមុំយន្តហោះនៃត្រីកោណកែងជាមួយកំពូល ទំមុំតិចជាង 360°
យើងទទួលបានថាផលបូកនៃមុំ dihedral នៃមុំ trihedral ដើមគឺធំជាង 180°
.
ទ្រព្យ ២.bisectors នៃត្រីកោណមួយប្រសព្វគ្នានៅចំណុចមួយ។
ទ្រព្យសម្បត្តិ 2" ។ប្លង់ bisectoral នៃមុំ dihedral នៃមុំ trihedral ប្រសព្វគ្នាតាមបណ្តោយបន្ទាត់ត្រង់មួយ។
ភស្តុតាងស្រដៀងនឹងករណីយន្តហោះ។ ពោលគឺអនុញ្ញាតឱ្យ SABC- មុំ trihedral ។ ប្លង់ទ្វេនៃមុំ dihedral អេសគឺជា GMT នៃមុំសមមូលពីមុខរបស់វា។ ASCនិង ASB. ស្រដៀងគ្នានេះដែរ យន្តហោះ bisector នៃមុំ dihedral SBគឺជា GMT នៃមុំសមមូលពីមុខរបស់វា។ ប៊ីអេសអេនិង BSC
.
បន្ទាត់នៃចំនុចប្រសព្វរបស់ពួកគេ។ ដូច្នេះនឹងមានភាពស្មើគ្នាពីមុខទាំងអស់នៃមុំត្រីកោណ ហើយដូច្នេះ ប្លង់ទ្វេនៃមុំ dihedral នឹងឆ្លងកាត់វា SC
.
ទ្រព្យ ៣.ផ្នែកកាត់កែងនៃជ្រុងនៃត្រីកោណមួយប្រសព្វគ្នានៅចំណុចមួយ។
ទ្រព្យសម្បត្តិ 3" ។យន្តហោះដែលឆ្លងកាត់ bisectors នៃមុខនៃមុំ trihedral និងកាត់កែងទៅនឹងមុខទាំងនេះប្រសព្វគ្នាតាមបណ្តោយបន្ទាត់ត្រង់មួយ។
ភ័ស្តុតាងគឺស្រដៀងនឹងភស្តុតាងនៃទ្រព្យសម្បត្តិពីមុន។
ទ្រព្យ ៤.មេដ្យាននៃត្រីកោណមួយប្រសព្វគ្នានៅចំណុចមួយ។
ទ្រព្យសម្បត្តិ 4" ។យន្តហោះដែលឆ្លងកាត់គែមនៃមុំត្រីកោណ និងផ្នែកនៃមុខទល់មុខប្រសព្វគ្នាតាមបន្ទាត់ត្រង់មួយ។
ភស្តុតាង។
ពិចារណាមុំត្រីកោណ SABC, SA = SB = SC(រូបទី 5) ។ បន្ទាប់មក bisectors អេស
1 ,
SB 1 ,
SC 1 ជ្រុង BSC, ASC, ASB
គឺជាមេដ្យាននៃត្រីកោណដែលត្រូវគ្នា។ ដូច្នេះ អេ
1 ,
ប៊ីប៊ី 1 ,
ស៊ី.ស៊ី 1 - ត្រីកោណមាត្រ ABC. អនុញ្ញាតឱ្យមាន អូគឺជាចំណុចប្រសព្វរបស់ពួកគេ។ ត្រង់ ដូច្នេះមានក្នុងយន្តហោះទាំងបីដែលចាត់ទុកថាជាបន្ទាត់នៃចំណុចប្រសព្វរបស់វា។


ទ្រព្យ ៥.រយៈកំពស់នៃត្រីកោណប្រសព្វគ្នានៅចំណុចមួយ។
ទ្រព្យ ៥"។ យន្តហោះដែលឆ្លងកាត់គែមនៃមុំត្រីកោណ និងកាត់កែងទៅមុខទល់មុខ ប្រសព្វគ្នាតាមបន្ទាត់ត្រង់មួយ។
ភស្តុតាង។
ពិចារណាមុំបីជ្រុងជាមួយចំនុចកំពូល សនិងឆ្អឹងជំនី ក, ខ, គ។បញ្ជាក់ ក
1 ,
ខ 1 ,
គ 1 - បន្ទាត់ប្រសព្វនៃមុខដែលមានយន្តហោះឆ្លងកាត់គែមដែលត្រូវគ្នា និងកាត់កែងទៅនឹងមុខទាំងនេះ (រូបភាព 6) ។ ជួសជុលចំណុចមួយ។ គនៅលើគែម គហើយទម្លាក់កាត់កែងពីវា។ CA
1
និង ស៊ី.ប៊ី 1 នៅត្រង់ ក 1 និង ខ
1 .
បញ្ជាក់ កនិង ខចំនុចប្រសព្វនៃបន្ទាត់ CA
1 និង ស៊ី.ប៊ី
1 ជាមួយត្រង់ កនិង ខ. បន្ទាប់មក អេស
1
គឺជាការព្យាករ អេ
1
ទៅគែម BSC. ជា BCកាត់កែង អេស
1 បន្ទាប់មកវាកាត់កែង និង អេ
1 .
ដូចគ្នានេះដែរ ACកាត់កែង ប៊ីប៊ី
1 . ដូច្នេះ អេ
1 និង ប៊ីប៊ី
1
គឺជារយៈកំពស់នៃត្រីកោណ ABC. អនុញ្ញាតឱ្យមាន អូគឺជាចំណុចប្រសព្វរបស់ពួកគេ។ យន្តហោះឆ្លងកាត់បន្ទាត់ត្រង់ កនិង ក
1 ,
ខនិង ខ
1
កាត់កែងទៅនឹងយន្តហោះ ABCដូច្នេះហើយ បន្ទាត់នៃចំនុចប្រសព្វរបស់ពួកគេ។ ដូច្នេះកាត់កែង ABC. មានន័យថា ដូច្នេះកាត់កែង AB. នៅម្ខាងទៀត, សហកាត់កែង AB. ដូច្នេះយន្តហោះឆ្លងកាត់គែម គនិង ដូច្នេះនឹងកាត់កែងទៅម្ខាង។
ទ្រព្យ ៦ (ទ្រឹស្តីបទស៊ីនុស) ។
នៅក្នុងត្រីកោណមួយ។ ABCជាមួយភាគី ក, ខ, គរៀងៗខ្លួន យើងមានសមភាព ក
៖ អំពើបាប A=b៖ អំពើបាប B=c៖ អំពើបាប គ.
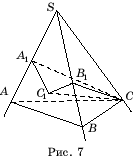
ទ្រព្យសម្បត្តិ 6" ។អនុញ្ញាតឱ្យ a, b, g - ជ្រុងសំប៉ែតនៃមុំ trihedral, ក, ខ, គគឺជាមុំ dihedral ទល់មុខរបស់ពួកគេ។ បន្ទាប់មក sin a : sin ក= sin b : sin ខ= sin g : sin គ.
ភស្តុតាង។អនុញ្ញាតឱ្យមាន SABC- មុំ trihedral ។ ទម្លាក់ពីចំណុច គកាត់កែង ស៊ី.ស៊ី
1
ទៅយន្តហោះ ASBនិងកាត់កែង CA
1
នៅលើគែម អេស(រូបភាពទី 7) ។ បន្ទាប់មកមុំ CA
1 គ 1 នឹងជាមុំលីនេអ៊ែរនៃមុំ dihedral ក. ដូច្នេះ ស៊ី.ស៊ី
1
=
CA១ បាប ក
=
SCបាប b sin ក.
ដូចគ្នានេះដែរវាត្រូវបានបង្ហាញថា ស៊ី.ស៊ី
1
= ស៊ី.ប៊ី១ បាប b=SCអំពើបាប
ដូចជានៅក្នុង ខ.
ដូច្នេះអំពើបាបសមភាពខអំពើបាប ក =បាប ក អំពើបាប ខដូច្នេះហើយ អំពើបាបសមភាពដូចជានៅក្នុង ក= sinb ៖ អំពើបាប ខ. នៅក្នុងវិធីស្រដៀងគ្នានេះ យើងបង្ហាញថាសមភាពមានបាបខ: បាប ខ= sin g : sin គ.
ទ្រព្យ ៧.ប្រសិនបើរង្វង់មួយអាចត្រូវបានចារឹកក្នុងរាងបួនជ្រុងប៉ោង នោះផលបូកនៃភាគីទល់មុខគឺស្មើគ្នា។
ទ្រព្យសម្បត្តិ 7" ។ប្រសិនបើស្វ៊ែរអាចត្រូវបានចារឹកក្នុងមុំ tetrahedral ប៉ោង នោះផលបូកនៃមុំយន្តហោះទល់មុខគឺស្មើគ្នា។
អក្សរសិល្ប៍
1. Hadamard J. ធរណីមាត្របឋម។ ផ្នែកទី II ។ ស្តេរ៉េអូមេទ្រី។ - អិមៈ Uchpedgiz ឆ្នាំ 1938 ។
2. Perepelkin D.I. វគ្គសិក្សានៃធរណីមាត្របឋម។ ផ្នែកទី II ។ ធរណីមាត្រក្នុងលំហ។ - M.-L. : Gostekhizdat ឆ្នាំ 1949 ។
3. សព្វវចនាធិប្បាយគណិតវិទ្យាបឋម។ សៀវភៅ IV ។ ធរណីមាត្រ។ - អិម; ១៩៦៣។
4. Smirnova I.M. នៅក្នុងពិភពនៃ polyhedrons ។ - អិមៈ ការត្រាស់ដឹង ឆ្នាំ ១៩៩៥។
មុំ dihedral គឺជាតួលេខដែលបង្កើតឡើងដោយពាក់កណ្តាលយន្តហោះពីរដែលមានបន្ទាត់ត្រង់ធម្មតាដែលចងពួកវា ប្លង់ពាក់កណ្តាលត្រូវបានគេហៅថា មុខ ហើយបន្ទាត់ត្រង់ដែលចងពួកវាត្រូវបានគេហៅថាគែមនៃមុំ dihedral ។
រូបភាព 142 បង្ហាញមុំ dihedral ជាមួយគែម a និងប្រឈមមុខនឹង a និង (3.
យន្តហោះកាត់កែងទៅគែមនៃមុំ dihedral កាត់មុខរបស់វាតាមបន្ទាត់ពាក់កណ្តាលពីរ។ មុំដែលបង្កើតឡើងដោយបន្ទាត់ពាក់កណ្តាលទាំងនេះត្រូវបានគេហៅថាមុំលីនេអ៊ែរនៃមុំ dihedral ។ រង្វាស់នៃមុំ dihedral មួយត្រូវបានយកជារង្វាស់នៃមុំលីនេអ៊ែរដែលត្រូវគ្នា។ ប្រសិនបើតាមរយៈចំណុច A នៃគែម a នៃមុំ dihedral យើងគូរប្លង់ y កាត់កែងទៅគែមនេះ នោះវានឹងប្រសព្វគ្នានឹងយន្តហោះ a និង (3 តាមបន្ទាត់ពាក់កណ្តាល (រូបភាព 142); មុំលីនេអ៊ែរនៃ dihedral ដែលបានផ្តល់ឱ្យ មុំ។ រង្វាស់ដឺក្រេនៃមុំលីនេអ៊ែរនេះគឺជារង្វាស់ដឺក្រេនៃមុំ dihedral ។ ការវាស់វែងមុំ dihedral មិនអាស្រ័យលើជម្រើសនៃមុំលីនេអ៊ែរទេ។
មុំត្រីកោណគឺជាតួរលេខដែលបង្កើតឡើងដោយមុំសំប៉ែតបី (រូបភាព 143)។ មុំទាំងនេះត្រូវបានគេហៅថាមុខនៃមុំត្រីកោណ ហើយជ្រុងរបស់វាត្រូវបានគេហៅថាគែម។ ចំនុចកំពូលទូទៅនៃមុំសំប៉ែតត្រូវបានគេហៅថា vertex នៃមុំ trihedral ។ មុំ dihedral ដែលបង្កើតឡើងដោយមុខនិងផ្នែកបន្ថែមរបស់ពួកគេត្រូវបានគេហៅថាមុំ dihedral នៃមុំ trihedral ។
ស្រដៀងគ្នានេះដែរ គោលគំនិតនៃមុំពហុកោណ ត្រូវបានកំណត់ជាតួរលេខដែលផ្សំឡើងដោយមុំសំប៉ែត (រូបភាព ១៤៤)។ សម្រាប់មុំពហុកោណ គោលគំនិតនៃមុខ គែម និងមុំ dihedral ត្រូវបានកំណត់តាមរបៀបដូចគ្នាទៅនឹងមុំត្រីកោណ។


ពហុកោណគឺជាតួដែលផ្ទៃរបស់វាមានចំនួនកំណត់នៃពហុកោណរាបស្មើ (រូបភាព 145) ។
ពហុកោណត្រូវបានគេហៅថាប៉ោងប្រសិនបើវាមានទីតាំងនៅម្ខាងនៃយន្តហោះនៃពហុកោណនីមួយៗនៅលើផ្ទៃរបស់វា (រូបភាព 145, ក, ខ) ។ ផ្នែកទូទៅនៃយន្តហោះបែបនេះ និងផ្ទៃនៃប៉ោងប៉ោងត្រូវបានគេហៅថា មុខ។ មុខនៃពហុកោណប៉ោងគឺជាពហុកោណប៉ោង។ ជ្រុងនៃមុខត្រូវបានគេហៅថា គែមនៃ polyhedron ហើយកំពូលត្រូវបានគេហៅថា vertices នៃ polyhedron ។
និយមន័យ។ ចូរយើងយកមុំជាច្រើន (រូបភាពទី 37)៖ ASB, BSC, CSD ដែលនៅជាប់គ្នាជាស៊េរី មានទីតាំងនៅក្នុងប្លង់តែមួយជុំវិញចំនុចរួម S ។
អនុញ្ញាតឱ្យយើងបង្វិលប្លង់មុំ ASB ជុំវិញផ្នែកទូទៅ SB ដើម្បីឱ្យយន្តហោះនេះបង្កើតមុំ dihedral មួយចំនួនជាមួយនឹងយន្តហោះ BSC ។ បន្ទាប់មកដោយមិនផ្លាស់ប្តូរមុំ dihedral លទ្ធផលយើងបង្វិលវាជុំវិញបន្ទាត់ត្រង់ SC ដូច្នេះយន្តហោះ BSC ធ្វើឱ្យមុំ dihedral មួយចំនួនជាមួយនឹងយន្តហោះ CSD ។ ចូរបន្តការបង្វិលបន្តបន្ទាប់គ្នាជុំវិញផ្នែករួមនីមួយៗ។ ប្រសិនបើក្នុងករណីនេះផ្នែកចុងក្រោយនៃ SF ត្រូវបានផ្សំជាមួយផ្នែកទីមួយនៃ SA នោះតួលេខមួយត្រូវបានបង្កើតឡើង (រូបភាព 38) ដែលត្រូវបានគេហៅថា មុំ polyhedral. មុំ ASB, BSC, ... ត្រូវបានគេហៅថា ជ្រុងរាបស្មើឬ មុខ, ភាគីរបស់ពួកគេ SA, SB, ... ត្រូវបានគេហៅថា ឆ្អឹងជំនីនិងចំណុចកំពូលរួម S- កិច្ចប្រជុំកំពូលមុំពហុមុខ។

គែមនីមួយៗក៏ជាគែមនៃមុំ dihedral មួយចំនួនផងដែរ។ ដូច្នេះ នៅក្នុងមុំពហុធា មានមុំ dihedral ច្រើន និងមុំសំប៉ែតច្រើន ដូចមានគែមទាំងអស់នៅក្នុងវា។ ចំនួនមុខតូចបំផុតនៅក្នុងមុំពហុកោណគឺបី; មុំនេះត្រូវបានគេហៅថា ត្រីវិស័យ. អាចមានមុំបួនជ្រុង ប្រាំជ្រុង។ល។
មុំពហុកែងត្រូវបានតាងដោយអក្សរ S តែមួយដាក់នៅចំនុចកំពូល ឬដោយអក្សរស៊េរី SABCDE ដែលទីមួយកំណត់ចំនុចកំពូល ហើយមួយទៀតជាគែមតាមលំដាប់នៃទីតាំងរបស់វា។
មុំពហុកែងត្រូវបានគេហៅថាប៉ោង ប្រសិនបើវាស្ថិតនៅម្ខាងនៃយន្តហោះនៃមុខនីមួយៗ ដែលត្រូវបានពង្រីកដោយគ្មានកំណត់។ ជាឧទាហរណ៍ មុំបែបនេះគឺជាមុំដែលបង្ហាញក្នុងគំនូរលេខ 38។ ផ្ទុយទៅវិញ មុំក្នុងគំនូរលេខ 39 មិនអាចត្រូវបានគេហៅថាប៉ោងបានទេ ដោយសារវាស្ថិតនៅលើផ្នែកទាំងពីរនៃមុខ ASB ឬមុខ BSC ។

ប្រសិនបើមុខទាំងអស់នៃមុំពហុកោណត្រូវបានប្រសព្វគ្នាដោយយន្តហោះ នោះពហុកោណមួយត្រូវបានបង្កើតឡើងនៅក្នុងផ្នែក ( abcde ) នៅក្នុងមុំពហុកោណប៉ោង ពហុកោណនេះក៏ប៉ោងផងដែរ។
យើងនឹងពិចារណាតែមុំពហុកែងប៉ោងប៉ុណ្ណោះ។
ទ្រឹស្តីបទ។ នៅក្នុងមុំបីជ្រុង មុំសំប៉ែតនីមួយៗគឺតិចជាងផលបូកនៃមុំសំប៉ែតពីរផ្សេងទៀត។
អនុញ្ញាតឱ្យនៅក្នុងមុំ trihedral SABC (រូបភាព 40) ធំបំផុតនៃមុំផ្ទះល្វែងគឺមុំ ASC ។

ចូរយើងគូរមុំ ASD នៅលើមុំនេះ ដែលស្មើនឹងមុំ ASB ហើយគូរបន្ទាត់ត្រង់មួយចំនួន AC ប្រសព្វ SD នៅចំណុចខ្លះ D. ដាក់ SB = SD ។ ការភ្ជាប់ B ជាមួយ A និង C យើងទទួលបាន \(\Delta\)ABC ដែលក្នុងនោះ
AD+DC< АВ + ВС.
ត្រីកោណ ASD និង ASB គឺត្រូវគ្នាព្រោះពួកវានីមួយៗមានមុំស្មើគ្នារវាងភាគីស្មើគ្នា៖ ដូច្នេះ AD = AB ។ ដូច្នេះប្រសិនបើយើងបោះបង់ចោលពាក្យស្មើគ្នា AD និង AB នៅក្នុងវិសមភាពដែលបានមកពីនោះ យើងទទួលបាន DC នោះ។< ВС.
ឥឡូវនេះយើងកត់សំគាល់ថាត្រីកោណ SCD និង SCB មានភាគីទាំងពីរនៃមួយស្មើនឹងពីរជ្រុងនៃម្ខាងទៀត ហើយជ្រុងទីបីមិនស្មើគ្នា។ ក្នុងករណីនេះមុំធំជាងស្ថិតនៅទល់មុខនឹងធំជាងនៃភាគីទាំងនេះ; មានន័យថា
∠CSD< ∠ CSВ.
ការបន្ថែមមុំ ASD ទៅផ្នែកខាងឆ្វេងនៃវិសមភាពនេះ ហើយមុំ ASB ស្មើនឹងវាទៅផ្នែកខាងស្តាំ យើងទទួលបានវិសមភាពដែលត្រូវបានទាមទារដើម្បីបញ្ជាក់៖
∠ ASC< ∠ CSB + ∠ ASB.
យើងបានបង្ហាញថាសូម្បីតែមុំសំប៉ែតធំបំផុតក៏តិចជាងផលបូកនៃមុំពីរផ្សេងទៀតដែរ។ ដូច្នេះទ្រឹស្តីបទត្រូវបានបញ្ជាក់។
ផលវិបាក។ ដកពីផ្នែកទាំងពីរនៃវិសមភាពចុងក្រោយនៅក្នុងមុំ ASB ឬក្នុងមុំ CSB; យើងទទួលបាន:
∠ASC - ∠ASB< ∠ CSB;
∠ASC - ∠CSB< ∠ ASB.
ដោយពិចារណាលើវិសមភាពទាំងនេះពីស្តាំទៅឆ្វេង ហើយពិចារណាថាមុំ ASC ជាមុំធំបំផុតនៃមុំទាំងបីគឺធំជាងភាពខុសគ្នានៃមុំពីរផ្សេងទៀត យើងសន្និដ្ឋានថា នៅក្នុងមុំបីជ្រុង មុំយន្តហោះនីមួយៗគឺធំជាងភាពខុសគ្នានៃមុំពីរផ្សេងទៀត។.
ទ្រឹស្តីបទ។ នៅក្នុងមុំពហុកែងប៉ោង ផលបូកនៃមុំប្លង់ទាំងអស់គឺតិចជាង 4d (360°) .
ចូរប្រសព្វមុខគ្នា (រូបភាពទី 41) នៃមុំប៉ោង SABCDE ជាមួយប្លង់ខ្លះ។ ពីនេះនៅក្នុងផ្នែកយើងទទួលបានប៉ោងមួយ។ ន- ហ្គុន ABCDE ។

ការអនុវត្តទ្រឹស្តីបទដែលបានបង្ហាញមុននេះចំពោះមុំត្រីកោណនីមួយៗដែលមានចំណុចកំពូលនៅចំណុច A, B, C, D និង E, paholim៖
∠ABC< ∠ABS + ∠SВC, ∠BCD < ∠BCS + ∠SCD и т. д.
ចូរយើងបន្ថែមវិសមភាពទាំងអស់នេះតាមពាក្យ។ បន្ទាប់មកនៅផ្នែកខាងឆ្វេងយើងទទួលបានផលបូកនៃមុំទាំងអស់នៃពហុកោណ ABCDE ដែលស្មើនឹង 2 ឌីន - 4ឃ និងនៅខាងស្តាំ - ផលបូកនៃមុំនៃត្រីកោណ ABS, SBC ។ល។ លើកលែងតែមុំទាំងនោះដែលស្ថិតនៅត្រង់ចំនុចកំពូល S. បង្ហាញពីផលបូកនៃមុំចុងក្រោយទាំងនេះដោយអក្សរ X យើងទទួលបានបន្ទាប់ពីការបន្ថែម៖
2ឌីន - 4ឃ < 2dn - x .
ពីភាពខុសគ្នា ២ ឌីន - 4ឃ និង ២ dn - x minuends គឺដូចគ្នា ដូច្នេះសម្រាប់ភាពខុសគ្នាទីមួយតិចជាងទីពីរ វាចាំបាច់ថា subtrahend 4 ឃ គឺច្រើនជាងដក X ; មានន័យថា ៤ ឃ > X , i.e. X < 4ឃ .
ករណីសាមញ្ញបំផុតនៃភាពស្មើគ្នានៃមុំ trihedral
ទ្រឹស្តីបទ។ មុំ Trihedral គឺស្មើគ្នាប្រសិនបើពួកគេមាន៖
1) ដោយមុំ dihedral ស្មើគ្នាដែលរុំព័ទ្ធរវាងមុំយន្តហោះស្មើគ្នា និងគម្លាតស្មើគ្នា, ឬ
2) តាមបណ្តោយមុំយន្តហោះស្មើគ្នាដែលបានរុំព័ទ្ធរវាងមុំ dihedral ពីរដែលមានគម្លាតស្មើគ្នា និងស្មើគ្នា.
1) ទុក S និង S 1 ជាមុំត្រីកោណពីរ (រូបភាព 42) ដែលក្នុងនោះ ∠ASB = ∠A 1 S 1 B 1 , ∠ASC = ∠A 1 S 1 C 1 (ហើយមុំស្មើគ្នាទាំងនេះមានទីតាំងស្មើគ្នា) និង dihedral មុំ AS គឺស្មើនឹងមុំ dihedral A 1 S 1 ។

ចូរយើងបង្កប់មុំ S 1 ទៅក្នុងមុំ S ដើម្បីឱ្យចំនុច S 1 និង S បន្ទាត់ S 1 A 1 និង SA និងយន្តហោះ A 1 S 1 B 1 និង ASB ស្របគ្នា។ បន្ទាប់មកគែម S 1 B 1 នឹងទៅតាមបណ្តោយ SB (ដោយសារតែសមភាពនៃមុំ A 1 S 1 B 1 និង ASB) យន្តហោះ A 1 S 1 C 1 នឹងទៅតាមបណ្តោយ ASC (ដោយសារតែសមភាពនៃមុំ dihedral) ។ ហើយគែម S 1 C 1 នឹងទៅតាមបណ្តោយគែម SC (ដោយសារតែសមភាពនៃមុំ A 1 S 1 C 1 និង ASC) ។ ដូច្នេះមុំ trihedral នឹងត្រូវបានបញ្ចូលគ្នាដោយគែមទាំងអស់របស់ពួកគេ i.e. ពួកគេនឹងស្មើគ្នា។
2) លក្ខណៈវិនិច្ឆ័យទី 2 ដូចជាទី 1 ត្រូវបានបង្ហាញដោយការបង្កប់។
មុំពហុធាស៊ីមេទ្រី
ដូចដែលអ្នកបានដឹងហើយថាមុំបញ្ឈរគឺស្មើគ្នានៅពេលដែលវាមកដល់មុំដែលបង្កើតឡើងដោយបន្ទាត់ត្រង់ឬប្លង់។ តោះមើលថាតើសេចក្តីថ្លែងការណ៍នេះពិតសម្រាប់មុំពហុធា។

យើងបន្ត (រូបភាពទី 43) គែមទាំងអស់នៃមុំ SABCDE ហួសពីចំនុចកំពូល S បន្ទាប់មកមុំពហុកែងមួយទៀត SA 1 B 1 C 1 D 1 E 1 ត្រូវបានបង្កើតឡើង ដែលអាចត្រូវបានគេហៅថា បញ្ឈរដោយគោរពទៅជ្រុងទីមួយ។ វាងាយមើលឃើញថា មុំទាំងពីរមានប្លង់ស្មើគ្នា និងមុំ dihedral រៀងគ្នា ប៉ុន្តែទាំងពីរស្ថិតនៅក្នុងលំដាប់បញ្ច្រាស។ ជាការពិតណាស់ ប្រសិនបើយើងស្រមៃមើលអ្នកសង្កេតការណ៍ដែលមើលពីខាងក្រៅមុំពហុកែងនៅចំនុចកំពូលរបស់វា នោះគែម SA, SB, SC, SD, SE នឹងហាក់បីដូចជាគាត់មានទីតាំងនៅក្នុងទិសដៅច្រាសទ្រនិចនាឡិកា ខណៈកំពុងមើលមុំ SA 1 B 1 C 1 D 1 E 1 គាត់ឃើញគែម SA 1 , SВ 1 , ... ដែលមានទីតាំងនៅតាមទ្រនិចនាឡិកា។
មុំ Polyhedral ដែលមានប្លង់ស្មើគ្នា និងមុំ dihedral ប៉ុន្តែស្ថិតនៅក្នុងលំដាប់បញ្ច្រាស មិនអាចរួមបញ្ចូលគ្នាបានទេនៅពេលបង្កប់។ នោះមានន័យថាពួកគេមិនស្មើគ្នា។ មុំបែបនេះត្រូវបានគេហៅថា ស៊ីមេទ្រី(ទាក់ទងទៅនឹងកំពូល S) ។ បន្ថែមទៀតអំពីស៊ីមេទ្រីនៃតួលេខនៅក្នុងលំហ នឹងត្រូវបានពិភាក្សាដូចខាងក្រោម។
សម្ភារៈផ្សេងៗ№1 Date05.09.14
ប្រធានបទធរណីមាត្រ
ថ្នាក់ 11
ប្រធានបទមេរៀន៖ គំនិតនៃមុំពហុកោណ។ មុំត្រីកោណ។
គោលបំណងនៃមេរៀន៖
ណែនាំគំនិត៖“ មុំត្រីកោណ”“ មុំពហុកោណ”“ ពហុកោណ”;
ដើម្បីឱ្យសិស្សស្គាល់ពីធាតុនៃមុំត្រីកោណ និងពហុកោណ ពហុហេដរ៉ុន ក៏ដូចជានិយមន័យនៃមុំពហុកោណប៉ោង និងលក្ខណៈសម្បត្តិនៃមុំសំប៉ែតនៃមុំពហុកោណ។
ដើម្បីបន្តការងារលើការអភិវឌ្ឍនៃតំណាងទំហំ និងការស្រមើលស្រមៃតាមលំហ ក៏ដូចជាការគិតឡូជីខលរបស់សិស្ស។
ប្រភេទមេរៀន៖ រៀនសម្ភារៈថ្មី។
ក្នុងអំឡុងពេលថ្នាក់
1. ពេលរៀបចំ។
ជំរាបសួរសិស្ស ពិនិត្យមើលការត្រៀមខ្លួនរបស់ថ្នាក់សម្រាប់មេរៀន រៀបចំការយកចិត្តទុកដាក់របស់សិស្ស បង្ហាញពីគោលបំណងទូទៅនៃមេរៀន និងផែនការរបស់វា។
2. ការបង្កើតគំនិតថ្មី និងវិធីសាស្រ្តនៃសកម្មភាព។
កិច្ចការ៖ ដើម្បីធានាបាននូវការយល់ឃើញ ការយល់ដឹង និងការទន្ទេញនៃសម្ភារៈសិក្សាដោយសិស្ស។ ដើម្បីធានាថាសិស្សស្ទាត់ជំនាញវិធីសាស្រ្តក្នុងការផលិតឡើងវិញនូវសម្ភារៈដែលបានសិក្សា ដើម្បីលើកកម្ពស់ការយល់ដឹងផ្នែកទស្សនវិជ្ជានៃគោលគំនិត ច្បាប់ ច្បាប់ រូបមន្តដែលត្រូវបានផ្សំឡើង។ ដើម្បីបង្កើតភាពត្រឹមត្រូវ និងការយល់ដឹងអំពីសម្ភារៈសិក្សាដោយសិស្ស ដើម្បីកំណត់ចន្លោះប្រហោងក្នុងការយល់ដឹងបឋម ដើម្បីអនុវត្តការកែតម្រូវ។ ដើម្បីធានាថាសិស្សានុសិស្សបានផ្សារភ្ជាប់បទពិសោធន៍ប្រធានបទរបស់ពួកគេជាមួយនឹងសញ្ញានៃចំណេះដឹងវិទ្យាសាស្ត្រ។
សូមឱ្យកាំរស្មីបីត្រូវបានផ្តល់ឱ្យក, ខ និងs s ចំណុចចាប់ផ្តើមទូទៅអូ (រូបភាព 1.1) ។ កាំរស្មីទាំងបីនេះមិនចាំបាច់ស្ថិតនៅលើយន្តហោះតែមួយទេ។ នៅក្នុងរូបភាព 1.2 កាំរស្មីខ និងជាមួយ ដេកក្នុងយន្តហោះR កាំរស្មីមួយ។ក មិនកុហកនៅក្នុងយន្តហោះនេះទេ។
កាំរស្មីក, ខ និងជាមួយ គូកំណត់មុំសំប៉ែតបីដែលសម្គាល់ដោយធ្នូ (រូបភាព 1.3) ។
ពិចារណាលើតួរលេខដែលមានមុំបីដែលបានបង្ហាញខាងលើ និងផ្នែកនៃលំហដែលជាប់នឹងមុំសំប៉ែតទាំងនេះ។ តួលេខនេះត្រូវបានគេហៅថាមុំ trihedral
(រូបភាពទី 2) ។
កាំរស្មីក, ខ និងជាមួយ បានហៅគែមនៃមុំ trihedral, និងជ្រុង៖ = AOC = AOB
=
BOC
,
កំណត់មុំត្រីកោណ - របស់វា។មុខ។
ជ្រុងទាំងនេះបង្កើតបាន។ផ្ទៃ trihedral ។
ចំណុចអូ
បានហៅចំនុចកំពូលនៃមុំត្រីកោណ។
មុំ trihedral អាចត្រូវបានសម្គាល់ដូចខាងក្រោម: OABC

ដោយបានពិនិត្យដោយប្រុងប្រយ័ត្ននូវមុំពហុកែងទាំងអស់ដែលបង្ហាញក្នុងរូបភាពទី 3 យើងអាចសន្និដ្ឋានបានថា មុំពហុកែងនីមួយៗមានចំនួនគែម និងមុខដូចគ្នា៖

4 មុខនិងកំពូលមួយ;
ជ្រុងឆកោនមាន 6 គែម 6 មុខ និងមួយ vertex ។ល។
ជ្រុងប្រាំជ្រុងមាន 5 គែម 5 មុខ និងមួយ vertex;
មុំ Polyhedral គឺ ប៉ោង និង មិនប៉ោង។
ស្រមៃថាយើងបានយកកាំរស្មីចំនួនបួនដែលមានប្រភពដើមទូទៅ ដូចក្នុងរូបភាពទី 4។ ក្នុងករណីនេះ យើងទទួលបានមុំ polyhedral មិនប៉ោង។
និយមន័យ 1. មុំពហុកោណត្រូវបានគេហៅថាមុំប៉ោងប្រសិនបើគាត់ស្ថិតនៅម្ខាងនៃយន្តហោះនៃមុខនីមួយៗ។
ម្យ៉ាងវិញទៀត មុំប៉ោងប៉ោងតែងតែអាចដាក់ដោយមុខណាមួយរបស់វានៅលើយន្តហោះមួយចំនួន។ អ្នកអាចមើលឃើញថាក្នុងករណីដែលបង្ហាញក្នុងរូបភាពទី 4 នេះមិនតែងតែអាចធ្វើទៅបានទេ។ មុំ tetrahedral ដែលបង្ហាញក្នុងរូបភាពទី 4 គឺមិនប៉ោង។
ចំណាំថានៅក្នុងមេរៀនរបស់យើង ប្រសិនបើយើងនិយាយថា "មុំពហុកោណ" យើងមានន័យថាវាប៉ោង។ ប្រសិនបើមុំ polyhedral ដែលត្រូវបានចាត់ទុកថាមិនមែនជាប៉ោង នេះនឹងត្រូវបានពិភាក្សាដោយឡែកពីគ្នា។
លក្ខណៈសម្បត្តិនៃជ្រុងយន្តហោះនៃជ្រុងពហុហិដ
ទ្រឹស្តីបទ ១.មុំសំប៉ែតនីមួយៗនៃមុំត្រីកោណគឺតិចជាងផលបូកនៃមុំរាបស្មើពីរផ្សេងទៀត។
ទ្រឹស្តីបទ ២.ផលបូកនៃតម្លៃនៃមុំយន្តហោះទាំងអស់នៃមុំពហុកែងប៉ោងគឺតិចជាង 360°។
3. កម្មវិធី។ ការបង្កើតជំនាញនិងសមត្ថភាព។
គោលបំណង៖ ដើម្បីធានាថាសិស្សអនុវត្តចំណេះដឹង និងវិធីសាស្រ្តនៃសកម្មភាពដែលពួកគេត្រូវការសម្រាប់ SW ដើម្បីបង្កើតលក្ខខណ្ឌសម្រាប់សិស្សក្នុងការកំណត់អត្តសញ្ញាណវិធីផ្ទាល់ខ្លួននៃការអនុវត្តអ្វីដែលពួកគេបានរៀន។
6. ដំណាក់កាលព័ត៌មានអំពីកិច្ចការផ្ទះ។
គោលបំណង៖ ដើម្បីធានាថាសិស្សយល់អំពីគោលបំណង ខ្លឹមសារ និងវិធីសាស្រ្តធ្វើកិច្ចការផ្ទះ។
§1(1.1, 1.2) ទំ។ 4, លេខ 9 ។
7. សង្ខេបមេរៀន។
គោលបំណង៖ ដើម្បីផ្តល់ការវាយតម្លៃគុណភាពនៃការងាររបស់ថ្នាក់ និងសិស្សម្នាក់ៗ។
8. ដំណាក់កាលនៃការឆ្លុះបញ្ចាំង។
កិច្ចការ៖ ដើម្បីផ្តួចផ្តើមការឆ្លុះបញ្ចាំងរបស់សិស្សលើការវាយតម្លៃខ្លួនឯងអំពីសកម្មភាពរបស់ពួកគេ។ ដើម្បីធានាថាសិស្សរៀនពីគោលការណ៍នៃការគ្រប់គ្រងខ្លួនឯង និងកិច្ចសហប្រតិបត្តិការ។
ការសន្ទនាលើ៖
តើអ្នកឃើញអ្វីគួរឱ្យចាប់អារម្មណ៍នៅក្នុងមេរៀន?
អ្វីដែលមិនច្បាស់?
តើគ្រូគួរយកចិត្តទុកដាក់លើអ្វីក្នុងមេរៀនបន្ទាប់?
តើអ្នកនឹងវាយតម្លៃការងាររបស់អ្នកក្នុងថ្នាក់យ៉ាងដូចម្តេច?
