ដំណោះស្រាយក្រាហ្វិកនៃសមីការ quadratic ដើម្បីពង្រឹងសមត្ថភាពបង្កើតក្រាហ្វនៃមុខងារផ្សេងៗ។ ដើម្បីបង្កើតសមត្ថភាពក្នុងការដោះស្រាយសមីការការ៉េជាក្រាហ្វិក។ គម្រោងលើប្រធានបទ "ការផ្លាស់ប្តូរក្រាហ្វនៃមុខងារ"

ដំណោះស្រាយក្រាហ្វិកនៃសមីការ quadratic ដើម្បីពង្រឹងសមត្ថភាពបង្កើតក្រាហ្វនៃមុខងារផ្សេងៗ។ ដើម្បីបង្កើតសមត្ថភាពក្នុងការដោះស្រាយសមីការការ៉េជាក្រាហ្វិក។ Brdsk 2009 ស្ថាប័នអប់រំក្រុង - Economic Lyceum មេរៀនទូទៅលើប្រធានបទ "មុខងារបួនជ្រុង" ពិជគណិតថ្នាក់ទី 8 គ្រូបង្រៀន Fedoseeva T.M.

ការធ្វើផែនការអនុគមន៍ quadratic កំណត់ទិសដៅនៃសាខា៖ a> 0 branch up; ក 0 សាខាឡើង; a"> 0 សាខាឡើង; a"> 0 សាខាឡើង; a" title="(!LANG:ការកំណត់មុខងាររាងការ៉េ កំណត់ទិសដៅសាខា៖ a>0 សាខាឡើងលើ; a"> title="ការធ្វើផែនការអនុគមន៍ quadratic កំណត់ទិសដៅនៃសាខា៖ a> 0 branch up; ក"> !}

0 សាខាត្រូវបានដឹកនាំឡើងលើ; 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ យើងរកឃើញចំណុច" title="(!LANG: ចូរយើងរៀបចំមុខងារ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1>0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ការស្វែងរកចំណុចមួយ។" class="link_thumb"> 3 !}ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1> 0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ យើងរកឃើញចំនុចប្រសព្វជាមួយអ័ក្ស OX: x 1 \u003d -1; x 2 \u003d 3 1 វិធីដើម្បីដោះស្រាយសមីការ x 2 -2x-3 \u003d 0 y x ដោះស្រាយសមីការ x 2 +2x-3 \u003d 0 0 សាខាត្រូវបានដឹកនាំឡើងលើ; 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ យើងរកឃើញចំណុច "\u003e 0 សាខាត្រូវបានតម្រង់ទៅខាងលើ; 2) កំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្ស ចំណុចត្រួតពិនិត្យប៉ារ៉ាបូឡា៖ (0: -3), (3; 0) និងស៊ីមេទ្រីអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ស្វែងរកចំណុចប្រសព្វជាមួយអ័ក្ស OX៖ x 1 \u003d -1; x 2 \u003d 3 1 វិធីដើម្បីដោះស្រាយសមីការ x 2 -2x-3 \u003d 0 y x 0 1 - 4 23 ដោះស្រាយសមីការ x 2 + 2x-3 \u003d 0 "\u003e 0 សាខាត្រូវបានដឹកនាំឡើងលើ; 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ស្វែងរកចំណុច "title="(!LANG៖ ចូរបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1>0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ការស្វែងរកចំណុចមួយ។"> title="ចូរយើងបង្កើតក្រាហ្វនៃអនុគមន៍ y=x 2 -2x-3 ដោយប្រើក្បួនដោះស្រាយ៖ 1) a=1> 0 សាខាត្រូវបានតម្រង់ទៅខាងលើ។ 2) ចំនុចកំពូល y o \u003d y (1) \u003d 1-2-3 \u003d -4 A (1; -4) x \u003d 1 - អ័ក្សនៃប៉ារ៉ាបូឡា ចំណុចត្រួតពិនិត្យ៖ (0: -3), (3 ; 0) និងស៊ីមេទ្រីចំពោះពួកគេអំពីអ័ក្ស x = 1 យើងបង្កើតប៉ារ៉ាបូឡា។ ការស្វែងរកចំណុចមួយ។"> !}

វិធីទីពីរ៖ ក) ។ ចូរបែងចែកសមីការ x 2 −2x-3=0 ជាផ្នែក x 2 = 2x+3 ចូរយើងសរសេរអនុគមន៍ពីរ y= x 2 ; y \u003d 2x + 3 យើងបង្កើតក្រាហ្វនៃមុខងារទាំងនេះនៅក្នុងប្រព័ន្ធកូអរដោនេមួយ។ abscissas នៃចំនុចប្រសព្វគឺជាឫសគល់នៃសមីការ។ 0 1 x y ដោះស្រាយសមីការ x 2 +2x-3=0

វិធីទីបី៖ x 2 -3 \u003d 2x y \u003d x 2 -3; y=2x យើងបង្កើតក្រាហ្វនៃមុខងារទាំងនេះនៅក្នុងប្រព័ន្ធកូអរដោនេមួយ។ abscissas នៃចំនុចប្រសព្វគឺជាឫសគល់នៃសមីការ។ 0 1 x y ដោះស្រាយសមីការ x 2 +2x-3=0

ដំណោះស្រាយក្រាហ្វិកនៃសមីការ

សួស្តីឆ្នាំ ២០០៩

សេចក្តីផ្តើម

តម្រូវការដើម្បីដោះស្រាយសមីការបួនជ្រុងនៅសម័យបុរាណគឺបណ្តាលមកពីតម្រូវការក្នុងការដោះស្រាយបញ្ហាទាក់ទងនឹងការស្វែងរកតំបន់នៃដី និងផែនដីនៃធម្មជាតិយោធា ក៏ដូចជាការអភិវឌ្ឍន៍តារាសាស្ត្រ និងគណិតវិទ្យាខ្លួនឯង។ ជនជាតិបាប៊ីឡូនបានដឹងពីរបៀបដោះស្រាយសមីការបួនជ្រុងប្រហែលឆ្នាំ 2000 មុនគ។ ច្បាប់សម្រាប់ការដោះស្រាយសមីការទាំងនេះដែលមានចែងនៅក្នុងអត្ថបទរបស់បាប៊ីឡូន គឺស្របគ្នានឹងសមីការសម័យទំនើប ប៉ុន្តែគេមិនដឹងថាតើជនជាតិបាប៊ីឡូនចូលមកក្បួននេះដោយរបៀបណានោះទេ។

រូបមន្តសម្រាប់ដោះស្រាយសមីការការ៉េនៅអឺរ៉ុបត្រូវបានបង្កើតឡើងជាលើកដំបូងក្នុងសៀវភៅ Abacus ដែលសរសេរក្នុងឆ្នាំ ១២០២ ដោយគណិតវិទូជនជាតិអ៊ីតាលី Leonardo Fibonacci។ សៀវភៅរបស់គាត់បានរួមចំណែកដល់ការរីករាលដាលនៃចំណេះដឹងពិជគណិតមិនត្រឹមតែនៅក្នុងប្រទេសអ៊ីតាលីប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងនៅក្នុងប្រទេសអាល្លឺម៉ង់ បារាំង និងបណ្តាប្រទេសអឺរ៉ុបផ្សេងទៀតផងដែរ។

ប៉ុន្តែច្បាប់ទូទៅសម្រាប់ការដោះស្រាយសមីការបួនជ្រុងជាមួយនឹងការបន្សំដែលអាចធ្វើបានទាំងអស់នៃមេគុណ b និង c ត្រូវបានបង្កើតឡើងនៅក្នុងទ្វីបអឺរ៉ុបតែនៅក្នុងឆ្នាំ 1544 ដោយ M. Stiefel ។

នៅឆ្នាំ 1591 ហ្វ្រង់ស្វ័រវៀត បានណែនាំរូបមន្តសម្រាប់ដោះស្រាយសមីការការ៉េ។

ប្រភេទមួយចំនួននៃសមីការការ៉េអាចត្រូវបានដោះស្រាយនៅក្នុងបាប៊ីឡូនបុរាណ។

Diophantus នៃ Alexandria និង អេកលីដ , អាល់-Khwarizmiនិង Omar Khayyamដោះស្រាយសមីការតាមធរណីមាត្រ និងក្រាហ្វិក។

នៅថ្នាក់ទី 7 យើងបានសិក្សាមុខងារ y \u003d C, y= kx , y = kx + ម , y = x 2 ,y = - x 2 , នៅថ្នាក់ទី ៨ - y = √ x , y = |x |, y= ពូថៅ 2 + bx + គ , y = k / x. នៅក្នុងសៀវភៅសិក្សាពិជគណិតថ្នាក់ទី៩ ខ្ញុំបានឃើញមុខងារដែលខ្ញុំមិនទាន់ស្គាល់៖ y= x 3 , y= x 4 ,y= x 2 ន , y= x - 2 ន , y= 3 √x , ( x – ក ) 2 + (y - ខ ) 2 = r 2 និងអ្នកដទៃ។ មានច្បាប់សម្រាប់បង្កើតក្រាហ្វនៃមុខងារទាំងនេះ។ ខ្ញុំឆ្ងល់ថាតើមានមុខងារផ្សេងទៀតដែលគោរពច្បាប់ទាំងនេះដែរឬទេ?

ការងាររបស់ខ្ញុំគឺសិក្សាក្រាហ្វនៃមុខងារ និងដោះស្រាយសមីការក្រាហ្វិក។

1. តើមានមុខងារអ្វីខ្លះ

ក្រាហ្វនៃអនុគមន៍គឺជាសំណុំនៃចំណុចទាំងអស់នៃប្លង់កូអរដោនេ អេស៊ីសស៊ីស ដែលស្មើនឹងតម្លៃនៃអាគុយម៉ង់ ហើយការចាត់តាំងគឺស្មើនឹងតម្លៃដែលត្រូវគ្នានៃអនុគមន៍។

អនុគមន៍លីនេអ៊ែរត្រូវបានផ្តល់ដោយសមីការ y= kx + ខកន្លែងណា kនិង ខ- លេខមួយចំនួន។ ក្រាហ្វនៃមុខងារនេះគឺជាបន្ទាត់ត្រង់។

អនុគមន៍សមាមាត្របញ្ច្រាស y= k / xដែលជាកន្លែងដែល k¹ 0. ក្រាហ្វនៃអនុគមន៍នេះត្រូវបានគេហៅថាអ៊ីពែបូឡា។

មុខងារ ( x – ក ) 2 + (y – ខ ) 2 = r 2 កន្លែងណា ក , ខនិង r- លេខមួយចំនួន។ ក្រាហ្វនៃអនុគមន៍នេះគឺជារង្វង់នៃកាំ r ដែលស្ថិតនៅកណ្តាលចំណុច A ( ក , ខ).

មុខងារបួនជ្រុង y = ពូថៅ 2 + bx + គកន្លែងណា ក, ខ , ជាមួយ- លេខមួយចំនួននិង ក¹ 0. ក្រាហ្វនៃអនុគមន៍នេះគឺជាប៉ារ៉ាបូឡា។

សមីការ y 2 ( ក – x ) = x 2 ( ក + x ) . ក្រាហ្វនៃសមីការនេះនឹងជាខ្សែកោងដែលហៅថា ស្ត្រូហ្វីត។

សមីការ ( x 2 + y 2 ) 2 = ក ( x 2 – y 2 ) . ក្រាហ្វនៃសមីការនេះត្រូវបានគេហៅថា Bernoulli lemniscate ។

សមីការ។ ក្រាហ្វនៃសមីការនេះត្រូវបានគេហៅថា astroid ។

ខ្សែកោង (x 2 y 2 - 2 a x) 2 \u003d 4 a 2 (x 2 + y 2). ខ្សែកោងនេះត្រូវបានគេហៅថា cardioid ។

មុខងារ៖ y= x 3 - ប៉ារ៉ាបូឡាគូប, y= x 4 , y = 1/ x 2 .

2. គំនិតនៃសមីការ ដំណោះស្រាយក្រាហ្វិករបស់វា។

សមីការគឺជាកន្សោមដែលមានអថេរ។

ដោះស្រាយសមីការ- នេះមានន័យថាស្វែងរកឫសគល់របស់វាទាំងអស់ ឬបង្ហាញថាវាមិនមាន។

ឫសគល់នៃសមីការគឺជាលេខដែលនៅពេលជំនួសទៅក្នុងសមីការ បង្កើតសមភាពលេខត្រឹមត្រូវ។

ការដោះស្រាយសមីការក្រាហ្វិកអនុញ្ញាតឱ្យអ្នកស្វែងរកតម្លៃពិតប្រាកដ ឬប្រហាក់ប្រហែលនៃឫស អនុញ្ញាតឱ្យអ្នកស្វែងរកចំនួនឫសនៃសមីការ។

នៅពេលគូរក្រាហ្វ និងដោះស្រាយសមីការ លក្ខណៈសម្បត្តិនៃអនុគមន៍មួយត្រូវបានប្រើប្រាស់ ដូច្នេះវិធីសាស្ត្រនេះត្រូវបានគេហៅថាជាក្រាហ្វិកមុខងារ។

ដើម្បីដោះស្រាយសមីការ យើងបែងចែកវាជាពីរផ្នែក ណែនាំមុខងារពីរ បង្កើតក្រាហ្វរបស់ពួកគេ ស្វែងរកកូអរដោនេនៃចំនុចប្រសព្វនៃក្រាហ្វ។ abscissas នៃចំនុចទាំងនេះគឺជាឫសគល់នៃសមីការ។

3. ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វនៃអនុគមន៍មួយ។

ដឹងពីក្រាហ្វនៃមុខងារ y= f ( x ) អ្នកអាចគ្រោងមុខងារ y= f ( x + ម ) ,y= f ( x )+ លីត្រនិង y= f ( x + ម )+ លីត្រ. ក្រាហ្វទាំងអស់នេះត្រូវបានទទួលពីក្រាហ្វនៃអនុគមន៍ y= f ( x ) ដោយប្រើការបំប្លែងការបកប្រែប៉ារ៉ាឡែល៖ បើក │ ម │ មាត្រដ្ឋានឯកតាទៅខាងស្តាំឬខាងឆ្វេងតាមអ័ក្ស x និងនៅលើ │ លីត្រ │ មាត្រដ្ឋានឯកតាឡើងលើឬចុះតាមអ័ក្ស y .

4. ដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ

ដោយប្រើឧទាហរណ៍នៃអនុគមន៍ quadratic យើងនឹងពិចារណាដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ។ ក្រាហ្វនៃអនុគមន៍ quadratic គឺប៉ារ៉ាបូឡា។

តើជនជាតិក្រិចបុរាណដឹងអ្វីខ្លះអំពីប៉ារ៉ាបូឡា?

និមិត្តសញ្ញាគណិតវិទ្យាសម័យទំនើបមានដើមកំណើតនៅសតវត្សទី 16 ។

គណិតវិទូក្រិកបុរាណមិនមានវិធីសាស្ត្រកូអរដោណេ ឬគោលគំនិតនៃអនុគមន៍ទេ។ ទោះជាយ៉ាងណាក៏ដោយលក្ខណៈសម្បត្តិរបស់ប៉ារ៉ាបូឡាត្រូវបានសិក្សាដោយពួកគេយ៉ាងលំអិត។ ការច្នៃប្រឌិតរបស់គណិតវិទូបុរាណគឺពិតជាអស្ចារ្យណាស់ ព្រោះពួកគេអាចប្រើតែគំនូរ និងការពិពណ៌នាដោយពាក្យសំដីនៃភាពអាស្រ័យ។

ភាគច្រើនបានរុករកយ៉ាងពេញលេញនូវប៉ារ៉ាបូឡា អ៊ីពែបូឡា និងពងក្រពើ Apollonius នៃ Pergaដែលរស់នៅក្នុងសតវត្សទី 3 មុនគ។ គាត់ក៏បានផ្តល់ឈ្មោះដល់ខ្សែកោងទាំងនេះ និងចង្អុលបង្ហាញនូវលក្ខខណ្ឌអ្វីដែលចំនុចដែលស្ថិតនៅលើខ្សែកោងជាក់លាក់ណាមួយពេញចិត្ត (បន្ទាប់ពីទាំងអស់ វាមិនមានរូបមន្តទេ!)

មានក្បួនដោះស្រាយសម្រាប់បង្កើតប៉ារ៉ាបូឡា៖

យើងរកឃើញកូអរដោនេនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡា A (x 0; y 0)៖ x 0 =- ខ /2 ក ;

Y 0 \u003d ពូថៅប្រហែល 2 + ក្នុង 0 + c;

យើងរកឃើញអ័ក្សស៊ីមេទ្រីនៃប៉ារ៉ាបូឡា (បន្ទាត់ត្រង់ x \u003d x 0);

ការចងក្រងតារាងតម្លៃសម្រាប់ចំណុចត្រួតពិនិត្យអគារ;

យើងសាងសង់ចំណុចដែលទទួលបាន និងបង្កើតចំណុចស៊ីមេទ្រីទៅនឹងពួកវាដោយគោរពតាមអ័ក្សស៊ីមេទ្រី។

1. ចូរយើងបង្កើតប៉ារ៉ាបូឡាតាមក្បួនដោះស្រាយ y = x 2 – 2 x – 3 . Abscissas នៃចំនុចប្រសព្វជាមួយអ័ក្ស xនិងជាឫសគល់នៃសមីការការ៉េ x 2 – 2 x – 3 = 0.

មានវិធីប្រាំយ៉ាងដើម្បីដោះស្រាយសមីការនេះតាមក្រាហ្វិក។

2. ចូរបំបែកសមីការជាពីរមុខងារ៖ y = x 2 និង y = 2 x + 3

3. ចូរបំបែកសមីការជាពីរមុខងារ៖ y = x 2 –3 និង y =2 x. ឫសនៃសមីការគឺជា abscissas នៃចំនុចប្រសព្វនៃ parabola ជាមួយបន្ទាត់។

4. បំប្លែងសមីការ x 2 – 2 x – 3 = 0 ដោយជ្រើសរើសការ៉េពេញលើមុខងារ៖ y = ( x –1) 2 និង y =4. ឫសនៃសមីការគឺជា abscissas នៃចំនុចប្រសព្វនៃ parabola ជាមួយបន្ទាត់។

5. យើងបែងចែកពាក្យតាមពាក្យទាំងពីរផ្នែកនៃសមីការ x 2 – 2 x – 3 = 0 នៅលើ x, យើងទទួលបាន x – 2 – 3/ x = 0 ចូរបែងចែកសមីការនេះជាមុខងារពីរ៖ y = x – 2, y = 3/ x . ឫសគល់នៃសមីការគឺ abscissas នៃចំនុចប្រសព្វនៃបន្ទាត់ និងអ៊ីពែបូឡា។

5. ដំណោះស្រាយក្រាហ្វិកនៃសមីការដឺក្រេ ន

ឧទាហរណ៍ ១ដោះស្រាយសមីការ x 5 = 3 – 2 x .

y = x 5 , y = 3 – 2 x .

ចម្លើយ៖ x = ១.

ឧទាហរណ៍ ២ដោះស្រាយសមីការ 3 √ x = 10 – x .

ឫសគល់នៃសមីការនេះគឺជា abscissa នៃចំនុចប្រសព្វនៃក្រាហ្វនៃមុខងារពីរ៖ y = 3 √ x , y = 10 – x .

ចម្លើយ៖ x=8 ។

សេចក្តីសន្និដ្ឋាន

ពិចារណាក្រាហ្វិកមុខងារ៖ y= ពូថៅ 2 + bx + គ , y = k / x , y = √ x , y = |x |, y= x 3 , y= x 4 ,y= 3 √x , ខ្ញុំបានកត់សម្គាល់ឃើញថាក្រាហ្វទាំងអស់នេះត្រូវបានបង្កើតឡើងស្របតាមច្បាប់នៃការបកប្រែប៉ារ៉ាឡែលទាក់ទងទៅនឹងអ័ក្ស xនិង y .

ដោយប្រើឧទាហរណ៍នៃការដោះស្រាយសមីការ quadratic យើងអាចសន្និដ្ឋានថាវិធីសាស្ត្រក្រាហ្វិចក៏អាចអនុវត្តបានចំពោះសមីការដឺក្រេ n ។

វិធីសាស្រ្តក្រាហ្វិកសម្រាប់ការដោះស្រាយសមីការគឺស្រស់ស្អាត និងអាចយល់បាន ប៉ុន្តែពួកគេមិនផ្តល់ការធានា 100% នៃការដោះស្រាយសមីការណាមួយឡើយ។ abscissas នៃចំនុចប្រសព្វនៃក្រាហ្វអាចប្រហាក់ប្រហែល។

នៅថ្នាក់ទី 9 និងនៅក្នុងថ្នាក់ជាន់ខ្ពស់ខ្ញុំនឹងនៅតែស្គាល់មុខងារផ្សេងទៀត។ ខ្ញុំចាប់អារម្មណ៍ចង់ដឹងថាតើមុខងារទាំងនោះគោរពតាមច្បាប់នៃការបកប្រែប៉ារ៉ាឡែលនៅពេលគូរក្រាហ្វិករបស់ពួកគេ។

នៅឆ្នាំក្រោយ ខ្ញុំក៏ចង់ពិចារណាពីបញ្ហានៃដំណោះស្រាយក្រាហ្វិកនៃប្រព័ន្ធសមីការ និងវិសមភាព។

អក្សរសិល្ប៍

1. ពិជគណិត។ ថ្នាក់ទី 7 ។ ផ្នែកទី 1. សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ / A.G. Mordkovich ។ ទីក្រុងម៉ូស្គូ: Mnemosyne, 2007 ។

2. ពិជគណិត។ ថ្នាក់ទី ៨ ។ ផ្នែកទី 1. សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ / A.G. Mordkovich ។ ទីក្រុងម៉ូស្គូ: Mnemosyne, 2007 ។

3. ពិជគណិត។ ថ្នាក់ទី 9 ផ្នែកទី 1. សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ / A.G. Mordkovich ។ ទីក្រុងម៉ូស្គូ: Mnemosyne, 2007 ។

4. Glazer G.I. ប្រវត្តិគណិតវិទ្យានៅសាលា។ ថ្នាក់ VII-VIII ។ - អិមៈ ការត្រាស់ដឹង ឆ្នាំ១៩៨២។

5. ទិនានុប្បវត្តិគណិតវិទ្យា№5 2009; លេខ 8 2007; លេខ 23 2008 ។

6. ដំណោះស្រាយក្រាហ្វិកនៃសមីការ គេហទំព័រអ៊ីនធឺណិត៖ Tol WIKI; stimul.biz/en; wiki.iot.ru/images; berdsk.edu; pege 3–6.htm ។

ដំណោះស្រាយក្រាហ្វិកនៃសមីការ

សួស្តីឆ្នាំ ២០០៩

សេចក្តីផ្តើម

Diophantus នៃ Alexandria និង អេកលីដ, អាល់-Khwarizmiនិង Omar Khayyamដោះស្រាយសមីការតាមធរណីមាត្រ និងក្រាហ្វិក។

នៅថ្នាក់ទី 7 យើងបានសិក្សាមុខងារ y \u003d C, y=kx, y =kx+ ម, y =x 2,y = -x 2, នៅថ្នាក់ទី ៨ - y = √x, y =|x|, y=ពូថៅ2 + bx+ គ, y =k/ x. នៅក្នុងសៀវភៅសិក្សាពិជគណិតថ្នាក់ទី៩ ខ្ញុំបានឃើញមុខងារដែលខ្ញុំមិនទាន់ស្គាល់៖ y=x 3, y=x 4,y=x 2n, y=x- 2n, y= 3√x, (x– ក) 2 + (y -ខ) 2 = r 2 និងអ្នកដទៃ។ មានច្បាប់សម្រាប់បង្កើតក្រាហ្វនៃមុខងារទាំងនេះ។ ខ្ញុំឆ្ងល់ថាតើមានមុខងារផ្សេងទៀតដែលគោរពច្បាប់ទាំងនេះដែរឬទេ?

ការងាររបស់ខ្ញុំគឺសិក្សាក្រាហ្វនៃមុខងារ និងដោះស្រាយសមីការក្រាហ្វិក។

1. តើមុខងារអ្វីខ្លះ

អនុគមន៍លីនេអ៊ែរត្រូវបានផ្តល់ដោយសមីការ y=kx+ ខកន្លែងណា kនិង ខ- លេខមួយចំនួន។ ក្រាហ្វនៃមុខងារនេះគឺជាបន្ទាត់ត្រង់។

អនុគមន៍សមាមាត្របញ្ច្រាស y=k/ xដែលជាកន្លែងដែល k ¹ 0. ក្រាហ្វនៃអនុគមន៍នេះត្រូវបានគេហៅថាអ៊ីពែបូឡា។

មុខងារ (x– ក) 2 + (y -ខ) 2 = r2 កន្លែងណា ក, ខនិង r- លេខមួយចំនួន។ ក្រាហ្វនៃអនុគមន៍នេះគឺជារង្វង់នៃកាំ r ដែលស្ថិតនៅកណ្តាលចំណុច A ( ក, ខ).

មុខងារបួនជ្រុង y= ពូថៅ2 + bx+ គកន្លែងណា ក,ខ, ជាមួយ- លេខមួយចំនួននិង ក¹ 0. ក្រាហ្វនៃអនុគមន៍នេះគឺជាប៉ារ៉ាបូឡា។

សមីការ នៅ2 (ក– x) = x2 (ក+ x) . ក្រាហ្វនៃសមីការនេះនឹងជាខ្សែកោងដែលហៅថា ស្ត្រូហ្វីត។

/>សមីការ (x2 + y2 ) 2 = ក(x2 – y2 ) . ក្រាហ្វនៃសមីការនេះត្រូវបានគេហៅថា Bernoulli lemniscate ។

សមីការ។ ក្រាហ្វនៃសមីការនេះត្រូវបានគេហៅថា astroid ។

ខ្សែកោង (x2 y2 - 2 ក x)2 =4 ក2 (x2 +y2 ) . ខ្សែកោងនេះត្រូវបានគេហៅថា cardioid ។

មុខងារ៖ y=x 3 - ប៉ារ៉ាបូឡាគូប, y=x 4, y = 1/x 2.

2. គំនិតនៃសមីការ ដំណោះស្រាយក្រាហ្វិករបស់វា។

សមីការគឺជាកន្សោមដែលមានអថេរ។

3. ក្បួនដោះស្រាយសម្រាប់បង្កើតក្រាហ្វនៃអនុគមន៍មួយ។

ដឹងពីក្រាហ្វនៃមុខងារ y=f(x) អ្នកអាចគ្រោងមុខងារ y=f(x+ ម) ,y=f(x)+ លីត្រនិង y=f(x+ ម)+ លីត្រ. ក្រាហ្វទាំងអស់នេះត្រូវបានទទួលពីក្រាហ្វនៃអនុគមន៍ y=f(x) ដោយប្រើការបំប្លែងការបកប្រែប៉ារ៉ាឡែល៖ បើក │ ម│ មាត្រដ្ឋានឯកតាទៅខាងស្តាំឬខាងឆ្វេងតាមអ័ក្ស x និងនៅលើ │ លីត្រ│ មាត្រដ្ឋានឯកតាឡើងលើឬចុះតាមអ័ក្ស y.

4. ដំណោះស្រាយក្រាហ្វិកនៃសមីការការ៉េ

តើជនជាតិក្រិចបុរាណដឹងអ្វីខ្លះអំពីប៉ារ៉ាបូឡា?

និមិត្តសញ្ញាគណិតវិទ្យាសម័យទំនើបមានដើមកំណើតនៅសតវត្សទី 16 ។

មានក្បួនដោះស្រាយសម្រាប់បង្កើតប៉ារ៉ាបូឡា៖

ស្វែងរកកូអរដោនេនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡា A (x0; y0)៖ X=- ខ/2 ក;

y0=aho2+in0+s;

រកអ័ក្សស៊ីមេទ្រីនៃប៉ារ៉ាបូឡា (បន្ទាត់ត្រង់ x=x0);

PAGE_BREAK--

ការចងក្រងតារាងតម្លៃសម្រាប់ចំណុចត្រួតពិនិត្យអគារ;

1. ចូរយើងបង្កើតប៉ារ៉ាបូឡាតាមក្បួនដោះស្រាយ y= x2 – 2 x– 3 . Abscissas នៃចំនុចប្រសព្វជាមួយអ័ក្ស xនិងជាឫសគល់នៃសមីការការ៉េ x2 – 2 x– 3 = 0.

មានវិធីប្រាំយ៉ាងដើម្បីដោះស្រាយសមីការនេះតាមក្រាហ្វិក។

2. ចូរបំបែកសមីការជាពីរមុខងារ៖ y= x2 និង y= 2 x+ 3

3. ចូរបំបែកសមីការជាពីរមុខងារ៖ y= x2 –3 និង y=2 x. ឫសនៃសមីការគឺជា abscissas នៃចំនុចប្រសព្វនៃ parabola ជាមួយបន្ទាត់។

4. បំប្លែងសមីការ x2 – 2 x– 3 = 0 ដោយជ្រើសរើសការ៉េពេញលើមុខងារ៖ y= (x–1) 2 និង y=4. ឫសនៃសមីការគឺជា abscissas នៃចំនុចប្រសព្វនៃ parabola ជាមួយបន្ទាត់។

5. យើងបែងចែកពាក្យតាមពាក្យទាំងពីរផ្នែកនៃសមីការ x2 – 2 x– 3 = 0 នៅលើ x, យើងទទួលបាន x– 2 – 3/ x= 0 ចូរបែងចែកសមីការនេះជាមុខងារពីរ៖ y= x– 2, y= 3/ x. ឫសគល់នៃសមីការគឺ abscissas នៃចំនុចប្រសព្វនៃបន្ទាត់ និងអ៊ីពែបូឡា។

5. ដំណោះស្រាយក្រាហ្វិកនៃសមីការដឺក្រេន

ឧទាហរណ៍ ១ដោះស្រាយសមីការ x5 = 3 – 2 x.

y= x5 , y= 3 – 2 x.

ចម្លើយ៖ x = ១.

ឧទាហរណ៍ ២ដោះស្រាយសមីការ 3 √ x= 10 – x.

ឫសគល់នៃសមីការនេះគឺជា abscissa នៃចំនុចប្រសព្វនៃក្រាហ្វនៃមុខងារពីរ៖ y= 3 √ x, y= 10 – x.

ចម្លើយ៖ x=8 ។

សេចក្តីសន្និដ្ឋាន

ពិចារណាក្រាហ្វិកមុខងារ៖ y=ពូថៅ2 + bx+ គ, y =k/ x, y = √x, y =|x|, y=x 3, y=x 4,y= 3√x, ខ្ញុំបានកត់សម្គាល់ឃើញថាក្រាហ្វទាំងអស់នេះត្រូវបានបង្កើតឡើងស្របតាមច្បាប់នៃការបកប្រែប៉ារ៉ាឡែលទាក់ទងទៅនឹងអ័ក្ស xនិង y.

អក្សរសិល្ប៍

5. ទិនានុប្បវត្តិគណិតវិទ្យា№5 2009; លេខ 8 2007; លេខ 23 2008 ។

នៅក្នុងមេរៀនវីដេអូនេះ ប្រធានបទ “មុខងារ y \u003d x 2 ។ ដំណោះស្រាយក្រាហ្វិកនៃសមីការ។ ក្នុងអំឡុងពេលមេរៀននេះ សិស្សនឹងអាចស្គាល់ពីវិធីថ្មីនៃការដោះស្រាយសមីការ - ក្រាហ្វិក ដែលផ្អែកលើចំណេះដឹងអំពីលក្ខណៈសម្បត្តិនៃក្រាហ្វិកមុខងារ។ គ្រូនឹងបង្ហាញអ្នកពីរបៀបដោះស្រាយក្រាហ្វិចនៃអនុគមន៍ y=x 2 ។

ប្រធានបទ៖មុខងារ

មេរៀន៖មុខងារ. ដំណោះស្រាយក្រាហ្វិកនៃសមីការ

ដំណោះស្រាយក្រាហ្វិកនៃសមីការគឺផ្អែកលើចំណេះដឹងនៃក្រាហ្វិកមុខងារ និងលក្ខណៈសម្បត្តិរបស់វា។ យើងរាយមុខងារដែលក្រាហ្វដែលយើងដឹង៖

1) ក្រាហ្វគឺជាបន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស x ឆ្លងកាត់ចំណុចមួយនៅលើអ័ក្ស y ។ ពិចារណាឧទាហរណ៍៖ y=១៖

សម្រាប់តម្លៃផ្សេងគ្នា យើងទទួលបានគ្រួសារនៃបន្ទាត់ត្រង់ស្របទៅនឹងអ័ក្ស x ។

2) អនុគមន៍សមាមាត្រដោយផ្ទាល់ ក្រាហ្វនៃអនុគមន៍នេះគឺជាបន្ទាត់ត្រង់ឆ្លងកាត់ប្រភពដើម។ ពិចារណាឧទាហរណ៍មួយ៖

យើងបានបង្កើតក្រាហ្វទាំងនេះរួចហើយនៅក្នុងមេរៀនមុន សូមចាំថា ដើម្បីកសាងបន្ទាត់នីមួយៗ អ្នកត្រូវជ្រើសរើសចំណុចដែលពេញចិត្ត ហើយយកប្រភពដើមជាចំណុចទីពីរ។

រំលឹកឡើងវិញនូវតួនាទីនៃមេគុណ k: នៅពេលដែលមុខងារកើនឡើង មុំរវាងបន្ទាត់ត្រង់ និងទិសដៅវិជ្ជមាននៃអ័ក្ស x គឺស្រួច; នៅពេលដែលអនុគមន៍ថយចុះ មុំរវាងបន្ទាត់ត្រង់ និងទិសវិជ្ជមាននៃអ័ក្ស x គឺមានភាពស្រអាប់។ លើសពីនេះទៀតមានទំនាក់ទំនងដូចខាងក្រោមរវាងប៉ារ៉ាម៉ែត្រពីរ k នៃសញ្ញាដូចគ្នា: សម្រាប់ k វិជ្ជមានវាកាន់តែធំមុខងារកើនឡើងលឿនហើយសម្រាប់អវិជ្ជមានមុខងារថយចុះលឿនជាងមុនសម្រាប់តម្លៃធំនៃ k ម៉ូឌុល។

3) មុខងារលីនេអ៊ែរ។ នៅពេលដែល - យើងទទួលបានចំណុចប្រសព្វជាមួយអ័ក្ស y ហើយបន្ទាត់ទាំងអស់នៃប្រភេទនេះឆ្លងកាត់ចំណុច (0; m) ។ លើសពីនេះទៀតនៅពេលដែលមុខងារកើនឡើងមុំរវាងបន្ទាត់និងទិសដៅវិជ្ជមាននៃអ័ក្ស x គឺស្រួច; នៅពេលដែលអនុគមន៍ថយចុះ មុំរវាងបន្ទាត់ត្រង់ និងទិសវិជ្ជមាននៃអ័ក្ស x គឺមានភាពស្រអាប់។ ហើយជាការពិតណាស់តម្លៃ k ប៉ះពាល់ដល់អត្រានៃការផ្លាស់ប្តូរតម្លៃនៃអនុគមន៍។

៤). ក្រាហ្វនៃមុខងារនេះគឺជាប៉ារ៉ាបូឡា។

ពិចារណាឧទាហរណ៍។

ឧទាហរណ៍ទី 1 - ដោះស្រាយសមីការក្រាហ្វិក៖

យើងមិនស្គាល់មុខងារនៃប្រភេទនេះទេ ដូច្នេះយើងត្រូវបំប្លែងសមីការដែលបានផ្តល់ឱ្យ ដើម្បីដំណើរការជាមួយមុខងារដែលគេស្គាល់៖

យើងទទួលបានមុខងារដែលធ្លាប់ស្គាល់នៅក្នុងផ្នែកទាំងពីរនៃសមីការ៖

តោះបង្កើតក្រាហ្វនៃមុខងារ៖

ក្រាហ្វមានចំនុចប្រសព្វពីរ៖ (-1; 1); (២; ៤)

តោះពិនិត្យមើលថាតើដំណោះស្រាយត្រូវបានរកឃើញត្រឹមត្រូវឬអត់ ជំនួសកូអរដោនេទៅក្នុងសមីការ៖

ចំណុចទីមួយត្រូវបានរកឃើញត្រឹមត្រូវ។

, , , , , ,

ចំណុចទីពីរក៏ត្រូវបានរកឃើញយ៉ាងត្រឹមត្រូវ។

ដូច្នេះដំណោះស្រាយនៃសមីការគឺ និង

យើងធ្វើសកម្មភាពស្រដៀងគ្នាទៅនឹងឧទាហរណ៍មុន៖ យើងបំប្លែងសមីការដែលបានផ្តល់ឱ្យទៅជាមុខងារដែលយើងស្គាល់ គ្រោងក្រាហ្វរបស់ពួកគេ ស្វែងរកចរន្តប្រសព្វ ហើយពីទីនេះយើងបង្ហាញពីដំណោះស្រាយ។

យើងទទួលបានមុខងារពីរ៖

តោះបង្កើតក្រាហ្វ៖

ក្រាហ្វទាំងនេះមិនមានចំនុចប្រសព្វ ដែលមានន័យថាសមីការដែលបានផ្តល់ឱ្យមិនមានដំណោះស្រាយទេ។

សេចក្តីសន្និដ្ឋាន៖ នៅក្នុងមេរៀននេះ យើងបានពិនិត្យឡើងវិញនូវមុខងារដែលយើងស្គាល់ និងក្រាហ្វរបស់ពួកគេ ចងចាំលក្ខណៈសម្បត្តិរបស់វា និងពិចារណាវិធីក្រាហ្វិកដើម្បីដោះស្រាយសមីការ។

1. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. et al.ពិជគណិត 7. ការបោះពុម្ពលើកទី 6 ។ M. : ការត្រាស់ដឹង។ ឆ្នាំ ២០១០

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. ពិជគណិត 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. និងផ្សេងៗទៀត ពិជគណិត 7 .M.: ការអប់រំ។ ២០០៦

កិច្ចការទី 1: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et al.ពិជគណិត 7, លេខ 494, ទំព័រ 110;

កិច្ចការទី 2: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. និងផ្សេងៗទៀត។ពិជគណិតទី 7 លេខ 495 ធាតុ 110;

កិច្ចការទី 3: Makarychev Yu.N., Mindyuk N.G., Neshkov K.I. et al.ពិជគណិត 7, លេខ 496, ទំព័រ 110;

វិទ្យាស្ថាន DAGESTAN សម្រាប់ការអភិវឌ្ឍន៍វិជ្ជាជីវៈ

បុគ្គលិកគរុកោសល្យ

នាយកដ្ឋានអប់រំរូបវិទ្យា និងគណិតវិទ្យា និង ICT

គម្រោង

លើប្រធានបទ៖

« សំណង់ និង ទំ កំណែទម្រង់

ក្រាហ្វិកមុខងារ

នៅក្នុងគណិតវិទ្យាសាលា »

Rabadanov P.A.

គ្រូបង្រៀនគណិតវិទ្យា

MBOU "អនុវិទ្យាល័យ Kochubey"

ស្រុក Tarumovsky

ឆ្នាំ 2015

1. សេចក្តីផ្តើម…………………………………………………………………..៣

2. ជំពូក ខ្ញុំ. ការពិនិត្យឡើងវិញនៃអក្សរសិល្ប៍លើប្រធានបទនៃគម្រោង…………………………………….៥

3. ជំពូក II. ផ្នែកជាក់ស្តែង៖

៣.១. វិធីសាស្រ្តជាមូលដ្ឋានសម្រាប់បំប្លែងក្រាហ្វមុខងារ …………. ៧

3.2. ការធ្វើផែនការស្មើគ្នានិងមុខងារសេស…………….. 10

3.3. ការធ្វើផែនការមុខងារបញ្ច្រាស………………………… 11

3.4. ការខូចទ្រង់ទ្រាយ (ការបង្ហាប់និងភាពតានតឹង) នៃក្រាហ្វ………………….12

3.5 ការរួមបញ្ចូលគ្នានៃការផ្ទេរ ការឆ្លុះបញ្ចាំង និងការខូចទ្រង់ទ្រាយ……………………13

៤.ភារកិច្ចសម្រាប់ដំណោះស្រាយឯករាជ្យ……………………………...១៤

៥.សេចក្តីសន្និដ្ឋាន………………………………………………………………… ១៥

៦.សេចក្តីសន្និដ្ឋាន…………………………………………………………………..១៧

ការណែនាំ

ការបំប្លែងក្រាហ្វមុខងារគឺជាគោលគំនិតគណិតវិទ្យាជាមូលដ្ឋានមួយដែលទាក់ទងដោយផ្ទាល់ទៅនឹងសកម្មភាពជាក់ស្តែង។ ក្រាហ្វឆ្លុះបញ្ចាំងពីភាពប្រែប្រួល និងថាមវន្តនៃពិភពពិត ទំនាក់ទំនងទៅវិញទៅមកនៃវត្ថុពិត និងបាតុភូត។

បន្ទាត់មុខងារគឺជាប្រធានបទមូលដ្ឋានដែលគ្របដណ្តប់នៅក្នុងការប្រឡងថ្នាក់មូលដ្ឋាន និងបង្រួបបង្រួមរដ្ឋ។ដូចគ្នានេះផងដែរគំនិតគណិតវិទ្យាជាច្រើនត្រូវបានពិចារណាដោយវិធីសាស្ត្រក្រាហ្វិក។ ឧទាហរណ៍ទៅបួនជ្រុងមុខងារត្រូវបានណែនាំ និងសិក្សាដោយទំនាក់ទំនងជិតស្និទ្ធជាមួយសមីការ quadratic និងវិសមភាព។ដូច្នេះវាធ្វើតាមនោះ។ការបង្រៀនសិស្សពីរបៀបបង្កើត និងបំប្លែងក្រាហ្វនៃមុខងារ គឺជាកិច្ចការសំខាន់មួយនៃការបង្រៀនគណិតវិទ្យានៅសាលា។

ការសិក្សាអំពីមុខងារធ្វើឱ្យវាអាចរកឃើញអំពីដែននៃនិយមន័យ និងវិសាលភាពនៃមុខងារ វិសាលភាពការថយចុះឬបង្កើនអត្រា, asymtotes, ចន្លោះពេលsign constancy ។ល។ ទោះយ៉ាងណាក៏ដោយ ដើម្បីបង្កើតក្រាហ្វkov មុខងារជាច្រើនអាចជាប្រើវិធីសាស្រ្តមួយចំនួនធ្វើឱ្យវាកាន់តែងាយស្រួលអគារ។ ដូច្នេះ សិស្សគួរមានសមត្ថភាពក្នុងការបង្កើតក្រាហ្វតាមគ្រោងការណ៍វិធីសាស្ត្រ។

ខាងលើកំណត់ភាពពាក់ព័ន្ធ ប្រធានបទស្រាវជ្រាវ។

វត្ថុនៃការសិក្សា គឺជាការសិក្សាអំពីការបំប្លែងក្រាហ្វបន្ទាត់មុខងារក្នុងគណិតវិទ្យាសាលា។

មុខវិជ្ជាសិក្សា - ដំណើរការនៃការបង្កើត និងបំប្លែងក្រាហ្វមុខងារនៅក្នុងអនុវិទ្យាល័យ។

គោលបំណងនៃការសិក្សា៖ ការអប់រំ មាននៅក្នុងការកំណត់អត្តសញ្ញាណគ្រោងការណ៍វិធីសាស្រ្តសម្រាប់ការសាងសង់ និងការបំប្លែងក្រាហ្វនៃមុខងារមួយ;កំពុងអភិវឌ្ឍ - ការអភិវឌ្ឍនៃអរូបី, ក្បួនដោះស្រាយ, ការគិតឡូជីខល, ការស្រមើលស្រមៃទំហំ;អប់រំ - ការអប់រំនៃវប្បធម៌ក្រាហ្វិករបស់សិស្សសាលា, ការបង្កើតជំនាញផ្លូវចិត្ត។

គោលដៅនាំឱ្យមានការសម្រេចចិត្តដូចខាងក្រោមភារកិច្ច:

1. វិភាគការអប់រំ និងវិធីសាស្រ្តលើបញ្ហាដែលកំពុងសិក្សា។

2. កំណត់គ្រោងការណ៍វិធីសាស្រ្តការបំប្លែងក្រាហ្វមុខងារក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា។

3. ជ្រើសរើសមធ្យោបាយ និងមធ្យោបាយដែលមានប្រសិទ្ធភាពបំផុត។ការស្ថាបនា និងការផ្លាស់ប្តូរក្រាហ្វមុខងារនៅក្នុងសាលាមធ្យមសិក្សារួមចំណែកដល់៖ ការបញ្ចូលអត្ថន័យនៃសម្ភារៈអប់រំ; បង្កើនសកម្មភាពយល់ដឹងរបស់សិស្ស; ការអភិវឌ្ឍសមត្ថភាពច្នៃប្រឌិតរបស់ពួកគេ។

សម្មតិកម្មស្រាវជ្រាវ៖ ការបង្កើតជំនាញក្រាហ្វិកក្នុងដំណើរការសិក្សាមុខងារ និងការអប់រំនៃវប្បធម៌ក្រាហ្វិករបស់សិស្សនឹង មានប្រសិទ្ធភាពប្រសិនបើសិស្សមានគ្រោងការណ៍វិធីសាស្រ្តសម្រាប់ការសាងសង់ និងបំប្លែងក្រាហ្វមុខងារនៅក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា។

ជំពូក ខ្ញុំ . ការវាយតម្លៃអក្សរសិល្ប៍លើប្រធានបទនៃគម្រោង។

ក្នុងការរៀបចំសម្រាប់គម្រោង យើងបានសិក្សាអក្សរសិល្ប៍ដូចខាងក្រោមៈ

Sivashinsky, I. Kh. ទ្រឹស្តីបទ និងបញ្ហាក្នុងពិជគណិត មុខងារបឋម - M., 2002. - 115 p.

Gelfand, I. M., Glagoleva, E. G., Shnol, E. E. មុខងារ និងក្រាហ្វ (បច្ចេកទេសមូលដ្ឋាន) - M., 1985. - 120 s

V.Z.Zaitsev, V.V. Ryzhkov, M.I. ស្កែនវី។ គណិតវិទ្យាបឋម - អិម, ឆ្នាំ ២០១០ (ផ្សាយឡើងវិញ) ។ - 590 ទំ។

Kuzmin, M. K. ការសាងសង់ក្រាហ្វនៃអនុគមន៍ - J. គណិតវិទ្យានៅសាលា។ - 2003. - លេខ 5 ។ - ស ៦១-៦២។

Shilov G.E. តើធ្វើដូចម្តេចដើម្បីកសាងតារាង? - M. , 1982 ។

អ៊ីសាក តាណាតា។ ការបំប្លែងធរណីមាត្រនៃក្រាហ្វនៃមុខងារ - MTsNMO, 2012

អេវាត្រូវបានកត់សម្គាល់ថាសមត្ថភាពក្នុងការ "អាន" ឥរិយាបទនៃមុខងារនៅលើសំណុំជាក់លាក់មួយដោយប្រើក្រាហ្វត្រូវបានប្រើមិនត្រឹមតែនៅក្នុងវគ្គសិក្សានៃគណិតវិទ្យាប៉ុណ្ណោះទេប៉ុន្តែថែមទាំងនៅក្នុងសកម្មភាពជាក់ស្តែងនៃមនុស្សម្នាក់ដែលគាត់ត្រូវដោះស្រាយជាមួយក្រាហ្វិកជាក់លាក់ផងដែរ។ តំណាងនៃភាពអាស្រ័យ។ ដូច្នេះ សិស្សគួរតែអាចកំណត់លក្ខណៈសម្បត្តិមួយចំនួនរបស់វាពីក្រាហ្វនៃអនុគមន៍មួយ។

សម្ភារៈទ្រឹស្តីសម្រាប់ការផ្លាស់ប្តូរក្រាហ្វត្រូវបានបញ្ជាក់យ៉ាងតឹងរ៉ឹងនៅក្នុង។ បច្ចេកទេសនេះត្រូវបានអមដោយរូបភាពជាមួយគំនូរ ឧទាហរណ៍នៃភាពស្មុគស្មាញផ្សេងៗគ្នា និងដំណោះស្រាយរបស់ពួកគេ ដែលធ្វើឱ្យវាអាចធ្វើទៅបានដើម្បីពង្រឹងចំណេះដឹង និងគ្រោងមុខងារស្មុគស្មាញ។

តំណាងឱ្យវគ្គបណ្តុះបណ្តាលអេឡិចត្រូនិច បរិមាណ និងខ្លឹមសារដែលត្រូវនឹងតម្រូវការសម្រាប់វគ្គសិក្សាគណិតវិទ្យានៅវិទ្យាល័យ។ សម្ភារៈទ្រឹស្តីត្រូវបានគាំទ្រដោយគំនូរជីវចលក្រាហ្វិកដែលផ្តល់នូវការតំណាងដែលមើលឃើញនៃប្រធានបទដែលកំពុងសិក្សា។ វគ្គសិក្សារួមមានម៉ូឌុលចំនួនបី៖ ម៉ូឌុលសិក្សាសម្ភារៈទ្រឹស្តី ម៉ូឌុលពិនិត្យដោយខ្លួនឯង និងម៉ូឌុលត្រួតពិនិត្យចំណេះដឹង។

ពី , , គ្រោងការណ៍គំនូសតាងវិធីសាស្រ្ត ឧទាហរណ៍សម្រាប់ការងារឯករាជ្យត្រូវបានប្រើសម្រាប់ផ្នែកជាក់ស្តែងនៃគម្រោង។

ការសន្និដ្ឋានទៅជំពូកទី 1

ការសិក្សាអក្សរសិល្ប៍អប់រំ និងវិធីសាស្រ្តត្រូវបានអនុញ្ញាត៖

1. កំណត់គ្រោងការណ៍វិធីសាស្រ្តសិក្សា បង្កើត និងបំប្លែងក្រាហ្វនៃមុខងារក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា។

2. ជ្រើសរើសមធ្យោបាយ និងមធ្យោបាយដែលមានប្រសិទ្ធភាពបំផុត។ការស្ថាបនា និងការផ្លាស់ប្តូរក្រាហ្វមុខងារក្នុងគណិតវិទ្យាសាលា,រួមចំណែក៖

assimilation អត្ថន័យនៃសម្ភារៈអប់រំ;

បង្កើនសកម្មភាពយល់ដឹងរបស់សិស្ស;

ការអភិវឌ្ឍសមត្ថភាពច្នៃប្រឌិតរបស់ពួកគេ។

3. បង្ហាញថា បន្ទាត់មុខងារមានឥទ្ធិពលយ៉ាងសំខាន់ក្នុងការសិក្សាអំពីគោលគំនិតផ្សេងៗក្នុងគណិតវិទ្យា។

ជំពូកទី 2. ផ្នែក EMPIRICAL

នៅក្នុងជំពូកនេះ យើងនឹងពិចារណាអំពីវិធីសាស្ត្រសំខាន់ៗសម្រាប់បំប្លែងក្រាហ្វមុខងារ និងផ្តល់គ្រោងការណ៍វិធីសាស្រ្តសម្រាប់ការសាងសង់បន្សំផ្សេងៗនៃក្រាហ្វសម្រាប់មុខងារផ្សេងៗ។

២.១. បច្ចេកទេសជាមូលដ្ឋានសម្រាប់ការបំប្លែងក្រាហ្វមុខងារ

ការបកប្រែតាមអ័ក្ស y

f ( x ) f ( x )+ ខ .

សម្រាប់ការធ្វើផែនការមុខងារy = f( x) + ខដានអ៊ីម៖

1. បង្កើតក្រាហ្វមុខងារy= f( x)

2. ផ្លាស់ទីអ័ក្សabscissa នៅលើ| ខ| ឯកតាឡើងនៅខ>0 ឬនៅ| ខ| បរិភោគក្រាបចុះនៅខ < 0. ទទួលបាននៅក្នុងប្រព័ន្ធថ្មី។ក្រាហ្វឌីណាត គឺជាក្រាហ្វនៃមុខងារមួយ។y = f( x) + ខ.

2. ផ្ទេរ តាម អ័ក្ស abscissa

f ( x ) f ( x + ក ) .

y = f( x+ ក) ដានអ៊ីម៖

3. កំណត់មុខងារនៃទម្រង់ y = f (- x )

f (x ) f (- x ).

ដើម្បីគូរមុខងារy = f( - x) ដូចតទៅ៖

គ្រោងមុខងារមួយ។y = f( x)

ឆ្លុះបញ្ចាំងវាមកវិញទាក់ទងទៅនឹងអ័ក្ស y

ក្រាហ្វលទ្ធផលគឺក្រាហ្វមុខងារy = f( - X).

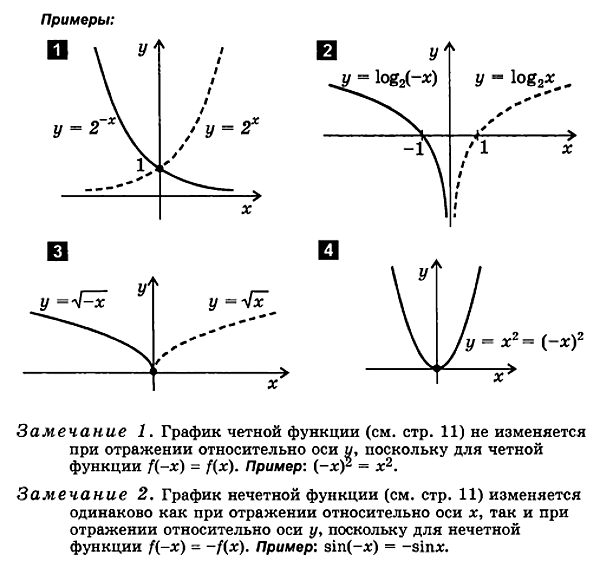
4. កំណត់មុខងារនៃទម្រង់ y= - f ( x )

f ( x ) - f ( x )

- f( x) ដូចតទៅ៖

គ្រោងមុខងារមួយ។y= f( x)

ឆ្លុះបញ្ចាំងពីអ័ក្ស x

២.២. ការធ្វើផែនការស្មើគ្នា និង លក្ខណៈពិសេសប្លែក

នៅពេលគ្រោងសម្រាប់មុខងារគូ និងសេស វាងាយស្រួលប្រើលក្ខណៈសម្បត្តិខាងក្រោម៖

1. ក្រាហ្វនៃស៊ីមមេតមុខងារគូRicen ទាក់ទងទៅនឹងអ័ក្ស y ។

2. ក្រាហ្វនៃមុខងារសេសគឺស៊ីមេទ្រីអំពីប្រភពដើម។

ដើម្បីបង្កើតក្រាហ្វនៃអនុគមន៍គូ និងសេស វាគ្រប់គ្រាន់ដើម្បីគូសតែសាខាខាងស្ដាំនៃក្រាហ្វសម្រាប់តម្លៃវិជ្ជមាននៃអាគុយម៉ង់។ សាខាខាងឆ្វេងត្រូវបានបញ្ចប់ដោយស៊ីមេទ្រីអំពីប្រភពដើមសម្រាប់មុខងារសេស និងអំពីអ័ក្ស y សម្រាប់អនុគមន៍គូ។

ដើម្បីកំណត់មុខងារស្មើ y = f ( x ) បន្ទាប់ពី បទភ្លេង៖

បង្កើតសាខានៃក្រាហ្វនៃមុខងារនេះតែនៅក្នុងជួរនៃតម្លៃវិជ្ជមាននៃអាគុយម៉ង់ x≥0 ។

អូតាមដានសាខានេះអំពីអ័ក្ស y

ដើម្បីរៀបចំមុខងារសេស y = f ( x ) ដូចខាងក្រោម៖

បង្កើតសាខាក្រាហ្វនៃមុខងារនេះតែនៅក្នុងផ្ទៃដីនៃតម្លៃវិជ្ជមាននៃអាគុយម៉ង់ (х≥0) ។

អូតាមដានសាខានេះដោយគោរពតាមប្រភពដើមទៅតំបន់នៃតម្លៃ x អវិជ្ជមាន។

២.៣. ការធ្វើផែនការមុខងារបញ្ច្រាស

ដូចដែលបានកត់សម្គាល់រួចហើយ មុខងារផ្ទាល់ និងបញ្ច្រាសបង្ហាញទំនាក់ទំនងដូចគ្នារវាងអថេរx និង y ជាមួយនឹងភាពខុសគ្នាតែមួយគត់ដែលនៅក្នុងមុខងារបញ្ច្រាសទាំងនេះអថេរបានផ្លាស់ប្តូរតួនាទី ដែលស្មើនឹងការផ្លាស់ប្តូរសញ្ញាណនៃអ័ក្សកូអរដោនេ។ ដូច្នេះកាលវិភាគអនុគមន៍បញ្ច្រាសគឺស៊ីមេទ្រីទៅនឹងក្រាហ្វនៃអនុគមន៍ផ្ទាល់អំពី bisectorខ្ញុំនិងIIIមុំសំរបសំរួល,i.e. ត្រង់y = x ។ ដូច្នេះយើងទទួលបានច្បាប់បន្ទាប់។

ដើម្បីកំណត់មុខងារ y = (x) បញ្ច្រាសទៅមុខងារy = f( x) គួរតែត្រូវបានសាងសង់កាលវិភាគy = f( x) ហើយឆ្លុះបញ្ចាំងវាដោយគោរពតាមបន្ទាត់ត្រង់ y = x ។

២.៤. ការខូចទ្រង់ទ្រាយ (ការបង្ហាប់និងភាពតានតឹង) នៃក្រាហ្វ

1. ការបង្ហាប់ (ការពង្រីក) នៃក្រាហ្វតាមអ័ក្ស y

f ( x ) ក ∙ f ( x ).

ដើម្បីគូរមុខងារy= ក∙ f( x) ដូចតទៅ៖

8. ការបង្ហាប់ (ការពង្រីក) នៃក្រាហ្វតាមអ័ក្ស x

f( x)

ដើម្បីកំណត់មុខងារ y= f( x) ដូចខាងក្រោម៖

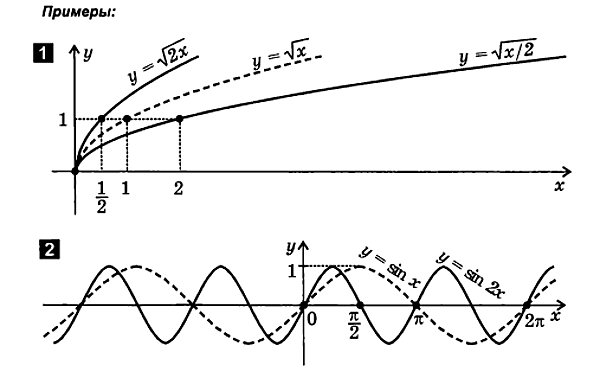
២.៥. ការរួមបញ្ចូលគ្នានៃការបកប្រែ ការឆ្លុះបញ្ចាំង និងការខូចទ្រង់ទ្រាយ

ជាញឹកញាប់ណាស់នៅពេលគូរក្រាហ្វិកមុខងារសម្រាប់ផ្លាស់ប្តូរការរួមបញ្ចូលគ្នា.

ការអនុវត្តប្រកបដោយនិរន្តរភាពនៃបច្ចេកទេសឥរិយាបថបែបនេះមួយចំនួនអនុញ្ញាតឱ្យមានភាពសាមញ្ញយ៉ាងខ្លាំងក្នុងការកសាងក្រាហ្វដោយប្រើមុខងារដែលកំពុងដំណើរការហើយជារឿយៗកាត់បន្ថយវានៅចុងបញ្ចប់ទៅការស្ថាបនាមុខងារបឋមដ៏សាមញ្ញបំផុតមួយ។កិច្ចការ។ ពិចារណាពីរបៀបដែលនៅក្នុងទិដ្ឋភាពខាងលើវាដូចខាងក្រោមបង្កើតក្រាហ្វិកមុខងារ។

ចូរយើងកត់សំគាល់ថាវាដល់ពេលហើយ។វាគឺជាទីប្រឹក្សាដើម្បីអនុវត្តការចតសាមញ្ញនៅក្នុងអ្នកស្នងបន្ទាប់ភាព។

ការប្រើភាពស្មើគ្នាឬមុខងារចម្លែក។

ការផ្ទេរអ័ក្ស។

ការឆ្លុះបញ្ចាំងនិងការខូចទ្រង់ទ្រាយ។

ការសាងសង់ក្រាហ្វត្រូវបានអនុវត្តតាមលំដាប់បញ្ច្រាស។

ឧទាហរណ៍។ គ្រោងមុខងារមួយ។

ការសាងសង់នឹងត្រូវបានអនុវត្តតាមជំហានដូចខាងក្រោមៈ

1. គ្រោងលោការីតធម្មជាតិ:

2. ច្របាច់ទៅអ័ក្សអូយ2 ដង:;
3. បង្ហាញស៊ីមេទ្រីអំពីអ័ក្សអូយ: ;
4. ផ្លាស់ទីតាមអ័ក្សOXនៅលើ(!!!) ទៅខាងស្តាំ៖:

5. បង្ហាញស៊ីមេទ្រីអំពីអ័ក្សOX: ;
6. ផ្លាស់ទីតាមអ័ក្សអូយ3 គ្រឿងឡើង៖:

ឧទាហរណ៍នៃការសាងសង់ និងការបំប្លែងក្រាហ្វិកមុខងារ

ឧទាហរណ៍ ១ គ្រោងមុខងារមួយ។.

ដំបូងគូរក្រាហ្វស៊ីនុស រយៈពេលរបស់វាគឺស្មើនឹង:

ក្រាហ្វមុខងារទទួលបានដោយការបង្ហាប់ក្រាហ្វពីរដងទៅអ័ក្ស y ។កំណត់ហេតុ .

គ្រោងមុខងារមួយ។នៅ = 2 cosX.

គ្រោងមុខងារមួយ។y = អំពើបាបx .

សេចក្តីសន្និដ្ឋាន

ក្នុងអំឡុងពេលនៃការងារលើការងារគម្រោង អក្សរសិល្ប៍អប់រំ និងវិធីសាស្រ្តផ្សេងៗលើបញ្ហានេះត្រូវបានវិភាគ។ លទ្ធផលនៃការសិក្សាបានធ្វើឱ្យវាអាចកំណត់អត្តសញ្ញាណលក្ខណៈវិជ្ជមានបំផុតនៃការសិក្សាការសាងសង់ និងការបំប្លែងក្រាហ្វនៃអនុគមន៍នៅក្នុងវគ្គសិក្សាគណិតវិទ្យារបស់សាលា

គោលដៅចម្បងនៃគម្រោងគឺដើម្បីអភិវឌ្ឍជំនាញ និងសមត្ថភាពរបស់សិស្សក្នុងការអាន និងគូរគំនូរ ដើម្បីបង្កើតវិធីសាស្រ្តសមហេតុផលនៃសកម្មភាពឯករាជ្យ។

តម្រូវការក្នុងការធ្វើឱ្យប្រសើរឡើងនូវការអប់រំក្រាហ្វិកទាំងមូលត្រូវបានកំណត់មិនត្រឹមតែដោយតម្រូវការផលិតកម្មទំនើបប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងដោយតួនាទីនៃក្រាហ្វិកក្នុងការអភិវឌ្ឍន៍ការគិតបច្ចេកទេស និងសមត្ថភាពយល់ដឹងរបស់សិស្សផងដែរ។ សមត្ថភាពរបស់មនុស្សម្នាក់ក្នុងដំណើរការព័ត៌មានក្រាហ្វិកគឺជាសូចនាករមួយនៃការអភិវឌ្ឍន៍ផ្លូវចិត្តរបស់គាត់។ ដូច្នេះ ការបណ្តុះបណ្តាលក្រាហ្វិកគួរតែក្លាយជាធាតុសំខាន់នៃការបណ្តុះបណ្តាលអប់រំទូទៅ។

ការរកឃើញ

ដូច្នេះ គម្រោងដែលបានបង្កើត "ការសាងសង់ និងការផ្លាស់ប្តូរក្រាហ្វមុខងារ" ដែលឧទ្ទិសដល់គោលគំនិតកណ្តាលនៃគណិតវិទ្យា - ការពឹងផ្អែកមុខងារ គឺផ្តោតលើការរៀបចំប្រព័ន្ធ និងការពង្រីកចំណេះដឹងរបស់សិស្ស។ ការសិក្សាអំពីវិធីសាស្រ្តជាក់លាក់សម្រាប់បំប្លែងក្រាហ្វមុខងារត្រូវបានអនុវត្តតាមវិធីវិភាគ និងក្រាហ្វិកតាមគ្រោងការណ៍វិធីសាស្រ្តដ៏តឹងរឹង។ សម្ភារៈដែលប្រមូលបានអាចប្រើប្រាស់ក្នុងថ្នាក់រៀន និងសម្រាប់ការបណ្តុះបណ្តាលសិស្សដោយខ្លួនឯង។ ទម្រង់ និងវិធីសាស្រ្តផ្សេងៗនៃការរៀបចំ និងការបណ្តុះបណ្តាលអាចត្រូវបានប្រើដើម្បីដឹកនាំថ្នាក់។

វិបផតថលសម្រាប់សិស្ស។ ការបណ្តុះបណ្តាលខ្លួនឯង

អត្ថបទ​ដែល​ទាក់ទង

អត្ថបទដែលទាក់ទង