A função y=f(x) é chamada diferenciável em algum ponto x 0 se tiver uma certa derivada neste ponto, ou seja, se o limite da relação existe e é finito.

Se uma função é diferenciável em cada ponto de um determinado segmento [a; b] ou intervalo (a; b), então dizemos que é diferenciável no intervalo [a; b] ou, respectivamente, no intervalo (a; b).

O seguinte teorema é válido, estabelecendo a conexão entre funções diferenciáveis ​​e contínuas.

Teorema. Se a função y=f(x) é diferenciável em algum ponto x 0, então ela é contínua neste ponto.

Assim, da diferenciabilidade de uma função segue-se a sua continuidade.

Prova. Se então

onde b é uma quantidade infinitesimal, ou seja, uma quantidade tendendo a zero quando Dx>0. Mas então

Dy=f "(x 0) Dx+bDx=> Dy>0 em Dx>0, ou seja, f(x) - f(x 0)>0 em x>x 0,

e isso significa que a função f(x) é contínua no ponto x 0 . Q.E.D.

Assim, a função não pode ter derivada em pontos de descontinuidade. O inverso não é verdadeiro: existem funções contínuas que não são diferenciáveis ​​em alguns pontos (ou seja, não possuem derivada nesses pontos).

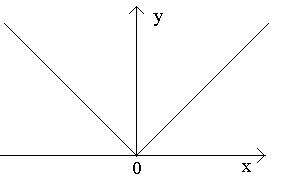
Vejamos os pontos a, b, c na figura.

No ponto a para Dx>0, a razão não tem limite (já que os limites unilaterais são diferentes para Dx>0-0 e Dx>0+0). No ponto A do gráfico não existe uma tangente específica, mas existem duas tangentes unidirecionais diferentes com inclinações de 1 e 2. Este tipo de ponto é denominado ponto de canto.

No ponto b para Dx>0, a razão é de sinal constante e infinitamente grande. A função tem derivada infinita. Neste ponto o gráfico tem uma tangente vertical. Tipo de ponto - “ponto de inflexão” com tangente vertical.

No ponto c, as derivadas unilaterais são quantidades infinitamente grandes de sinais diferentes. Neste ponto, o gráfico tem duas tangentes verticais mescladas. Tipo - "ponto de retorno" com tangente vertical - um caso especial de ponto de canto.

1. Considere a função y=|x|. Esta função é contínua no ponto

Vamos mostrar que não tem derivada neste ponto.

f(0+Dx) = f(Dx) = |Dx|. Portanto, Дy = f(Дx) - f(0) = |Дx|

Mas então no Dx< 0 (т.е. при Дx стремящемся к 0 слева)

E quando Dx > 0

Assim, a razão para Dx>0 à direita e à esquerda tem limites diferentes, o que significa que a razão não tem limite, ou seja, derivada da função y=|x| não existe no ponto x= 0. Geometricamente, isso significa que no ponto x = 0 esta “curva” não possui uma tangente específica (neste ponto existem duas).

2. A função é definida e contínua em toda a reta numérica. Vamos descobrir se esta função tem uma derivada em x= 0.

Consequentemente, a função em consideração não é diferenciável no ponto x= 0. A tangente à curva neste ponto forma um ângulo p/2 com o eixo das abcissas, ou seja, coincide com o eixo Oy.

3 Definição da derivada de uma função em um ponto Seja a função f(x) definida em uma determinada vizinhança do ponto x 0. DEFINIÇÃO. Se houver um limite (finito) da relação, então f(x) é chamado de ponto diferenciável x 0, e o próprio limite é chamado de derivada da função f(x) no ponto x 0 e é denotado por f " (x 0), ou seja, vamos denotar x = x – x 0 é o incremento do argumento ao passar do ponto x 0 para o ponto x, e y = f(x 0 + x) – f(x 0) é o incremento correspondente da função. Então a derivada da função f(x) no ponto x 0 é o limite da razão entre o incremento da função e o incremento do argumento que a causou, quando o incremento do argumento tende a zero.

4 Exemplo 1. Damos exemplos de cálculo das derivadas de algumas das funções elementares mais simples, com base na definição da derivada. y = a x (0 0. Assumindo que | x | 0 é um ponto arbitrário, então 0.Assumindo que | x | 0 é um ponto arbitrário, então">

0.Assumindo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então (sinx) = cosx, x R." title=" 5 Exemplo 3. Vamos considerar x 0 > 0. Supondo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então ( senx) = cosx, x R." class="link_thumb"> 5 !} 5 Exemplo 3. Considere x 0 > 0. Assumindo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então (sinx) = cosx, x R. 0.Assumindo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então (sinx) = cosx, x R."> 0. Supondo que | x | 0 – ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então (sinx) = cosx, x R."> 0. Assumindo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então (sinx) = cosx, x R." title=" 5 Exemplo 3. Vamos considerar x 0 > 0. Supondo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então ( senx) = cosx, x R."> title="5 Exemplo 3. Considere x 0 > 0. Assumindo que | x | 0 é um ponto arbitrário, então Exemplo 4. y = sinx, x R. Pegue x 0 R e calcule o incremento da função neste ponto: Então (sinx) = cosx, x R."> !}

6 TEOREMA. Se uma função f(x) é diferenciável em um ponto x 0, então ela é contínua nesse ponto. Prova. Deixe existir Então A partir daqui obtemos que f (x) – f (x 0) = f "(x 0) (x – x 0) + (x – x 0)α(x) para x x 0. Ou seja, f( x) é contínuo no ponto x 0. Continuidade da função diferenciável (1)

7 NOTA. A continuidade de uma função num ponto não é condição suficiente para a existência de uma derivada nesse ponto. Exemplo 5. f(x) = x. Vamos estudar o comportamento de f (x) nas proximidades de x 0 = 0. Aqui f (x) f (0) = 0 em x 0. Isso é a função é contínua no ponto x 0 = 0. Considere x y 0 O limite não existe, pois Então, a função f (x) = x não tem derivada no ponto x = 0, embora seja contínua neste apontar

8 Exemplo x y 0 em x 0. em x 0. Isso é f(x) é contínuo no ponto x = 0. Ou seja, f(x) não tem derivada no ponto x = 0 e, portanto, não é diferenciável neste ponto. Vamos estudar o comportamento de f(x) nas proximidades do ponto x = 0.

9 Seja a função y = f(x) diferenciável no ponto x 0. Então, de acordo com (1), seu incremento no ponto x 0 pode ser escrito como y = f(x 0 + x) – f(x 0) = f ( x 0) x + o(x) em x. O diferencial da função f (x 0) x é o linear principal em relação a x parte do incremento da função y = f(x) no ponto x 0 é chamado de diferencial da função no ponto x 0 com o incremento x e é denotado df(x 0 ; x) ou df(x 0 ) ou df ou dу. y = f(x 0 + x) – f(x 0) = df(x 0; x) + o(x) em x. DEFINIÇÃO. A parte principal do incremento, linear em relação a x. Um infinitesimal de ordem superior a x. Agora o incremento da função pode ser escrito assim:

10 NOTA. O incremento x é frequentemente denotado pelo símbolo dx e é chamado de diferencial da variável independente. Assim, o diferencial de uma função no ponto x 0 pode ser escrito na forma df(x 0) = f "(x 0) dx. Se uma função é diferenciável em cada ponto de um determinado intervalo, então seu diferencial dy é uma função de x e dx: dy = f "(x)dx. A partir daqui, em particular, obtemos uma expressão para a derivada, ou seja, a derivada pode ser considerada como a razão entre o diferencial de uma função e o diferencial da variável independente.

11 Significado geométrico de derivada e diferencial Deixe a função y = f(x) ser definida em U(x 0) e diferenciável no ponto x 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + y 0 L – secante L 0 – tangente x y = f(x 0 + x) – f(x 0) em x devido à continuidade da função. A tangente ao gráfico da função y = f(x) no ponto M 0 é a posição limite da secante L em x. y Se a função é diferenciável no ponto x 0, então na equação secante y/ x f (x 0) em x e a equação tangente tem a forma y = y 0 + f (x 0) (x – x 0).

12 М0М0 М x0x0 x 0 + x dy = df(x 0; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o (x) para x 0 L0L0 tg = f (x 0) Se y/ x para x, então a linha reta x = x 0 resultante da equação secante é chamada de tangente vertical ao gráfico da função no ponto M 0. Da equação da tangente obtemos y – y 0 = f (x 0) (x – x 0) = df (x 0) – incremento da ordenada da tangente ao passar do ponto x 0 para o ponto x. A normal ao gráfico de uma função no ponto M 0 é uma reta perpendicular à tangente que passa pelo ponto M 0. Sua equação tem a forma y = y 0 – 1/f (x 0) (x – x 0). L 1 – normal

13 Aplicações físicas da derivada e diferencial Se S(t) é o caminho percorrido por um ponto material no tempo t, então S "(t) é a velocidade instantânea do ponto material, e dS = S "(t)dt é a distância que o ponto material percorreria no período de tempo de t a t + dt, se estivesse se movendo a uma velocidade igual à velocidade instantânea no momento t. Se Q(t) é a quantidade de eletricidade que flui através da seção transversal do condutor no tempo t, então Q "(t) = I é a intensidade da corrente. Se N(t) é a quantidade de substância formada no tempo t durante uma reação química, então N "(t) – taxa de reação química.

Se a função sim = f(x) é diferenciável em algum ponto x = x 0, então é contínuo neste ponto.

Assim, a função não pode ter derivada em pontos de descontinuidade. A conclusão oposta está incorreta, ou seja, do fato de que em algum momento x = x 0 função sim = f(x) é contínuo não significa que seja diferenciável neste ponto. Por exemplo, a função sim = |x| contínuo para todos x (–< X < ), но в точке x= 0 não tem derivada. Neste ponto não há tangente ao gráfico. Existe uma tangente direita e uma tangente esquerda, mas elas não coincidem.

21 Encontrando regras Produção valores

Regra 1. Se as funções y = f(x) e y = g(x) têm uma derivada no ponto x, então sua soma também tem uma derivada no ponto x, e a derivada da soma é igual à soma das derivadas:
(f(x) + 8(x))" =f(x)+ (x).
Na prática, esta regra é formulada de forma mais resumida: a derivada de uma soma é igual à soma de suas derivadas.
Por exemplo,
Regra 2. Se a função y = f(x) tem uma derivada no ponto x, então a função y = kf(x) também tem uma derivada no ponto x, e:

Na prática, esta regra é formulada de forma mais resumida: o fator constante pode ser retirado do sinal da derivada. Por exemplo,

Regra 3. Se as funções y=f(x) e y =g(x) têm uma derivada no ponto x, então seu produto também tem uma derivada no ponto x, e:

Na prática, esta regra é formulada da seguinte forma: a derivada do produto de duas funções é igual à soma dos dois termos. O primeiro termo é o produto da derivada da primeira função e da segunda função, e o segundo termo é o produto da primeira função e da derivada da segunda função.
Por exemplo:
Regra 4. Se as funções y = f(x) e y=g(x) têm uma derivada em então o quociente tem uma derivada no ponto x, e:

Tabela de derivadas complexas

22 Diferença. funcional no ponto

Função sim=f(x) é dito diferenciável no ponto x 0 se seu incremento for Δ sim(x 0,Δ x) pode ser representado como

Δ sim(x 0,Δ x)=AΔ x+ó(Δ x).

Parte linear principal AΔ x incrementos Δ simé chamado de diferencial desta função no ponto x 0, correspondente ao incremento Δ x, e é denotado pelo símbolo morrer(x 0,Δ x).

Para que a função sim=f(x) era diferenciável no ponto x 0, é necessário e suficiente que a derivada exista f′( x 0), e a igualdade é verdadeira A=f′( x 0).

A expressão para o diferencial tem a forma

morrer(x 0,dx)=f′( x 0)dx,

Onde dx=Δ x.

23 Prod. Complexo Função

Derivada de uma função complexa. Derivada de uma função especificada parametricamente

Deixar sim – função complexa x, ou seja sim = f(você), você = g(x), ou

Se g(x) E f(você) – funções diferenciáveis ​​de seus argumentos, respectivamente, em pontos x E você = g(x), então a função complexa também é diferenciável no ponto x e é encontrado pela fórmula

Derivada de uma função dada parametricamente.

24 Prod. e dif. Ordem mais alta

Agora deixe a derivada de ordem ser definida em uma certa vizinhança do ponto e ser diferenciável. Então

Se uma função tem uma derivada parcial em relação a uma das variáveis ​​em algum domínio D, então a referida derivada, sendo ela mesma uma função de, pode ter derivadas parciais em relação à mesma ou a qualquer outra variável em algum ponto. Para a função original, essas derivadas serão derivadas parciais de segunda ordem (ou segundas derivadas parciais).

Uma derivada parcial de segunda ordem ou superior tomada em relação a diferentes variáveis ​​é chamada de derivada parcial mista. Por exemplo,

Diferencial de pedido n, Onde n > 1, de uma função em algum ponto é chamada de diferencial neste ponto da diferencial de ordem (n-1), aquilo é

Para uma função que depende de uma variável, a segunda e a terceira diferenciais são assim:

A partir daqui podemos derivar uma visão geral do diferencial nª ordem da função:

25 Teoremas de Fermat, Rolle, Langrange

v Teorema de Fermat: Deixe a função ser definida e atingir seus valores máximo e mínimo ( M E eu) em alguns dos . Se houver uma derivada em , então ela será necessariamente igual a 0.

Prova: Existe. Há duas possibilidades:

1) , => , => .

2) , => , => .

De 1) e 2) segue-se que

v Teorema de Rolle (sobre as raízes da derivada): Seja a função contínua e diferenciável e assuma os mesmos valores nas extremidades do segmento: . Então há pelo menos um ponto de, a derivada em que.

v Prova: alcances contínuos em M E eu. Então dois casos são possíveis:

2) o maior valor é alcançado dentro do intervalo segundo o teorema de Fermat.

v Teorema de Langrage (sobre incrementos finais): Deixe a função ser contínua e derivável em . Então há pelo menos um de , para o qual vale a seguinte igualdade: .

Prova: vamos apresentar a função . (contínuo e diferenciável em ).

Existe uma função que satisfaz o Teorema de Rolle, para a qual:,,,,.

· a função é chamada aumentando estritamente em se

· a função é chamada diminuindo em se

· a função é chamada diminuindo estritamente em se

Definição: A derivada de uma função em um ponto é o limite para o qual tende a razão entre seu incremento naquele ponto e o incremento correspondente do argumento quando este tende a zero:

Ou seja, se definido em, então

Teorema 1:

O gráfico de uma função tem uma tangente não vertical se e somente se existe um valor finito da derivada dessa função em um determinado ponto.

Prova:

Seja um valor f’()-finito, então

Que haja uma tangente não vertical => que haja uma tangente finita.

A secante tende à tangente.

O teorema foi provado.

Ticket 2 Continuidade de uma função com derivada.

Uma função f (x), definida em alguma vizinhança de um ponto a, é chamada contínua neste ponto se

Teorema: (uma condição necessária para a existência de uma derivada)

Se uma função é finita num ponto, ela não é contínua nesse ponto.

Prova:

Portanto, é contínuo em um ponto.

O teorema foi provado.

Comente : a afirmação inversa não é verdadeira; se uma função é contínua num ponto, então não se segue que ela tenha uma derivada nesse ponto.

Declaração : Se uma função tem derivadas à direita e à esquerda em um ponto, então ela é contínua tanto à direita quanto à esquerda.

Bilhete 3

Derivada de uma soma, produto, quociente.

Derivada da função inversa.

Definição de uma função diferenciável. Condição necessária e suficiente para diferenciabilidade.

Deixe a função ter uma derivada em um ponto (finito): .

Então, para valores suficientemente pequenos, podemos escrevê-lo como uma soma e alguma função, que denotamos por, que tende a zero junto com:,

e o incremento em um ponto pode ser escrito como:

ou (1) ,

afinal, a expressão é entendida como uma função tal que sua razão tende a zero junto com.

Explicação:

Definição .

Uma função é dita diferenciável em um ponto se seu incremento puder ser representado como: (2),

onde A não depende, mas geralmente depende.

Teorema 1:

Para que uma função seja diferenciável num ponto, é necessário e suficiente que ela tenha uma derivada finita nesse ponto.

Prova:

Suficiência da condição foi provado acima: da existência de uma derivada finita seguiu-se a possibilidade de representação na forma (1), onde podemos colocar.

Condição de necessidade . Seja a função diferenciável em um ponto. Então de (2), assumindo, obtemos.

O limite do lado direito em existe e é igual a A:.

Isso significa que existe uma derivada. O teorema foi provado.

Bilhete 6 Diferencial de uma função, seu significado geométrico.

Se a função f tem uma derivada f΄(x ó ) no ponto x ó, então há um limite onde Δ f=f(x ó + Δ x)-f(x ó ) ,,ou onde UMA=f΄(x ó ) .

Definição:

Função f diferenciável no ponto x ó, se seu incremento puder ser representado como:

Onde AΔ x=df. (*)

O diferencial é a parte linear principal do incremento da função.

Se existe uma derivada finita f΄(x ó ) no ponto x ó, então a função f(x)é diferenciável neste ponto.

A recíproca também é verdadeira: se a função f diferenciável no ponto x ó, ou seja seu incremento pode ser representado na forma (*), então tem uma derivada no ponto x ó, igual a A:

Significado geométrico do diferencial:

A E B– pontos do gráfico f(x), correspondente aos valores x ó E (x ó + Δ x) variável independente. Ordenadas de pontos A E B respectivamente igual f(x ó ) E f(x ó + Δ x). Incremento de função Δ f=f(x ó + Δ x)-f(x ó ) no ponto x ó igual ao comprimento do segmento BD e pode ser representado como a soma Δ f=BD=DC+CB, Onde DC=tgαΔ x=f΄(x ó ) Δ x E α é o ângulo entre a tangente no ponto A ao gráfico e à direção positiva do eixo x. A partir disso fica claro que CC existe uma função diferencial f no ponto x ó :

DC=df=f΄(x ó ) Δ x.

Ao mesmo tempo, a participação do segundo membro C. B. incrementos Δ f contabilizar o valor. Este valor, em geral Δ x, talvez até maior que o termo principal, mas é um infinitesimal de ordem superior que Δ x, quando Δ x→0.

PROPRIEDADES DAS FUNÇÕES CONTÍNUAS EM UMA ENTREVISTA

Consideremos algumas propriedades de funções contínuas em um intervalo. Apresentamos essas propriedades sem provas.

Função y =f(x) chamado contínuo no segmento [a, b], se for contínuo em todos os pontos internos deste segmento e em suas extremidades, ou seja, em pontos a E b, é contínuo à direita e à esquerda, respectivamente.

Teorema 1. Uma função contínua no intervalo [ a, b], pelo menos em um ponto deste segmento assume o maior valor e pelo menos em um ponto o menor.

O teorema afirma que se uma função y =f(x)é contínuo no intervalo [ a, b], então há pelo menos um ponto x 1 Î [ a, b] tal que o valor da função f(x) neste ponto será o maior de todos os seus valores neste segmento: f(x 1) ≥ f(x). Da mesma forma, existe tal ponto x 2, em que o valor da função será o menor de todos os valores do segmento: f(x 1) ≤ f(x).

É claro que pode haver vários desses pontos; por exemplo, a figura mostra que a função f(x) assume o menor valor em dois pontos x 2 E x 2 ".

Comente. A afirmação do teorema pode se tornar incorreta se considerarmos o valor da função no intervalo ( a, b). Na verdade, se considerarmos a função y = x em (0, 2), então é contínuo neste intervalo, mas não atinge nem o maior nem o menor valor dele: atinge esses valores nas extremidades do intervalo, mas as extremidades não pertencem para o nosso domínio.

Além disso, o teorema deixa de ser verdadeiro para funções descontínuas. Dê um exemplo.

Consequência. Se a função f(x)é contínuo em [ a, b], então é limitado neste segmento.

Teorema 2. Deixe a função y =f(x)é contínuo no intervalo [ a, b] e nas extremidades deste segmento assume valores de sinais diferentes, então há pelo menos um ponto dentro do segmento x = C, em que a função vai para zero: f(C)= 0, onde um< C< b

Este teorema tem um significado geométrico simples: se os pontos do gráfico de uma função contínua y =f(x), correspondendo às extremidades do segmento [ a, b] ficam em lados opostos do eixo Boi, então este gráfico intercepta o eixo em pelo menos um ponto do segmento Boi. Funções descontínuas podem não ter esta propriedade.

Este teorema admite a seguinte generalização.

Teorema 3 (teorema do valor intermediário). Deixe a função y =f(x)é contínuo no intervalo [ a, b] E f(a) = UMA, f(b) = B. Então para qualquer número C, concluído entre A E B, existe um tal ponto dentro deste segmento CÎ [ a, b], O que f(c) = C.

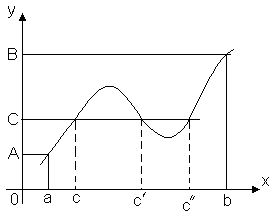
Este teorema é geometricamente óbvio. Considere o gráfico da função y =f(x). Deixar f(a) = UMA, f(b) = B. Então qualquer linha reta y = C, Onde C– qualquer número entre A E B, cruzará o gráfico da função em pelo menos um ponto. A abscissa do ponto de intersecção será esse valor x = C, em qual f(c) = C.

Assim, uma função contínua, passando de um valor para outro, passa necessariamente por todos os valores intermediários. Em particular:

Consequência. Se a função y =f(x)é contínuo ao longo de um determinado intervalo e assume o maior e o menor valor, então nesse intervalo ele assume pelo menos uma vez qualquer valor contido entre seus menores e maiores valores.

DERIVADO E SUAS APLICAÇÕES. DEFINIÇÃO DE DERIVADO

Vamos ter alguma função y=f(x), definido em algum intervalo. Para cada valor de argumento x deste intervalo a função y=f(x) tem um certo significado.

Considere dois valores de argumento: inicial x 0 e novo x.

Diferença x-x 0 é chamado incrementando o argumento x no ponto x 0 e é denotado Δx. Por isso, Δx = x – x 0 (o incremento do argumento pode ser positivo ou negativo). Desta igualdade segue que x=x 0 +Δx, ou seja o valor inicial da variável recebeu algum incremento. Então, se no ponto x 0 valor da função era f(x 0 ), então em um novo ponto x a função assumirá o valor f(x) = f(x 0 +Δx).

Diferença sim 0 =f(x) –f(x 0 ) chamado incremento de função y =f(x) no ponto x 0 e é indicado pelo símbolo Δy. Por isso,

Δy = f(x) – f(x 0 ) =f(x 0 +Δx) - f(x 0 ) .

(1)

Normalmente, o valor inicial do argumento x 0 é considerado fixo e o novo valor x- variável. Então sim 0 =f(x 0 ) acaba sendo constante e y =f(x)- variável. Incrementos Δy E Δx também serão variáveis ​​e a fórmula (1) mostra que Dyé uma função de uma variável Δx.

Vamos criar a razão entre o incremento da função e o incremento do argumento

Vamos encontrar o limite desta razão em Δx→0. Se este limite existir, então ele é chamado de derivada desta função f(x) no ponto x 0 e denotar f "(x 0). Então,

Derivado esta função y =f(x) no ponto x 0 é chamado de limite da razão de incremento da função Δ sim para o incremento do argumento Δ x, quando este tende arbitrariamente a zero.

Observe que para a mesma função a derivada em pontos diferentes x pode assumir valores diferentes, ou seja, a derivada pode ser considerada como uma função do argumento x. Esta função é designada f "(x)

A derivada é denotada pelos símbolos f "(x),y", . O valor específico da derivada em x = uma denotado por f "(a) ou sim "| x=uma.

A operação de encontrar a derivada de uma função f(x)é chamado de diferenciação desta função.

Para encontrar diretamente a derivada por definição, você pode usar o seguinte: regra prática:

Exemplos.

SENTIDO MECÂNICO DE DERIVADO

É sabido pela física que a lei do movimento uniforme tem a forma s = v t, Onde é– o caminho percorrido até o momento do tempo t, v– velocidade do movimento uniforme.

No entanto, porque A maioria dos movimentos que ocorrem na natureza são desiguais, então em geral a velocidade e, conseqüentemente, a distância é vai depender do tempo t, ou seja será uma função do tempo.

Então, deixe um ponto material se mover em linha reta em uma direção de acordo com a lei s=s(t).

Vamos marcar um determinado momento t 0. Neste ponto o ponto ultrapassou o caminho s=s(t 0 ). Vamos determinar a velocidade v ponto material em um momento no tempo t 0 .

Para fazer isso, vamos considerar algum outro momento t 0 + Δ t. Corresponde ao caminho percorrido s =s(t 0 + Δ t). Então, durante um período de tempo Δ t o ponto percorreu o caminho Δs =s(t 0 + Δ t)–s(t).

Vamos considerar a atitude. É chamada de velocidade média no intervalo de tempo Δ t. A velocidade média não pode caracterizar com precisão a velocidade de movimento de um ponto no momento t 0 (porque o movimento é desigual). Para expressar com mais precisão essa velocidade verdadeira usando a velocidade média, é necessário considerar um período de tempo mais curto Δ t.

Então, a velocidade do movimento em um determinado momento t 0 (velocidade instantânea) é o limite da velocidade média no intervalo de t 0 a t 0 +Δ t, quando Δ t→0:

,

aqueles. velocidade irregular esta é a derivada da distância percorrida em relação ao tempo.

SIGNIFICADO GEOMÉTRICO DA DERIVADA

Vamos primeiro introduzir a definição de uma tangente a uma curva em um determinado ponto.

Vamos ter uma curva e um ponto fixo nela M 0(veja a figura) Considere outro ponto M esta curva e desenhe uma secante M 0 M. Se o ponto M começa a se mover ao longo da curva, e o ponto M 0 permanece imóvel, então a secante muda de posição. Se, com aproximação ilimitada do ponto M ao longo de uma curva até um ponto M 0 em qualquer lado a secante tende a ocupar a posição de uma certa linha reta M 0 T, então direto M 0 T chamada de tangente à curva em um determinado ponto M 0.

Que., tangente para a curva em um determinado ponto M 0 chamada de posição limite da secante M 0 M quando ponto M tende ao longo da curva até um ponto M 0.

Consideremos agora a função contínua y=f(x) e a curva correspondente a esta função. Com algum valor X 0 função assume valor y 0 =f(x 0). Esses valores x 0 e sim 0 na curva corresponde a um ponto M 0 (x 0 ; y 0). Vamos dar o argumento x0 incremento Δ X. O novo valor do argumento corresponde ao valor incrementado da função sim 0 +Δ y=f(x 0 –Δ x). Nós entendemos o ponto M(x 0+Δ x; e 0+Δ e). Vamos desenhar uma secante M 0 M e denotamos por φ o ângulo formado por uma secante com a direção positiva do eixo Boi. Vamos fazer uma relação e observar isso.

Se agora Δ x→0, então, devido à continuidade da função Δ no→0 e, portanto, o ponto M, movendo-se ao longo da curva, aproxima-se indefinidamente do ponto M 0. Então a secante M 0 M tenderá a assumir a posição de uma tangente à curva no ponto M 0, e o ângulo φ→α em Δ x→0, onde α denota o ângulo entre a tangente e a direção positiva do eixo Boi. Como a função tan φ depende continuamente de φ para φ≠π/2, então para φ→α tan φ → tan α e, portanto, a inclinação da tangente será:

aqueles. f"(x)= tg α .

Assim, geometricamente y "(x 0) representa a inclinação da tangente ao gráfico desta função no ponto x0, ou seja para um determinado valor do argumento x, a derivada é igual à tangente do ângulo formado pela tangente ao gráfico da função f(x) no ponto apropriado M 0 (x; y) com direção de eixo positiva Boi.

Exemplo. Encontre a inclinação da tangente à curva y = x 2 no ponto M(-1; 1).

Já vimos anteriormente que ( x 2)" = 2X. Mas o coeficiente angular da tangente à curva é tan α = sim"| x=-1 = – 2.

DIFERENCIABILIDADE DE FUNÇÕES. CONTINUIDADE DA FUNÇÃO DIFERENCIÁVEL

Função y=f(x) chamado diferenciável em algum ponto x 0 se tiver uma certa derivada neste ponto, ou seja, se o limite da relação existe e é finito.

Se uma função é diferenciável em cada ponto de um determinado segmento [ A; b] ou intervalo ( A; b), então eles dizem que ela diferenciável no segmento [ A; b] ou, respectivamente, no intervalo ( A; b).

O seguinte teorema é válido, estabelecendo a conexão entre funções diferenciáveis ​​e contínuas.

Teorema. Se a função y=f(x) diferenciável em algum ponto x0, então é contínuo neste ponto.

Assim, da diferenciabilidade de uma função segue-se a sua continuidade.

Prova. Se , Que

,

onde α é uma quantidade infinitesimal, ou seja, uma quantidade tendendo a zero como Δ x→0. Mas então

Δ sim=f "(x0) Δ x+αΔ x=> Δ sim→0 em Δ x→0, ou seja f(x) –f(x 0)→0 em x→x 0 , o que significa que a função f(x) contínuo em um ponto x 0. Q.E.D.

Assim, a função não pode ter derivada em pontos de descontinuidade. O inverso não é verdadeiro: existem funções contínuas que não são diferenciáveis ​​em alguns pontos (ou seja, não possuem derivada nesses pontos).

Considere os pontos da figura uma, b, c.

No ponto a em Δ x→0 a razão não tem limite (já que os limites unilaterais são diferentes para Δ x→0–0 e Δ x→0+0). No ponto A gráfico não há tangente definida, mas existem duas tangentes unidirecionais diferentes com inclinações Para 1 e Para 2. Este tipo de ponto é denominado ponto de canto.

No ponto b em Δ x A razão →0 é um sinal constante de quantidade infinitamente grande. A função tem uma derivada infinita. Neste ponto o gráfico tem uma tangente vertical. Tipo de ponto - “ponto de inflexão” com tangente vertical.

No ponto c derivadas unilaterais são quantidades infinitamente grandes de sinais diferentes. Neste ponto, o gráfico possui duas tangentes verticais mescladas. Tipo - "cúspide" com tangente vertical - um caso especial de ponto angular.