На этом уроке мы повторим теорию и докажем теорему-признак перпендикулярности прямой и плоскости.
В начале урока вспомним определение прямой, перпендикулярной к плоскости. Далее рассмотрим и докажем теорему-признак перпендикулярности прямой и плоскости. Для доказательства этой теоремы вспомним свойство серединного перпендикуляра.
Далее решим несколько задач на перпендикулярность прямой и плоскости.

Тема: Перпендикулярность прямой и плоскости

Урок: Признак перпендикулярности прямой и плоскости

На этом уроке мы повторим теорию и докажем теорему-признак перпендикулярности прямой и плоскости .

Определение . Прямая а называется перпендикулярной к плоскости α, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Доказательство .

Пусть нам дана плоскость α. В этой плоскости лежат две пересекающиеся прямые p и q . Прямая а перпендикулярна прямой p и прямой q . Нам нужно доказать, что прямая а перпендикулярна плоскости α, то есть, что прямая а перпендикулярна любой прямой, лежащей в плоскости α.

Напоминание .

Для доказательства нам нужно вспомнить свойства серединного перпендикуляра к отрезку. Серединный перпендикуляр р к отрезку АВ - это геометрическое место точек, равноудаленных от концов отрезка. То есть, если точка С лежит на серединном перпендикуляре р, то АС = ВС .

Пусть точка О - точка пересечения прямой а и плоскости α (рис. 2). Без ограничения общность, будем считать, что прямые p и q пересекаются в точке О . Нам нужно доказать перпендикулярность прямой а к произвольной прямой m из плоскости α.

Проведем через точку О прямую l , параллельно прямой m. На прямой а отложим отрезки ОА и ОВ , причем ОА = ОВ , то есть точка О - середина отрезка АВ . Проведем прямую PL , .

Прямая р перпендикулярна прямой а (из условия), (по построению). Значит, р АВ . Точка Р лежит на прямой р . Значит, РА = РВ .

Прямая q перпендикулярна прямой а (из условия), (по построению). Значит, q - серединный перпендикуляр к отрезку АВ . Точка Q лежит на прямой q . Значит, QА = QВ .

Треугольники АР Q и ВР Q равны по трем сторонам (РА = РВ , QА = QВ, Р Q - общая сторона). Значит, углы АР Q и ВР Q равны.

Треугольники А PL и BPL равны по углу и двум прилежащим сторонам (∠АР L = ∠ВР L, РА = РВ , PL - общая сторона). Из равенства треугольников получаем, что AL = BL .

Рассмотрим треугольник ABL. Он равнобедренный, так как AL = BL. В равнобедренном треугольнике медиана LО является и высотой, то есть прямая LО перпендикулярна АВ .

Мы получили, что прямая а перпендикулярна прямой l, а значит, и прямой m, что и требовалось доказать.

Точки А, М, О лежат на прямой, перпендикулярной к плоскости α, а точки О, В, С и D лежат в плоскости α (рис. 3). Какие из следующих углов являются прямыми: ?

Решение

Рассмотрим угол . Прямая АО перпендикулярна плоскости α, а значит, прямая АО перпендикулярна любой прямой, лежащей в плоскости α, в том числе прямой ВО . Значит, .

Рассмотрим угол . Прямая АО перпендикулярна прямой ОС , значит, .

Рассмотрим угол . Прямая АО перпендикулярна прямой О D , значит, . Рассмотрим треугольник DAO . В треугольнике может быть только один прямой угол. Значит, угол DAM - не является прямым.

Рассмотрим угол . Прямая АО перпендикулярна прямой О D , значит, .

Рассмотрим угол . Это угол в прямоугольном треугольнике BMO , он не может быть прямым, так как угол МОВ - прямой.

Ответ : .

В треугольнике АВС дано: , АС = 6 см, ВС = 8 см, СМ - медиана (рис. 4). Через вершину С проведена прямая СК , перпендикулярная к плоскости треугольника АВС , причем СК = 12 см. Найдите КМ .

Решение :

Найдем длину АВ по теореме Пифагора: (см).

По свойству прямоугольного треугольника середина гипотенузы М равноудалена от вершин треугольника. То есть СМ = АМ = ВМ , (см).

Рассмотрим треугольник КСМ . Прямая КС перпендикулярна плоскости АВС , а значит, КС перпендикулярна СМ . Значит, треугольник КСМ - прямоугольный. Найдем гипотенузу КМ из теоремы Пифагора: (см).

1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. - 5-е издание, исправленное и дополненное - М.: Мнемозина, 2008. - 288 с.: ил.

Задания 1, 2, 5, 6 стр. 57

2. Дайте определение перпендикулярности прямой и плоскости.

3. Укажите в кубе пару - ребро и грань, которые являются перпендикулярными.

4. Точка К лежит вне плоскости равнобедренного треугольника АВС и равноудалена от точек В и С . М - середина основания ВС . Докажите, что прямая ВС перпендикулярна плоскости АКМ .

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Yandex.RTB R-A-339285-1

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Определение 1

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается « ⊥ », а запись принимает вид a ⊥ b , что значит, прямая a перпендикулярна прямой b .

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые O x , O z , O y перпендикулярны попарно: O x и O z , O x и O y , O y и O z .

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Теорема 1

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b .

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Доказательство 1

Пусть введена прямоугольная декартова система координат О х у с заданными уравнениями прямой на плоскости, которые определяют прямые a и b . Направляющие векторы прямых a и b обозначим a → и b → . Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a → и b → . Это возможно только при скалярном произведении векторов a → = (a x , a y) и b → = (b x , b y) равном нулю, а запись имеет вид a → , b → = a x · b x + a y · b y = 0 . Получим, что необходимым и достаточным условием перпендикулярности прямых a и b , находящихся в прямоугольной системе координат О х у на плоскости, является a → , b → = a x · b x + a y · b y = 0 , где a → = (a x , a y) и b → = b x , b y - это направляющие векторы прямых a и b .

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b .

Пример 1

Заданы три точки A (8 , 6) , B (6 , 3) , C (2 , 10) в прямоугольной системе координат О х у. Определить, прямые А В и А С перпендикулярны или нет.

Решение

Прямые А В и А С имеют направляющие векторы A B → и A C → соответственно. Для начала вычислим A B → = (- 2 , - 3) , A C → = (- 6 , 4) . Получим, что векторы A B → и A C → перпендикулярны из свойства о скалярном произведении векторов, равном нулю.

A B → , A C → = (- 2) · (- 6) + (- 3) · 4 = 0

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Пример 2

Определить, заданные прямые x - 1 2 = y - 7 3 и x = 1 + λ y = 2 - 2 · λ перпендикулярны или нет.

Решение

a → = (2 , 3) является направляющим вектором заданной прямой x - 1 2 = y - 7 3 ,

b → = (1 , - 2) является направляющим вектором прямой x = 1 + λ y = 2 - 2 · λ .

Перейдем к вычислению скалярного произведения векторов a → и b → . Выражение будет записано:

a → , b → = 2 · 1 + 3 · - 2 = 2 - 6 ≠ 0

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a → , b → = a x · b x + a y · b y + a z · b z = 0 , где a → = (a x , a y , a z) и b → = (b x , b y , b z) являются направляющими векторами прямых a и b .

Пример 3

Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x 2 = y - 1 = z + 1 0 и x = λ y = 1 + 2 · λ z = 4 · λ

Решение

Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a → = (2 , - 1 , 0) и b → = (1 , 2 , 4) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.

Выражение примет вид a → , b → = 2 · 1 + (- 1) · 2 + 0 · 4 = 0 .

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Теорема 2

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b , это и есть необходимое и достаточное условие.

Доказательство 2

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида A x + B y + C = 0 , уравнения прямой в отрезках вида x a + y b = 1 , уравнения прямой с угловым коэффициентом вида y = k x + b координаты векторов возможно найти.

Пример 4

Выяснить, перпендикулярны ли прямые 3 x - y + 2 = 0 и x 3 2 + y 1 2 = 1 .

Решение

Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что n α → = (3 , - 1) - это нормальный вектор для прямой 3 x - y + 2 = 0 .

Упростим уравнение x 3 2 + y 1 2 = 1 до вида 2 3 x + 2 y - 1 = 0 . Теперь четко видны координаты нормального вектора, которые запишем в такой форме n b → = 2 3 , 2 .

Векторы n a → = (3 , - 1) и n b → = 2 3 , 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0 . Получим n a → , n b → = 3 · 2 3 + (- 1) · 2 = 0 .

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y = k 1 x + b 1 , а прямая b - y = k 2 x + b 2 , отсюда следует, что нормальные векторы будут иметь координаты (k 1 , - 1) и (k 2 , - 1) . Само условие перпендикулярности сводится к k 1 · k 2 + (- 1) · (- 1) = 0 ⇔ k 1 · k 2 = - 1 .

Пример 5

Выяснить, перпендикулярны ли прямые y = - 3 7 x и y = 7 3 x - 1 2 .

Решение

Прямая y = - 3 7 x имеет угловой коэффициент, равный - 3 7 , а прямая y = 7 3 x - 1 2 - 7 3 .

Произведение угловых коэффициентов дает значение - 1 , - 3 7 · 7 3 = - 1 , то есть прямые являются перпендикулярными.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Теорема 3

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Доказательство 3

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Пример 6

Определить, являются ли заданные прямые x - y - 1 = 0 и x 0 = y - 4 2 перпендикулярными.

Решение

Получаем, что нормальный вектор прямой x - y - 1 = 0 имеет координаты n a → = (1 , - 1) , а b → = (0 , 2) - направляющий вектор прямой x 0 = y - 4 2 .

Отсюда видно, что векторы n a → = (1 , - 1) и b → = (0 , 2) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t , чтобы выполнялось равенство n a → = t · b → . Отсюда вывод, что прямые не являются перпендикулярными.

Ответ: прямые не перпендикулярны.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Понятие перпендикулярных плоскостей

При пересечении двух плоскостей у нас получается $4$ двугранных угла. Два угла равны $\varphi $, а два другие равны ${180}^0-\varphi $.

Определение 1

Углом между плоскостями называется минимальный из двугранных углов, образованных этими плоскостями.

Определение 2

Две пересекающиеся плоскости называются перпендикулярными, если угол между этими плоскостями равен $90^\circ$ (рис. 1).

Рисунок 1. Перпендикулярные плоскости

Признак перпендикулярности двух плоскостей

Теорема 1

Если прямая плоскости перпендикулярна другой плоскости, то эти плоскости перпендикулярны друг другу.

Доказательство.

Пусть нам даны плоскости $\alpha $ и $\beta $, которые пересекаются по прямой $AC$. Пусть прямая $AB$, лежащая в плоскости $\alpha $ перпендикулярна плоскости $\beta $ (рис. 2).

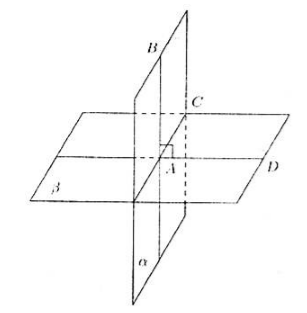
Рисунок 2.

Так как прямая $AB$ перпендикулярна плоскости $\beta $, то она перпендикулярна и прямой $AC$. Проведем дополнительно прямую $AD$ в плоскости $\beta $, перпендикулярно прямой $AC$.

Получаем, что угол $BAD$ - линейный угол двугранного угла, равный $90^\circ$. То есть, по определению 1, угол между плоскостями равен $90^\circ$, значит, данные плоскости перпендикулярны.

Теорема доказана.

Из этой теоремы следует следующая теорема.

Теорема 2

Если плоскость перпендикулярна прямой, по которой пересекаются две другие плоскости, то она перпендикулярна и этим плоскостям.

Доказательство.

Пусть нам даны две плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Плоскость $\gamma $ перпендикулярна прямой $c$ (рис. 3)

Рисунок 3.

Так как прямая $c$ принадлежит плоскости $\alpha $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\alpha $ и $\gamma $ перпендикулярны.

Так как прямая $c$ принадлежит плоскости $\beta $ и плоскость $\gamma $ перпендикулярна прямой $c$, то, по теореме 1, плоскости $\beta $ и $\gamma $ перпендикулярны.

Теорема доказана.

Для каждой из этих теорем справедливы и обратные утверждения.

Примеры задач

Пример 1

Пусть нам дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Найти все пары перпендикулярных плоскостей (рис. 5).

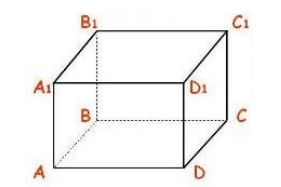
Рисунок 4.

Решение.

По определению прямоугольного параллелепипеда и перпендикулярных плоскостей видим следующие восемь пар перпендикулярных между собой плоскостей: $(ABB_1)$ и $(ADD_1)$, $(ABB_1)$ и $(A_1B_1C_1)$, $(ABB_1)$ и $(BCC_1)$, $(ABB_1)$ и $(ABC)$, $(DCC_1)$ и $(ADD_1)$, $(DCC_1)$ и $(A_1B_1C_1)$, $(DCC_1)$ и $(BCC_1)$, $(DCC_1)$ и $(ABC)$.

Пример 2

Пусть нам даны две взаимно перпендикулярные плоскости. Из точки одной плоскости проведен перпендикуляр к другой плоскости. Доказать, что эта прямая лежит в данной плоскости.

Доказательство.

Пусть нам даны перпендикулярные плоскости $\alpha $ и $\beta $, пересекающиеся по прямой $c$. Из точки $A$ плоскости $\beta $ проведен перпендикуляр $AC$ к плоскости $\alpha $. Предположим, что $AC$ не лежит в плоскости $\beta $ (рис. 6).

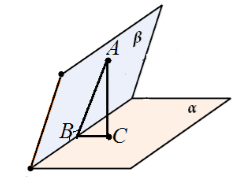
Рисунок 5.

Рассмотрим треугольник $ABC$. Он является прямоугольным с прямым углом $ACB$. Следовательно, $\angle ABC\ne {90}^0$.

Но, с другой стороны, $\angle ABC$ является линейным углом двугранного угла, образованного этими плоскостями. То есть двугранный угол, образованный этими плоскостями не равняется 90 градусам. Получаем, что угол между плоскостями не равен $90^\circ$. Противоречие. Следовательно, $AC$ лежит в плоскости $\beta $.

На этом уроке мы повторим теорию и докажем теорему-признак перпендикулярности прямой и плоскости.
В начале урока вспомним определение прямой, перпендикулярной к плоскости. Далее рассмотрим и докажем теорему-признак перпендикулярности прямой и плоскости. Для доказательства этой теоремы вспомним свойство серединного перпендикуляра.
Далее решим несколько задач на перпендикулярность прямой и плоскости.

Тема: Перпендикулярность прямой и плоскости

Урок: Признак перпендикулярности прямой и плоскости

На этом уроке мы повторим теорию и докажем теорему-признак перпендикулярности прямой и плоскости .

Определение . Прямая а называется перпендикулярной к плоскости α, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Доказательство .

Пусть нам дана плоскость α. В этой плоскости лежат две пересекающиеся прямые p и q . Прямая а перпендикулярна прямой p и прямой q . Нам нужно доказать, что прямая а перпендикулярна плоскости α, то есть, что прямая а перпендикулярна любой прямой, лежащей в плоскости α.

Напоминание .

Для доказательства нам нужно вспомнить свойства серединного перпендикуляра к отрезку. Серединный перпендикуляр р к отрезку АВ - это геометрическое место точек, равноудаленных от концов отрезка. То есть, если точка С лежит на серединном перпендикуляре р, то АС = ВС .

Пусть точка О - точка пересечения прямой а и плоскости α (рис. 2). Без ограничения общность, будем считать, что прямые p и q пересекаются в точке О . Нам нужно доказать перпендикулярность прямой а к произвольной прямой m из плоскости α.

Проведем через точку О прямую l , параллельно прямой m. На прямой а отложим отрезки ОА и ОВ , причем ОА = ОВ , то есть точка О - середина отрезка АВ . Проведем прямую PL , .

Прямая р перпендикулярна прямой а (из условия), (по построению). Значит, р АВ . Точка Р лежит на прямой р . Значит, РА = РВ .

Прямая q перпендикулярна прямой а (из условия), (по построению). Значит, q - серединный перпендикуляр к отрезку АВ . Точка Q лежит на прямой q . Значит, QА = QВ .

Треугольники АР Q и ВР Q равны по трем сторонам (РА = РВ , QА = QВ, Р Q - общая сторона). Значит, углы АР Q и ВР Q равны.

Треугольники А PL и BPL равны по углу и двум прилежащим сторонам (∠АР L = ∠ВР L, РА = РВ , PL - общая сторона). Из равенства треугольников получаем, что AL = BL .

Рассмотрим треугольник ABL. Он равнобедренный, так как AL = BL. В равнобедренном треугольнике медиана LО является и высотой, то есть прямая LО перпендикулярна АВ .

Мы получили, что прямая а перпендикулярна прямой l, а значит, и прямой m, что и требовалось доказать.

Точки А, М, О лежат на прямой, перпендикулярной к плоскости α, а точки О, В, С и D лежат в плоскости α (рис. 3). Какие из следующих углов являются прямыми: ?

Решение

Рассмотрим угол . Прямая АО перпендикулярна плоскости α, а значит, прямая АО перпендикулярна любой прямой, лежащей в плоскости α, в том числе прямой ВО . Значит, .

Рассмотрим угол . Прямая АО перпендикулярна прямой ОС , значит, .

Рассмотрим угол . Прямая АО перпендикулярна прямой О D , значит, . Рассмотрим треугольник DAO . В треугольнике может быть только один прямой угол. Значит, угол DAM - не является прямым.

Рассмотрим угол . Прямая АО перпендикулярна прямой О D , значит, .

Рассмотрим угол . Это угол в прямоугольном треугольнике BMO , он не может быть прямым, так как угол МОВ - прямой.

Ответ : .

В треугольнике АВС дано: , АС = 6 см, ВС = 8 см, СМ - медиана (рис. 4). Через вершину С проведена прямая СК , перпендикулярная к плоскости треугольника АВС , причем СК = 12 см. Найдите КМ .

Решение :

Найдем длину АВ по теореме Пифагора: (см).

По свойству прямоугольного треугольника середина гипотенузы М равноудалена от вершин треугольника. То есть СМ = АМ = ВМ , (см).

Рассмотрим треугольник КСМ . Прямая КС перпендикулярна плоскости АВС , а значит, КС перпендикулярна СМ . Значит, треугольник КСМ - прямоугольный. Найдем гипотенузу КМ из теоремы Пифагора: (см).

1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. - 5-е издание, исправленное и дополненное - М.: Мнемозина, 2008. - 288 с.: ил.

Задания 1, 2, 5, 6 стр. 57

2. Дайте определение перпендикулярности прямой и плоскости.

3. Укажите в кубе пару - ребро и грань, которые являются перпендикулярными.

4. Точка К лежит вне плоскости равнобедренного треугольника АВС и равноудалена от точек В и С . М - середина основания ВС . Докажите, что прямая ВС перпендикулярна плоскости АКМ .

В этой статье мы поговорим о перпендикулярности прямой и плоскости. Сначала дано определение прямой, перпендикулярной к плоскости, приведена графическая иллюстрация и пример, показано обозначение перпендикулярных прямой и плоскости. После этого сформулирован признак перпендикулярности прямой и плоскости. Далее получены условия, позволяющие доказывать перпендикулярность прямой и плоскости, когда прямая и плоскость заданы некоторыми уравнениями в прямоугольной системе координат в трехмерном пространстве. В заключении показаны подробные решения характерных примеров и задач.

Навигация по странице.

Перпендикулярные прямая и плоскость – основные сведения.

Рекомендуем для начала повторить определение перпендикулярных прямых , так как определение прямой, перпендикулярной к плоскости, дается через перпендикулярность прямых.

Определение.

Говорят, что прямая перпендикулярна к плоскости , если она перпендикулярна любой прямой, лежащей в этой плоскости.

Также можно сказать, что плоскость перпендикулярна к прямой, или прямая и плоскость перпендикулярны.

Для обозначения перпендикулярности используют значок вида «». То есть, если прямая c перпендикулярна к плоскости , то можно кратко записать .

В качестве примера прямой, перпендикулярной к плоскости, можно привести прямую, по которой пересекаются две смежных стены комнаты. Эта прямая перпендикулярна к плоскости и к плоскости потолка. Канат в спортивном зале можно также рассматривать как отрезок прямой, перпендикулярной к плоскости пола.

В заключении этого пункта статьи отметим, что если прямая перпендикулярна к плоскости, то угол между прямой и плоскостью считается равным девяноста градусам.

Перпендикулярность прямой и плоскости - признак и условия перпендикулярности.

На практике часто возникает вопрос: «Перпендикулярны ли заданные прямая и плоскость»? Для ответа на него существует достаточное условие перпендикулярности прямой и плоскости , то есть, такое условие, выполнение которого гарантирует перпендикулярность прямой и плоскости. Это достаточное условие называют признаком перпендикулярности прямой и плоскости. Сформулируем его в виде теоремы.

Теорема.

Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Доказательство признака перпендикулярности прямой и плоскости Вы можете посмотреть в учебнике геометрии за 10 -11 классы.

При решении задач на установление перпендикулярности прямой и плоскости также часто применяется следующая теорема.

Теорема.

Если одна из двух параллельных прямых перпендикулярна к плоскости, то и вторая прямая перпендикулярна к плоскости.

В школе рассматривается много задач, для решения которых применяется признак перпендикулярности прямой и плоскости, а также последняя теорема. Здесь мы не будем на них останавливаться. В этом пункте статьи основное внимание сосредоточим на применении следующего необходимого и достаточного условия перпендикулярности прямой и плоскости.

Это условие можно переписать в следующем виде.

Пусть - направляющий вектор прямой a , а - нормальный вектор плоскости . Для перпендикулярности прямой a и плоскости необходимо и достаточно, чтобы выполнялось и : , где t – некоторое действительное число.

Доказательство этого необходимого и достаточного условия перпендикулярности прямой и плоскости основано на определениях направляющего вектора прямой и нормального вектора плоскости.

Очевидно, это условие удобно использовать для доказательства перпендикулярности прямой и плоскости, когда легко находятся координаты направляющего вектора прямой и координаты нормального вектора плоскости в зафиксированной в трехмерном пространстве. Это справедливо для случаев, когда заданы координаты точек, через которые проходят плоскость и прямая, а также для случаев, когда прямую определяют некоторые уравнения прямой в пространстве , а плоскость задана уравнением плоскости некоторого вида.

Рассмотрим решения нескольких примеров.

Пример.

Докажите перпендикулярность прямой и плоскости .

Решение.

Нам известно, что числа, стоящие в знаменателях канонических уравнений прямой в пространстве , являются соответствующими координатами направляющего вектора этой прямой. Таким образом, - направляющий вектор прямой .

Коэффициенты при переменных x , y и z в общем уравнении плоскости являются координатами нормального вектора этой плоскости, то есть, - нормальный вектор плоскости .

Проверим выполнение необходимого и достаточного условия перпендикулярности прямой и плоскости.

Так как , то векторы и связаны соотношением , то есть, они коллинеарны. Следовательно, прямая перпендикулярна плоскости .

Пример.

Перпендикулярны ли прямая и плоскость .

Решение.

Найдем направляющий вектор заданной прямой и нормальный вектор плоскости, чтобы проверить выполнений необходимого и достаточного условия перпендикулярности прямой и плоскости.

Направляющим вектором прямой является