SLIDE 4
View document content
"How to solve probability problems"
Mitrofanova Snezhana Viktorovna, MBOU "Verkhovskaya School" Vologda Region
Subject: Workshop on solving problems in the theory of probability.
SLIDE 1
How to solve probability problems?
Probability. What is it?
SLIDE 2
Probability theory, as the name suggests, deals with probabilities. We are surrounded by many things and phenomena about which, no matter how advanced science is, it is impossible to make accurate predictions. We do not know which card we will draw at random from the deck or how many days it will rain in May, but having some Additional information, we can make predictions and calculate the probabilities of these random events.
Thus, we are faced with the basic concept random event - these are phenomena, the behavior of which cannot be predicted, or it is an experiment, the result of which cannot be calculated in advance, etc. It is the probabilities of events that are calculated in typical tasks USE.
SLIDE 2 (ONE AGAIN)
Probability- this is some, strictly speaking, a function that takes values from 0 to 1 and characterizes a given random event.
Then we use sample diagram, which should be used to solve the standard learning objectives to calculate the probability of a random event,
SLIDE 3
and then below with examples I will illustrate its application.
Find the main question of the task (find what is the outcome of the task, find favorable outcomes.)
Select a formula (or several) for the solution.
SLIDE 4
WHY DO WE READ TASKS CAREFULLY?
Of the 20 tickets offered in the exam, the student can answer only 17. What is the probability that the student will be able to answer the ticket chosen at random?
Of the 20 tickets offered in the exam, the student can answer only 17. What is the probability that the student will not be able to answer the ticket chosen at random?
SLIDE 5,6,7


SLIDE 8.9



SLIDE 10
Task 1.
SLIDE 11
Decision.

SLIDE 12
0.5 0.25= 0.125
SLIDE 13
Task 2.
SLIDE 14
Decision.
P(M)=P(ABD)+P(ABE)+P(ACF)
SLIDE 15

SLIDE 16

SLIDE 17

SLIDE 18

SLIDE 19, 20
Task 4.
View presentation content
"Presentation"

How to solve problems
on probability?
Mitrofanova Snezhana Viktorovna,
mathematic teacher
MBOU "Verkhovskaya School"
Vologda region

Probability. What is it ?
Probability is a function that takes values from 0 to 1.

Approximate scheme , which should be used to solve standard educational problems for calculating the probability:
Find the main question of the problem
The formula (or several) for the solution is selected.

Of the 20 tickets offered in the exam, the student can answer only 17. What is the probability that the student will be able to answer the ticket chosen at random?
Of the 20 tickets offered in the exam, the student can answer only 17. What is the probability that the student will not be able to answer the ticket chosen at random?

Probability events is the ratio of the number of outcomes that favor its occurrence to the number of all outcomes (incompatible, the only possible and equally possible):





Problems solved by constructing a tree of probabilities.
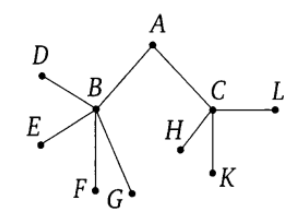
Task 1. Pavel Ivanovich takes a walk from point A along the paths of the park. At each fork, he randomly chooses the next track without going back. The track diagram is shown in the figure. Find the probability that Pavel Ivanovich will hit point G.
Decision.
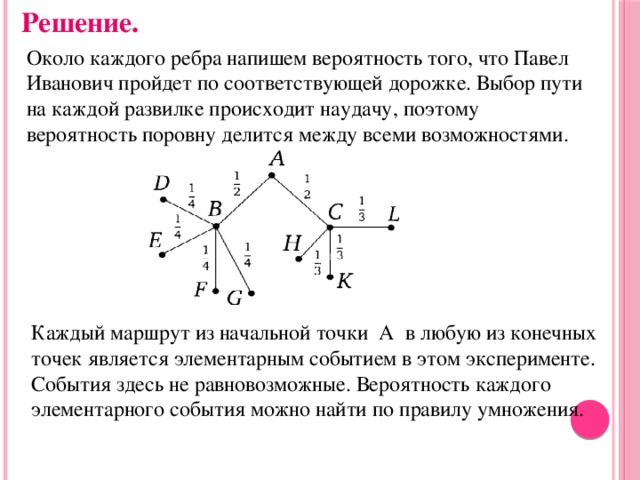
Next to each edge write the probability that Pavel Ivanovic will pass along the corresponding track. The choice of the path at each fork occurs at random, so the probability is equally divided among all possibilities.
Each route from start point A to any of the end points is an elementary event in this experiment. Events here are not equally likely. The probability of each elementary event can be found by the multiplication rule.
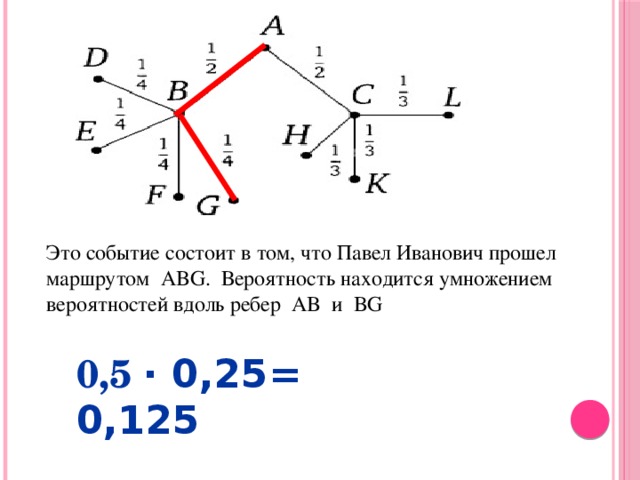
This event consists in the fact that Pavel Ivanovich passed the ABG route. The probability is found by multiplying the probabilities along the edges AB and BG
0,5 0.25= 0.125
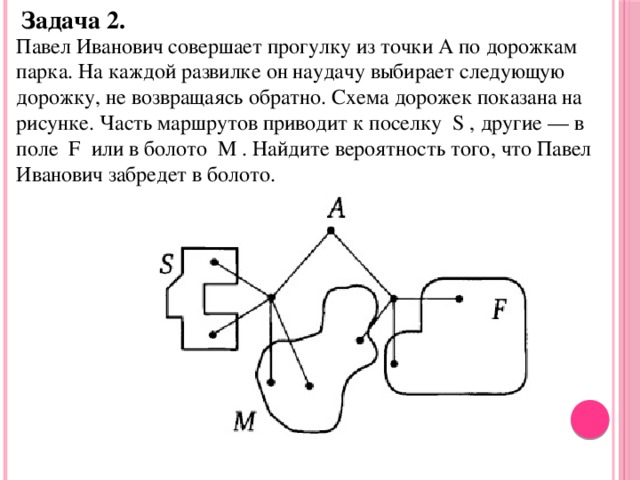
Task 2.
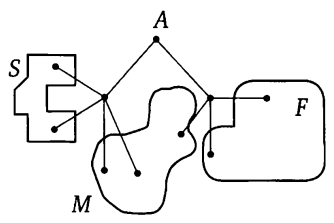
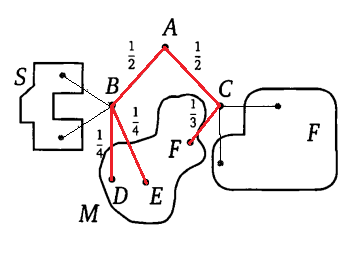
Pavel Ivanovich takes a walk from point A along the paths of the park. At each fork, he randomly chooses the next path without going back. The track diagram is shown in the figure. Some of the routes lead to the village S , others - to the field F or to the swamp M . Find the probability that Pavel Ivanovich wanders into the swamp.
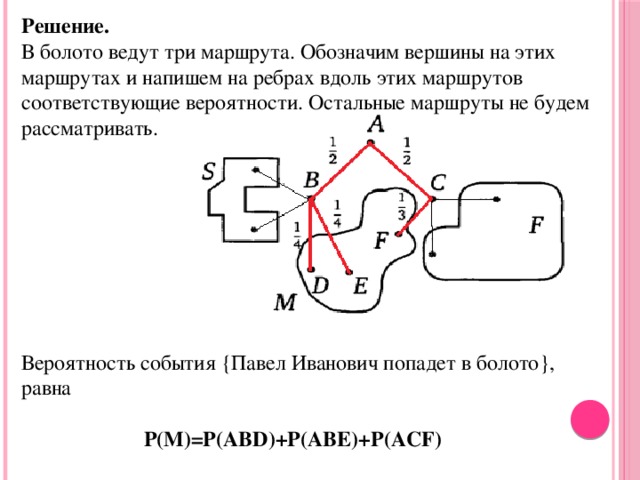
Decision. Three routes lead to the swamp. We denote the vertices on these routes and write the corresponding probabilities on the edges along these routes. Other routes will not be considered.
The probability of an event (Pavel Ivanovich will fall into a swamp) is equal to
P(M)=P(ABD)+P(ABE)+P(ACF)


Answer: 0,125

Task 4. Two factories of the same firm produce the same mobile phones.
The first factory produces 30% of all phones of this brand, and the second - the rest of the phones.
It is known that of all phones produced by the first factory, 1% have hidden defects, and 1.5% of all phones manufactured by the second factory.
Find the probability that a phone of this brand bought in a store has a hidden defect.
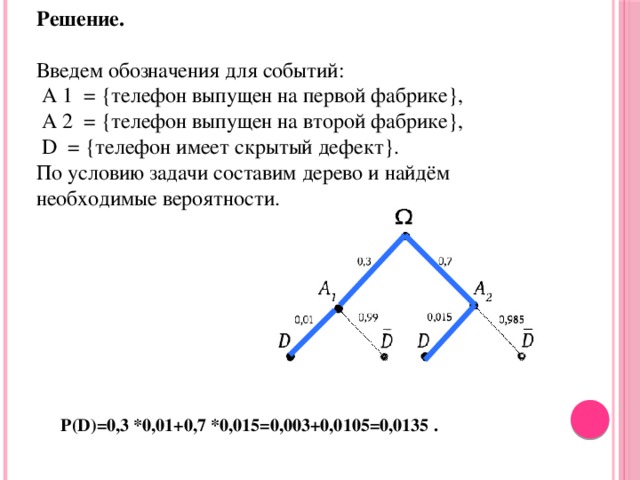
Decision. Let's introduce the notation for the events: A 1 = (the phone is released at the first factory), A 2 = (the phone is released at the second factory), D = (the phone has a hidden defect). According to the condition of the problem, we will make a tree and find the necessary probabilities.
P(D)=0.3 *0.01+0.7 *0.015=0.003+0.0105=0.0135 .
USE TEST - 2017 IN MATHEMATICS
PROFILE LEVEL
OPTION 4
Part 1
1. By tariff plan"Just Like Day" company cellular communication every evening withdraws 18 rubles from the subscriber's account. If there is less than 18 rubles left on the account, then the next morning the number is blocked until the account is replenished. This morning, Lisa had 500 rubles in her account. How many days (including today) will she be able to use her phone without topping up her account?
2. When the flashlight is on, the battery is gradually discharged, and the voltage in electrical circuit the flashlight falls. The figure shows the dependence of the voltage in the circuit on the operating time of the flashlight. On the horizontal axis indicates the operating time of the flashlight in hours, vertical axis- voltage in volts. Determine from the figure what voltage will be in the circuit after 15 hours of operation of the flashlight. Give your answer in volts.
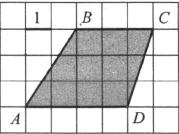
3. Find the area trapezoid ABCD shown on checkered paper with a cell size of 1 x 1 (see Fig.).
4. Pavel Ivanovich takes a walk from point A along the paths of the park. At each fork, he randomly chooses the next path without going back. The track diagram is shown in the figure. Find the probability that Pavel Ivanovich will hit point G.

5. Find the root of the equation
![]()
6. Quadrilateral ABCD is inscribed in a circle. Angle ABC is 132°, angle ABD is 61°. Find the angle CAD. Give your answer in degrees.

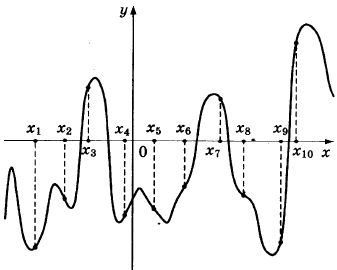
7. The figure shows a graph of the function y \u003d f (x) and ten points on the x-axis: x 1, x 2, x 3, ..., x 10. At how many of these points is the derivative f"(x) of the function f(x) positive?
8. A concrete ball weighs 0.5 tons. How many tons will the ball weigh twice larger radius made from the same concrete?
Part 2
9. Find the value of the expression
10. Ratio useful action some engine is determined by the formula
![]()
At what value of the heater temperature T 1 (in degrees Kelvin) will the efficiency of this engine be 80% if the refrigerator temperature T 2 = 200 K?
11. Pants are 30% more expensive than a shirt and 22% cheaper than a jacket. By what percent is the shirt cheaper than the jacket?
12. Find highest value functions
y \u003d 13x - 13tg x - 18
on the segment.
13. a) Solve the equation
b) Find all the roots of this equation, belonging to the segment [−3; 1].
14. In the right triangular prism ABCA 1 B 1 C 1 base side AB = 7√3, and side rib AA 1 = 8.
a) Prove that the plane BCA 1 is perpendicular to the plane passing through the edge AA 1 and the midpoint of the edge B 1 C 1 .
b) Find the tangent of the angle between the planes BCA 1 and BB 1 C 1.
15. Solve the inequality
![]()
16. On AC and BC sides triangle ABC the squares ACDE and BFKC are constructed outside the triangle. Point M is the midpoint of side AB.
a) Prove that CM = 1/2 DK.
b) Find the distance from point M to the centers of the squares, if AC = 14, BC = 16 and angle ACB = 150°.
17. In two regions there are 50 workers each, each of whom is ready to work 10 hours a day in the extraction of aluminum or nickel. In the first region, one worker produces 0.2 kg of aluminum or 0.1 kg of nickel per hour. In the second mining area X kg of aluminum per day requires x 2 man-hours of labor, and for extraction at kg of nickel per day is required for 2 man-hours of labor.
Both regions supply the mined metal to the plant, where an alloy of aluminum and nickel is produced for the needs of industry, in which 1 kg of aluminum accounts for 2 kg of nickel. At the same time, the regions agree among themselves to mine metals so that the plant can produce the largest number alloy. How many kilograms of alloy under such conditions can the plant produce daily?
"Point fluctuation" - Intermediate situation. The motion is damped and aperiodic. 5. Linear oscillations. 7. Free vibrations with viscous resistance. General solution = common decision+ private solution homogeneous heterogeneous. 1. Examples of oscillations. Harmonic driving force. Free vibrations caused by a driving force.
"The derivative of the function at a point" - What is the value of the derivative of the function y \u003d f (x) at point B? The figure shows a graph of the derivative y= f‘(x) of the function f(x) defined on the interval (-3;3). What value does the derivative of the functions y= f(x) take at point A? What angle does the tangent to the graph of the function form with the positive direction of the x-axis?
"Critical points of the function" - Among the critical points there are extremum points. Necessary condition extremum. Critical points functions Points of extremums. Definition. Extreme points (repetition). But, if f "(x0) = 0, then it is not necessary that the point x0 will be an extremum point. Examples. Critical points.
"Point coordinates" - Symmetry of the point about the abscissa axis (Ox). The body of the lizard is symmetrical about a straight line. The human body has an axis of symmetry. In nature, the structure of animal bodies also obeys the laws of symmetry. Point B (3; 6) is symmetrical to point B (3; - 6), located below the x-axis. Conclusion: Semirichnik is a rare plant, but the seven petals of the flower have bilateral symmetry.
"South Africa National Parks" - "Journey to Republic of South Africa". Nearby is the famous Tugela waterfall (948 m) of five cascades. The third day National parks and reserves. First day The capital of South Africa. The cost of hotel rooms starts from $400. A rainbow glows in a cloud of water dust rising 100 meters.
"Four remarkable points of the triangle" - The perpendicular dropped from the vertex of the triangle to the line containing the opposite side is called. Height. The median of a triangle. Problem number 1. The height of the triangle. Segment AN is a perpendicular dropped from point A to line a, if. A line segment that connects a vertex to a midpoint opposite side, is called.
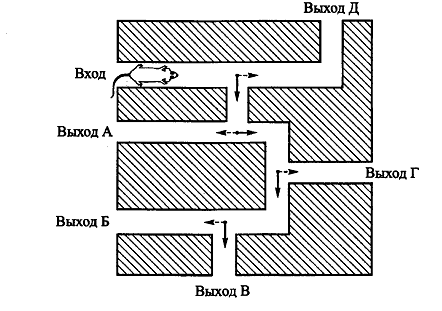
The pensioner walks along the paths of the park. At each fork, he randomly chooses the next path without going back. The track diagram is shown in the figure. The pensioner starts walking at point A. Find the probability that he will come to point F.
The solution of the problem
AT this lesson an example of solving the problem using probability theory is shown. For successful solution problem, you need to know that probability is the degree of possibility of the occurrence of some event, or the ratio of the number of favorable outcomes to the total number of possible outcomes. Thus, the solution of the problem is reduced to the application of the probability theory formula: , where is a favorable number of outcomes, and - total number outcomes. The solution of the problem is divided into stages. First, the probability is determined that the pensioner will start the walk exactly from the path , while Then the probability is calculated that the walk will continue along the route , while By the probabilities multiplication theorem: the probability of producing several events is equal to the product of the probabilities of these events, and the probability of each following on The order of the event is calculated assuming that all the previous ones have taken place. Thus, the result of calculating the product is the desired answer.
This task is similar to tasks of type B6, so it can be successfully used as a preparation for the exam in mathematics.
