Свободное падение. Движение тела, брошенного вертикально вверх.
Свободное падение.
Определение: Движение тела в поле сил тяжести, в отсутствии сил сопротивления, вблизи поверхности земли.
Замечание: Свободное падение - частный случай равноускоренного движения. Ускорение свободного падения g=9,8\frac{м}{c^{2}} . Везде в ЕГЭ g принято за 10\frac{м}{c^{2}} .
Пусть тело отпустили с высоты h без начальной скорости.
Общая формула:
В данном случае: y_{0}=0 ; V_{0y}=0 ; a_{x}=g
То есть: y=\frac{gt^{2}}{2}
Пусть t_{n} - время падения, тогда y=\frac{gt_{n}^{2}}{2}\Rightarrow t_{n}=\sqrt{\frac{2h}{g}}
Общая формула для скорости: V_{y}=V_{0y}+a_{y}t
В данном случае: V_{0y}=0 ; a_{y}=g\Rightarrow V_{y}=gt .
V_{k}=gt_{n} - конечная скорость
V_{k}=g\sqrt{\frac{2h}{g}}=\sqrt{\frac{g^{2}2h}{g}}=\sqrt{2gh}
Движение тела, брошенного вертикально вверх.

Н - минимальная высота подъема
Общая формула:
y=y_{0}+V_{0y}t+\frac{a_{y}t^{2}}{2} - где y_{0}=0\Rightarrow y=V_{0y}t+\frac{a_{y}t^{2}}{2} .
y=V_{0}t-\frac{gt^{2}}{2} - так как: V_{0y}=V_{0} ; a_{y}=-g .
y=V_{0}t-\frac{gt^{2}}{2} - так как: V_{y}=V_{0}-gt ; (из общей формулы V_{y}=V_{0y}+a_{y}t при V_{0y}=V_{0} ; a_{y}=-g .
Скорость в верхней точке подъема V_{y}=0 .
V_{0}-gt_{n}=0\Rightarrow t_{n}=\frac{V_{0}}{g} - время подъема.
Время падения:
t_{падения}=t_{n}=\frac{V_{0}}{g}
Полное время полета:
t_{полное}=2t_{n}=\frac{2V_{0}}{g}
Начальная и конечная скорость:
V_{k}=V_{0}=\sqrt{2gH}
Максимальная высота подъема:
H=y\left(t_{n}\right)=V_{0}t_{n}-\frac{gt_{n}^{2}}{2}=V_{0}\frac{V_{0}}{g}-\frac{g}{2}\cdot \frac{V_{0}^{2}}{g^{2}}=\frac{V_{0}^{2}}{g}-\frac{V_{0}^{2}}{2g}=\frac{V_{0}^{2}}{g}\left(1-\frac{1}{2}\right)=\frac{1}{2}\frac{V_{0}^{2}}{g}
H=\frac{V_{0}^{2}}{2g}
Отзывы
|
Александра |
|
Наталья Львовна замечательный преподаватель по физике, который превосходно подготовит вас к ЕГЭ. Пришла к ней не с нулевыми знаниями, но хорошими их назвать нельзя. Хоть я и начала заниматься с января, мы успели пройти все темы на дополнительных занятиях. Каждая тема была разобрана и были прорешаны все типы задач, которые могли встретиться на экзамене. И действительно, на ЕГЭ я не столкнулась с трудностями в решении задач и написала экзамен на 94 балла. Очень советую этого преподавателя! |
|
Илья |
|
Заниматься у Натальи Львовны я начал с середины января, сразу после новогодних каникул. До начала занятий, были пробные экзамены по физике, а также подготовка к экзамену в школе, но результат был 60-70 баллов, при этом я получал отличные оценки по предмету. Занятия с Натальей Львовной проходили плодотворно и интересно, с этим репетитором по физзике я смог расширить свои знания, а также закрепить школьную программу. Пройдя весенние интенсивы, я вышел на экзамен уверенным в своем результате. Получив 85 баллов, я смог поступить в желаемый ВУЗ с 1 волной. Хочу еще раз отблагодарить репетитора, который помог мне приблизиться к своим целям, сдать единый государственный экзамен на нужные баллы, поступить в вуз и начать обучение будущей профессии. |
|
Татьяна |
|
Моя дочь Полина училась в школе с «гуманитарным уклоном». Основными предметами с первого класса для неё были иностранные языки. Но, когда встал вопрос выбора профессии, дочь захотела поступать в технический ВУЗ. Очевидно, что школьная программа - не резиновая, и не удивительно, что при 8 учебных часах иностранных языков у неё был только один урок физики в неделю. Пришлось срочно искать решение. Нам повезло - мы нашли прекрасного репетитора по физике. |
^ 3. Движение тела, брошенного вертикально вверх, вертикально вниз. Вывод формулы для времени движения тела брошенного вертикально с высоты h.
Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г. Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же . До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.
Ускорение, с которым падают на Землю тела, называется ускорением свободного падения
. Вектор ускорения свободного падения обозначается символом он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение g
оказывается неодинаковым, изменяясь примерно от 9,83 м/с 2 на полюсах до 9,78 м/с 2 на экваторе. Обычно, если в расчетах не требуется высокая точность, то числовое значение g
у поверхности Земли принимают равным 9,8 м/с 2 или даже 10 м/с 2 .
А . Простым примером свободного падения
является падение тела с некоторой высоты h
без начальной скорости
. Свободное падение является прямолинейным движением с постоянным ускорением.
. Простым примером свободного падения
является падение тела с некоторой высоты h
без начальной скорости
. Свободное падение является прямолинейным движением с постоянным ускорением.
Если направить координатную ось OY
вертикально вниз, совместив начало координат с местом начала падения, тогда поверхность Земли имеет координату 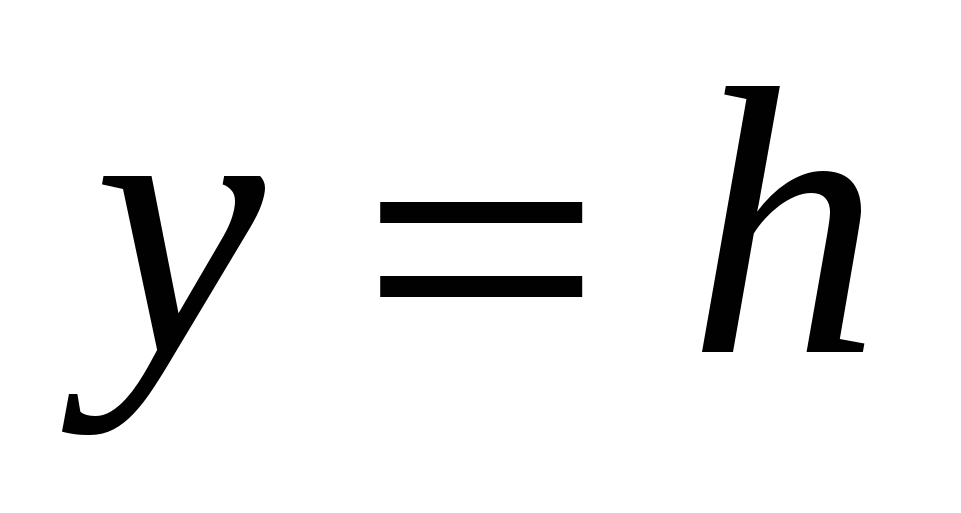 .
.
 , координата
, координата  .
.
В момент падения  - время свободного падения определяется высотой с которой падает тело.
- время свободного падения определяется высотой с которой падает тело.
Скорость тела в момент падения: 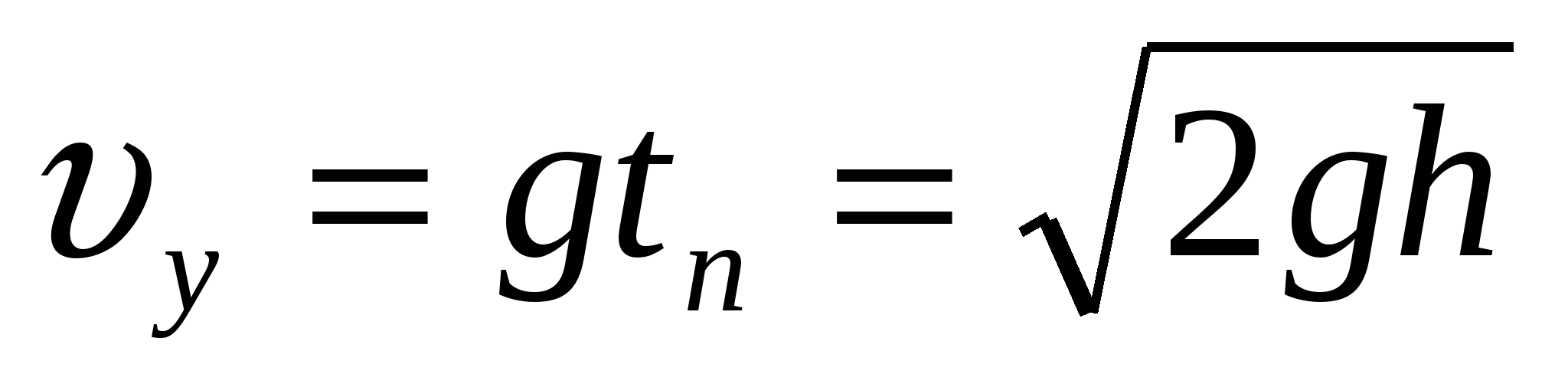 - так же однозначно определяется высотой, с которой упало тело.
- так же однозначно определяется высотой, с которой упало тело.
Б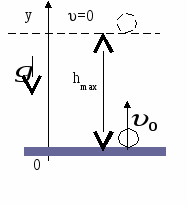 . Движение тела брошенного вертикально вверх с некоторой начальной скоростью.
. Движение тела брошенного вертикально вверх с некоторой начальной скоростью.
Направим координатную ось OY
Скорость тела в проекции на выбранную ось изменяется по закону 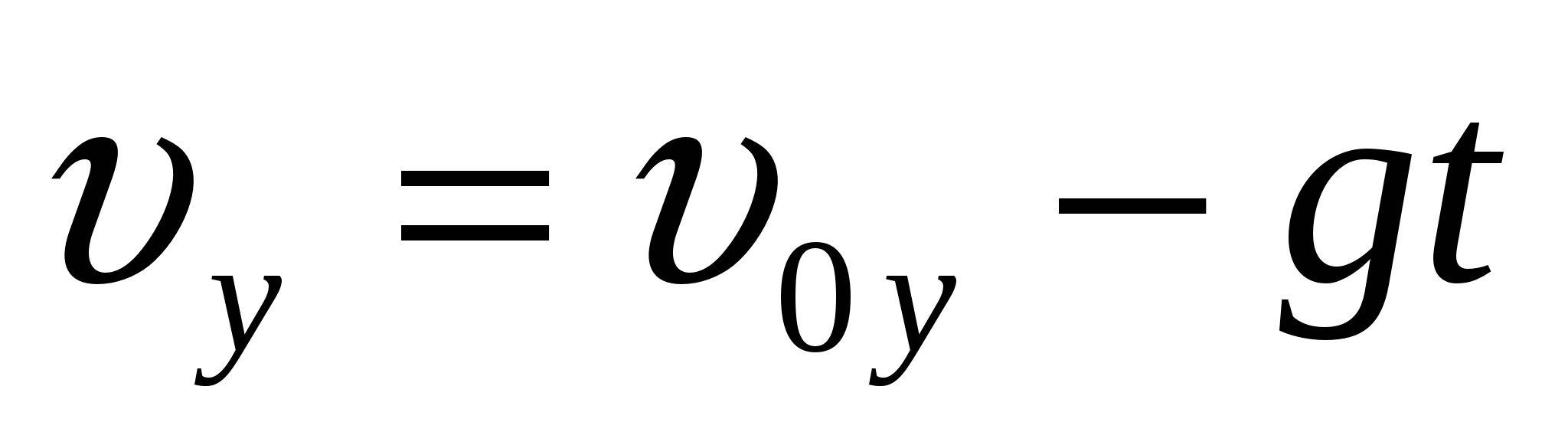 , координата
, координата  .
.
В верхней точке траектории 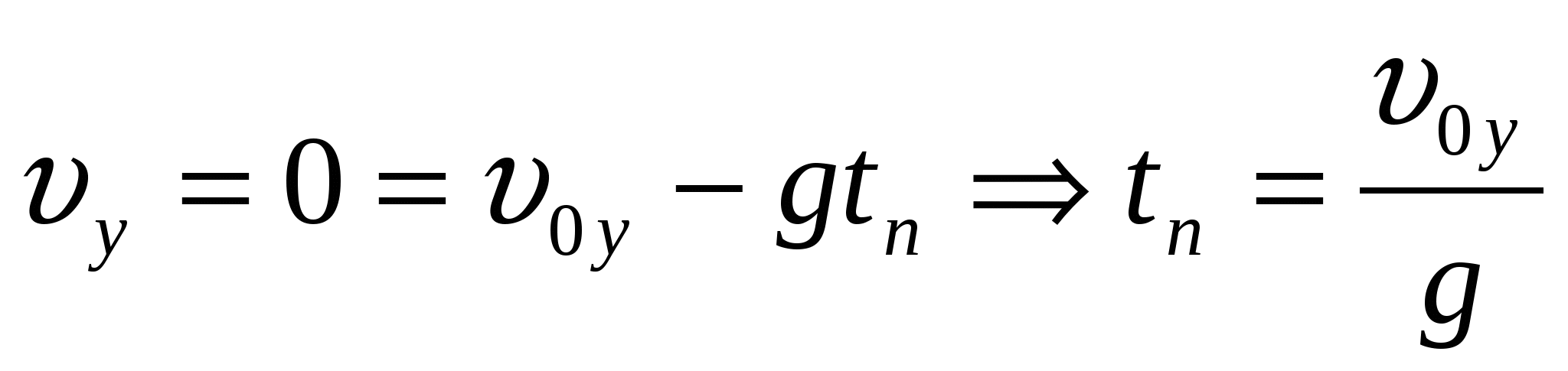 - время подъема определяется начальной скоростью тела. Если пренебречь сопротивлением воздуха, то время падения и время подъема будут равны. Т.е. время движения (до поверхности земли)
- время подъема определяется начальной скоростью тела. Если пренебречь сопротивлением воздуха, то время падения и время подъема будут равны. Т.е. время движения (до поверхности земли)  .
.
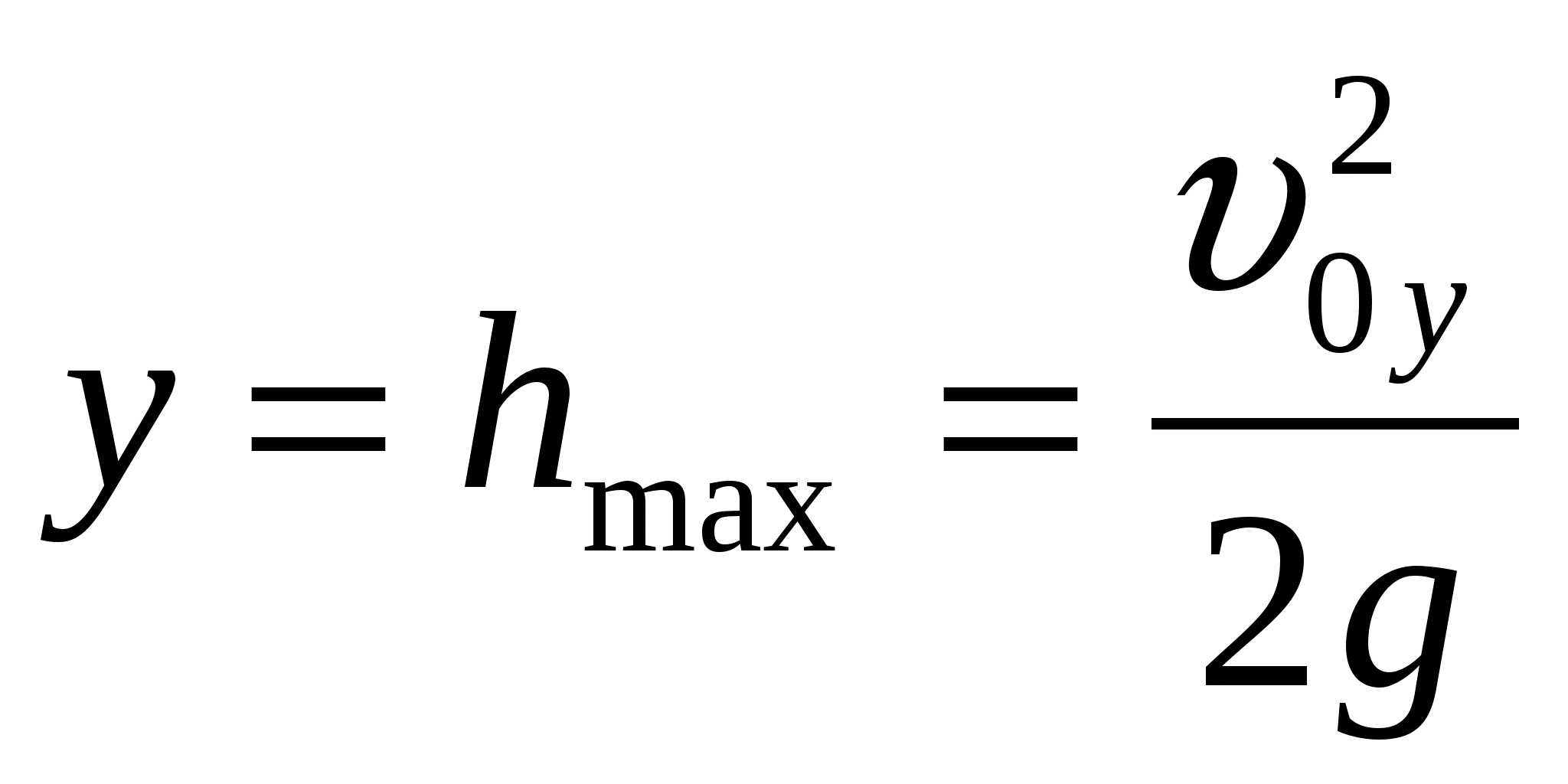 . Из верхней точки траектории тело падает свободно. Скорость тела в момент падения на землю равна начальной скорости. Скорость тела на высоте h соответствующего закону сохранения энергии.
. Из верхней точки траектории тело падает свободно. Скорость тела в момент падения на землю равна начальной скорости. Скорость тела на высоте h соответствующего закону сохранения энергии.
^
4. Движение тела брошенного под углом к горизонту. Вывод формул дальности полета, максимальной высоты подъема, времени движения
Н аправим координатную ось OY
вертикально вверх, совместив начало координат с точкой бросания.
аправим координатную ось OY
вертикально вверх, совместив начало координат с точкой бросания.
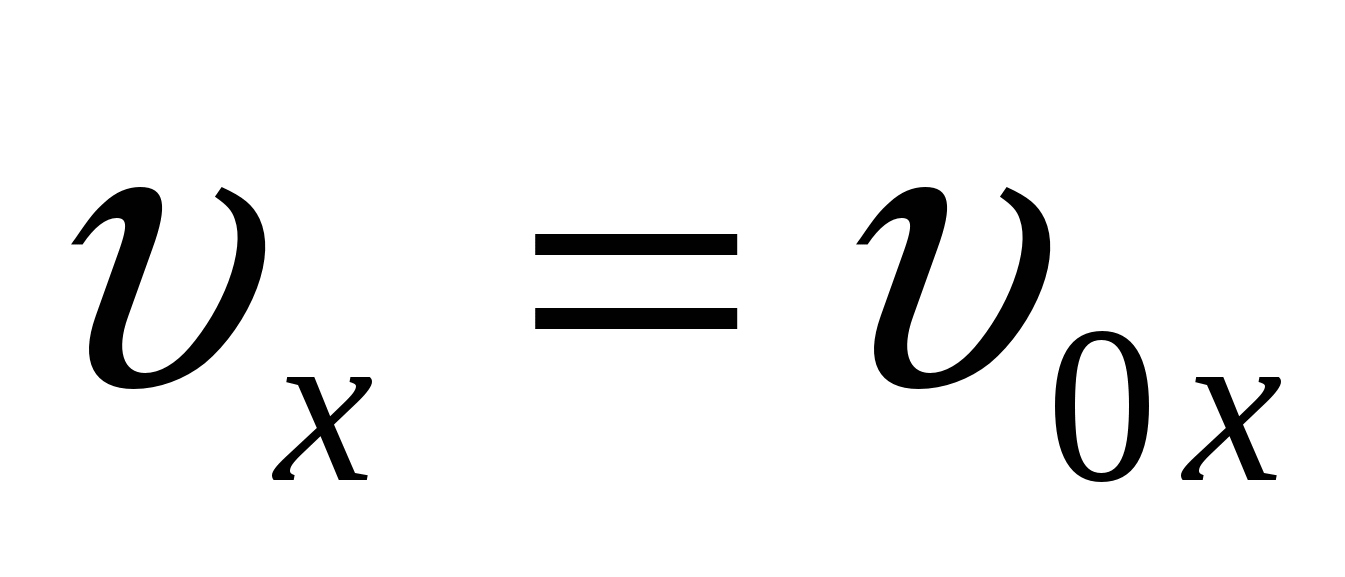 . Из рисунка:
. Из рисунка:  и
и ![]() .
.
Координаты: 
В верхней точке траектории 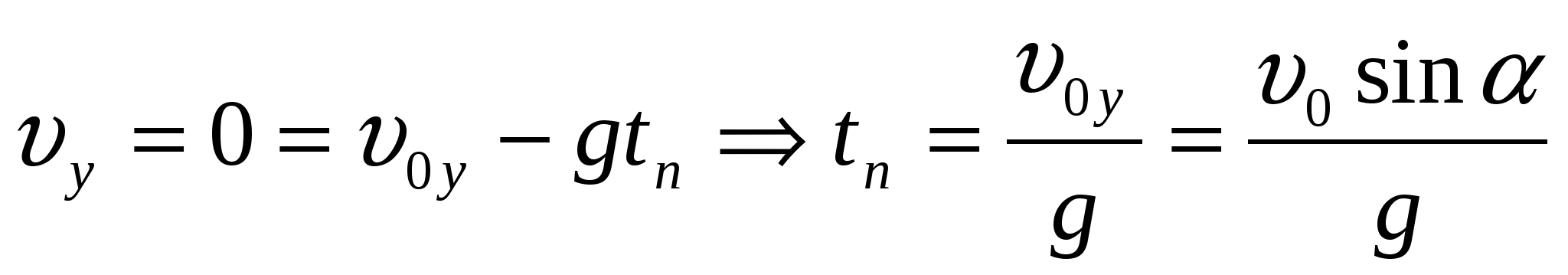 - время подъема определяется вертикальной составляющей начальной скорости тела. Если пренебречь сопротивлением воздуха, то время падения и время подъема будут равны. Т.е. время движения (до поверхности земли)
- время подъема определяется вертикальной составляющей начальной скорости тела. Если пренебречь сопротивлением воздуха, то время падения и время подъема будут равны. Т.е. время движения (до поверхности земли)  .
.
Из уравнения зависимости координаты от времени максимальная высота подъема  . Скорость тела в момент падения на землю равна по модулю начальной скорости, но проекция скорости на ось у меняет знак на противоположный. Скорость тела на высоте h соответствующего закону сохранения энергии.
. Скорость тела в момент падения на землю равна по модулю начальной скорости, но проекция скорости на ось у меняет знак на противоположный. Скорость тела на высоте h соответствующего закону сохранения энергии.
Дальность полета по горизонтали .
Из приведенных формул следует, что дальность полета будет максимальной для угла 45
^ 5. Движение тела, брошенного горизонтально. Вывод формулы траектории движения, вывод формул для времени падения и дальности полета
Н аправим координатную ось OY
вертикально вниз, совместив начало координат с местом начала падения, тогда поверхность Земли имеет координату .
аправим координатную ось OY
вертикально вниз, совместив начало координат с местом начала падения, тогда поверхность Земли имеет координату .
В горизонтальном направлении никакие силы на тело не действуют, поэтому горизонтальная составляющая скорости не меняется. По вертикали скорость тела изменяет сила тяжести, т.е. тело движется с постоянным ускорением , направленным вертикально вниз. Скорость тела в проекции на выбранные оси изменяется по закону: и  . Координаты:
. Координаты:  Если исключить из этих уравнений время движения
Если исключить из этих уравнений время движения  - получили уравнение траектории – ветвь параболы.
- получили уравнение траектории – ветвь параболы.
Вдоль оси у тело свободно падает. В момент падения - время свободного падения определяется высотой с которой падает тело.
Скорость тела в момент падения может быть определена из закона сохранения энергии:  .
.
Дальность полета тела по горизонтали  - зависит от высоты и начальной скорости тела.
- зависит от высоты и начальной скорости тела.
При движении по криволинейной траектории скорости направлена по касательной к траектории.
^
6. Движение тела по окружности с постоянной по модулю скоростью. Угловая скорость, угол поворота, период обращения, частота. Связь между угловой и линейной скоростью.
Д вижение тела по окружности
является частным случаем криволинейного движения. Наряду с вектором перемещения
вижение тела по окружности
является частным случаем криволинейного движения. Наряду с вектором перемещения  удобно рассматривать угловое перемещение
Δφ (или угол поворота
), измеряемое в радианах
(рис.). Длина дуги связана с углом поворота соотношением Δl
= R
Δφ. При малых углах поворота Δl
≈ Δs
.
удобно рассматривать угловое перемещение
Δφ (или угол поворота
), измеряемое в радианах
(рис.). Длина дуги связана с углом поворота соотношением Δl
= R
Δφ. При малых углах поворота Δl
≈ Δs
.
Угловой скоростью
ω тела в данной точке круговой траектории называют предел (при Δt
→ 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt
:  . Угловая скорость измеряется в рад/с
. Связь между модулем линейной скорости υ и угловой скоростью ω: υ = ωR
. Угловая скорость измеряется в рад/с
. Связь между модулем линейной скорости υ и угловой скоростью ω: υ = ωR
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора скорости.
Каждый оборот тело совершает за один и тот же промежуток времени – период Т (время одного оборота). Число оборотов за 1 с называется частотой  [об/с]. Частота оказывается величиной обратной периоду.
[об/с]. Частота оказывается величиной обратной периоду.
Из определения скорости 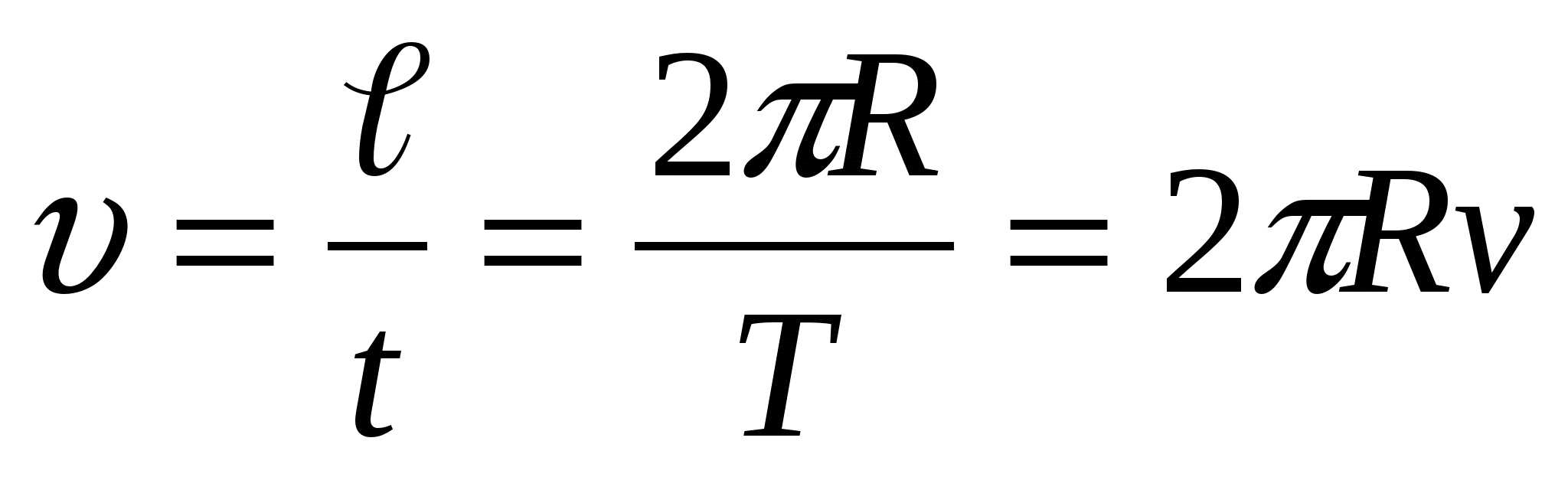 .
.
Из определения угловой скорости 
нормальным
или
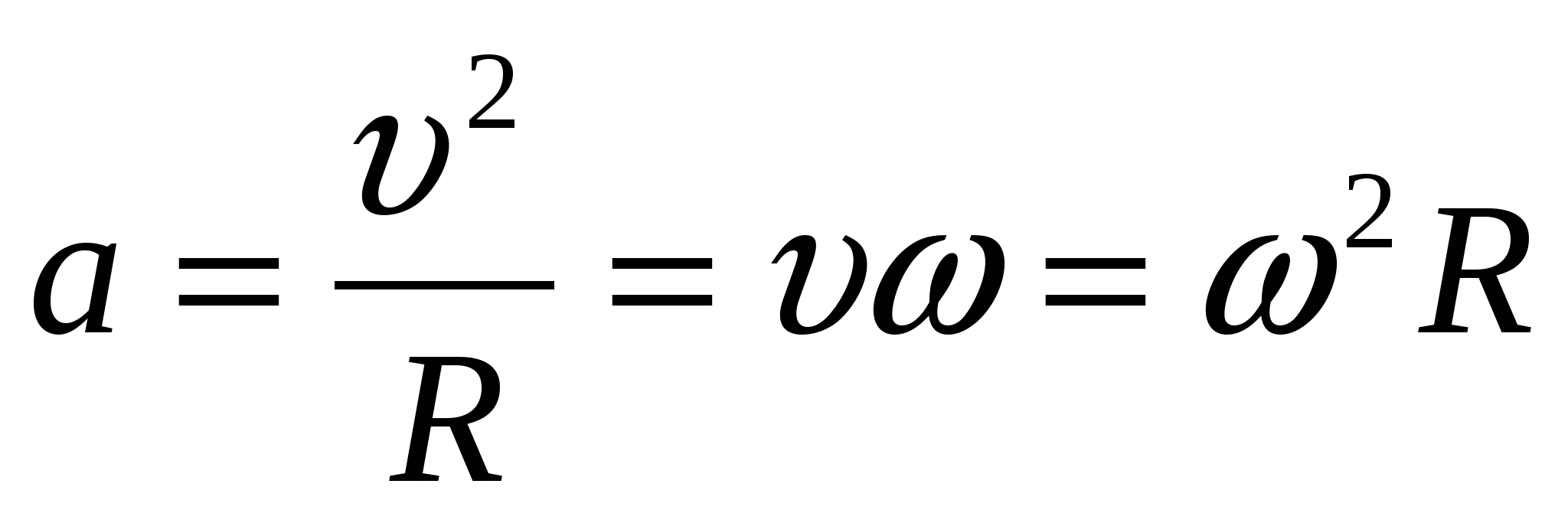
t
^
7. Центростремительное ускорение (вывод формулы).
Равномерное движение тела по окружности является движением с ускорением. Ускорение направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением . Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:
Д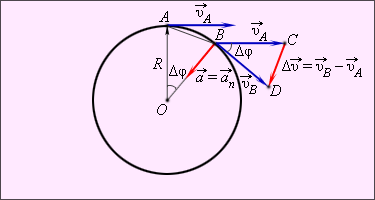 ля доказательства этого выражения рассмотрим изменение вектора скорости за малый промежуток времени Δt
. По определению ускорения
ля доказательства этого выражения рассмотрим изменение вектора скорости за малый промежуток времени Δt
. По определению ускорения 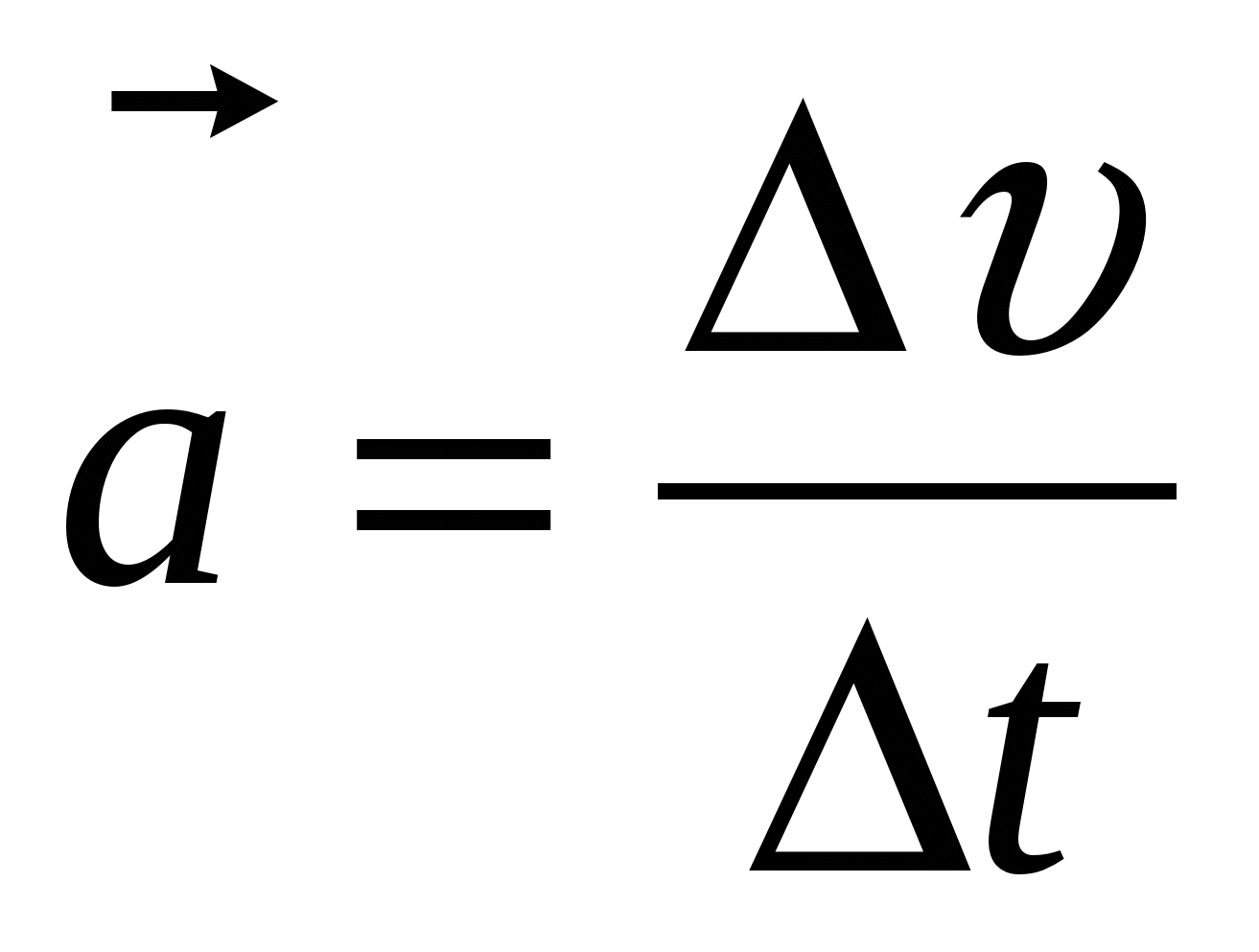
Векторы скоростей  и
и  в точках A
и B
направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ A
= υ B
= υ.
в точках A
и B
направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υ A
= υ B
= υ.
Из подобия треугольников OAB
и BCD
(рис.) следует:  .
.
При малых значениях угла Δφ = ωΔt
расстояние |AB
| =Δs
≈ υΔt
. Так как |OA
| = R
и |CD
| = Δυ, из подобия треугольников на рис. получаем: 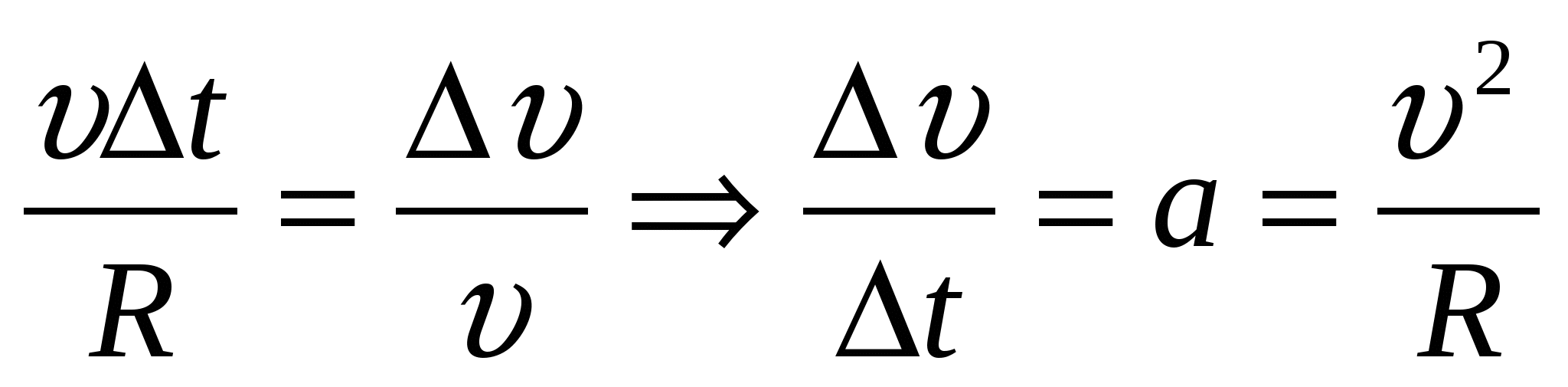 .
.
При малых углах Δφ направление вектора приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt → 0. При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.
Центростремительное ускорение показывает как быстро изменяется направление скорости. Любое криволинейное движение – это движение с ускорением.
^ 9. Закон сохранения импульса (вывод, границы применения)
Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела
(или количеством движения
). Импульс тела – векторная величина. 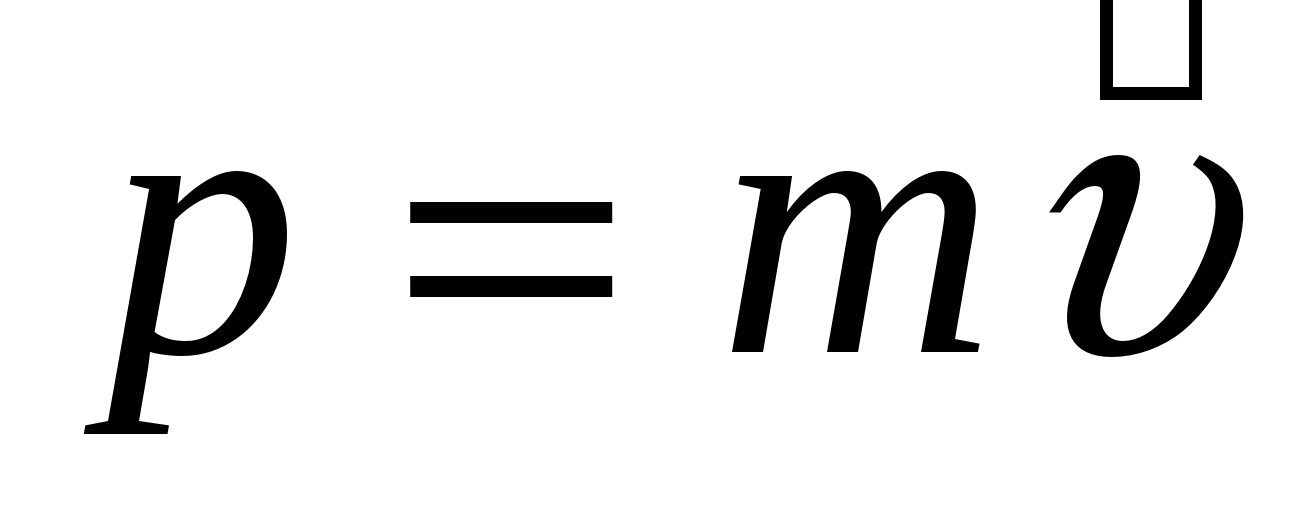 . Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с)
.
. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с)
.
Физическая величина, равная произведению силы на время ее действия, называется импульсом силы
 . Импульс силы также является векторной величиной.
. Импульс силы также является векторной величиной.
В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы
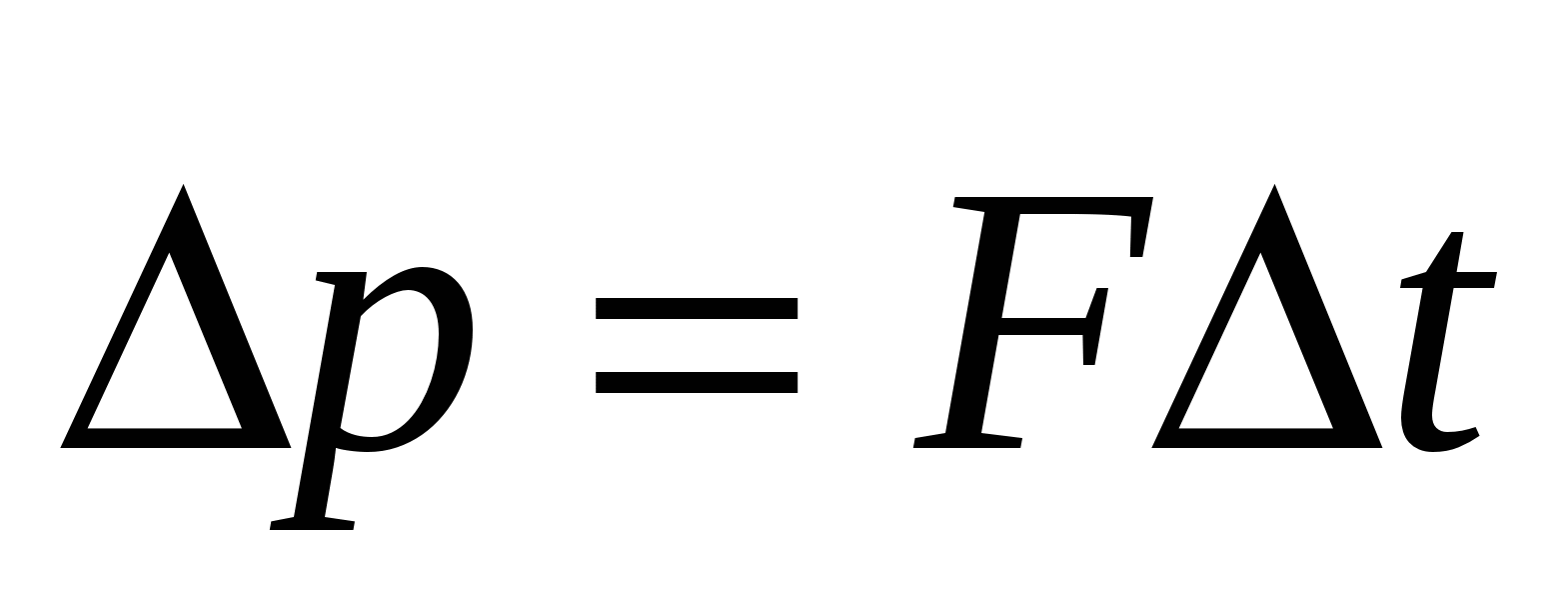
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу . Это векторное равенство может быть записано в проекциях на координатные оси, например F x Δt = Δp x . Таким образом, изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось. При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу.
Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой . Импульс системы тел равен векторной сумме импульсов тел, составляющих эту систему:
^ В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса . Он является следствием из второго и третьего законов Ньютона.
Р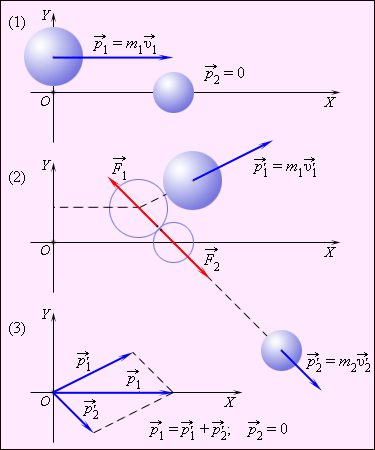 ассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через
ассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через  и
и  . По третьему закону Ньютона если эти тела взаимодействуют в течение времени t
, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:
. По третьему закону Ньютона если эти тела взаимодействуют в течение времени t
, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:  . Применим к этим телам второй закон Ньютона:
. Применим к этим телам второй закон Ньютона:  и
и 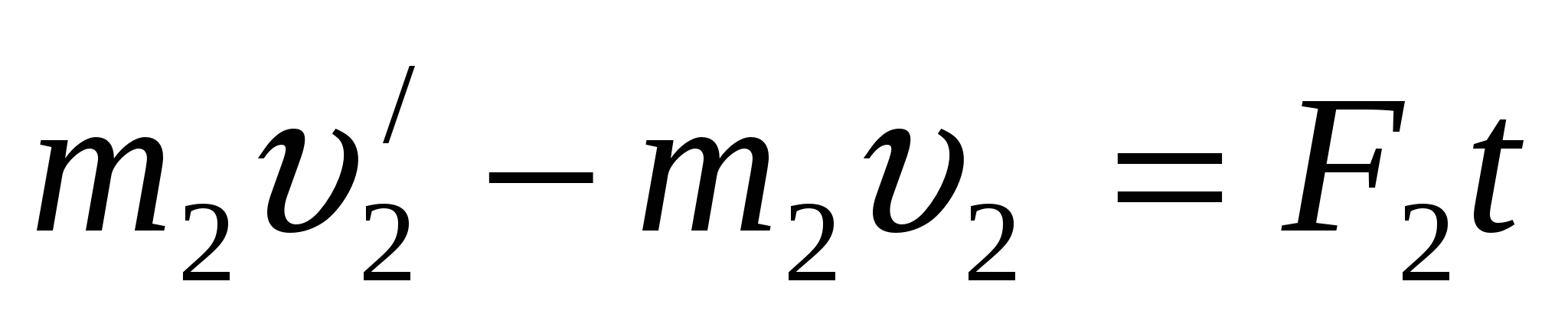 , где
, где  и
и  – импульсы тел в начальный момент времени,
– импульсы тел в начальный момент времени, 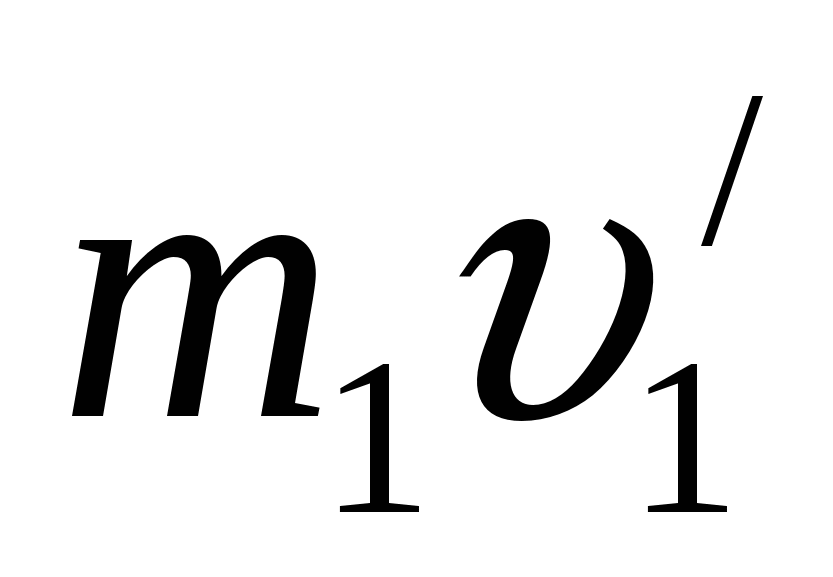 и
и 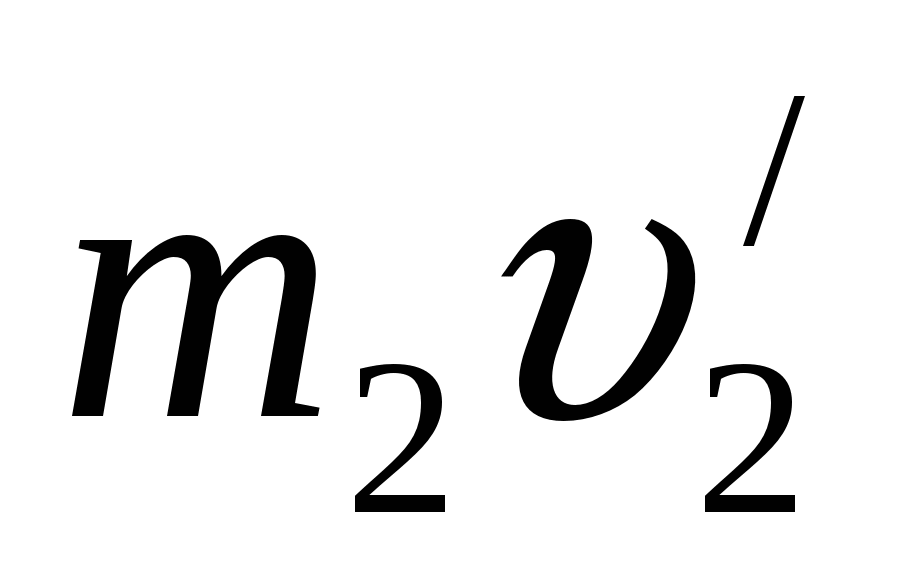 – импульсы тел в конце взаимодействия. Из этих соотношений следует:
– импульсы тел в конце взаимодействия. Из этих соотношений следует:
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.
^ Закон сохранения импульса выполняется и для проекций векторов на каждую ось.
Примером может служить реактивное движение . При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела.
На принципе отдачи основано реактивное движение . В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью относительно ракеты.
Закон сохранения импульса можно применять для всех быстро протекающих процессов: столкновения, удар, взрыв – когда время взаимодействия тел мало.
^ 10. Гидростатическое давление (вывод формулы). Сила Архимеда (вывод формулы). Условие плавания тел.
Основным отличием жидкостей от твердых (упругих) тел является способность легко изменять свою форму. Части жидкости могут свободно сдвигаться, скользя друг относительно друга. Поэтому жидкость принимает форму сосуда, в который она налита. В жидкость, как и в газообразную среду, можно погружать твердые тела. В отличие от газов жидкости практически несжимаемы.
На тело, погруженное в жидкость или газ, действуют силы, распределенные по поверхности тела. Для описания таких распределенных сил вводится новая физическая величина – давление .
Давление определяется как отношение модуля силы действующей перпендикулярно поверхности, к площади S
этой поверхности: 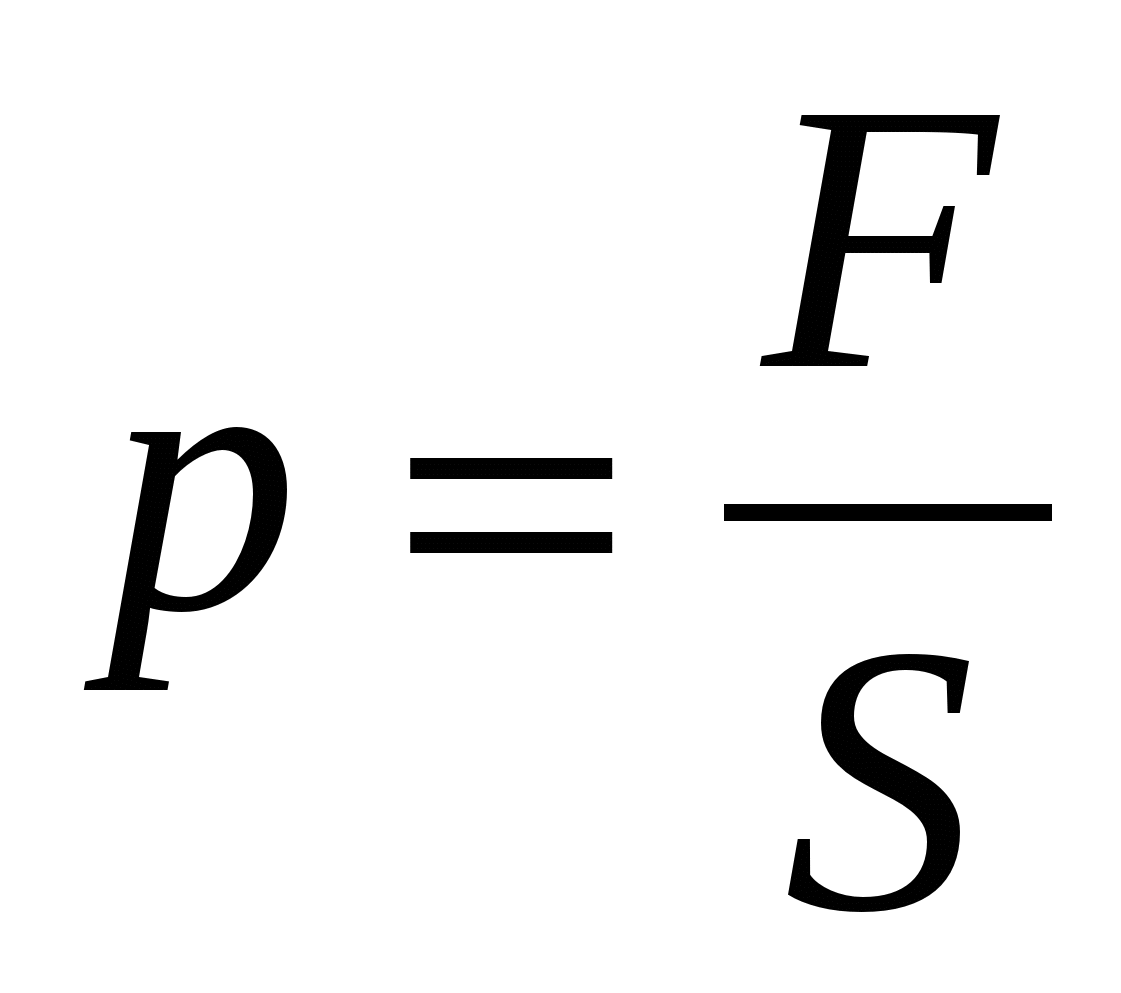 . В системе СИ давление измеряется в паскалях (Па)
: 1 Па = 1 Н/м 2 . Часто используются внесистемные единицы: нормальная атмосфера (атм)
и миллиметр ртутного столба (мм Hg)
: 1 атм = 101325 Па = 760 мм Hg
. В системе СИ давление измеряется в паскалях (Па)
: 1 Па = 1 Н/м 2 . Часто используются внесистемные единицы: нормальная атмосфера (атм)
и миллиметр ртутного столба (мм Hg)
: 1 атм = 101325 Па = 760 мм Hg
Ф ранцузский ученый Б. Паскаль
в середине XVII века эмпирически установил закон, названный законом Паскаля
: Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.
ранцузский ученый Б. Паскаль
в середине XVII века эмпирически установил закон, названный законом Паскаля
: Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.
Для иллюстрации закона Паскаля на рис. изображена небольшая прямоугольная призма, погруженная в жидкость. Если предположить, что плотность материала призмы равна плотности жидкости, то призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т. е. силы, действующие на единицу площади поверхности каждой грани, одинаковы: p 1 = p 2 = p 3 = p .
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты h
и площади основания S
равна весу столба жидкости mg
, где m
= ρghS
– масса жидкости в сосуде, ρ – плотность жидкости. Следовательно  . Такое же давление на глубине h
в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Давление столба жидкости ρgh
называют гидростатическим давлением
.
. Такое же давление на глубине h
в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Давление столба жидкости ρgh
называют гидростатическим давлением
.
Если жидкость находится в цилиндре под поршнем, то действуя на поршень некоторой внешней силой можно создавать в жидкости дополнительное давление p 0 = F / S , где S – площадь поршня.
Таким образом, полное давление в жидкости на глубине h
можно записать в виде: 
И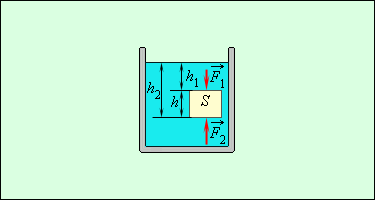 з-за разности давлений в жидкости на разных уровнях возникает выталкивающая
или архимедова
сила
з-за разности давлений в жидкости на разных уровнях возникает выталкивающая
или архимедова
сила  .
.
Рис. поясняет появление архимедовой силы. В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S . Разность давлений на нижнюю и верхнюю грани есть: Δp = p 2 – p 1 = ρgh. Поэтому выталкивающая сила будет направлена вверх, и ее модуль равен F А = F 2 – F 1 = S Δp = ρgSh = ρgV, где V – объем вытесненной телом жидкости, а ρV – ее масса. Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом. Это утверждение, называемое законом Архимеда , справедливо для тел любой формы.
Из закона Архимеда вытекает, что если средняя плотность тела ρ т больше плотности жидкости (или газа) ρ, тело будет опускаться на дно. Если же ρ т
^
11. Механическая работа. Кинетическая энергия. Доказательство теоремы об изменении кинетической энергии
Механическая работа - это физическая величина, являющаяся количественной характеристикой действия силы F на тело, приводящее к изменению скорости. Работа силы равна скалярному произведению силы на перемещение A =  =Fscosα = F x Δx + F y Δy + F z Δz (1).
=Fscosα = F x Δx + F y Δy + F z Δz (1).
Работа силы может быть положительной, отрицательной или равной нулю.
Если угол между вектором силы и вектором перемещения острый – работа силы положительная; равен 90 - работа равна нулю; тупой – работа силы отрицательная.
^ Работа всех приложенных сил равна работе равнодействующей силы
Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. Эту связь проще всего установить, рассматривая движение тела вдоль прямой линии под действием постоянной силы  . В этом случае векторы силы, перемещения, скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F
, s
, υ и a
как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A
= Fs
.
. В этом случае векторы силы, перемещения, скорости и ускорения направлены вдоль одной прямой, и тело совершает прямолинейное равноускоренное движение. Направив координатную ось вдоль прямой движения, можно рассматривать F
, s
, υ и a
как алгебраические величины (положительные или отрицательные в зависимости от направления соответствующего вектора). Тогда работу силы можно записать как A
= Fs
.
При равноускоренном движении перемещение s
может быть выражено формулой  . Отсюда следует, что
. Отсюда следует, что 
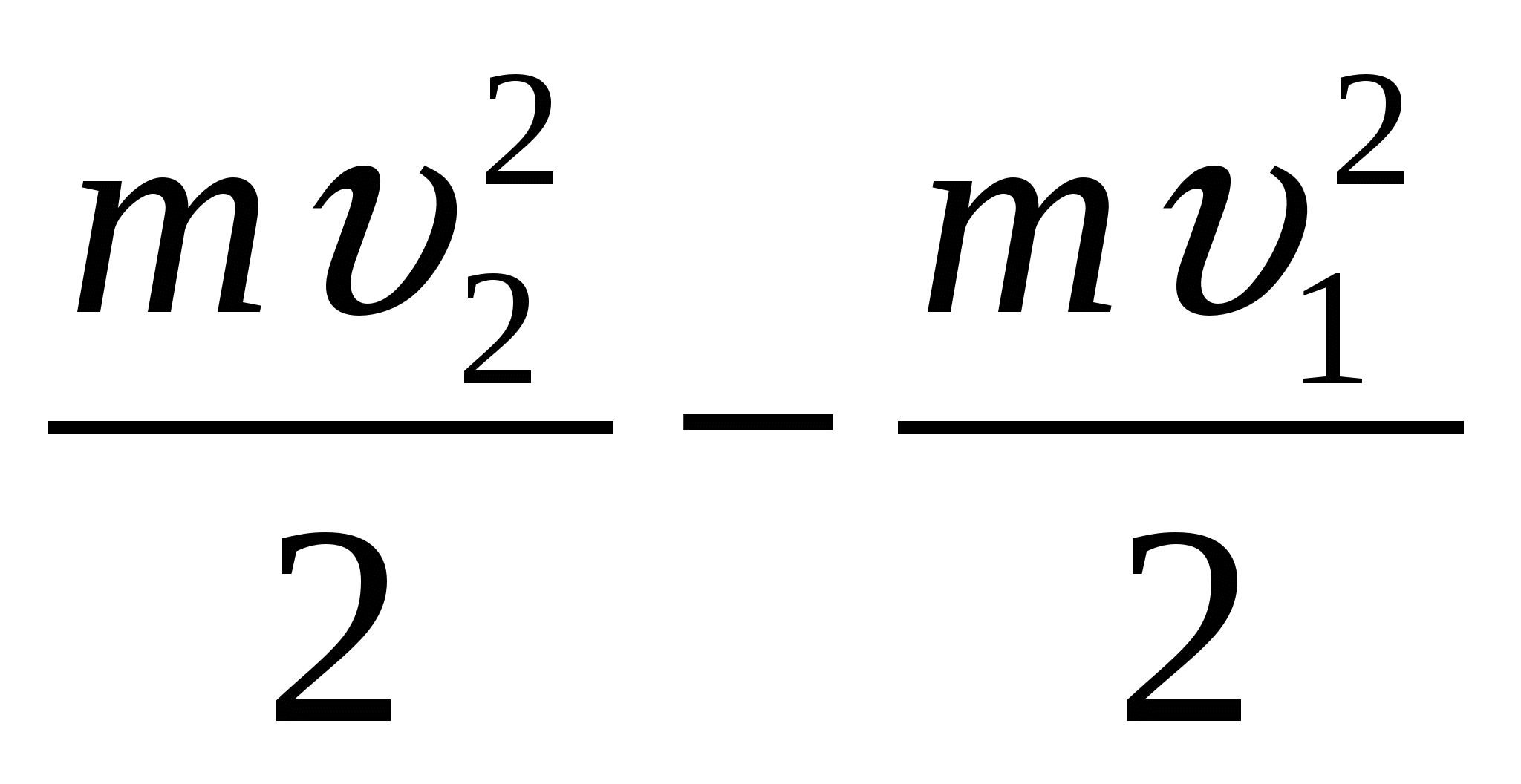 (2). Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
(2). Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией
тела: 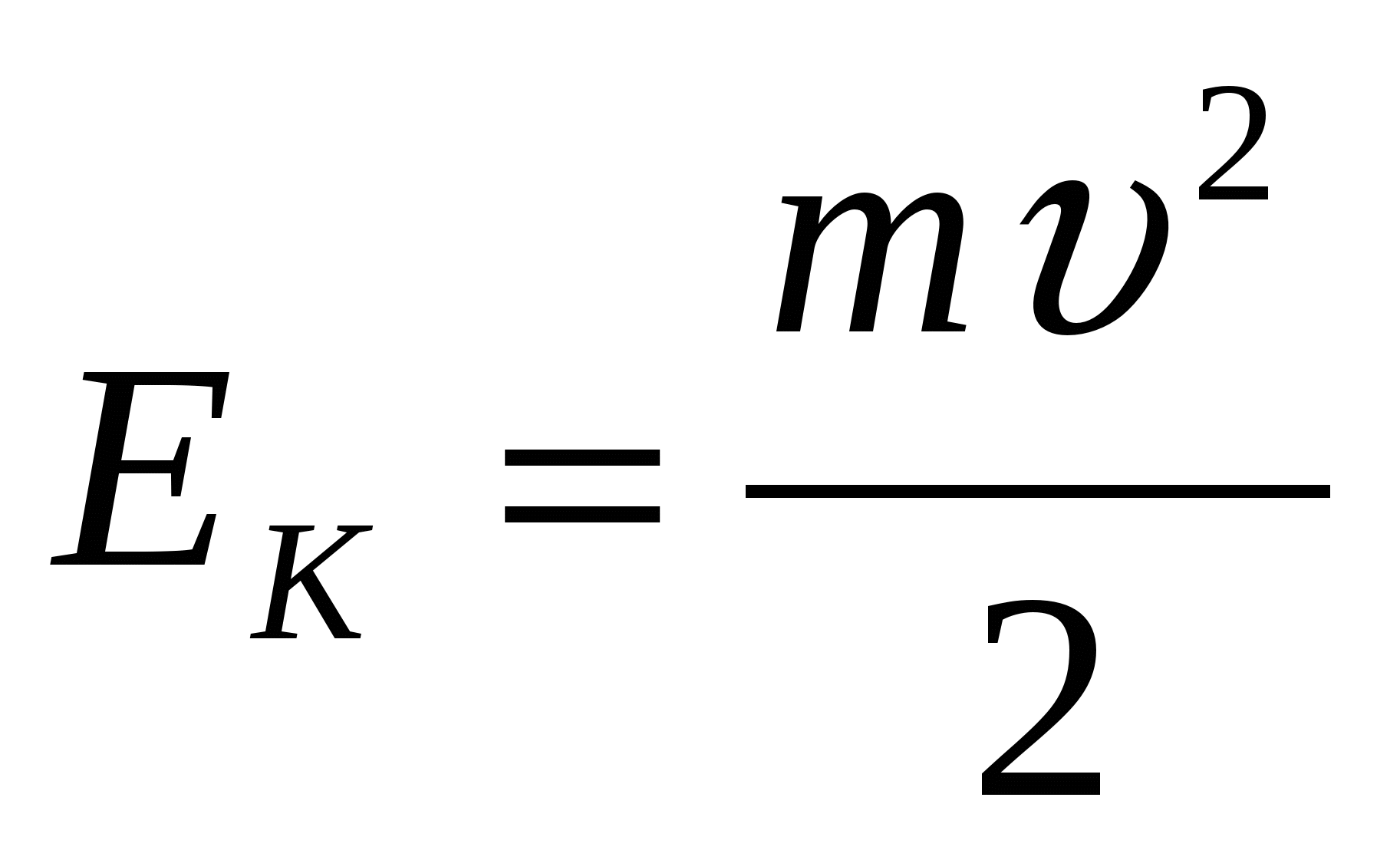 . ^
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии
. Это утверждение соответствующее формуле (2) называют теоремой об изменении кинетической энергии
. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
. ^
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии
. Это утверждение соответствующее формуле (2) называют теоремой об изменении кинетической энергии
. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
К инетическая энергия – это энергия движения. Кинетическая энергия тела массой m
, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:
инетическая энергия – это энергия движения. Кинетическая энергия тела массой m
, движущегося со скоростью равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:  Если тело движется со скоростью то для его полной остановки необходимо совершить работу .
Если тело движется со скоростью то для его полной остановки необходимо совершить работу .
Формулу (1) для вычисления работы силы можно применять только в том случае, если сила – величина постоянная. Работу переменной силы можно найти как площадь фигуры под графиком зависимости силы от перемещения.
Примером силы, модуль которой зависит от координаты, может служить сила упругости пружины, подчиняющаяся закону Гука .
^
12. Работа силы тяжести и силы упругости, потенциальная энергия деформированной пружины (вывод формулы) и тела поднятого над Землей.
В физике наряду с кинетической энергией или энергией движения важную роль играет понятие потенциальной энергии
или энергии взаимодействия тел
.
Потенциальная энергия определяется взаимным положением тел или частей одного и того же тела (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела . Такие силы называются консервативными . Работа консервативных сил на замкнутой траектории равна нулю .
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести 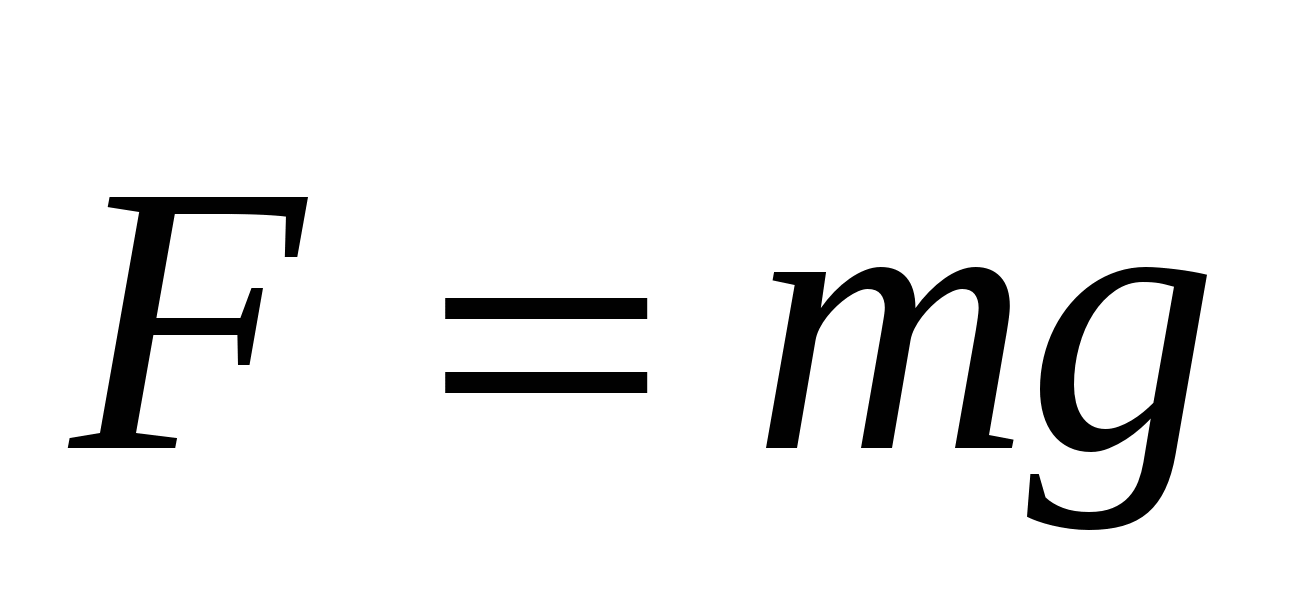 . Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения на ось OY
, направленную вертикально. При подъеме тела вверх сила тяжести совершает отрицательную работу, при спуске - положительную. Если тело переместилось из точки, расположенной на высоте h
1 , в точку, расположенную на высоте h
2 от начала координатной оси OY
то сила тяжести совершила работу A
= –mg
(h
2 – h
1) = –(mgh
2 – mgh
1)
. Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения на ось OY
, направленную вертикально. При подъеме тела вверх сила тяжести совершает отрицательную работу, при спуске - положительную. Если тело переместилось из точки, расположенной на высоте h
1 , в точку, расположенную на высоте h
2 от начала координатной оси OY
то сила тяжести совершила работу A
= –mg
(h
2 – h
1) = –(mgh
2 – mgh
1)
Эта работа равна изменению некоторой физической величины mgh , взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести E р = mgh. Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
^ Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком. A = –(E р2 – E р1)
Потенциальная энергия E р зависит от выбора нулевого уровня, т. е. от выбора начала координат оси OY . Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔE р = E р2 – E р1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
П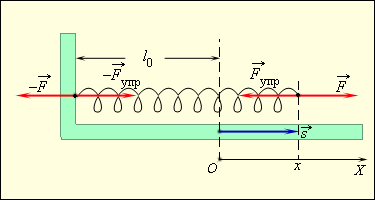 онятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами. Можно просто удлинить пружину на величину x
, или сначала удлинить ее на 2x
, а затем уменьшить удлинение до значения x
и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x
в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A
, взятой с противоположным знаком: где k
– жесткость пружины.
онятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами. Можно просто удлинить пружину на величину x
, или сначала удлинить ее на 2x
, а затем уменьшить удлинение до значения x
и т. д. Во всех этих случаях сила упругости совершает одну и ту же работу, которая зависит только от удлинения пружины x
в конечном состоянии, если первоначально пружина была недеформирована. Эта работа равна работе внешней силы A
, взятой с противоположным знаком: где k
– жесткость пружины.
М одуль силы упругости зависит от координаты. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины. Зависимость модуля внешней силы от координаты x
изображается на графике прямой линией (рис.). По площади треугольника на рис. можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:
одуль силы упругости зависит от координаты. Для того, чтобы растянуть пружину, к ней нужно приложить внешнюю силу модуль которой пропорционален удлинению пружины. Зависимость модуля внешней силы от координаты x
изображается на графике прямой линией (рис.). По площади треугольника на рис. можно определить работу, совершенную внешней силой, приложенной к правому свободному концу пружины:  .
.
Этой же формулой выражается работа, совершенная внешней силой при сжатии пружины. В обоих случаях работа упругой силы равна по модулю работе внешней силы и противоположна ей по знаку.
Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, т. е. сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину Потенциальная энергия упруго деформированного тела
равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. 
Если в начальном состоянии пружина уже была деформирована, а ее удлинение было равно x
1 , тогда при переходе в новое состояние с удлинением x
2 сила упругости совершит работу, равную изменению потенциальной энергии, взятому с противоположным знаком:  . Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
. Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
Свойством консервативности наряду с силой тяжести и силой упругости обладают некоторые другие виды сил, например, сила электростатического взаимодействия между заряженными телами. Сила трения не обладает этим свойством. Работа силы трения зависит от пройденного пути. Понятие потенциальной энергии для силы трения вводить нельзя.
