Definisi 9.3. vektor X ditelepon vektor sendiri matriks TETAPI jika ada nomor seperti itu λ, bahwa persamaan itu berlaku: TETAPI X= λ X, yaitu, hasil penerapan ke X transformasi linier yang diberikan oleh matriks TETAPI, adalah perkalian vektor ini dengan bilangan λ . Nomor itu sendiri λ ditelepon nomor sendiri matriks TETAPI.

Mengganti ke dalam rumus (9.3) x` j = x j , kami memperoleh sistem persamaan untuk menentukan koordinat vektor eigen:

. (9.5)

Sistem homogen linier ini akan memiliki solusi non-trivial hanya jika determinan utamanya adalah 0 (aturan Cramer). Dengan menuliskan kondisi ini dalam bentuk:

kita mendapatkan persamaan untuk menentukan nilai eigen λ ditelepon persamaan karakteristik. Secara singkat dapat digambarkan sebagai berikut:

| A-λE | = 0, (9.6)

karena ruas kirinya adalah determinan matriks A-λE. Polinomial terhadap | A-λE| ditelepon polinomial karakteristik matriks a.

Sifat-sifat polinomial karakteristik:

1) Polinomial karakteristik dari transformasi linier tidak bergantung pada pilihan basis. Bukti. (lihat (9.4)), tetapi Akibatnya, . Dengan demikian, tidak tergantung pada pilihan dasar. Oleh karena itu, dan | A-λE| tidak berubah saat transisi ke basis baru.

2) Jika matriks TETAPI transformasi linier adalah simetris(itu. a ij = a ji), maka semua akar persamaan karakteristik (9.6) adalah bilangan real.

Sifat-sifat nilai eigen dan vektor eigen:

1) Jika kita memilih basis dari vektor eigen x 1, x 2, x 3 sesuai dengan nilai eigen 1 , 2 , 3 matriks TETAPI, maka pada basis ini transformasi linier A memiliki matriks diagonal:

(9.7) Bukti properti ini mengikuti definisi vektor eigen.

2) Jika nilai eigen transformasi TETAPI berbeda, maka vektor eigen yang bersesuaian dengannya bebas linier.

3) Jika polinomial karakteristik dari matriks TETAPI memiliki tiga akar yang berbeda, maka dalam beberapa basis matriks TETAPI memiliki bentuk diagonal.

Mari kita cari nilai eigen dan vektor eigen dari matriks Mari kita buat persamaan karakteristik: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Temukan koordinat vektor eigen yang sesuai dengan setiap nilai yang ditemukan λ. Dari (9.5) berikut bahwa jika X (1) ={x 1 , x 2 , x 3) adalah vektor eigen yang bersesuaian dengan λ 1 = -2, maka

adalah sistem kolaboratif tetapi tidak pasti. Solusinya dapat ditulis sebagai X (1) ={sebuah,0,-sebuah), di mana a adalah bilangan apa saja. Khususnya, jika Anda memerlukan | x (1) |=1, X (1) =

Substitusi ke dalam sistem (9.5) λ 2 =3, kami mendapatkan sistem untuk menentukan koordinat vektor eigen kedua - x (2) ={y1,y2,y3}:

, di mana X (2) ={b,-b,b) atau, asalkan | x (2) |=1, x (2) =

Untuk λ 3 = 6 tentukan vektor eigennya x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) atau dalam versi yang dinormalisasi

x (3) = Dapat dilihat bahwa X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = SM- 2bc + bc= 0. Jadi, vektor eigen dari matriks ini adalah ortogonal berpasangan.

Kuliah 10

Bentuk kuadrat dan hubungannya dengan matriks simetris. Sifat-sifat vektor eigen dan nilai eigen dari matriks simetris. Pengurangan bentuk kuadrat menjadi bentuk kanonik.

Definisi 10.1.bentuk kuadrat variabel nyata x 1, x 2,…, x n polinomial derajat kedua sehubungan dengan variabel-variabel ini disebut, yang tidak mengandung istilah bebas dan istilah derajat pertama.

Contoh bentuk kuadrat:

(n = 2),

(n = 3). (10.1)

Ingat definisi matriks simetris yang diberikan dalam kuliah terakhir:

Definisi 10.2. Matriks persegi disebut simetris, jika , yaitu, jika elemen matriks simetris terhadap diagonal utama adalah sama.

Sifat-sifat nilai eigen dan vektor eigen dari matriks simetris:

1) Semua nilai eigen dari matriks simetris adalah nyata.

Bukti (untuk n = 2).

Biarkan matriks TETAPI seperti: . Mari kita buat persamaan karakteristiknya:

(10.2) Cari diskriminannya:

Oleh karena itu, persamaan hanya memiliki akar real.

2) Vektor eigen dari matriks simetris adalah ortogonal.

Bukti (untuk n= 2).

Koordinat vektor eigen dan harus memenuhi persamaan.

Matriks tipe diagonal paling sederhana disusun. Timbul pertanyaan apakah tidak mungkin menemukan basis di mana matriks operator linier akan memiliki bentuk diagonal. Dasar seperti itu ada.
Biarkan ruang linier R n dan operator linier A yang bekerja di dalamnya diberikan; dalam hal ini, operator A mengambil R n ke dalam dirinya sendiri, yaitu, A:R n → R n .

Definisi. Sebuah vektor bukan nol disebut vektor eigen dari operator A jika operator A diterjemahkan ke dalam vektor collinear untuk itu, yaitu . Bilangan disebut nilai eigen atau nilai eigen dari operator A yang bersesuaian dengan vektor eigen .
Kami mencatat beberapa sifat nilai eigen dan vektor eigen.
1. Setiap kombinasi linear dari vektor eigen dari operator A yang berkorespondensi dengan nilai eigen yang sama adalah vektor eigen dengan nilai eigen yang sama.
2. Vektor eigen operator A dengan nilai eigen berbeda berpasangan 1 , 2 , …, m bebas linier.
3. Jika nilai eigen λ 1 =λ 2 = m = , maka nilai eigen sesuai dengan tidak lebih dari m vektor eigen bebas linier.

Jadi, jika ada n vektor eigen yang bebas linier sesuai dengan nilai eigen yang berbeda λ 1 , 2 , …, n , maka mereka bebas linier, oleh karena itu, mereka dapat diambil sebagai basis ruang R n . Mari kita cari bentuk matriks operator linier A berdasarkan vektor eigennya, di mana kita bertindak dengan operator A berdasarkan vektor dasar: kemudian .
Dengan demikian, matriks operator linier A berdasarkan vektor eigennya memiliki bentuk diagonal, dan nilai eigen operator A berada pada diagonal.
Apakah ada dasar lain di mana matriks memiliki bentuk diagonal? Jawaban atas pertanyaan ini diberikan oleh teorema berikut.

Dalil. Matriks operator linier A pada basis (i = 1..n) berbentuk diagonal jika dan hanya jika semua vektor basis adalah vektor eigen dari operator A.

Aturan untuk mencari nilai eigen dan vektor eigen

Biarkan vektor , di mana x 1 , x 2 , …, x n - koordinat vektor relatif terhadap basis dan merupakan vektor eigen dari operator linier A yang sesuai dengan nilai eigen , yaitu . Relasi ini dapat ditulis dalam bentuk matriks

. (*)

Persamaan (*) dapat dianggap sebagai persamaan untuk mencari , dan , yaitu, kita tertarik pada solusi non-trivial, karena vektor eigen tidak boleh nol. Diketahui bahwa solusi nontrivial dari sistem persamaan linear homogen ada jika dan hanya jika det(A - E) = 0. Jadi, agar menjadi nilai eigen dari operator A, det(A - E perlu dan cukup bahwa det(A - E) ) = 0.
Jika persamaan (*) ditulis secara rinci dalam bentuk koordinat, maka kita mendapatkan sistem persamaan linier homogen:

(1)
di mana adalah matriks dari operator linier.

Sistem (1) memiliki solusi bukan nol jika determinannya D sama dengan nol

Kami mendapat persamaan untuk menemukan nilai eigen.
Persamaan ini disebut persamaan karakteristik, dan ruas kirinya disebut polinomial karakteristik dari matriks (operator) A. Jika polinomial karakteristik tidak memiliki akar real, maka matriks A tidak memiliki vektor eigen dan tidak dapat direduksi menjadi bentuk diagonal.
Misalkan 1 , 2 , …, n adalah akar-akar real dari persamaan karakteristik, dan mungkin ada kelipatan di antara mereka. Mengganti nilai-nilai ini pada gilirannya menjadi sistem (1), kami menemukan vektor eigen.

Contoh 12. Operator linier A bekerja di R 3 sesuai dengan hukum , dimana x 1 , x 2 , .., x n adalah koordinat vektor di basis , , . Temukan nilai eigen dan vektor eigen dari operator ini.
Larutan. Kami membangun matriks operator ini:
.
Kami menyusun sistem untuk menentukan koordinat vektor eigen:

Kami menyusun persamaan karakteristik dan menyelesaikannya:

.
1,2 = -1, 3 = 3.
Mensubstitusikan = -1 ke dalam sistem, kita memperoleh:
atau
Karena , maka ada dua variabel terikat dan satu variabel bebas.
Biarkan x 1 menjadi tidak diketahui gratis, maka Kami memecahkan sistem ini dengan cara apa pun dan menemukan solusi umum dari sistem ini: Sistem dasar solusi terdiri dari satu solusi, karena n - r = 3 - 2 = 1.
Himpunan vektor eigen yang sesuai dengan nilai eigen = -1 memiliki bentuk: , di mana x 1 adalah bilangan apa pun selain nol. Mari kita pilih satu vektor dari himpunan ini, misalnya dengan menetapkan x 1 = 1: .
Dengan argumen yang sama, kami menemukan vektor eigen yang sesuai dengan nilai eigen = 3: .
Dalam ruang R 3 basis terdiri dari tiga vektor bebas linier, tetapi kita hanya memperoleh dua vektor eigen bebas linier, yang darinya basis di R 3 tidak dapat dibentuk. Akibatnya, matriks A dari operator linier tidak dapat direduksi menjadi bentuk diagonal.

Contoh 13 Diberikan matriks .
1. Buktikan bahwa vektor adalah vektor eigen dari matriks A. Temukan nilai eigen yang sesuai dengan vektor eigen ini.
2. Tentukan basis di mana matriks A berbentuk diagonal.
Larutan.
1. Jika , maka adalah vektor eigen

.
Vektor (1, 8, -1) adalah vektor eigen. Nilai eigen = -1.
Matriks memiliki bentuk diagonal pada basis yang terdiri dari vektor eigen. Salah satunya terkenal. Mari kita cari sisanya.
Kami mencari vektor eigen dari sistem:

Persamaan karakteristik: ;
(3 + )[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
1 = -3, 2 = 1, 3 = -1.
Temukan vektor eigen yang sesuai dengan nilai eigen = -3:

Pangkat matriks sistem ini sama dengan dua dan sama dengan jumlah yang tidak diketahui, oleh karena itu sistem ini hanya memiliki solusi nol x 1 = x 3 = 0. x 2 di sini dapat berupa apa saja selain nol, misalnya, x 2 = 1. Jadi, vektor (0 ,1,0) adalah vektor eigen yang bersesuaian dengan = -3. Mari kita periksa:
.
Jika = 1, maka diperoleh sistem
Pangkat matriks adalah dua. Coret persamaan terakhir.
Biarkan x 3 menjadi tidak diketahui gratis. Kemudian x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Dengan asumsi x 3 = 1, kita memiliki (-3,-9,1) - sebuah vektor eigen yang sesuai dengan nilai eigen = 1. Periksa:

.
Karena nilai eigennya nyata dan berbeda, vektor-vektor yang bersesuaian dengannya bebas linier, sehingga dapat diambil sebagai basis dalam R 3 . Jadi, pada dasarnya , , matriks A berbentuk:
.
Tidak setiap matriks dari operator linier A:R n → R n dapat direduksi menjadi bentuk diagonal, karena untuk beberapa operator linier mungkin ada kurang dari n vektor eigen bebas linier. Namun, jika matriksnya simetris, maka tepat m vektor bebas linier berkorespondensi dengan akar persamaan karakteristik multiplisitas m.

Definisi. Matriks simetris adalah matriks persegi di mana elemen-elemen yang simetris terhadap diagonal utama adalah sama, yaitu di mana .
Catatan. 1. Semua nilai eigen dari matriks simetris adalah nyata.
2. Vektor eigen dari matriks simetris yang bersesuaian dengan nilai eigen yang berbeda berpasangan adalah ortogonal.
Sebagai salah satu dari banyak aplikasi peralatan yang dipelajari, kami mempertimbangkan masalah penentuan bentuk kurva orde kedua.

Dengan matriks A, jika ada bilangan l sehingga AX = lX.

Dalam hal ini, nomor l disebut nilai eigen operator (matriks A) yang bersesuaian dengan vektor X.

Dengan kata lain, vektor eigen adalah vektor yang, di bawah aksi operator linier, berubah menjadi vektor collinear, yaitu. kalikan saja dengan beberapa angka. Sebaliknya, vektor yang tidak tepat lebih sulit untuk diubah.

Kami menulis definisi vektor eigen sebagai sistem persamaan:

Mari kita pindahkan semua suku ke ruas kiri:

Sistem terakhir dapat dituliskan dalam bentuk matriks sebagai berikut:

(A - lE)X \u003d O

Sistem yang dihasilkan selalu memiliki solusi nol X = O. Sistem yang semua suku bebasnya sama dengan nol disebut homogen. Jika matriks sistem seperti itu persegi, dan determinannya tidak sama dengan nol, maka menurut rumus Cramer, kita akan selalu mendapatkan solusi unik - nol. Dapat dibuktikan bahwa sistem memiliki solusi bukan-nol jika dan hanya jika determinan matriks ini sama dengan nol, yaitu

|A - lE| = = 0

Persamaan dengan l yang tidak diketahui ini disebut persamaan karakteristik (polinomial karakteristik) matriks A (operator linier).

Dapat dibuktikan bahwa polinomial karakteristik dari operator linier tidak bergantung pada pilihan basis.

Sebagai contoh, mari kita cari nilai eigen dan vektor eigen dari operator linier yang diberikan oleh matriks A = .

Untuk melakukan ini, kami membuat persamaan karakteristik |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; nilai eigen l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

Untuk menemukan vektor eigen, kami memecahkan dua sistem persamaan

(A + 5E) X = O

(A - 7E) X = O

Untuk yang pertama, matriks yang diperluas akan berbentuk

,

dari mana x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, mis. X (1) \u003d (- (2/3) s; s).

Untuk yang kedua, matriks yang diperluas akan berbentuk

,

dari mana x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, mis. X (2) \u003d ((2/3) s 1; s 1).

Jadi, vektor eigen dari operator linier ini adalah semua vektor berbentuk (-(2/3)c; c) dengan nilai eigen (-5) dan semua vektor berbentuk ((2/3)c 1 ; c 1) dengan nilai eigen 7 .

Dapat dibuktikan bahwa matriks operator A pada basis yang terdiri dari vektor-vektor eigennya adalah diagonal dan berbentuk:

,

di mana l adalah nilai eigen dari matriks ini.

Kebalikannya juga benar: jika matriks A pada beberapa basis diagonal, maka semua vektor dari basis ini akan menjadi vektor eigen dari matriks ini.

Dapat juga dibuktikan bahwa jika suatu operator linier memiliki n nilai eigen yang berbeda secara berpasangan, maka vektor eigen yang bersesuaian adalah bebas linier, dan matriks dari operator ini pada basis yang bersesuaian memiliki bentuk diagonal.

Mari kita jelaskan ini dengan contoh sebelumnya. Mari kita ambil nilai tak-nol sembarang c dan c 1 , tetapi sedemikian rupa sehingga vektor X (1) dan X (2) bebas linier, mis. akan membentuk dasar. Misalnya, biarkan c \u003d c 1 \u003d 3, lalu X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Mari kita verifikasi independensi linier dari vektor-vektor ini:

12 0. Dalam basis baru ini, matriks A akan berbentuk A * = .

Untuk memverifikasi ini, kami menggunakan rumus A * = C -1 AC. Mari kita cari C -1 dulu.

C -1 = ;

Bentuk kuadrat

bentuk kuadrat f (x 1, x 2, x n) dari n variabel disebut jumlah, yang setiap sukunya merupakan kuadrat dari salah satu variabel, atau hasil kali dua variabel yang berbeda, diambil dengan koefisien tertentu: f (x 1 , x 2, x n) = (a ij = a ji).

Matriks A, terdiri dari koefisien-koefisien ini, disebut matriks bentuk kuadrat. Selalu simetris matriks (yaitu, matriks simetris tentang diagonal utama, a ij = a ji).

Dalam notasi matriks, bentuk kuadrat memiliki bentuk f(X) = X T AX, di mana

Memang

Sebagai contoh, mari kita tulis bentuk kuadrat dalam bentuk matriks.

Untuk melakukan ini, kami menemukan matriks berbentuk kuadrat. Elemen diagonalnya sama dengan koefisien pada kuadrat variabel, dan elemen lainnya sama dengan setengah dari koefisien yang sesuai dari bentuk kuadrat. Itu sebabnya

Biarkan kolom-matriks variabel X diperoleh dengan transformasi linier tak-degenerasi dari kolom-matriks Y, yaitu. X = CY, di mana C adalah matriks tak-degenerasi orde n. Maka bentuk kuadrat f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Jadi, dengan transformasi linier non-degenerasi C, matriks berbentuk kuadrat berbentuk: A * = C T AC.

Sebagai contoh, mari kita cari bentuk kuadrat f(y 1, y 2) yang diperoleh dari bentuk kuadrat f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 dengan transformasi linier.

Bentuk kuadrat disebut resmi(Memiliki tampilan kanonik) jika semua koefisiennya a ij = 0 untuk i j, mis.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Matriksnya adalah diagonal.

Dalil(buktinya tidak diberikan di sini). Setiap bentuk kuadrat dapat direduksi menjadi bentuk kanonik menggunakan transformasi linier non-degenerasi.

Sebagai contoh, mari kita reduksi ke bentuk kanonik menjadi bentuk kuadrat
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Untuk melakukan ini, pertama-tama pilih kotak penuh untuk variabel x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Sekarang kita pilih kotak penuh untuk variabel x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Kemudian transformasi linier non-degenerasi y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 dan y 3 \u003d x 3 membawa bentuk kuadrat ini ke bentuk kanonik f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Perhatikan bahwa bentuk kanonik dari bentuk kuadrat didefinisikan secara ambigu (bentuk kuadrat yang sama dapat direduksi menjadi bentuk kanonik dengan cara yang berbeda). Namun, bentuk kanonik yang diperoleh dengan berbagai metode memiliki sejumlah sifat umum. Secara khusus, jumlah suku dengan koefisien positif (negatif) dari bentuk kuadrat tidak bergantung pada bagaimana bentuk direduksi menjadi bentuk ini (misalnya, dalam contoh yang dipertimbangkan akan selalu ada dua koefisien negatif dan satu positif). Sifat ini disebut hukum inersia bentuk kuadrat.

Mari kita verifikasi ini dengan mengurangi bentuk kuadrat yang sama ke bentuk kanonik dengan cara yang berbeda. Mari kita mulai transformasi dengan variabel x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, di mana y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6 ) x 3 dan y 3 = x 1 . Di sini, koefisien negatif -3 pada y 1 dan dua koefisien positif 3 dan 2 pada y 2 dan y 3 (dan menggunakan metode lain, kami mendapatkan koefisien negatif (-5) pada y 2 dan dua koefisien positif: 2 pada y 1 dan 1/20 untuk y 3).

Perlu juga diperhatikan bahwa pangkat suatu matriks berbentuk kuadrat, disebut pangkat dari bentuk kuadrat, sama dengan jumlah koefisien bukan-nol dari bentuk kanonik dan tidak berubah dalam transformasi linier.

Bentuk kuadrat f(X) disebut positif (negatif) yakin, jika untuk semua nilai variabel yang tidak serentak sama dengan nol, maka bernilai positif, yaitu f(X) > 0 (negatif, mis.
f(X)< 0).

Misalnya, bentuk kuadrat f 1 (X) \u003d x 1 2 + x 2 2 pasti positif, karena adalah jumlah kuadrat, dan bentuk kuadrat f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 pasti negatif, karena mewakili itu dapat direpresentasikan sebagai f 2 (X) \u003d - (x 1 - x 2) 2.

Dalam kebanyakan situasi praktis, agak lebih sulit untuk menetapkan definisi-tanda dari bentuk kuadrat, jadi salah satu teorema berikut digunakan untuk ini (kami merumuskannya tanpa bukti).

Dalil. Suatu bentuk kuadrat adalah definit positif (negatif) jika dan hanya jika semua nilai eigen matriksnya positif (negatif).

Dalil(Kriteria Sylvester). Suatu bentuk kuadrat adalah definit positif jika dan hanya jika semua minor utama dari matriks bentuk ini adalah positif.

Mayor (sudut) minor Orde ke-k dari matriks A orde ke-n disebut determinan matriks, yang terdiri dari k baris dan kolom pertama matriks A ().

Perhatikan bahwa untuk bentuk kuadrat pasti negatif, tanda-tanda dari minor utama bergantian, dan minor orde pertama harus negatif.

Sebagai contoh, kita periksa bentuk kuadrat f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 untuk definiteness tanda.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Oleh karena itu, bentuk kuadrat adalah definit positif.

Metode 2. Minor utama dari matriks orde pertama A D 1 = a 11 = 2 > 0. Minor utama orde kedua D 2 = = 6 - 4 = 2 > 0. Oleh karena itu, menurut kriteria Sylvester, bentuk kuadrat adalah definit positif.

Kami memeriksa bentuk kuadratik lain untuk kepastian tanda, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metode 1. Mari kita buat matriks berbentuk kuadrat = . Persamaan karakteristik akan memiliki bentuk = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Oleh karena itu, bentuk kuadrat adalah definit negatif.

Metode 2. Minor utama dari matriks orde pertama A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Oleh karena itu, menurut kriteria Sylvester, bentuk kuadratnya pasti negatif (tanda-tanda dari minor utama bergantian, mulai dari minus).

Dan sebagai contoh lain, kami memeriksa bentuk kuadrat f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 untuk kepastian tanda.

Metode 1. Mari kita buat matriks berbentuk kuadrat = . Persamaan karakteristik akan memiliki bentuk = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Salah satu angka ini negatif dan yang lainnya positif. Tanda-tanda nilai eigen berbeda. Oleh karena itu, bentuk kuadrat tidak dapat berupa pasti negatif atau positif, mis. bentuk kuadrat ini tidak tanda-pasti (dapat mengambil nilai dari tanda apa pun).

Metode 2. Minor utama dari matriks orde pertama A D 1 = a 11 = 2 > 0. Minor utama orde kedua D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

SISTEM PERSAMAAN LINIER HOMOGEN

Sistem persamaan linear homogen adalah sistem yang berbentuk

Jelas bahwa dalam kasus ini , karena semua elemen dari salah satu kolom dalam determinan ini sama dengan nol.

Karena yang tidak diketahui ditemukan oleh rumus , maka dalam kasus ketika 0, sistem memiliki solusi nol yang unik x = kamu = z= 0. Namun, dalam banyak masalah, pertanyaan apakah sistem homogen memiliki solusi selain nol merupakan hal yang menarik.

Dalil. Agar sistem persamaan linier homogen memiliki solusi bukan nol, perlu dan cukup bahwa 0.

Jadi, jika determinannya adalah 0, maka sistem tersebut memiliki solusi unik. Jika 0, maka sistem persamaan linear homogen memiliki banyak solusi.

Contoh.

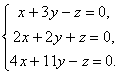
Vektor Eigen dan Matriks Nilai Eigen

Biarkan matriks persegi diberikan , X adalah beberapa kolom matriks yang tingginya bertepatan dengan orde matriks SEBUAH. .

Dalam banyak masalah, kita harus mempertimbangkan persamaan untuk X

dimana adalah suatu bilangan. Jelas bahwa untuk setiap persamaan ini memiliki solusi nol .

Bilangan yang persamaan ini memiliki solusi bukan nol disebut nilai eigen matriks SEBUAH, sebuah X untuk seperti itu disebut vektor sendiri matriks SEBUAH.

Tentukan vektor eigen dari matriks SEBUAH. Karena E∙X=X, maka persamaan matriks dapat ditulis ulang menjadi atau . Dalam bentuk yang diperluas, persamaan ini dapat ditulis ulang sebagai sistem persamaan linier. Betulkah .

Dan maka dari itu

Jadi, kami mendapatkan sistem persamaan linier homogen untuk menentukan koordinat x 1, x2, x 3 vektor X. Agar sistem memiliki solusi bukan-nol, perlu dan cukup bahwa determinan sistem sama dengan nol, yaitu.

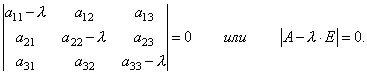
Ini adalah persamaan derajat 3 terhadap . Ini disebut persamaan karakteristik matriks SEBUAH dan berfungsi untuk menentukan nilai eigen .

Setiap nilai eigen sesuai dengan vektor eigen X, yang koordinatnya ditentukan dari sistem pada nilai yang sesuai.

Contoh.

ALJABAR VEKTOR. KONSEP VEKTOR

Saat mempelajari berbagai cabang fisika, ada besaran yang sepenuhnya ditentukan dengan menetapkan nilai numeriknya, misalnya, panjang, luas, massa, suhu, dll. Nilai seperti itu disebut skalar. Namun, selain mereka, ada juga besaran, untuk penentuannya, selain nilai numerik, juga perlu diketahui arahnya di ruang angkasa, misalnya, gaya yang bekerja pada tubuh, kecepatan dan percepatan. tubuh ketika bergerak di ruang angkasa, kekuatan medan magnet pada titik tertentu di ruang angkasa dan lain-lain. Besaran yang demikian disebut besaran vektor.

Mari kita perkenalkan definisi yang ketat.

Segmen terarah Mari kita sebut segmen, relatif terhadap ujung yang diketahui yang mana yang pertama dan mana yang kedua.

vektor segmen terarah disebut, memiliki panjang tertentu, mis. Ini adalah segmen dengan panjang tertentu, di mana salah satu titik yang membatasinya diambil sebagai awal, dan yang kedua - sebagai akhir. Jika sebuah SEBUAH adalah awal dari vektor, B adalah ujungnya, maka vektor dilambangkan dengan simbol, selain itu vektor sering dilambangkan dengan satu huruf . Pada gambar, vektor ditunjukkan oleh segmen, dan arahnya oleh panah.

modul atau panjangnya vektor disebut panjang segmen berarah yang mendefinisikannya. Dilambangkan dengan || atau ||.

Yang disebut vektor nol, yang awal dan akhirnya bertepatan, juga akan disebut sebagai vektor. Hal ini ditandai. Vektor nol tidak memiliki arah yang pasti dan modulusnya sama dengan nol ||=0.

Vektor dan disebut kolinear jika mereka terletak pada garis yang sama atau pada garis paralel. Dalam hal ini, jika vektor dan sama-sama diarahkan, kita akan menulis , sebaliknya.

Vektor yang terletak pada garis lurus yang sejajar dengan bidang yang sama disebut sebidang.

Dua vektor dan disebut setara jika mereka segaris, memiliki arah yang sama, dan sama panjang. Dalam hal ini, tulis .

Dari definisi kesetaraan vektor, sebuah vektor dapat dipindahkan sejajar dengan dirinya sendiri dengan menempatkan titik asalnya di sembarang titik dalam ruang.

Sebagai contoh.

OPERASI LINEAR PADA VEKTOR

1. Mengalikan vektor dengan angka.

   Hasil kali vektor dengan bilangan adalah vektor baru sedemikian sehingga:

   Hasil kali vektor dan bilangan dilambangkan dengan .

   

   Sebagai contoh, adalah vektor yang arahnya sama dengan vektor dan memiliki panjang setengah dari vektor .

   Operasi yang dimasukkan memiliki yang berikut: properti:

2. Penambahan vektor.

   Membiarkan dan menjadi dua vektor sewenang-wenang. Ambil titik sewenang-wenang HAI dan membangun sebuah vektor. Setelah itu, dari titik SEBUAH menyisihkan vektor. Vektor yang menghubungkan awal vektor pertama dengan akhir vektor kedua disebut jumlah dari vektor-vektor ini dan dilambangkan .

   

   Rumusan definisi penjumlahan vektor disebut aturan jajaran genjang, karena jumlah vektor yang sama dapat diperoleh sebagai berikut. Sisihkan dari intinya HAI vektor dan . Bangun jajar genjang pada vektor-vektor ini OABC. Karena vektor , maka vektor , yang merupakan diagonal jajaran genjang yang ditarik dari titik HAI, jelas akan menjadi jumlah vektor .

   

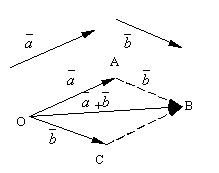
   Sangat mudah untuk memeriksa berikut ini sifat penjumlahan vektor.

3. Perbedaan vektor.

   Suatu vektor yang collinear terhadap suatu vektor yang sama panjang dan berlawanan arah disebut di depan vektor untuk vektor dan dilambangkan dengan . Vektor yang berlawanan dapat dianggap sebagai hasil perkalian vektor dengan bilangan = -1: .