Gambarlah poligon di atas kertas kotak-kotak. Misalnya seperti yang ditunjukkan pada Gambar 1.

Mari kita coba menghitung luasnya sekarang. Bagaimana cara melakukannya? Mungkin cara termudah adalah memecahnya menjadi segitiga siku-siku dan persegi panjang, yang luasnya sudah mudah dihitung dan dijumlahkan hasilnya. Metode yang saya gunakan sederhana, tetapi sangat rumit, dan selain itu, tidak cocok untuk semua poligon.

Pertimbangkan poligon bilangan bulat sederhana non-degenerasi (yaitu, terhubung - dua titiknya dapat dihubungkan oleh kurva kontinu yang seluruhnya terkandung di dalamnya, dan semua simpulnya memiliki koordinat bilangan bulat, batasnya adalah polyline terhubung tanpa persimpangan sendiri, dan memiliki bujur sangkar yang tidak nol). Untuk menghitung luas poligon semacam itu, Anda dapat menggunakan teorema berikut:

teorema Pick. Membiarkan menjadi jumlah titik integer di dalam poligon, menjadi jumlah titik integer pada batasnya, dan menjadi luasnya. Kemudian rumus pilih:

Contoh. Untuk poligon pada Gambar 1 (titik kuning), (titik biru, jangan lupa simpulnya!), jadi satuan persegi.

Bukti teorema Pick. Pertama, perhatikan bahwa rumus Pick benar untuk kuadrat satuan. Memang, dalam hal ini kita memiliki

Pertimbangkan sebuah persegi panjang dengan sisi-sisi yang terletak pada garis kisi. Biarkan panjang sisinya sama dengan dan. Kami memiliki dalam kasus ini dan, menurut rumus Pick,

Pertimbangkan sekarang segitiga siku-siku dengan kaki terletak pada sumbu koordinat. Segitiga seperti itu diperoleh dari persegi panjang dengan sisi dan, dipertimbangkan dalam kasus sebelumnya, dengan memotongnya secara diagonal. Biarkan titik-titik bilangan bulat terletak pada diagonal. Kemudian untuk kasus ini kita mendapatkan itu

Sekarang perhatikan segitiga sembarang. Ini dapat diperoleh dengan memotong beberapa segitiga siku-siku dan, mungkin, persegi panjang dari persegi panjang (lihat gambar 2 dan 3). Karena rumus Pick benar untuk persegi panjang dan segitiga siku-siku, kita mendapatkan bahwa itu juga berlaku untuk segitiga sembarang.

Tetap mengambil langkah terakhir: pindah dari segitiga ke poligon. Poligon apa pun dapat dibagi menjadi segitiga (misalnya, dengan diagonal). Oleh karena itu, kita hanya perlu membuktikan bahwa ketika menambahkan segitiga apa pun ke poligon arbitrer, rumus Pick tetap benar.

Biarkan poligon dan segitiga memiliki sisi yang sama. Asumsikan bahwa rumus Pick berlaku untuk, dan kami akan membuktikan bahwa itu juga benar untuk poligon yang diperoleh dari penjumlahan. Karena dan memiliki sisi yang sama, semua titik bilangan bulat yang terletak di sisi ini, kecuali dua simpul, menjadi titik interior poligon baru. Simpul akan menjadi titik batas. Mari kita tunjukkan jumlah titik yang sama dengan dan dapatkan

Jumlah titik integer interior poligon baru,

Jumlah titik batas untuk poligon baru.

Dari persamaan tersebut kita peroleh

Karena kita mengasumsikan bahwa teorema ini benar untuk dan untuk secara terpisah, maka

Dengan demikian, rumus Pick terbukti.

Rumus ini ditemukan oleh ahli matematika Austria Peak Georg Aleksandrov (1859 – 1943) pada tahun 1899. Selain rumus ini, Georg Pick menemukan teorema Pick, Pick - Julia, Pick - Nevalina, membuktikan ketidaksetaraan Schwarz - Pick. PADA Lampiran 1 Anda dapat melihat tugas non-standar yang telah saya pertimbangkan untuk menerapkan rumus Pick.

Formula Puncak

1. Perkenalan

2. Rumus puncak. Bukti I

Bukti II.

Bukti dari Sh.

3. Tugas.

4. Rumus luas poligon ditinjau dari koordinat titik-titiknya.

5. Tugas.

6. Sastra

rumus puncak.

1. Perkenalan.

Kami menarik kebijaksanaan dari sejarah,

dalam puisi - kecerdasan,

dalam matematika - wawasan.

F. Daging babi asap

Plot akan terungkap pada selembar kertas kotak-kotak biasa.

Garis di sepanjang sisi sel membentuk kisi, dan simpul sel adalah simpul dari kisi ini. Mari menggambar poligon pada lembar dengan simpul di simpul dan menemukan areanya.

Anda dapat mencarinya dengan berbagai cara. Misalnya, Anda dapat memotong poligon menjadi bentuk yang cukup sederhana, menemukan areanya, dan menjumlahkannya.

Tapi di sini kita berada dalam banyak masalah. Sosok itu mudah dipecah menjadi persegi panjang, trapesium, dan segitiga, dan luasnya dihitung dengan mudah.

Meskipun poligon terlihat cukup sederhana, akan membutuhkan banyak usaha untuk menghitung luasnya. Bagaimana jika poligon terlihat lebih menarik? Ternyata area poligon yang simpulnya terletak di simpul kisi dapat dihitung lebih sederhana: ada rumus yang menghubungkan luasnya dengan jumlah simpul yang terletak di dalam dan di perbatasan poligon. Rumus yang luar biasa dan sederhana ini disebut rumus Pick.

2. Rumus puncak.

Simpul poligon (tidak harus cembung) terletak di simpul kisi bilangan bulat. Di dalamnya terletak B node dari kisi, dan di perbatasan node G. Mari kita buktikan bahwa luasnya adalah B + – 1 (rumus Puncak).

Bukti I

Pertimbangkan poligon yang simpulnya berada di simpul kisi bilangan bulat, yaitu, mereka memiliki koordinat bilangan bulat.

Kami membagi poligon menjadi segitiga dengan simpul di simpul kisi, yang tidak mengandung simpul baik di dalam maupun di samping.

Menunjukkan:

n adalah jumlah sisi poligon,

m adalah jumlah segitiga dengan simpul pada simpul kisi yang tidak mengandung simpul baik di dalam maupun di samping,

B adalah jumlah node di dalam poligon,

adalah jumlah simpul di sisi, termasuk simpul.

Luas semua segitiga ini sama dan sama.

Jadi, luas poligon adalah
.

180 0 m .

Sekarang mari kita cari jumlah ini dengan cara yang berbeda.

Jumlah sudut dengan simpul pada setiap simpul internal adalah 360 0 .

Maka jumlah sudut dengan simpul di semua simpul internal sama dengan 360 0 V.

Jumlah total sudut pada simpul di sisi, tetapi tidak di simpul, adalah 180 0 (G - n).

Jumlah sudut pada titik sudut poligon adalah 180 0 ( n – 2) .

Jumlah sudut semua segitiga adalah 360 0 V + 180 0 (G - n) + 180 0 (n – 2).

jadi 180 0 m\u003d 360 0 V + 180 0 (G - n) + 180 0 (n – 2),

180 0 m\u003d 360 0 V + 180 0 G - 180 0 n + 180 0 n– 180 0 2,

180 0 m\u003d 360 0 V + 180 0 G– 360 0,

= B + – 1 ,

dari mana kita memperoleh ekspresi untuk luas S poligon:

S= B + – 1 ,

dikenal sebagai rumus Pick.

Pada gambar: V = 24, D = 9, oleh karena itu,S = 24 + – 1 = 27,5.

Temukan luas poligon pertama menggunakan rumus Puncak:

B = 28 (titik hijau);

D = 20 (titik biru).

Kita dapatkan, S =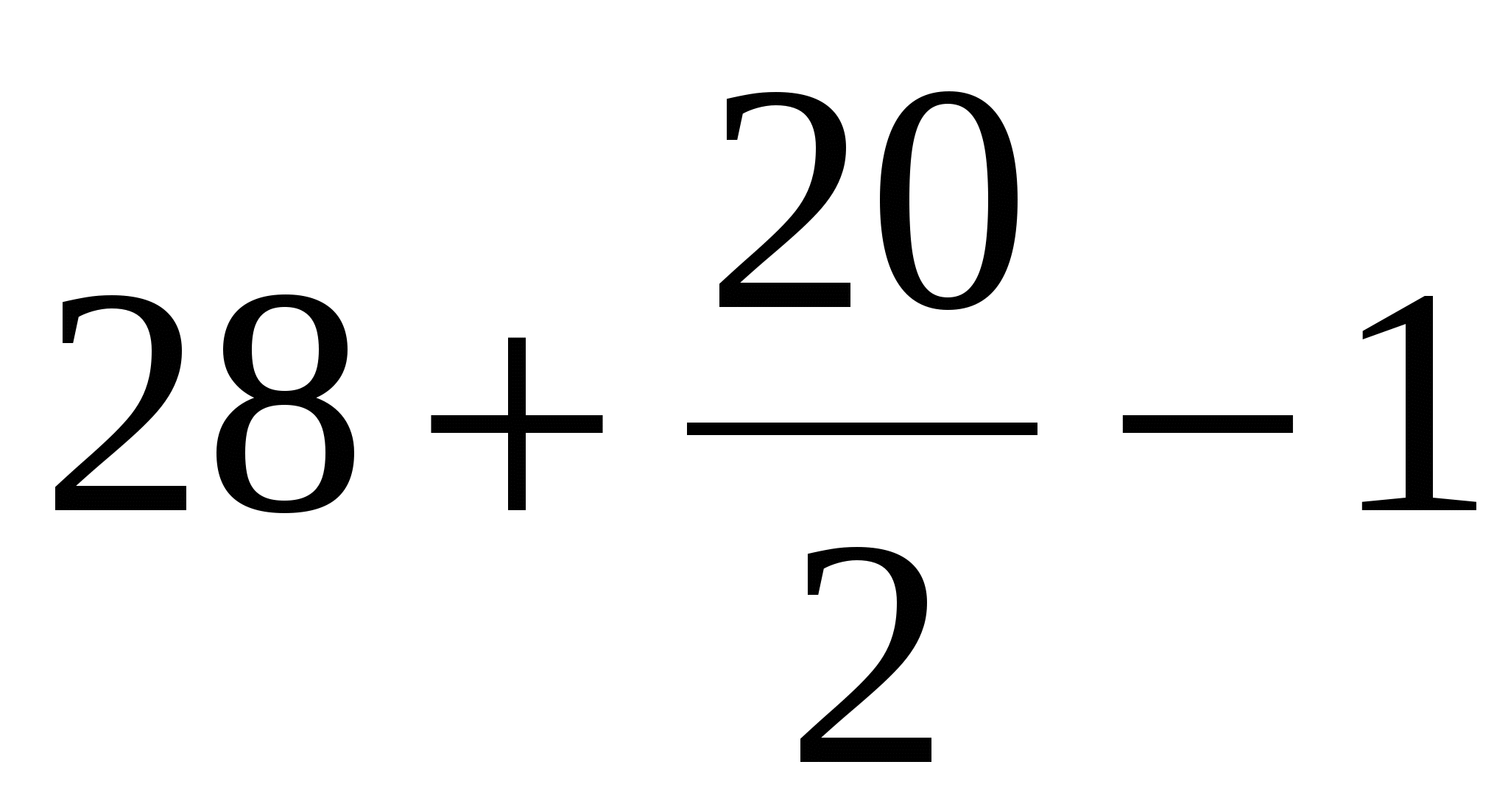
= 37 satuan persegi

Bukti II.

Untuk setiap poligon M dengan simpul-simpul pada simpul-simpul kisi bilangan bulat, kami menetapkan bilangan f (M) =
, di mana penjumlahan adalah semua simpul kisi milik M, dan sudut didefinisikan sebagai berikut: =
untuk titik interior poligon, =
untuk titik batas selain titik, dan – sudut pada simpul, jika simpul yang diberikan adalah simpul. Sangat mudah untuk melihat bahwa f (M) =
+
= B + – 1. Tetap memeriksa apakah angka f (M) sama dengan luas poligon M.

Biarkan poligon M dipotong menjadi poligon M 1 dan M 2 dengan simpul di simpul kisi. Maka f(M) = f(M 1) + f(M 2), karena untuk setiap simpul sudutnya bertambah. Oleh karena itu, jika rumus Pick benar untuk dua poligon M, M 1 dan M 2, maka ini juga benar untuk poligon ketiga.

Jika M adalah persegi panjang dengan sisi p dan q, diarahkan sepanjang garis kisi, maka

f (M) = (p – 1)(q – 1) +
= pq.

Dalam hal ini, rumus Pick adalah valid. Dengan memotong persegi panjang M secara diagonal menjadi segitiga M 1 dan M 2 dan menggunakan fakta bahwa f (M) = f (M 1) + f (M 2) dan f (M 1) = f (M 2), mudah untuk membuktikan validitas rumus Pick untuk setiap segitiga siku-siku dengan kaki yang diarahkan sepanjang garis kisi. Dengan memotong beberapa segitiga seperti itu dari persegi panjang, segitiga apa pun dapat diperoleh.

Untuk melengkapi pembuktian rumus Pick, perlu diperhatikan bahwa poligon apa pun dapat dipotong menjadi segitiga dengan diagonal yang tidak berpotongan.

Bukti dari Sh.

Hubungan antara luas gambar dan jumlah simpul yang termasuk dalam gambar ini sangat jelas dalam kasus persegi panjang.

Membiarkan ABCD- persegi panjang dengan simpul di simpul dan sisi sepanjang garis kisi.

Dilambangkan dengan PADA jumlah node yang terletak di dalam persegi panjang, dan melalui G adalah jumlah node pada batasnya. Pindahkan kisi setengah sel ke kanan dan setengah sel ke bawah.

Kemudian wilayah persegi panjang dapat "didistribusikan" antara node sebagai berikut: masing-masing dari PADA node "mengontrol" seluruh sel dari grid yang digeser, masing-masing dari G- 4 node batas non-sudut - setengah dari sel, dan masing-masing titik sudut - seperempat sel. Jadi, luas persegi panjang S adalah

Jadi, untuk persegi panjang dengan simpul di simpul dan sisi sepanjang garis kisi, kami telah menetapkan rumus:

Mari kita buktikan bahwa rumus ini benar tidak hanya untuk persegi panjang, tetapi juga untuk poligon arbitrer dengan simpul di simpul kisi.

Dilambangkan dengan S m daerah poligonM dengan simpul pada simpul, dan melaluiP m - nilai
, di manaPADA m adalah jumlah node di dalamM, sebuah G m adalah jumlah node pada batas. Maka rumus Pick dapat ditulis sebagai
.

Kami membagi bukti rumus menjadi beberapa langkah.

Langkah 1.

Jika poligonM dengan simpul di simpul grid dipotong menjadi 2 poligonM 1 dan M 2 , juga memiliki simpul hanya pada node grid, maka
. Biarkan poligonM dipotong menjadi poligonM 1 dan M 2 dengan simpul di simpul oleh segmen AB. Semua node, kecuali yang jatuh pada segmenAB, memberikan kontribusi yang sama pada ruas kiri dan kanan rumus. Pertimbangkan node yang terletak pada segmen AB.

Jika simpul tersebut terletak di antara A dan B (misalnya, C), maka untuk poligonM itu internal, dan untuk poligonM 1 dan M 2 - batas. Oleh karena itu, kontribusinya untukP m sama dengan 1, dan di setiap ekspresi
dan
– 0,5 masing-masing, yaitu kontribusi dari simpul tersebut keP m dan
adalah sama.

Pertimbangkan node A dan B. Mereka adalah batas keduanya untuk M, dan untuk M 1 , M 2 .

Oleh karena itu, kontribusi masing-masing node ini untukP m adalah 0,5 a
- satuan. Ini berarti bahwa kontribusi total node A dan B terhadapP m sama dengan 1, yaitu 1 lebih kecil dari kontribusinya terhadap
. Tetapi
, sebuah .

Dari total "kontribusi" semua node P m 1 dikurangi dari
2 dikurangi, dan ini mengkompensasi perbedaan kontribusi node A dan B.

Jadi,
.

Langkah 2

Jika poligon M dengan simpul di node grid dipotong menjadi dua poligon M 1 dan M 2 (juga dengan simpul di simpul) dan rumusnya benar untuk beberapa dua poligon MM 1 , M 2 , maka itu juga berlaku untuk poligon ketiga.

Mari, misalnya, itu benar untukM 1 dan M 2 , itu adalah
. Kemudian (pada langkah pertama), tapi pada langkah pertama), ekspresi terakhir sama denganP m , dan kesetaraan
dan ada rumus Pick.

Langkah 3

Mari kita buktikan rumus Pick untuk segitiga siku-siku dengan simpul di simpul kisi dan kaki terletak di garis kisi.

Segi tiga ABC bangun persegi panjang ABCD .

Untuk persegi panjang, rumus Pick benar: S ABCD = P ABCD . Menurut langkah pertama P ABCD = P ABC + P ACD , P ABC = P ACD , jadi P ABCD = 2P ABC . Tetapi S ABCD = 2 S ABC . Itu sebabnya S ABC = P ABC .

Langkah 4

Rumus Pick benar untuk segitiga arbitrer dengan simpul di node grid.

Setelah memeriksa gambarnya, mudah untuk memahami: segitiga apa pun dapat diperoleh dengan "memotong" dari beberapa persegi panjang dengan sisi-sisi yang membentang di sepanjang garis kisi, beberapa persegi panjang dan segitiga siku-siku dengan kaki pada garis kisi. Dan karena rumus Pick benar untuk persegi panjang dan segitiga siku-siku, maka (ingat langkah 2) juga berlaku untuk segitiga aslinya.

Kami telah membuktikan bahwa jika poligon dapat dipotong menjadi segitiga dengan simpul di simpul grid, maka rumus Pick benar untuk itu.

3. Tugas.

Hitunglah luas bangun-bangun tersebut:

1
.

B=9

G = 4

B=9

G = 5

Menghitung luas suatu bangun.

Pilih Metode

Karya seorang siswa kelas 5B MBOU sekolah menengah No. 23 di Irkutsk

Balsukova Alexandra

Ketua: Khodyreva T.G.

2014

Menghitung luas suatu bangun. Pilih Metode

Objek studi : tugas di atas kertas kotak-kotak

Subyek studi : masalah untuk menghitung luas poligon pada kertas kotak-kotak, metode dan teknik untuk menyelesaikannya.

Metode penelitian Kata kunci: perbandingan, generalisasi, analogi, studi literatur dan sumber internet, analisis informasi.

Tujuan studi:

pilih informasi utama, menarik, dan dapat dipahami

Menganalisis dan mengatur informasi yang diterima

Temukan berbagai metode dan teknik untuk memecahkan masalah pada kertas kotak-kotak

periksa rumus untuk menghitung luas bentuk geometris menggunakan rumus Puncak

Buat presentasi elektronik dari karya untuk mempresentasikan materi yang dikumpulkan

Geometri adalah alat yang paling ampuh untuk menyempurnakan kemampuan mental kita dan memungkinkan kita untuk berpikir dan bernalar dengan benar.

(G. Galileo)

Relevansi topik

Gairah untuk matematika sering dimulai dengan memikirkan suatu masalah. Jadi, ketika mempelajari topik "Area poligon", muncul pertanyaan apakah ada tugas yang berbeda dari tugas yang dipertimbangkan dalam buku teks. Tugas-tugas tersebut termasuk tugas-tugas di atas kertas kotak-kotak. Apa kekhasan masalah seperti itu, apakah ada metode dan teknik khusus untuk memecahkan masalah di atas kertas kotak-kotak. Di kelas matematika, guru memperkenalkan kami pada metode yang menarik untuk menghitung poligon. Saya mulai mempelajari literatur, sumber daya Internet tentang topik ini. Tampaknya hal-hal menarik dapat ditemukan di bidang kotak-kotak, yaitu, di selembar kertas tak berujung, berjajar ke dalam kotak yang identik. Ternyata tugas yang terkait dengan kertas kotak-kotak cukup beragam. Saya belajar bagaimana menghitung luas poligon yang digambar pada selembar kertas kotak-kotak. Untuk banyak tugas di atas kertas dalam sangkar tidak ada aturan umum untuk penyelesaian, metode dan teknik khusus. Ini adalah properti mereka yang menentukan nilainya untuk pengembangan bukan keterampilan atau keterampilan pendidikan tertentu, tetapi secara umum kemampuan untuk berpikir, merenungkan, menganalisis, mencari analogi, yaitu tugas-tugas ini mengembangkan keterampilan berpikir dalam arti luas.

Dan saya juga belajar bahwa tugas-tugas seperti itu dipertimbangkan dalam kontrol dan pengukuran bahan GIA dan Unified State Examination. Oleh karena itu, saya menganggap studi materi ini berguna untuk penerapannya tidak hanya dalam proses pendidikan lebih lanjut, tetapi juga untuk memecahkan masalah Olimpiade yang tidak standar.

2.Konsep wilayah

Kotak- karakteristik numerik dari sosok geometris dua dimensi, yang menunjukkan ukuran gambar ini. Secara historis, perhitungan luas disebut . Suatu bangun yang memiliki luas disebut mengkuadratkan .

Luas bangun datar dalam hal geometri

1. Kotak- ukuran bangun datar dalam kaitannya dengan gambar standar, yang merupakan persegi dengan sisi sama dengan satu panjang.

2. Kotak- karakteristik numerik yang dikaitkan dengan angka datar dari kelas tertentu (misalnya, poligon). Luas persegi dengan sisi sama dengan satuan panjang, diambil sama dengan satuan luas

3. Kotak- nilai positif, nilai numerik yang memiliki sifat-sifat berikut:

 Angka yang sama memiliki luas yang sama;

 Jika suatu bangun dibagi menjadi bagian-bagian yang merupakan bangun sederhana (yaitu, yang dapat dibagi menjadi sejumlah segitiga datar yang terbatas), maka luas gambar ini sama dengan jumlah luasnya bagian;

 Luas persegi dengan sisi sama dengan satuan ukuran sama dengan satu.

Dengan demikian, kita dapat menyimpulkan bahwa luas bukanlah nilai tertentu, tetapi hanya memberikan beberapa karakteristik kondisional dari bangun datar. Untuk menemukan luas angka sewenang-wenang, perlu untuk menentukan berapa banyak kotak dengan sisi yang sama dengan satu panjang yang dikandungnya. Sebagai contoh, mari kita ambil persegi panjang di mana satu sentimeter persegi cocok tepat 6 kali. Artinya luas persegi panjang tersebut adalah 6 cm2.

Pemilihan luas bujur sangkar dengan sisi yang sama dengan satuan ukuran sebagai satuan minimum pengukuran untuk semua luas bukanlah suatu kebetulan. Ini adalah hasil kesepakatan antara orang-orang yang muncul dalam proses seleksi "alami" berabad-abad. Selain itu, ada usulan lain untuk satuan ukuran. Jadi, misalnya, diusulkan untuk mengambil luas segitiga sama sisi sebagai unit (yaitu, setiap angka datar dapat direpresentasikan sebagai "jumlah" dari sejumlah segitiga sama sisi), yang akan mengarah ke perubahan dalam representasi numerik daerah.

Dengan demikian, rumus untuk menghitung luas muncul dalam matematika dan tidak segera disadari oleh seseorang - ini banyak ilmuwan yang hidup di era yang berbeda dan negara yang berbeda. (Formula yang salah tidak mendapat tempat dalam sains dan terlupakan). Rumus-rumus yang benar dilengkapi, dikoreksi, dan dibuktikan selama ribuan tahun, hingga mencapai kita dalam bentuk modernnya.

Tentu saja pengukuran luas terdiri dari membandingkan luas gambar yang diberikan dengan luas gambar yang diambil sebagai unit pengukuran. Sebagai hasil perbandingan, diperoleh angka tertentu - nilai numerik dari luas gambar yang diberikan. Angka ini menunjukkan berapa kali luas suatu bangun tertentu lebih besar (atau lebih kecil) dari luas bangun tersebut, yang diambil sebagai satuan luas.

T Dengan demikian, kita dapat menyimpulkan bahwa luas adalah besaran buatan, yang secara historis diperkenalkan oleh manusia untuk mengukur beberapa properti dari bangun datar. Kebutuhan untuk memasukkan nilai seperti itu disebabkan oleh meningkatnya kebutuhan untuk mengetahui seberapa besar wilayah ini atau itu, berapa banyak biji-bijian yang dibutuhkan untuk menabur ladang atau menghitung luas permukaan lantai untuk mendekorasi ubin hias.

Formula Puncak

Untuk memperkirakan luas poligon pada kertas kotak-kotak, cukup menghitung berapa banyak sel yang dicakup oleh poligon ini (kami mengambil luas sel sebagai satu kesatuan). Lebih tepatnya, jikaS adalah luas poligon, B adalah jumlah sel yang terletak seluruhnya di dalam poligon, dan G adalah jumlah sel yang memiliki interior. Kami hanya akan mempertimbangkan poligon seperti itu, semua simpulnya terletak di simpul kertas kotak-kotak - di mana garis kisi poligon berpotongan setidaknya satu titik yang sama.

Luas segitiga apa pun yang digambar di atas kertas kotak-kotak dapat dengan mudah dihitung dengan menyatakannya sebagai jumlah atau selisih luas segitiga siku-siku dan persegi panjang yang sisi-sisinya mengikuti garis kisi-kisi yang melewati titik sudut segitiga yang digambar.

Untuk menghitung luas poligon semacam itu, Anda dapat menggunakan teorema berikut:

Dalil . Membiarkan - jumlah titik integer di dalam poligon, - jumlah titik integer pada batasnya, - daerahnya. Kemudianrumus pilih:

Contoh. Untuk poligon pada gambarL = 7 (titik merah), 9 (titik hijau), jadiS = 7+ 9/2 -1 = 10,5 satuan persegi.

Teorema Pick- hasil klasik dan .

Luas segitiga dengan simpul di simpul dan tidak mengandung simpul baik di dalam maupun di sisi (kecuali simpul) sama dengan 1/2. Fakta ini.

3. Sejarah

Rumus Pick ditemukan oleh matematikawan Austria Georg Alexander (1859-1942) di . Pada usia 16 tahun, Georg menyelesaikan sekolah dan masuk. Pada usia 20 ia menerima hak untuk mengajar fisika dan matematika. Pada tahun 1884 Peak pergi ke ke . Di sana dia bertemu dengan murid lain dari Klein,. Kemudian, pada tahun 1885, ia kembali kedi mana ia menghabiskan sisa karir ilmiahnya.

Georg Pick berteman dengan Einstein. Pick dan Einstein tidak hanya berbagi minat ilmiah, tetapi juga menyukai musik. Pick, yang bermain dalam kuartet yang terdiri dari profesor universitas, memperkenalkan Einstein kepada masyarakat ilmiah dan musik di Praha.

Lingkaran minat matematika Peak sangat luas. Secara khusus, ia memiliki lebih dari 50 karya ilmiah. Teorema Pick, yang ditemukan olehnya pada tahun 1899, dikenal luas untuk menghitung luas poligon. Di Jerman, teorema ini termasuk dalam buku pelajaran sekolah.

4.Aplikasi dari rumus Pick

Rumus Pick digunakan tidak hanya untuk menghitung luas poligon, tetapi juga untuk memecahkan banyak masalah pada level Olympiad.

Beberapa contoh penggunaan rumus Pick saat menyelesaikan masalah:

1) Raja catur berkeliling papan 8 × 8 sel, setelah mengunjungi masing-masing

lapangan rumah tepat sekali dan dengan langkah terakhir kembali ke aslinya

bidang. Garis putus-putus yang menghubungkan secara seri pusat-pusat bidang yang

raja berlalu, tidak memiliki persimpangan sendiri. Daerah mana yang bisa?

batasi garis putus-putus ini? (Sisi sel adalah 1.)

Segera mengikuti dari rumus Pick bahwa area yang dibatasi oleh lo-

mana adalah 64/2 1 = 31; di sini simpul kisi adalah pusat 64

bidang dan, dengan asumsi, mereka semua terletak pada batas poligon. Jadi

Jadi, meskipun ada cukup banyak "lintasan" raja seperti itu, tetapi semuanya

batas poligon dengan luas yang sama.

Tugas dari bahan kontrol dan pengukuran GIA dan Unified State Examination

Tugas B3

Temukan luas gambar yang digambarkan pada kertas kotak-kotak dengan ukuran sel 1 cm 1 cm (lihat Gambar). Berikan jawaban Anda dalam sentimeter persegi.

4. Kesimpulan

Dalam proses penelitian, saya mempelajari referensi, literatur sains populer. Saya mengetahui bahwa masalah menemukan luas poligon dengan simpul di simpul kisi menginspirasi matematikawan Austria Pick pada tahun 1899 untuk membuktikan formula Pick yang luar biasa.

Sebagai hasil dari pekerjaan saya, saya memperluas pengetahuan saya tentang pemecahan masalah di atas kertas kotak-kotak, menentukan sendiri klasifikasi masalah yang sedang dipelajari, dan menjadi yakin akan keragamannya.

Saya belajar bagaimana menghitung luas poligon yang digambar pada lembar kotak-kotak.Tugas-tugas yang dianggap memiliki tingkat kesulitan yang berbeda - dari yang sederhana hingga Olimpiade. Setiap orang dapat menemukan di antara mereka tugas-tugas dengan tingkat kerumitan yang layak, mulai dari mana, akan dimungkinkan untuk beralih ke penyelesaian yang lebih sulit.

Saya sampai pada kesimpulan bahwa topik yang menarik minat saya cukup beragam, tugas pada kertas kotak-kotak beragam, metode dan teknik untuk menyelesaikannya juga beragam. Oleh karena itu, saya memutuskan untuk terus bekerja ke arah ini.

5. Literatur yang digunakan:

1. N.B. Vasil'ev, "Formula Sekitar Pilihan," Kvant. - 1974. - No. 12

2. Kokse Prasolov VV Tugas dalam planimetri. - M.: MTsNMO, 2006.t e r G.S.M. Pengantar geometri. - M.: Nauka, 1966

3. Roslova L.O., Sharygin I.F. Pengukuran. - M.: Ed. "Dunia Terbuka", 2005.

sumber daya internet:

:

Umpan balik tentang pekerjaan

“Perhitungan luas bangun datar. Pilih Metode"

Pertimbangan topik ini akan meningkatkan aktivitas kognitif siswa, yang nantinya dalam pelajaran geometri akan mulai melihat keselarasan gambar dan akan berhenti menganggap geometri (dan matematika pada umumnya) sebagai ilmu yang membosankan.

Diulas oleh guru matematika

Khodyreva Tatyana Georgievna

Ada formula luar biasa yang memungkinkan Anda menghitung daerah poligon di grid koordinat hampir tanpa kesalahan. Itu bahkan bukan formula, itu nyata dalil. Sekilas mungkin terlihat rumit. Tetapi itu cukup untuk menyelesaikan beberapa tugas - dan Anda akan memahami betapa kerennya fitur ini. Jadi silakan!

Mari kita mulai dengan definisi baru:

Sebuah node tumpukan koordinat adalah setiap titik yang terletak di persimpangan garis vertikal dan horizontal dari grid ini.

Penamaan:

Pada gambar pertama, node tidak ditandai sama sekali. Yang kedua memiliki 4 node. Akhirnya, pada gambar ketiga, semua 16 node ditandai.

Apa hubungannya dengan masalah B5? Faktanya adalah bahwa simpul poligon dalam masalah seperti itu selalu terletak di node dari grid. Akibatnya, teorema berikut bekerja untuk mereka:

Dalil. Pertimbangkan poligon pada kisi koordinat yang simpulnya terletak pada simpul dari kisi ini. Maka luas poligon tersebut adalah :

dimana n adalah jumlah node di dalam poligon yang diberikan, k adalah jumlah node yang terletak pada batasnya (boundary node).

Sebagai contoh, pertimbangkan segitiga biasa pada kisi koordinat dan coba tandai simpul internal dan batas.

Gambar pertama menunjukkan segitiga biasa. Pada gambar kedua, node internalnya ditandai, yang jumlahnya n = 10. Pada gambar ketiga, node yang terletak di perbatasan ditandai, totalnya ada k = 6.

Mungkin banyak pembaca yang belum paham cara menghitung angka n dan k. Mulailah dengan node internal. Semuanya jelas di sini: kami melukis segitiga dengan pensil dan melihat berapa banyak simpul yang diarsir.

Dengan node batas, ini sedikit lebih rumit. perbatasan poligon - garis putus-putus tertutup, yang memotong grid koordinat di banyak titik. Cara termudah adalah dengan menandai beberapa titik "awal", dan kemudian mengelilingi sisanya.

Node batas hanya akan menjadi titik-titik pada polyline di mana mereka berpotongan secara bersamaan tiga baris:

1. Sebenarnya, garis putus-putus;
2. Garis kisi horizontal;
3. garis vertikal.

Mari kita lihat bagaimana semuanya bekerja dalam masalah nyata.

Sebuah tugas. Cari luas segitiga jika ukuran sel 1 x 1 cm:

Pertama, mari kita tandai simpul yang terletak di dalam segitiga, serta di perbatasannya:

Ternyata hanya ada satu simpul internal: n = 1. Ada enam simpul batas: tiga bertepatan dengan simpul segitiga, dan tiga lagi terletak di samping. Jumlah k = 6.

Sekarang kita hitung luasnya menggunakan rumus:

Itu saja! Masalah terpecahkan.

Sebuah tugas. Cari luas segi empat yang digambar di atas kertas kotak-kotak dengan ukuran sel 1 cm kali 1 cm Berikan jawaban Anda dalam sentimeter persegi.

Sekali lagi, kami menandai simpul internal dan batas. Ada n = 2 simpul internal, simpul batas: k = 7, 4 di antaranya adalah titik sudut segi empat, dan 3 lagi terletak di sisi.

Tetap mengganti angka n dan k dalam rumus luas:

Perhatikan contoh terakhir. Masalah ini sebenarnya diusulkan pada pekerjaan diagnostik pada tahun 2012. Jika Anda bekerja sesuai dengan skema standar, Anda harus melakukan banyak konstruksi tambahan. Dan dengan metode simpul, semuanya diselesaikan hampir secara lisan.

Catatan penting tentang area

Tapi formula bukanlah segalanya. Mari kita tulis ulang rumusnya sedikit, bawa istilahnya ke sisi kanan ke penyebut yang sama. Kita mendapatkan:

Angka n dan k adalah jumlah node, mereka selalu bilangan bulat. Jadi pembilangnya juga bilangan bulat. Kami membaginya dengan 2, yang menyiratkan fakta penting:

Daerah selalu dinyatakan bilangan bulat atau pecahan. Apalagi di akhir pecahan selalu ada "lima persepuluh": 10.5; 17,5 dll.

Jadi, luas dalam soal B5 selalu dinyatakan sebagai bilangan bulat atau pecahan dalam bentuk ***.5. Jika jawabannya berbeda, berarti telah terjadi kesalahan di suatu tempat. Ingatlah hal ini ketika Anda mengikuti ujian matematika yang sebenarnya!

Untuk menggunakan pratinjau presentasi, buat akun Google (akun) dan masuk: https://accounts.google.com

Teks slide:

Diselesaikan oleh siswa sekolah menengah No. 7 8 "A" kelas Yunosheva Ksenia Instruktur: Babina Natalya Alekseevna Salsk 2011 "Formula Puncak"

Tujuan pekerjaan: Mengetahui keberadaan yang lain, berbeda dari kurikulum sekolah, rumus untuk mencari luas kisi poligon. Area penerapan formula yang diinginkan.

Pengantar. Pendidikan matematika yang diterima di sekolah pendidikan umum merupakan komponen penting dari pendidikan umum dan budaya umum manusia modern. Pada tahap ini, sistem sekolah dirancang untuk pendidikan sebelas tahun. Semua siswa di akhir kelas sebelas harus mengikuti Ujian Negara Terpadu, yang akan menunjukkan tingkat pengetahuan yang diperoleh selama belajar di sekolah. Namun kurikulum sekolah tidak selalu memberikan cara yang paling rasional untuk memecahkan masalah. Misalnya melihat hasil UN tahun 2010 ini, terlihat jelas banyak siswa yang kehilangan poin karena mengerjakan tugas B6. Saya mulai mencari cara untuk menghemat waktu dan memecahkan masalah ini dengan benar.

Tugas B6. Gambar digambarkan pada kertas kotak-kotak dengan sel berukuran 1 cm kali 1 cm (lihat gambar). Temukan luasnya dalam sentimeter persegi.

Jadi, untuk tetap menyelesaikan tugas ini, saya perlu menerapkan rumus untuk mencari luas, yang kita pelajari di kelas 8. Tapi itu akan memakan banyak waktu, dan saya harus menjawab pertanyaan itu secepat mungkin, karena waktu untuk ujian sangat terbatas. Oleh karena itu, setelah melakukan penelitian, saya menemukan bahwa ada teorema Pick, yang tidak dipelajari dalam kurikulum sekolah, tetapi akan membantu saya mengatasi tugas lebih cepat.

Referensi sejarah. Georg Alexander Pick (10 Agustus 1859 – 26 Juli 1942) adalah seorang matematikawan Austria. Dia meninggal di kamp konsentrasi Terezin. Diketahui hari ini karena rumus Pick untuk menentukan luas kisi poligon. Ia menerbitkan rumusnya dalam sebuah makalah pada tahun 1899, rumus itu menjadi populer ketika Hugo Steinhaus memasukkannya ke dalam Mathematical Pictures edisi 1969. Pick belajar di Universitas Wina dan menyelesaikan PhD-nya pada tahun 1880. Setelah menerima gelar doktor, ia diangkat sebagai asisten Ernest Mach di Universitas Scherl-Ferdinand di Praha. Ia menjadi guru di sana pada tahun 1881. Mengambil cuti dari universitas pada tahun 1884, ia mulai bekerja dengan Felix Klein di Universitas Leipzig. Dia tetap di Praha sampai pensiun pada tahun 1927, ketika dia kembali ke Wina. Pick mengetuai komite di Universitas Praha Jerman (saat itu) yang mengangkat Albert Einstein sebagai profesor fisika matematika pada tahun 1911. Pick terpilih sebagai anggota Akademi Ilmu Pengetahuan dan Seni Ceko, tetapi dikeluarkan setelah Nazi mengambil alih Praha. Setelah pensiun pada tahun 1927, Pick kembali ke Wina, kota tempat ia dilahirkan. Setelah Anschluss, ketika Nazi memasuki Austria pada 12 Maret 1938, Pieck kembali ke Praha. Pada bulan Maret 1939, Nazi menginvasi Cekoslowakia. Georg dikirim ke kamp konsentrasi Terezin pada 13 Juli 1942. Dia meninggal dua minggu kemudian.

teorema Pick. Teorema Pick adalah hasil klasik dari geometri kombinatorial dan geometri bilangan. Luas poligon dengan simpul bilangan bulat sama dengan jumlah B + D/2 - 1, di mana B adalah jumlah titik bilangan bulat di dalam poligon, dan D adalah jumlah titik bilangan bulat pada batas poligon.

Sebuah bukti menyanjung teorema Pick. Setiap poligon tersebut dapat dengan mudah dibagi menjadi segitiga dengan simpul pada simpul kisi, tidak mengandung simpul baik di dalam maupun di samping. Dapat ditunjukkan bahwa luas semua segitiga ini sama dan sama dengan 1/2, dan, oleh karena itu, luas poligon sama dengan setengah dari jumlah T. Untuk menemukan nomor ini, kami dilambangkan dengan n jumlah sisi poligon, dengan i - jumlah simpul di dalamnya dan b - jumlah simpul di sisi, termasuk simpul. Jumlah sudut semua segitiga adalah . Sekarang mari kita cari jumlah ini dengan cara yang berbeda. Jumlah sudut dengan simpul di sembarang simpul internal adalah 2 , yaitu jumlah total sudut tersebut adalah 2 i ; jumlah total sudut pada simpul di sisi, tetapi tidak di simpul, adalah (b - n) , dan jumlah sudut pada simpul poligon adalah (n - 2) . Jadi, T \u003d 2i + (b - n) + (n - 2) , dari mana kita memperoleh ekspresi untuk luas S poligon, yang dikenal sebagai rumus Pick. Misalnya, pada gambar b = 9, i = 24, maka luas poligon adalah 27,5.

Aplikasi. Jadi, kembali ke tugas B6. Nah, dengan mengetahui rumus baru, kita bisa dengan mudah mencari luas segi empat ini. Karena B adalah 5; D - 14, lalu 5 + 14: 2-1 \u003d 11 (cm kuadrat) Luas segi empat ini adalah 11 cm kuadrat.

Dengan menggunakan rumus yang sama, kita dapat menemukan luas segitiga. Karena B-14, G-10, maka 14+10:2-1=18 (cm persegi) Luas segitiga ini adalah 18 cm kuadrat.

Jika B-9, D-12, maka: 9+12:2-1=14 (cm kuadrat) Luas segi empat ini adalah 14 cm kuadrat.

Lingkup rumus. Selain fakta bahwa rumus itu digunakan dalam berbagai macam ujian, tugas, dan sebagainya, itu menyertai seluruh dunia di sekitar kita.

Menurut rumus Puncak S = B + ½ G-1 1) badan B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) ekor B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

Menurut rumus Peak S \u003d B + G-1 B \u003d 36, G \u003d 21 S \u003d 36 + 21 -1 \u003d 36 + 10.5-1 \u003d 45.5

Kesimpulan. Akibatnya, saya sampai pada kesimpulan bahwa ada banyak cara berbeda untuk menyelesaikan masalah area yang tidak dipelajari dalam kurikulum sekolah, dan menunjukkannya dengan menggunakan rumus Pick sebagai contoh.

Direktori. Sebuah poligon tanpa self-intersection disebut poligon kisi jika semua simpulnya berada pada titik-titik dengan koordinat bilangan bulat (dalam sistem koordinat Cartesian). Suatu titik pada bidang koordinat disebut bilangan bulat jika kedua koordinatnya bilangan bulat.