គោលបំណងនៃមេរៀន៖
ដើម្បីបង្កើតចំណេះដឹង ជំនាញ និងសមត្ថភាពនៃការអនុវត្តប្រកបដោយប្រសិទ្ធភាពនៃវិធីសាស្រ្តទូទៅនៃចន្លោះពេល ដោយផ្អែកលើលក្ខណៈសម្បត្តិនៃមុខងារបន្ត។
បង្កើតក្បួនដោះស្រាយនៃសកម្មភាពដែលនាំទៅដល់ការបំប្លែងសមមូល;
បង្រៀនខ្លួនឯងឱ្យអនុវត្តវានៅពេលដោះស្រាយវិសមភាព;
ដើម្បីអនុវត្តការផ្ទេរចំណេះដឹង ជំនាញ និងសមត្ថភាពទៅកាន់លក្ខខណ្ឌថ្មី។
ការអប់រំ៖ ការរៀបចំប្រព័ន្ធ ការបង្រួបបង្រួម ទូទៅនៃចំណេះដឹង ជំនាញ និងសមត្ថភាព។
ការអប់រំ៖ ការអប់រំអំពីតម្រូវការសម្រាប់ការជជែកវែកញែកជាប់លាប់ពេញលេញ ភាពត្រឹមត្រូវ ឯករាជ្យភាព។
ការអភិវឌ្ឍន៍៖ ការអភិវឌ្ឍន៍តក្កវិជ្ជាគណិតវិទ្យា ការបង្កើតទម្រង់នៃការគិតបែបគណិតវិទ្យា (ការវិភាគច្បាស់លាស់នៃវគ្គនៃហេតុផល) ការចាប់អារម្មណ៍លើការយល់ដឹង។
១) សេចក្តីផ្តើម ការកំណត់គោលដៅ និងគោលបំណងនៃមេរៀន - ២ នាទី។
2) ពិនិត្យកិច្ចការផ្ទះ - 2 នាទី។ (ការងារផ្នែកខាងមុខ, ការគ្រប់គ្រងខ្លួនឯង) ។
3) ការបញ្ជាក់គណិតវិទ្យានៃដំណាក់កាលនៃការដោះស្រាយវិសមភាពដោយវិធីសាស្ត្រចន្លោះពេល - 4 នាទី (ចម្លើយសិស្សដែលបានរៀបចំ) ។
4) ពាក្យដដែលៗនៃលក្ខណៈសម្បត្តិនៃវិសមភាព - 2 នាទី។
5) ការរៀបចំសម្រាប់ការបញ្ចូល (សិក្សា) នៃសម្ភារៈអប់រំថ្មីតាមរយៈការធ្វើឡើងវិញ និងការធ្វើបច្ចុប្បន្នភាពចំណេះដឹងមូលដ្ឋាន - 5 នាទី។ (ការងារផ្នែកខាងមុខ ចម្លើយចំពោះសំណួរ ស្ថានភាពបញ្ហា)។
6) វិធីសាស្រ្តចន្លោះពេលទូទៅសម្រាប់ការដោះស្រាយវិសមភាព ការយល់ដឹងដំបូង - 13 នាទី។ (ដំណោះស្រាយរួមនៃវិសមភាពដោយវិធីសាស្ត្រនៃចន្លោះពេល៖ នៅលើក្តារ និងក្នុងសៀវភៅកត់ត្រា)។
7) ព័ត៌មានអំពីកិច្ចការផ្ទះ ការណែនាំសម្រាប់ធ្វើវា - 1 នាទី។
៨) ការបង្រួបបង្រួមចំណេះដឹងថ្មី - ១៥ នាទី។ (ការងារឯករាជ្យ - ជម្រើសទី 1) ។
9) សង្ខេបមេរៀន ការឆ្លុះបញ្ចាំង - 1 នាទី។
១) សេចក្តីផ្តើម ការកំណត់គោលដៅ និងគោលបំណងនៃមេរៀន។ (រឿងគ្រូ)
1) តម្រូវការសម្រាប់ការអនុវត្តកាន់តែទូលំទូលាយនៃវិធីសាស្រ្តនៃចន្លោះពេលនៅក្នុងសាលារៀនត្រូវបានកំណត់ដោយមនោគមវិជ្ជានៃដំណើរការទាំងមូលនៃការបង្រៀនគណិតវិទ្យា។ ចំនុចនោះគឺថាបន្ទាត់មុខងារ (ជាខ្សែសំខាន់មួយក្នុងការសិក្សាអំពីមូលដ្ឋានគ្រឹះនៃគណិតវិទ្យា) ទទួលបានការគាំទ្រផ្នែកបច្ចេកវិទ្យាដ៏មានឥទ្ធិពល។ វិធីសាស្រ្តនៃចន្លោះពេលគឺផ្អែកលើលក្ខណៈសំខាន់ៗនៃការពឹងផ្អែកមុខងារដូចជាសូន្យនៃអនុគមន៍ ចន្លោះពេលនៃសញ្ញាថេរ និង monotonicity របស់វា។ បន្ទាប់មកប្រភពដើមមុខងារនៃសមីការ និងវិសមភាព ក៏ដូចជាវិធីសាស្រ្តសម្រាប់ដំណោះស្រាយរបស់ពួកគេកាន់តែច្បាស់។ ប្រភេទនៃការបន្តនៃមុខងារមួយ អាកប្បកិរិយានៃក្រាហ្វរបស់វានៅក្នុងតំបន់ជុំវិញនៃចំណុចនៃភាពមិនទៀងទាត់គ្មានកំណត់ ទ្រឹស្តីបទនៅលើឫស ភាពជាប់លាប់នៃសញ្ញា ចំណុចខ្លាំង និងប្រភេទរបស់វាកាន់តែមើលឃើញ។ ហើយទាំងអស់នេះត្រូវបានភ្ជាប់សរីរាង្គទៅជាមុខងារទាំងមូល។
ម៉្យាងវិញទៀត ធរណីមាត្រនៃវត្ថុនៃការសិក្សាដែលបានប្រើគឺមានតម្លៃមិនអាចកាត់ថ្លៃបាន ពោលគឺឧ។ ដោយមើលឃើញ ជាន័យធៀបបង្ហាញឧបករណ៍គណិតវិទ្យាដែលបានប្រើទាំងអស់នៃការពឹងផ្អែកមុខងារ។
គោលការណ៍ជាមូលដ្ឋាននៃវិធីសាស្ត្រចន្លោះពេល៖
- មុខងារ (ទូទៅ) វិធីសាស្រ្ត;
- ការពឹងផ្អែកលើធរណីមាត្រនៃលក្ខណៈសម្បត្តិមុខងារ;
- ការមើលឃើញស្រាវជ្រាវ។
នេះនាំឱ្យមានគុណសម្បត្តិដូចខាងក្រោមនៃវិធីសាស្រ្តបើប្រៀបធៀបទៅនឹងអ្នកផ្សេងទៀតដែលបានប្រើក្នុងប្រភេទនៃភារកិច្ចដូចគ្នា: ភាពសាមញ្ញនិងល្បឿននៃការសម្រេចបាននូវគោលដៅ; ភាពមើលឃើញ (និងសមត្ថភាពក្នុងការត្រួតពិនិត្យឬពិនិត្យពីរដង); សេដ្ឋកិច្ចក្នុងការគណនាធនធាននិងពេលវេលា; វិសាលភាពនៃការគ្របដណ្តប់នៃស្ថានភាពទាំងមូល ការបង្កើត និងការអភិវឌ្ឍជំនាញនៃការគិត និងការវិភាគទូទៅ ក៏ដូចជាជំនាញដែលភ្ជាប់ជាមួយនេះ ដើម្បីធ្វើការសន្និដ្ឋានឡូជីខល។
2) ពិនិត្យកិច្ចការផ្ទះ។(ស្លាយលេខ ៤)
3) រឿងអំពីវិធីសាស្រ្តនៃចន្លោះពេលសម្រាប់ដោះស្រាយវិសមភាព។ (សិស្សឆ្លើយ)។
រូបមន្តគណិតវិទ្យានៃដំណោះស្រាយវិសមភាពដោយវិធីសាស្រ្តនៃចន្លោះពេល។
1) ពិចារណាវិសមភាព៖ (x-2)(x-3)> 0 ។ (ស្លាយលេខ ៥)
អ្នកអាចដោះស្រាយវាដូចនេះ៖ ផលិតផល (គុណតម្លៃ) នៃកត្តាពីរគឺវិជ្ជមានប្រសិនបើ និងលុះត្រាតែកត្តាទាំងពីរមានសញ្ញាដូចគ្នា ពោលគឺឧ។ វិសមភាពគឺស្មើនឹងការរួមបញ្ចូលគ្នានៃប្រព័ន្ធពីរ៖ (ស្លាយលេខ ៦)
![]()
ពីប្រព័ន្ធទីមួយយើងទទួលបាន x>3 ពី x ទីពីរ< 2.
ដំណោះស្រាយគឺជាការរួបរួមនៃដំណោះស្រាយនៃប្រព័ន្ធទាំងពីរ។
ចម្លើយ៖ ![]()
វិធីសាស្ត្រក្រាហ្វិក (ស្លាយលេខ ៧)
វិធីសាស្រ្តមួយទៀតគឺ វិធីសាស្រ្តចន្លោះពេល(ស្លាយលេខ ៨) ។
គំនិតរបស់គាត់មានដូចខាងក្រោម។
នៅលើបន្ទាត់ពិត សម្គាល់សូន្យ (ឫស) នៃពហុធា (x-2)(x-3) ឈរ
នៅផ្នែកខាងឆ្វេងនៃវិសមភាព, i.e. លេខ 2 និង 3 ។
នៅពេល x>3 (នៅខាងស្តាំនៃឫសធំ) បន្ទាប់មក (x-2)(x-3)>0 ដោយសារកត្តានីមួយៗគឺវិជ្ជមាន។
ប្រសិនបើអ្នកផ្លាស់ទីតាមអ័ក្សក្នុងទិសដៅអវិជ្ជមាន នោះនៅពេលអ្នកឆ្លងកាត់ចំនុច x=3 កត្តា (x-3) នឹងផ្លាស់ប្តូរសញ្ញា។ នៅក្នុងផលិតផល (x-2) (x-3) កត្តាអវិជ្ជមានមួយនឹងលេចឡើង ជាលទ្ធផល (x-2) (x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.
ឥឡូវនេះវាងាយស្រួលក្នុងការសរសេរដំណោះស្រាយវិសមភាព៖
សេចក្តីសន្និដ្ឋាន៖ ផលិតផលអាចផ្លាស់ប្តូរសញ្ញាបានលុះត្រាតែឆ្លងកាត់ចំនុច x=2 និង x=3
ដូច្នេះហើយ រក្សាសញ្ញានៅលើចន្លោះពេលនីមួយៗដែលទទួលបាន។
នៅក្នុងឧទាហរណ៍ដ៏សាមញ្ញនេះ វាងាយស្រួលក្នុងការយល់អំពីគំនិតនៃវិធីសាស្ត្រចន្លោះពេល ប៉ុន្តែវាមិនបង្ហាញពីគុណសម្បត្តិគួរឱ្យកត់សម្គាល់ណាមួយឡើយ។
សនិទានភាពនៃវិធីសាស្រ្តចន្លោះពេល អំណាចរបស់វា យើងនឹងពិចារណាឧទាហរណ៍ខាងក្រោម (ស្លាយលេខ 9, 10,11, 12))
2) ដោះស្រាយវិសមភាព (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10)> 0 ។
ដើម្បីដោះស្រាយវិសមភាពនេះដោយប្រើសំណុំនៃប្រព័ន្ធ មួយនឹងត្រូវពិចារណាលើសំណុំនៃប្រព័ន្ធ 512 ដែលមានវិសមភាពចំនួន 10 នៅក្នុងប្រព័ន្ធនីមួយៗ។
ចូរយើងប្រើវិធីសាស្ត្រចន្លោះពេល។ យើងសម្គាល់លេខសូន្យនៃពហុនាមនៅលើបន្ទាត់ពិត។ នៅចន្លោះពេល x> 10 ពហុធានឹងវិជ្ជមាន ដោយសារកត្តានីមួយៗគឺវិជ្ជមាន។ នៅពេលឆ្លងកាត់ឫសបន្ទាប់នីមួយៗ ពហុធានឹងផ្លាស់ប្តូរសញ្ញា ដោយសារកត្តាអវិជ្ជមានបន្ថែមនឹងបង្ហាញនៅក្នុងផលិតផល។ ឥឡូវនេះវាងាយស្រួលក្នុងការសរសេរដំណោះស្រាយចំពោះវិសមភាពដោយប្រើសញ្ញាឆ្លាស់គ្នា។

គុណសម្បត្តិនៃវិធីសាស្ត្រចន្លោះពេល។
- ភាពសាមញ្ញនិងល្បឿននៃការសម្រេចបាននូវគោលដៅ;
- ភាពមើលឃើញ (និងសមត្ថភាពក្នុងការត្រួតពិនិត្យឬពិនិត្យពីរដង);
- ការថយចុះគួរឱ្យកត់សម្គាល់នៃចំនួនការងារគណនានិងពេលវេលា;
- វិសាលភាពនៃការគ្របដណ្តប់នៃស្ថានភាពទាំងមូល;
- ការបង្កើត និងអភិវឌ្ឍជំនាញការគិត និងការវិភាគទូទៅ ក៏ដូចជាជំនាញពាក់ព័ន្ធដើម្បីទាញការសន្និដ្ឋានឡូជីខល។
មតិយោបល់។ វាងាយស្រួលណាស់ក្នុងការដោះស្រាយវិសមភាព ដែលផ្នែកខាងឆ្វេងត្រូវបានបង្កើតជាកត្តា ព្រោះវាមិនពិបាកក្នុងការស្វែងរកលេខសូន្យ (ឫស)។
កិច្ចការ៖ ដោះស្រាយវិសមភាពដោយប្រើវិធីសាស្ត្រចន្លោះពេល (x+3) 3 (x-4) 2 (x-5)> 0(ស្លាយទី ១៣)
4) ពាក្យដដែលៗនៃលក្ខណៈសម្បត្តិនៃវិសមភាព។
ក) សំណួរ៖ តើវិសមភាពអ្វីទៅដែលហៅថាសមមូល?
(វិសមភាពពីរត្រូវបានគេនិយាយថាស្មើនឹងប្រសិនបើដំណោះស្រាយណាមួយចំពោះវិសមភាពទីមួយគឺជាដំណោះស្រាយចំពោះទីពីរ ហើយផ្ទុយទៅវិញដំណោះស្រាយណាមួយចំពោះវិសមភាពទីពីរគឺជាដំណោះស្រាយចំពោះទីមួយ)។
ឬ៖ វិសមភាពពីរត្រូវបានគេនិយាយថាសមមូល ប្រសិនបើសំណុំនៃដំណោះស្រាយរបស់ពួកគេគឺដូចគ្នា។
ស្លាយ 14. ពាក្យដដែលៗនៃលក្ខណៈសម្បត្តិនៃវិសមភាព។
ស្លាយទី ១៥ ឆ្លើយសំណួរ ហើយពន្យល់។
តើវិសមភាពស្មើគ្នាទេ?
1) 4x-5<0 и 4х<5
2) -2x+5>0 និង 2x-5<0
3) -3x 2 +5x-7>0 និង 3x 2 -5x+7<0
4) (x+1)>0 និង (x 2 +5x+10)(x+1)>0
5) ការងារផ្ទាល់មាត់ក្នុងការរៀបចំសម្រាប់ការបញ្ចូល (សិក្សា) នៃសម្ភារៈអប់រំថ្មីតាមរយៈការធ្វើឡើងវិញនិងការធ្វើបច្ចុប្បន្នភាពនៃចំណេះដឹងមូលដ្ឋាន។
ស្លាយ 16. និយមន័យនៃអនុគមន៍បន្តនៅចំណុចមួយ។
ស្លាយ 17. ទ្រព្យសម្បត្តិនៃមុខងារបន្ត។
ស្លាយ 18. ស្វែងរកចន្លោះនៃការបន្ត។

ស្លាយ 19. ស្វែងរកកំហុស។




ស្លាយ 20. ដោះស្រាយវិសមភាពដោយពាក្យសំដី,  ដោយប្រើគំនូសតាង។
ដោយប្រើគំនូសតាង។
ស្លាយ 21, 22. ការជំនួសវិសមភាពជាមួយនឹងលក្ខខណ្ឌសមមូល។
ដោះស្រាយវិសមភាព
វិសមភាពនេះគឺស្មើនឹងលក្ខខណ្ឌ f(x) <
0 រាប់ ![]()
ដូច្នេះ យើងត្រូវស្វែងរកតម្លៃទាំងអស់នៃ x ដែលលក្ខខណ្ឌ f(x) < 0.
6) វិធីសាស្រ្តចន្លោះពេលទូទៅសម្រាប់ការដោះស្រាយវិសមភាព ការយល់ដឹងដំបូង - 10 នាទី។ (ដំណោះស្រាយរួមនៃវិសមភាពដោយវិធីសាស្ត្រនៃចន្លោះពេល៖ នៅលើក្តារ និងក្នុងសៀវភៅកត់ត្រា)។
ស្លាយ ២៣. ក្បួនដោះស្រាយ។ វិធីសាស្រ្តទូទៅសម្រាប់ការដោះស្រាយវិសមភាព។
ដំណោះស្រាយវិសមភាព f(x)> 0, f(x) > 0, f(x)<0, f(x)< 0 ដោយវិធីសាស្ត្រចន្លោះពេល។ (គ្រោងការណ៍)
ស្លាយ 24 និង 25. ការដោះស្រាយវិសមភាពដោយក្បួនដោះស្រាយ។ (មតិចំពោះចំណុចទាំងអស់នៃក្បួនដោះស្រាយ) ។
ស្លាយ 26 ។ រូបភាពក្រាហ្វិកនៃដំណោះស្រាយចំពោះវិសមភាពនេះ។
ស្លាយ 27. ដោះស្រាយវិសមភាពនៅលើក្តារ និងក្នុងសៀវភៅកត់ត្រា ![]() .
.
ស្លាយទី 28. រូបភាពក្រាហ្វិកនៃដំណោះស្រាយចំពោះវិសមភាពនេះ។
ស្លាយ 29. ដោះស្រាយវិសមភាពនៅលើក្តារ និងក្នុងសៀវភៅកត់ត្រា
ស្លាយទី 30. រូបភាពក្រាហ្វិកនៃដំណោះស្រាយចំពោះវិសមភាពនេះ។
ស្លាយទី ៣១, ៣២. ដោះស្រាយវិសមភាពដោយពាក្យសំដី តាមរូបភាព
7) ព័ត៌មានអំពីកិច្ចការផ្ទះ។(ដោះស្រាយដោយវិធីសាស្ត្រចន្លោះពេល ជម្រើសលេខ 2)
8) ការបង្រួបបង្រួមចំណេះដឹងថ្មី (ការងារឯករាជ្យ ជម្រើសលេខ 1) ។
9) សង្ខេបមេរៀន ការគ្រប់គ្រងខ្លួនឯងលើដំណោះស្រាយដែលត្រៀមរួចជាស្រេច (ស្លាយ 33, 34, 35) ពាក្យដដែលៗនៃក្បួនដោះស្រាយនៃវិធីសាស្រ្តទូទៅនៃចន្លោះពេល និងកម្មវិធីរបស់វា។
10) ការវិភាគលើការរួមផ្សំនៃសម្ភារៈ និងការចាប់អារម្មណ៍របស់សិស្សក្នុងប្រធានបទ។វិធីសាស្រ្តនេះគឺមានលក្ខណៈជាសកលសម្រាប់ដោះស្រាយវិសមភាពណាមួយ រួមទាំងសនិទានភាពជាមួយនឹងម៉ូឌុល អិចស្ប៉ូណង់ស្យែល អិចស្ប៉ូណង់ស្យែល លោការីត ចាប់តាំងពីវិធីសាស្ត្រចន្លោះពេលកាត់បន្ថយដំណោះស្រាយវិសមភាពទៅនឹងការដោះស្រាយសមីការ ការស្វែងរកដែននិយមន័យ និងតម្លៃនៃមុខងារនៅចំណុចមួយ មិនបង្កឱ្យមានការលំបាក។ ប៉ុន្តែខ្ញុំត្រូវតែផ្តល់ឧទាហរណ៍នៃវិសមភាពដែលការប្រើប្រាស់វិធីសាស្រ្តនេះមិនសមហេតុផល ដែលវាសមហេតុផលជាងដើម្បីអនុវត្តវិធីសាស្រ្តផ្សេងទៀតសម្រាប់ការដោះស្រាយវិសមភាព។
បទបង្ហាញ "ការអនុវត្តបន្តក្នុងការដោះស្រាយវិសមភាព" ។ (៣៥ ស្លាយ)
![]()
និយមន័យ 4. មុខងារមួយត្រូវបានគេហៅថាបន្តនៅលើផ្នែកមួយប្រសិនបើវាបន្តនៅគ្រប់ចំណុចនៃផ្នែកនេះ (នៅចំណុច a វាបន្តនៅខាងស្តាំ ពោលគឺ ហើយនៅចំណុច b វាបន្តនៅខាងឆ្វេង ឧ)។
មុខងារបឋមមូលដ្ឋានទាំងអស់គឺបន្តនៅក្នុងដែននៃនិយមន័យរបស់វា។
លក្ខណៈសម្បត្តិនៃមុខងារបន្តលើផ្នែកមួយ៖
- 1) ប្រសិនបើមុខងារបន្តនៅលើផ្នែកមួយ នោះវាត្រូវបានចងនៅលើផ្នែកនេះ (ទ្រឹស្តីបទ Weierstrass ដំបូង)។
- 2) ប្រសិនបើមុខងារបន្តនៅលើផ្នែកមួយ នោះនៅលើផ្នែកនេះវាឈានដល់តម្លៃអប្បបរមា និងតម្លៃអតិបរមារបស់វា (ទ្រឹស្តីបទ Weierstrass ទីពីរ) (សូមមើលរូបទី 2)។
- 3) ប្រសិនបើមុខងារបន្តនៅលើផ្នែកមួយ ហើយយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងរបស់វា នោះយ៉ាងហោចណាស់មានចំណុចមួយនៅក្នុងផ្នែកនោះ (ទ្រឹស្តីបទ Bolzano-Cauchy)។
ចំណុចបំបែកមុខងារ និងចំណាត់ថ្នាក់របស់វា។
ផ្នែកចំណុចបន្តមុខងារ
ចំណុចដែលលក្ខខណ្ឌបន្តមិនត្រូវបានគេហៅថាចំណុចមិនបន្តនៃអនុគមន៍នេះ។ ប្រសិនបើជាចំណុចដាច់នៃអនុគមន៍ នោះយ៉ាងហោចណាស់លក្ខខណ្ឌមួយក្នុងចំណោមលក្ខខណ្ឌទាំងបីសម្រាប់ការបន្តនៃអនុគមន៍ដែលបានបញ្ជាក់ក្នុងនិយមន័យ 1, 2 មិនពេញចិត្តនៅក្នុងវា ពោលគឺ៖
1) អនុគមន៍ត្រូវបានកំណត់នៅតំបន់ជុំវិញចំណុច ប៉ុន្តែមិនបានកំណត់នៅចំណុចខ្លួនវាទេ។ ដូច្នេះមុខងារដែលបានពិចារណាក្នុងឧទាហរណ៍ទី 2 ក) មានការសម្រាកនៅចំណុចមួយ ដោយសារវាមិនត្រូវបានកំណត់នៅចំណុចនេះ។

2) អនុគមន៍ត្រូវបានកំណត់នៅចំណុចមួយនិងសង្កាត់របស់វាមានដែនកំណត់ម្ខាងហើយប៉ុន្តែមិនស្មើគ្នាទៅវិញទៅមក: . ឧទាហរណ៍ អនុគមន៍ពីឧទាហរណ៍ 2 ខ) ត្រូវបានកំណត់នៅចំណុចមួយ និងសង្កាត់របស់វា ប៉ុន្តែចាប់តាំងពី ក។

៣) អនុគមន៍ត្រូវបានកំណត់នៅត្រង់ចំណុច និងជុំវិញរបស់វា មានដែនកំណត់ម្ខាង ហើយវាស្មើគ្នាទៅវិញទៅមក ប៉ុន្តែមិនស្មើតម្លៃនៃអនុគមន៍ត្រង់ចំណុច ៖ ។ ឧទាហរណ៍មុខងារ។ នេះគឺជាចំណុចបំបែក៖ នៅចំណុចនេះ មុខងារត្រូវបានកំណត់ មានដែនកំណត់ម្ខាង និងស្មើគ្នាទៅវិញទៅមក ប៉ុន្តែ ឧ.
ចំណុចបំបែកមុខងារត្រូវបានចាត់ថ្នាក់ដូចខាងក្រោម។
និយមន័យ 5. ចំនុចមួយត្រូវបានគេហៅថាចំនុចមិនបន្តនៃប្រភេទទីមួយនៃអនុគមន៍ប្រសិនបើមានដែនកំណត់កំណត់ហើយនៅចំណុចនេះ ប៉ុន្តែវាមិនស្មើគ្នានឹងគ្នា : . បន្ទាប់មកបរិមាណត្រូវបានគេហៅថាលោតនៃអនុគមន៍នៅចំណុច។
និយមន័យ ៦. ចំណុចមួយត្រូវបានគេហៅថាចំណុចនៃភាពមិនដំណើរការដែលអាចដកចេញបាននៃអនុគមន៍ ប្រសិនបើនៅចំណុចនេះមានដែនកំណត់កំណត់ ហើយពួកវាស្មើនឹងគ្នាទៅវិញទៅមក៖ ប៉ុន្តែមុខងារខ្លួនវាមិនត្រូវបានកំណត់នៅចំណុច ឬត្រូវបានកំណត់ ប៉ុន្តែ។
និយមន័យ 7. ចំនុចមួយត្រូវបានគេហៅថាចំនុចមិនបន្តនៃប្រភេទទីពីរនៃអនុគមន៍ ប្រសិនបើនៅចំណុចនេះយ៉ាងហោចណាស់មួយនៃដែនកំណត់ម្ខាង (ឬ) មិនមាន ឬស្មើនឹងភាពគ្មានកំណត់។
ឧទាហរណ៍ 3. ស្វែងរកចំនុចបំបែកនៃមុខងារខាងក្រោម ហើយកំណត់ប្រភេទរបស់វា៖ ក) ខ)


ការសម្រេចចិត្ត។ ក) មុខងារត្រូវបានកំណត់ និងបន្តនៅលើចន្លោះពេល u ចាប់តាំងពីចន្លោះពេលនីមួយៗទាំងនេះត្រូវបានផ្តល់ដោយអនុគមន៍បឋមបន្ត។ ដូច្នេះ ចំនុចបំបែកនៃអនុគមន៍ដែលបានផ្តល់ឱ្យអាចជាចំណុចទាំងនោះដែលមុខងារផ្លាស់ប្តូរការចាត់តាំងវិភាគរបស់វា ពោលគឺឧ។ ពិន្ទុ i. ចូរយើងស្វែងរកដែនកំណត់ម្ខាងនៃមុខងារនៅចំណុច៖
ដោយសារដែនកំណត់ម្ខាងមាន ហើយមានកំណត់ ប៉ុន្តែមិនស្មើគ្នា ចំណុចនោះគឺជាចំណុចមិនបន្តនៃប្រភេទទីមួយ។ មុខងារលោត៖
សម្រាប់ចំណុចមួយដែលយើងរកឃើញ។
ការបន្តនៃមុខងារនៅលើចន្លោះពេលមួយ។
| ឈ្មោះប៉ារ៉ាម៉ែត្រ | អត្ថន័យ |
| ប្រធានបទអត្ថបទ៖ | ការបន្តនៃមុខងារនៅលើចន្លោះពេលមួយ។ |
| Rubric (ប្រភេទប្រធានបទ) | គណិតវិទ្យា |
និយមន័យ។អនុគមន៍ត្រូវបានគេហៅថាបន្តនៅលើចន្លោះពេលមួយ ប្រសិនបើវាបន្តនៅគ្រប់ចំណុចនៃចន្លោះពេលនេះ។
ប្រសិនបើមុខងារត្រូវបានកំណត់សម្រាប់ X=កហើយនៅត្រង់ណា f(X) = f(ក),
បន្ទាប់មកពួកគេនិយាយថា f(X) នៅចំណុច និងបន្តនៅខាងស្តាំ. ដូចគ្នានេះដែរប្រសិនបើ f(X) = f(ខ) បន្ទាប់មកយើងនិយាយថានៅចំណុចនោះ។ ខមុខងារនេះ។ បន្ត.
និយមន័យ។មុខងារត្រូវបានគេហៅថាជាបន្តនៅលើផ្នែក [ ក, ខ] ប្រសិនបើវាបន្តនៅចំនុចនីមួយៗរបស់វា (នៅចំណុច កបន្តនៅខាងស្តាំនៅចំណុចមួយ។ ខបន្តនៅខាងឆ្វេង) ។
តម្លៃខ្ពស់បំផុតមុខងារ នៅ = f(x) នៅលើផ្នែក [ ក, ខ f(x 1) នោះ។ f(x) £ f(x 1) សម្រាប់មនុស្សគ្រប់គ្នា X Î [ ក, ខ].
តម្លៃទាបបំផុត។មុខងារ នៅ = f(x) នៅលើផ្នែក [ ក, ខ] វាជាទម្លាប់ក្នុងការហៅតម្លៃរបស់វា។ f(x 2) នោះ។ f(x) ³ f(x 2) សម្រាប់មនុស្សគ្រប់គ្នា X Î [ ក, ខ].
អនុគមន៍ដែលបន្តនៅចន្លោះពេលមួយមានលក្ខណៈសម្បត្តិសំខាន់មួយចំនួនដែលត្រូវបានបង្ហាញដោយទ្រឹស្តីបទខាងក្រោម។
ទ្រឹស្តីបទ ៣.៣.១.មុខងារបន្តនៅលើផ្នែក [ ក, ខ] ឈានដល់តម្លៃអប្បបរមារបស់វានៅលើវា។ មនិងតម្លៃដ៏អស្ចារ្យបំផុត។ មនោះគឺមានចំណុចបែបនេះ x 1 និង x 2 នៃផ្នែកនេះ, ដែល f(x 1) = ម, f(x 2) = ម.
ទ្រឹស្តីបទមានអត្ថន័យធរណីមាត្រសាមញ្ញ (សូមមើលរូបភាពទី 2) ។
 |
ទ្រឹស្តីបទ ៣.៣.២.ក្នុងករណីមុខងារ នៅ = f(x) គឺបន្តនៅលើផ្នែក [ ក, ខ] ហើយយកតម្លៃមិនស្មើគ្នានៅចុងរបស់វា។ f(ក) = ក, f(ខ) = B, A ¹ B, បន្ទាប់មក អ្វីក៏ដោយ លេខ C រវាង A និង B វាមានចំនុចមួយ។ ជាមួយ Î [ ក, ខ] បែបនោះ។ f(ជាមួយ) = គ.
អត្ថន័យធរណីមាត្រនៃទ្រឹស្តីបទត្រូវបានបង្ហាញនៅក្នុងរូបភាពទី 3 ។ បន្ទាត់ត្រង់ណាមួយ។ នៅ= C ដែល A< C < B (или A >C > B) ប្រសព្វក្រាហ្វនៃអនុគមន៍ នៅ = f(x).
ផលវិបាក។ប្រសិនបើមុខងារបន្តនៅលើផ្នែកមួយ ហើយយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងរបស់វា នោះយ៉ាងហោចណាស់មានចំណុចមួយនៅលើផ្នែកនេះដែលមុខងារបាត់។
អត្ថន័យធរណីមាត្រនៃលទ្ធផលត្រូវបានបង្ហាញនៅក្នុងរូបភាពទី 4 ។

សំណួរសម្រាប់ការគ្រប់គ្រងខ្លួនឯង
1. តើមុខងារអ្វីទៅហៅថាបន្តនៅចំណុចមួយ?
2. ផ្តល់និយមន័យសមមូលមួយបន្ថែមទៀតតាមរយៈការបង្កើនមុខងារ និងអាគុយម៉ង់។
3. តើអ្វីអាចនិយាយបានអំពីផលបូក ភាពខុសគ្នា ផលិតផល និងផលគុណនៃអនុគមន៍បន្តពីរ?
4. តើតម្លៃអ្វីខ្លះនៃអាគុយម៉ង់ដែលអនុគមន៍សនិទាន និងប្រភាគ-សនិទានទាំងមូលបន្ត?
5. តើមុខងារស្មុគស្មាញបន្តនៅចំណុចមួយនៅពេលណា?
6. ដូចម្តេចដែលហៅថាចំណុចបំបែកនៃមុខងារ?
7. តើចំនុចណាខ្លះដែលហៅថាចំនុចដាច់នៃប្រភេទទីមួយ?
8. តើតម្លៃអ្វីជាធម្មតាត្រូវបានគេហៅថាលោតមុខងារ?
9. ពន្យល់ពីគោលគំនិតនៃ "ចំណុចបំបែកដែលអាចដកចេញបាន" ។ ផ្តល់ឧទាហរណ៍។
10. តើចំនុចណាខ្លះដែលហៅថាចំនុចដាច់នៃប្រភេទទីពីរ? ផ្តល់ឧទាហរណ៍។
11. ពន្យល់ពីគោលគំនិត៖ ""ការបន្តនៅចន្លោះពេល", ""បន្តនៅខាងស្តាំ", ""បន្តនៅខាងឆ្វេង"", ""បន្តនៅផ្នែក""។
12. កំណត់តម្លៃធំបំផុត និងតូចបំផុតនៃមុខងារ។
13. បង្កើតទ្រឹស្តីបទស្តីពីទំនាក់ទំនងនៃការបន្តលើផ្នែកដែលមានតម្លៃធំបំផុត និងតូចបំផុតនៃអនុគមន៍។ ពន្យល់វាជាមួយរូបភាព។
14. បង្កើតទ្រឹស្តីបទស្តីពីការភ្ជាប់រវាងការបន្តនៃអនុគមន៍នៅលើផ្នែកមួយ និងផ្នែកនៃតម្លៃអនុគមន៍។ បង្ហាញអត្ថន័យធរណីមាត្ររបស់វានៅក្នុងរូប។
15. ផ្តល់លទ្ធផលនៃទ្រឹស្តីបទខាងលើ និងការបកស្រាយធរណីមាត្ររបស់វា។
ធម្មទេសនា №៤
ប្រធានបទមេរៀន៖ ដេរីវេនៃមុខងារ
ផែនការបង្រៀន៖គំនិតនៃនិស្សន្ទវត្ថុ អត្ថន័យធរណីមាត្រ និងរូបវន្តរបស់វា។ ច្បាប់ជាមូលដ្ឋាននៃភាពខុសគ្នា។ ដេរីវេនៃមុខងារស្មុគស្មាញ។ កម្មវិធីមួយចំនួននៃដេរីវេ។
៤.១. គំនិតនៃនិស្សន្ទវត្ថុ អត្ថន័យធរណីមាត្រ និងរូបវន្តរបស់វា។
ពិចារណាមុខងារ នៅ = f(x) បានបញ្ជាក់ក្នុងចន្លោះពេល] ក, ខ[។ អនុញ្ញាតឱ្យមាន XÎ ] ក, ខ[ និង X Î ] ក, ខ[, បន្ទាប់មកមុខងារបង្កើននៅចំណុច X 0 ត្រូវបានបង្ហាញដោយរូបមន្ត D នៅ = f(x 0+D X) – f(x 0).
និយមន័យ។ ដេរីវេនៃអនុគមន៍ y = f(x) នៅចំណុច X 0 ជាធម្មតាត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍នេះទៅនឹងការបង្កើននៃអាគុយម៉ង់ នៅពេលក្រោយមានទំនោរទៅសូន្យ៖
f'(x 0) = ![]() ឬ y"(x 0) =.
ឬ y"(x 0) =.
អត្ថន័យធរណីមាត្រនៃដេរីវេ៖ ដេរីវេនៃអនុគមន៍នេះនៅចំណុចមួយគឺស្មើនឹងតង់សង់នៃមុំរវាងអ័ក្សអុក និងតង់សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅចំណុចដែលត្រូវគ្នា (សូមមើលរូបទី 1)៖
f"(x 0) = តាន់ ក.
និយមន័យ. ប្រសិនបើមុខងារ f(x) ត្រូវបានកំណត់នៅលើចន្លោះពេល [ ក, ខ] គឺបន្តនៅគ្រប់ចំណុចនៃចន្លោះពេល ( ក, ខ), នៅចំណុច កបន្តនៅខាងស្តាំនៅចំណុចមួយ។ ខគឺបន្តនៅខាងឆ្វេង បន្ទាប់មកយើងនិយាយថាមុខងារ f(x) បន្តលើផ្នែក [ក, ខ].
នៅក្នុងពាក្យផ្សេងទៀតមុខងារ f(x) គឺបន្តនៅលើផ្នែក [ ក, ខ] ប្រសិនបើលក្ខខណ្ឌបីត្រូវបានបំពេញ៖
1) "x 0 Î( ក, ខ): f(x) = f(x 0);
2) f(x) = f(ក);
3) f(x) = f(ខ).
សម្រាប់មុខងារដែលបន្តនៅចន្លោះពេលមួយ យើងពិចារណាអំពីលក្ខណៈសម្បត្តិមួយចំនួន ដែលយើងបង្កើតជាទម្រង់នៃទ្រឹស្តីបទខាងក្រោមដោយគ្មានភស្តុតាង។
ទ្រឹស្តីបទ ១. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅលើផ្នែក [ ក, ខ] បន្ទាប់មកវាឈានដល់តម្លៃតូចបំផុត និងធំបំផុតរបស់វានៅលើផ្នែកនេះ។
ទ្រឹស្តីបទនេះចែងថា (រូប ១.១៥) ថានៅលើផ្នែក [ ក, ខ] មានចំណុចបែបនេះ x 1 នោះ។ f(x 1) £ f(x) សម្រាប់ណាមួយ។ xពី [ ក, ខ] ហើយថាមានចំណុចមួយ។ x 2 (x 2 អូ[ ក, ខ]) បែបនេះ " xÎ[ ក, ខ] (f(x 2) ³ f(x)).
អត្ថន័យ f(x 1) គឺធំបំផុតសម្រាប់មុខងារដែលបានផ្តល់ឱ្យនៅលើ [ ក, ខ], ក f(x 2) - តូចបំផុត។ បញ្ជាក់៖ f(x 1) = ម, f(x 2) =ម. ចាប់តាំងពី f(x) វិសមភាពខាងក្រោមមាន៖ " xÎ[ ក, ខ] ម£ f(x) £ មបន្ទាប់មកយើងទទួលបានកូរ៉ូឡារីខាងក្រោមពីទ្រឹស្តីបទទី១។
ផលវិបាក. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅលើផ្នែកមួយ បន្ទាប់មកវាត្រូវបានចងនៅលើផ្នែកនេះ។
ទ្រឹស្តីបទ ២. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅលើផ្នែក [ ក, ខ] ហើយយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងផ្នែក បន្ទាប់មកមានចំណុចខាងក្នុងបែបនេះ x 0 ផ្នែក [ ក, ខ] ដែលមុខងារប្រែទៅជា 0, i.e. $ x 0 Î ( ក, ខ) (f(x 0) = 0).
ទ្រឹស្តីបទនេះចែងថាក្រាហ្វនៃអនុគមន៍ y=f(x), បន្តនៅលើចន្លោះពេល [ ក, ខ] ឆ្លងកាត់អ័ក្ស គោយ៉ាងហោចណាស់ម្តងប្រសិនបើតម្លៃ f(ក) និង f(ខ) មានសញ្ញាផ្ទុយ។ ដូច្នេះ (រូបភាព ១.១៦) f(ក) > 0, f(ខ) < 0 и функция f(x) បាត់នៅចំណុច x 1 , x 2 , x 3 .
ទ្រឹស្តីបទ ៣. អនុញ្ញាតឱ្យមុខងារ f(x) គឺបន្តនៅលើផ្នែក [ ក, ខ], f(ក) = ក, f(ខ) = ខនិង ក¹ ខ. (រូបភាព 1.17) ។ បន្ទាប់មកសម្រាប់លេខណាមួយ។ គ, បានបញ្ចប់រវាងលេខ កនិង ខមានចំណុចខាងក្នុងបែបនេះ x 0 ផ្នែក [ ក, ខ] អ្វី f(x 0) = គ.
ផលវិបាក. ប្រសិនបើមុខងារ f(x) គឺបន្តនៅលើផ្នែក [ ក, ខ], ម- តម្លៃតូចបំផុត។ f(x), ម- តម្លៃធំបំផុតនៃមុខងារ f(x) នៅលើផ្នែក [ ក, ខ] បន្ទាប់មកអនុគមន៍យក (យ៉ាងហោចណាស់ម្តង) តម្លៃណាមួយ។ មរវាង មនិង មដូច្នេះហើយផ្នែក [ m, M] គឺជាសំណុំនៃតម្លៃទាំងអស់នៃអនុគមន៍ f(x) នៅលើផ្នែក [ ក, ខ].
ចំណាំថាប្រសិនបើមុខងារបន្តនៅចន្លោះពេល ( ក, ខ) ឬមាននៅលើផ្នែក [ ក, ខ] នៃចំណុចមិនបន្តបន្ទាប់ ទ្រឹស្តីបទ 1, 2, 3 ឈប់ជាការពិតសម្រាប់មុខងារបែបនេះ។
សរុបសេចក្តី សូមពិចារណាទ្រឹស្តីបទស្តីពីអត្ថិភាពនៃអនុគមន៍បញ្ច្រាសមួយ។
សូមចាំថាចន្លោះពេលគឺជាផ្នែក ចន្លោះពេល ឬចន្លោះពេលពាក់កណ្តាលកំណត់ ឬគ្មានកំណត់។
 |
ទ្រឹស្តីបទ ៤. អនុញ្ញាតឱ្យមាន f(x) គឺបន្តនៅចន្លោះពេល Xកើនឡើង (ឬថយចុះ) ដោយ Xនិងមានជួរតម្លៃ យ. បន្ទាប់មកសម្រាប់មុខងារ y=f(x) មានមុខងារបញ្ច្រាស x= j(y) កំណត់នៅលើចន្លោះពេល យបន្តនិងបង្កើន (ឬថយចុះ) លើ យជាមួយនឹងអត្ថន័យជាច្រើន។ X.
មតិយោបល់. អនុញ្ញាតឱ្យមុខងារ x= j(y) គឺបញ្ច្រាសសម្រាប់មុខងារ f(x) ចាប់តាំងពីអាគុយម៉ង់ជាធម្មតាត្រូវបានតំណាងដោយ xនិងមុខងារតាមរយៈ yបន្ទាប់មកយើងសរសេរអនុគមន៍ច្រាសជា y=j(x).
ឧទាហរណ៍ ១. មុខងារ y=x 2 (រូបភាព 1.8, ក) នៅលើសំណុំ X= ប្រសិនបើវាបន្តនៅគ្រប់ចំណុចខាងក្នុងនៃផ្នែកនេះ ហើយនៅចុងបញ្ចប់របស់វា i.e. នៅចំនុច កនិង ខគឺបន្តនៅខាងស្តាំ និងខាងឆ្វេង រៀងគ្នា។
ទ្រឹស្តីបទ ១.មុខងារបន្តនៅលើផ្នែក [ ក, ខ] យ៉ាងហោចណាស់នៅចំណុចមួយនៃផ្នែកនេះយកតម្លៃធំបំផុត ហើយយ៉ាងហោចណាស់នៅចំណុចមួយ - តូចបំផុត។
ទ្រឹស្តីបទចែងថាប្រសិនបើមុខងារ y = f(x)បន្តនៅលើចន្លោះពេល [ ក, ខ] បន្ទាប់មកយ៉ាងហោចណាស់មានចំណុចមួយ។ x ១ Î [ ក, ខ] ដូចនេះតម្លៃនៃមុខងារ f(x)នៅចំណុចនេះនឹងជាតម្លៃធំបំផុតនៃតម្លៃទាំងអស់របស់វានៅលើផ្នែកនេះ៖ f(x1) ≥ f(x). ដូចគ្នានេះដែរមានចំណុចបែបនេះ x2ដែលក្នុងនោះតម្លៃនៃអនុគមន៍នឹងតូចបំផុតនៃតម្លៃទាំងអស់នៅលើផ្នែក៖ f(x 1) ≤ f(x).
វាច្បាស់ណាស់ថាវាអាចមានចំណុចបែបនេះជាច្រើនឧទាហរណ៍តួលេខបង្ហាញថាមុខងារ f(x)យកតម្លៃតូចបំផុតនៅពីរចំណុច x2និង x 2 ".
មតិយោបល់. សេចក្តីថ្លែងការណ៍នៃទ្រឹស្តីបទអាចក្លាយទៅជាមិនពិត ប្រសិនបើយើងពិចារណាតម្លៃនៃអនុគមន៍នៅលើចន្លោះពេល ( ក, ខ) ជាការពិតប្រសិនបើយើងពិចារណាមុខងារ y=xនៅលើ (0, 2) បន្ទាប់មកវាបន្តនៅលើចន្លោះពេលនេះ ប៉ុន្តែមិនឈានដល់តម្លៃអតិបរមា ឬអប្បបរមារបស់វានៅក្នុងវាទេ៖ វាឈានដល់តម្លៃទាំងនេះនៅចុងបញ្ចប់នៃចន្លោះពេល ប៉ុន្តែចុងបញ្ចប់មិនមែនជារបស់យើងទេ។ តំបន់។
ដូចគ្នានេះផងដែរ ទ្រឹស្តីបទឈប់ជាការពិតសម្រាប់មុខងារមិនបន្ត។ ផ្តល់ឧទាហរណ៍មួយ។
ផលវិបាក។ប្រសិនបើមុខងារ f(x)បន្តនៅ [ ក, ខ] បន្ទាប់មកវាត្រូវបានកំណត់នៅលើចន្លោះពេលនេះ។
ទ្រឹស្តីបទ ២.អនុញ្ញាតឱ្យមុខងារ y = f(x)បន្តនៅលើចន្លោះពេល [ ក, ខ] ហើយយកតម្លៃនៃសញ្ញាផ្សេងគ្នានៅចុងផ្នែកនេះ បន្ទាប់មកមានយ៉ាងហោចណាស់មួយចំណុចនៅខាងក្នុងផ្នែក x=Cកន្លែងដែលមុខងារបាត់៖ f(C)= 0 ដែល ក< C< b

ទ្រឹស្តីបទនេះមានអត្ថន័យធរណីមាត្រសាមញ្ញ៖ ប្រសិនបើចំនុចនៃក្រាហ្វនៃអនុគមន៍បន្ត y = f(x)ដែលត្រូវគ្នាទៅនឹងចុងបញ្ចប់នៃផ្នែក [ ក, ខ] ដេកនៅលើជ្រុងម្ខាងនៃអ័ក្ស គោបន្ទាប់មកក្រាហ្វនេះយ៉ាងហោចណាស់នៅចំណុចមួយនៃផ្នែកកាត់អ័ក្ស គោ. មុខងារមិនបន្តអាចមិនមានទ្រព្យសម្បត្តិនេះទេ។
ទ្រឹស្តីបទនេះទទួលយកការទូទៅដូចខាងក្រោម។
ទ្រឹស្តីបទ ៣ (ទ្រឹស្តីបទស្តីពីតម្លៃមធ្យម)។អនុញ្ញាតឱ្យមុខងារ y = f(x)បន្តនៅលើចន្លោះពេល [ ក, ខ] និង f(a) = ក, f (b) = ខ. បន្ទាប់មកសម្រាប់លេខណាមួយ។ គរវាង កនិង ខមានចំណុចបែបនេះនៅក្នុងផ្នែកនេះ។ គÎ [ ក, ខ] អ្វី f (c) = គ.

ទ្រឹស្តីបទនេះគឺជាក់ស្តែងតាមធរណីមាត្រ។ ពិចារណាក្រាហ្វនៃមុខងារ y = f(x). អនុញ្ញាតឱ្យមាន f(a) = ក, f (b) = ខ. បន្ទាប់មកបន្ទាត់ណាមួយ។ y=Cកន្លែងណា គ- លេខណាមួយរវាង កនិង ខ, ប្រសព្វក្រាហ្វនៃអនុគមន៍យ៉ាងហោចណាស់នៅចំណុចមួយ។ abscissa នៃចំនុចប្រសព្វនឹងជាតម្លៃនោះ។ x=Cនៅឯណា f (c) = គ.
ដូច្នេះ មុខងារបន្តមួយ ឆ្លងកាត់ពីតម្លៃមួយទៅតម្លៃមួយទៀត ចាំបាច់ឆ្លងកាត់តម្លៃមធ្យមទាំងអស់។ ជាពិសេស:
ផលវិបាក។ប្រសិនបើមុខងារ y = f(x)គឺបន្តនៅចន្លោះពេលខ្លះ ហើយទទួលយកតម្លៃធំបំផុត និងតូចបំផុត បន្ទាប់មកនៅចន្លោះពេលនេះ វាត្រូវចំណាយពេលយ៉ាងហោចណាស់ម្តង តម្លៃណាមួយរវាងតម្លៃតូចបំផុត និងធំបំផុតរបស់វា។
ដេរីវេ និងកម្មវិធីរបស់វា។ និយមន័យដេរីវេ
តោះមានមុខងារខ្លះ y=f(x),កំណត់នៅចន្លោះពេលខ្លះ។ សម្រាប់តម្លៃអាគុយម៉ង់នីមួយៗ xពីចន្លោះពេលនេះមុខងារ y=f(x)មានអត្ថន័យជាក់លាក់។
ពិចារណាតម្លៃអាគុយម៉ង់ពីរ៖ ដំបូង x 0 និងថ្មី។ x.

ភាពខុសគ្នា x–x 0 ត្រូវបានគេហៅថា ការបង្កើនអាគុយម៉ង់ xនៅចំណុច x 0 និងតំណាង Δx. ដូច្នេះ ∆x = x − x 0 (ការបង្កើនអាគុយម៉ង់អាចជាវិជ្ជមាន ឬអវិជ្ជមាន)។ ពីសមភាពនេះវាធ្វើតាមនោះ។ x=x 0 +Δx, i.e. តម្លៃដំបូងនៃអថេរបានទទួលការបន្ថែមមួយចំនួន។ បន្ទាប់មកប្រសិនបើនៅចំណុច x 0 តម្លៃមុខងារគឺ f(x 0 ), បន្ទាប់មកនៅចំណុចថ្មី។ xមុខងារនឹងយកតម្លៃ f(x) = f(x 0 +∆x).
ភាពខុសគ្នា y-y 0 = f(x) – f(x 0 ) បានហៅ ការបង្កើនមុខងារ y = f(x)នៅចំណុច x 0 និងត្រូវបានតំណាងដោយនិមិត្តសញ្ញា Δy. ដូច្នេះ
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ) . | (1) |
ជាធម្មតាតម្លៃដំបូងនៃអាគុយម៉ង់ x 0 ត្រូវបានចាត់ទុកថាថេរ និងតម្លៃថ្មី។ x- អថេរ។ បន្ទាប់មក y 0 = f(x 0 ) ប្រែទៅជាថេរនិង y = f(x)- អថេរ។ ការកើនឡើង Δyនិង Δxក៏នឹងក្លាយជាអថេរ ហើយរូបមន្ត (1) បង្ហាញថា ឌីគឺជាមុខងារនៃអថេរ Δx.
ផ្សំសមាមាត្រនៃការកើនឡើងនៃអនុគមន៍ទៅនឹងការកើនឡើងនៃអាគុយម៉ង់
អនុញ្ញាតឱ្យយើងរកឃើញដែនកំណត់នៃទំនាក់ទំនងនេះនៅ Δx→0. ប្រសិនបើដែនកំណត់នេះមាន នោះវាត្រូវបានគេហៅថាដេរីវេនៃមុខងារនេះ។ f(x)នៅចំណុច x 0 និងសម្គាល់ f "(x 0). ដូច្នេះ
ដេរីវេមុខងារនេះ។ y = f(x)នៅចំណុច x 0 ត្រូវបានគេហៅថាដែនកំណត់នៃសមាមាត្របង្កើននៃអនុគមន៍Δ yដល់ការកើនឡើងនៃអាគុយម៉ង់ Δ xនៅពេលក្រោយមានទំនោរទៅសូន្យតាមអំពើចិត្ត។
ចំណាំថាសម្រាប់មុខងារដូចគ្នា ដេរីវេនៅចំណុចផ្សេងគ្នា xអាចទទួលយកតម្លៃផ្សេងគ្នា, i.e. ដេរីវេអាចត្រូវបានគេគិតថាជាមុខងារនៃអាគុយម៉ង់ x. មុខងារនេះត្រូវបានសម្គាល់ f "(x)
ដេរីវេត្រូវបានតំណាងដោយនិមិត្តសញ្ញា f "(x), y", . តម្លៃជាក់លាក់នៃដេរីវេនៅ x = កតំណាង f "(ក) ឬ y "| x=a.
ប្រតិបត្តិការនៃការស្វែងរកដេរីវេនៃអនុគមន៍មួយ។ f(x)ត្រូវបានគេហៅថាភាពខុសគ្នានៃមុខងារនេះ។
ដើម្បីស្វែងរកដោយផ្ទាល់នូវដេរីវេតាមនិយមន័យ អ្នកអាចអនុវត្តដូចខាងក្រោម ច្បាប់នៃមេដៃ:
ឧទាហរណ៍។
អត្ថន័យមេកានិកនៃដេរីវេ
វាត្រូវបានគេស្គាល់ពីរូបវិទ្យាថាច្បាប់នៃចលនាឯកសណ្ឋានមានទម្រង់ s = v tកន្លែងណា ស- ផ្លូវបានធ្វើដំណើរដល់ចំណុចទាន់ពេលវេលា t, vគឺជាល្បឿននៃចលនាឯកសណ្ឋាន។
ទោះយ៉ាងណាក៏ដោយចាប់តាំងពី ភាគច្រើននៃចលនាដែលកើតឡើងនៅក្នុងធម្មជាតិគឺមិនស្មើគ្នា បន្ទាប់មកនៅក្នុងករណីទូទៅ ល្បឿន ហើយជាលទ្ធផល ចម្ងាយ សនឹងអាស្រ័យលើពេលវេលា t, i.e. នឹងជាមុខងារនៃពេលវេលា។
ដូច្នេះសូមឲ្យចំណុចសម្ភារៈរំកិលត្រង់ក្នុងទិសមួយទៅតាមច្បាប់ s=s(t)។
ចំណាំមួយភ្លែតនៅក្នុងពេលវេលា t 0. ដោយចំណុចនេះចំណុចបានឆ្លងកាត់ផ្លូវ s=s(t 0 ). ចូរយើងកំណត់ល្បឿន vចំណុចសម្ភារៈនៅពេល t 0 .
ដើម្បីធ្វើដូច្នេះ សូមពិចារណាពេលវេលាផ្សេងទៀតនៅក្នុងពេលវេលា t 0 + Δ t. វាត្រូវនឹងចម្ងាយដែលបានធ្វើដំណើរ s =s(t 0 + Δ t) បន្ទាប់មកសម្រាប់ចន្លោះពេល Δ tចំណុចបានធ្វើដំណើរតាមផ្លូវ Δs =s(t 0 + Δ t)–s(t)
ចូរយើងពិចារណាទំនាក់ទំនង។ វាត្រូវបានគេហៅថាល្បឿនមធ្យមក្នុងចន្លោះពេល Δ t. ល្បឿនមធ្យមមិនអាចកំណត់លក្ខណៈល្បឿននៃចលនានៃចំណុចណាមួយបានត្រឹមត្រូវទេនៅពេលនេះ t 0 (ដោយសារតែចលនាមិនស្មើគ្នា) ។ ដើម្បីបង្ហាញឱ្យកាន់តែច្បាស់នូវល្បឿនពិតនេះដោយប្រើល្បឿនមធ្យម អ្នកត្រូវប្រើចន្លោះពេលតូចជាង Δ t.
ដូច្នេះល្បឿននៃចលនានៅពេលកំណត់ t 0 (ល្បឿនភ្លាមៗ) គឺជាដែនកំណត់នៃល្បឿនមធ្យមក្នុងចន្លោះពេលពី t 0 ទៅ t 0 +Δ tនៅពេលដែល Δ t→0:
![]() ,
,
ទាំងនោះ។ ល្បឿននៃចលនាមិនស្មើគ្នាគឺជាដេរីវេនៃចម្ងាយធ្វើដំណើរដោយគោរពតាមពេលវេលា។

អត្ថន័យធរណីមាត្រនៃដេរីវេ
ចូរយើងណែនាំនិយមន័យនៃតង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ។
សូមឱ្យយើងមានខ្សែកោងនិងចំណុចថេរនៅលើវា។ ម ០(សូមមើលរូប) សូមពិចារណាចំណុចមួយទៀត មខ្សែកោងនេះហើយគូរវិនាទី ម 0 ម. ប្រសិនបើចំណុច មចាប់ផ្តើមផ្លាស់ទីតាមខ្សែកោង និងចំណុច ម ០នៅស្ថានភាព ឃ្លាផ្លាស់ប្តូរទីតាំងរបស់ខ្លួន។ ប្រសិនបើជាមួយនឹងការប៉ាន់ស្មានគ្មានដែនកំណត់នៃចំណុច មកោងទៅចំណុច ម ០នៅផ្នែកខាងណាមួយ សេកមានទំនោរទៅរកទីតាំងនៃបន្ទាត់ត្រង់ជាក់លាក់មួយ។ ម 0 ធបន្ទាប់មកបន្ទាត់ត្រង់ ម 0 ធត្រូវបានគេហៅថាតង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ ម ០.
នោះ., តង់សង់ទៅខ្សែកោងនៅចំណុចដែលបានផ្តល់ឱ្យ ម ០ហៅថាទីតាំងកំណត់នៃសេកាន ម 0 មនៅពេលដែលចំណុច មទំនោរតាមបណ្តោយខ្សែកោងទៅចំណុចមួយ។ ម ០.
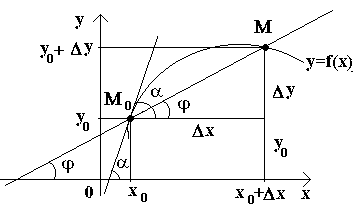
ឥឡូវនេះសូមពិចារណាអំពីមុខងារបន្ត y=f(x)និងខ្សែកោងដែលត្រូវគ្នានឹងមុខងារនេះ។ សម្រាប់តម្លៃមួយចំនួន Xមុខងារ 0 យកតម្លៃមួយ។ y0=f(x0)។តម្លៃទាំងនេះ x 0 និង y 0 នៅលើខ្សែកោងត្រូវគ្នាទៅនឹងចំណុចមួយ។ M 0 (x 0; y 0) ។ចូរយើងផ្តល់អំណះអំណាង x0បង្កើន Δ X. តម្លៃថ្មីនៃអាគុយម៉ង់ត្រូវគ្នាទៅនឹងតម្លៃបន្ថែមនៃអនុគមន៍ y 0 +Δ y=f(x 0 –Δ x). យើងទទួលបានចំណុចមួយ។ ម(x ០+Δ x; y ០+Δ y)ចូរគូរឃ្លាមួយ ម 0 មនិងសម្គាល់ដោយ φ មុំដែលបង្កើតឡើងដោយសេកង់ជាមួយនឹងទិសដៅវិជ្ជមាននៃអ័ក្ស គោ. ចូរយើងបង្កើតទំនាក់ទំនងមួយ ហើយកត់សម្គាល់។
ប្រសិនបើឥឡូវនេះ Δ x→ 0 បន្ទាប់មកដោយសារតែការបន្តនៃអនុគមន៍ Δ នៅ→0 ហើយដូច្នេះចំណុច មផ្លាស់ទីតាមខ្សែកោង ចូលទៅជិតចំណុចមិនកំណត់ ម ០. បន្ទាប់មកសេក ម 0 មទំនោរនឹងយកទីតាំងនៃតង់សង់ទៅខ្សែកោងនៅចំណុច ម ០, និងមុំφ→αនៅΔ x→0 ដែល α បង្ហាញពីមុំរវាងតង់សង់ និងទិសដៅវិជ្ជមាននៃអ័ក្ស គោ. ដោយសារអនុគមន៍ tg φ បន្តអាស្រ័យលើφនៅφ≠π/2 បន្ទាប់មកនៅφ→α tg φ→ tg α ហើយដូច្នេះជម្រាលនៃតង់សង់នឹងមានៈ
![]()
ទាំងនោះ។ f"(x)= tgα ។
ដូច្នេះធរណីមាត្រ y "(x 0)តំណាងឱ្យជម្រាលនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍នេះនៅចំណុច x0, i.e. សម្រាប់តម្លៃដែលបានផ្តល់ឱ្យនៃអាគុយម៉ង់ xដេរីវេគឺស្មើនឹងតង់ហ្សង់នៃមុំដែលបង្កើតឡើងដោយតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ f(x)នៅចំណុចដែលត្រូវគ្នា។ M 0 (x; y)ជាមួយនឹងទិសដៅអ័ក្សវិជ្ជមាន គោ។
ឧទាហរណ៍។ស្វែងរកជម្រាលនៃតង់សង់ទៅខ្សែកោង y = x 2 នៅចំណុច ម(-1; 1).
យើងបានឃើញរួចហើយថា ( x 2)" = 2X. ប៉ុន្តែជម្រាលនៃតង់សង់ទៅខ្សែកោងគឺ tg α = y"|x=-1=-2.
ភាពខុសគ្នានៃមុខងារ។ ការបន្តនៃមុខងារដែលអាចផ្លាស់ប្តូរបាន។
មុខងារ y=f(x)បានហៅ ខុសគ្នានៅចំណុចណាមួយ។ x 0 ប្រសិនបើវាមានដេរីវេជាក់លាក់នៅចំណុចនេះ i.e. ប្រសិនបើដែនកំណត់នៃទំនាក់ទំនងមាន ហើយមានកំណត់។
ប្រសិនបើមុខងារអាចខុសគ្នានៅគ្រប់ចំណុចនៃផ្នែកខ្លះ [ ក; ខ] ឬចន្លោះពេល ( ក; ខ) បន្ទាប់មកពួកគេនិយាយថាវា។ ខុសគ្នានៅលើផ្នែក [ ក; ខ] ឬរៀងគ្នាក្នុងចន្លោះពេល ( ក; ខ).
ទ្រឹស្តីបទខាងក្រោមមានសុពលភាព ដែលបង្កើតការតភ្ជាប់រវាងមុខងារផ្សេងគ្នា និងបន្ត។
ទ្រឹស្តីបទ។ប្រសិនបើមុខងារ y=f(x)ខុសគ្នាត្រង់ចំណុចណាមួយ។ x0បន្ទាប់មកវាបន្តនៅចំណុចនេះ។
ដូច្នេះ ភាពខុសគ្នានៃមុខងារបង្កប់ន័យបន្តរបស់វា។
ភស្តុតាង. ប្រសិនបើ ក ![]() បន្ទាប់មក
បន្ទាប់មក
![]() ,
,
ដែល α គឺជាតម្លៃគ្មានកំណត់ ពោលគឺឧ។ បរិមាណទំនោរទៅសូន្យនៅ Δ x→0. ប៉ុន្តែបន្ទាប់មក
Δ y=f "(x0) Δ x+αΔ x=> Δ y→ 0 នៅ Δ x→ 0, ឧ។ f(x) - f(x0)→ 0 នៅ x→x 0 ដែលមានន័យថាមុខងារ f(x)បន្តនៅចំណុច x 0. Q.E.D.
ដូច្នេះ នៅចំនុចដាច់ មុខងារមិនអាចមានដេរីវេទេ។ សេចក្តីថ្លែងការសន្ទនាគឺមិនពិតទេ៖ មានមុខងារបន្តដែលមិនមានភាពខុសគ្នានៅចំណុចមួយចំនួន (នោះគឺពួកគេមិនមានដេរីវេនៅចំណុចទាំងនេះទេ)។
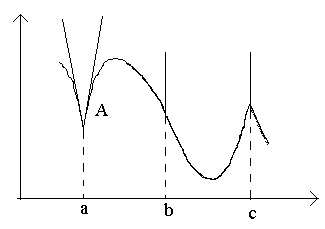
ពិចារណាចំណុចនៅក្នុងរូបភាព ក, ខ, គ។
នៅចំណុច កនៅ Δ x→0 ទំនាក់ទំនងមិនមានដែនកំណត់ទេ (ព្រោះដែនកំណត់ម្ខាងគឺខុសគ្នាសម្រាប់ Δ x→ 0–0 និង Δ x→0+0)។ នៅចំណុច កក្រាហ្វមិនមានតង់សង់ដែលបានកំណត់ទេ ប៉ុន្តែមានតង់សង់ម្ខាងពីរផ្សេងគ្នាដែលមានជម្រាល ទៅ 1 និង ទៅ២. ចំណុចប្រភេទនេះត្រូវបានគេហៅថា ចំណុចជ្រុង។
នៅចំណុច ខនៅ Δ x→ 0 សមាមាត្រគឺជាសញ្ញាថេរ តម្លៃដ៏ធំគ្មានកំណត់។ អនុគមន៍មានដេរីវេគ្មានកំណត់។ នៅចំណុចនេះ ក្រាហ្វមានតង់សង់បញ្ឈរ។ ប្រភេទចំណុច - "ចំណុចបញ្ឆេះ" ដែលមានតង់សង់បញ្ឈរ។
នៅចំណុច គនិស្សន្ទវត្ថុម្ខាងគឺមានចំនួនច្រើនឥតកំណត់នៃសញ្ញាផ្សេងគ្នា។ នៅចំណុចនេះ ក្រាហ្វមានតង់សង់បញ្ឈរពីរបញ្ចូលគ្នា។ ប្រភេទ - "cusp" ជាមួយតង់សង់បញ្ឈរ - ករណីពិសេសនៃចំណុចជ្រុង។

