តម្លៃរំពឹងទុក។ ការរំពឹងទុកគណិតវិទ្យាអថេរចៃដន្យដាច់ដោយឡែក Xដែលយកចំនួនកំណត់នៃតម្លៃ Xខ្ញុំជាមួយនឹងប្រូបាប៊ីលីតេ រខ្ញុំ, ត្រូវបានគេហៅថាផលបូក:

ការរំពឹងទុកគណិតវិទ្យាអថេរចៃដន្យបន្ត Xត្រូវបានគេហៅថាអាំងតេក្រាលនៃផលិតផលនៃតម្លៃរបស់វា។ Xនៅលើដង់ស៊ីតេនៃការចែកចាយប្រូបាប៊ីលីតេ f(x):

(6ខ)

អាំងតេក្រាល​មិន​ត្រឹមត្រូវ (៦ ខ) ត្រូវ​បាន​សន្មត​ថា​ជា​ការ​រួម​គ្នា​យ៉ាង​ពិត​ប្រាកដ (បើ​មិន​ដូច្នេះ​ទេ​យើង​និយាយ​ថា​ការ​រំពឹង​ទុក​ ម(X) មិន​មាន​ទេ)។ ការរំពឹងទុកគណិតវិទ្យាមានលក្ខណៈពិសេស មធ្យមអថេរចៃដន្យ X. វិមាត្ររបស់វាស្របគ្នានឹងវិមាត្រនៃអថេរចៃដន្យ។

លក្ខណៈសម្បត្តិនៃការរំពឹងទុកគណិតវិទ្យា៖

ការបែកខ្ញែក។ ការបែកខ្ញែកអថេរចៃដន្យ Xលេខត្រូវបានគេហៅថា:

ការបែកខ្ញែកគឺ លក្ខណៈនៃការបែកខ្ញែកតម្លៃនៃអថេរចៃដន្យ Xទាក់ទងទៅនឹងតម្លៃមធ្យមរបស់វា។ ម(X) វិមាត្រនៃវ៉ារ្យង់គឺស្មើនឹងវិមាត្រនៃអថេរចៃដន្យការ៉េ។ ដោយផ្អែកលើនិយមន័យនៃវ៉ារ្យង់ (8) និងការរំពឹងទុកគណិតវិទ្យា (5) សម្រាប់អថេរចៃដន្យដាច់ដោយឡែក និង (6) សម្រាប់អថេរចៃដន្យបន្ត យើងទទួលបានកន្សោមស្រដៀងគ្នាសម្រាប់វ៉ារ្យ៉ង់៖

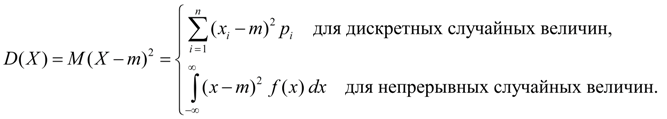(9)

នៅទីនេះ ម = ម(X).

លក្ខណៈសម្បត្តិបែកខ្ញែក៖

គម្លាតស្តង់ដារ៖

(11)

ដោយសារវិមាត្រនៃគម្លាតស្តង់ដារគឺដូចគ្នាទៅនឹងអថេរចៃដន្យ វាញឹកញាប់ជាងវ៉ារ្យង់ដែលប្រើជារង្វាស់នៃការបែកខ្ចាត់ខ្ចាយ។

ពេលចែកចាយ។ គោលគំនិតនៃការរំពឹងទុកគណិតវិទ្យា និងបំរែបំរួលគឺជាករណីពិសេសនៃគោលគំនិតទូទៅសម្រាប់លក្ខណៈលេខនៃអថេរចៃដន្យ - ពេលចែកចាយ. ពេលចែកចាយនៃអថេរចៃដន្យត្រូវបានណែនាំជាការរំពឹងទុកគណិតវិទ្យានៃមុខងារសាមញ្ញមួយចំនួននៃអថេរចៃដន្យ។ ដូច្នេះ, ពេលនៃលំដាប់ kទាក់ទងទៅនឹងចំណុច X 0 ត្រូវបានគេហៅថាការរំពឹងទុក ម(X–X 0 )k. ពេលវេលាទាក់ទងនឹងប្រភពដើម X= 0 ត្រូវបានគេហៅថា គ្រាដំបូងហើយត្រូវបានសម្គាល់៖

(12)

ពេលដំបូងនៃលំដាប់ទីមួយគឺជាមជ្ឈមណ្ឌលចែកចាយនៃអថេរចៃដន្យដែលត្រូវបានពិចារណា៖

(13)

ពេលវេលាទាក់ទងនឹងមជ្ឈមណ្ឌលចែកចាយ X= មបានហៅ ចំណុចកណ្តាលហើយត្រូវបានសម្គាល់៖

(14)

ពី (7) វាដូចខាងក្រោមថាពេលកណ្តាលនៃលំដាប់ទីមួយតែងតែស្មើនឹងសូន្យ:

គ្រាកណ្តាលមិនអាស្រ័យលើប្រភពដើមនៃតម្លៃនៃអថេរចៃដន្យនោះទេ ចាប់តាំងពីជាមួយនឹងការផ្លាស់ប្តូរដោយតម្លៃថេរ។ ជាមួយកណ្តាលនៃការចែកចាយរបស់វាត្រូវបានផ្លាស់ប្តូរដោយតម្លៃដូចគ្នា។ ជាមួយហើយគម្លាតពីចំណុចកណ្តាលមិនផ្លាស់ប្តូរទេ៖ X – ម = (X – ជាមួយ) – (ម – ជាមួយ).
ឥឡូវនេះវាច្បាស់ណាស់។ ការបែកខ្ញែក- នេះ។ ពេលកណ្តាលលំដាប់ទីពីរ:

ភាពមិនស៊ីមេទ្រី។ ពេលកណ្តាលនៃលំដាប់ទីបី:

(17)

បម្រើដើម្បីវាយតម្លៃ ភាពមិនច្បាស់នៃការចែកចាយ. ប្រសិនបើការបែងចែកគឺស៊ីមេទ្រីអំពីចំណុច X= មបន្ទាប់មកពេលកណ្តាលនៃលំដាប់ទីបីនឹងស្មើនឹងសូន្យ (ក៏ដូចជាពេលកណ្តាលនៃការបញ្ជាទិញសេសទាំងអស់)។ ដូច្នេះ ប្រសិនបើពេលកណ្តាលនៃលំដាប់ទីបីខុសពីសូន្យ នោះការចែកចាយមិនអាចស៊ីមេទ្រីបានទេ។ ទំហំនៃការ asymmetry ត្រូវបានប៉ាន់ប្រមាណដោយប្រើវិមាត្រ មេគុណ asymmetry:

(18)

សញ្ញានៃមេគុណ asymmetry (18) បង្ហាញពី asymmetry ផ្នែកខាងស្តាំ ឬខាងឆ្វេង (រូបភាព 2) ។

អង្ករ។ 2. ប្រភេទនៃ asymmetry នៃការចែកចាយ។

លើស។ ពេលកណ្តាលនៃលំដាប់ទីបួន៖

(19)

បម្រើដើម្បីវាយតម្លៃអ្វីដែលគេហៅថា kurtosisដែលកំណត់កម្រិតនៃភាពចោត (ចង្អុល) នៃខ្សែកោងចែកចាយនៅជិតមជ្ឈមណ្ឌលចែកចាយ ដោយគោរពតាមខ្សែកោងចែកចាយធម្មតា។ ចាប់តាំងពីសម្រាប់ការចែកចាយធម្មតាបរិមាណដែលបានយកជា kurtosis គឺ:

(20)

នៅលើរូបភព។ 3 បង្ហាញឧទាហរណ៍នៃខ្សែកោងការចែកចាយជាមួយនឹងតម្លៃផ្សេងគ្នានៃ kurtosis ។ សម្រាប់ការចែកចាយធម្មតា។ អ៊ី= 0. ខ្សែកោងដែលមានកំពូលខ្ពស់ជាងធម្មតាមាន kurtosis វិជ្ជមាន ហើយអ្នកដែលមានកំពូលរាបស្មើមាន kurtosis អវិជ្ជមាន។

អង្ករ។ 3. ខ្សែកោងចែកចាយដែលមានកម្រិតនៃភាពចោតខុសៗគ្នា (kurtosis) ។

ពេលវេលាលំដាប់ខ្ពស់នៅក្នុងកម្មវិធីវិស្វកម្មនៃស្ថិតិគណិតវិទ្យាជាធម្មតាមិនត្រូវបានប្រើទេ។

ម៉ូដ ដាច់អថេរចៃដន្យ គឺជាតម្លៃដែលទំនងបំផុតរបស់វា។ ម៉ូដ បន្តអថេរចៃដន្យគឺជាតម្លៃរបស់វាដែលដង់ស៊ីតេប្រូបាប៊ីលីតេអតិបរមា (រូបភាពទី 2) ។ ប្រសិនបើខ្សែកោងការចែកចាយមានអតិបរមាមួយ នោះការចែកចាយត្រូវបានគេហៅថា មិនធម្មតា. ប្រសិនបើខ្សែកោងការចែកចាយមានច្រើនជាងមួយអតិបរមា នោះការចែកចាយត្រូវបានគេហៅថា polymodal. ពេលខ្លះមានការចែកចាយដែលខ្សែកោងមិនមានអតិបរមា ប៉ុន្តែអប្បបរមា។ ការចែកចាយបែបនេះត្រូវបានគេហៅថា ថ្នាំប្រឆាំងមេរោគ. ក្នុង​ករណី​ទូទៅ របៀប​និង​ការ​រំពឹង​ទុក​តាម​គណិតវិទ្យា​នៃ​អថេរ​ចៃដន្យ​មិន​ស្រប​គ្នា។ ក្នុងករណីជាក់លាក់មួយសម្រាប់ ម៉ូឌុល, i.e. មានរបៀបមួយ ការចែកចាយស៊ីមេទ្រី ហើយផ្តល់ថាមានការរំពឹងទុកតាមគណិតវិទ្យា ក្រោយមកទៀតស្របគ្នាជាមួយនឹងរបៀប និងចំណុចកណ្តាលនៃស៊ីមេទ្រីនៃការចែកចាយ។

មធ្យម អថេរចៃដន្យ Xគឺជាអត្ថន័យរបស់វា។ ខ្ញុំដែលសមភាពទទួលបាន៖ i.e. វាទំនងជាស្មើគ្នាដែលអថេរចៃដន្យ Xនឹងតិចឬច្រើន។ ខ្ញុំ. ធរណីមាត្រ មធ្យមគឺជា abscissa នៃចំណុចដែលតំបន់នៅក្រោមខ្សែកោងចែកចាយត្រូវបានបែងចែកជាពាក់កណ្តាល (រូបភាព 2) ។ នៅក្នុងករណីនៃការចែកចាយម៉ូឌុលស៊ីមេទ្រី មធ្យម របៀប និងមធ្យមគឺដូចគ្នា។

របៀបគឺជាតម្លៃដែលទំនងបំផុតនៃអថេរចៃដន្យ។ ជាមួយនឹងការចែកចាយស៊ីមេទ្រីទាក់ទងនឹងមធ្យម របៀបនេះស្របគ្នានឹងការរំពឹងទុកគណិតវិទ្យា។ ប្រសិនបើតម្លៃនៃអថេរចៃដន្យមិនធ្វើម្តងទៀតនោះ គ្មានរបៀបទេ។

ចំណុចនៅលើអ័ក្ស x ដែលត្រូវគ្នានឹងអតិបរមានៃខ្សែកោងដង់ស៊ីតេនៃការចែកចាយត្រូវបានគេហៅថា របៀប ពោលគឺ របៀបគឺជាតម្លៃដែលទំនងបំផុតនៃអថេរចៃដន្យ។ ទោះយ៉ាងណាក៏ដោយ របៀបមិនមានសម្រាប់ការចែកចាយទាំងអស់ទេ។ ឧទាហរណ៍មួយគឺការចែកចាយឯកសណ្ឋាន។ ក្នុងករណីនេះនិយមន័យនៃមជ្ឈមណ្ឌលចែកចាយជារបៀបគឺមិនអាចទៅរួចទេ។ ម៉ូតត្រូវបានសំដៅជាទូទៅថាជា Mo ។

មានគោលគំនិតនៃរបៀប និងមធ្យមនៃអថេរចៃដន្យ។

វាច្បាស់ណាស់ថានៅក្នុងករណីនៃមេដ្យានស៊ីមេទ្រីស្របគ្នាជាមួយនឹងរបៀបនិងការរំពឹងទុកគណិតវិទ្យា។

ដោយផ្អែកលើការពិតដែលថារបៀបមិនផ្អែកលើការវាស់វែងតែមួយទេ ប៉ុន្តែនៅលើបរិមាណដ៏ធំនៃការសង្កេត វាមិនអាចត្រូវបានចាត់ទុកថាជាអថេរចៃដន្យនោះទេ។ ទំហំនៃរបៀបមិនត្រូវបានប៉ះពាល់ដោយប្រភេទផ្សេងៗនៃការពន្យារពេលក្នុងការងារ និងការបាត់បង់អត្រាធម្មតារបស់វា។

ពេលខ្លះនៅពេលវិភាគការចែកចាយជាក់ស្តែង គោលគំនិតនៃរបៀប និងមធ្យមនៃការចែកចាយត្រូវបានគេប្រើ "... Mode គឺជាតម្លៃដែលទំនងបំផុតនៃអថេរចៃដន្យ។

ការបកស្រាយប្រូបាប៊ីលីតេបន្ថែមនៃបាតុភូតឆ្នោតគឺជាគំនិតនៃការចែកចាយប្រូបាប៊ីលីតេនៃអថេរចៃដន្យ។ វាត្រូវបានប្រើដើម្បីកំណត់ប្រូបាប៊ីលីតេដែលអថេរចៃដន្យនឹងយកតម្លៃមួយឬផ្សេងទៀតនៃតម្លៃដែលអាចធ្វើបានរបស់វា។ សម្គាល់ដោយ y អថេរចៃដន្យ និងដោយ y តម្លៃដែលអាចធ្វើបានរបស់វា។ បន្ទាប់មកសម្រាប់អថេរចៃដន្យដាច់ដោយឡែក ដែលអាចទទួលយកតម្លៃដែលអាចធ្វើបាន Y, y2, US, ។ .., yn ទម្រង់ដ៏ងាយស្រួលនៃការចែកចាយប្រូបាប៊ីលីតេ គួរតែត្រូវបានចាត់ទុកថាជាការពឹងផ្អែក P(y = y) ដែលជាធម្មតាត្រូវបានគេហៅថាស៊េរីប្រូបាប៊ីលីតេ ស៊េរីការចែកចាយ n ។ នៅក្នុងការអនុវត្ត សម្រាប់ការវាយតម្លៃទូទៅនៃប្រតិបត្តិការនៃការបែងចែកប្រូបាប៊ីលីតេនៃតម្លៃហានិភ័យ អ្វីដែលគេហៅថាជាលេខ និងលក្ខណៈផ្សេងទៀតនៃការចែកចាយលទ្ធផលចៃដន្យត្រូវបានគេប្រើជាញឹកញាប់៖ ការរំពឹងទុកគណិតវិទ្យា វ៉ារ្យ៉ង់ គម្លាតស្តង់ដារ មេគុណបំរែបំរួល របៀប មធ្យម។ ។ល។ (សូមមើលឧទាហរណ៍ និងផ្សេងៗទៀត។ )។ ម្យ៉ាងវិញទៀត សម្រាប់ការយល់ឃើញរហ័ស និងទូលំទូលាយ សហគ្រិនស្វែងរក (ឬអ្នកសាមញ្ញ

ដោយផ្អែកលើទិន្នន័យរបស់គណៈកម្មាធិការស្ថិតិរដ្ឋនៃសហភាពសូវៀតស្តីពីការបែងចែកចំនួនប្រជាជនដោយប្រាក់ចំណូលសរុបសម្រាប់មនុស្សម្នាក់ យើងនឹងព្យាយាមប្រៀបធៀបសូចនាករនៃប្រាក់ចំណូលមធ្យម មធ្យម និងមធ្យម (តារាងទី 1)។ តារាងបង្ហាញថាប្រាក់ចំណូលជាមធ្យមក្នុងលក្ខខណ្ឌដាច់ខាតលើសពីចំណូលមធ្យម និងមធ្យម ហើយកំណើនរបស់វាកើតឡើងជាចម្បងដោយសារតែការកើនឡើងនៃសមាមាត្រនៃអ្នកដែលមានប្រាក់ចំណូលខ្ពស់ ពោលគឺការប្រើប្រាស់សូចនាករប្រាក់ចំណូលជាមធ្យមនាំឱ្យមានការប៉ាន់ប្រមាណយ៉ាងខ្លាំង។ នៃកម្រិតប្រាក់ចំណូលនៃចំនួនប្រជាជនភាគច្រើន និងក្នុងកម្រិតធំលាក់បាំងដំណើរការនៃភាពខុសគ្នារបស់ពួកគេ។ តម្លៃនៃប្រាក់ចំណូលតាមទម្រង់ ទំនាញឆ្ពោះទៅរកក្រុមចែកចាយទាប ហើយងាកចេញពីប្រាក់ចំណូលមធ្យមចុះក្រោម។ ទោះយ៉ាងណាក៏ដោយ ការវាយលុកនៃរបៀបក្នុងចន្លោះពេលមួយ ឬមួយផ្សេងទៀត ជាញឹកញាប់ចៃដន្យនៅក្នុងធម្មជាតិ ការផ្លាស់ប្តូរតិចតួចក្នុងការចែកចាយ - ហើយរបៀបនឹងស្ថិតនៅក្នុងចន្លោះពេលជិតខាងរួចហើយ។ ឧទាហរណ៍នៅឆ្នាំ 1989 កម្រិតប្រាក់ចំណូលទូទៅបំផុតគឺពី 100 ទៅ 125 រូប្លិ (16.1% នៃចំនួនប្រជាជនបានទទួលប្រាក់ចំណូលបែបនេះ) ប៉ុន្តែដោយសារតែការផ្លាស់ប្តូរតិចតួចនៃប្រាក់ចំណូលដែលបានកើតឡើងនៅក្នុង 1989-1990 ចន្លោះពេលទូទៅបំផុតបានប្រែទៅជា ចន្លោះពេលខាងក្រោម (125-150 rubles): ហើយតម្លៃនៃម៉ូដខ្លួនវាបានកើនឡើង 15,6 rubles ។ លើសពីនេះ ចំណែកនៃចំនួនប្រជាជននៅក្នុងចន្លោះពេលនៃប្រាក់ចំណូលម៉ូឌុលអាចលើសពីភាគហ៊ុនផ្សេងទៀតបន្តិច។

ដើម្បី​កំណត់​លក្ខណៈ​មជ្ឈមណ្ឌល​ចែកចាយ​នៃ​អថេរ​ចៃដន្យ​លោការីត​ធម្មតា​ a មួយ​អាច​ប្រើ​រួម​ជាមួយ​នឹង​ការ​រំពឹង​ទុក​ខាង​គណិត​វិទ្យា​ដែល​បាន​គណនា​រួច​ហើយ​ Ma ជា​របៀប

របៀប - ម៉ូដ។ តម្លៃដែលទំនងបំផុតនៃអថេរចៃដន្យ។

ម៉ូដ - គំនិត

បន្ថែមពីលើការរំពឹងទុក និងការបែងចែកតាមគណិតវិទ្យា លក្ខណៈលេខមួយចំនួនត្រូវបានប្រើប្រាស់ក្នុងទ្រឹស្តីប្រូបាប៊ីលីតេ ដែលឆ្លុះបញ្ចាំងពីលក្ខណៈជាក់លាក់នៃការចែកចាយ។

និយមន័យ។ របៀប Mo(X) នៃអថេរចៃដន្យ X គឺជាតម្លៃដែលទំនងបំផុតរបស់វា។(សម្រាប់ប្រូបាប៊ីលីតេ r rឬដង់ស៊ីតេប្រូបាប៊ីលីតេ

ប្រសិនបើប្រូបាប៊ីលីតេ ឬប្រូបាប៊ីលីតេនៃប្រូបាប៊ីលីតេឈានដល់អតិបរមាមិនមែនមួយទេ ប៉ុន្តែនៅចំណុចជាច្រើន ការចែកចាយត្រូវបានគេហៅថា polymodal(រូបភាព 3.13) ។

ម៉ូដ ស្លែ),ដែលប្រូបាប៊ីលីតេ R (ឬដង់ស៊ីតេប្រូបាប៊ីលីតេ (p(x)) ឈានដល់អតិបរមាសកល ត្រូវបានគេហៅថា តម្លៃទំនងបំផុត។អថេរចៃដន្យ (ក្នុងរូប ៣.១៣ នេះ។ Mo(X) ២).

និយមន័យ។ មធ្យម Me(X) នៃអថេរចៃដន្យ X គឺជាតម្លៃរបស់វា។, សម្រាប់អ្វីដែល

ទាំងនោះ។ ប្រូបាប៊ីលីតេដែលអថេរចៃដន្យ Xយកតម្លៃតិចជាងមធ្យម រោម)ឬធំជាងវា ដូចគ្នា និងស្មើ 1/2 ។ បន្ទាត់បញ្ឈរតាមធរណីមាត្រ X = រោម) ឆ្លងកាត់ចំនុចដែលមាន abscissa ស្មើនឹង រោម) បែងចែកផ្ទៃនៃតួរលេខនៃខ្សែកោងចែកចាយជាពីរផ្នែកស្មើគ្នា (រូបភាព 3.14)។ ជាក់ស្តែងនៅចំណុច X = រោម)មុខងារចែកចាយគឺស្មើនឹង 1/2, i.e. P(ខ្ញុំ(X))= 1/2 (រូបភាព 3.15) ។

ចំណាំទ្រព្យសម្បត្តិសំខាន់នៃមធ្យមនៃអថេរចៃដន្យ៖ ការរំពឹងទុកគណិតវិទ្យានៃតម្លៃដាច់ខាតនៃគម្លាតនៃអថេរចៃដន្យ X ពីតម្លៃថេរ C គឺតិចតួចបំផុតបន្ទាប់មក, នៅពេលដែល C ថេរនេះស្មើនឹងមធ្យម Me(X) = m, i.e.

(ទ្រព្យសម្បត្តិគឺស្រដៀងគ្នាទៅនឹងទ្រព្យសម្បត្តិ (3.10") នៃអប្បបរមានៃការ៉េមធ្យមនៃគម្លាតនៃអថេរចៃដន្យពីការរំពឹងទុកគណិតវិទ្យារបស់វា)។

O ឧទាហរណ៍ 3.15 ។ ស្វែងរករបៀប មធ្យម និងមធ្យមនៃអថេរចៃដន្យ X sដង់ស៊ីតេប្រូបាប៊ីលីតេ φ(x) = 3x 2 សម្រាប់ xx ។

ការសម្រេចចិត្ត។ខ្សែកោងការចែកចាយត្រូវបានបង្ហាញនៅក្នុងរូបភព។ ៣.១៦. ជាក់ស្តែង ដង់ស៊ីតេប្រូបាប៊ីលីតេ φ(x) គឺអតិបរមានៅ X= Mo(X) = 1.

មធ្យម រោម) = ខ យើងរកឃើញពីលក្ខខណ្ឌ (៣.២៨)៖

កន្លែងណា

ការរំពឹងទុកគណិតវិទ្យាត្រូវបានគណនាដោយរូបមន្ត (3.25)៖

ការរៀបចំពិន្ទុគ្នាទៅវិញទៅមក M(X) > ខ្ញុំ(X) និង ស្លែ) នៅក្នុងលំដាប់ឡើងនៃ abscissa ត្រូវបានបង្ហាញនៅក្នុងរូបភព។ ៣.១៦. ?

រួមជាមួយនឹងលក្ខណៈលេខដែលបានកត់សម្គាល់ខាងលើ គោលគំនិតនៃបរិមាណ និងពិន្ទុភាគរយត្រូវបានប្រើដើម្បីពិពណ៌នាអថេរចៃដន្យមួយ។

និយមន័យ។ កម្រិតបរិមាណ y-quantile )

ត្រូវបានគេហៅថាតម្លៃ x q នៃអថេរចៃដន្យ , ដែលមុខងារចែកចាយរបស់វាយកតម្លៃស្មើនឹង d, i.e.

បរិមាណមួយចំនួនបានទទួលឈ្មោះពិសេស។ ជាក់ស្តែងខាងលើ មធ្យម អថេរចៃដន្យគឺ 0.5 កម្រិត quantile, i.e. ខ្ញុំ (X) \u003d x 05 ។ quantiles dg 0 2 5 និង x 075 ត្រូវបានគេដាក់ឈ្មោះរៀងៗខ្លួន ទាបជាង និង ត្រីមាសខាងលើK

ទាក់ទងយ៉ាងជិតស្និទ្ធទៅនឹងគោលគំនិតនៃបរិមាណគឺជាគំនិត ពិន្ទុភាគរយ។នៅក្រោម ចំណុច YuOuHo-noi បរិមាណបង្កប់ន័យ x x (( , ទាំងនោះ។ តម្លៃនៃអថេរចៃដន្យមួយ។ x, នៅក្រោមនោះ។

0 ឧទាហរណ៍ 3.16 ។ យោងតាមឧទាហរណ៍ 3.15 ស្វែងរកបរិមាណ x ០៣ និង 30% ចំណុចអថេរចៃដន្យ x.

ការសម្រេចចិត្ត។ យោងតាមរូបមន្ត (3.23) មុខងារចែកចាយ

យើងរកឃើញបរិមាណ r 0 z ពីសមីការ (3.29) i.e. x$៣ \u003d 0.3 ពីកន្លែងដែល L "oz -0.67 ។ ស្វែងរកចំណុច 30% នៃអថេរចៃដន្យ x, ឬបរិមាណ x 0 7 ពីសមីការ x$7 = 0.7, whence x 0 7 "0.89 ។ ?

ក្នុង​ចំណោម​លក្ខណៈ​លេខ​នៃ​អថេរ​ចៃដន្យ គ្រា​ដំបូង និង​កណ្តាល​គឺ​មាន​សារៈសំខាន់​ជា​ពិសេស។

និយមន័យ។ ពេលចាប់ផ្តើមលំដាប់ k-th នៃអថេរចៃដន្យ X គឺជាការរំពឹងទុកតាមគណិតវិទ្យានៃអំណាច k-th នៃអថេរនេះ :

និយមន័យ។ ពេលកណ្តាលលំដាប់ k-th នៃអថេរចៃដន្យ X គឺជាការរំពឹងទុកគណិតវិទ្យានៃកម្រិត k-th នៃគម្លាតនៃអថេរចៃដន្យ X ពីការរំពឹងទុកគណិតវិទ្យារបស់វា។:

រូបមន្តសម្រាប់គណនាគ្រាសម្រាប់អថេរចៃដន្យដាច់ដោយឡែក (យកតម្លៃ x ១ ជាមួយនឹងប្រូបាប៊ីលីតេ p,) និងបន្ត (ជាមួយនឹងដង់ស៊ីតេប្រូបាប៊ីលីតេ cp(x)) ត្រូវបានផ្តល់ឱ្យក្នុងតារាង។ ៣.១.

តារាង 3.1

វាងាយស្រួលមើលថានៅពេលណា k = 1 ពេលដំបូងនៃអថេរចៃដន្យ Xគឺជាការរំពឹងទុកគណិតវិទ្យារបស់វា, i.e. h x \u003d M [X) \u003d a,នៅ ទៅ= 2 គ្រាកណ្តាលទីពីរគឺការបែកខ្ញែក, i.e. ទំ 2 = T)(X)។

គ្រាកណ្តាល p A អាចត្រូវបានបញ្ជាក់នៅក្នុងលក្ខខណ្ឌនៃគ្រាដំបូងដោយប្រើរូបមន្ត៖

ល។

ឧទាហរណ៍ គ ៣ \u003d M (X-a) * \u003d M (X * -ZaX 2 + Za 2 X-a-\u003e) \u003d M (X *) ~ -ZaM (X 2) + Za 2 M (X) ~ a3 \u003d y 3 -Zy ^ + Zy (y, -y ^ \u003d y 3 - Zy ^ + 2y ^ (នៅពេលទាញយក យើងបានពិចារណាថា ក = M(X)= V, - តម្លៃមិនចៃដន្យ) ។ ?

ដូចដែលបានកត់សម្គាល់ខាងលើការរំពឹងទុកគណិតវិទ្យា M(X),ឬពេលដំបូងដំបូងកំណត់លក្ខណៈតម្លៃមធ្យម ឬទីតាំង ចំណុចកណ្តាលនៃការចែកចាយអថេរចៃដន្យ Xនៅលើបន្ទាត់លេខ; ការបែកខ្ញែក អូ)ឬពេលកណ្តាលទីពីរ p 2 , - s t s - ការចែកចាយខ្ចាត់ខ្ចាយ Xទាក់ទង M(X)ពេលវេលាលំដាប់ខ្ពស់បម្រើសម្រាប់ការពិពណ៌នាលម្អិតបន្ថែមទៀតនៃការចែកចាយ។

ពេលកណ្តាលទីបី p 3 បម្រើដើម្បីកំណត់លក្ខណៈ asymmetry នៃការចែកចាយ (skewness) ។ វាមានវិមាត្រនៃគូបនៃអថេរចៃដន្យមួយ។ ដើម្បីទទួលបានតម្លៃគ្មានវិមាត្រ វាត្រូវបានបែងចែកដោយប្រហែល 3 ដែល a គឺជាគម្លាតស្តង់ដារនៃអថេរចៃដន្យ x.តម្លៃដែលទទួលបាន ប៉ុន្តែបានហៅ មេគុណនៃ asymmetry នៃអថេរចៃដន្យមួយ។

ប្រសិនបើការចែកចាយមានភាពស៊ីមេទ្រីទាក់ទងទៅនឹងការរំពឹងទុកគណិតវិទ្យា នោះមេគុណភាពមិនច្បាស់គឺ A = 0 ។

នៅលើរូបភព។ 3.17 បង្ហាញខ្សែកោងចែកចាយពីរ៖ I និង II ។ ខ្សែកោង I មានភាពវិជ្ជមាន (ខាងស្តាំ) asymmetry (L> 0) ហើយខ្សែកោង II មានអវិជ្ជមាន (ខាងឆ្វេង) (L

ពេលកណ្តាលទីបួន p 4 បម្រើដើម្បីកំណត់លក្ខណៈនៃភាពចោត (កំពូលនៃកំពូលឬផ្ទះល្វែង - ប្រកាស) នៃការចែកចាយ។

ម៉ូដ- តម្លៃនៅក្នុងសំណុំនៃការសង្កេតដែលកើតឡើងញឹកញាប់បំផុត។

ម៉ូ \u003d X Mo + h Mo * (f Mo - f Mo-1): ((f Mo - f Mo-1) + (f Mo - f Mo + 1)),

នៅទីនេះ X Mo គឺជាព្រំដែនខាងឆ្វេងនៃចន្លោះម៉ូឌុល h Mo គឺជាប្រវែងនៃចន្លោះម៉ូឌុល f Mo-1 គឺជាប្រេកង់នៃចន្លោះពេល premodal f Mo គឺជាប្រេកង់នៃចន្លោះ modal f Mo +1 គឺជា ភាពញឹកញាប់នៃចន្លោះពេលក្រោយ។

របៀបនៃការចែកចាយបន្តយ៉ាងពិតប្រាកដ គឺជាចំណុចណាមួយនៃដង់ស៊ីតេចែកចាយអតិបរមាក្នុងតំបន់។ សម្រាប់ការចែកចាយដាច់ពីគ្នា របៀបមួយគឺជាតម្លៃណាមួយ a i ដែលប្រូបាប៊ីលីតេ p i គឺធំជាងប្រូបាប៊ីលីតេនៃតម្លៃជិតខាង

មធ្យមអថេរចៃដន្យបន្ត Xតម្លៃរបស់វាត្រូវបានគេហៅថា Me ដែលវាប្រហែលស្មើគ្នាថាតើអថេរចៃដន្យនឹងប្រែទៅជាតិច ឬច្រើន ខ្ញុំ, i.e.

M e \u003d (n + 1) / 2 P(X < ខ្ញុំ) = P(X > ខ្ញុំ)

ចែកចាយស្មើៗគ្នា NEW

សូម្បីតែការចែកចាយ។អថេរចៃដន្យបន្តត្រូវបានគេហៅថាចែកចាយស្មើៗគ្នានៅលើផ្នែក () ប្រសិនបើមុខងារដង់ស៊ីតេនៃការចែកចាយរបស់វា (រូបភាព 1.6, ក) មើល​ទៅ​ដូច​ជា:

ការកំណត់៖ - ​​SW ត្រូវបានចែកចាយស្មើៗគ្នា។

ដូច្នោះហើយមុខងារចែកចាយនៅលើផ្នែក (រូបភាព 1.6, ខ):

អង្ករ។ ១.៦. មុខងារនៃអថេរចៃដន្យដែលចែកចាយស្មើៗគ្នានៅលើ [ ក,ខ]: ក- ដង់ស៊ីតេប្រូបាប៊ីលីតេ f(x); ខ- ការចែកចាយ ច(x)

ការរំពឹងទុកគណិតវិទ្យា និងភាពខុសគ្នានៃ RV នេះត្រូវបានកំណត់ដោយកន្សោម៖

ដោយសារតែស៊ីមេទ្រីនៃមុខងារដង់ស៊ីតេវាស្របគ្នាជាមួយមធ្យម។ ម៉ូតមិនមានការចែកចាយឯកសណ្ឋានទេ។

ឧទាហរណ៍ 4 ពេលវេលារង់ចាំសម្រាប់ចម្លើយចំពោះការហៅទូរសព្ទគឺជាអថេរចៃដន្យដែលគោរពច្បាប់ចែកចាយឯកសណ្ឋានក្នុងចន្លោះពី 0 ទៅ 2 នាទី។ ស្វែងរកមុខងារចែកចាយអាំងតេក្រាល និងឌីផេរ៉ង់ស្យែលនៃអថេរចៃដន្យនេះ។

27. ច្បាប់ធម្មតានៃការចែកចាយប្រូបាប៊ីលីតេ

អថេរចៃដន្យបន្ត x មានការចែកចាយធម្មតាជាមួយប៉ារ៉ាម៉ែត្រ៖ m,s> 0 ប្រសិនបើដង់ស៊ីតេចែកចាយប្រូបាប៊ីលីតេមានទម្រង់៖

ដែល៖ m ជា​ការ​រំពឹង​ទុក​តាម​គណិតវិទ្យា s ជា​គម្លាត​ស្តង់ដារ។

ការចែកចាយធម្មតាត្រូវបានគេហៅថា Gaussian បន្ទាប់ពីគណិតវិទូអាល្លឺម៉ង់ Gauss ។ ការពិតដែលថាអថេរចៃដន្យមានការចែកចាយធម្មតាជាមួយប៉ារ៉ាម៉ែត្រ: m, , ត្រូវបានតំណាងដូចខាងក្រោម: N (m, s), ដែល: m = a = M [X];

ជាញឹកញយ នៅក្នុងរូបមន្ត ការរំពឹងទុកគណិតវិទ្យាត្រូវបានតាងដោយ ក . ប្រសិនបើអថេរចៃដន្យត្រូវបានចែកចាយយោងទៅតាមច្បាប់ N(0,1) នោះវាត្រូវបានគេហៅថាតម្លៃធម្មតាធម្មតា ឬស្តង់ដារ។ មុខងារចែកចាយសម្រាប់វាមានទម្រង់៖

ក្រាហ្វនៃដង់ស៊ីតេនៃការចែកចាយធម្មតាដែលត្រូវបានគេហៅថាខ្សែកោងធម្មតាឬខ្សែកោង Gaussian ត្រូវបានបង្ហាញនៅក្នុងរូបភាព 5.4 ។

អង្ករ។ ៥.៤. ដង់ស៊ីតេចែកចាយធម្មតា។

លក្ខណៈសម្បត្តិអថេរចៃដន្យជាមួយច្បាប់ចែកចាយធម្មតា។

1. ប្រសិនបើ បន្ទាប់មកដើម្បីស្វែងរកប្រូបាប៊ីលីតេដែលតម្លៃនេះធ្លាក់ចូលទៅក្នុងចន្លោះពេលដែលបានផ្តល់ឱ្យ ( x 1; x 2) រូបមន្តត្រូវបានប្រើ៖

2. ប្រូបាប៊ីលីតេដែលគម្លាតនៃអថេរចៃដន្យពីការរំពឹងទុកគណិតវិទ្យារបស់វានឹងមិនលើសពីតម្លៃ (ជាតម្លៃដាច់ខាត) គឺស្មើនឹង៖

3. "ច្បាប់បី Sigma". ប្រសិនបើអថេរចៃដន្យ នោះវាពិតជាប្រាកដណាស់ថាតម្លៃរបស់វាត្រូវបានផ្ទុកនៅក្នុងចន្លោះ ()។ (ប្រូបាប៊ីលីតេនៃការហួសពីព្រំដែនទាំងនេះគឺ 0.0027។) ច្បាប់អនុញ្ញាតដោយដឹងពីប៉ារ៉ាម៉ែត្រ (និង) ដើម្បីកំណត់ចន្លោះពេលនៃតម្លៃជាក់ស្តែងនៃអថេរចៃដន្យ។

ការចែកចាយអិចស្ប៉ូណង់ស្យែល

អថេរចៃដន្យ X មានការចែកចាយអិចស្ប៉ូណង់ស្យែលជាមួយប៉ារ៉ាម៉ែត្រ ប្រសិនបើដង់ស៊ីតេរបស់វាមានទម្រង់

ការរួមបញ្ចូលដង់ស៊ីតេ យើងទទួលបានមុខងារចែកចាយអិចស្ប៉ូណង់ស្យែល៖

លក្ខណៈសំខាន់នៃការចែកចាយអិចស្ប៉ូណង់ស្យែល៖

ប្លង់ដង់ស៊ីតេ និងមុខងារនៃការចែកចាយអិចស្ប៉ូណង់ស្យែលលទ្ធផល