1. កិច្ចការ។
នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ កសមីការ ( ក - 1)x 2 + 2x + ក- 1 = 0 មានឫសមួយពិតប្រាកដ?

1. ការសម្រេចចិត្ត។
នៅ ក= 1 សមីការមានទម្រង់ 2 x= 0 ហើយច្បាស់ជាមានឫសតែមួយ x= 0. ប្រសិនបើ កលេខ 1 បន្ទាប់មកសមីការនេះគឺ quadratic និងមានឫសតែមួយសម្រាប់តម្លៃទាំងនោះនៃប៉ារ៉ាម៉ែត្រដែលការរើសអើងនៃ trinomial ការ៉េស្មើនឹងសូន្យ។ សមីការអ្នករើសអើងទៅសូន្យ យើងទទួលបានសមីការសម្រាប់ប៉ារ៉ាម៉ែត្រ ក 4ក 2 - 8ក= 0, មកពីណា ក= 0 ឬ ក = 2.

1. ចម្លើយ៖សមីការមានឫសតែមួយនៅ ក O(0; 1; 2) ។

2. ភារកិច្ច។
ស្វែងរកតម្លៃប៉ារ៉ាម៉ែត្រទាំងអស់។ កដែលសមីការមានឫសពីរផ្សេងគ្នា x 2 +4ពូថៅ+8ក+3 = 0.
2. ការសម្រេចចិត្ត។
សមីការ x 2 +4ពូថៅ+8ក+3 = 0 មានឫសពីរផ្សេងគ្នាប្រសិនបើ និងបានតែប្រសិនបើ ឃ = 16ក 2 -4(8ក+3) > 0. យើងទទួលបាន (បន្ទាប់ពីកាត់បន្ថយដោយកត្តារួមនៃ 4) 4 ក 2 -8ក-3> 0 មកពីណា

2. ចម្លើយ៖

កអូ (-Ґ ; 1 -

គ ៧ ២

) និង (1 +

គ ៧ ២

; Ґ ).

3. ភារកិច្ច។
វាត្រូវបានគេស្គាល់ថា
f 2 (x) = 6x-x 2 -6.
ក) ក្រាហ្វនៃមុខងារ f 1 (x) នៅ ក = 1.
ខ) តម្លៃអ្វី កក្រាហ្វិកមុខងារ f 1 (x) និង f 2 (x) មានចំណុចរួមតែមួយ?

3. ដំណោះស្រាយ។
3. ក.តោះ​ប្រែ​ក្លាយ f 1 (x) តាមវិធីខាងក្រោម
ក្រាហ្វនៃមុខងារនេះ។ ក= 1 ត្រូវបានបង្ហាញក្នុងរូបនៅខាងស្តាំ។
3. ខ.យើងកត់សំគាល់ភ្លាមៗថាក្រាហ្វមុខងារ y = kx+ខនិង y = ពូថៅ 2 +bx+គ (កលេខ 0) ប្រសព្វគ្នាត្រង់ចំណុចតែមួយ ប្រសិនបើសមីការការ៉េ kx+ខ = ពូថៅ 2 +bx+គមានឫសតែមួយ។ ការប្រើប្រាស់ទិដ្ឋភាព f 1 នៃ 3. ក, យើងស្មើភាពរើសអើងនៃសមីការ ក = 6x-x២-៦ ដល់សូន្យ។ ពីសមីការ 36-24-4 ក= 0 យើងទទួលបាន ក= 3. ធ្វើដូចគ្នាជាមួយនឹងសមីការ 2 x-ក = 6x-x២-៦ រក ក= 2. វាងាយស្រួលក្នុងការផ្ទៀងផ្ទាត់ថាតម្លៃប៉ារ៉ាម៉ែត្រទាំងនេះបំពេញលក្ខខណ្ឌនៃបញ្ហា។ ចម្លើយ៖ ក= 2 ឬ ក = 3.

4. ភារកិច្ច។
ស្វែងរកតម្លៃទាំងអស់។ កក្រោមដែលសំណុំនៃដំណោះស្រាយនៃវិសមភាព x 2 -2ពូថៅ-3ក i 0 មានផ្នែក។

4. ដំណោះស្រាយ។
កូអរដោនេទីមួយនៃចំនុចកំពូលនៃប៉ារ៉ាបូឡា f(x) = x 2 -2ពូថៅ-3កគឺស្មើនឹង x 0 = ក. ពីលក្ខណៈសម្បត្តិនៃអនុគមន៍ quadratic លក្ខខណ្ឌ f(x) i 0 នៅលើចន្លោះពេលគឺស្មើនឹងចំនួនសរុបនៃប្រព័ន្ធបី
មានដំណោះស្រាយពីរយ៉ាងពិតប្រាកដ?

5. ការសម្រេចចិត្ត។
ចូរយើងសរសេរសមីការនេះឡើងវិញក្នុងទម្រង់ x 2 + (2ក-2)x - 3ក+7 = 0. នេះគឺជាសមីការបួនជ្រុង វាមានដំណោះស្រាយពីរយ៉ាងពិតប្រាកដ ប្រសិនបើការរើសអើងរបស់វាខ្លាំងជាងសូន្យ។ ការគណនាការរើសអើង យើងទទួលបានថាលក្ខខណ្ឌសម្រាប់ការមានឫសគល់ពីរយ៉ាងពិតប្រាកដគឺការបំពេញវិសមភាព។ ក 2 +ក-6 > 0. ការដោះស្រាយវិសមភាព យើងរកឃើញ ក < -3 или ក> 2. ជាក់ស្តែង វិសមភាពទីមួយមិនមានដំណោះស្រាយជាលេខធម្មជាតិទេ ហើយដំណោះស្រាយធម្មជាតិតូចបំផុតទីពីរគឺលេខ 3 ។

5. ចម្លើយ៖ 3.

6. កិច្ចការ (10 ក្រឡា)
ស្វែងរកតម្លៃទាំងអស់។ កដែលក្រាហ្វនៃអនុគមន៍ ឬបន្ទាប់ពីការបំលែងជាក់ស្តែង។ ក-2 = | 2-ក| . សមីការចុងក្រោយគឺស្មើនឹងវិសមភាព កខ្ញុំ ២.

6. ចម្លើយ៖ កអូ ហើយមិនអាស្រ័យលើសញ្ញានៃអ្នករើសអើងនោះទេ។ តោះបង្កើតគំនូរព្រាង (សម្រាប់ D>0)

https://pandia.ru/text/78/525/images/image020_10.jpg" width="624" height="209 src=">

សម្រាប់ករណីនីមួយៗនៃចំនួនបី ក) ខ) គ) តម្លៃតូចបំផុតនៃអនុគមន៍ f(t) = t2-8at+7a2

នៅលើផ្នែកត្រូវបានសម្រេចរៀងគ្នានៅចំណុច x = 1, x = 2a, x = 1/4 ។ បន្ទាប់មកសំណួរដែលត្រូវឆ្លើយគឺជាដំណោះស្រាយនៃចំនួនសរុបនៃប្រព័ន្ធបី៖

1≤4a 1/4<4а<1 4а<1/4

f(1)<0 или f(4а)<0 или f(1/4)<0

a≥1/4 1/16<а<1/4 а≤1/16

1 - 8a + 7a2<0 или 16а2 – 32а2 + 7а2<0 или 1/16 – 2а + 7а2<0.

ចម្លើយ៖ 1/28<а<1.

កិច្ចការសាកល្បង

មួយ) សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a តើក្រាហ្វនៃអនុគមន៍ y = 2x – a និង y = (a + 1)x2 + 1 ប្រសព្វគ្នានៅចំណុចតែមួយ?

២). ស្វែងរកតម្លៃទាំងអស់នៃប៉ារ៉ាម៉ែត្រ a ដែលក្រាហ្វនៃអនុគមន៍ y = (a + 5)x2 - 1 និង

y \u003d (3a + 15) x - 4 មិនមានចំណុចរួមទេ?

៣). សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a តើសមីការ (a +4)x2 +6x –1 = 0 មានដំណោះស្រាយតែមួយគត់?

៤). សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a តើសមីការ (2a + 8) x2 − (a + 4) x + 3 = 0 មានដំណោះស្រាយតែមួយគត់?

៥). សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a តើសមីការមានដំណោះស្រាយច្រើនជាងមួយ?

ក) (a + 6)x2 - 8x + a \u003d 0

b) a (2a + 4) x2 − (a + 2) x − 5a − 10 = 0 ។

៦). ស្វែងរកតម្លៃទាំងអស់នៃប៉ារ៉ាម៉ែត្រ k ដែលខ្សែកោង y = x2 + kx + 4 ប៉ះអ័ក្ស x ។

៧). តើអ្វីទៅជាតម្លៃចំនួនគត់តូចបំផុតនៃប៉ារ៉ាម៉ែត្រ k សម្រាប់ត្រីកោណការ៉េ

(k–2)x2+8x+k+4 គឺវិជ្ជមានសម្រាប់តម្លៃពិតទាំងអស់នៃ x?

ប្រាំបី) ។ លេខ x, y, ហើយមានដូចជា x + y = a −1, x2 + y2 = 5a2 − 3a + 0.5 ។ តើតម្លៃនៃប៉ារ៉ាម៉ែត្រ a តើផលិតផល xy យកតម្លៃអតិបរមាដែរឬទេ?

ប្រាំបួន). លេខ x, y, និង​ដូច​ជា x + y = a +1, xy = a2 - 3a + 4. សម្រាប់​តម្លៃ​អ្វី​នៃ​ប៉ារ៉ាម៉ែត្រ

ហើយផលបូក x2 + y2 យកតម្លៃអតិបរមា?

ដប់) ។ ស្វែងរកតម្លៃធំបំផុត និងតូចបំផុត 1 នៃអនុគមន៍ y \u003d 2x2 - 2ax + នៅលើផ្នែក

ដប់មួយ) ។ ស្វែងរកតម្លៃធំបំផុតនៃត្រីកោណការ៉េ 1 - (a - 2) x - x2 នៅលើផ្នែក

១២). នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ a គឺជាតម្លៃតូចបំផុតនៃអនុគមន៍ y = x2 + (a + 4) x + 2a + 3 នៅលើចម្រៀកស្មើនឹង -4?

ដប់បី) ។ តើតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ a គឺជាតម្លៃតូចបំផុតនៃអនុគមន៍ y \u003d x2 - (a + 2) x + a2 នៅលើផ្នែក [-1; 1] ស្មើនឹង 4?

ដប់បួន) ។ នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ a គឺជាតម្លៃអតិបរមានៃអនុគមន៍

f (x) \u003d - (1 / a) x + (7 / a) 3-x - 3a2 នៅលើផ្នែក [-1; 0] គឺអវិជ្ជមាន?

ចម្លើយចំពោះកិច្ចការសាកល្បង

1) a=-2, a=-1, a=0 ។

2) –19/3<а≤-5.

3) a=-4, a=-13 ។

5) ក) -8<а<-6 и -6<а<2

ខ) a=-2; -1/40 0.

១០) ប្រសិនបើ ក<-2, то наименьшее значение функции при х=-1 и равно 3+2а, наибольшее значение функции при х=1 и равно 3–2а;

ប្រសិនបើ -2≤a<0, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=1 и равно 3–2а;

ប្រសិនបើ 0≤a<2, то наименьшее значение функции при х= хо и равно 1–а2/2, наибольшее значение функции при х=-1 и равно 3+2а;

ប្រសិនបើ a≥2 បន្ទាប់មកតម្លៃតូចបំផុតនៃអនុគមន៍នៅ x = 1 និងស្មើនឹង 3–2a តម្លៃធំបំផុតនៃអនុគមន៍នៅ x=-1 និងស្មើនឹង 3+2a;

១១) ប្រសិនបើ a≤0 បន្ទាប់មក -6a2-a+2 ប្រសិនបើ 0<а<8/5, то 2- 6а +а2/4, если а ≥8/5, то 19а-6а2 -14

១៣) a=-2 ឬ a=(1+√21)/2

១៤) |a|>(7√3)/12.

ទីតាំងនៃឫសនៃត្រីកោណការ៉េ

ពិចារណាបញ្ហាធម្មតាមួយចំនួនដែលទាក់ទងនឹងទីតាំងនៃឫសនៃត្រីកោណកែង ax2 + bx + c ។ យើងនឹងអនុវត្តហេតុផលទាំងអស់ដោយសន្មតថា a > 0 ។ ប្រសិនបើ ក<0,то рассуждения проводятся аналогично.

លេខកិច្ចការ 1 ។

នៅក្រោមលក្ខខណ្ឌណាដែលឫសទាំងពីរនៃសមីការ quadratic ax2 + bx + c = 0 (មិនចាំបាច់ខុសគ្នាទេ) ធំជាងចំនួនដែលបានផ្តល់ឱ្យ k?

ការសម្រេចចិត្ត។

យើងបង្កើតក្រាហ្វិចនៃអនុគមន៍នៃត្រីកោណការ៉េ y= ax2+bx+c ដែល x1 និង x2 បំពេញលក្ខខណ្ឌ៖ x1>k, x2>k ។ អនុញ្ញាតឱ្យ f(x)=ax2+bx+c។ ក្រាហ្វ y = f(x) ឆ្លងកាត់អ័ក្ស OX (D>0) ឬប៉ះវា (D=0)។ បន្ទាប់មក វាចាំបាច់ដើម្បីបំពេញលក្ខខណ្ឌ៖ х>к, y(к)>0។ ប្រសិនបើ ក< 0 условие: х1>k, x2>k ត្រូវបានកំណត់ដោយប្រព័ន្ធវិសមភាព៖

https://pandia.ru/text/78/525/images/image023_20.gif" width="14" height="86">

រូប ៤

កិច្ចការ ១១.ស្វែងរកតម្លៃទាំងអស់នៃប៉ារ៉ាម៉ែត្រ a ដែលឫសទាំងអស់នៃសមីការ

x2–6ax+2–2a+9a2 = 0 ច្រើនជាង 3 ។

ការសម្រេចចិត្ត។

ប្រសិនបើលក្ខខណ្ឌតម្រូវត្រូវបានបំពេញ មុខតំណែងខាងក្រោមនៃប៉ារ៉ាបូឡាអាចធ្វើទៅបាន ដែលជាក្រាហ្វនៃអនុគមន៍ f(x)= x2–6ax+2–2a+9a2

រូប ៥

តោះដោះស្រាយប្រព័ន្ធវិសមភាព៖

https://pandia.ru/text/78/525/images/image026_8.jpg" align="left" width="324" height="239 src=">

វាគ្រប់គ្រាន់ដើម្បីបំពេញលក្ខខណ្ឌ៖ y(k)<0, если а >0.ពេល ក<0, y(к) > 0.

អង្ករ។ ៦

កិច្ចការ 12 ។ស្វែងរកតម្លៃទាំងអស់នៃប៉ារ៉ាម៉ែត្រ a ដែល 1 ស្ថិតនៅចន្លោះឫសនៃសមីការ x2–2ax+3–4a+2a2=0 ។

ការសម្រេចចិត្ត។

ដោយសារមេគុណនាំមុខគឺវិជ្ជមាន វាគ្រប់គ្រាន់ដើម្បីបំពេញលក្ខខណ្ឌ f(1)<0, где f(х)=х2–2ах+3–4а+2а2

4–6a+2a2<0, 1<а<2.

ចម្លើយ៖ 1<а<2

លេខកិច្ចការ 3 ។នៅក្រោមលក្ខខណ្ឌបែបណាដែលឫសមួយនៃសមីការការ៉េ ax2 + bx + c = 0 ដែលមានឫសផ្សេងគ្នា ស្ថិតនៅលើចន្លោះពេល (k, e)?

អនុញ្ញាតឱ្យយើងបង្កើតក្រាហ្វិកតាមគ្រោងការណ៍ y = ax2 + bx + c យោងទៅតាមលក្ខខណ្ឌនៃបញ្ហានេះសម្រាប់ a > 0 ។

https://pandia.ru/text/78/525/images/image028_8.jpg" width="623" height="246 src=">

ដោះស្រាយវិសមភាព៖ f(1) f(2)<0.

(a2+8a+7)(a2+14a+16)<0

7-√33< а<-7; -7+√33<а<-1.

ចម្លើយ៖ -7-√33< а<-7; -7+√33<а<-1.

កិច្ចការ 14 ។ស្វែងរកតម្លៃទាំងអស់នៃប៉ារ៉ាម៉ែត្រ a ដែលសមីការ 2cos(2x)+2asin(x)+a-1=0 មានដំណោះស្រាយតែមួយគត់នៅលើចន្លោះពេល (-π/2;0)។

ការសម្រេចចិត្ត.

2cos(2x)+2a sinx+a-1=0

2(1–2 sin2х)+ 2a sinx+a–1=0

4 sin2х–2а sinx –a–1=0

អនុញ្ញាតឱ្យ sinx=t ចាប់តាំងពី -π/2<х<0, то -1< t <0

ស្វែងរកតម្លៃទាំងនោះនៃប៉ារ៉ាម៉ែត្រ a ដែលសមីការ 4t2– 2at–a–1=0 មានដំណោះស្រាយតែមួយគត់នៅលើចន្លោះពេល (-1; 0) ។

សមីការ 4t2– 2at–a–1=0 មានដំណោះស្រាយតែមួយគត់នៅលើចន្លោះពេល (-1; 0) ប្រសិនបើ៖

មួយ) D \u003d 0 D / 4 \u003d (a + 2) 2 D \u003d 0 សម្រាប់ \u003d -2 ។

២). ពិចារណាអនុគមន៍ f(t)= 4t2– 2at–a–1

យើងបង្កើតក្រាហ្វិចនៃអនុគមន៍ y=f(t)

https://pandia.ru/text/78/525/images/image030_16.gif" width="14" height="50 src=">

f(0) f(1) ≤0 a≤-3; a≥-1

ចម្លើយ៖ a≤-3; a≥-1; a=-2.

លេខកិច្ចការ 4 ។នៅក្រោមលក្ខខណ្ឌណាដែលឫសទាំងពីរ (មិនចាំបាច់ខុសគ្នា) នៃសមីការ quadratic ax2 + bx + c ស្ថិតនៅលើផ្នែក [k; អ៊ី]។ ពិចារណានៅក្រោមលក្ខខណ្ឌ a> 0 ។ អនុញ្ញាតឱ្យមានអនុគមន៍ f(x)= ax2+bx+c

https://pandia.ru/text/78/525/images/image032_14.gif" width="14" height="110">D≥0

k≤ ho≤ e

កិច្ចការ ១៥. ស្វែងរកតម្លៃទាំងនោះនៃប៉ារ៉ាម៉ែត្រ a ដែលឫសទាំងអស់នៃសមីការ

х2- 2(а–3)х–а +3=0 កុហកក្នុងចន្លោះពេល (-3; 0)។

ការសម្រេចចិត្ត។

បានផ្តល់ថាយ៉ាងហោចណាស់មានឫសមួយ ក្រាហ្វនៃអនុគមន៍ f (x) \u003d x2- 2 (a-3) x-a + 3 អាចត្រូវបានកំណត់តាមគ្រោងការណ៍តាមវិធីមួយក្នុងចំណោមពីរ

https://pandia.ru/text/78/525/images/image034_12.gif" width="14" height="110">D≥0 4(а – 3)(а – 2) ≥0

3<хо<0 3<а – 3 <0 1,2<а≤2.

f(-3) >0 5а ដល់ 6>0

f(0)>0 -а+3>0

សមីការ sin x − 1 + a = sin x − 2 ។ sin x − 2 sin x − 3 ដំណោះស្រាយ។ ការកំណត់ t = sin x យើងកាត់បន្ថយសមីការទៅជាទម្រង់នៅ 2 − 5at + 6a − 1 = 0 ។ ប្រសិនបើ a = 0 នោះគ្មានដំណោះស្រាយទេ។ សម្រាប់ a = 0 និងក្រោមលក្ខខណ្ឌ a ∈ (−∞; −4] ∪ (0; +∞) √ 2 + 4a យើងទទួលបានឫសនៃសមីការ t1,2 = 5a ± 2aa ។ ចាប់តាំងពីចំនុចកំពូលនៃប៉ារ៉ាបូឡា f (t) = at2 − 5at + 6a − 1 មានទីតាំងនៅចំណុច tв = 2 , 5 លក្ខខណ្ឌ |t|1 សម្រាប់ឫសតូចបំផុតនឹងពេញចិត្ត ប្រសិនបើមុខងារមានសញ្ញាផ្សេងគ្នានៅចុងផ្នែក [− 1; 1]: f (−1) f (1) 0 ឬ (2a−1)(12a−1) 0. ដំណោះស្រាយចំពោះវិសមភាព 1 ចុងក្រោយគឺចន្លោះពេល a ∈ 12 ;1 .2 √ a2 ចម្លើយ៖ ប្រសិនបើ a ∈ 12 ;2: x = (−1)n arcsin 5a− 2a +4a +πn, n∈Z, 1 1 មិនមានដំណោះស្រាយសម្រាប់ a ផ្សេងទៀតទេ បញ្ហា 6.7 សម្រាប់តម្លៃណាមួយនៃប៉ារ៉ាម៉ែត្រ a មុខងារ f (x) = 8ax − a sin 6x − 7x − sin 5x កំពុងកើនឡើងនៅលើអ័ក្សពិតទាំងមូល ហើយគ្មានចំនុចសំខាន់ទេ? ដំណោះស្រាយ។ 6a cos 6x − 7 − 5 cos 5x ។ បញ្ហាអាចត្រូវបានកែទម្រង់ដូចខាងក្រោមៈ ដែលវិសមភាព 6a cos 6x + 5 cos 5x< 8a − 7 справедливо для любого x? Так как последнее неравенство должно выполняться для любого значения x, оно должно быть справедливо и для x = 0, от- куда 6a + 5 < 8a − 7 или a >6. ពិចារណាឥឡូវនេះថា 6a cos 6x + 5 cos 5x 6|a| +5< 8a − 7, приходим к выводу, что при a >6 វិសមភាពមានសុពលភាពសម្រាប់ x ណាមួយ។ ចម្លើយ៖ a > 6. បញ្ហាសម្រាប់ដំណោះស្រាយឯករាជ្យ បញ្ហា 6.8 ។ (SGAU) អាស្រ័យលើតម្លៃនៃប៉ារ៉ាម៉ែត្រ a ដោះស្រាយសមីការ cos4 x − (a + 2) cos2 x √ a − 3 = 0. − ចំលើយ៖ ប្រសិនបើ a ∈ [−3; −2] : x = arccos a + 3 + πk, k ∈ Z, ប្រសិនបើ a ∈ [−3; −2]៖ គ្មានដំណោះស្រាយ។ បញ្ហា 6.9 ។ (SGAU) អាស្រ័យលើតម្លៃនៃប៉ារ៉ាម៉ែត្រ a ដោះស្រាយសមីការ sin4 x + cos4 x + sin 2x + a = 0. 61 √ ចម្លើយ៖ ប្រសិនបើ a ∈ − 3 ; 2: x = 1 (−1)k arcsin(1− 2a−3) + πk, 2 1 2 3 ; ១៖ គ្មានដំណោះស្រាយ។ ប្រសិនបើ a ∈ − 2 2 k ∈ Z, បញ្ហា 6.10 ។ (SGAU) សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a ធ្វើសមីការ (a2 +8a+16)(2−2 cos x− sin2 x)+(32+2a2 +16a)(cos x−1)+3a+10 =0 ដំណោះស្រាយ? ចម្លើយ៖ ក< − 10 ; −3 < a < −2. 3 Задача 6.11. (СГАУ) При каких значениях параметра a урав- нение loga−2 17 + cos x − sin x = 3 8 имеет решение? √ 2 3 Ответ: a ∈ 2 5 ; 3 ∪ 3; 2 + 26 . 2 Задача 6.12. (СГАУ) При каких значениях параметра a урав- нение loga+1 25 + cos x − 2 sin x = 3 8 2 имеет решение? √3 37 Ответ: a ∈ − 1 ; 0 ∪ 0; 2 − 1 . 2 Задача 6.13. (ЕГЭ) При каких значениях параметра a значение выражения 2+cos x·(3 cos x+a sin x) не равно нулю ни при каких значениях x? √ √ Ответ: a ∈ −2 10; 2 10 . Задача 6.14. (ЕГЭ) При каких значениях параметра a значение выражения 3 + sin x · (2 sin x + a cos x) будет равно −1 хотя бы при одном значении x? √ √ Ответ: a ∈ −∞; −4 6 ∪ 4 6; +∞ . Задача 6.15. (ЕГЭ) При каких значениях параметра a сумма loga (sin x + 2) и loga (sin x + 3) будет равна единице хотя бы при одном значении x? Ответ: a ∈ [ 2; 12 ]. Задача 6.16. (СГАУ) При каких значениях параметра α систе- ма 4 sin x · sin y · cos(x + y) − 0,5 = 0 x−y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. 62 Ответ: Если α = 2πn: x = ±π 6 + π(k+n) π y = ±6 + π(k−n); если α = π+2πn: x = ±π 3 + π + π(k+n) 2 y = ±π 3 − π + π(k−n), 2 n, k ∈ Z. Задача 6.17. (СГАУ) При каких значениях параметра α систе- ма 2 sin x · cos y · sin(x − y) + 0,25 = 0 x+y =α имеет решения? Найдите эти решения в зависимости от значений параметра α. Ответ: Если α = π +2πn: x = (−1)k+1 π + π + π (2n+k) 2 12 4 2 k π + π + π (2n−k); y = (−1) 12 4 2 если α = − 2 π +2πn: x = (−1)k π − π + π (2n+k) 12 4 2 y = (−1) k+1 π − π + π (2n−k), 12 4 2 n, k ∈ Z. Задача 6.18. (СГАУ) При каких значениях параметра a нера- венство √ 2 2 (sin x − cos x) − a + 7 log 2a+34 15 <0 35 выполняется для любых значений x? 1 Ответ: a ∈ (−17; −12) ∪ 2 ; 3 . Задача 6.19. (СГАУ) При каких значениях параметра a нера- венство √ log 3−2a 3 sin x + 3 3 cos x − 2a − 12 >0 23 28 រក្សាតម្លៃណាមួយនៃ x? ចម្លើយ៖ a ∈ (−∞; −23) ∪ (−10; −9) ។ បញ្ហា 6.20 ។ អាស្រ័យលើតម្លៃនៃប៉ារ៉ាម៉ែត្រ a ដោះស្រាយវិសមភាព cos x 2 − a2 ។ ចម្លើយ៖ |a| √ : x ∈ R, 1 ១<|a| √3: x ∈ arccos(2−a2)+2πk; π− arccos(2−a2)+2πk , |a|>៣៖ គ្មានដំណោះស្រាយ។ k∈Z បញ្ហា 6.21 ។ សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a តើសមីការ tg x (a + 1) tg2 x − 2 cos x + a = 0 មិនមានដំណោះស្រាយទេ? ចម្លើយ៖ ក -៣; a 1. 63 មគ្គុទ្ទេសក៍សិក្សា PROBLEM with PARAMETERS ចងក្រងដោយ៖ Efimov Evgeny Alexandrovich Kolomiets Lyudmila Vadimovna ការវាយអក្សរ និងប្លង់កុំព្យូទ័រ E.A. សាកលវិទ្យាល័យ Efimov Samara State Aerospace បានដាក់ឈ្មោះតាម Academician S.P. មហាក្សត្រី។ 443086, Samara, Moscow highway, 34. - RIO Samara State Aerospace University ដាក់ឈ្មោះតាម Academician S.P. មហាក្សត្រី។ 443086, Samara, ផ្លូវហាយវេទីក្រុងម៉ូស្គូ, 34 ។

ក្រសួងអប់រំ និងវិទ្យាសាស្ត្រនៃតំបន់សាម៉ារ៉ា

ស្ថាប័នអប់រំស្វយ័តរដ្ឋនៃការអប់រំវិជ្ជាជីវៈបន្ថែម (ការអភិវឌ្ឍន៍គុណវុឌ្ឍិ) នៃអ្នកឯកទេស

វិទ្យាស្ថានតំបន់សាម៉ារ៉ាសម្រាប់ការអភិវឌ្ឍន៍វិជ្ជាជីវៈ

និង​ការ​បណ្ដុះបណ្ដាល​កម្មករ​ផ្នែក​អប់រំ​ឡើងវិញ

ការងារចុងក្រោយ

នៅលើវគ្គបណ្តុះបណ្តាលកម្រិតខ្ពស់

នេះបើយោងតាម ​​WB IOCH

"លក្ខណៈពិសេសនៃវិធីសាស្រ្តនៃការបង្រៀនដើម្បីដោះស្រាយបញ្ហាជាមួយនឹងប៉ារ៉ាម៉ែត្រនៅក្នុងបរិបទនៃការផ្លាស់ប្តូរទៅស្តង់ដារអប់រំថ្មី"

(15.06 - 19.06.2015)

ការរចនាប្រព័ន្ធពហុកម្រិតនៃកិច្ចការដែលមានប៉ារ៉ាម៉ែត្រប្រធានបទ៖

"ដេរីវេ"

សម្តែង៖

Valieva F.G.,

គ្រូគណិតវិទ្យា

GBOU អនុវិទ្យាល័យពួកគេ។ M.K. Ovsyannikova

ជាមួយ។ អ៊ីសាកាឡា

សាម៉ារ៉ា

ឆ្នាំ 2015

កំណត់ចំណាំពន្យល់

ឈ្មោះពេញ (ឈ្មោះពេញ)

Valieva Fanuzya Galimzyanovna

កន្លែងធ្វើការ

GBOU អនុវិទ្យាល័យពួកគេ។ M.K. ភូមិ Ovsyannikova នៃ Isakly,

ស្រុក Isaklinsky តំបន់ Samara

ទីតាំង

គ្រូគណិតវិទ្យា

រឿង

គណិតវិទ្យា

ថ្នាក់

គោលដៅ៖

1. ការអនុវត្តតម្រូវការនៃស្តង់ដារអប់រំរបស់រដ្ឋសហព័ន្ធ LLC នៅពេលសិក្សាប្រធានបទ៖ "ដេរីវេ"

   ទូទៅនិងការរៀបចំប្រព័ន្ធនៃចំណេះដឹងនិងវិធីសាស្រ្តនៃសកម្មភាពលើប្រធានបទ "ដេរីវេ"; ការបង្កើតជំនាញដើម្បីដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ។

   ការអភិវឌ្ឍន៍នៃការស្រាវជ្រាវ និងសកម្មភាពយល់ដឹង។

គំនិតនៃការអភិវឌ្ឍន៍ខាងវិញ្ញាណនិងសីលធម៌និងការអប់រំបុគ្គលិកលក្ខណៈរបស់ពលរដ្ឋនៃប្រទេសរុស្ស៊ីគឺជាមូលដ្ឋានវិធីសាស្រ្តសម្រាប់ការអភិវឌ្ឍន៍ និងការអនុវត្តស្តង់ដារអប់រំរបស់រដ្ឋសហព័ន្ធសម្រាប់ការអប់រំទូទៅ។

ស្តង់ដារអប់រំរបស់រដ្ឋសហព័ន្ធសម្រាប់ការអប់រំទូទៅជាមូលដ្ឋានលើមុខវិជ្ជាគណិតវិទ្យារបស់សាលា។

ស្តង់ដារគឺផ្អែកលើវិធីសាស្រ្តសកម្មភាពប្រព័ន្ធ។

ស្តង់ដារបង្កើតតម្រូវការសម្រាប់លទ្ធផលនៃការធ្វើជាម្ចាស់ដោយសិស្សនៃកម្មវិធីអប់រំចម្បងនៃការអប់រំទូទៅជាមូលដ្ឋាន:

ផ្ទាល់ខ្លួន;

ប្រធានបទ;

ប្រធានបទ។

ភារកិច្ច:

- ការអប់រំ៖ វិភាគ និងស្វែងយល់ពីអត្ថបទនៃកិច្ចការ កំណត់អត្តសញ្ញាណ និងបង្កើតគោលដៅនៃការយល់ដឹងដោយឯករាជ្យ កែទម្រង់លក្ខខណ្ឌ បង្កើតខ្សែសង្វាក់នៃហេតុផល វាយតម្លៃយ៉ាងត្រចះត្រចង់នូវចម្លើយដែលបានទទួល ការស្ថាបនាសេចក្តីថ្លែងការណ៍ដោយស្មារតី និងតាមអំពើចិត្ត ជ្រើសរើសវិធីដែលមានប្រសិទ្ធភាពបំផុតដើម្បីដោះស្រាយ។ បញ្ហា, បង្កើតនិងបង្កើតបញ្ហាមួយ, ដាក់ចេញសម្មតិកម្មនិងបង្ហាញអំពីភាពត្រឹមត្រូវរបស់ពួកគេ, ការអាន semantic;

- អភិវឌ្ឍន៍៖ ការកំណត់គោលដៅ, រៀបចំផែនការសកម្មភាពរបស់ពួកគេអាស្រ័យលើលក្ខខណ្ឌជាក់លាក់; ការឆ្លុះបញ្ចាំងពីវិធីសាស្រ្ត និងលក្ខខណ្ឌនៃសកម្មភាព ការគ្រប់គ្រង និងការវាយតម្លៃនៃដំណើរការ និងលទ្ធផលនៃសកម្មភាព ការគ្រប់គ្រងខ្លួនឯង។តាមរយៈការដោះស្រាយបញ្ហា ដើម្បីបង្កើតសកម្មភាពច្នៃប្រឌិត និងផ្លូវចិត្តរបស់សិស្ស គុណភាពបញ្ញា៖ សមត្ថភាពក្នុងការ "មើលឃើញ" បញ្ហា សកម្មភាពវាយតម្លៃ ឯករាជ្យភាព ភាពបត់បែននៃការគិត។

- ការអប់រំ៖ ការបង្កើតអារម្មណ៍ សមត្ថភាពក្នុងការស្តាប់ និងចូលទៅក្នុងកិច្ចសន្ទនា ដើម្បីចូលរួមក្នុងការពិភាក្សារួមគ្នាអំពីបញ្ហា បណ្តុះទំនួលខុសត្រូវ និងភាពត្រឹមត្រូវ។

ភារកិច្ច ជាមួយនឹងប៉ារ៉ាម៉ែត្រ - ទាំងនេះគឺជាការងារមិនស្តង់ដារ, i.e.មិនធម្មតាទាំងក្នុងទម្រង់ និងខ្លឹមសារ និងវិធីសាស្រ្តនៃដំណោះស្រាយ។ តួនាទីបែបនេះភារកិច្ច, សារៈសំខាន់និងអត្ថប្រយោជន៍របស់ពួកគេសម្រាប់ការអភិវឌ្ឍនៃការគិតឡូជីខល, វិចារណញាណ,សមត្ថភាពច្នៃប្រឌិតរបស់សិស្ស ការបង្កើតគណិតវិទ្យាខ្ពស់របស់ពួកគេ។វប្បធម៌មានទំហំធំណាស់។ វាត្រូវបានគេដឹងថាអ្នកអប់រំប្រឈមមុខនឹងការធ្ងន់ធ្ងរបញ្ហាវិធីសាស្រ្តក្នុងការបង្រៀនដើម្បីដោះស្រាយបញ្ហាបែបនេះ ទោះបីជាមានវត្តមានក៏ដោយ។មួយចំនួនធំនៃការបង្រៀន និងអត្ថបទទិនានុប្បវត្តិ។ ហេតុផលសម្រាប់ការនេះគឺច្បាស់ណាស់៖ យុទ្ធសាស្ត្រចម្បងនៃការអប់រំគណិតវិទ្យានៅសាលាគឺការអភិវឌ្ឍន៍ជំនាញ និងសមត្ថភាពសម្រាប់ដោះស្រាយបញ្ហាស្តង់ដារមួយចំនួន ដែលភាគច្រើនទាក់ទងនឹងបច្ចេកទេសនៃការផ្លាស់ប្តូរពិជគណិត។ សមីការ (វិសមភាព) ជាមួយនឹងប៉ារ៉ាម៉ែត្រសំដៅទៅលើប្រភេទផ្សេងគ្នានៃភារកិច្ច - ភារកិច្ចសម្រាប់ដំណោះស្រាយដែលដំបូងបង្អស់សមត្ថភាពក្នុងការអនុវត្ត - ជួនកាលមានសាខាណាស់ - ការសាងសង់ឡូជីខលនិងការស្រាវជ្រាវគឺចាំបាច់។

ការដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រតម្រូវឱ្យមានការស្រាវជ្រាវ ទោះបីជាពាក្យនេះមិនត្រូវបានលើកឡើងនៅក្នុងសេចក្តីថ្លែងការណ៍បញ្ហាក៏ដោយ។ ការអនុវត្តមេកានិកនៃរូបមន្តគឺមិនគ្រប់គ្រាន់ទេ ចាំបាច់ត្រូវយល់អំពីគំរូ សមត្ថភាពក្នុងការវិភាគករណីជាក់លាក់មួយ ដោយផ្អែកលើលក្ខណៈសម្បត្តិទូទៅដែលគេស្គាល់នៃវត្ថុ ភាពស៊ីសង្វាក់គ្នា និងភាពស៊ីសង្វាក់គ្នាក្នុងដំណោះស្រាយ សមត្ថភាពក្នុងការផ្សំករណីជាក់លាក់ដែលបានពិចារណា។ ទៅជាលទ្ធផលតែមួយ។ នេះ​មក​ពី​ការ​លំបាក​ដែល​សិស្ស​មាន​ក្នុង​ការ​ដោះស្រាយ​បញ្ហា​បែប​នេះ។

នាពេលបច្ចុប្បន្ននេះ គំនិតនៃការរួមបញ្ចូលគ្នារវាងការរៀនដើម្បីដោះស្រាយបញ្ហាជាមួយនឹងការរៀនរចនាពួកវាបានរីករាលដាលយ៉ាងខ្លាំង។ តាមរយៈការសាងសង់ភារកិច្ច យើងនឹងយល់ពីដំណើរការនៃការបង្កើតកិច្ចការថ្មី។ ការ​សាង​បញ្ហា​គឺ​ផ្អែក​លើ​សមត្ថភាព​បង្កើត​ត្រីកោណមាត្រ​ការ៉េ។ ក្នុងករណីនេះ បច្ចេកទេសផ្សេងៗត្រូវបានប្រើប្រាស់៖ ភាពស្រដៀងគ្នា បំរែបំរួលនៃមេគុណនៃត្រីកោណការ៉េ បំរែបំរួលនៃអថេរថ្មី បំរែបំរួលនៃតម្រូវការការងារ។ មុខងារស្មុគ្រស្មាញកាន់តែច្រើនអាចដើរតួជាមេគុណ និងអថេរថ្មី។ ដូច្នេះអ្នកអាចប្រើ trinomial ការ៉េដែលនឹងជួយក្នុងការរៀបចំពាក្យដដែលៗនៃមុខងារស្មុគ្រស្មាញបន្ថែមទៀត៖ អិចស្ប៉ូណង់ស្យែល លោការីត ត្រីកោណមាត្រ។ នៅលើដៃមួយអ្នកត្រូវដឹងពីលក្ខណៈសម្បត្តិនៃត្រីកោណការ៉េហើយម្យ៉ាងវិញទៀតលក្ខណៈសម្បត្តិនៃមុខងារត្រូវបានធ្វើម្តងទៀតដោយហេតុនេះអាចសម្រេចបាននូវការរួមបញ្ចូលគ្នានៃបញ្ហា។

ជម្រើសនៃបញ្ហាជាមួយនឹងប៉ារ៉ាម៉ែត្រសម្រាប់ការបង្រៀនដំណោះស្រាយ និងការរចនារបស់ពួកគេអាចត្រូវបានពន្យល់ដោយកាលៈទេសៈដូចខាងក្រោមៈ

នៅពេលដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ ពាក្យផ្ទួនកើតឡើង ហើយជាលទ្ធផល ភាពស៊ីជម្រៅ និងរឹងមាំនៃបញ្ហាកម្មវិធី។

ការដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ ពង្រីកការយល់ដឹងគណិតវិទ្យា ផ្តល់នូវវិធីសាស្រ្តថ្មីក្នុងការដោះស្រាយបញ្ហា។

មានការអភិវឌ្ឍនៃគណិតវិទ្យា ការគិតឡូជីខល សមត្ថភាពក្នុងការវិភាគ ប្រៀបធៀប ទូទៅ;

ជំនាញសម្រាប់ការងារស្រាវជ្រាវត្រូវបានទទួល;

ជំនួយក្នុងការរៀបចំសម្រាប់ការប្រឡង;

មានការបង្កើតបុគ្គលិកលក្ខណៈដូចជាការឧស្សាហ៍ព្យាយាម, គោលបំណង, ការតស៊ូ, ឆន្ទៈ, ភាពត្រឹមត្រូវ។

បានបង្កើត UUD ក្នុងក្របខ័ណ្ឌនៃស្តង់ដារអប់រំរដ្ឋសហព័ន្ធ នៅពេលដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ៖

ដំណាក់កាលនៃការដោះស្រាយបញ្ហា

បង្កើត UUD

ការវិភាគស្ថានភាព(សេចក្តីផ្តើមនៃអក្សរ)

• ការកំណត់គោលដៅ;

  ការបន្លិចព័ត៌មានសម្ភារៈ;

  ការបង្កើតបញ្ហា និងការព្យាករណ៍ដំណោះស្រាយ;

  អរូបី;

  ភាពស្រដៀងគ្នា;

  ចំណាត់ថ្នាក់ (អក្សរសាស្ត្រ);

  សកម្មភាពនិមិត្តសញ្ញា។

គ្រោងការណ៍កត់ត្រាស្ថានភាពនៃបញ្ហាក្នុងទម្រង់ជាតារាង ដ្យាក្រាម ក្រាហ្វជាមួយអក្សរដែលបានបញ្ចូល

• ការធ្វើផែនការ;

  ការរៀបចំប្រព័ន្ធ;

  សកម្មភាពនិមិត្តសញ្ញា;

  ការធ្វើគំរូ។

ការកសាងគំរូ(ស្វែងរក analogue ការទាក់ទាញនៃច្បាប់ដែលគេស្គាល់ពីគណិតវិទ្យា ឬរូបវិទ្យា)

• ការបង្កើតវិធីសាស្រ្តសម្រាប់ការដោះស្រាយ zalachi;

  ការកែតម្រូវលក្ខខណ្ឌ;

  ការធ្វើគំរូក្នុងទម្រង់ក្រាហ្វិក។

ការដោះស្រាយសមីការ ប្រព័ន្ធ ។ល។(ស្វែងរកមិនស្គាល់)

• ការវិភាគនិងការកំណត់អត្តសញ្ញាណព័ត៌មានសម្ភារៈ;

  លទ្ធផលនៃផលវិបាក;

  ការកសាងខ្សែសង្វាក់នៃហេតុផលមួយ;

  ការអភិវឌ្ឍនិងការធ្វើតេស្តសម្មតិកម្ម;

  ការផ្លាស់ប្តូរគំរូ។

ការបកស្រាយគំរូ(ការផ្ទៀងផ្ទាត់ និងវាយតម្លៃដំណោះស្រាយ ឫសគល់)

• ការវិភាគ;

  លទ្ធផលនៃផលវិបាក;

  ការបញ្ជាក់;

  សកម្មភាពនិមិត្តសញ្ញា (ការបកស្រាយ) ។

សិក្សា(ការបង្កើតទូទៅនៃបញ្ហា ឬវិធីសាស្រ្តសម្រាប់ដោះស្រាយវាសម្រាប់លក្ខខណ្ឌដែលបានកែប្រែ វិធីសាស្រ្តផ្សេងទៀតក្នុងការដោះស្រាយ)

• ការវិភាគ;

  ការសំយោគ;

  ស្វែងរក analogues;

  ការកសាងខ្សែសង្វាក់នៃហេតុផលមួយ;

  សមត្ថភាពក្នុងការបញ្ជូនមាតិកាដោយសង្ខេប;

  ដ្យាក្រាមជំនាញ និមិត្តសញ្ញា គំរូ;

  ការបង្កើតវិធីដោះស្រាយបញ្ហានៃការស្វែងរក ធម្មជាតិប្រកបដោយការច្នៃប្រឌិត។

ការឆ្លុះបញ្ចាំង

• ការបង្កើតអត្ថន័យ;

  ការធ្វើផែនការ;

  ការត្រួតពិនិត្យ;

  ការកែតម្រូវ;

  ថ្នាក់;

  បទបញ្ជាខ្លួនឯងតាមឆន្ទៈ;

  ការត្រៀមខ្លួនសម្រាប់ការអភិវឌ្ឍន៍ខ្លួនឯង, សម្រាប់ការអប់រំខ្លួនឯង;

  សមត្ថភាពក្នុងការកំណត់ដោយឯករាជ្យនូវគោលដៅនៃការបណ្តុះបណ្តាលរបស់ពួកគេ;

  កំណត់និងបង្កើតភារកិច្ចថ្មីសម្រាប់ខ្លួនអ្នក;

  អភិវឌ្ឍការជម្រុញ និងផលប្រយោជន៍នៃសកម្មភាពអប់រំរបស់ពួកគេ។

ប្រព័ន្ធកិច្ចការច្រើនកម្រិត

មូលដ្ឋាននៃវិធីសាស្រ្តបង្រៀនដោយផ្អែកលើប្រព័ន្ធពហុកម្រិតនៃភារកិច្ចគឺការអភិវឌ្ឍន៍បន្តិចម្តង ៗ នៃប្លុកនៃម៉ាទ្រីសរបស់វា។ លក្ខណៈសំខាន់នៃបច្ចេកទេសនេះគឺថានៅកម្រិតនីមួយៗ i.e. នៅពេលធ្វើជាម្ចាស់លើជួរឈរដែលត្រូវគ្នានៃម៉ាទ្រីស សិស្សរាល់ពេលដែលជួបប្រទះស្ថានភាពសិក្សាទាំងបីប្រភេទដែលកើតឡើងនៅពេលដោះស្រាយបញ្ហា។

ប្រព័ន្ធពហុកម្រិតនៃកិច្ចការសម្រាប់ប្រធានបទនីមួយៗនៃវគ្គសិក្សាត្រូវបានបង្កើតឡើងដោយប្រើតំណាងម៉ាទ្រីសរបស់វា ដោយគូសបញ្ជាក់ពីបញ្ជីចំណាត់ថ្នាក់នៃធាតុមូលដ្ឋាននៃខ្លឹមសារនៃការអប់រំ និងកិច្ចការមូលដ្ឋានដែលត្រូវគ្នានឹងពួកគេ ហើយនៅលើដៃម្ខាង និងកម្រិតនៃការរៀន។ ដែលឆ្លុះបញ្ចាំងពីសមត្ថភាពក្នុងការដោះស្រាយបញ្ហាដែលធ្លាប់ស្គាល់ កែប្រែ និងការងារដែលមិនធ្លាប់ស្គាល់។

ម៉ាទ្រីសនៃប្រព័ន្ធកិច្ចការប្រធានបទមាន 3 ជួរដែលត្រូវគ្នាទៅនឹងស្ថានភាពសិក្សាបីប្រភេទដែលកើតឡើងនៅពេលដោះស្រាយបញ្ហា និងន ជួរឈរឆ្លុះបញ្ចាំងពីចំនួនកិច្ចការមូលដ្ឋាននៃប្រធានបទ។ តារាង (ម៉ាទ្រីស) បែបនេះតំណាងឱ្យប្រព័ន្ធនៃកិច្ចការនៃប្រធានបទនេះជួយឱ្យមានការបំពេញពេញលេញនៅកម្រិតនីមួយៗនៃសមាសធាតុគណិតវិទ្យា និងសកម្មភាព (ការបង្កើត UUD) ហើយដោយហេតុនេះអនុវត្តលក្ខណៈវិនិច្ឆ័យសម្រាប់ភាពពេញលេញនៃប្រធានបទ និងសកម្មភាព (មានន័យថា UUD ការយល់ដឹង) ប្រព័ន្ធនៃភារកិច្ចអប់រំ។ ក្នុងពេលជាមួយគ្នានេះ ប្រសិនបើកិច្ចការមូលដ្ឋាននៅក្នុងប្រព័ន្ធដើរតួនាទីជាប្រភេទនៃសមាហរណកម្មនៃធាតុផ្សំនៃប្រធានបទ នោះនៅពេលរចនា និងអនុវត្តដំណើរការសិក្សា តួនាទីស្រដៀងគ្នាគួរតែត្រូវបានលេងដោយសកម្មភាពសិក្សាជាសកល (វិធីសាស្រ្តទូទៅ និង បច្ចេកទេសនៃសកម្មភាព) ក្នុងស្ថានភាពដែលបានជ្រើសរើស។

សកម្មភាពអប់រំក្នុងការដោះស្រាយបញ្ហាដែលរួមបញ្ចូលក្នុងជួរទីមួយនៃម៉ាទ្រីសគឺមានលក្ខណៈបន្តពូជ (សកម្មភាពអប់រំទូទៅដូចជាការចាត់ថ្នាក់ ការសង្ខេបក្រោមគំនិត ការទទួលបានលទ្ធផល សកម្មភាព ការកសាងខ្សែសង្វាក់តក្កវិជ្ជានៃហេតុផល ភស្តុតាង។ល។ ) ត្រូវ​បាន​ប្រើ។ ភារកិច្ចដែលពាក់ព័ន្ធគឺខុសគ្នា។ទំនាក់ទំនងច្បាស់លាស់ រវាងទិន្នន័យ និងធាតុដែលត្រូវការ (ស្គាល់ និងមិនស្គាល់)។ សិស្សកំណត់អត្តសញ្ញាណ (ទទួលស្គាល់កិច្ចការដែលធ្លាប់ស្គាល់នៅក្នុងចំនួនស្រដៀងគ្នា) ផលិតឡើងវិញនូវវិធីសាស្រ្តដែលបានសិក្សា ឬក្បួនដោះស្រាយនៃសកម្មភាព អនុវត្តចំណេះដឹងដែលទទួលបានក្នុងន័យជាក់ស្តែងសម្រាប់ថ្នាក់ការងារដែលគេស្គាល់មួយចំនួន និងទទួលបានព័ត៌មានថ្មីដោយផ្អែកលើការអនុវត្តគំរូសកម្មភាពដែលបានសិក្សា។ .

នៅពេលដោះស្រាយកិច្ចការនៃជួរទីពីរ សកម្មភាពសិក្សាបន្តពូជត្រូវបានផ្សំជាមួយសកម្មភាពស្ថាបនាឡើងវិញ ដែលគំរូនៃសកម្មភាពមិនត្រូវបានផលិតឡើងវិញពីការចងចាំនោះទេ ប៉ុន្តែត្រូវបានបង្កើតឡើងវិញក្រោមលក្ខខណ្ឌដែលបានកែប្រែខ្លះ (នៅទីនេះ សកម្មភាពអប់រំទូទៅដូចជាការជ្រើសរើស និងការបង្កើត គោលដៅនៃការយល់ដឹង ការស្វែងរក និងការជ្រើសរើសព័ត៌មានចាំបាច់ សកម្មភាពជានិមិត្តរូប រួមទាំងការធ្វើគំរូគណិតវិទ្យា រចនាសម្ព័ន្ធចំណេះដឹង)។

ជាចុងក្រោយ នៅពេលដោះស្រាយបញ្ហានៃខ្សែទី 3 សកម្មភាពអប់រំគឺមានលក្ខណៈច្នៃប្រឌិតនៃការស្រាវជ្រាវ។ សិស្សត្រូវតែអាចរុករកក្នុងស្ថានភាពថ្មី និងបង្កើតកម្មវិធីសកម្មភាពថ្មីជាមូលដ្ឋាន (ដាក់សម្មតិកម្ម ពិនិត្យ៖ បញ្ជាក់ ឬបដិសេធ ដាក់ចេញថ្មី ។ល។ អនុវត្តសកម្មភាពស្រាវជ្រាវ)។ ការដោះស្រាយបញ្ហានៃប្លុកដែលត្រូវគ្នាតម្រូវឱ្យសិស្សមានមូលនិធិយ៉ាងទូលំទូលាយនៃក្បួនដោះស្រាយដែលបានបង្ហាញឱ្យឃើញ និងដាក់ឱ្យប្រើប្រាស់យ៉ាងឆាប់រហ័ស។ សមត្ថភាពក្នុងការសរសេរកូដឡើងវិញយ៉ាងឆាប់រហ័សពីទម្រង់សញ្ញា-និមិត្តសញ្ញាទៅជាក្រាហ្វិកមួយ ហើយផ្ទុយទៅវិញ ពីក្រាហ្វិកទៅជាសញ្ញា-និមិត្តសញ្ញាមួយ; ចក្ខុវិស័យជាប្រព័ន្ធនៃវគ្គសិក្សា។ ក្នុងពេលជាមួយគ្នានេះ វាមិនគ្រាន់តែពាក់ព័ន្ធនឹងការប្រើប្រាស់ក្បួនដោះស្រាយចាស់ក្នុងលក្ខខណ្ឌថ្មី និងការកើនឡើងនៃភាពស្មុគស្មាញផ្នែកបច្ចេកទេសប៉ុណ្ណោះទេ ប៉ុន្តែត្រូវបានសម្គាល់ដោយភាពមិនច្បាស់លាស់នៃកម្មវិធី និងការរួមបញ្ចូលគ្នានៃក្បួនដោះស្រាយដែលបានសិក្សា។ ភារកិច្ចនៃកម្រិតនេះមានរចនាសម្ព័ន្ធឡូជីខលដ៏ស្មុគស្មាញនិងត្រូវបានកំណត់ដោយវត្តមានការតភ្ជាប់មិនទាន់ឃើញច្បាស់ រវាងទិន្នន័យ និងធាតុដែលអ្នកកំពុងស្វែងរក។ ភារកិច្ចបែបនេះជាធម្មតាត្រូវបានផ្តល់ជូនជាការលំបាកបំផុតក្នុងការប្រឡងចូលសាកលវិទ្យាល័យដែលមានតម្រូវការខ្ពស់សម្រាប់ការរៀបចំគណិតវិទ្យារបស់អ្នកដាក់ពាក្យ និងនៅក្នុងកិច្ចការ 17, 18, 20, 21 នៃ KIM USE ។

ប្រព័ន្ធពហុកម្រិតនៃភារកិច្ចលើប្រធានបទ "ដេរីវេ"

№ ទំ/ទំ

ឈ្មោះភារកិច្ច

ប្រភេទភារកិច្ច

ការគណនាដេរីវេតាមនិយមន័យ។

៣៣

MOH

NZ

ការស្វែងរកដេរីវេនៃផលបូក ផលិតផល មុខងារឯកជន

៣៣

MOH

NZ

ការស៊ើបអង្កេតលើភាពឯកតានៃមុខងារ

៣៣

មុខងារ កើនឡើងតាមបន្ទាត់លេខទាំងមូល?

MOH

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រមុខងារ ថយចុះសម្រាប់តម្លៃទាំងអស់។ ?

NZ

ស្វែងរកសំណុំនៃលេខទាំងអស់ a សម្រាប់មុខងារនីមួយៗf(x) = អំពើបាប 2 x – 8(ក + 1) sinx + (4 ក 2 + 8 ក – 14) xកំពុងកើនឡើងនៅលើបន្ទាត់ពិតទាំងមូល ហើយមិនមានចំណុចសំខាន់ទេ។

ការស្វែងរកចំណុចខ្លាំង

៣៣

មាន​ចំណុច​កំណត់​មួយ?

MOH

កំណត់តម្លៃនៃប៉ារ៉ាម៉ែត្រ មុខងារអតិបរមាគឺ 9

NZ

សម្រាប់តម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ a មុខងារf(x) = (ក 2 – 3 ក + 2) (cos 2 – អំពើបាប 2 + (ក – 1) x + អំពើបាប1 មិនមានចំណុចសំខាន់ទេ?

ការស្វែងរកតម្លៃធំបំផុត និងតូចបំផុតនៃអនុគមន៍បន្តមួយនៅលើចន្លោះពេល និងអាចខុសគ្នានៅលើចន្លោះពេលមួយ

៣៣

ស្វែងយល់ថាតើតម្លៃអ្វីខ្លះនៃប៉ារ៉ាម៉ែត្រក តម្លៃមុខងារតូចបំផុត។y = x 2 -12 x + ក នៅលើផ្នែកគឺសូន្យ។

MOH

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ តម្លៃមុខងារតូចបំផុត។ស្មើ

NZ

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រមុខងារ យកតម្លៃតិចជាង 5 សម្រាប់ណាមួយ។

បញ្ចប់ការរុករក និងរៀបចំផែនការ

៣៣

3+3x2

MOH

នៅតម្លៃនៃប៉ារ៉ាម៉ែត្រ a គឺជាអប្បបរមានៃអនុគមន៍ f(x) = ax 2 − 6ax + a 2 − 9 ស្មើនឹង 1 ?

NZ

សមីការនៃតង់សង់ទៅក្រាហ្វនៃអនុគមន៍នៅចំណុចដែលបានផ្តល់ឱ្យ

៣៣

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រត្រង់ គឺតង់សង់ទៅក្រាហ្វនៃអនុគមន៍ ?

MOH

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ តង់សង់​ទៅ​ក្រាហ្វិក​មុខងារ កាត់ចេញពីត្រីមាសទីមួយ ត្រីកោណ isosceles ជាមួយផ្ទៃ

NZ

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ គូសនៅចំណុចប្រសព្វរបស់វាជាមួយអ័ក្ស, បង្កើតជាមុំមួយ។

ការអនុវត្តនៃដេរីវេក្នុងការដោះស្រាយបញ្ហាក្នុងធរណីមាត្រ រូបវិទ្យា និងសេដ្ឋកិច្ច

៣៣

អ្វីដែលគួរជាជ្រុងនៃចតុកោណកែងជាមួយបរិវេណទំពង្រីកតំបន់របស់វា?

MOH

បង្អួច​មាន​រាង​ចតុកោណ​ដែល​ចង​នៅ​លើ​កំពូល​ដោយ​រង្វង់​មូល (រូបភាព​ទី ៣)។ បរិវេណនៃបង្អួចគឺ P. កំណត់កាំនៃពាក់កណ្តាលរង្វង់ R ដែលតំបន់នៃបង្អួចគឺធំជាងគេ។

NZ

រូបភាពនៃកម្ពស់ a ត្រូវបានព្យួរនៅលើជញ្ជាំងតាមរបៀបដែលគែមខាងក្រោមរបស់វាមានឯកតា h ខាងលើកម្រិតភ្នែករបស់អ្នកសង្កេតការណ៍។ តើអ្នកសង្កេតគួរស្ថិតនៅចម្ងាយប៉ុន្មាន x ពីជញ្ជាំង ដើម្បីឱ្យមុំមើលនៃគំនូរមានទំហំធំជាងគេ (រូបភាពទី 7 ក)?

ដំណោះស្រាយ

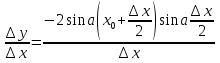
ការសម្រេចចិត្ត :

1. អនុគមន៍ f(x) ថយចុះសម្រាប់តម្លៃទាំងអស់នៃ x ប្រសិនបើដេរីវេ

f′(x) = 6ax 2 + 18ax + 30a = 6a(x 2 + 3x + 5)< 0

សម្រាប់ x ទាំងអស់។

2. ដូច្នេះហើយ យើងរកឃើញថា ក< 0.

3 . ចម្លើយ៖ ក (–∞; 0).

1. ស្វែងរកសំណុំនៃលេខទាំងអស់ a សម្រាប់មុខងារនីមួយៗ f (x) \u003d sin 2x - 8 (a + 1) sinx + (4a 2 + 8a - 14) x កំពុងកើនឡើងនៅលើបន្ទាត់ពិតទាំងមូល ហើយមិនមាន មានចំណុចសំខាន់។

1. សម្រាប់ a ថេរណាមួយ មុខងារនេះអាចខុសគ្នានៅគ្រប់ចំណុចនៅលើបន្ទាត់ពិត។

2. ដោយសារអនុគមន៍ f(x) កំពុងកើនឡើង វិសមភាព f′(x) ≥ 0 ត្រូវតែរក្សានៅចំនុច x នីមួយៗ។

3. លើសពីនេះ f(x) មិនមានចំណុចសំខាន់ទេ ដូច្នេះសម្រាប់ x ណាមួយ វិសមភាព f′(x) ≠ 0 ត្រូវតែរក្សា។

4. ដូច្នេះ ប្រសិនបើអនុគមន៍បំពេញលក្ខខណ្ឌនៃបញ្ហានោះ រាល់ x វិសមភាព f (x) > 0 ត្រូវតែពេញចិត្ត។

5. ម្យ៉ាងវិញទៀត ប្រសិនបើវិសមភាព f′(x) > 0 រក្សាសម្រាប់ x ទាំងអស់ នោះមុខងារច្បាស់ជាមិនមានចំណុចសំខាន់ ហើយកំពុងកើនឡើង។

6. ស្វែងរកដេរីវេនៃមុខងារនេះ៖

f′( x) = 2 cos 2 x – 8( ក + 1) cosx + 4 ក 2 + 8 ក – 14.

ឥឡូវនេះបញ្ហាអាចត្រូវបានកែទម្រង់ដូចខាងក្រោម: ស្វែងរកតម្លៃទាំងអស់នៃប៉ារ៉ាម៉ែត្រ a សម្រាប់នីមួយៗសម្រាប់ x វិសមភាព។

cos 2x − 4(a + 1) cos x + 2a 2 + 4a – 7 > 0 ។(1)

7. ផ្តល់ថា cos 2x = 2 cos 2 x − 1 និងការកំណត់ cos x = t ដែល −1 ≤ t ≤ 1 យើងសរសេរវិសមភាព (1) ឡើងវិញដូចខាងក្រោម៖

2t 2 – 1 – 4 (a + 1) t + 2a 2 + 4a – 7 > 0,

ឬ

t 2 - 2 (a + 1) t + ក 2 + 2a – 4 > 0. (2)

8. កំណត់មុខងារនៅខាងឆ្វេងនៃវិសមភាព (2) ដោយ ϕ(t) យើងផ្តល់រូបមន្តថ្មីនៃបញ្ហាដើម៖ ស្វែងរកតម្លៃទាំងអស់នៃ a សម្រាប់តម្លៃនីមួយៗនៃអនុគមន៍ ϕ( t) នៅចន្លោះពេល [–1; 1] វិជ្ជមាន។

9. ដេរីវេ ϕ′(t) = 2t − 2(a + 1) បាត់នៅ t 0 = ក + ១ ។

10. តម្លៃតូចបំផុតនៃអនុគមន៍ ϕ(t) នៅលើចន្លោះពេល [–1; 1] គឺ៖

ϕ (–១) = ក 2 + 4a – 1,ប្រសិនបើa + 1 ≤ −1;

ϕ (a + 1) = -5,ប្រសិនបើ –1 < a + 1 < 1;

ϕ(1) = ក 2 – 5 ប្រសិនបើ a + 1 ≥ 1 ។

11. ចាប់តាំងពីតម្លៃតូចបំផុតនៃអនុគមន៍ ϕ(t) នៅលើផ្នែក [–1; 1] ត្រូវតែជាវិជ្ជមាន បន្ទាប់មកតម្លៃនៃប៉ារ៉ាម៉ែត្រដែលពេញចិត្តនឹងលក្ខខណ្ឌនៃបញ្ហាជារបស់ចន្លោះពេលពីរ៖ a ≤ -2 និង a ≥ 0 ។

12. ប្រសិនបើ a ≤ −2 នោះតម្លៃដែលចង់បាននៃប៉ារ៉ាម៉ែត្រ a បំពេញវិសមភាព a 2 + 4a – 1 > 0 ។

13. ប្រសិនបើ a ≥ 0 នោះតម្លៃដែលចង់បាននៃប៉ារ៉ាម៉ែត្រ a បំពេញវិសមភាព a 2 – 5 > 0.

14. ដូចនេះ សំណុំនៃតម្លៃដែលចង់បាន a គឺជាការរួបរួមនៃដំណោះស្រាយនៃប្រព័ន្ធវិសមភាពពីរ៖

(3)

a ≥ 0

ក 2 -5 > 0 (4)

15. សំណុំនៃដំណោះស្រាយចំពោះប្រព័ន្ធ (3) គឺជាចន្លោះពេល –∞< a < –2 –√5 , а множество решений системы (4)- промежуток a >√5 .

១៦.ចម្លើយ៖ ក (–∞; –2 –√5) (√5; +∞).

1. ដោយសារអនុគមន៍នេះមានភាពខុសប្លែកគ្នានៅលើបន្ទាត់ពិតទាំងមូល ចំនុចសំខាន់នៃអនុគមន៍ f(x) គឺជាចំនុចដែលដេរីវេទី f′(x) = 0 ។

2. ក្នុងករណីនេះយើងមាន f (x) =(a–1)(a–2) (–sin+ (ក - ១) ។

3. ជាក់ស្តែងប្រសិនបើ a = 1 បន្ទាប់មក f (x) = 0 សម្រាប់ x ណាមួយ។ R, i.e.

សម្រាប់អនុគមន៍ដែលបានផ្តល់ឱ្យ ចំនុចនីមួយៗ x R គឺសំខាន់។

4. សន្មតថា ក 1. បន្ទាប់មកសមីការ f (x) = 0 យកទម្រង់

(a - 2) អំពើបាប = 2. (1)

វាធ្វើតាមថាប្រសិនបើ |a – 2|< 2, т. е. если a (0; 1) (1; 4),

បន្ទាប់មកសមីការ (1) មិនមានឫសគល់ទេ ដូច្នេះហើយសម្រាប់តម្លៃដែលបានបង្ហាញនៃ a មុខងារ f(x) មិនមានចំណុចសំខាន់ទេ។

5 . ចម្លើយ៖ ក (0; 1) (1; 4).

តម្លៃតូចបំផុតនៃភាគយក និងតម្លៃធំបំផុតនៃភាគបែងត្រូវបានសម្រេចនៅតម្លៃផ្សេងគ្នានៃ x ។ ដូច្នេះ ដើម្បីស្វែងរកតម្លៃតូចបំផុតនៃអនុគមន៍ វាជាការងាយស្រួលក្នុងការប្រើដេរីវេ។ ចូរយើងសរសេរឡើងវិញនូវវិសមភាពក្នុងទម្រង់

កន្លែងណាt=3- cos 2 x, t

ស្វែងរកតម្លៃតូចបំផុតនៃមុខងារf( t) = , នៅលើផ្នែក. ចាប់តាំងពីដេរីវេf "( t) = អវិជ្ជមាននៅtបន្ទាប់មកfថយចុះ ហើយយកតម្លៃតូចបំផុតនៅt=3, f ឈ្មោះ = f(3) = .

ចម្លើយ៖ក

តើអ្វីទៅជា k ធម្មជាតិតូចបំផុតដែលសមីការ x 3+3x2 – 45x + k = 0 មានឫសតែមួយ?

1. សាងសង់គំនូសតាងនៃក្រាហ្វនៃអនុគមន៍ y 1 = x 3 + 3x 2 – 45x និងកំណត់តម្លៃធម្មជាតិតូចបំផុតនៃ k ដែលក្រាហ្វនេះកាត់បន្ទាត់ y 2 = –k ត្រង់ចំណុចមួយ។

2. ក) D(y 1 ) = R;

បូ 1 / = 3x 2 + 6x - 45; 1 / ក្នុងចន្លោះពេល (–∞; –5), (–5; 3) និង (3; +∞) ត្រូវបានបង្ហាញនៅក្នុងរូបភព។ 1. នៅក្នុងរូបភព។ 2 គឺជាការតំណាងគំនូសតាងនៃក្រាហ្វនៃអនុគមន៍ y 1 .

3. ជាក់ស្តែង សមីការនេះមានដំណោះស្រាយតែមួយគត់ប្រសិនបើ –k> 175 ឬ –k< –81, т. е. k < –175 или k >81. តម្លៃធម្មជាតិតូចបំផុតនៃ k គឺ 82 ។

៤.ចំលើយ៖ k = ៨២.

តើតម្លៃនៃប៉ារ៉ាម៉ែត្រ a ជាអប្បបរមានៃអនុគមន៍ f(x) = ax2 – 6ax + a2 – 9 ស្មើនឹង 1?

1. f′(x) = −6x 2 + 6x + 12 ។

2. y′ = 0 សម្រាប់ x 1 = 2.

6. ចម្លើយ៖ a = 2 ។

នៅតម្លៃនៃប៉ារ៉ាម៉ែត្រ a គឺជាអប្បបរមានៃអនុគមន៍ f(x) = –2x 3 + 3x 2 + 12x + 4a គឺ 1 ?

សម្រាប់តម្លៃនៃប៉ារ៉ាម៉ែត្រ a គឺបន្ទាត់ y=ax-2 តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=1+ln⁡ x?

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=a-x^2 កាត់ចេញត្រីកោណ isosceles ដែលមានផ្ទៃដី 9/32 ពីត្រីមាសទីមួយ

ជា តាមលក្ខខណ្ឌ តង់សង់ត្រូវប្រសព្វអនុគមន៍ក្នុងត្រីមាសមានន័យថា. ត្រីកោណ isosceles គឺជាត្រីកោណកែង ដូច្នេះមុំផ្សេងទៀតគឺស្មើគ្នា, ប៉ុន្តែតើតង់ហ្សង់កើតឡើងនៅពេលណា ចំណុចទំនាក់ទំនងនៃតង់សង់ជាមួយក្រាហ្វតាមអ័ក្ស x គឺស្មើនឹង . យោងតាមរូបមន្តតង់សង់ទៅក្រាហ្វ ចាប់តាំងពីតំបន់នៃត្រីកោណមួយគួរតែ បន្ទាប់មក ជា ត្រីមាស។កន្លែងណា

នៅតម្លៃអ្វីនៃប៉ារ៉ាម៉ែត្រ a តង់សង់ទៅក្រាហ្វនៃអនុគមន៍ y=4x^2-|a|x ដែលគូរនៅចំណុចប្រសព្វរបស់វាជាមួយអ័ក្ស x បង្កើតជាមុំ 60° រវាងពួកវា

តើជ្រុងនៃចតុកោណជាមួយបរិមាត្រ P គួរតែជាជ្រុងណាសម្រាប់ផ្ទៃដីរបស់វាអតិបរមា?

បង្អួច​មាន​រាង​ចតុកោណ​ដែល​ចង​នៅ​លើ​កំពូល​ដោយ​រង្វង់​មូល (រូបភាព​ទី ៣)។ បរិវេណនៃបង្អួចគឺ P. កំណត់កាំនៃពាក់កណ្តាលរង្វង់ R ដែលតំបន់នៃបង្អួចគឺធំជាងគេ។

រូបភាពនៃកម្ពស់ a ត្រូវបានព្យួរនៅលើជញ្ជាំងតាមរបៀបដែលគែមខាងក្រោមរបស់វាមានឯកតា h ខាងលើកម្រិតភ្នែករបស់អ្នកសង្កេតការណ៍។ តើអ្នកសង្កេតគួរស្ថិតនៅចម្ងាយប៉ុន្មាន x ពីជញ្ជាំង ដើម្បីឱ្យមុំមើលនៃគំនូរមានទំហំធំជាងគេ (រូបភាពទី 7 ក)?

អក្សរសិល្ប៍

Azarov A.I., Barvenov S.A., Fedosenko V.S.វិធីសាស្រ្តក្នុងការដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ។ គណិតវិទ្យាសម្រាប់សិស្សវិទ្យាល័យ។ Minsk: "Aversev", ឆ្នាំ 2003 ។

V.S. Vysotsky, ភារកិច្ចជាមួយប៉ារ៉ាម៉ែត្រសម្រាប់ការរៀបចំសម្រាប់ការប្រឡង

Gorshtein P.I., Polonsky V.B., Yakir M.S. ភារកិច្ចជាមួយប៉ារ៉ាម៉ែត្រ។ - K. : RIA "អត្ថបទ"; MP "OKO", 1992. -290 ទំ។

Kachalova G.A. អំពីតម្រូវការក្នុងការរួមបញ្ចូលបន្ទាត់មាតិកា - វិធីសាស្រ្ត "បញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ" នៅក្នុងម៉ូឌុលអប់រំ "មូលដ្ឋានគ្រឹះនៃគណិតវិទ្យា" //បញ្ហាł yMię dzynarodowej Naukowi- PraktycznejkonferencjiPostę ទំó wwnauce. Nowepoglą ឌី, បញ្ហា, innowacje. 29.07.2012. - 31.07.2012. część 2. - Łoឃź, 2012. - S. 67–70 ។

Kozko A. I., Panferov V. S., Sergeev I. N., Chirsky V. G. USE 2011. គណិតវិទ្យា។ កិច្ចការ C5 ។ ភារកិច្ចដែលមានប៉ារ៉ាម៉ែត្រ / Ed ។ A.L. Semenova និង I.V. Yashchenko ។ - M.: MTsNMO, 2011.-144 ទំ។

Rodionov E.M. ការដោះស្រាយបញ្ហាជាមួយប៉ារ៉ាម៉ែត្រ។ M.: MP "Rus-90", ឆ្នាំ 1995