គូរពហុកោណនៅលើក្រដាសគូស។ ឧទាហរណ៍ដូចជាបង្ហាញក្នុងរូបភាពទី 1 ។

តោះព្យាយាមគណនាតំបន់របស់វាឥឡូវនេះ។ តើត្រូវធ្វើដូចម្តេច? ប្រហែលជាវិធីងាយស្រួលបំផុតគឺបំបែកវាទៅជាត្រីកោណកែង និងចតុកោណកែង ដែលជាផ្នែកដែលងាយស្រួលក្នុងការគណនា និងបន្ថែមលទ្ធផលរួចហើយ។ វិធីសាស្រ្តដែលខ្ញុំបានប្រើគឺសាមញ្ញ ប៉ុន្តែពិបាកខ្លាំង ហើយក្រៅពីនេះ វាមិនស័ក្តិសមសម្រាប់ពហុកោណទាំងអស់។

ពិចារណាពហុកោណចំនួនគត់សាមញ្ញដែលមិនខូចទ្រង់ទ្រាយ (នោះគឺវាត្រូវបានតភ្ជាប់ - ចំណុចទាំងពីររបស់វាអាចត្រូវបានតភ្ជាប់ដោយខ្សែកោងបន្តដែលមានទាំងស្រុងនៅក្នុងវា ហើយចំនុចកំពូលរបស់វាទាំងអស់មានកូអរដោណេចំនួនគត់ ព្រំដែនរបស់វាគឺជាប៉ូលីលីនដែលតភ្ជាប់ដោយគ្មាន ផ្លូវប្រសព្វដោយខ្លួនឯង ហើយវាមានការ៉េមិនសូន្យ)។ ដើម្បីគណនាផ្ទៃនៃពហុកោណបែបនេះ អ្នកអាចប្រើទ្រឹស្តីបទខាងក្រោម៖

ទ្រឹស្តីបទជ្រើសរើស។ទុកជាចំនួនពិន្ទុចំនួនគត់នៅខាងក្នុងពហុកោណ ជាចំនួនគត់នៃចំនុចគត់នៅលើព្រំដែនរបស់វា និងជាតំបន់របស់វា។ បន្ទាប់មក រូបមន្តជ្រើសរើស:

ឧទាហរណ៍។សម្រាប់ពហុកោណក្នុងរូបភាពទី 1 (ចំណុចពណ៌លឿង) (ចំណុចពណ៌ខៀវ កុំភ្លេចចំណុចកំពូល!) ដូច្នេះ ឯកតាការ៉េ។

ភស្តុតាងនៃទ្រឹស្តីបទ Pick ។ដំបូង ចំណាំថារូបមន្តរបស់ Pick គឺពិតសម្រាប់ឯកតាការ៉េ។ ជាការពិតក្នុងករណីនេះយើងមាន

ពិចារណាចតុកោណកែងដែលមានជ្រុងដេកលើបន្ទាត់បន្ទះឈើ។ សូមឱ្យប្រវែងនៃជ្រុងរបស់វាស្មើនិង។ យើងមាននៅក្នុងករណីនេះ ហើយយោងទៅតាមរូបមន្តជ្រើសរើស។

ឥឡូវនេះ សូមពិចារណាត្រីកោណកែងដែលមានជើងដេកលើអ័ក្សកូអរដោណេ។ ត្រីកោណបែបនេះត្រូវបានទទួលពីចតុកោណជាមួយជ្រុងហើយពិចារណានៅក្នុងករណីមុនដោយកាត់វាតាមអង្កត់ទ្រូង។ ទុកអោយចំនុចចំនួនគត់ស្ថិតនៅលើអង្កត់ទ្រូង។ បន្ទាប់មកសម្រាប់ករណីនេះយើងទទួលបាននោះ។

ឥឡូវពិចារណាត្រីកោណដែលបំពាន។ វាអាចត្រូវបានទទួលបានដោយការកាត់ចេញត្រីកោណមុំខាងស្តាំជាច្រើន ហើយប្រហែលជាចតុកោណកែងពីចតុកោណកែង (សូមមើលរូបភាពទី 2 និងទី 3)។ ដោយសាររូបមន្តរបស់ Pick គឺពិតសម្រាប់ទាំងចតុកោណកែង និងត្រីកោណកែង យើងទទួលបានថាវាក៏នឹងជាការពិតសម្រាប់ត្រីកោណដែលបំពានផងដែរ។

វានៅសល់ដើម្បីអនុវត្តជំហានចុងក្រោយ: ផ្លាស់ទីពីត្រីកោណទៅពហុកោណ។ ពហុកោណណាមួយអាចត្រូវបានបែងចែកទៅជាត្រីកោណ (ឧទាហរណ៍ដោយអង្កត់ទ្រូង) ។ ដូច្នេះហើយ យើងគ្រាន់តែត្រូវបញ្ជាក់ថា នៅពេលបន្ថែមត្រីកោណណាមួយទៅពហុកោណតាមអំពើចិត្ត រូបមន្តរបស់ Pick នៅតែជាការពិត។

សូមឱ្យពហុកោណ និងត្រីកោណមានជ្រុងរួម។ សន្មតថារូបមន្តរបស់ Pick មានសុពលភាពសម្រាប់ ហើយយើងនឹងបង្ហាញថាវាក៏នឹងជាការពិតសម្រាប់ពហុកោណដែលទទួលបានពីការបន្ថែម។ ដោយសារ​តែ​មាន​ផ្នែក​រួម ចំណុច​ចំនួនគត់​ទាំងអស់​ដែល​នៅ​ខាង​នេះ លើក​លែង​តែ​កំពូល​ពីរ ក្លាយ​ជា​ចំណុច​ខាងក្នុង​នៃ​ពហុកោណ​ថ្មី។ ចំនុចកំពូលនឹងក្លាយជាចំណុចព្រំដែន។ អនុញ្ញាតឱ្យយើងកំណត់ចំនួននៃចំណុចទូទៅដោយនិងទទួលបាន

ចំនួននៃចំណុចចំនួនគត់ខាងក្នុងនៃពហុកោណថ្មី,

ចំនួននៃចំណុចព្រំដែនសម្រាប់ពហុកោណថ្មី។

ពីសមភាពទាំងនេះយើងទទួលបាន

ចាប់តាំងពីយើងសន្មត់ថាទ្រឹស្តីបទគឺពិតសម្រាប់ និងសម្រាប់ដាច់ដោយឡែកពីគ្នា។

ដូច្នេះរូបមន្ត Pick ត្រូវបានបង្ហាញ។

រូបមន្តនេះត្រូវបានរកឃើញដោយគណិតវិទូជនជាតិអូទ្រីស Peak Georg Aleksandrov (1859 - 1943) ក្នុងឆ្នាំ 1899 ។ បន្ថែមពីលើរូបមន្តនេះ Georg Pick បានរកឃើញ Pick, Pick - Julia, Pick - Nevalina theorems បានបង្ហាញឱ្យឃើញពីវិសមភាព Schwarz - Pick ។ អេ ឧបសម្ព័ន្ធ ១អ្នកអាចឃើញកិច្ចការមិនស្តង់ដារដែលខ្ញុំបានពិចារណាសម្រាប់ការអនុវត្តរូបមន្តជ្រើសរើស។

រូបមន្តកំពូល

1 ។ សេចក្ដីណែនាំ

2. រូបមន្តកំពូល។ ភស្តុតាង I.

ភស្តុតាង II.

ភស្តុតាងរបស់ Sh.

3. កិច្ចការ។

4. រូបមន្តសម្រាប់ផ្ទៃនៃពហុកោណក្នុងលក្ខខណ្ឌនៃកូអរដោនេនៃចំនុចកំពូល។

5. ភារកិច្ច។

6. អក្សរសាស្ត្រ

រូបមន្តកំពូល។

1 ។ សេចក្ដីណែនាំ។

យើងទាញប្រាជ្ញាពីប្រវត្តិសាស្ត្រ

នៅក្នុងកំណាព្យ - ប្រាជ្ញា,

នៅក្នុងគណិតវិទ្យា - ការយល់ដឹង។

F. Bacon

គ្រោងនឹងលាតត្រដាងនៅលើក្រដាសធម្មតាមួយ។

បន្ទាត់ដែលនៅតាមបណ្តោយជ្រុងនៃកោសិកាបង្កើតជាក្រឡាចត្រង្គ ហើយចំនុចកំពូលនៃក្រឡាគឺជាថ្នាំងនៃក្រឡាចត្រង្គនេះ។ ចូរ​គូរ​ពហុកោណ​នៅលើ​សន្លឹក​ដោយ​ដាក់​បញ្ឈរ​នៅ​ថ្នាំង ហើយ​ស្វែងរក​ផ្ទៃ​របស់វា។

អ្នកអាចស្វែងរកវាតាមវិធីផ្សេងៗគ្នា។ ឧទាហរណ៍ អ្នក​អាច​កាត់​ពហុកោណ​ជា​រាង​សាមញ្ញ​គួរសម ស្វែងរក​តំបន់​របស់​វា ហើយ​បន្ថែម​វា​ឡើង។

ប៉ុន្តែនៅទីនេះយើងជួបបញ្ហាច្រើន។ តួលេខនេះត្រូវបានបំបែកយ៉ាងងាយស្រួលទៅជាចតុកោណ ចតុកោណកែង និងត្រីកោណ ហើយផ្ទៃដីរបស់វាត្រូវបានគណនាយ៉ាងងាយស្រួល។

ទោះបីជាពហុកោណមើលទៅសាមញ្ញគ្រប់គ្រាន់ក៏ដោយ វានឹងត្រូវការការងារច្រើនដើម្បីគណនាផ្ទៃដីរបស់វា។ ចុះ​បើ​ពហុកោណ​មើល​ទៅ​សង្ហា​ជាង? វាប្រែថាតំបន់នៃពហុកោណដែលកំពូលរបស់វាមានទីតាំងនៅថ្នាំងនៃក្រឡាចត្រង្គអាចត្រូវបានគណនាយ៉ាងសាមញ្ញជាងនេះទៅទៀត: មានរូបមន្តដែលទាក់ទងនឹងតំបន់របស់ពួកគេទៅនឹងចំនួនថ្នាំងដែលស្ថិតនៅខាងក្នុងនិងនៅលើព្រំដែននៃពហុកោណ។ រូបមន្តដ៏អស្ចារ្យ និងសាមញ្ញនេះត្រូវបានគេហៅថារូបមន្តជ្រើសរើស។

2. រូបមន្តកំពូល។

ចំនុចកំពូលនៃពហុកោណ (មិនចាំបាច់ប៉ោងទេ) មានទីតាំងនៅថ្នាំងនៃបន្ទះឈើចំនួនគត់។ នៅខាងក្នុងវាស្ថិតនៅលើថ្នាំង B នៃបន្ទះឈើ និងនៅលើព្រំដែននៃថ្នាំង G ។ អនុញ្ញាតឱ្យយើងបង្ហាញថាតំបន់របស់វាគឺ B + - 1 (រូបមន្តរបស់ Peak) ។

ភស្តុតាង I.

ពិចារណាពហុកោណដែលចំនុចកំពូលស្ថិតនៅត្រង់ថ្នាំងនៃបន្ទះឈើចំនួនគត់ ពោលគឺពួកគេមានកូអរដោណេចំនួនគត់។

យើងបែងចែកពហុកោណទៅជាត្រីកោណដែលមានចំនុចបញ្ឈរនៅថ្នាំងនៃបន្ទះឈើដែលមិនមានថ្នាំងខាងក្នុងឬនៅលើជ្រុង។

បញ្ជាក់៖

នគឺជាចំនួនជ្រុងនៃពហុកោណ

មគឺ​ជា​ចំនួន​ត្រីកោណ​ដែល​មាន​បន្ទាត់​បញ្ឈរ​នៅ​ថ្នាំង​នៃ​បន្ទះ​ឈើ​ដែល​មិន​មាន​ថ្នាំង​ទាំង​ខាង​ក្នុង ឬ​នៅ​លើ​ជ្រុង

B គឺជាចំនួនថ្នាំងនៅខាងក្នុងពហុកោណ

Г គឺជាចំនួនថ្នាំងនៅសងខាង រួមទាំងចំនុចកំពូល។

តំបន់នៃត្រីកោណទាំងអស់នេះគឺដូចគ្នា និងស្មើគ្នា។

ដូច្នេះ​ហើយ​ផ្ទៃ​ពហុកោណ​គឺ
.

180 0 ម .

ឥឡូវនេះ ចូរយើងស្វែងរកផលបូកនេះតាមរបៀបផ្សេង។

ផលបូកនៃមុំដែលមានចំនុចកំពូលនៅថ្នាំងខាងក្នុងណាមួយគឺ 360 0 ។

បន្ទាប់មកផលបូកនៃមុំដែលមានចំនុចកំពូលនៅថ្នាំងខាងក្នុងទាំងអស់គឺ 360 0 V ។

ផលបូកសរុបនៃមុំនៅថ្នាំងនៅសងខាង ប៉ុន្តែមិនមែននៅចំនុចកំពូលទេ គឺ 180 0 (G - ន).

ផលបូកនៃមុំនៅចំនុចកំពូលនៃពហុកោណគឺ 180 0 ( ន – 2) .

ផលបូកសរុបនៃមុំនៃត្រីកោណទាំងអស់គឺ 360 0 V + 180 0 (G - ន) + 180 0 (ន – 2).

ដូច្នេះ 1800 ម\u003d 360 0 V + 180 0 (G - ន) + 180 0 (ន – 2),

180 0 ម\u003d 360 0 V + 180 0 G - 180 0 ន + 180 0 ន– ១៨០០ ២,

180 0 ម\u003d 360 0 V + 180 0 G– 360 0,

= ខ + – 1 ,

តើនៅពេលណាដែលយើងទទួលបានកន្សោមសម្រាប់ផ្ទៃ S នៃពហុកោណ៖

ស= ខ + – 1 ,

គេស្គាល់ថាជារូបមន្តរបស់ Pick ។

នៅក្នុងរូបភាព៖ V = 24, D = 9 ដូច្នេះស = 24 + – 1 = 27,5.

ស្វែងរកផ្ទៃនៃពហុកោណដំបូងដោយប្រើរូបមន្ត Peak៖

B = 28 (ចំណុចពណ៌បៃតង);

D = 20 (ចំណុចពណ៌ខៀវ) ។

យើងទទួលបាន S =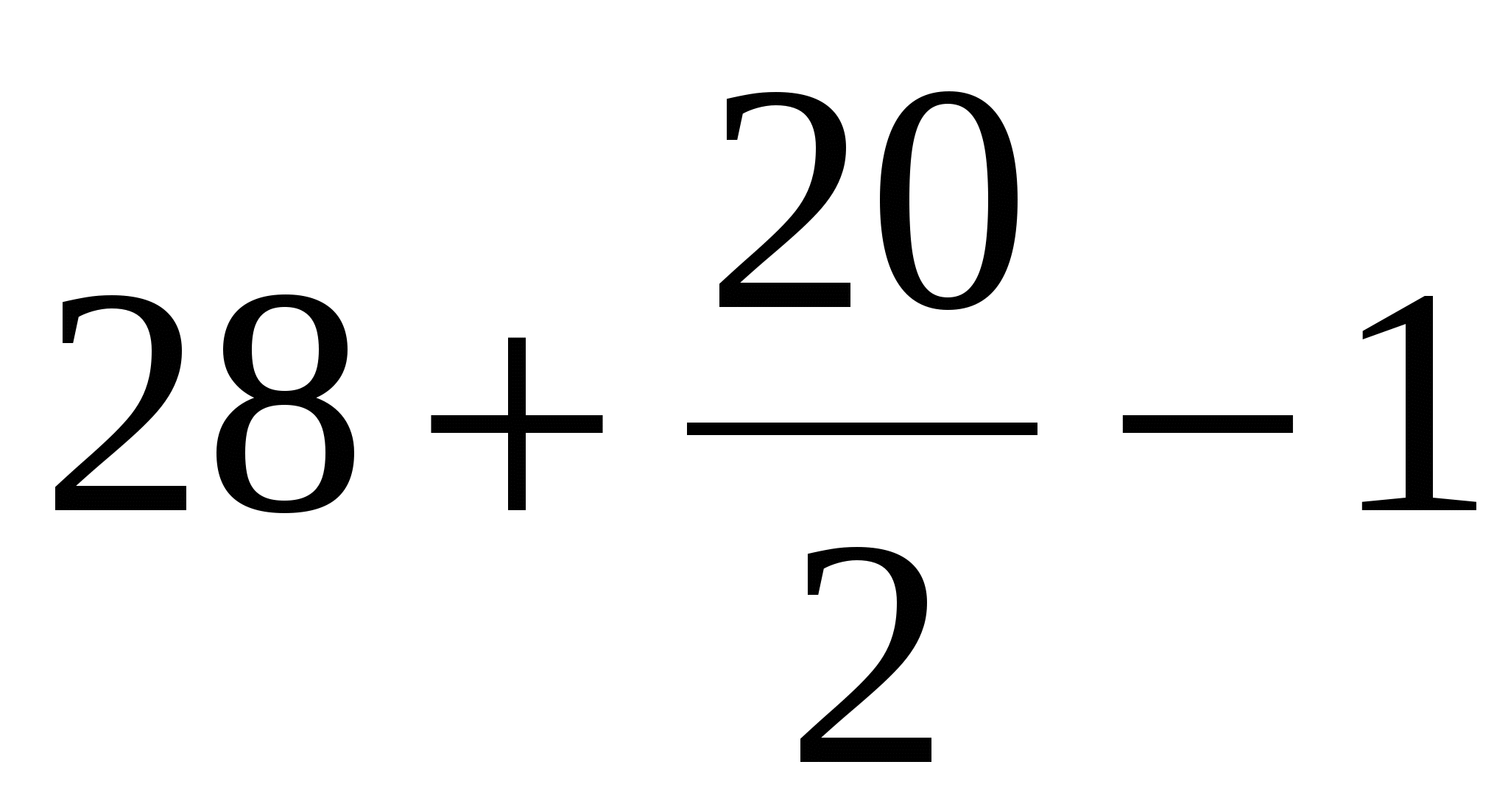
= 37 យូនីតការ៉េ

ភស្តុតាង II.

ទៅពហុកោណ M នីមួយៗដែលមានចំនុចកំពូលនៅថ្នាំងនៃបន្ទះឈើចំនួនគត់ យើងកំណត់លេខ f (M) =
ដែលជាកន្លែងដែលការបូកសរុបគឺនៅលើថ្នាំងបន្ទះឈើទាំងអស់ដែលជាកម្មសិទ្ធិរបស់ M និងមុំ ត្រូវបានកំណត់ដូចខាងក្រោមៈ =
សម្រាប់ចំណុចខាងក្នុងនៃពហុកោណ =
សម្រាប់ចំណុចព្រំដែនក្រៅពីចំនុចកំពូល និង - មុំនៅចំនុចកំពូល ប្រសិនបើថ្នាំងដែលបានផ្តល់ជាចំនុចកំពូល។ វាងាយមើលថា f (M) =
+
= ខ + – 1. វានៅសល់ដើម្បីពិនិត្យមើលថាចំនួន f (M) គឺស្មើនឹងផ្ទៃនៃពហុកោណ M ។

អនុញ្ញាតឱ្យពហុកោណ M ត្រូវបានកាត់ចូលទៅក្នុងពហុកោណ M 1 និង M 2 ដោយដាក់បញ្ឈរនៅថ្នាំងនៃបន្ទះឈើ។ បន្ទាប់មក f(M) = f(M 1) + f(M 2) ព្រោះសម្រាប់ថ្នាំងនីមួយៗ មុំបូក។ ដូច្នេះ ប្រសិនបើរូបមន្តរបស់ Pick គឺពិតសម្រាប់ពហុកោណពីរ M, M 1 និង M 2 នោះ វាក៏ពិតសម្រាប់ពហុកោណទាំងពីរផងដែរ។

ប្រសិនបើ M ជាចតុកោណកែង ទំនិង qដឹកនាំតាមបន្ទាត់បន្ទះឈើ បន្ទាប់មក

f (M) = (p − 1)(q − 1) +
= pq ។

ក្នុងករណីនេះ រូបមន្តរបស់ Pick មានសុពលភាព។ ដោយកាត់ចតុកោណកែង M តាមអង្កត់ទ្រូងទៅជាត្រីកោណ M 1 និង M 2 ហើយប្រើការពិតថា f (M) = f (M 1) + f (M 2) និង f (M 1) = f (M 2) វាងាយស្រួល។ ដើម្បីបញ្ជាក់សុពលភាពនៃរូបមន្តរបស់ Pick សម្រាប់ត្រីកោណកែងណាមួយដែលមានជើងតម្រង់តាមបន្ទាត់នៃបន្ទះឈើ។ តាមរយៈការកាត់ត្រីកោណបែបនេះជាច្រើនចេញពីចតុកោណកែង ត្រីកោណណាមួយអាចទទួលបាន។

ដើម្បីបំពេញភស្តុតាងនៃរូបមន្តរបស់ Pick វានៅតែត្រូវកត់សម្គាល់ថាពហុកោណណាមួយអាចត្រូវបានកាត់ជាត្រីកោណដោយអង្កត់ទ្រូងដែលមិនប្រសព្វគ្នា។

ភស្តុតាងរបស់ Sh.

ការតភ្ជាប់រវាងផ្ទៃនៃតួលេខមួយ និងចំនួនថ្នាំងដែលធ្លាក់ចូលទៅក្នុងតួលេខនេះគឺច្បាស់ជាពិសេសនៅក្នុងករណីនៃចតុកោណកែង។

អនុញ្ញាតឱ្យមាន ABCD- ចតុកោណកែង​ដែល​មាន​ចំណុច​បញ្ឈរ​នៅ​ថ្នាំង និង​ជ្រុង​ដែល​ដើរ​តាម​បន្ទាត់​ក្រឡាចត្រង្គ។

បញ្ជាក់ដោយ អេចំនួនថ្នាំងដែលស្ថិតនៅខាងក្នុងចតុកោណកែង និងតាមរយៈ ជីគឺជាចំនួនថ្នាំងនៅលើព្រំដែនរបស់វា។ ផ្លាស់ទីក្រឡាពាក់កណ្តាលក្រឡាមួយទៅខាងស្តាំ និងពាក់កណ្តាលក្រឡាចុះក្រោម។

បន្ទាប់មកទឹកដីនៃចតុកោណអាចត្រូវបាន "ចែកចាយ" រវាងថ្នាំងដូចខាងក្រោម: នីមួយៗនៃ អេថ្នាំង "គ្រប់គ្រង" ក្រឡាទាំងមូលនៃក្រឡាចត្រង្គដែលបានផ្លាស់ប្តូរ នីមួយៗនៃ ជី- ថ្នាំងមិនជ្រុងព្រំដែនចំនួន 4 - ពាក់កណ្តាលនៃក្រឡា ហើយចំនុចជ្រុងនីមួយៗ - មួយភាគបួននៃក្រឡា។ ដូច្នេះ​ហើយ​ផ្ទៃ​នៃ​ចតុកោណ​ S គឺ​

ដូច្នេះ​សម្រាប់​ចតុកោណកែង​ជាមួយ​ចំណុច​កំពូល​នៅ​ថ្នាំង និង​ជ្រុង​ដែល​នៅ​តាម​បន្ទាត់​ក្រឡាចត្រង្គ យើង​បាន​បង្កើត​រូបមន្ត

ចូរយើងបញ្ជាក់ថារូបមន្តនេះគឺពិតមិនត្រឹមតែសម្រាប់ចតុកោណកែងប៉ុណ្ណោះទេ ប៉ុន្តែក៏សម្រាប់ពហុកោណតាមអំពើចិត្តដែលមានចំនុចកំពូលនៅថ្នាំងក្រឡាចត្រង្គផងដែរ។

បញ្ជាក់ដោយ ស ម តំបន់ពហុកោណម ជាមួយចំនុចកំពូលនៅថ្នាំង និងតាមរយៈទំ ម - តម្លៃ
កន្លែងណាអេ ម គឺជាចំនួនថ្នាំងនៅខាងក្នុងមក ជី ម គឺជាចំនួនថ្នាំងនៅលើព្រំដែន។ បន្ទាប់មករូបមន្តជ្រើសរើសអាចត្រូវបានសរសេរជា
.

យើងបែងចែកភស្តុតាងនៃរូបមន្តទៅជាជំហានជាច្រើន។

ជំហានទី 1 ។

ប្រសិនបើពហុកោណម ជាមួយនឹងចំនុចកំពូលនៅថ្នាំងក្រឡាចត្រង្គកាត់ជា 2 ពហុកោណម 1 និង ម 2 , ក៏មានចំនុចកំពូលតែនៅថ្នាំងក្រឡាចត្រង្គ
. អនុញ្ញាតឱ្យពហុកោណម កាត់ចូលទៅក្នុងពហុកោណម 1 និង ម 2 ជាមួយចំនុចកំពូលនៅថ្នាំងដោយផ្នែកមួយ។ AB ថ្នាំងទាំងអស់ លើកលែងតែថ្នាំងដែលធ្លាក់លើផ្នែកAB, ផ្តល់ការរួមចំណែកដូចគ្នាទៅនឹងផ្នែកខាងឆ្វេង និងខាងស្តាំនៃរូបមន្ត។ ពិចារណាថ្នាំងដែលស្ថិតនៅលើផ្នែក AB ។

ប្រសិនបើថ្នាំងបែបនេះស្ថិតនៅចន្លោះ A និង B (ឧទាហរណ៍ C) បន្ទាប់មកសម្រាប់ពហុកោណម វាជាផ្នែកខាងក្នុង និងសម្រាប់ពហុកោណម 1 និង ម 2 - ព្រំដែន។ ដូច្នេះការរួមចំណែករបស់គាត់។ទំ ម ស្មើ 1 និងក្នុងកន្សោមនីមួយៗ
និង
- 0.5 នីមួយៗ ពោលគឺការរួមចំណែករបស់ថ្នាំងបែបនេះចំពោះទំ ម និង
គឺស្មើគ្នា។

ពិចារណាថ្នាំង A និង B. ពួកគេមានព្រំដែនទាំងពីរសម្រាប់ ម, និងសម្រាប់ ម 1 , ម 2 .

ដូច្នេះការរួមចំណែកនៃថ្នាំងនីមួយៗទាំងនេះទៅទំ ម គឺ 0.5 a
- ឯកតា។ នេះមានន័យថាការរួមចំណែកសរុបនៃថ្នាំង A និង B ទៅទំ ម ស្មើនឹង 1 ដែលជា 1 តិចជាងការរួមចំណែករបស់ពួកគេ។
. ប៉ុន្តែ
, ក .

ពី "ការរួមចំណែក" សរុបនៃថ្នាំងទាំងអស់។ ទំ ម 1 ត្រូវបានដកពី
2 ត្រូវបានដក ហើយនេះផ្តល់សំណងសម្រាប់ភាពខុសគ្នានៃការរួមចំណែកនៃថ្នាំង A និង B ។

ដូច្នេះ
.

ជំហានទី 2

ប្រសិនបើពហុកោណ មជាមួយចំនុចកំពូលនៅថ្នាំងក្រឡាចត្រង្គកាត់ជាពហុកោណពីរ ម 1 និង ម 2 (ក៏មានចំនុចកំពូលនៅថ្នាំង) ហើយរូបមន្តគឺពិតសម្រាប់ពហុកោណពីរ ម 1 , ម 2 បន្ទាប់មក វាក៏ជាការពិតសម្រាប់ពហុកោណទីបី។

ជាឧទាហរណ៍សូមឱ្យវាជាការពិតសម្រាប់ម 1 និង ម 2 , i.e
. បន្ទាប់មក (ជំហានដំបូង), ប៉ុន្តែនៅលើ ជំហានដំបូង) កន្សោមចុងក្រោយគឺស្មើនឹងទំ ម , និងសមភាព
ហើយមានរូបមន្តជ្រើសរើស។

ជំហានទី 3

ចូរយើងបង្ហាញរូបមន្តរបស់ Pick សម្រាប់ត្រីកោណកែងដែលមានចំនុចកំពូលនៅថ្នាំងក្រឡាចត្រង្គ និងជើងដែលស្ថិតនៅលើបន្ទាត់ក្រឡាចត្រង្គ។

ត្រីកោណ ABCបង្កើតជាចតុកោណ ABCD .

សម្រាប់រាងចតុកោណ រូបមន្តរបស់ Pick គឺត្រឹមត្រូវ៖ ស ABCD = ភី ABCD . នេះបើយោងតាមជំហានដំបូង ទំ ABCD = ភី ABC + ទំ ACD , ទំ ABC = ភី ACD , ដូច្នេះ ទំ ABCD = 2 ភី ABC . ប៉ុន្តែ ស ABCD = 2 ស ABC . ដូច្នេះ ស ABC = ភី ABC .

ជំហានទី 4

រូបមន្ត​របស់ Pick គឺ​ត្រឹមត្រូវ​សម្រាប់​ត្រីកោណ​តាម​អំពើ​ចិត្ត​ដែល​មាន​បន្ទាត់​បញ្ឈរ​នៅ​ថ្នាំង​ក្រឡាចត្រង្គ។

ដោយបានពិនិត្យមើលតួលេខ វាងាយស្រួលយល់៖ ត្រីកោណបែបនេះអាចទទួលបានដោយ "កាត់ចេញ" ពីចតុកោណកែងមួយចំនួនដែលមានជ្រុងរត់តាមបន្ទាត់ក្រឡាចត្រង្គ ចតុកោណកែងជាច្រើន និងត្រីកោណមុំខាងស្តាំដែលមានជើងនៅលើបន្ទាត់ក្រឡាចត្រង្គ។ ហើយដោយសាររូបមន្តរបស់ Pick គឺពិតសម្រាប់ចតុកោណកែង និងត្រីកោណកែង ដូច្នេះ (ចងចាំជំហានទី 2) វាក៏ពិតសម្រាប់ត្រីកោណដើម។

យើង​បាន​បង្ហាញ​ថា ប្រសិនបើ​ពហុកោណ​អាច​ត្រូវ​បាន​កាត់​ជា​ត្រីកោណ​ជាមួយ​បន្ទាត់​បញ្ឈរ​នៅ​ចំណុច​នៃ​ក្រឡាចត្រង្គ នោះ​រូបមន្ត​របស់ Pick គឺ​ពិត​សម្រាប់​វា។

3. កិច្ចការ។

ស្វែងរកតំបន់នៃតួលេខ៖

1
.

B=9

G = ៤

B=9

G = ៥

ការគណនាផ្ទៃដីនៃតួលេខ។

ជ្រើសរើសវិធីសាស្រ្ត

ការងាររបស់សិស្សនៃថ្នាក់ 5B MBOU អនុវិទ្យាល័យលេខ 23 នៅ Irkutsk

Balsukova អាឡិចសាន់ត្រា

ក្បាល៖ Khodyreva T.G.

២០១៤

ការគណនាផ្ទៃដីនៃតួលេខ។ ជ្រើសរើសវិធីសាស្រ្ត

វត្ថុនៃការសិក្សា ៖ កិច្ចការនៅលើក្រដាសគូស

ប្រធានបទនៃការសិក្សា ៖ បញ្ហា​សម្រាប់​ការ​គណនា​ផ្ទៃ​ពហុកោណ​លើ​ក្រដាស​គូសធីក វិធីសាស្ត្រ និង​បច្ចេកទេស​សម្រាប់​ដោះស្រាយ​ពួកវា។

វិធីសាស្រ្តស្រាវជ្រាវ ពាក្យគន្លឹះ៖ ការប្រៀបធៀប, ទូទៅ, ភាពស្រដៀងគ្នា, ការសិក្សាអក្សរសិល្ប៍ និងធនធានអ៊ីនធឺណិត, ការវិភាគព័ត៌មាន។

គោលបំណងនៃការសិក្សា៖

ជ្រើសរើសព័ត៌មានសំខាន់ៗ គួរឱ្យចាប់អារម្មណ៍ និងអាចយល់បាន។

វិភាគនិងរៀបចំព័ត៌មានដែលទទួលបាន

ស្វែងរកវិធីសាស្រ្ត និងបច្ចេកទេសផ្សេងៗសម្រាប់ដោះស្រាយបញ្ហានៅលើក្រដាសត្រួតពិនិត្យ

ពិនិត្យរូបមន្តសម្រាប់គណនាផ្ទៃនៃរាងធរណីមាត្រដោយប្រើរូបមន្ត Peak

បង្កើតបទបង្ហាញអេឡិចត្រូនិចនៃការងារដើម្បីបង្ហាញសម្ភារៈដែលប្រមូលបាន។

ធរណីមាត្រគឺជាឧបករណ៍ដ៏មានឥទ្ធិពលបំផុតសម្រាប់ការកែលម្អនៃមហាវិទ្យាល័យផ្លូវចិត្តរបស់យើង ហើយអាចឱ្យយើងគិត និងវែកញែកបានត្រឹមត្រូវ។

(G. Galileo)

ភាពពាក់ព័ន្ធនៃប្រធានបទ

ចំណង់ចំណូលចិត្តចំពោះគណិតវិទ្យាជារឿយៗចាប់ផ្តើមដោយការគិតអំពីបញ្ហា។ ដូច្នេះនៅពេលសិក្សាប្រធានបទ "តំបន់ពហុកោណ" សំណួរកើតឡើងថាតើមានភារកិច្ចដែលខុសពីភារកិច្ចដែលបានពិចារណានៅក្នុងសៀវភៅសិក្សាដែរឬទេ។ ការងារបែបនេះរួមមានការងារនៅលើក្រដាសគូស។ តើអ្វីជាភាពពិសេសនៃបញ្ហាបែបនេះ តើមានវិធីសាស្រ្ត និងបច្ចេកទេសពិសេសសម្រាប់ដោះស្រាយបញ្ហានៅលើក្រដាសត្រួតពិនិត្យដែរឬទេ? នៅក្នុងថ្នាក់គណិតវិទ្យា គ្រូបានណែនាំយើងអំពីវិធីសាស្រ្តដ៏គួរឱ្យចាប់អារម្មណ៍មួយសម្រាប់ការគណនាពហុកោណ។ ខ្ញុំចាប់ផ្តើមសិក្សាអក្សរសិល្ប៍ ធនធានអ៊ីនធឺណិតលើប្រធានបទនេះ។ វាហាក់ដូចជាថាវត្ថុដ៏គួរឱ្យចាប់អារម្មណ៍អាចត្រូវបានរកឃើញនៅលើយន្តហោះដែលមានការត្រួតពិនិត្យ ពោលគឺនៅលើក្រដាសគ្មានទីបញ្ចប់ដែលតម្រង់ជួរចូលទៅក្នុងការ៉េដូចគ្នា។ វាប្រែថាភារកិច្ចដែលភ្ជាប់ជាមួយក្រដាសត្រួតពិនិត្យមានភាពចម្រុះណាស់។ ខ្ញុំបានរៀនពីរបៀបគណនាផ្ទៃនៃពហុកោណដែលគូរនៅលើក្រដាសដែលគូស។ សម្រាប់កិច្ចការជាច្រើននៅលើក្រដាសនៅក្នុងទ្រុងមិនមានច្បាប់ទូទៅសម្រាប់ដោះស្រាយទេ វិធីសាស្ត្រ និងបច្ចេកទេសជាក់លាក់។ នេះគឺជាទ្រព្យសម្បត្តិរបស់ពួកគេដែលកំណត់តម្លៃរបស់ពួកគេសម្រាប់ការអភិវឌ្ឍន៍មិនមែនជាជំនាញ ឬជំនាញអប់រំជាក់លាក់ណាមួយនោះទេ ប៉ុន្តែជាទូទៅសមត្ថភាពក្នុងការគិត ឆ្លុះបញ្ចាំង វិភាគ រកមើលភាពស្រដៀងគ្នា ពោលគឺការងារទាំងនេះអភិវឌ្ឍជំនាញគិតក្នុងន័យទូលំទូលាយបំផុត។

ហើយខ្ញុំក៏បានរៀនផងដែរថា ភារកិច្ចបែបនេះត្រូវបានពិចារណាក្នុងការត្រួតពិនិត្យ និងវាស់វែងសម្ភារៈនៃ GIA និងការប្រឡងរដ្ឋបង្រួបបង្រួម។ ដូច្នេះហើយ ខ្ញុំចាត់ទុកការសិក្សាអំពីសម្ភារៈនេះមានប្រយោជន៍សម្រាប់កម្មវិធីរបស់វា មិនត្រឹមតែក្នុងដំណើរការអប់រំបន្ថែមប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងសម្រាប់ដោះស្រាយបញ្ហា Olympiad ដែលមិនមានលក្ខណៈស្តង់ដារផងដែរ។

2.គំនិតនៃតំបន់

ការ៉េ- លក្ខណៈលេខនៃតួលេខធរណីមាត្រពីរវិមាត្របង្ហាញទំហំនៃតួលេខនេះ។ តាមប្រវត្តិសាស្ត្រ ការគណនាតំបន់ត្រូវបានគេហៅថា . តួលេខដែលមានតំបន់ត្រូវបានគេហៅថា ការ៉េ .

តំបន់នៃតួលេខផ្ទះល្វែងមួយនៅក្នុងលក្ខខណ្ឌនៃធរណីមាត្រ

1. ការ៉េ- រង្វាស់នៃតួរលេខសំប៉ែត ទាក់ទងទៅនឹងតួរលេខស្តង់ដារ ដែលជាការ៉េដែលមានជ្រុងម្ខាងស្មើនឹងប្រវែងមួយ។

2. ការ៉េ- លក្ខណៈលេខដែលសន្មតថាជាតួលេខរាបស្មើនៃថ្នាក់ជាក់លាក់មួយ (ឧទាហរណ៍ ពហុកោណ)។ តំបន់នៃការ៉េដែលមានផ្នែកម្ខាងស្មើនឹងឯកតានៃប្រវែងមួយយកស្មើនឹងឯកតានៃផ្ទៃដី

3. ការ៉េ- តម្លៃវិជ្ជមាន តម្លៃលេខដែលមានលក្ខណៈសម្បត្តិដូចខាងក្រោមៈ

 តួលេខស្មើគ្នាមានតំបន់ស្មើគ្នា;

 ប្រសិនបើតួលេខមួយត្រូវបានបែងចែកទៅជាផ្នែកដែលជាតួលេខសាមញ្ញ (ពោលគឺអ្នកដែលអាចត្រូវបានបែងចែកទៅជាចំនួនកំណត់នៃត្រីកោណរាបស្មើ) នោះផ្ទៃដីនៃតួលេខនេះគឺស្មើនឹងផលបូកនៃផ្ទៃដីរបស់វា ផ្នែក;

 ផ្ទៃដីនៃការ៉េដែលមានផ្នែកម្ខាងស្មើនឹងឯកតារង្វាស់គឺស្មើនឹងមួយ។

ដូច្នេះយើងអាចសន្និដ្ឋានបានថាតំបន់នេះមិនមែនជាតម្លៃជាក់លាក់នោះទេ ប៉ុន្តែគ្រាន់តែផ្តល់លក្ខណៈតាមលក្ខខណ្ឌមួយចំនួននៃតួលេខផ្ទះល្វែងប៉ុណ្ណោះ។ ដើម្បីស្វែងរកផ្ទៃដីនៃតួលេខដែលបំពានវាចាំបាច់ត្រូវកំណត់ថាតើការ៉េប៉ុន្មានដែលមានផ្នែកម្ខាងស្មើនឹងប្រវែងមួយវាមាន។ ជាឧទាហរណ៍ ចូរយើងយកចតុកោណកែងដែលមួយសង់ទីម៉ែត្រត្រូវគ្នានឹង 6 ដង។ នេះមានន័យថាផ្ទៃដីនៃចតុកោណកែងគឺ 6 cm2 ។

ជម្រើសនៃតំបន់នៃការ៉េដែលមានផ្នែកម្ខាងស្មើនឹងឯកតារង្វាស់ដែលជាឯកតារង្វាស់អប្បបរមាសម្រាប់គ្រប់តំបន់ទាំងអស់គឺមិនចៃដន្យទេ។ នេះគឺជាលទ្ធផលនៃកិច្ចព្រមព្រៀងរវាងមនុស្សដែលបានក្រោកឡើងនៅក្នុងដំណើរការនៃការជ្រើសរើស "ធម្មជាតិ" ដែលមានអាយុកាលរាប់សតវត្ស។ លើសពីនេះទៀតមានសំណើផ្សេងទៀតសម្រាប់ឯកតារង្វាស់។ ដូច្នេះ ជាឧទាហរណ៍ វាត្រូវបានស្នើឡើងដើម្បីយកតំបន់នៃត្រីកោណសមភាពជាឯកតាបែបនេះ (ឧទាហរណ៍ តួលេខផ្ទះល្វែងណាមួយអាចត្រូវបានតំណាងថាជា "ផលបូក" នៃចំនួនជាក់លាក់នៃត្រីកោណសមភាព) ដែលនឹងនាំទៅដល់ ការផ្លាស់ប្តូរនៅក្នុងតំណាងលេខនៃតំបន់។

ដូច្នេះ រូបមន្តសម្រាប់ការគណនាតំបន់បានលេចឡើងក្នុងគណិតវិទ្យា ហើយមិនត្រូវបានដឹងភ្លាមៗដោយមនុស្សម្នាក់នោះទេ - នេះ អ្នកវិទ្យាសាស្ត្រជាច្រើនរស់នៅក្នុងសម័យកាល និងប្រទេសផ្សេងៗគ្នា។ (រូបមន្តខុស រកមិនឃើញកន្លែងនៅក្នុងវិទ្យាសាស្រ្ត ហើយបានចូលទៅក្នុងការភ្លេចភ្លាំង)។ រូបមន្តពិតត្រូវបានបំពេញបន្ថែម កែ និងបញ្ជាក់ក្នុងរយៈពេលរាប់ពាន់ឆ្នាំ រហូតទាល់តែពួកគេបានមកដល់យើងក្នុងទម្រង់ទំនើបរបស់ពួកគេ។

ពិតប្រាកដ​ណាស់ ការវាស់វែងតំបន់មាននៅក្នុងការប្រៀបធៀបផ្ទៃនៃតួលេខដែលបានផ្តល់ឱ្យជាមួយនឹងផ្ទៃនៃតួលេខដែលបានយកជាឯកតារង្វាស់។ ជាលទ្ធផលនៃការប្រៀបធៀបចំនួនជាក់លាក់មួយត្រូវបានទទួល - តម្លៃជាលេខនៃតំបន់នៃតួលេខដែលបានផ្តល់ឱ្យ។ លេខនេះបង្ហាញពីចំនួនដងនៃផ្ទៃដីនៃតួលេខដែលបានផ្តល់ឱ្យគឺធំជាង (ឬតិចជាង) ជាងផ្ទៃដីនៃតួលេខ ដែលយកជាឯកតានៃផ្ទៃដី។

ធ ដូច្នេះហើយ យើងអាចសន្និដ្ឋានបានថា តំបន់នោះគឺជាបរិមាណសិប្បនិម្មិត ដែលមនុស្សបានណែនាំជាប្រវត្តិសាស្ត្រ ដើម្បីវាស់ស្ទង់ទ្រព្យសម្បត្តិមួយចំនួននៃតួលេខរាបស្មើ។ តម្រូវការក្នុងការបញ្ចូលតម្លៃបែបនេះគឺដោយសារតែការកើនឡើងនៃតម្រូវការដើម្បីដឹងថាទំហំនេះ ឬទឹកដីនោះមានទំហំប៉ុនណា ត្រូវការគ្រាប់ធញ្ញជាតិប៉ុន្មានដើម្បីសាបព្រួសវាលស្រែ ឬគណនាផ្ទៃកម្រាលសម្រាប់តុបតែងក្បឿងលម្អ។

រូបមន្តកំពូល

ដើម្បីប៉ាន់ស្មានផ្ទៃដីនៃពហុកោណនៅលើក្រដាសគូស វាគ្រប់គ្រាន់ដើម្បីគណនាថាតើក្រឡាពហុកោណនេះគ្របដណ្តប់ប៉ុន្មាន (យើងយកផ្ទៃដីនៃក្រឡាជាឯកតា)។ កាន់តែច្បាស់ប្រសិនបើស គឺជាតំបន់នៃពហុកោណ B គឺជាចំនួនកោសិកាដែលស្ថិតនៅខាងក្នុងពហុកោណ ហើយ G គឺជាចំនួនកោសិកាដែលមានផ្នែកខាងក្នុង។ យើងនឹងពិចារណាតែពហុកោណបែបនេះប៉ុណ្ណោះ ចំណុចកំពូលទាំងអស់ដែលស្ថិតនៅលើថ្នាំងនៃក្រដាសគូសធីក - នៅក្នុងកន្លែងដែលបន្ទាត់ក្រឡាចត្រង្គនៃពហុកោណប្រសព្វគ្នាយ៉ាងហោចណាស់ចំណុចរួមមួយ។

ផ្ទៃនៃត្រីកោណណាមួយដែលគូរនៅលើក្រដាសគូសអាចគណនាបានយ៉ាងងាយស្រួលដោយតំណាងឱ្យវាជាផលបូក ឬភាពខុសគ្នានៃតំបន់នៃត្រីកោណមុំខាងស្តាំ និងចតុកោណកែងដែលជ្រុងរបស់វាតាមបន្ទាត់ក្រឡាចត្រង្គឆ្លងកាត់ចំនុចកំពូលនៃត្រីកោណដែលបានគូរ។

ដើម្បីគណនាផ្ទៃនៃពហុកោណបែបនេះ អ្នកអាចប្រើទ្រឹស្តីបទខាងក្រោម៖

ទ្រឹស្តីបទ . អនុញ្ញាតឱ្យមាន - ចំនួន​ចំនួន​គត់​ក្នុង​ពហុកោណ​, - ចំនួននៃចំនួនគត់នៅលើព្រំដែនរបស់វា, - តំបន់របស់វា។ បន្ទាប់មករូបមន្តជ្រើសរើស:

ឧទាហរណ៍។ សម្រាប់ពហុកោណក្នុងរូបអិល = 7 (ចំណុចក្រហម), 9 (ចំណុចពណ៌បៃតង) ដូច្នេះស = 7+ 9/2 -1 = 10,5 ឯកតាការ៉េ។

ទ្រឹស្តីបទជ្រើសរើស- លទ្ធផលបុរាណ និង .

ផ្ទៃនៃត្រីកោណដែលមានចំនុចកំពូលនៅថ្នាំង និងគ្មានថ្នាំងខាងក្នុង ឬនៅលើជ្រុង (លើកលែងតែកំពូល) គឺស្មើនឹង 1/2 ។ ការពិតនេះ។

3. ប្រវត្តិសាស្ត្រ

រូបមន្ត Pick ត្រូវបានរកឃើញដោយគណិតវិទូជនជាតិអូទ្រីស Georg Alexander (1859-1942) នៅក្នុង . នៅអាយុ 16 ឆ្នាំ Georg បានបញ្ចប់ការសិក្សាហើយចូល. នៅអាយុ 20 ឆ្នាំគាត់បានទទួលសិទ្ធិបង្រៀនរូបវិទ្យានិងគណិតវិទ្យា។ នៅឆ្នាំ 1884 Peak បានទៅទៅ . នៅទីនោះគាត់បានជួបសិស្សម្នាក់ទៀតរបស់ Klein ។. ក្រោយមកនៅឆ្នាំ 1885 គាត់បានត្រលប់ទៅដែលជាកន្លែងដែលគាត់បានចំណាយពេលដែលនៅសល់នៃអាជីពវិទ្យាសាស្ត្ររបស់គាត់។

Georg Pick គឺជាមិត្តនឹង Einstein ។ Pick និង Einstein មិនត្រឹមតែចែករំលែកចំណាប់អារម្មណ៍ខាងវិទ្យាសាស្ត្រប៉ុណ្ណោះទេ ប៉ុន្តែក៏មានចំណង់ចំណូលចិត្តចំពោះតន្ត្រីផងដែរ។ Pick ដែលលេងក្នុងក្រុមដែលមានសាស្ត្រាចារ្យនៅសកលវិទ្យាល័យ បានណែនាំ Einstein ដល់សង្គមវិទ្យាសាស្ត្រ និងតន្ត្រីនៅទីក្រុង Prague ។

រង្វង់នៃចំណាប់អារម្មណ៍គណិតវិទ្យារបស់ Peak គឺធំទូលាយណាស់។ ជាពិសេស​គាត់​មាន​ឯកសារ​វិទ្យាសាស្ត្រ​ជាង ៥០ ។ ទ្រឹស្តីបទរបស់ Pick ត្រូវបានរកឃើញដោយគាត់ក្នុងឆ្នាំ 1899 ត្រូវបានគេស្គាល់យ៉ាងទូលំទូលាយសម្រាប់ការគណនាតំបន់នៃពហុកោណ។ នៅប្រទេសអាឡឺម៉ង់ ទ្រឹស្តីបទនេះត្រូវបានបញ្ចូលក្នុងសៀវភៅសិក្សារបស់សាលា។

4.កម្មវិធីនៃរូបមន្តជ្រើសរើស

រូបមន្ត Pick ត្រូវបានប្រើមិនត្រឹមតែដើម្បីគណនាតំបន់នៃពហុកោណប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងដើម្បីដោះស្រាយបញ្ហាជាច្រើននៃកម្រិតអូឡាំពិកផងដែរ។

ឧទាហរណ៍មួយចំនួននៃការប្រើប្រាស់រូបមន្តរបស់ Pick នៅពេលដោះស្រាយបញ្ហា៖

1) ស្តេចអុកបានដើរជុំវិញក្តារក្រឡា 8 × 8 ដោយបានទៅលេងនីមួយៗ

វាលផ្ទះពិតប្រាកដតែម្តង ហើយជាមួយនឹងការផ្លាស់ប្តូរចុងក្រោយត្រឡប់ទៅដើមវិញ។

វាល។ ខ្សែ​ដែល​ខូច​តភ្ជាប់​ជា​ស៊េរី​កណ្តាល​វាល​នោះ។

ស្តេចយាងកាត់ ពុំមានផ្លូវប្រសព្វ។ តំបន់ណាដែលអាចធ្វើបាន

កំណត់ខ្សែដែលខូចនេះ? (ផ្នែកម្ខាងនៃក្រឡាគឺ 1 ។ )

វាធ្វើតាមរូបមន្ត Pick ភ្លាមៗ ដែលតំបន់ជាប់នឹង lo-

ម៉ាណាគឺ 64/2 − 1 = 31; នៅទីនេះថ្នាំងបន្ទះឈើគឺជាចំណុចកណ្តាល 64

វាល និងតាមការសន្មត ពួកវាទាំងអស់ស្ថិតនៅលើព្រំដែននៃពហុកោណ។ ដូច្នេះ

ដូច្នេះ ថ្វីត្បិតតែមាន "គន្លង" របស់ព្រះរាជាច្រើនណាស់ ប៉ុន្តែសុទ្ធតែមានទាំងអស់។

កំណត់ពហុកោណនៃផ្ទៃស្មើគ្នា។

ភារកិច្ចពីវត្ថុបញ្ជានិងវាស់វែងនៃ GIA និងការប្រឡងរដ្ឋបង្រួបបង្រួម

កិច្ចការ B3

ស្វែងរកផ្ទៃនៃរូបដែលបង្ហាញនៅលើក្រដាសគូសដែលមានទំហំក្រឡា 1 សង់ទីម៉ែត្រ 1 សង់ទីម៉ែត្រ (សូមមើលរូបភព) ។ ផ្តល់ចម្លើយរបស់អ្នកជាសង់ទីម៉ែត្រការ៉េ។

4. សេចក្តីសន្និដ្ឋាន

នៅក្នុងដំណើរការនៃការស្រាវជ្រាវ ខ្ញុំបានសិក្សាឯកសារយោង ដែលជាអក្សរសិល្ប៍វិទ្យាសាស្ត្រដ៏ពេញនិយម។ ខ្ញុំបានដឹងថាបញ្ហានៃការស្វែងរកផ្ទៃនៃពហុកោណដែលមានចំនុចកំពូលនៅចំនុចនៃក្រឡាចត្រង្គបានបំផុសគំនិតគណិតវិទូជនជាតិអូទ្រីស Pick ក្នុងឆ្នាំ 1899 ដើម្បីបង្ហាញពីរូបមន្ត Pick ដ៏អស្ចារ្យ។

ជាលទ្ធផលនៃការងាររបស់ខ្ញុំ ខ្ញុំបានពង្រីកចំណេះដឹងរបស់ខ្ញុំក្នុងការដោះស្រាយបញ្ហានៅលើក្រដាសត្រួតពិនិត្យ ដោយកំណត់សម្រាប់ខ្លួនខ្ញុំផ្ទាល់នូវចំណាត់ថ្នាក់នៃបញ្ហាដែលកំពុងសិក្សា ហើយបានជឿជាក់លើភាពចម្រុះរបស់ពួកគេ។

ខ្ញុំបានរៀនពីរបៀបគណនាផ្ទៃនៃពហុកោណដែលគូរនៅលើសន្លឹកគូសធីក។ កិច្ចការដែលបានពិចារណាមានកម្រិតពិបាកខុសគ្នា - ពីសាមញ្ញទៅ Olympiad ។ មនុស្សគ្រប់រូបអាចស្វែងរកកិច្ចការនៃកម្រិតដែលអាចធ្វើទៅបាននៃភាពស្មុគស្មាញ ដោយចាប់ផ្តើមពីនោះ វានឹងអាចបន្តទៅការដោះស្រាយកិច្ចការដែលពិបាកជាងនេះ។

ខ្ញុំបានសន្និដ្ឋានថាប្រធានបទដែលខ្ញុំចាប់អារម្មណ៍គឺមានច្រើនមុខ កិច្ចការនៅលើក្រដាសគូសត្រូវមានភាពចម្រុះ វិធីសាស្រ្ត និងបច្ចេកទេសសម្រាប់ដោះស្រាយក៏មានភាពចម្រុះផងដែរ។ ដូច្នេះហើយ ខ្ញុំបានសម្រេចចិត្តបន្តធ្វើការក្នុងទិសដៅនេះ។

5. អក្សរសិល្ប៍ដែលបានប្រើ៖

1. N. B. Vasil'ev "ជុំវិញរូបមន្តជ្រើសរើស" Kvant ។ - 1974. - លេខ 12

2. Kokse Prasolov VV Tasks in planimetry ។ - M.: MTsNMO, 2006.t e r G.S.M. ការណែនាំអំពីធរណីមាត្រ។ - អិមៈ ណៅកា ឆ្នាំ ១៩៦៦

3. Roslova L.O., Sharygin I.F. ការ​វាស់។ - M. : Ed ។ "Open World", ឆ្នាំ 2005 ។

ធនធានអ៊ីនធឺណិត:

:

មតិយោបល់លើការងារ

"ការគណនាតំបន់នៃតួលេខយន្តហោះ។ វិធីសាស្រ្តជ្រើសរើស"

ការពិចារណាលើប្រធានបទនេះនឹងបង្កើនសកម្មភាពនៃការយល់ដឹងរបស់សិស្ស ដែលនៅពេលក្រោយក្នុងមេរៀនធរណីមាត្រនឹងចាប់ផ្តើមឃើញភាពចុះសម្រុងគ្នានៃគំនូរ ហើយនឹងឈប់យល់ឃើញថាធរណីមាត្រ (និងគណិតវិទ្យាជាទូទៅ) ជាវិទ្យាសាស្ត្រគួរឱ្យធុញ។

ពិនិត្យឡើងវិញដោយគ្រូគណិតវិទ្យា

Khodyreva Tatyana Georgievna

មានរូបមន្តដ៏អស្ចារ្យដែលអនុញ្ញាតឱ្យអ្នករាប់ តំបន់ពហុកោណនៅលើក្រឡាចត្រង្គកូអរដោនេស្ទើរតែគ្មានកំហុស។ វាមិនមែនជារូបមន្តទេ វាជាការពិត ទ្រឹស្តីបទ. នៅ glance ដំបូងវាហាក់ដូចជាស្មុគស្មាញ។ ប៉ុន្តែវាគ្រប់គ្រាន់ដើម្បីដោះស្រាយកិច្ចការពីរបី - ហើយអ្នកនឹងយល់ថាលក្ខណៈពិសេសនេះត្រជាក់ប៉ុណ្ណា។ ដូច្នេះទៅមុខ!

ចូរចាប់ផ្តើមជាមួយនឹងនិយមន័យថ្មី៖

ថ្នាំងជង់កូអរដោណេគឺជាចំណុចណាមួយដែលស្ថិតនៅចំនុចប្រសព្វនៃបន្ទាត់បញ្ឈរ និងផ្ដេកនៃក្រឡាចត្រង្គនេះ។

ការកំណត់:

នៅក្នុងរូបភាពទី 1 ថ្នាំងមិនត្រូវបានសម្គាល់ទាល់តែសោះ។ ទីពីរមាន 4 ថ្នាំង។ ទីបំផុតនៅក្នុងរូបភាពទី 3 ថ្នាំងទាំង 16 ត្រូវបានសម្គាល់។

តើ​នេះ​មាន​បញ្ហា​អ្វី​ខ្លះ​ចំពោះ​បញ្ហា B5? ការពិតគឺថាចំនុចកំពូលនៃពហុកោណនៅក្នុងបញ្ហាបែបនេះ ជានិច្ចដេកនៅចំនុចនៃក្រឡាចត្រង្គ។ ជាលទ្ធផល ទ្រឹស្តីបទខាងក្រោមដំណើរការសម្រាប់ពួកគេ៖

ទ្រឹស្តីបទ។ ពិចារណាពហុកោណនៅលើក្រឡាចត្រង្គកូអរដោណេដែលកំពូលស្ថិតនៅត្រង់ចំណុចនៃក្រឡាចត្រង្គនេះ។ បន្ទាប់មកផ្ទៃនៃពហុកោណគឺ៖

ដែល n ជាចំនួនថ្នាំងនៅខាងក្នុងពហុកោណដែលបានផ្តល់ឱ្យ k គឺជាចំនួនថ្នាំងដែលស្ថិតនៅលើព្រំដែនរបស់វា (ថ្នាំងព្រំដែន)។

ជាឧទាហរណ៍ ចូរយើងពិចារណាត្រីកោណធម្មតានៅលើក្រឡាចត្រង្គកូអរដោនេ ហើយព្យាយាមសម្គាល់ថ្នាំងខាងក្នុង និងព្រំដែន។

រូបភាពទីមួយបង្ហាញពីត្រីកោណធម្មតា។ នៅលើរូបភាពទី 2 ថ្នាំងខាងក្នុងរបស់វាត្រូវបានសម្គាល់ដែលចំនួនគឺ n = 10 ។ នៅលើរូបភាពទី 3 ថ្នាំងដែលស្ថិតនៅលើព្រំដែនត្រូវបានសម្គាល់វាមាន k = 6 ក្នុងចំណោមពួកគេសរុប។

ប្រហែលជាអ្នកអានជាច្រើនមិនយល់ពីរបៀបរាប់លេខ n និង k ។ ចាប់ផ្តើមជាមួយថ្នាំងខាងក្នុង។ អ្វីគ្រប់យ៉ាងគឺជាក់ស្តែងនៅទីនេះ: យើងគូរលើត្រីកោណដោយខ្មៅដៃហើយមើលថាតើថ្នាំងប៉ុន្មានត្រូវបានស្រមោល។

ជាមួយនឹងថ្នាំងព្រំដែន វាមានភាពស្មុគស្មាញបន្តិច។ ព្រំដែនពហុកោណ - បិទបន្ទាត់ខូចដែលប្រសព្វក្រឡាចត្រង្គកូអរដោនេនៅចំណុចជាច្រើន។ មធ្យោបាយងាយស្រួលបំផុតគឺសម្គាល់ចំណុច "ចាប់ផ្តើម" មួយចំនួន ហើយបន្ទាប់មកបន្តទៅកន្លែងដែលនៅសល់។

ថ្នាំងព្រំដែននឹងគ្រាន់តែជាចំណុចទាំងនោះនៅលើបន្ទាត់ប៉ូលីលីនដែលពួកវាប្រសព្វក្នុងពេលដំណាលគ្នា។ បីបន្ទាត់:

1. តាមពិតបន្ទាត់ខូច;
2. បន្ទាត់ក្រឡាចត្រង្គផ្ដេក;
3. បន្ទាត់បញ្ឈរ។

តោះមើលរបៀបដែលវាដំណើរការទាំងអស់នៅក្នុងបញ្ហាជាក់ស្តែង។

កិច្ចការ។ រកផ្ទៃនៃត្រីកោណប្រសិនបើទំហំក្រឡាគឺ 1 x 1 សង់ទីម៉ែត្រ៖

ដំបូង​យើង​សម្គាល់​ថ្នាំង​ដែល​ស្ថិត​នៅ​ខាង​ក្នុង​ត្រីកោណ ព្រម​ទាំង​ព្រំដែន​របស់វា៖

វាប្រែថាមានថ្នាំងខាងក្នុងតែមួយ: n = 1. មានថ្នាំងព្រំដែនប្រាំមួយ: បីស្របគ្នា។ ជាមួយត្រីកោណបញ្ឈរនិងបីទៀតដេកនៅសងខាង។ សរុប k = 6 ។

ឥឡូវនេះយើងគណនាផ្ទៃដីដោយប្រើរូបមន្ត៖

អស់ហើយ! បញ្ហាត្រូវបានដោះស្រាយ។

កិច្ចការ។ រកផ្ទៃនៃរាងបួនជ្រុងដែលគូរលើក្រដាសគូសដែលមានទំហំក្រឡា 1 សង់ទីម៉ែត្រ គុណនឹង 1 សង់ទីម៉ែត្រ។ ផ្តល់ចម្លើយរបស់អ្នកជាសង់ទីម៉ែត្រការ៉េ។

ជាថ្មីម្តងទៀត យើងសម្គាល់ថ្នាំងខាងក្នុង និងព្រំដែន។ មាន n = 2 nodes ខាងក្នុង។​ nodes boundary: k = 7 ដែលក្នុងនោះមាន 4 ចំនុចកំពូលនៃបួនជ្រុងនិង 3 ទៀតដេកនៅសងខាង។

វានៅសល់ដើម្បីជំនួសលេខ n និង k ក្នុងរូបមន្តតំបន់៖

យកចិត្តទុកដាក់លើឧទាហរណ៍ចុងក្រោយ។ បញ្ហានេះត្រូវបានស្នើឡើងយ៉ាងពិតប្រាកដនៅឯការងារធ្វើរោគវិនិច្ឆ័យក្នុងឆ្នាំ 2012។ ប្រសិនបើអ្នកធ្វើការតាមគ្រោងការណ៍ស្តង់ដារនោះអ្នកនឹងត្រូវធ្វើសំណង់បន្ថែមជាច្រើន។ ហើយដោយវិធីសាស្រ្តនៃការ knots អ្វីគ្រប់យ៉ាងត្រូវបានដោះស្រាយស្ទើរតែផ្ទាល់មាត់។

ចំណាំសំខាន់លើតំបន់

ប៉ុន្តែរូបមន្តមិនមែនជាអ្វីគ្រប់យ៉ាងទេ។ ចូរយើងសរសេររូបមន្តឡើងវិញបន្តិច ដោយនាំយកពាក្យនៅខាងស្តាំ ទៅភាគបែងរួម. យើង​ទទួល​បាន:

លេខ n និង k គឺជាចំនួនថ្នាំង ពួកគេតែងតែជាចំនួនគត់។ ដូច្នេះ ភាគយកទាំងមូលក៏ជាចំនួនគត់ផងដែរ។ យើងបែងចែកវាដោយ 2 ដែលបង្កប់ន័យការពិតសំខាន់មួយ:

តំបន់តែងតែត្រូវបានបង្ហាញ ចំនួនទាំងមូលឬប្រភាគ. លើសពីនេះទៅទៀត នៅចុងបញ្ចប់នៃប្រភាគ វាតែងតែមាន "ប្រាំភាគដប់": 10.5; ១៧.៥ ជាដើម។

ដូច្នេះ ផ្ទៃក្នុងបញ្ហា B5 តែងតែត្រូវបានបង្ហាញជាចំនួនគត់ ឬប្រភាគនៃទម្រង់ ***.5 ។ បើ​ចម្លើយ​ខុស​គ្នា វា​មាន​ន័យ​ថា​មាន​កំហុស​នៅ​កន្លែង​ណា​មួយ។ ចងចាំចំណុចនេះនៅពេលអ្នកប្រឡងពិតប្រាកដក្នុងគណិតវិទ្យា!

ដើម្បីប្រើការមើលការបង្ហាញជាមុន បង្កើតគណនី Google (គណនី) ហើយចូល៖ https://accounts.google.com

ចំណងជើងស្លាយ៖

បញ្ចប់ដោយសិស្សនៃអនុវិទ្យាល័យលេខ 7 8 "A" ថ្នាក់ Yunosheva Ksenia គ្រូបង្រៀន: Babina Natalya Alekseevna Salsk ឆ្នាំ 2011 "រូបមន្តកំពូល"

គោលបំណងនៃការងារ៖ ស្វែងរកអត្ថិភាពនៃមួយទៀត ខុសពីកម្មវិធីសិក្សារបស់សាលា រូបមន្តសម្រាប់ស្វែងរកផ្ទៃនៃពហុកោណបន្ទះឈើ។ តំបន់នៃការអនុវត្តរូបមន្តដែលចង់បាន។

សេចក្តីផ្តើម។ ការអប់រំគណិតវិទ្យាដែលទទួលបាននៅក្នុងសាលាអប់រំទូទៅគឺជាធាតុផ្សំដ៏សំខាន់នៃការអប់រំទូទៅ និងវប្បធម៌ទូទៅរបស់មនុស្សសម័យទំនើប។ នៅដំណាក់កាលនេះ ប្រព័ន្ធសាលារៀនត្រូវបានរចនាឡើងសម្រាប់ការអប់រំដប់មួយឆ្នាំ។ សិស្សទាំងអស់នៅចុងបញ្ចប់នៃថ្នាក់ទី 11 នឹងត្រូវប្រឡង Unified State ដែលនឹងបង្ហាញពីកម្រិតនៃចំណេះដឹងដែលទទួលបាននៅពេលសិក្សានៅសាលា។ ប៉ុន្តែកម្មវិធីសិក្សារបស់សាលាមិនតែងតែផ្តល់នូវវិធីសមហេតុផលបំផុតក្នុងការដោះស្រាយបញ្ហាណាមួយនោះទេ។ ជាឧទាហរណ៍ បើក្រឡេកមើលលទ្ធផលនៃការប្រឡងរដ្ឋបង្រួបបង្រួមក្នុងឆ្នាំ 2010 វាច្បាស់ណាស់ថាសិស្សជាច្រើនបាត់បង់ពិន្ទុដោយសារតែកិច្ចការ B6 ។ ខ្ញុំបានកំណត់ដើម្បីរកវិធីសន្សំពេលវេលា និងដោះស្រាយបញ្ហានេះបានត្រឹមត្រូវ។

កិច្ចការ B6 ។ តួលេខត្រូវបានបង្ហាញនៅលើក្រដាសដែលមានក្រឡាទំហំ 1 សង់ទីម៉ែត្រ គុណនឹង 1 សង់ទីម៉ែត្រ (សូមមើលរូប)។ រកតំបន់របស់ពួកគេគិតជាសង់ទីម៉ែត្រការ៉េ។

ដូច្នេះដើម្បីនៅតែដោះស្រាយកិច្ចការនេះ ខ្ញុំត្រូវអនុវត្តរូបមន្តសម្រាប់ស្វែងរកតំបន់ដែលយើងសិក្សានៅថ្នាក់ទី ៨។ ប៉ុន្តែវានឹងចំណាយពេលច្រើន ហើយខ្ញុំត្រូវឆ្លើយសំណួរឱ្យបានលឿនតាមដែលអាចធ្វើទៅបាន ព្រោះ ពេលវេលាសម្រាប់ការប្រឡងត្រូវបានកំណត់យ៉ាងតឹងរ៉ឹង។ ដូច្នេះហើយ បន្ទាប់ពីធ្វើការស្រាវជ្រាវ ខ្ញុំបានរកឃើញថា មានទ្រឹស្តីបទរបស់ Pick ដែលមិនត្រូវបានសិក្សានៅក្នុងកម្មវិធីសិក្សារបស់សាលា ប៉ុន្តែវានឹងជួយឱ្យខ្ញុំដោះស្រាយកិច្ចការបានលឿនជាងមុន។

ឯកសារយោងប្រវត្តិសាស្ត្រ។ Georg Alexander Pick (ថ្ងៃទី 10 ខែសីហា ឆ្នាំ 1859 ដល់ថ្ងៃទី 26 ខែកក្កដា ឆ្នាំ 1942) គឺជាគណិតវិទូជនជាតិអូទ្រីស។ គាត់បានស្លាប់នៅក្នុងជំរុំប្រមូលផ្តុំ Terezin ។ វាត្រូវបានគេស្គាល់សព្វថ្ងៃនេះដោយសារតែរូបមន្តរបស់ Pick សម្រាប់កំណត់តំបន់នៃបន្ទះឈើនៃពហុកោណ។ គាត់បានបោះពុម្ភរូបមន្តរបស់គាត់នៅក្នុងក្រដាសមួយនៅឆ្នាំ 1899 វាបានក្លាយជាការពេញនិយមនៅពេលដែល Hugo Steinhaus បញ្ចូលវានៅក្នុងឆ្នាំ 1969 នៃរូបភាពគណិតវិទ្យា។ Pick បានសិក្សានៅសាកលវិទ្យាល័យ Vienna ហើយបានបញ្ចប់ថ្នាក់បណ្ឌិតរបស់គាត់នៅឆ្នាំ 1880 ។ បន្ទាប់ពីទទួលបានបណ្ឌិត គាត់ត្រូវបានតែងតាំងជាជំនួយការរបស់ Ernest Mach នៅសាកលវិទ្យាល័យ Scherl-Ferdinand ក្នុងទីក្រុង Prague ។ គាត់បានក្លាយជាគ្រូបង្រៀននៅទីនោះក្នុងឆ្នាំ 1881 ។ ដោយឈប់សម្រាកពីសាកលវិទ្យាល័យនៅឆ្នាំ 1884 គាត់បានចាប់ផ្តើមធ្វើការជាមួយ Felix Klein នៅសាកលវិទ្យាល័យ Leipzig ។ គាត់បានស្នាក់នៅទីក្រុង Prague រហូតដល់ការចូលនិវត្តន៍របស់គាត់នៅឆ្នាំ 1927 នៅពេលដែលគាត់បានត្រលប់ទៅទីក្រុងវីយែនវិញ។ Pick បានធ្វើជាប្រធានគណៈកម្មាធិការនៅ (ពេលនោះ) សាកលវិទ្យាល័យអាល្លឺម៉ង់ Prague ដែលបានតែងតាំងជាសាស្រ្តាចារ្យ Albert Einstein នៃរូបវិទ្យាគណិតវិទ្យាក្នុងឆ្នាំ 1911 ។ Pick ត្រូវបានជ្រើសរើសជាសមាជិកនៃបណ្ឌិត្យសភាវិទ្យាសាស្ត្រ និងសិល្បៈឆេក ប៉ុន្តែត្រូវបានបណ្តេញចេញបន្ទាប់ពីការកាន់កាប់របស់ណាស៊ីនៅទីក្រុងប្រាក។ បន្ទាប់ពីចូលនិវត្តន៍នៅឆ្នាំ 1927 Pick បានត្រលប់ទៅ Vienna ដែលជាទីក្រុងដែលគាត់កើត។ បន្ទាប់ពី Anschluss នៅពេលដែលពួកណាស៊ីបានចូលប្រទេសអូទ្រីសនៅថ្ងៃទី 12 ខែមីនាឆ្នាំ 1938 Pieck បានត្រឡប់ទៅទីក្រុង Prague វិញ។ នៅខែមីនាឆ្នាំ 1939 ពួកណាស៊ីបានលុកលុយប្រទេសឆេកូស្លូវ៉ាគី។ Georg ត្រូវបានបញ្ជូនទៅជំរុំប្រមូលផ្តុំ Terezin នៅថ្ងៃទី 13 ខែកក្កដា ឆ្នាំ 1942 ។ គាត់បានស្លាប់ពីរសប្តាហ៍ក្រោយមក។

ទ្រឹស្តីបទជ្រើសរើស។ ទ្រឹស្តីបទរបស់ Pick គឺជាលទ្ធផលបុរាណនៃធរណីមាត្រផ្សំ និងធរណីមាត្រនៃលេខ។ ផ្ទៃនៃពហុកោណដែលមានចំនួនគត់បញ្ឈរគឺស្មើនឹងផលបូក B + D / 2 - 1 ដែល B គឺជាចំនួននៃចំណុចចំនួនគត់នៅខាងក្នុងពហុកោណ ហើយ D គឺជាចំនួននៃចំនុចចំនួនគត់នៅលើព្រំដែននៃពហុកោណ។

ភស្តុតាងដ៏អស្ចារ្យនៃទ្រឹស្តីបទ Pick ។ ពហុកោណបែបនេះអាចបែងចែកយ៉ាងងាយស្រួលទៅជាត្រីកោណដែលមានចំណុចបញ្ឈរនៅថ្នាំងនៃបន្ទះឈើ ដោយគ្មានថ្នាំងខាងក្នុង ឬនៅសងខាង។ វាអាចត្រូវបានបង្ហាញថាផ្ទៃនៃត្រីកោណទាំងអស់នេះគឺដូចគ្នានិងស្មើ 1/2 ហើយដូច្នេះផ្ទៃនៃពហុកោណគឺស្មើនឹងពាក់កណ្តាលនៃចំនួនរបស់ពួកគេ T. ដើម្បីរកលេខនេះយើងកំណត់ដោយ n ចំនួនជ្រុងនៃពហុកោណដោយ i - ចំនួនថ្នាំងនៅខាងក្នុងវា និងដោយ ខ - ចំនួនថ្នាំងនៅសងខាងរួមទាំងកំពូល។ ផលបូកសរុបនៃមុំនៃត្រីកោណទាំងអស់គឺ πТ។ ឥឡូវនេះ ចូរយើងស្វែងរកផលបូកនេះតាមរបៀបផ្សេង។ ផលបូកនៃមុំដែលមានចំនុចកំពូលនៅថ្នាំងខាងក្នុងណាមួយគឺ 2 π ពោលគឺ ផលបូកសរុបនៃមុំបែបនេះគឺ 2 π i ; ផលបូកសរុបនៃមុំនៅថ្នាំងនៅសងខាង ប៉ុន្តែមិនមែននៅចំនុចកំពូលទេគឺ (b - n) π ហើយផលបូកនៃមុំនៅចំនុចកំពូលនៃពហុកោណគឺ (n - 2) π។ ដូច្នេះ π T \u003d 2i π + (b - n) π + (n - 2) π ដែលយើងទទួលបានកន្សោមសម្រាប់ផ្ទៃ S នៃពហុកោណ ដែលគេស្គាល់ថាជារូបមន្តជ្រើសរើស។ ឧទាហរណ៍ក្នុងរូបភាព b = 9, i = 24 ហើយដូច្នេះផ្ទៃនៃពហុកោណគឺ 27.5 ។

ការដាក់ពាក្យ។ ដូច្នេះត្រឡប់ទៅភារកិច្ច B6 ។ ឥឡូវនេះដោយដឹងពីរូបមន្តថ្មី យើងអាចរកឃើញតំបន់នៃរាងបួនជ្រុងនេះយ៉ាងងាយស្រួល។ ចាប់តាំងពី B គឺ 5; ឃ - 14 បន្ទាប់មក 5 + 14: 2-1 \u003d 11 (សង់ទីម៉ែត្រការ៉េ) តំបន់នៃការ៉េនេះគឺ 11 សង់ទីម៉ែត្រការ៉េ។

ដោយប្រើរូបមន្តដូចគ្នា យើងអាចរកឃើញផ្ទៃនៃត្រីកោណមួយ។ ចាប់តាំងពី B-14, G-10, បន្ទាប់មក 14+10:2-1=18 (សង់ទីម៉ែត្រការេ) តំបន់នៃត្រីកោណនេះគឺ 18 សង់ទីម៉ែត្រការ៉េ។

ប្រសិនបើ B-9, D-12, បន្ទាប់មក: 9+12:2-1=14 (សង់ទីម៉ែត្រការ៉េ) ផ្ទៃដីនៃការ៉េនេះគឺ 14 សង់ទីម៉ែត្រការ៉េ។

វិសាលភាពនៃរូបមន្ត។ បន្ថែមពីលើការពិតដែលថារូបមន្តត្រូវបានប្រើប្រាស់ក្នុងប្រភេទផ្សេងៗនៃការប្រឡង កិច្ចការ និងផ្សេងៗទៀត វាអមជាមួយពិភពលោកទាំងមូលជុំវិញយើង។

យោងតាមរូបមន្តរបស់ Peak S = B + ½ G-1 1) តួ B=9, G=26, S=9+½ 26-1=9+13-1= 21 2) កន្ទុយ B=0, G=8, S= 0 +½ 8 -1= 3 3) S= 21+3=24

យោងតាមរូបមន្តរបស់ Peak S \u003d B + ½ G-1 B \u003d 36, G \u003d 21 S \u003d 36 + ½ 21 -1 \u003d 36 + 10.5-1 \u003d 45.5

សេចក្តីសន្និដ្ឋាន។ ជាលទ្ធផល ខ្ញុំបានសន្និដ្ឋានថា មានវិធីផ្សេងគ្នាជាច្រើនក្នុងការដោះស្រាយបញ្ហាតំបន់ដែលមិនត្រូវបានសិក្សានៅក្នុងកម្មវិធីសិក្សារបស់សាលា ហើយបានបង្ហាញពួកគេដោយប្រើរូបមន្ត Pick ជាឧទាហរណ៍។

ថតឯកសារ។ ពហុកោណ​ដែល​គ្មាន​ប្រសព្វ​ខ្លួនឯង​ត្រូវ​បាន​ហៅ​ថា​ពហុកោណ​បន្ទះឈើ ប្រសិនបើ​ចំណុច​កំពូល​ទាំងអស់​របស់​វា​ស្ថិតនៅ​ចំណុច​ដែលមាន​កូអរដោណេ​ចំនួន​គត់ (នៅក្នុង​ប្រព័ន្ធ​កូអរដោណេ Cartesian)។ ចំណុចមួយនៅក្នុងយន្តហោះកូអរដោណេត្រូវបានគេហៅថាចំនួនគត់ ប្រសិនបើកូអរដោណេទាំងពីររបស់វាគឺជាចំនួនគត់។