វា​គឺ​ជា​រាង​បួន​ជ្រុង​ដែល​ភាគី​ទល់​មុខ​គឺ​ជា​គូ​ស្រប​គ្នា។

អចលនទ្រព្យ ១. អង្កត់ទ្រូងណាមួយនៃប្រលេឡូក្រាមចែកវាទៅជាត្រីកោណស្មើគ្នាពីរ។

ភស្តុតាង។ យោងតាមសញ្ញាទី II (ជ្រុងដេកនិងជ្រុងរួម) ។

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ទ្រព្យ ២. ក្នុងប្រលេឡូក្រាម ជ្រុងទល់មុខគឺស្មើគ្នា ហើយមុំទល់មុខគឺស្មើគ្នា។

ភស្តុតាង។
ដូចគ្នានេះដែរ

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ទ្រព្យសម្បត្តិ 3. ក្នុងប្រលេឡូក្រាមអង្កត់ទ្រូង ចំនុចប្រសព្វត្រូវបានបែងចែកជាពាក់កណ្តាល។

ភស្តុតាង។

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ទ្រព្យ ៤. មុំ bisector នៃ parallelogram ប្រសព្វ​ខាង​ទល់​មុខ បែងចែក​វា​ជា​ត្រីកោណ isosceles និង trapezoid ។ (ឆ. ពាក្យ - កំពូល - ពីរ isosceles ? -ka).

ភស្តុតាង។

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ទ្រព្យ ៥. នៅក្នុងប្រលេឡូក្រាម ចម្រៀកដែលមានចុងនៅសងខាង ឆ្លងកាត់ចំនុចប្រសព្វនៃអង្កត់ទ្រូងត្រូវបានបំបែកដោយចំនុចនេះ។

ភស្តុតាង។

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ទ្រព្យ ៦. មុំរវាងកម្ពស់ធ្លាក់ចុះពីចំណុចកំពូលនៃមុំ obtuse នៃប្រលេឡូក្រាមគឺស្មើនឹងមុំស្រួចនៃប្រលេឡូក្រាម។

ភស្តុតាង។

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ទ្រព្យ ៧. ផលបូកនៃមុំនៃប្រលេឡូក្រាមដែលនៅជាប់នឹងម្ខាងគឺ 180°។

ភស្តុតាង។

ទ្រឹស្តីបទបង្ហាញឱ្យឃើញ.

ការសាងសង់ផ្នែកនៃមុំមួយ។ លក្ខណៈសម្បត្តិនៃមុំ bisector នៃត្រីកោណមួយ។

1) សាងសង់កាំរស្មី DE បំពាន។

2) នៅលើកាំរស្មីដែលបានផ្តល់ឱ្យ បង្កើតរង្វង់តាមអំពើចិត្តដែលមានចំណុចកណ្តាលនៅចំនុចកំពូល និងដូចគ្នា
កណ្តាលនៅដើមនៃកាំរស្មីដែលបានសាងសង់។

3) F និង G - ចំនុចប្រសព្វនៃរង្វង់ជាមួយជ្រុងនៃមុំដែលបានផ្តល់ឱ្យ H - ចំនុចប្រសព្វនៃរង្វង់ជាមួយកាំរស្មីដែលបានសាងសង់

បង្កើតរង្វង់ដែលមានចំណុចកណ្តាលនៅចំណុច H និងកាំស្មើនឹង FG ។

5) ខ្ញុំ - ចំណុចប្រសព្វនៃរង្វង់នៃធ្នឹមដែលបានសាងសង់។

6) គូរបន្ទាត់កាត់ចំនុចកំពូល និង I ។

IDH - មុំដែលត្រូវការ។
)

អចលនទ្រព្យ ១. មុំ bisector នៃត្រីកោណមួយបែងចែកភាគីផ្ទុយគ្នាតាមសមាមាត្រទៅនឹងជ្រុងដែលនៅជាប់គ្នា។

ភស្តុតាង។ អនុញ្ញាតឱ្យ x, y ជាផ្នែកនៃចំហៀង c ។ យើងបន្តកាំរស្មី BC ។ នៅលើកាំរស្មី BC យើងគូរផ្នែក CK ពី C ស្មើនឹង AC ។

ភស្តុតាង

តោះគូរអង្កត់ទ្រូង AC ជាមុនសិន។ ត្រីកោណពីរត្រូវបានទទួល: ABC និង ADC ។

ដោយសារ ABCD គឺជាប្រលេឡូក្រាម ខាងក្រោមនេះជាការពិត៖

AD || BC \\ ព្រួញស្ដាំ \\ មុំ ១ = \\ មុំ ២ដូចជានិយាយកុហកឆ្លងកាត់។

AB || ស៊ីឌី \\ ព្រួញស្ដាំ \\ មុំ ៣ = មុំ ៤ដូចជានិយាយកុហកឆ្លងកាត់។

ដូច្នេះ \triangle ABC = \triangle ADC (ដោយលក្ខណៈទីពីរ៖ និង AC គឺជារឿងធម្មតា)។

ដូច្នេះហើយ \ ត្រីកោណ ABC = \ ត្រីកោណ ADC បន្ទាប់មក AB = ស៊ីឌី និង AD = BC ។

បញ្ជាក់!

2. មុំទល់មុខគឺដូចគ្នាបេះបិទ។

ភស្តុតាង

នេះ​បើ​តាម​ការ​បញ្ជាក់ លក្ខណៈសម្បត្តិ ១យើងដឹងរឿងនោះ។ \angle 1 = \angle 2, \angle 3 = \angle 4. ដូច្នេះផលបូកនៃមុំផ្ទុយគឺ៖ \angle 1 + \angle 3 = \angle 2 + \angle 4. ដោយពិចារណាថា \ ត្រីកោណ ABC = \ ត្រីកោណ ADC យើងទទួលបាន \angle A = \angle C, \angle B = \angle D ។

បញ្ជាក់!

3. អង្កត់ទ្រូងត្រូវបាន bisected ដោយចំនុចប្រសព្វ។

ភស្តុតាង

តោះគូរអង្កត់ទ្រូងមួយទៀត។

ដោយ ទ្រព្យ ១យើងដឹងថាភាគីទល់មុខគឺដូចគ្នាបេះបិទ៖ AB = CD ។ ជាថ្មីម្តងទៀតយើងកត់សំគាល់មុំស្មើគ្នាដែលនិយាយបញ្ច្រាស។

ដូច្នេះវាអាចមើលឃើញថា \ ត្រីកោណ AOB = \ ត្រីកោណ COD ដោយសញ្ញាទីពីរនៃសមភាពនៃត្រីកោណ (មុំពីរនិងជ្រុងមួយរវាងពួកវា) ។ នោះគឺ BO = OD (ទល់មុខ \angle 2 និង \angle 1) និង AO = OC (ទល់មុខ \angle 3 និង \angle 4 រៀងគ្នា)។

បញ្ជាក់!

លក្ខណៈប៉ារ៉ាឡែល

ប្រសិនបើមានតែសញ្ញាមួយនៅក្នុងបញ្ហារបស់អ្នក នោះតួលេខគឺជាប៉ារ៉ាឡែល ហើយអ្នកអាចប្រើលក្ខណៈសម្បត្តិទាំងអស់នៃតួលេខនេះ។

ដើម្បីទន្ទេញចាំបានកាន់តែប្រសើរ សូមចំណាំថា សញ្ញាប៉ារ៉ាឡែលនឹងឆ្លើយសំណួរខាងក្រោម − "តើធ្វើដូចម្តេចដើម្បីស្វែងយល់?". នោះ​គឺ​របៀប​ដើម្បី​រក​ឱ្យ​ឃើញ​ថា​តួ​លេខ​ដែល​បាន​ផ្តល់​ឱ្យ​គឺ​ជា​ប៉ារ៉ាឡែល​។

1. ប្រលេឡូក្រាមគឺជាចតុកោណដែលភាគីទាំងពីរស្មើគ្នា និងប៉ារ៉ាឡែល។

AB=CD; AB || ស៊ីឌី \\ ព្រួញស្ដាំ ABCD គឺជាប្រលេឡូក្រាម។

ភស្តុតាង

ចូរយើងពិចារណាលម្អិតបន្ថែមទៀត។ ហេតុអ្វី AD || BC?

\\ ត្រីកោណ ABC = \\ ត្រីកោណ ADC ដោយ ទ្រព្យ ១៖ AB = CD, AC គឺជារឿងធម្មតា ហើយ \angle 1 = \angle 2 ជា crosswise ជាមួយ AB និង CD ស្របគ្នា និង secant AC ។

ប៉ុន្តែប្រសិនបើ \triangle ABC = \triangle ADC បន្ទាប់មក \angle 3 = \angle 4 (ពួកវាស្ថិតនៅទល់មុខ AB និង CD រៀងគ្នា)។ ដូច្នេះ AD || BC (\ មុំ 3 និង \ មុំ 4 - កុហក​កាត់​ក៏​ស្មើគ្នា) ។

សញ្ញាដំបូងគឺត្រឹមត្រូវ។

2. ប្រលេឡូក្រាមគឺជាចតុកោណដែលភាគីទល់មុខស្មើគ្នា។

AB = CD , AD = BC \\ Rightarrow ABCD គឺជាប្រលេឡូក្រាម។

ភស្តុតាង

ចូរយើងពិចារណាលក្ខណៈពិសេសនេះ។ តោះគូរអង្កត់ទ្រូង AC ម្តងទៀត។

ដោយ ទ្រព្យ ១\\ ត្រីកោណ ABC = \\ ត្រីកោណ ACD ។

វាធ្វើតាមថា: \angle 1 = \angle 2 \ Rightarrow AD || BCនិង \angle 3 = \angle 4 \Rightarrow AB || ស៊ីឌីនោះគឺ ABCD គឺជាប៉ារ៉ាឡែល។

សញ្ញាទីពីរគឺត្រឹមត្រូវ។

3. ប្រលេឡូក្រាមគឺជាចតុកោណដែលមុំទល់មុខគឺស្មើគ្នា។

\angle A = \angle C , \angle B = \angle D \ Rightarrow ABCD- ប្រលេឡូក្រាម។

ភស្តុតាង

2 \alpha + 2 \beta = 360^(\circ)(ព្រោះ ABCD ជាចតុកោណកែង ហើយ \angle A = \angle C, \angle B = \angle D តាមអនុសញ្ញា)។

ដូច្នេះ \alpha + \beta = 180^(\circ) ។ ប៉ុន្តែ \alpha និង \beta គឺខាងក្នុងម្ខាងនៅ secant AB ។

ហើយការពិតថា \alpha + \beta = 180^(\circ) ក៏មានន័យថា AD || BC

នៅពេលដំណាលគ្នានោះ \alpha និង \beta គឺខាងក្នុងម្ខាងជាមួយ AD secant ។ ហើយនោះមានន័យថា AB || ស៊ីឌី។

សញ្ញាទីបីគឺត្រឹមត្រូវ។

4. ប្រលេឡូក្រាមគឺជាចតុកោណដែលអង្កត់ទ្រូងត្រូវបានបំបែកដោយចំនុចប្រសព្វ។

AO=OC; BO = OD \\ ប៉ារ៉ាឡែលព្រួញស្ដាំ។

ភស្តុតាង

BO=OD; AO = OC , \angle 1 = \angle 2 ជាបញ្ឈរ \\ ព្រួញស្ដាំ \\ ត្រីកោណ AOB = \\ ត្រីកោណ COD, \Rightarrow \angle 3 = \angle 4និង \Rightarrow AB || ស៊ីឌី។

ដូចគ្នាដែរ BO = OD ; AO=OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8និង \Rightarrow AD || BC

សញ្ញាទីបួនគឺត្រឹមត្រូវ។

ប្រធានបទមេរៀន

• លក្ខណៈសម្បត្តិនៃអង្កត់ទ្រូងនៃប្រលេឡូក្រាម។

គោលបំណងនៃមេរៀន

• ស្វែងយល់ពីនិយមន័យថ្មី ហើយរំលឹកឡើងវិញនូវអ្វីដែលបានសិក្សារួចហើយ។
• បង្កើត និងបញ្ជាក់ទ្រព្យសម្បត្តិនៃអង្កត់ទ្រូងនៃប្រលេឡូក្រាម។
• រៀនអនុវត្តលក្ខណៈសម្បត្តិនៃរាងក្នុងការដោះស្រាយបញ្ហា។
• ការអភិវឌ្ឍន៍ - ដើម្បីអភិវឌ្ឍការយកចិត្តទុកដាក់របស់សិស្ស, ការតស៊ូ, ការតស៊ូ, ការគិតឡូជីខល, ការនិយាយគណិតវិទ្យា។
• ការអប់រំ - តាមរយៈមេរៀនដើម្បីបណ្តុះអាកប្បកិរិយាយកចិត្តទុកដាក់ចំពោះគ្នាទៅវិញទៅមក, បណ្តុះសមត្ថភាពក្នុងការស្តាប់សមមិត្ត, ជំនួយទៅវិញទៅមក, ឯករាជ្យភាព។

គោលបំណងនៃមេរៀន

• ពិនិត្យមើលសមត្ថភាពរបស់សិស្សក្នុងការដោះស្រាយបញ្ហា។

ផែនការ​មេរៀន

1. សេចក្តីផ្តើម។
2. ពាក្យដដែលៗនៃសម្ភារៈដែលបានសិក្សាពីមុន។
3. Parallelogram លក្ខណៈសម្បត្តិនិងសញ្ញារបស់វា។
4. ឧទាហរណ៍នៃកិច្ចការ។
5. ពិនិត្យ​ដោយខ្លួនឯង។

សេចក្តីផ្តើម

"របកគំហើញវិទ្យាសាស្រ្តដ៏សំខាន់មួយ ផ្តល់នូវដំណោះស្រាយចំពោះបញ្ហាធំមួយ ប៉ុន្តែនៅក្នុងដំណោះស្រាយនៃបញ្ហាណាមួយ មានការរកឃើញមួយគ្រាប់។"

លក្ខណសម្បត្តិនៃជ្រុងផ្ទុយនៃប្រលេឡូក្រាម

ប្រលេឡូក្រាមមានភាគីផ្ទុយគ្នា។

ភស្តុតាង។

អនុញ្ញាតឱ្យ ABCD ជាប្រលេឡូក្រាមដែលបានផ្តល់ឱ្យ។ ហើយឱ្យអង្កត់ទ្រូងរបស់វាប្រសព្វគ្នាត្រង់ចំណុច O ។
ចាប់តាំងពី Δ AOB = Δ COD ដោយសញ្ញាដំបូងនៃសមភាពនៃត្រីកោណ (∠ AOB = ∠ COD ជាបញ្ឈរ AO = OC, DO = OB ដោយទ្រព្យសម្បត្តិនៃអង្កត់ទ្រូងប្រលេឡូក្រាម) បន្ទាប់មក AB = CD ។ ដូចគ្នានេះដែរពីសមភាពនៃត្រីកោណ BOC និង DOA វាធ្វើតាមថា BC = DA ។ ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

ទ្រព្យសម្បត្តិនៃមុំផ្ទុយនៃប្រលេឡូក្រាម

ប្រលេឡូក្រាមមានមុំទល់មុខ។

ភស្តុតាង។

អនុញ្ញាតឱ្យ ABCD ជាប្រលេឡូក្រាមដែលបានផ្តល់ឱ្យ។ ហើយឱ្យអង្កត់ទ្រូងរបស់វាប្រសព្វគ្នាត្រង់ចំណុច O ។
ពីលក្ខណៈសម្បត្តិនៃភាគីផ្ទុយនៃប្រលេឡូក្រាមដែលបានបង្ហាញនៅក្នុងទ្រឹស្តីបទនៅលើ Δ ABC = Δ CDA នៅលើភាគីទាំងបី (AB = CD, BC = DA ពីការបង្ហាញ, AC គឺទូទៅ) ។ វាធ្វើតាមពីសមភាពនៃត្រីកោណដែល ∠ABC = ∠CDA ។
វាត្រូវបានបញ្ជាក់ផងដែរថា ∠ DAB = ∠ BCD ដែលតាមពី ∠ ABD = ∠ CDB ។ ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

ទ្រព្យសម្បត្តិនៃអង្កត់ទ្រូងនៃប្រលេឡូក្រាម

អង្កត់ទ្រូង​នៃ​ប្រលេឡូក្រាម​ប្រសព្វ​គ្នា ហើយ​ចំណុច​ប្រសព្វ​ត្រូវ​បាន​កាត់​ជា​ពីរ។

ភស្តុតាង។

អនុញ្ញាតឱ្យ ABCD ជាប្រលេឡូក្រាមដែលបានផ្តល់ឱ្យ។ តោះគូរអង្កត់ទ្រូង AC ។ យើងសម្គាល់ចំណុចកណ្តាល O នៅលើវា។ នៅលើផ្នែកបន្តនៃផ្នែក DO យើងដាក់ផ្នែក OB 1 ស្មើនឹង DO ។
តាមទ្រឹស្តីបទមុន AB 1 CD គឺជាប្រលេឡូក្រាម។ ដូច្នេះ បន្ទាត់ AB 1 គឺស្របទៅនឹង DC ។ ប៉ុន្តែតាមរយៈចំណុច A មានតែបន្ទាត់មួយប៉ុណ្ណោះដែលអាចគូរស្របទៅនឹង DC ។ ដូច្នេះ បន្ទាត់ AB 1 ត្រូវគ្នានឹងបន្ទាត់ AB ។
វា​ត្រូវ​បាន​បញ្ជាក់​ផង​ដែរ​ថា BC 1 ត្រូវ​គ្នា​នឹង BC ។ ដូច្នេះចំណុច C ស្របគ្នានឹង C 1 ។ ប្រលេឡូក្រាម ABCD ស្របគ្នានឹងប្រលេឡូក្រាម AB 1 ស៊ីឌី។ ដូច្នេះ​អង្កត់ទ្រូង​នៃ​ប្រលេឡូក្រាម​ប្រសព្វ​គ្នា ហើយ​ចំណុច​ប្រសព្វ​ត្រូវ​បាន​បំបែក​ជា​ពីរ។ ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

នៅក្នុងសៀវភៅសិក្សាសម្រាប់សាលាធម្មតា (ឧទាហរណ៍នៅក្នុង Pogorelov) វាត្រូវបានបង្ហាញដូចខាងក្រោម: អង្កត់ទ្រូងបែងចែកប្រលេឡូក្រាមជា 4 ត្រីកោណ។ ពិចារណាមួយគូហើយរកឱ្យឃើញ - ពួកគេគឺស្មើគ្នា: មូលដ្ឋានរបស់ពួកគេគឺភាគីផ្ទុយគ្នាមុំដែលត្រូវគ្នានៅជាប់នឹងវាស្មើនឹងបញ្ឈរជាមួយបន្ទាត់ប៉ារ៉ាឡែល។ នោះគឺផ្នែកនៃអង្កត់ទ្រូងគឺស្មើគ្នា។ អ្វីគ្រប់យ៉ាង។

ទាំងអស់នោះឬ?
វាត្រូវបានបញ្ជាក់ខាងលើថាចំនុចប្រសព្វកាត់អង្កត់ទ្រូង - ប្រសិនបើវាមាន។ ការ​លើក​ឡើង​ខាង​លើ​មិន​បាន​បញ្ជាក់​ពី​អត្ថិភាព​របស់​វា​តាម​វិធី​ណា​មួយ​ឡើយ។ នោះគឺផ្នែកនៃទ្រឹស្តីបទ "អង្កត់ទ្រូងប៉ារ៉ាឡែលប្រសព្វ" នៅតែមិនអាចបញ្ជាក់បាន។

វាគួរឱ្យអស់សំណើចណាស់ដែលផ្នែកនេះពិបាកបញ្ជាក់។ ដោយវិធីនេះ នេះមកពីលទ្ធផលទូទៅជាងនេះ៖ សម្រាប់រាងបួនជ្រុងប៉ោងណាមួយ អង្កត់ទ្រូងនឹងប្រសព្វគ្នា សម្រាប់ការដែលមិនប៉ោងណាមួយពួកគេនឹងមិនធ្វើទេ។

នៅលើសមភាពនៃត្រីកោណតាមបណ្តោយចំហៀងនិងមុំពីរនៅជាប់នឹងវា (សញ្ញាទីពីរនៃសមភាពនៃត្រីកោណ) និងផ្សេងទៀត។

ទ្រឹស្តីបទស្តីពីសមភាពនៃត្រីកោណពីរនៅសងខាង និងមុំពីរនៅជាប់នឹងវា លោក Thales បានរកឃើញការអនុវត្តជាក់ស្តែងដ៏សំខាន់មួយ។ ឧបករណ៍កំណត់ចម្ងាយត្រូវបានសាងសង់នៅកំពង់ផែ Miletus ដែលកំណត់ចម្ងាយទៅកប៉ាល់នៅសមុទ្រ។ វា​មាន​ចង្កឹះ​បី A, B និង C (AB = BC) និង​បន្ទាត់​ត្រង់​សម្គាល់ SK ដែល​កាត់​កែង​ទៅ CA ។ នៅពេលដែលកប៉ាល់បានបង្ហាញខ្លួននៅលើបន្ទាត់ត្រង់ SC ចំនុច D ត្រូវបានគេរកឃើញថាចំនុច D, .B និង E ស្ថិតនៅលើបន្ទាត់ត្រង់ដូចគ្នា។ ដូចដែលបានបញ្ជាក់យ៉ាងច្បាស់ពីគំនូរ ចម្ងាយស៊ីឌីនៅលើដីគឺជាចម្ងាយដែលចង់បានទៅកាន់កប៉ាល់។

សំណួរ

1. តើអង្កត់ទ្រូងនៃការ៉េត្រូវបានបំបែកដោយចំនុចប្រសព្វឬ?
   
2. តើអង្កត់ទ្រូងនៃប្រលេឡូក្រាមស្មើគ្នាទេ?
3. តើមុំទល់មុខនៃប្រលេឡូក្រាមស្មើគ្នាទេ?
4. តើអ្វីជានិយមន័យនៃប្រលេឡូក្រាម?
5. តើ​មាន​លក្ខណៈ​ពិសេស​ប៉ុន្មាន​នៃ​ប្រលេឡូក្រាម?
   
6. តើ rhombus អាចជាប៉ារ៉ាឡែលបានទេ?
   

បញ្ជីប្រភពដែលបានប្រើ

1. Kuznetsov A.V. គ្រូបង្រៀនគណិតវិទ្យា (ថ្នាក់ទី ៥-៩) ទីក្រុងគៀវ
2. “ការប្រឡងបង្រួបបង្រួមរដ្ឋ 2006. គណិតវិទ្យា។ សម្ភារៈអប់រំ និងបណ្តុះបណ្តាលសម្រាប់ការរៀបចំសិស្ស / Rosobrnadzor, ISOP - M.: Intellect-Center, 2006 "
3. Mazur K. I. "ការដោះស្រាយបញ្ហាប្រកួតប្រជែងសំខាន់ៗក្នុងគណិតវិទ្យានៃការប្រមូលដែលបានកែសម្រួលដោយ M. I. Scanavi"
4. L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina "ធរណីមាត្រ, 7 - 9: សៀវភៅសិក្សាសម្រាប់ស្ថាប័នអប់រំ"

ធ្វើការលើមេរៀន

Kuznetsov A.V.

ប៉ូតាណាក់ S.A.

Evgeny Petrov

អ្នកអាចលើកជាសំណួរអំពីការអប់រំទំនើប បញ្ចេញគំនិត ឬដោះស្រាយបញ្ហាបន្ទាន់នៅ វេទិកាអប់រំជាកន្លែងដែលក្រុមប្រឹក្សាអប់រំនៃការគិត និងសកម្មភាពថ្មីៗជួបជាអន្តរជាតិ។ បានបង្កើត ប្លុកអ្នកនឹងមិនត្រឹមតែធ្វើឱ្យប្រសើរឡើងនូវឋានៈរបស់អ្នកជាគ្រូបង្រៀនដែលមានជំនាញប៉ុណ្ណោះទេប៉ុន្តែថែមទាំងរួមចំណែកយ៉ាងសំខាន់ក្នុងការអភិវឌ្ឍន៍សាលារៀននាពេលអនាគតផងដែរ។ សមាគមអ្នកដឹកនាំអប់រំបើកទ្វារទៅកាន់អ្នកឯកទេសលំដាប់កំពូល ហើយអញ្ជើញអ្នកឱ្យសហការក្នុងទិសដៅនៃការបង្កើតសាលាល្អបំផុតនៅក្នុងពិភពលោក។

មុខវិជ្ជា > គណិតវិទ្យា > គណិតវិទ្យាថ្នាក់ទី៨

ប៉ារ៉ាឡែល​គឺ​ជា​ចតុកោណ​ដែល​ភាគី​ទល់​មុខ​ស្រប​គ្នា ឧ. ដេកលើបន្ទាត់ប៉ារ៉ាឡែល

លក្ខណៈ​នៃ​ការ​ប៉ារ៉ាឡែល​:
ទ្រឹស្តីបទ ២២. ផ្នែកផ្ទុយនៃប្រលេឡូក្រាមគឺស្មើគ្នា។
ភស្តុតាង។ គូរអង្កត់ទ្រូង AC ក្នុងប្រលេឡូក្រាម ABCD ។ ត្រីកោណ ACD និង ACB គឺស្របគ្នាដែលមានជ្រុង AC ធម្មតា និងពីរគូនៃមុំស្មើគ្នា។ នៅជាប់នឹងវា៖ ∠ CAB = ∠ ACD, ∠ ASV = ∠ DAC (ជាមុំឆ្លងកាត់ជាមួយបន្ទាត់ប៉ារ៉ាឡែល AD និង BC) ។ ដូច្នេះ AB=CD និង BC=AD ជាជ្រុងដែលត្រូវគ្នានៃត្រីកោណស្មើគ្នា។ល។ សមភាពនៃត្រីកោណទាំងនេះក៏បង្កប់ន័យសមភាពនៃមុំដែលត្រូវគ្នានៃត្រីកោណផងដែរ៖
ទ្រឹស្តីបទ ២៣. មុំទល់មុខនៃប្រលេឡូក្រាមគឺ៖ ∠ A = ∠ C និង ∠ B = ∠ D ។
សមភាពនៃគូទីមួយបានមកពីសមភាពនៃត្រីកោណ ABD និង CBD ហើយទីពីរ - ABC និង ACD ។
ទ្រឹស្តីបទ ២៤. ជ្រុងជិតខាងនៃប្រលេឡូក្រាម i.e. មុំនៅជាប់នឹងម្ខាងបន្ថែមរហូតដល់ 180 ដឺក្រេ។
នេះគឺដោយសារតែពួកវាជាផ្នែកខាងក្នុងជ្រុងម្ខាង។
ទ្រឹស្តីបទ ២៥. អង្កត់ទ្រូងនៃប្រលេឡូក្រាមបត់គ្នាទៅវិញទៅមកនៅចំណុចប្រសព្វរបស់វា។
ភស្តុតាង។ ពិចារណាត្រីកោណ BOC និង AOD ។ យោងតាមទ្រព្យសម្បត្តិទីមួយ AD=BC ∠ ОАD=∠ OSV និង ∠ ОDA=∠ ОВС ដែលស្ថិតនៅលើបន្ទាត់ប៉ារ៉ាឡែល AD និង BC ។ ដូច្នេះ ត្រីកោណ BOC និង AOD គឺស្មើគ្នានៅចំហៀង និងមុំនៅជាប់នឹងវា។ ដូច្នេះ BO = OD និង AO = OC ជាជ្រុងដែលត្រូវគ្នានៃត្រីកោណស្មើគ្នា។ល។

លក្ខណៈប៉ារ៉ាឡែល
ទ្រឹស្តីបទ ២៦. ប្រសិនបើជ្រុងម្ខាងនៃចតុកោណកែងស្មើគ្នាជាគូ នោះវាជាប្រលេឡូក្រាម។
ភស្តុតាង។ អនុញ្ញាតឱ្យ ABCD ចតុកោណមានជ្រុង AD និង BC, AB និង CD រៀងគ្នាស្មើគ្នា (រូបភាព 2) ។ តោះគូរអង្កត់ទ្រូង AC ។ ត្រីកោណ ABC និង ACD មានបីជ្រុងស្មើគ្នា។ បន្ទាប់មកមុំ BAC និង DCA គឺស្មើគ្នា ហើយដូច្នេះ AB គឺស្របទៅនឹង CD ។ ភាពស្របគ្នានៃជ្រុង BC និង AD កើតឡើងពីសមភាពនៃមុំ CAD និង DIA ។
ទ្រឹស្តីបទ ២៧. ប្រសិនបើមុំទល់មុខនៃចតុកោណកែងគឺស្មើគ្នាជាគូ នោះវាគឺជាប្រលេឡូក្រាម។
ឲ្យ ∠ A=∠ C និង ∠ B=∠ D ។ ∠ A+∠ B+∠ C+∠ D=360 o បន្ទាប់មក ∠ A+∠ B=180 o ហើយជ្រុង AD និង BC គឺស្របគ្នា (ផ្អែកលើបន្ទាត់ប៉ារ៉ាឡែល)។ យើងក៏បង្ហាញភាពស្របគ្នានៃជ្រុង AB និង CD ហើយសន្និដ្ឋានថា ABCD គឺជាប៉ារ៉ាឡែលតាមនិយមន័យ។
ទ្រឹស្តីបទ ២៨. ប្រសិនបើជ្រុងជាប់គ្នានៃចតុកោណកែង i.e. មុំដែលនៅជាប់នឹងម្ខាងបន្ថែមរហូតដល់ 180 ដឺក្រេ បន្ទាប់មកវាគឺជាប្រលេឡូក្រាម។
ប្រសិនបើផ្នែកខាងក្នុងមុំម្ខាងបន្ថែមដល់ 180 ដឺក្រេ នោះបន្ទាត់គឺស្របគ្នា។ នេះមានន័យថា AB គឺជាគូនៃ CD ហើយ BC គឺជាគូនៃ AD ។ ចតុកោណ​ប្រែ​ជា​ប្រលេឡូក្រាម​តាម​និយមន័យ។
ទ្រឹស្តីបទ ២៩. ប្រសិនបើ​អង្កត់ទ្រូង​នៃ​ចតុកោណកែង​ត្រូវ​បាន​បែង​ចែក​ទៅ​វិញ​ទៅ​មក​នៅ​ចំណុច​ប្រសព្វ​ជា​ពាក់កណ្តាល នោះ​ចតុកោណ​គឺ​ជា​ប្រលេឡូក្រាម។
ភស្តុតាង។ ប្រសិនបើ AO = OC, BO = OD នោះត្រីកោណ AOD និង BOC គឺស្មើគ្នា ដោយសារមានមុំស្មើគ្នា (បញ្ឈរ) នៅចំនុចកំពូល O ដែលរុំព័ទ្ធរវាងគូនៃភាគីស្មើគ្នា។ ពីសមភាពនៃត្រីកោណ យើងសន្និដ្ឋានថា AD និង BC គឺស្មើគ្នា។ ជ្រុង AB និង CD ក៏ស្មើគ្នាដែរ ហើយ quadrangle ប្រែជា parallelogram យោងតាមលក្ខណៈពិសេស 1 ។
ទ្រឹស្តីបទ ៣០. ប្រសិនបើ quadrilateral មានគូស្មើគ្នា ភាគីប៉ារ៉ាឡែល នោះវាគឺជាប្រលេឡូក្រាម។
អនុញ្ញាតឱ្យភាគី AB និង CD ស្របគ្នា និងស្មើគ្នានៅក្នុង ABCD បួនជ្រុង។ គូរអង្កត់ទ្រូង AC និង BD ។ ពីភាពស្របគ្នានៃបន្ទាត់ទាំងនេះធ្វើតាមសមភាពនៃមុំឆ្លងកាត់ ABO = CDO និង BAO = OCD ។ ត្រីកោណ ABO និង CDO គឺស្មើគ្នានៅមុំចំហៀង និងនៅជាប់គ្នា។ ដូច្នេះ AO=OC, BO=OD, i.e. អង្កត់ទ្រូង​នៃ​ចំណុច​ប្រសព្វ​ត្រូវ​បាន​បែង​ចែក​ជា​ពាក់​ក​ណ្តា​ល ហើយ​ចតុកោណ​ប្រែ​ទៅ​ជា​ប្រលេឡូក្រាម​តាម​លក្ខណៈ​ពិសេស​ទី ៤។

នៅក្នុងធរណីមាត្រ ករណីពិសេសនៃប្រលេឡូក្រាមត្រូវបានពិចារណា។

គំនិតនៃប្រលេឡូក្រាម

និយមន័យ ១

ប៉ារ៉ាឡែលគឺជាចតុកោណកែងដែលភាគីទល់មុខស្របគ្នា (រូបភាពទី 1)។

រូបភាពទី 1 ។

ប្រលេឡូក្រាមមានលក្ខណៈសម្បត្តិសំខាន់ពីរ។ ចូរយើងពិចារណាពួកគេដោយគ្មានភស្តុតាង។

អចលនទ្រព្យ ១៖ ជ្រុងទល់មុខ និងមុំនៃប្រលេឡូក្រាមគឺស្មើគ្នា រៀងគ្នាទៅគ្នាទៅវិញទៅមក។

អចលនទ្រព្យ ២៖ អង្កត់ទ្រូង​ដែល​គូស​ក្នុង​ប្រលេឡូក្រាម​ត្រូវ​បាន​បំបែក​ដោយ​ចំណុច​ប្រសព្វ​របស់​វា។

លក្ខណៈ Parallelogram

ពិចារណាលក្ខណៈបីនៃប្រលេឡូក្រាម ហើយបង្ហាញវាក្នុងទម្រង់នៃទ្រឹស្តីបទ។

ទ្រឹស្តីបទ ១

ប្រសិនបើជ្រុងទាំងពីរនៃចតុកោណកែងស្មើគ្នាទៅវិញទៅមក ហើយស្របគ្នានោះ ចតុកោណនេះនឹងជាប្រលេឡូក្រាម។

ភស្តុតាង។

អនុញ្ញាតឱ្យយើងទទួលបាន $ABCD$ បួនជ្រុង។ ដែលក្នុងនោះ $AB||CD$ និង $AB=CD$ ចូរយើងគូរអង្កត់ទ្រូង $AC$ នៅក្នុងវា (រូបភាពទី 2)។

រូបភាពទី 2 ។

ពិចារណាបន្ទាត់ប៉ារ៉ាឡែល $AB$ និង $CD$ និងលេខរៀង $AC$ របស់ពួកគេ។ បន្ទាប់មក

\[\angle CAB=\angle DCA\]

ដូចជាជ្រុងឆ្លងកាត់។

យោងតាមលក្ខណៈវិនិច្ឆ័យ $I$ សម្រាប់សមភាពនៃត្រីកោណ។

ដោយសារ $AC$ គឺជាផ្នែកធម្មតារបស់ពួកគេ ហើយ $AB=CD$ តាមការសន្មត។ មធ្យោបាយ

\\[\angle DAC=\angle ACB\]

ពិចារណាបន្ទាត់ $AD$ និង $CB$ និងផ្នែក $AC$ របស់ពួកគេ; ដោយសមភាពចុងក្រោយនៃមុំឆ្លងកាត់ យើងទទួលបាន $AD||CB$ នោះ។) ដូច្នេះតាមនិយមន័យនៃ $1$ បួនជ្រុងនេះ គឺជាប្រលេឡូក្រាម។

ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

ទ្រឹស្តីបទ ២

ប្រសិនបើជ្រុងម្ខាងនៃចតុកោណកែងស្មើគ្នា នោះវាជាប្រលេឡូក្រាម។

ភស្តុតាង។

អនុញ្ញាតឱ្យយើងទទួលបាន $ABCD$ បួនជ្រុង។ ក្នុងនោះ $AD=BC$ និង $AB=CD$។ ចូរយើងគូរអង្កត់ទ្រូង $AC$ នៅក្នុងវា (រូបភាពទី 3)។

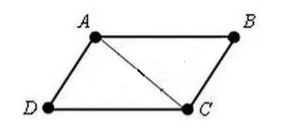
រូបភាពទី 3

ដោយហេតុថា $AD=BC$, $AB=CD$, និង $AC$ គឺជាផ្នែកទូទៅ បន្ទាប់មកដោយការសាកល្បងសមភាពត្រីកោណ $III$

\\[\ត្រីកោណ DAC=\ត្រីកោណ ACB\]

\\[\angle DAC=\angle ACB\]

ពិចារណាបន្ទាត់ $AD$ និង $CB$ និង secant $AC$ របស់ពួកគេ ដោយសមភាពចុងក្រោយនៃមុំនិយាយកុហក យើងទទួលបាន $AD||CB$ នោះ។ ដូច្នេះ តាមនិយមន័យនៃ $1$ បួនជ្រុងនេះគឺជាប្រលេឡូក្រាម។

\\[\angle DCA=\angle CAB\]

ពិចារណាបន្ទាត់ $AB$ និង $CD$ និង secant $AC$ របស់ពួកគេ ដោយសមភាពចុងក្រោយនៃមុំនិយាយកុហក យើងទទួលបាន $AB||CD$ នោះ។ ដូច្នេះ​តាម​និយមន័យ​ទី 1 ចតុកោណ​នេះ​គឺ​ជា​ប្រលេឡូក្រាម។

ទ្រឹស្តីបទត្រូវបានបញ្ជាក់។

ទ្រឹស្តីបទ ៣

ប្រសិនបើអង្កត់ទ្រូងដែលគូសក្នុងចតុកោណត្រូវបានបែងចែកទៅជាពីរផ្នែកស្មើគ្នាដោយចំនុចប្រសព្វរបស់វា នោះចតុកោណកែងនេះគឺជាប្រលេឡូក្រាម។

ភស្តុតាង។

អនុញ្ញាតឱ្យយើងទទួលបាន $ABCD$ បួនជ្រុង។ ចូរយើងគូរអង្កត់ទ្រូង $AC$ និង $BD$ នៅក្នុងវា។ អនុញ្ញាតឱ្យពួកគេប្រសព្វគ្នានៅចំណុច $O$ (រូបភាពទី 4) ។

រូបភាពទី 4

ដោយសារតាមលក្ខខណ្ឌ $BO=OD,\AO=OC$, និងមុំ $\angle COB=\angle DOA$ គឺបញ្ឈរ បន្ទាប់មកដោយការសាកល្បងសមភាពត្រីកោណ $I$,

\\[\ត្រីកោណ BOC=\ត្រីកោណ AOD\]

\\[\angle DBC=\angle BDA\]

ពិចារណាបន្ទាត់ $BC$ និង $AD$ និងលេខរៀង $BD$ របស់ពួកគេ ដោយសមភាពចុងក្រោយនៃមុំនិយាយកុហក យើងទទួលបាន $BC||AD$ នោះ។ ផងដែរ $BC=AD$។ ដូច្នេះ តាមទ្រឹស្តីបទ $1$ បួនជ្រុងនេះគឺជាប្រលេឡូក្រាម។