Para derivar a equação de Bernoulli, usamos um teorema bem conhecido da mecânica sobre a mudança energia cinética. Lembre-se de que este teorema é o seguinte: a variação na energia cinética 2 do corpo em consideração em algum de seu deslocamento é igual à soma do trabalho de todas as forças (externas e internas) aplicadas a dado corpo, no mesmo deslocamento.

Vamos pegar um fluxo elementar de um riacho (Fig. 3-20). Selecione as seções 1-1 e 2-2 algum compartimento de gotejamento AB. Denote por z 1 ez 2 os excessos das seções 1 -1 E 2 -2 acima do plano de comparação Oh, through - áreas de seções vivas do riacho nas seções 1-1i 2 -2.

Suponhamos que durante o tempo AB os jatos se moverão para a posição A"B" neste caso, a seção 1-1 do fluxo se moverá para uma distância e a seção 2 -2 gotas - na distância . notar que

Onde e 1 E E 2 - velocidades nas seções 1-1i 2 -2.

Argumentando, como em § 3-9, podemos mostrar que os volumes dos compartimentos elementares do gotejamento AA" E bb" são iguais, ou seja

volume (AA")= volume (BB") =(designação),

onde é a taxa de fluxo de fluido para o jato.

Vamos denotar a massa de um volume elementar por:

onde é a densidade do líquido.

Vamos agora encontrar a variação na energia cinética do compartimento AB ao movê-lo para a posição A"B" e o trabalho das forças aplicadas a este compartimento no deslocamento especificado.

1°. Mudança na energia cinética do compartimento AB ao movê-lo para a posição A"B". Vamos denotar a mudança mencionada na energia cinética (CE) através de b (CE). Então você pode escrever (veja a Figura 3-20):

(KE) \u003d KE (A "B") - KE (AB) \u003d KE (A "B -f BB") -

KE (AA "+ A" B) \u003d KE (BB ") - KE (AA"),

ou, dado (3-55),

Arroz. 3-20. Para a derivação da equação (3-60)

2°. O trabalho das forças ao mover o compartimento AB em posição A"B". Com o deslocamento indicado, obtemos o trabalho das seguintes forças.

1. O trabalho da gravidade. Como se vê, o efeito da ação da gravidade manifestou-se, por assim dizer, no fato de o compartimento AA" movido para a posição BB" (uma compartimento A "B ficou no lugar). Usando tal esquema condicional, o trabalho da gravidade (PCT) chegamos na forma

A justiça (3-57) pode ser justificada com mais rigor. Nós quebramos o compartimento A "B em compartimentos elementares de volume . Então o trabalho de gravidade desejado pode ser representado como:

Onde z", z", z",. . ., z(n) - elevações acima do plano 00 seções de limite que separam volumes elementares .

2. O trabalho das forças de pressão hidrodinâmica,
atuando em seções finais 1 -1 E 2 -2 compartimento
AB(do lado do líquido que o envolve). Este trabalho

onde e são as pressões hidrodinâmicas, respectivamente, nas seções 1 -1 e 2-2.

3. Trabalho forças externas a pressão do fluido circundante sobre o osso superfície lateral compartimento AB. Este trabalho é igual a zero, pois as forças são direcionadas perpendicularmente aos deslocamentos das partículas líquidas que se movem ao longo da superfície lateral do compartimento AB.

4. Trabalho forças internas pressão ( forças normais interações de partículas fluidas individuais que compõem o volume AB).

Essas forças são pareadas (com direções opostas) com os mesmos deslocamentos. A soma de seus trabalhos é zero.

5. O trabalho das forças de atrito externo e interno é igual a zero (forças de atrito no fluido ideal ausente).

3°. Conclusão final. Usando o teorema da variação de energia cinética, podemos escrever:

Vamos dividir esta expressão em , ou seja, vamos nos referir ao peso unitário do volume de líquido que passa no tempo b / através seção clara goteja. Neste caso, representamos a equação resultante na forma

Desde as seções 1-1 E 2 -2 foram planejados arbitrariamente, então (3-59) também pode ser reescrito na forma:

A equação (3-59) ou (3-60) é chamada de equação de Bernoulli. Foi obtido por Daniil Bernoulli em 1738. Esta equação aplica-se apenas a uma corrente elementar de um líquido ideal.

Atentemos também para o seguinte:

1) a equação de Bernoulli relaciona as quantidades z, p, e;

2) como pode ser visto em (3-60), no caso de um fluido ideal, a soma de três termos z,, é uma constante ao longo do fluxo considerado;

3) se o valor constante indicado para um determinado gotejamento for igual a Alt então, para o gotejamento vizinho, a soma dos três termos acima é igual a A 2 , e em " caso Geral A 1 ≠ A 2 ;

4) saber por um dado gotejamento valor constante A, e também sabendo para uma dada seção transversal de um jato de três quantidades ( z, eu, p) quaisquer duas quantidades, podemos, usando a equação de Bernoulli, encontrar a terceira quantidade desconhecida para a seção considerada do jato.

A equação (3-60) também pode ser obtida integrando as equações diferenciais de Euler (ver § 3-3) para qualquer sistema de forças de corpo atuando em um fluido e tendo um potencial (ver § 9-2). A equação (3-60) refere-se a uma linha de corrente específica (mais precisamente: a um fluxo elementar ao longo de uma linha de corrente específica). Essa equação costuma ser chamada de integral de Bernoulli.

Mais consideração detalhada esse assunto mostra que a equação de Bernoulli (integral de Bernoulli) acaba sendo válida tanto para o movimento permanente irrotacional (potencial) quanto para o movimento permanente de vórtice de um fluido ideal, desde que, no entanto, as forças de corpo que atuam no fluido tenham um potencial ( em particular, a gravidade, que tínhamos em mente acima). Ao considerar o movimento de vórtice constante de um fluido ideal a uma velocidade e incluído na equação de Bernoulli, segue entender (então mesmo como no caso de movimento irrotacional) a velocidade relacionada com um campo vetorial real refletindo o movimento do fluido em consideração (a decomposição do movimento em seus três tipos, explicada no § 3-4, não deve ser abordada aqui).

Também pode ser mostrado que no caso de: a) sem movimento de vórtice (potencial) de um fluido ideal e b) forças de corpo atuando no fluido, tendo um potencial, o valor A, que foi discutido acima, é o mesmo para todas as linhas de corrente que formam o fluxo: A 1 \u003d A 2 \u003d A 3 \u003d --- Nesse caso, a equação (3-60) passa a ser válida para toda a área ocupada pelo líquido, e não apenas para certas linhas de corrente.

Acima foram obtidas as equações diferenciais do movimento de um fluido ideal e a equação da continuidade do movimento, que formam um sistema fechado de equações. Para resolver problemas específicos de engenharia, é necessário saber encontrar as integrais dessas equações.

Antes de proceder à integração das equações de movimento de um fluido ideal, aceitamos as seguintes condições adicionais:

Projeções da aceleração da força corporal (em este caso gravidade) assumirá os seguintes valores quando selecionado; direção dos eixos coordenados:

X=0; Y=0; Z=-g.

Após a transformação obtemos:

Dividindo por g, obtemos:

Integrando esta equação diferencial em diferenciais totais, chegamos ao seguinte resultado:

Esta equação é chamada de equação D. Bernoulli, é válida para movimento estacionário de um fluido ideal.

Para duas seções arbitrárias de um stream elementar:

Esta é a equação de D. Bernoulli.

Significado geométrico e energéticoequações

D. Bernoulli

Todos os termos incluídos na equação de D. Bernoulli têm uma dimensão linear, por isso são geralmente chamados de alturas. Assim, os seguintes nomes para esses membros são geralmente aceitos:

z - altura geométrica ou geodésica;

Altura piezométrica ou altura de pressão;

- cabeçote dinâmico ou de velocidade;

É fácil ver o próximo significado geométrico A equação de D. Bernoulli, que é aquela no movimento estacionário de um fluido ideal, a soma de trêsalturas (geométricas, piezométricas e de velocidade) não sãovaria ao longo de um determinado fluxo elementar. Esta situação é claramente ilustrada na Fig. 1.

É possível interpretar o significado dos termos individuais da equação

Bernoulli é diferente. Foi mostrado acima que a soma

Representa a energia específica do fluido. Dessa forma, podemos supor que:

z - é a energia específica da posição;

energia de pressão;

Existe energia cinética específica.

O significado energético da equação de Bernoulli é que no movimento estacionário de um fluido ideala soma das energias específicas de posição, pressão e cinética não varia ao longo de um determinado jato elementar.

Arroz. 1

Energia específica total (ou seja, potencial + cinética) é chamada carga hidrodinâmica e é denotada . Assim, a equação de Bernoulli mostra que, sob o movimento estacionário de um fluido ideal para uma determinada corrente, a carga hidrodinâmica é um valor constante. No gráfico, a linha da cabeça hidrodinâmica é representada como uma linha horizontal.

A equação de D. Bernoulli para um fluxo elementar líquido real. Piezométrico e hidráulicoencostas.

Quando um fluido real se move entre correntes adjacentes, surgem forças de atrito, para superar as quais uma parte da energia do fluido é gasta. Portanto, a energia específica do líquido na seção transversal do jato elementar 2 -2 será menor que a energia específica do líquido na seção transversal 1-1 por alguma quantia , que é chamada de altura perdida ou energia específica perdida gasta para vencer a resistência hidráulica. Analiticamente, esta situação pode ser escrita da seguinte forma:

Por isso, no movimento estacionário de um líquido realsoma óssea de quatro alturas (geométrica, piezométricacéu, alta velocidade e perdido) ou, o que dá no mesmo, a somaquatro energias específicas (posição, pressão, cinética e perdida) não mudam ao longo do fluxo elementar dado.

É fácil representar graficamente a equação de Bernoulli para o caso em consideração. Para fazer isso, depois de escolher um plano de comparação horizontal arbitrário, coloque nele em cada seção a altura ; ; ; E . As extremidades dos segmentos z, conectados por uma curva suave, mostrarão a posição do eixo do gotejamento. Conectando as extremidades dos segmentos de uma curva suave, obtemos a chamada linha piezométrica. Colocando em cada seção da linha piezométrica segmentos iguais às pressões de velocidade e conectando suas extremidades com uma curva suave, obtemos uma linha de carga hidrodinâmica ou, como é freqüentemente chamada, uma linha hidráulica (Fig. 2). segmentos, igual às distâncias verticalmente da linha hidráulica a um plano horizontal passando acima do plano de comparação a uma altura igual à energia específica inicial, representam as perdas de energia por resistência hidráulica na seção inicial até a seção considerada.

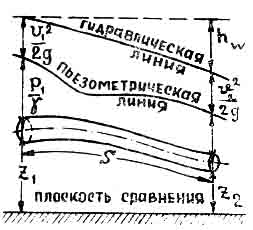
Arroz. 2

Chamemos a queda da linha hidráulica por unidade de comprimento da corrente elementar inclinação hidráulicaEU:

A inclinação hidráulica (Fig. 3) é sempre um valor positivo, pois a energia específica total da parte móvel do líquido diminui gradativamente à medida que se move ao longo do fluxo elementar, sendo gasta na superação das forças de atrito, transformando-se em energia térmica e dispersão.

Arroz. 3

O conceito de movimento fluido de mudança suave (mudança lenta)

No caso geral, com movimento estacionário, o escoamento do fluido pode ser representado como um conjunto de jatos elementares tendo vários significadosângulos de divergência e diferentes raios de curvatura. caso especial dvifluxo em que sofre uma ligeira deformaçãoíon, de modo que os filamentos elementares permaneçam paralelosou quase paralelas entre si (), e seus raios de curvatura são muito grandes valores (), chamado movimento de mudança suave ou mudança lenta.

EM o plano da seção livre do fluxo com uma mudança suavepressões hidrodinâmicas são distribuídas de acordo com as leis da hidrostática, o que significa que em uma determinada seção viva, a energia potencial específica de qualquer partícula é um valor constante:

Equação de D. Bernoulli para o fluxo de um fluido real.

Condições de aplicabilidade da equação D. Bernoulli.

Vamos estender a equação de Bernoulli para o fluxo permanente de um fluido real. Para fazer isso, escolhemos uma seção livre em uma seção fracamente deformada do fluxo, perto da qual o movimento pode ser considerado uma mudança suave.

Através desta seção, cada jato elementar no tempo dt energia é introduzida, o que, de acordo com o acima, acaba por ser igual a:

Tirando entre parênteses o peso do líquido que passa corte transversal um gotejamento por; vez dt, igual , reescreva esta expressão em seguinte formulário:

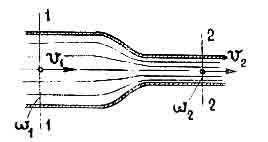
Arroz. 4

Vamos encontrar a energia total transportada pelo fluxo de fluido através da seção livre 1 - 1. Para fazer isso, obviamente, é necessário somar a expressão resultante sobre todas as correntes de uma determinada seção transversal livre. Então obtemos:

Então a energia total Acontece que igual à soma duas integrais representando, respectivamente, a energia potencial e cinética do escoamento.

Escrevemos a segunda integral da seguinte forma:

Esta integral representa, como já mencionado, a energia cinética transportada pelo escoamento através da seção 1-1 durante o tempo dt. Para calculá-lo, é necessário saber como as velocidades das partículas do fluido estão distribuídas na seção viva. Se calcularmos a energia cinética do fluxo assumindo que essas velocidades são constantes (ou seja, de acordo com a velocidade média do fluxo em uma determinada seção viva ), então obtemos:

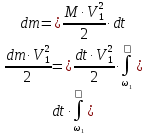
Essa expressão é sempre menor em magnitude do que a energia cinética real calculada a partir das velocidades reais. Vamos denotar a razão dessas duas quantidades:

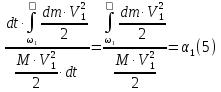
Como na seção de fluxo entre as seções 1-1 e 2-2 parte da energia do fluxo é gasta na superação da resistência hidráulica e é irreversivelmente convertida em energia térmica, . Também é óbvio que . A diferença entre essas energias específicas expressará a perda da energia específica do escoamento no trecho de movimento considerado:

Após integração e substituição, obtemos:

Coeficiente é chamado de coeficiente de cinéticafluxo de energia e é a razão da realenergia cinética do fluxo para a energia cinética, vocênumérico sob a suposição de que as velocidades em todos os pontos da seção livre são iguais à velocidade média do fluxo. é obvio que este coeficiente é sempre maior que um.

A equação resultante é a equação de D. Bernoulli para um escoamento estacionário de um fluido real.

Palestra número 8.

resistência hidráulica.

Classificação da resistência hidráulica e perda de carga.

Quando um fluido real se move, parte da energia do fluxo é gasta na superação de resistências hidráulicas, que são divididas em dois tipos:

1) resistência ao longo do comprimento do fluxo;

2) resistência local.

As resistências ao longo do comprimento do fluxo são resistências causadas por forças de atrito e dependem do comprimento do fluxo.

As resistências locais são aquelas causadas por uma mudança na direção ou magnitude da velocidade em diferentes seções do fluxo. Essas resistências são causadas por torneiras, válvulas de gaveta, válvulas em tubulações, expansão ou contração repentina do fluxo, etc.

Parte da energia do fluxo que é gasta para superar a resistência hidráulica é chamada de perda de carga ou perda de energia.

As perdas de pressão também são divididas em dois tipos:

1) perdas de carga ao longo do escoamento, que são causadas pela resistência hidráulica ao longo do escoamento ( h f);

2) perdas de pressão locais, que são causadas pela resistência hidráulica local ( h eu). Perdas totais cabeça:

h ω = . (1)

A perda de carga depende significativamente do modo de movimento do fluido.

laminar e regime turbulento s movimento fluido.

Existem dois modos de movimento do fluido: laminar e turbulento.

No modo de movimento laminar, as partículas do fluido se movem em jatos separados que não se misturam. Exemplos movimento laminar são: o movimento das águas subterrâneas, o movimento de líquidos com alta viscosidade através de dutos (óleo combustível, óleo, etc.), o movimento do sangue nos vasos sanguíneos.

No modo de movimento turbulento, correntes individuais são misturadas umas com as outras. O movimento turbulento é observado na natureza com muito mais frequência do que o movimento laminar. Um exemplo de movimento turbulento é o movimento da água em rios, canais, canos de água, etc.

A palavra "laminar" vem da palavra latina lamina - placa, tira, camada; A palavra "turbulento" vem da palavra latina turbulentus - errático.

A existência na natureza de dois modos de movimento de fluidos foi apontada pela primeira vez pelo notável russo professor cientista D. I. Mendeleev em 1880 em seu trabalho “Sobre resistência de fluidos e aeronáutica”.

Um estudo experimental dos modos de movimento foi realizado pelo cientista inglês O. Reynolds em 1883.

A experiência começa com uma passagem de tubo D líquidos em baixas velocidades. Ao mesmo tempo, a tinta é fornecida do tanque COM. Nesse caso, obtém-se a seguinte imagem (Fig. 1b): o jato colorido tem a forma de uma linha horizontal reta, enquanto o restante da massa do líquido em movimento permanece incolor. Conseqüentemente, neste caso, as partículas do fluxo colorido não se misturam com o restante do líquido e o modo de movimento do líquido no tubo D laminar.

Com um aumento gradual da velocidade no tubo D chega um momento em que o fluxo colorido desaparece e todo o líquido em movimento torna-se uniformemente colorido. Isso indica que as partículas do líquido no fluxo são misturadas, ou seja, no tubo D ocorre um regime turbulento (Fig. 1c).

Arroz. 1

A velocidade com que um modo de movimento muda para outro é chamada crítico. Existem duas velocidades críticas: a velocidade crítica superior V VC , em que o regime laminar de movimento passa para turbulento e a velocidade crítica mais baixa V nk - durante a transição reversa.

Com base em um estudo experimental dos modos de movimento, O. Reynolds forneceu um critério para estabelecer um ou outro modo de movimento.

O critério para determinar o modo de movimento do fluido é o chamado Número de Reynolds, que é denotado por Ré e é dada pela fórmula:

onde V está velocidade média movimentos de fluxo;

L é o tamanho geométrico característico da seção aberta do fluxo;

é o coeficiente cinemático de viscosidade.

O número de Reynolds correspondente à velocidade crítica superior é chamado de número de Reynolds crítico superior e é denotado por Re vk , neste número de Reynolds, o fluxo laminar torna-se turbulento.

O número de Reynolds correspondente à menor velocidade crítica é chamado de número de Reynolds crítico inferior e é denotado Ré nk ; neste número de Reynolds, o regime turbulento torna-se laminar.

Para o movimento de pressão em tubulações, os seguintes experimentos foram estabelecidos: valores numéricos número de Reynolds crítico:

Ré d (não) = 2000 2320;

Ré d (VC) = 10000 13000.

Um fluido real tem viscosidade e, quando se move, surge a resistência ao movimento. A resistência ao movimento é devido ao aparecimento de forças fricção interna. Quando uma corrente de um líquido real se move, a energia mecânica contida na corrente diminuirá ao longo dela, pois parte dela será gasta na superação da resistência, .

Essa energia é gasta em algum trabalho irreversível, ou seja, ao trabalho das forças de atrito, e se transforma em calor, que é dissipado.

Quanto mais longa a corrente, mais energia será gasta para vencer a resistência ao movimento.

Energia gasta em trabalho das forças de atrito, - perda de energia mecânica fluxos que se transformam em calor. As perdas de energia relacionadas ao peso unitário do líquido quando ele se move ao longo de uma corrente elementar são chamadas de perdas hidráulicas (perdas de energia específica).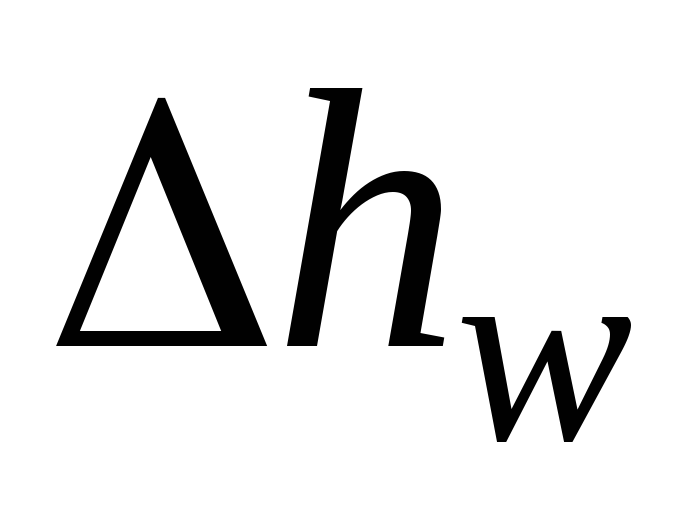

.

Considere um filete de um líquido real com movimento constante (Fig. 3.8).

Arroz. 3.8. Para a equação de Bernoulli para um gotejamento de um líquido real

A energia mecânica específica total de um gotejamento real em suas seções vivas 1-1 e 2-2 será

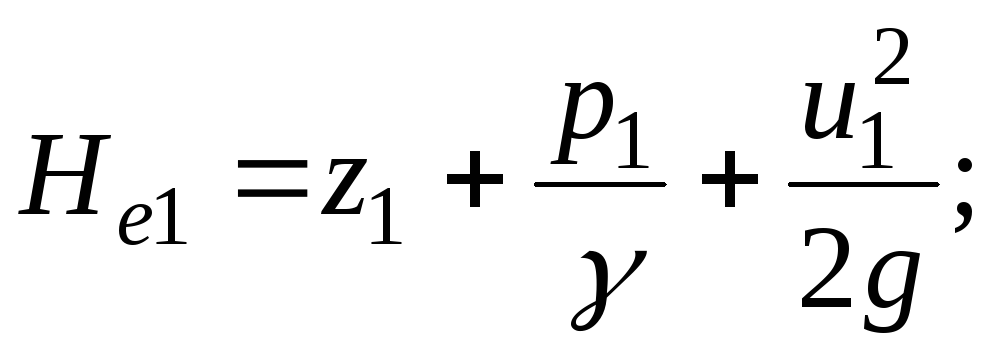
Perdas de energia mecânica específica devido ao atrito na área das seções vivas 1-1 e 2-2

(3.45)

Assim, a equação de Bernoulli para uma corrente elementar de um líquido real no caso de movimento estacionário pode ser representada como

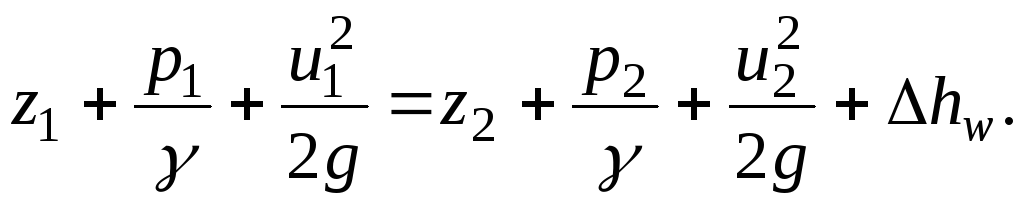(3.47)

Uma característica do movimento do fluido é o conceito de taludes piezométricos e hidráulicos.

Na fig. 3.8 mostra as curvas que caracterizam a equação de Bernoulli. A linha que passa pelos pontos correspondentes ao valor da altura piezométrica nas seções vivas 1-1 e 2-2 é linha piezométrica.

Inclinação piezométricaé a mudança na carga hidrostática do líquido ao longo da corrente, por unidade de comprimento. Na seção do córrego com um comprimento 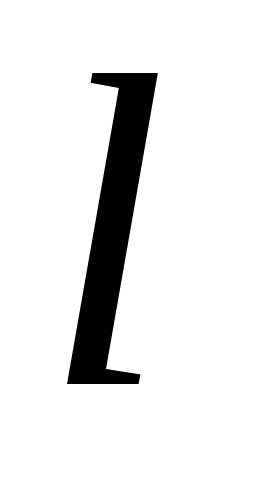entre as seções 1-1 e 2-2 inclinação piezométrica

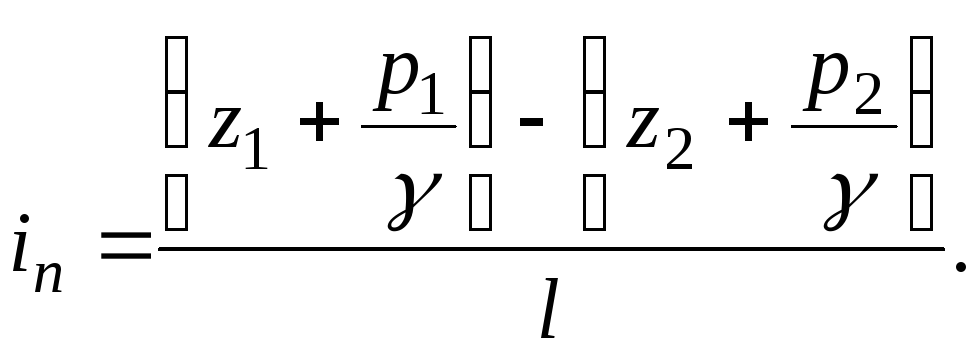(3.48)

Inclinação piezométrica correspondente a um comprimento infinitesimal

(no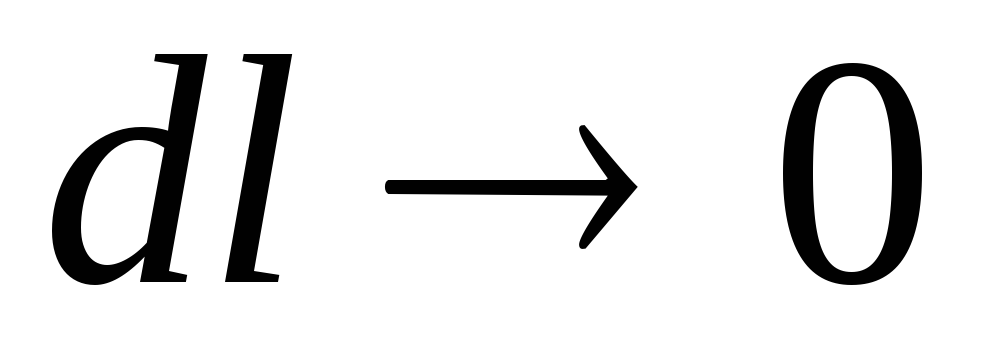

), - inclinação no ponto:

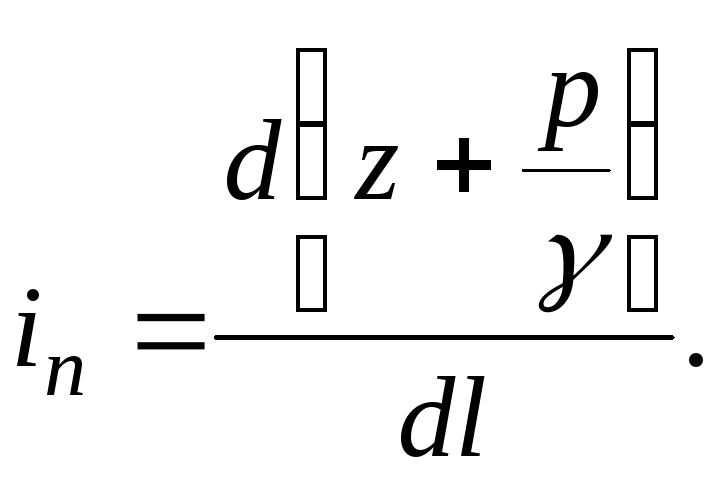(3.49)

A linha que passa pelos pontos de valores das energias mecânicas específicas nas seções vivas do filamento é pressãolinha(linha de pressão total). inclinação hidráulicaé a diminuição da energia mecânica específica total ao longo do filamento por unidade de comprimento:

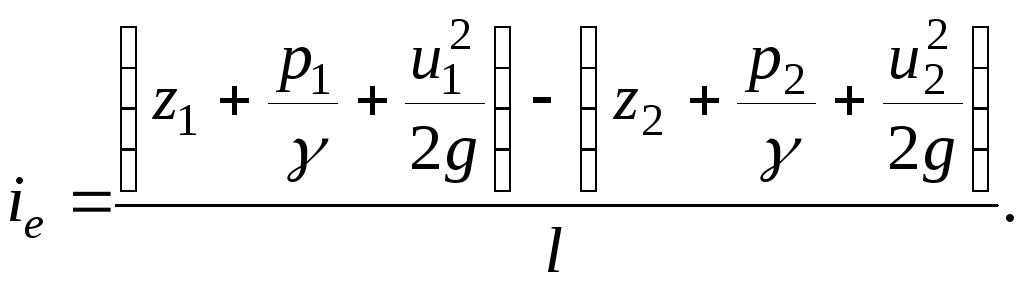(3.50)

Com uma diminuição elementar na energia específica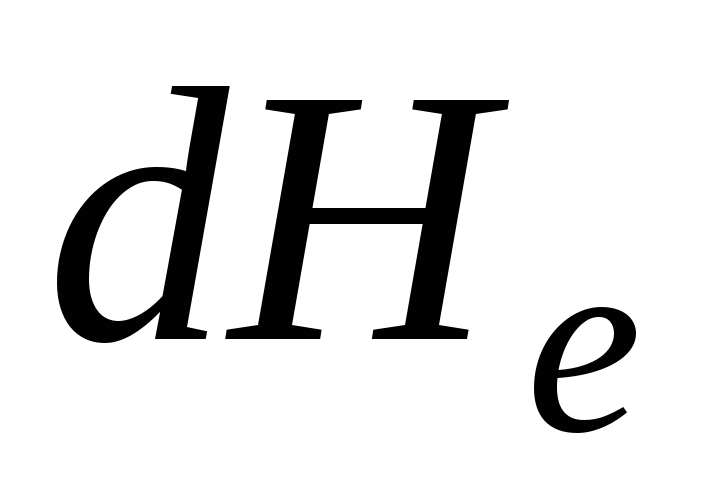

em uma área infinitesimal

inclinação hidráulica

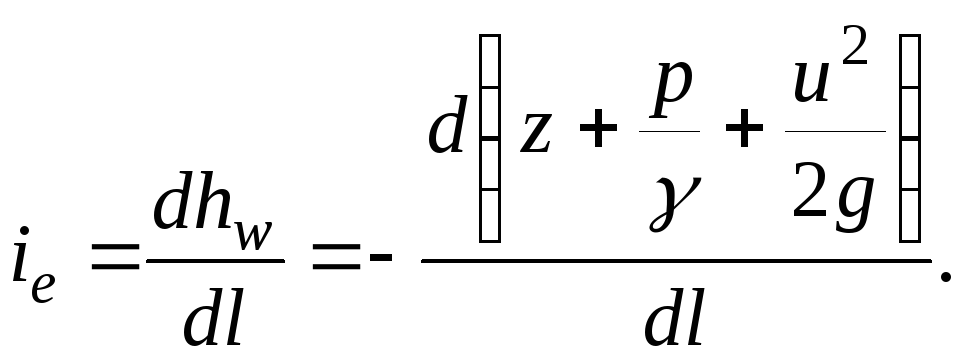(3.51)

Como a curva de carga total diminui ao longo do comprimento do filete, o sinal na expressão (3.51) menos [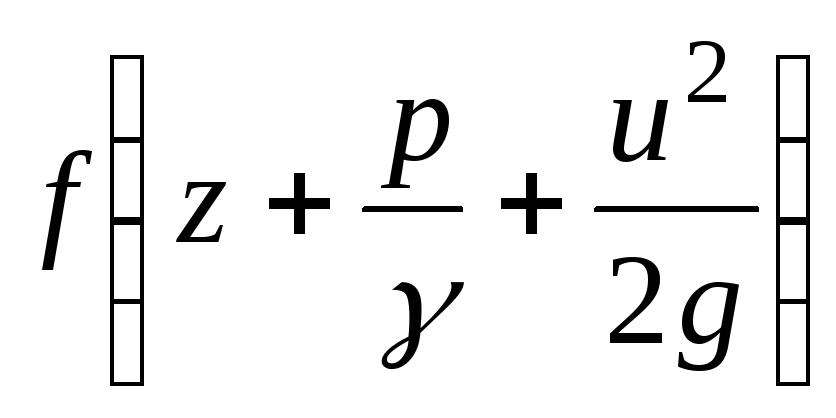

- função decrescente].

No caso de constância das seções vivas ao longo do comprimento do jato, a linha piezométrica e a linha de pressão total são paralelas.

3.9. Equações diferenciais do movimento de um fluido ideal (equação de Euler)

Em um espaço preenchido com uma densidade de fluido ideal em movimento , selecione um paralelepípedo elementar cujas arestas com lados

, ,

paralelas aos eixos coordenados (Fig. 3.9). Quando um fluido ideal se move, não há forças de atrito internas. Um volume elementar localizado em um paralelepípedo move-se com velocidade absoluta . As componentes desta velocidade ao longo dos eixos coordenados serão , , .

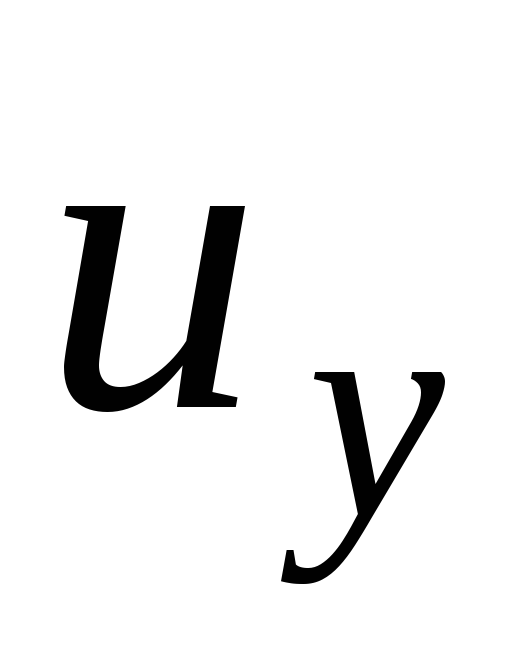As forças de massa e de superfície atuarão sobre o volume elementar. As forças de atrito durante o movimento do paralelepípedo são iguais a zero.

Massa de líquido no volume elementar de um paralelepípedo

(3.52)

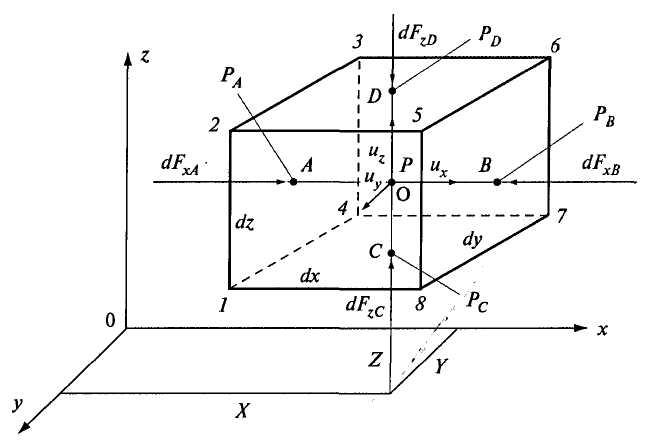
Arroz. 3.9. Para a derivação da equação de movimento de Euler

Projeções de forças de massa na direção eixos de coordenadas:

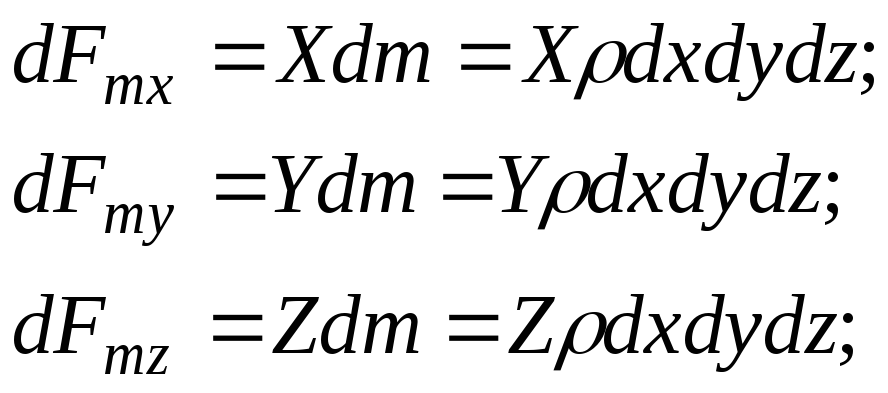(3.53)

Onde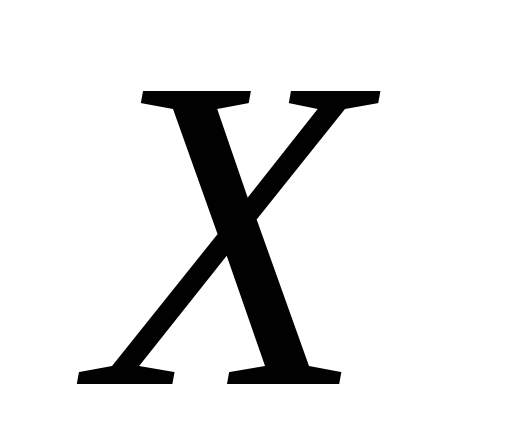

, , - componentes das forças unitárias do corpo em relação aos eixos , , (projeções da aceleração dessas forças).

As forças de superfície são determinadas pela pressão nas faces do paralelepípedo.

Seja a pressão hidrostática no centro de gravidade do paralelepípedo (ponto O) 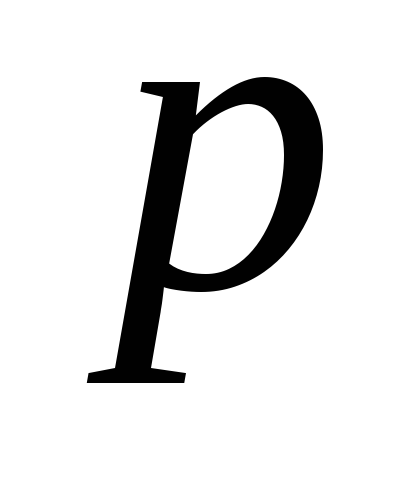, as coordenadas deste ponto , , .Velocidade de movimento neste ponto . As componentes desta velocidade ao longo dos eixos coordenados são , , .

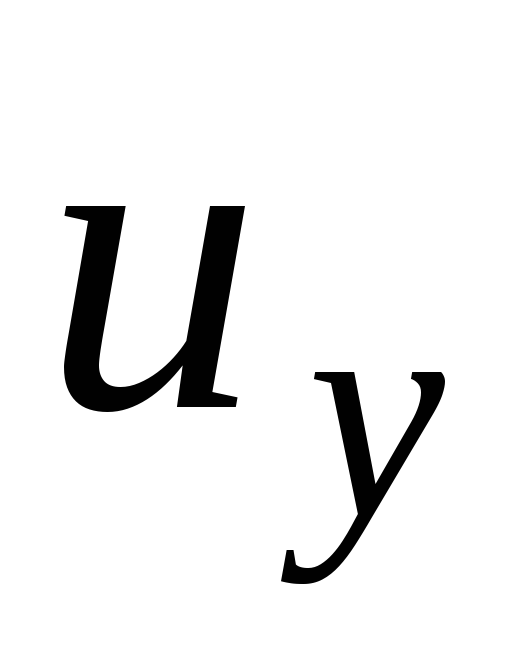Vamos desenhar através de t. Sobre uma linha horizontal paralela ao eixo . Pontos de interseção com as faces da caixa A (face 1234), B (face 5678). A pressão nesses pontos ao longo do eixo

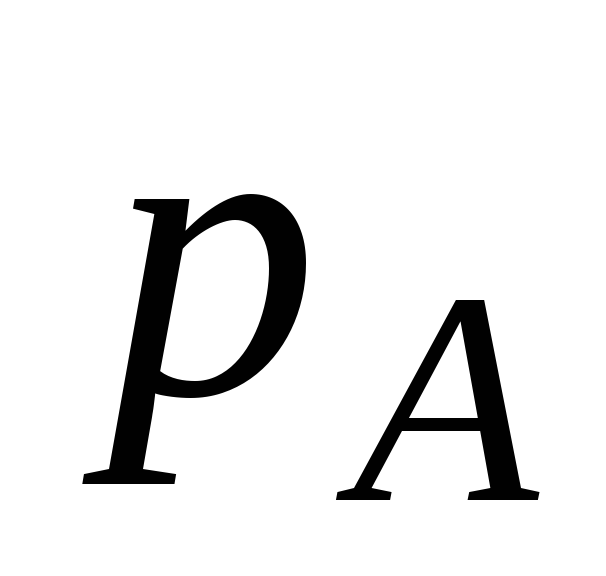E

.

Em um meio líquido contínuo, a pressão em um ponto é expressa por uma função contínua contínua das coordenadas da localização do ponto no espaço: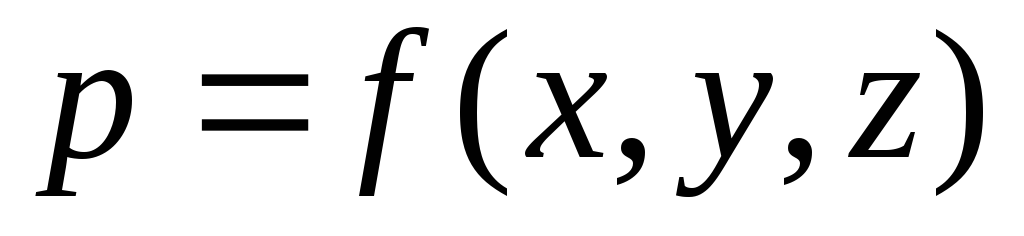

. A pressão hidrostática muda continuamente linearmente, e o incremento de pressão por unidade de comprimento elementar

-

-



-

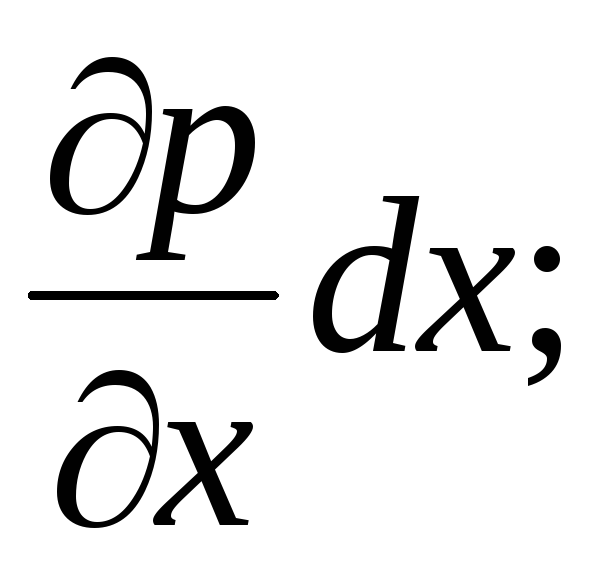
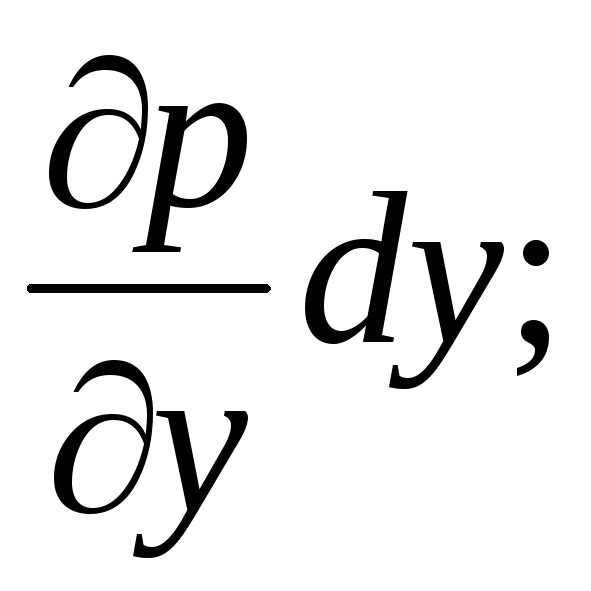
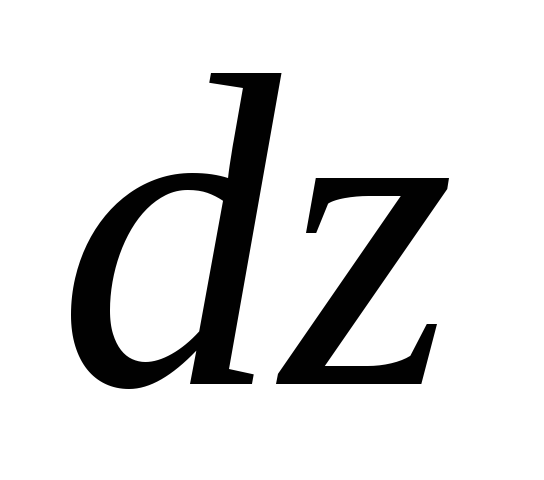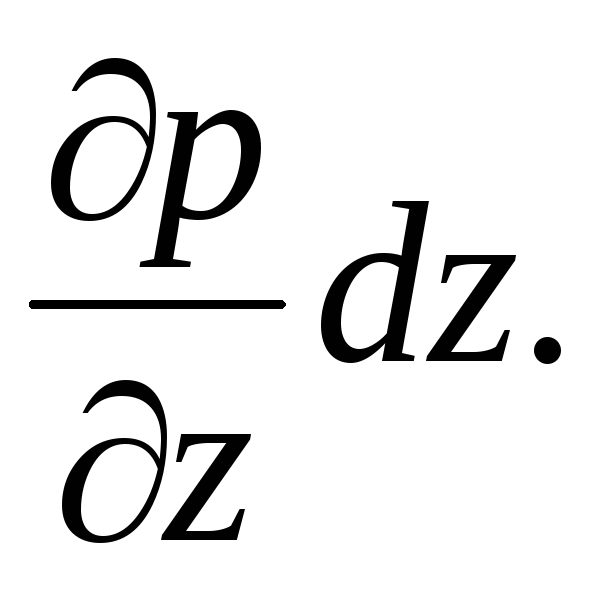
Consequentemente, as pressões nos pontos A e B irão diferir por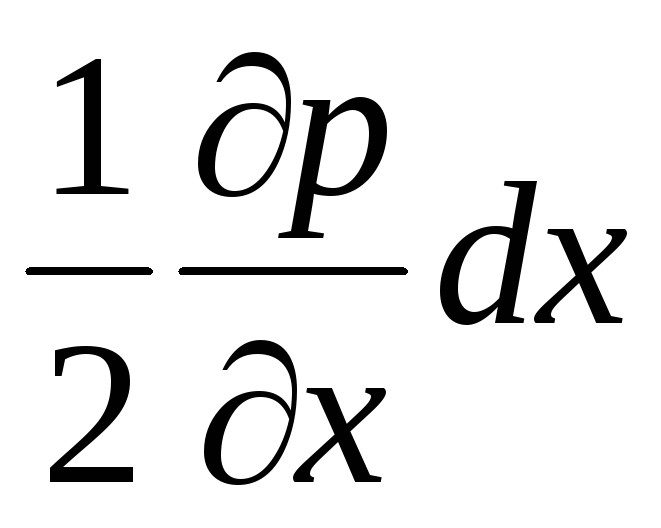

.

Expressamos as pressões nos pontos A e B da seguinte forma:

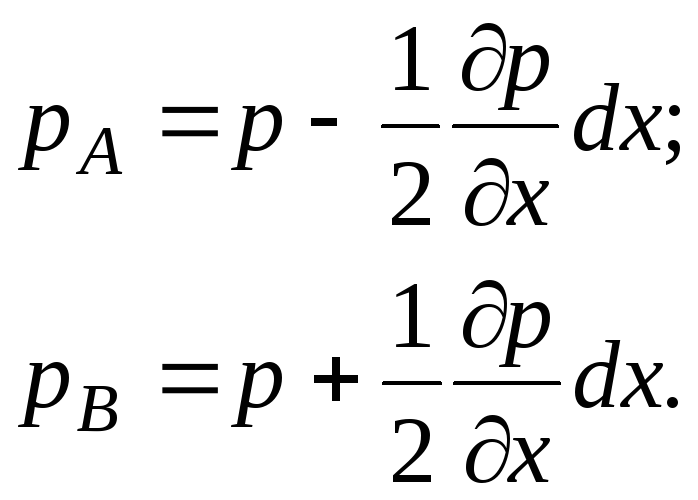(3.54)

Devido à pequena área das faces, podemos supor que as pressões

E

são as pressões hidrostáticas médias atuando nas faces 1234 e 5678. Forças de pressão de superfície nessas faces ao longo do eixo igual ao produto da pressão na área das faces:

(3.55)

Da mesma forma, as forças de pressão de superfície nas faces ao longo do eixo z (faces 1478 e 2365):

(3.56)

Você também pode definir forças de superfície em uma face ao longo do eixo .

Considere o equilíbrio de um paralelepípedo em um fluido em movimento usando Princípio de d'Alembert.

De acordo com o princípio de d'Alembert, a equação de movimento pode ser considerada como uma equação de equilíbrio se introduzirmos as forças de inércia. Suponhamos que um paralelepípedo de massa

movendo-se a uma velocidade , os componentes dessa velocidade , , .

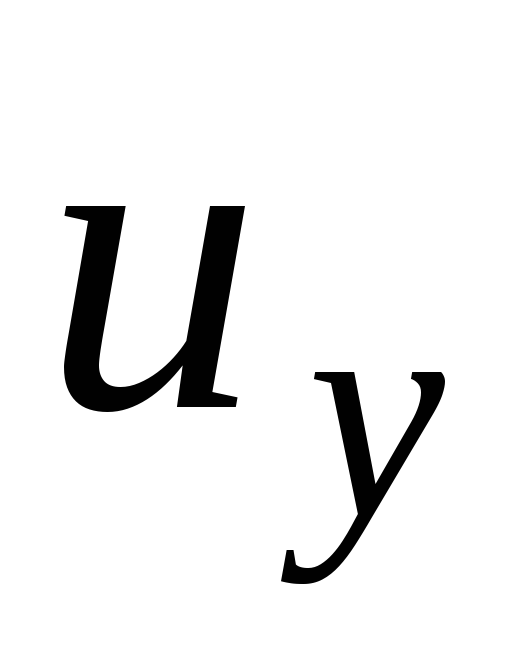força de inércia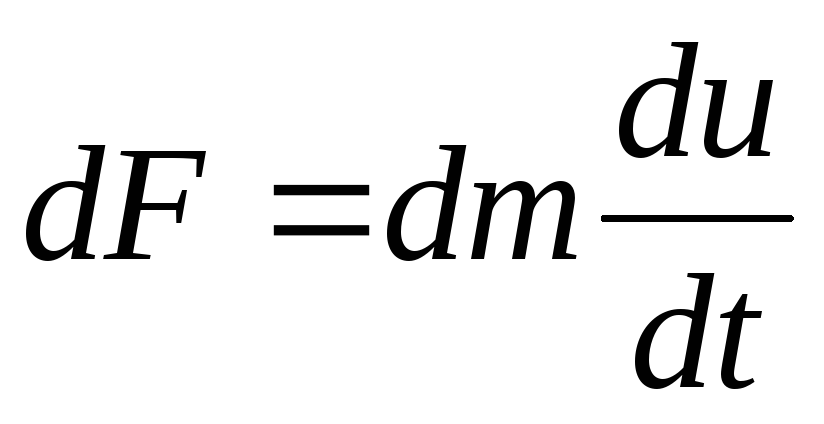

(- aceleração).

Projeções da força de inércia nos eixos coordenados correspondentes:

(3.57)

Onde 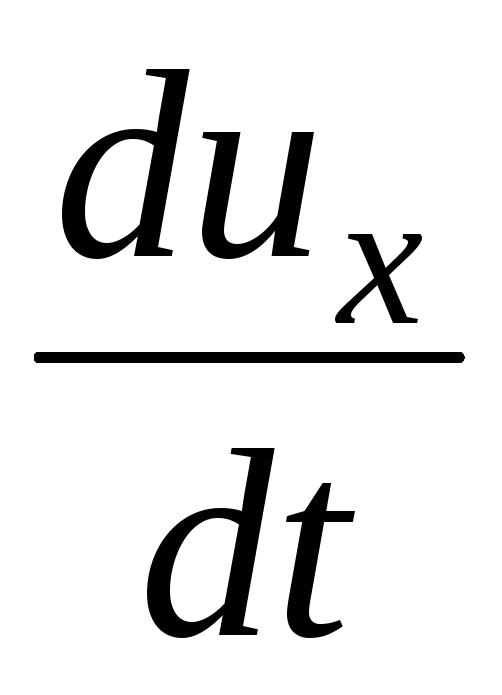,,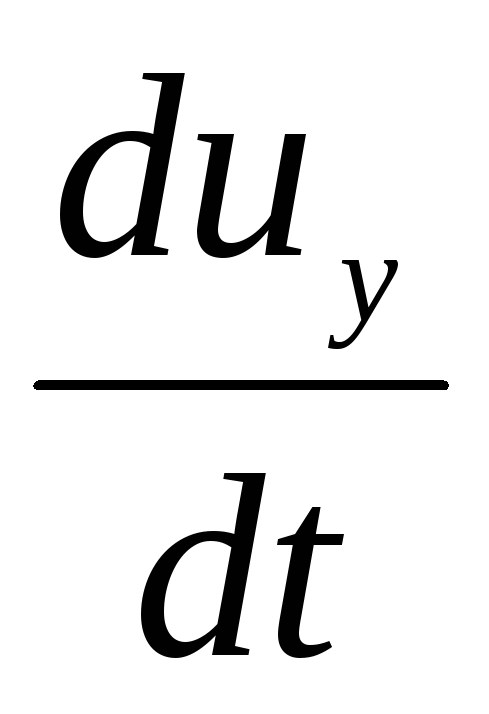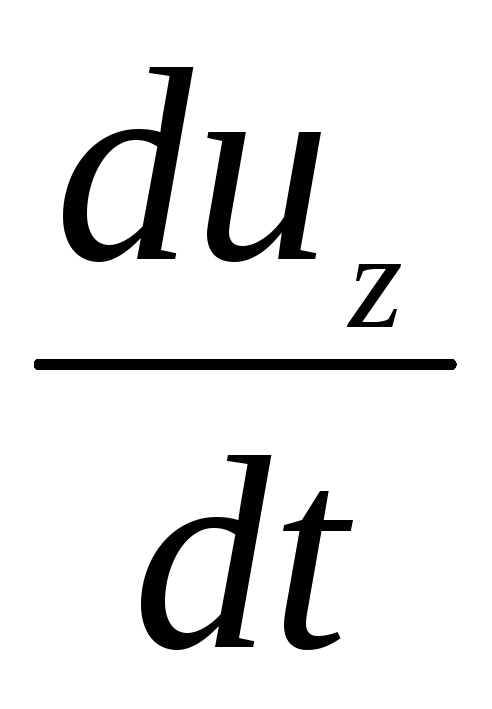- projeções de aceleração no eixo , , .

Vamos compor uma equação de equilíbrio para as forças que atuam no paralelepípedo fluido em consideração, levando em consideração a força de inércia ao longo dos eixos E :

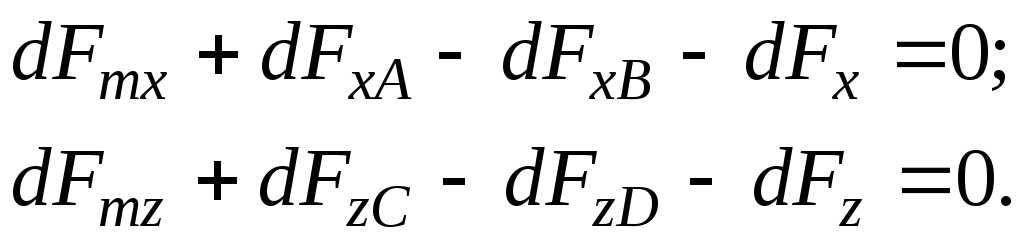(3.58)

Substituindo em (3.58) as dependências obtidas anteriormente (3.53), (3.55), (3.56) e (3.57), obtemos as seguintes equações

Abrindo os colchetes e dividindo as equações obtidas acima por

, escrever

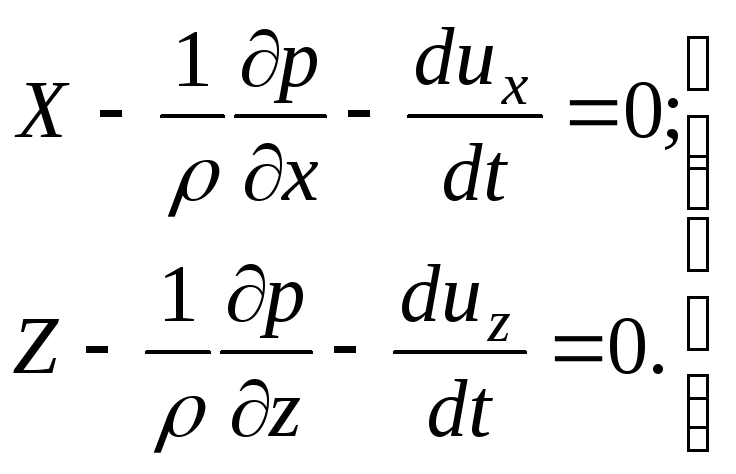(3.59)

Da mesma forma, você pode obter a equação para o eixo y:

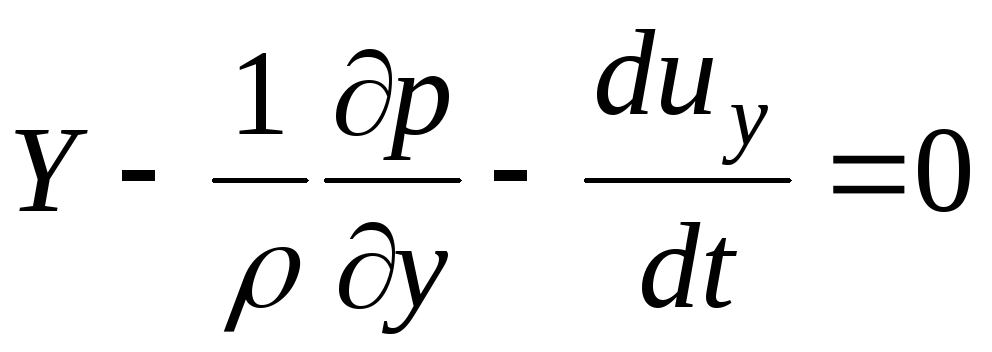(3.60)

As equações (3.59) e (3.60) podem ser escritas como um sistema de equações:

(3.61)

No caso geral, as quantidades , , são uma função das coordenadas , , , assim como o tempo . Portanto, o diferencial de velocidade total vai

Aceleração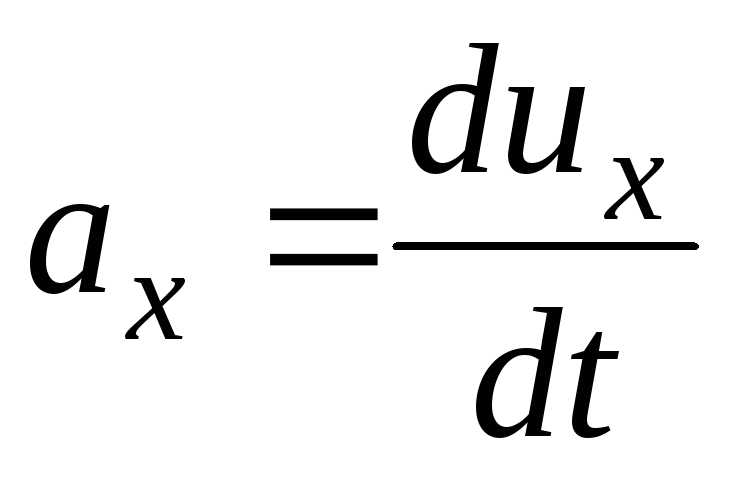

;

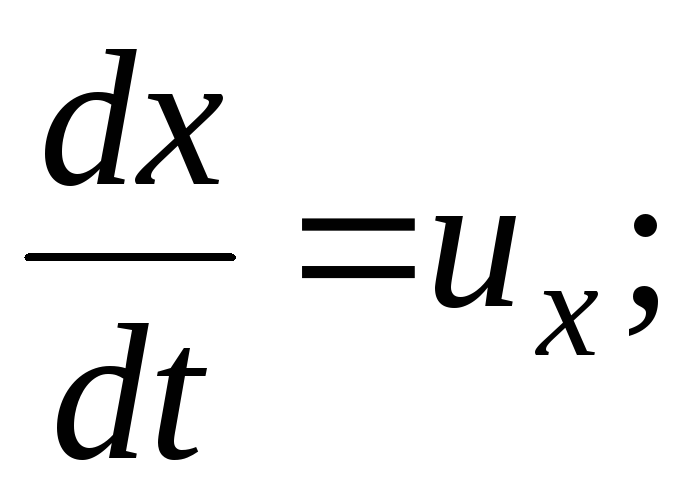
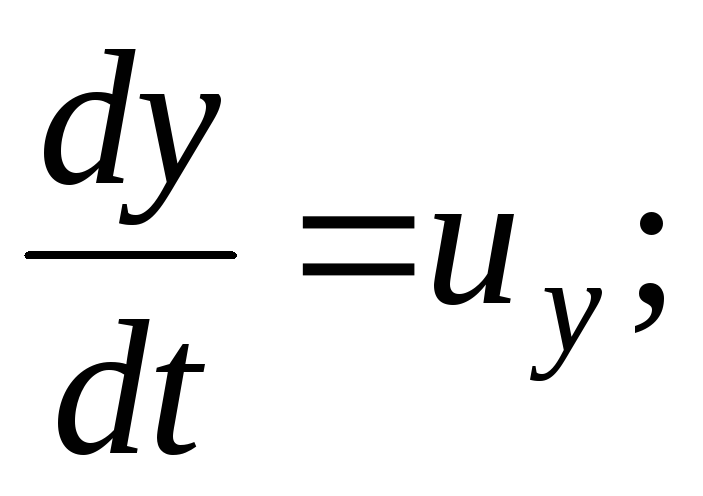
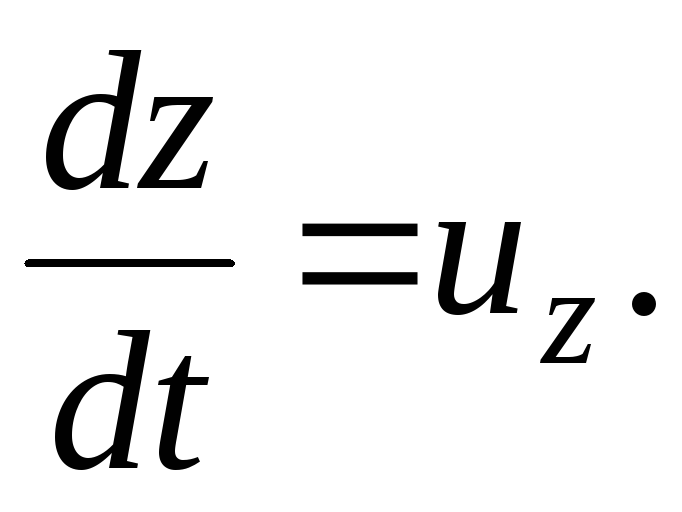
(3.64)

Da mesma forma, você pode obter os diferenciais de velocidade ,.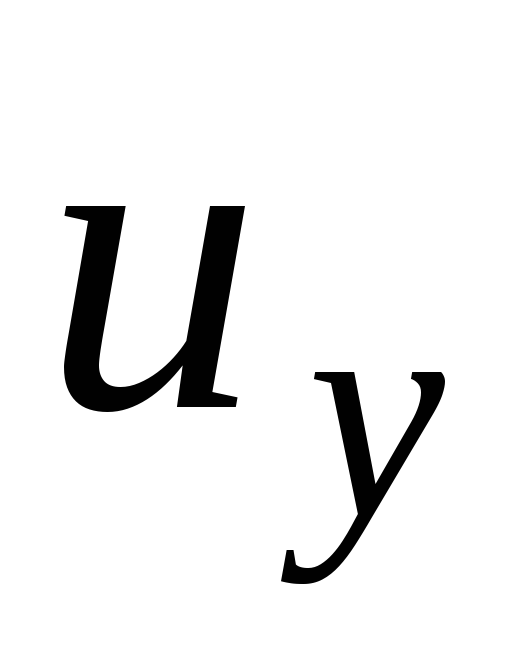

Depois de introduzir no sistema de equações (3.61) os diferenciais de velocidad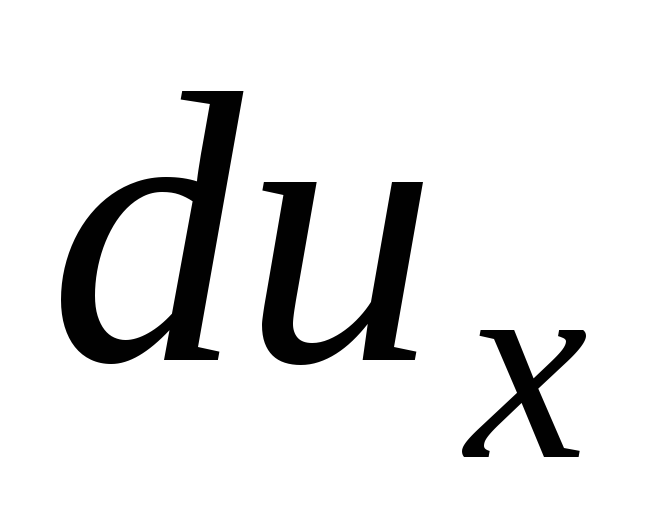e

,

E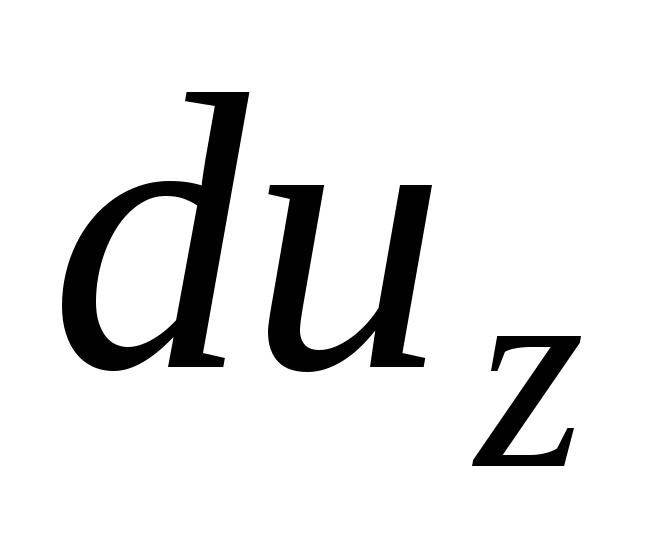

ela vai olhar

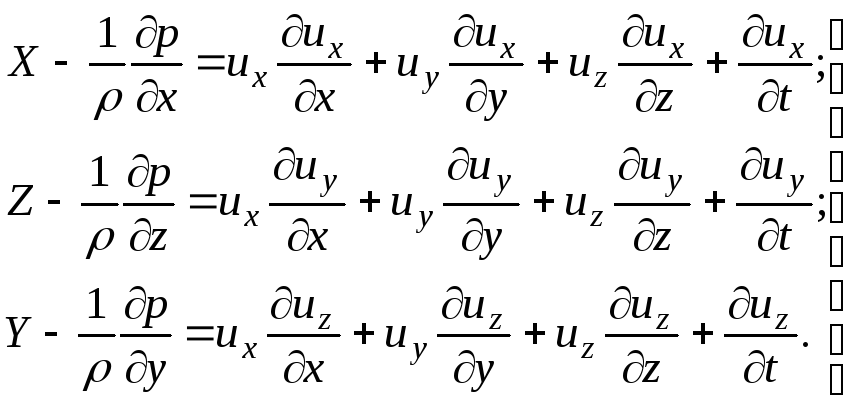(3.65)

Em caso de movimento constante

;

;

. (3.66)

As equações (3.65) são equações diferenciais do movimento de um fluido ideal (não viscoso) - equações de Euler. Essas equações foram obtidas por Euler em 1775.

As equações de Euler expressam a relação entre as projeções das forças atuantes, velocidades, pressão e densidade do fluido. As equações de Euler são muito importantes no estudo do movimento dos fluidos.

Para um fluido em repouso, temos

As equações diferenciais de Euler assumem a seguinte forma:

(3.67)

O sistema de equações diferenciais são as equações de equilíbrio do fluido.

A partir da equação de equilíbrio, pode-se obter a equação básica da hidrostática (2.2) (ver Apêndice).

Integração da equação de movimento de Euler. Integral de Bernoulli

Considere o movimento estacionário de um fluido ideal. Representamos as equações de Euler na forma (3.61). Multiplique a primeira das equações por

, o segundo - em e terceiro em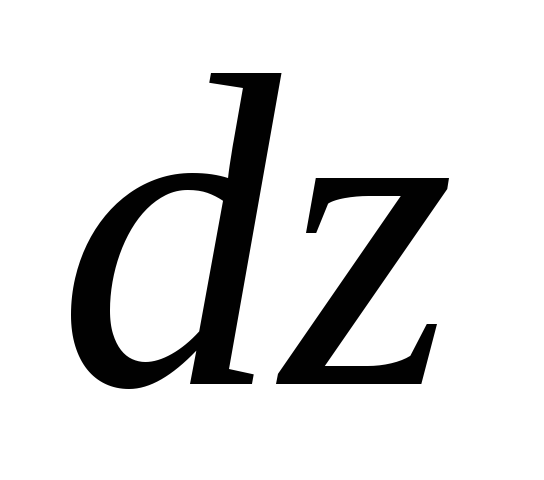

, Nós temos

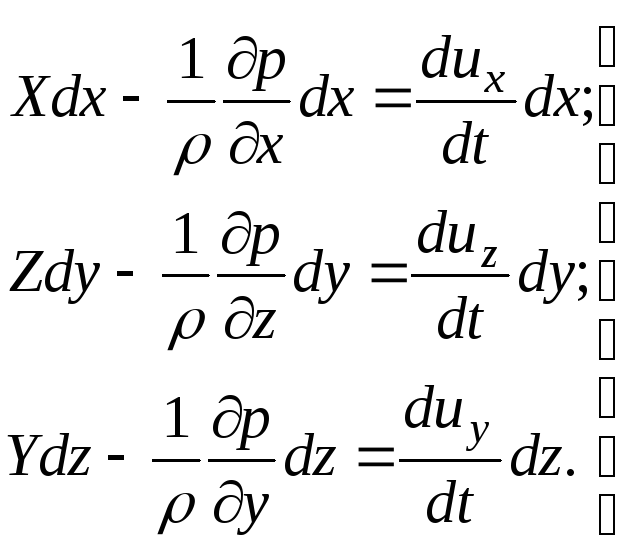(3.68)

Somamos termo a termo todas as três equações do sistema:

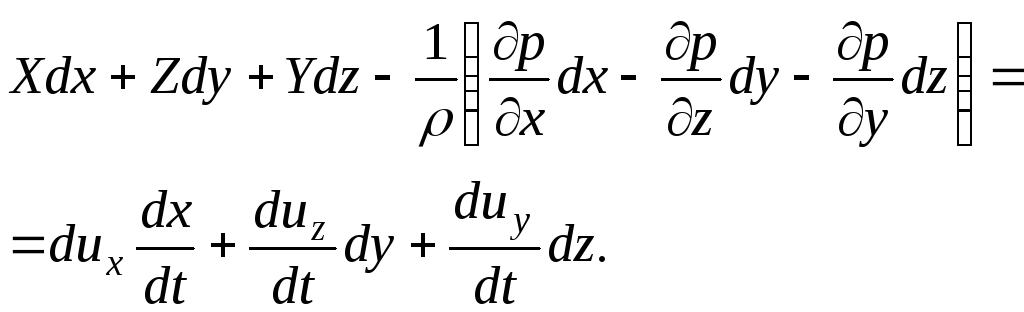(3.69)

Para um movimento estacionário, a pressão 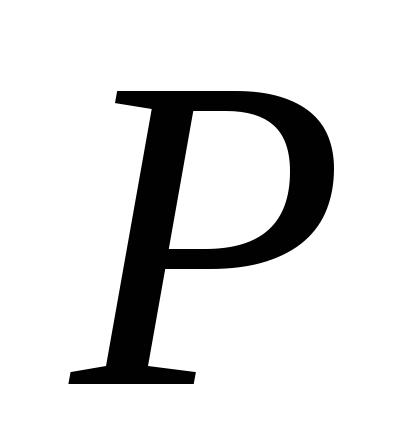em um ponto é uma função de suas coordenadas e não depende do tempo. Portanto, o diferencial de pressão é expresso em derivadas parciais:

.

Porque

;

E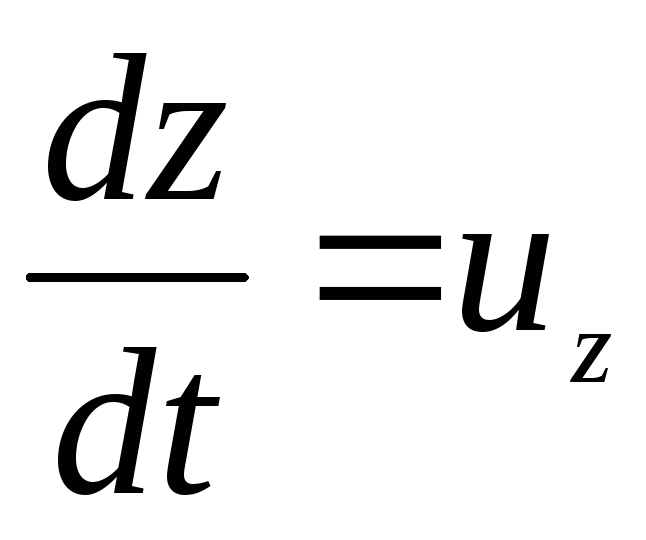

, então o último termo da equação (3.69)

Além do mais

;

;

.

Conseqüentemente, o lado direito da equação (3.69) assume a forma

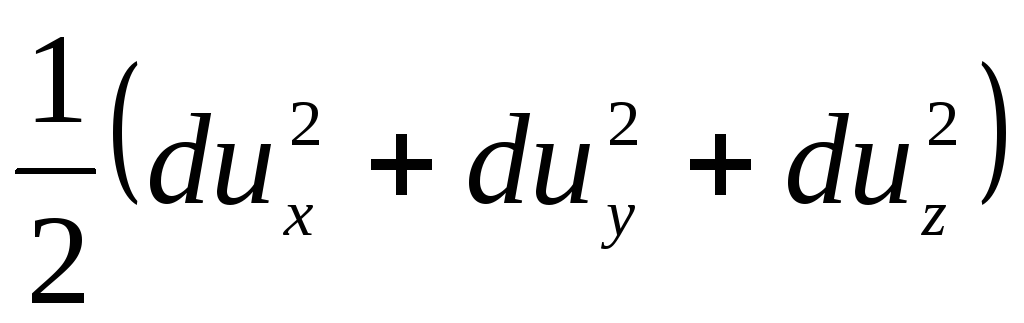. (3.71)

Velocidade total (absoluta) e é expressa através , , :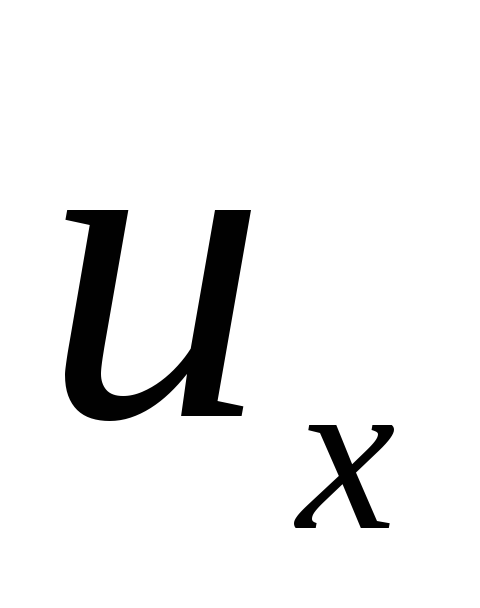

.

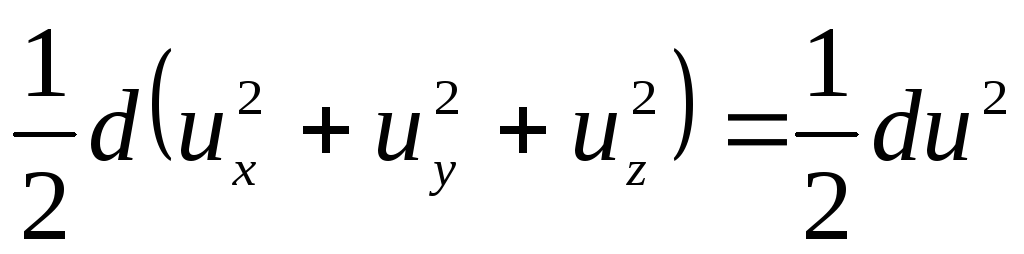. (3.72)

A equação (3.69) após a transformação pode ser reescrita da seguinte forma:

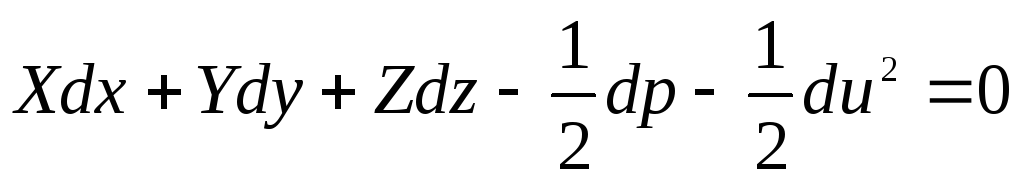. (3.73)

As três primeiras expressões nesta equação são o diferencial total da função de força (potencial) :

Assim, a equação (3.74) assume a forma

. (3.75)

Integrando a equação (3.75), obtemos

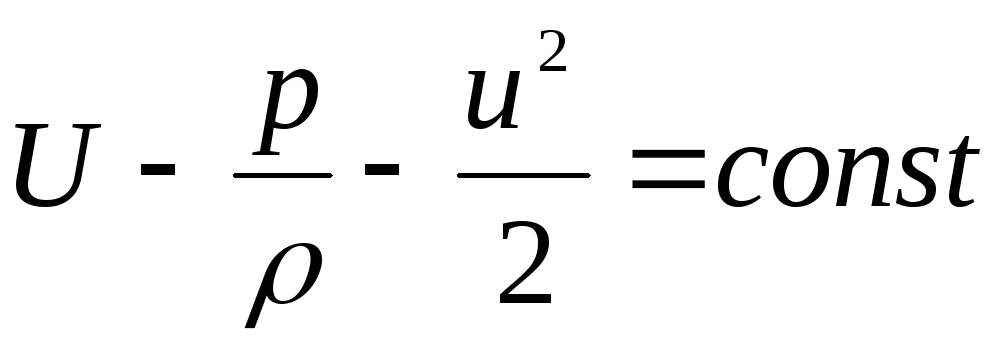. (3.76)

Essa expressão é chamada de integral de Bernoulli-Euler.

O trinômio resultante - a equação permanece inalterada ao longo da linha de corrente.

No caso em que o movimento ocorre sob a ação de apenas uma força de massa - a força da gravidade, então as forças unitárias de massa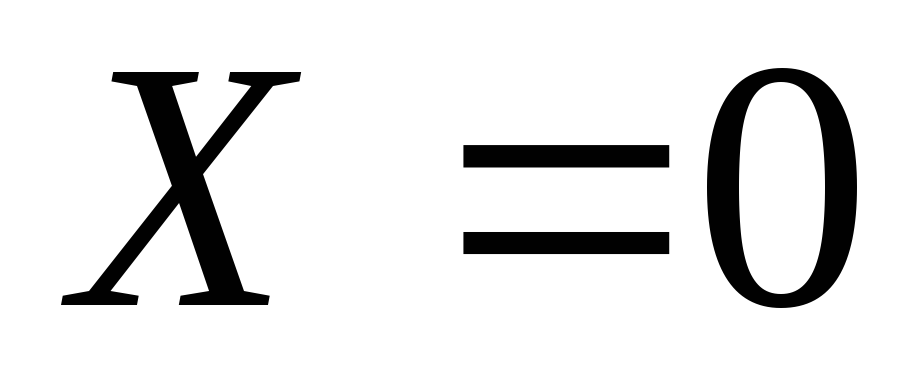

,

,

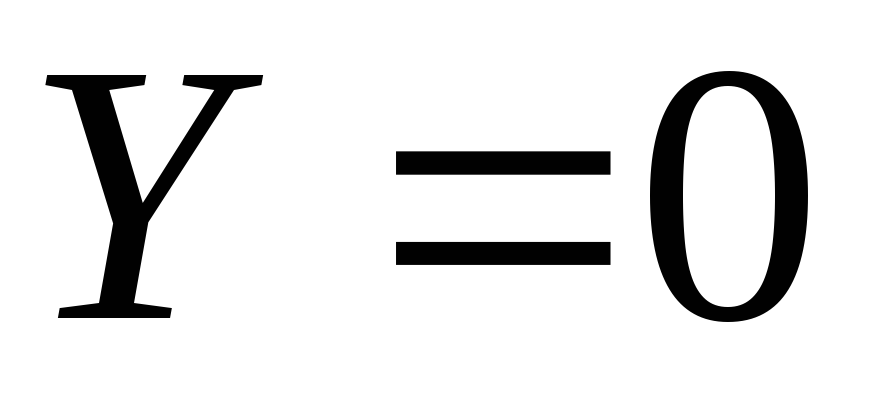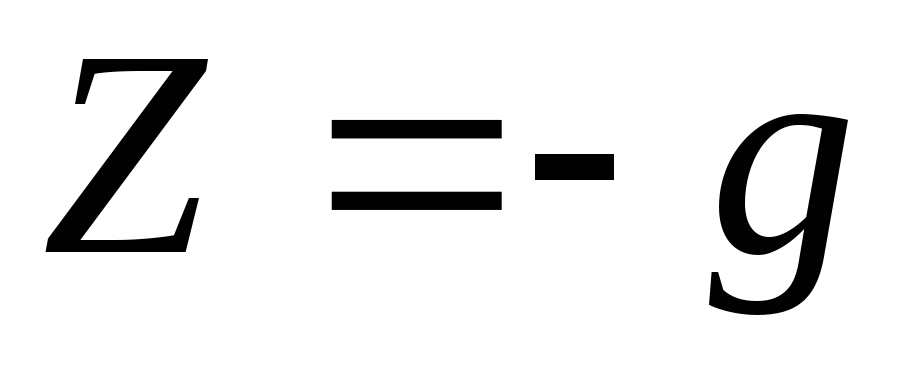(eixo direcionado verticalmente para cima). Diferencial de função de força

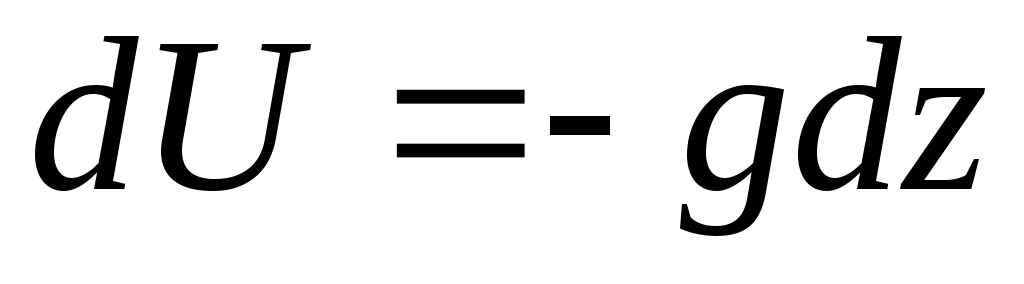. (3.77)

A equação (3.75) pode ser escrita da seguinte forma:

. (3.78)

Dividimos todos os termos da equação pela aceleração de queda livre , então obtemos

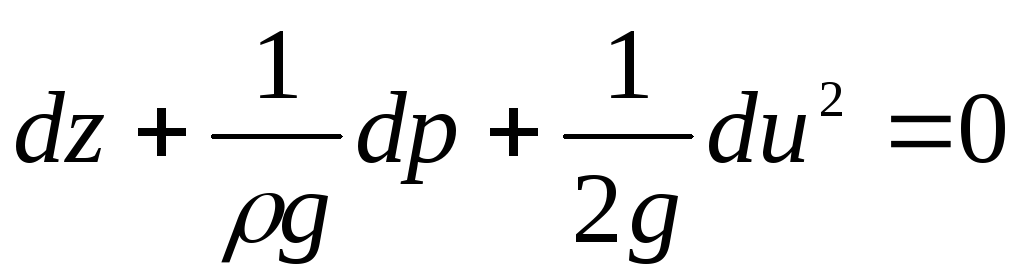. (3 79)

O incremento da soma de todos os três termos desta equação ao se mover ao longo da linha de corrente é igual a zero.

Integrando a equação diferencial (3.79), obtemos

. (3.80)

A soma de todos os termos ao longo da linha de corrente do líquido é um valor constante e, conseqüentemente, também é constante ao longo de uma corrente elementar ideal.

A equação (3.80), obtida usando a equação de movimento de Euler, para movimento permanente é a equação de Bernoulli. Uma equação idêntica foi obtida anteriormente de uma maneira diferente usando o teorema da energia cinética (3.43).

A equação (3.80), escrita para duas seções vivas de um fio, adquire a forma anteriormente conhecida

.
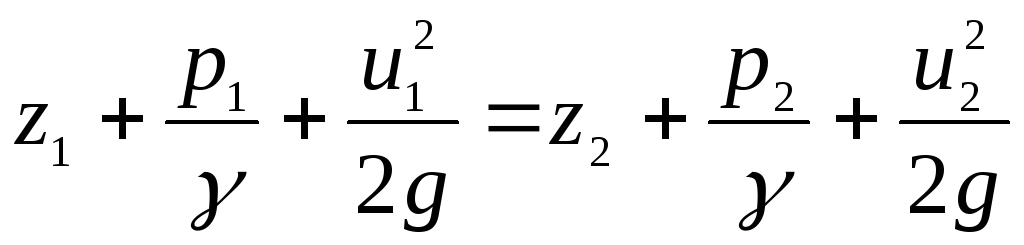